Abstract
A physiologic pharmacodynamic model was developed to jointly describe the effects of methylprednisolone (MPL) on adrenal suppression and glycemic control in normal rats. Six groups of animals were given MPL intravenously at 0, 10 and 50 mg/kg, or by subcutaneous 7 day infusion at rates of 0, 0.1 and 0.3 mg/kg/h. Plasma concentrations of MPL, corticosterone (CST), glucose and insulin were determined at various times up to 72 h after injection and 336 h after infusion. The pharmacokinetics of MPL was described by a two-compartment model. A circadian rhythm for CST was found in untreated rats with a stress-altered baseline caused by handling, which was captured by a circadian harmonic secretion rate with an increasing mesor. All drug treatments caused CST suppression. Injection of MPL caused temporary increases in glucose over 4 h. Insulin secretion was thereby stimulated yielding a later peak around 6 h. In turn, insulin can normalize glucose. However, long-term dosing caused continuous hyperglycemia during and after infusion. Hyperinsulinemia was achieved during infusion, but diminished immediately after dosing despite the high glucose concentration. The effects of CST and MPL on glucose production were described with a competitive stimulation function. A disease progression model incorporating reduced endogenous glucose uptake/utilization was used to describe glucose metabolism under different treatments. The results exemplify the roles of endogenous and exogenous hormones in mediating glucose dynamics. The pharmacokinetic/pharmacodynamic model is valuable for quantitating diabetogenic effects of corticosteroid treatments and provides mechanistic insights into the hormonal control of the metabolic system.
Keywords: corticosterone, methylprednisolone, pharmacodynamics, pharmacokinetics, glucose, insulin
Introduction
Endogenous corticosteroids have extensive effects on metabolism of carbohydrates, lipids, proteins and nucleic acids. Although they are secondary to insulin in regulating glucose metabolism in humans, these steroids work as the major inducers for gluconeogenesis and play a protective role against glucose deprivation, especially under stress and starvation [1]. The hormones can mobilize amino acids produced from peripheral tissues. Such gluconeogenic precursors can stimulate glucose synthesis in liver and kidney [2]. Corticosteroids also stimulate amino acid uptake by the liver and increase activity of several gluconeogenic enzymes via receptor/gene-mediated mechanisms.
Synthetic corticosteroids are potent antiinflammatory and immunosuppressive drugs and are used widely to treat diverse diseases. Some patients receive corticosteroid therapy for months or even years. The duration of treatment is largely limited by the appearance of adverse metabolic effects. Dosing with exogenous corticosteroids also inhibits their endogenous production via suppression of the hypothalamic-pituitary-adrenal axis, leading to adrenal insufficiency after withdrawal of long-term therapy. Numerous metabolic side effects such as osteoporosis, muscle wasting and steroid diabetes may evolve [3].
High corticosteroid concentrations increase hepatic glucose production and decrease glucose uptake/utilization in peripheral tissues [1]. They may also affect the quantities and/or functions of other hormones, such as insulin. Hyperglycemia and decreased carbohydrate tolerance can result [4], which may further lead to complications including steroid diabetes. In spite of the rich literature concerning corticosteroid effects on glucose regulation, limited information is available regarding the temporal patterns and the reversibility of dynamic changes. This is of special importance because of the long-term need for such therapy and the nature of diabetes as a progressive disease.
The development of mechanistic pharmacokinetic/pharmacodynamic (PK/PD) models for corticosteroid effects is essential for quantitative understanding of their actions and optimizing clinical usage. Characterizations of adrenal suppression and the joint effects of endogenous and exogenous corticosteroids on the biological system are important to assess their physiological roles and pharmacological impacts. The principal controlling signals for glucose homeostasis are glucose-induced insulin secretion, insulin-suppressed glucose production and insulin-induced glucose disposition. Simultaneous estimation of all system parameters that describe inter-regulations among glucose, insulin and endogenous steroid, as well as drug-specific parameters that describe corticosteroid potency assures the understanding of the control mechanisms of the system.
Recently, the effects of methylprednisolone (MPL) on glucose and insulin regulation were investigated in adrenalectomized (ADX) rats after both acute and chronic dosing [5]. A mechanism-based PK/PD model was developed quantitatively to describe the hyperglycemia and hyperinsulinemia after MPL treatment. However, the results and mathematical model presented in that report were limited by using ADX rats. Normal rats were used in the present study for their metabolic system with regular hormonal controls and allowing for suppression of endogenous CST. A mechanistic PD model was developed to describe the joint effects of exogenous and endogenous corticosteroids on glucose production, the inter-regulations between glucose and insulin, and the system impairment under chronic hyperglycemia. A comprehensive PK/PD model was sought to characterize effects produced by different MPL dosing regimens.
Methods
Animals and procedures
Two groups of male Wistar rats were purchased from Harlan-Sprague Dawley Inc. (Indianapolis, IN). One rat group weighed 225–275 g (n=12) and the other weighed 325–375 g (n=17). Rats weighing 225–275 g were further divided into three sub-groups (n=4/group) to receive a single injection of 0 (saline), 10 or 50 mg/kg MPL via the cannula over 30 s at 9:00 am. Rats with high body weights were also divided into three sub-groups to receive saline infusion or MPL infusion (n=4) at a rate of 0.1 (n=6) or 0.3 (n=7) mg/kg/h. The drug assay and other experimental procedures were identical to those described in the companion report [5,6].
Pharmacokinetic/pharmacodynamic model
Pharmacokinetics
The pharmacokinetics of MPL was described by a two-compartment model with bolus input (injection study) or zero-order input (k0, infusion study) [6]. Plasma MPL concentrations versus time from injection and infusion studies were fitted simultaneously. The pharmacokinetic parameters were then fixed in the following dynamic analysis.
Body weight
The effects of MPL on the total body weights of rats upon long-term dosing were described by indirect response model IV with the stimulation function applied to the degradation rate (Figure 3) [7]. Based on our previous experience, MPL does not have any direct effect on food intake. The weight loss effect of MPL is mainly catabolic in nature and was better described by indirect response model IV (stimulation of output) than I (inhibition of input) [8].
| (1) |
where Bwt0 represents the predose body weight at time zero and %Bwt represents the rat body weight expressed as a percentage of its predose body weight Bwt0 (i.e. %Bwt=Bwt/Bwt0*100%). Without drug treatment, body weight is controlled by the zero-order production rate constant and the first-order degradation rate constant . The and are drug-specific parameters representing the maximum stimulation of and the plasma MPL concentration required for half-maximal stimulation. Assuming rats will keep growing without drug administration, the system is not at steady-state at time zero. Once the steady-state body weight (%Bwtss=Bwtss/Bwt0) has been achieved, the system will produce the relationship:
| (2) |
Body weights of the three rat groups receiving 7 day infusions were fitted simultaneously using the proposed model. The initial condition for Equation (1) was fixed as 100%. The predose body weight Bwt0 was fixed as the mean body weight of 3–4 animals at time zero for each dose group.
Figure 3.
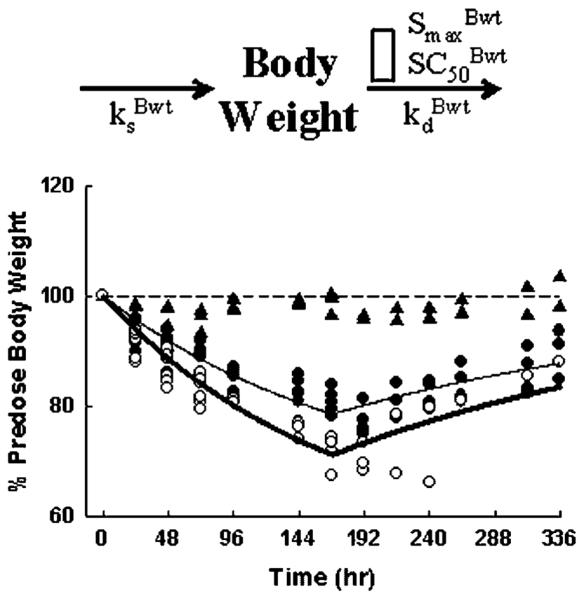
Indirect response model for effects of MPL on body weight (top) and the time course of changes in body weights for the saline (▲), 0.1 (●) and 0.3 (○) mg/kg/h infusion groups.. The open rectangle in top graph represents stimulation of body weight loss by MPL plasma concentration. Lines depict results of the simultaneous fittings with Equations (1) and (2). The PD parameters are listed in Table 2
Corticosterone
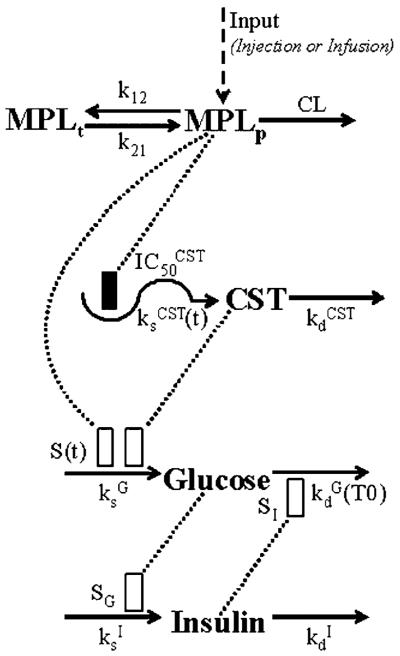
Plasma CST versus time was described by an indirect response model with circadian rhythmic secretion rate [7]. Administration of MPL caused CST suppression by inhibiting its endogenous production as depicted in the model shown in Figure 1:
| (3) |
This endogenous hormone is synthesized at the rate of and degraded at the rate of . The inhibition function driven by plasma MPL concentrations (MPLp) reduces CST production. It is assumed that MPL can fully suppress CST secretion and achieves 50% suppression at the concentration of . The initial condition of Equation (3) was fixed using mean values from 4–7 animals at time zero for each dose group (CST0).
Figure 1.
PK/PD model of MPL effects on adrenal suppression and glucose regulation. The dotted line and rectangles represent stimulation (open bar) and inhibition (solid bar) of the various processes via indirect mechanisms. Symbols are defined in the tables
The biorhythmic CST secretion rate was described by harmonic functions with a linearly increased mesor with time after 24 h:
| (4a) |
where
| (4b) |
| (4c) |
| (4d) |
| (4e) |
The period T was fixed as 24 h to represent a circadian rhythm. The value of n represents the frequency of the harmonic function, and a0, an, bn are Fourier coefficients. The mesor is constant for the first 24 h followed by a time-dependent increase with a linear slope. This alteration in baseline could be explained by the stress-induced CST secretion during animal handling, which was minimal during the first 24 h and evident afterwards.
Plasma concentrations of CST from control animals in the injection studies were subjected to Fourier analysis using the FOURPHARM software [9,10]. The harmonic functions that contributed more than 1% to the overall function of CST secretion rate were selected. The CST data from all animals were fitted simultaneously using the proposed model (Equations (3) and (4a–e)). Alternative models for CST secretion rates were also tested [11]. Once the parameters characterizing CST dynamics were obtained, they were fixed in the following data analysis.
Glucose-insulin dynamics
Based on the mechanisms described previously [5], a PD model incorporating corticosteroid stimulation of gluconeogenesis, glucose stimulation of insulin secretion, insulin stimulation of glucose utilization and hyperglycemic disease progression was developed as depicted in Figure 1. The effects of endogenous CST and exogenous MPL on glucose production were described with a joint additive stimulation function based on a competitive mechanism. The following equations were fitted to glucose and insulin data from all animals and treatments simultaneously:
| (5a) |
where
| (5b,c) |
| (6) |
where G and I represent glucose and insulin plasma concentrations. Glucose is constantly produced with a zero-order rate constant and utilized with a first-order rate constant . MPL and CST act competitively on glucose production presumably via stimulating gluconeogenesis. The Smax describes the maximum achievable stimulation of . The sensitivity parameters and represent the plasma concentrations of CST alone and MPL alone which produce half-maximal stimulation, and ξ is an index of the potency ratio of CST and MPL for glucose induction. Insulin is assumed to control glucose concentrations by stimulating its disposition with a linear efficiency constant (SI). The change of insulin from its baseline value at time zero (I0) was used to drive this stimulation effect.
Under hyperglycemic conditions, the glucose disposition rate decreases with time and is defined as:
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
where CSTbaseline, Gbaseline and Ibaseline represent the baseline plasma concentrations of CST, glucose and insulin for the treated group if no MPL was administered. The T0 is the duration of glucose concentration above its own baseline (Gbaseline). Because of the circadian biorhythms of endogenous CST, glucose and insulin would also yield a variable baseline without drug treatment. Using Gbaseline for each treatment group as standards for comparison was necessary for assessing the `real' hyperglycemic duration that was driving the disease progression. At time zero, the glucose disposition rate constant is at its baseline value , which represents the combination of endogenous glucose utilization and storage under physiological conditions. At high glucose concentrations, the inhibition of is dependent on the duration T0 and characterized by the maximum achievable inhibition , the hyperglycemic duration required for 50% maximal inhibition , and the Hill factor γG. This time-dependent decrease could be explained by the possible saturation, desensitization, or down-regulation of transporters/enzymes/receptors in glucose uptake, utilization and storage pathways.
As shown in Equation (6), insulin is produced with a zero-order rate constant and degraded with a first-order rate constant . Change of glucose from its steady-state value (Gss) can stimulate insulin production with a linear efficiency constant SG. Without MPL and insulin action, Gss is defined as:
| (12) |
At time zero, the system was assumed to be at its physiological steady-state and Equations (5a) and (6) yield:
| (13) |
| (14) |
where initial values of CST0, G0 and I0 were fixed as mean values from 4–7 animals at time zero for each dose group.
Other PD models containing competitive inhibition of glucose utilization by MPL and CST, or inhibition of glucose production by insulin were also tested. Methods of data analysis are the same as described previously [6,12].
Results
Pharmacokinetics
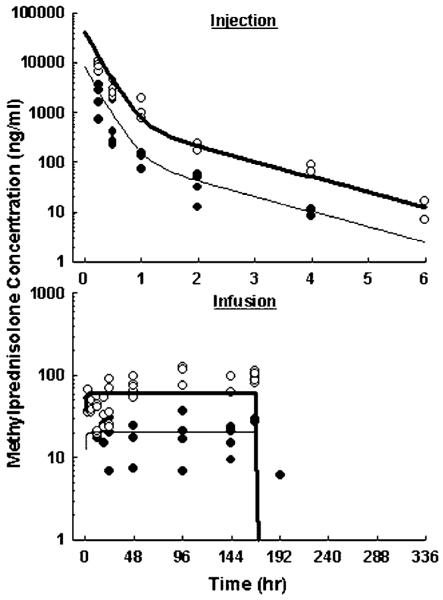
The plasma MPL concentration-time profiles are shown in Figure 2 and parameter estimates are listed in Table 1. The MPL exhibited a biexponential decline after injection and dropped below the detection limit after 4 and 6 h in low- and high-dose groups. Infusions produced constant MPL exposures for 7 days. The MPL concentrations reached steady-state quickly after pump implantation and rapidly diminished after pump removal, consistent with the short elimination half-life shown in the single-dose study. The two-compartment model captured all MPL time courses using one set of PK parameters. Model fitting yielded an elimination half-life of 1.0 h, and predicted steady-state concentrations of 20.4 and 61.1 ng/ml during low- and high-dose infusions.
Figure 2.
Pharmacokinetics of MPL upon administration of 10 (●) and 50 (◯) mg/kg intravenous injection (top), or 0.1 (●) and 0.3 (◯) mg/kg/h subcutaneous infusion for 7 days (bottom). Lines are results of the simultaneous fittings. The PK parameters are listed in Table 1
Table 1.
Pharmacokinetic parameters for methylprednisolone
| Parameter | Definition | Estimate | CV% |
|---|---|---|---|
| CL (l/h/kg) | Clearance | 4.91 | 10 |
| Vp (l/kg) | Central volume | 1.17 | 50 |
| k12 (h−1) | Rate constant | 0.39 | 10 |
| k21 (h−1) | Rate constant | 0.78 | 20 |
Body weight
Animals receiving saline infusion showed constant body weights (Figure 3). The MPL-treated rats lost body weights in relation to dose during the 7-day infusion, and slowly regained weights once MPL infusion was stopped at 168 h. No reduction in food consumption was observed in any animals. The low- (0.1 mg/kg/h) and high- (0.3 mg/kg/h) dose groups fell to 80.9±2.2% and 72.0±2.5% of predose body weight by the end of day 7. The lower body weight at day 8 (192 h), which appeared also in the control group, was possibly due to the effect of surgery at the end of infusion (pump removal under halothane). The proposed model satisfactorily captured the body weight changes after chronic MPL dosing with parameters listed in Table 2. The %Bwtss was fixed as 100% assuming that the system was at steady-state and the rats did not grow during the 2 week time period. The of 1.04 suggests that rats may lose weight to as low as 49.0% of predose body weights with maximum drug toxicity, assuming it will not be lethal. The of 16.4 ng/ml indicates that the MPL concentrations were maintained above its SC50 value during both infusions. The model predicted that rats could lose weight to as low as 63.4% and 54.9% of initial body weight with the low and high continuous infusion rates, which had not been achieved after 7 days.
Table 2.
Pharmacodynamic parameters for MPL effects on body weights
| Parameter | Definition (doses) | Estimate | CV% | |
|---|---|---|---|---|
|
|
Weight loss rate constant | 0.0033 | 10 | |
|
|
Maximal stimulation | 1.04 | 9 | |
|
|
Stimulation constant | 16.4 | 17 | |
| %Bwtss (%) | Maximal weight | 100 | Fixed | |
| Bwt0 (g) | Predose weight (0, 0.1, 0.3) | 356, 362, 354 | Fixed | |
|
|
Weight gain rate constant (0, 0.1, 0.3) | 117, 119, 117 | 10 |
Secondary parameter.
Corticosterone
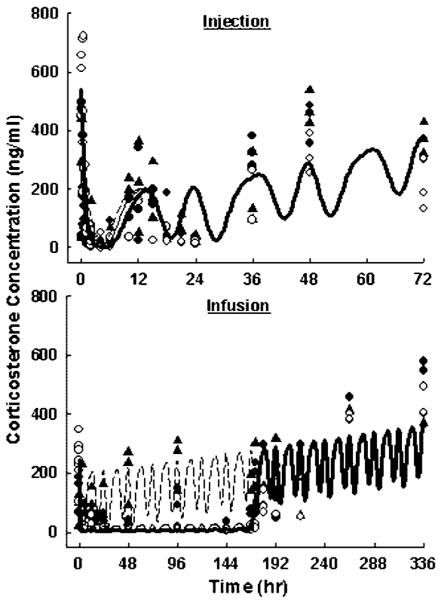
As shown in Figure 4, the baseline behavior of CST was assessed by the control animals in the injection study. The CST concentrations were high at 9:00 am (0 h) and 9:00 pm (12 h), and low at 1:00 pm (4 h) and 3:00 am (18 h). The CST baseline increased after 24 h. The time-dependent increase of CST was also present over 2 weeks in rats receiving saline infusion. The MPL caused moderate CST suppression after injection and full suppression during infusion. A similar increase of CST baseline was observed when the drug effect elapsed. The somewhat high variability was expected for endogenous CST concentrations because of its sensitivity to external disturbances.
Figure 4.
Plasma corticosterone versus time profiles upon administration of saline, 10 (●) and 50 (○) mg/kg MPL injection (top), or saline (▲), 0.1 (●) and 0.3 (○) mg/kg/h infusion for 7 days (bottom). Symbols are observed CST concentrations. Lines depict simultaneous fittings of CST with Equations (3) and (4). The PD parameters are listed in Table 3
The baseline CST concentration-time profile in rats receiving saline injection was well described by the multicomponent harmonic functions resulting from Fourier analysis. The harmonic function components n = 0, 2, 3, 1 contributed 76.7%, 15.1%, 3.32%, 3.11% to the overall function of , respectively. The proposed model successfully captured CST dynamics for all animal groups (Figure 4). Parameter estimates for CST dynamics are listed in Table 3. The linearly increased mesor with time illustrated the increasing baseline in control groups and the returning phase in MPL-treated groups. This elevation of CST secretion was applied after 24 h, because all rats were constrained in metabolic cages for frequent sampling with minimal handling in the first 24 h, but subsequent blood collections required handling which might be stressful thereby inducing CST secretion. Different slope factors for rats receiving injection and infusion was necessary to fit the data. This was likely due to the different handling frequency for blood sample collections and different experimental stress levels for rats in the injection and infusion groups. These differences are specific to the current experimental condition for rats and should not represent a practically meaningful difference for CST. The low of 2.42 ng/ml implies very high potency of MPL to inhibit CST secretion, which was fully suppressed during infusions. The complete suppression was not obvious after MPL injection due to the decreasing CST baseline at the same time.
Table 3.
Pharmacodynamic parameters for MPL effects on corticosterone
| Parameter | Definition (doses) | Estimate | CV% | ||||
|---|---|---|---|---|---|---|---|
| n | Harmonic | 0 | 1 | 2 | 3 | ||
| a n | Fourier coefficient | 124.3 | −33.3 | 77.0 | 34.2 | ||
| b n | Fourier coefficient | — | −12.1 | −12.9 | −13.1 | ||
|
|
Degradation rate constant | 1.40 | — a | ||||
| Slope injection (h−1) | Linear slope | 0.029 | — a | ||||
| Slope infusion (h−1) | Linear slope | 0.0040 | — a | ||||
|
|
Inhibition constant | 2.42 | — a | ||||
| CST0,injection (ng/ml) | Baseline CST (0, 10, 50) | 255, 262, 541 | Fixed | ||||
| CST0,infusion (ng/ml) | Baseline CST (0, 0.1, 0.3) | 195, 140, 243 | Fixed |
Not estimated.
Glucose-insulin dynamics
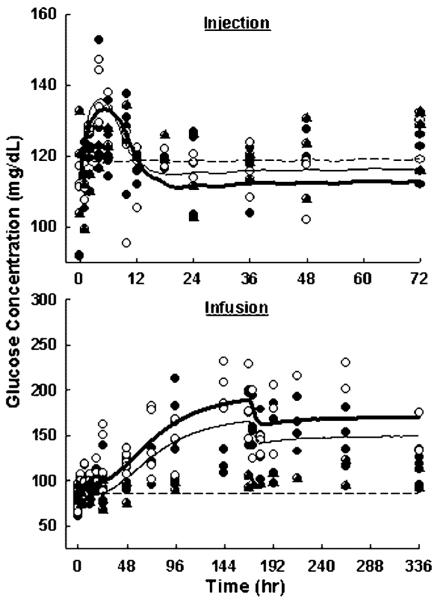
Glucose and insulin time profiles are shown in Figures 5 and 6. In rats receiving saline injection, glucose and insulin time courses showed no significant changes. This suggests that cannulation and animal handling had no effect on these biomarkers. Plasma glucose was temporarily increased from 88±7 to 130±16 mg/dl after 10 mg/kg MPL injection, and from 113±3 to 139±8 mg/dl after 50 mg/kg injection. Glucose concentrations peaked at around 4 h and quickly returned to baseline after 12 h. However, the profile difference between drug-treated and control groups was not statistically significant (p>0.05). There was also no significant difference between the two dose groups on glucose induction (p = 0.33). Plasma insulin increased from 1.00±0.20 to 3.45±0.38 ng/ml after the 10 mg/kg MPL injection, and from 0.99±0.26 to 3.06±0.76 ng/ml after the 50 mg/kg injection. Insulin profiles showed a delayed increase to a maximum at around 6 h followed by a slow return to baseline after 36 h. Corticosteroids do not have direct effects on insulin secretion [2], and such an increase was solely due to the elevated glucose level. Both drug-treated groups showed significantly different time profiles from the control group (p<0.0001). This insulin induction was not dose-dependent with p = 0.36. Both glucose and insulin showed reversible changes after single-dose administration, suggesting that system homeostasis was not disturbed.
Figure 5.
Plasma glucose versus time profiles upon administration of saline, 10 (●) and 50 (○) mg/kg MPL injection (top), or saline (▲), 0.1 (●) and 0.3 (○) mg/kg/h infusion for 7 days (bottom). Lines depict simultaneous fittings of glucose and insulin with Equations (5–14). The PD parameters are listed in Table 4
Figure 6.
Plasma insulin versus time profiles upon administration of saline, 10 (●) and 50 (○) mg/kg MPL injection (top), or saline (▲), 0.1 (●) and 0.3 (○) mg/kg/h MPL infusion for 7 days (bottom). Lines depict simultaneous fittings of glucose and insulin with Equations (5–14). The PD parameters are listed in Table 4
In control animals, glucose and insulin time courses showed no significant changes during and after saline infusion. This suggests that pump implantation and removal had no additional effects. During MPL infusion, glucose concentrations continuously rose from 70±8 to 178±28 mg/dl with 0.1 mg/kg/h infusion, and from 80±11 to 228±69 mg/dl with 0.3 mg/kg/h infusion. Glucose concentrations increased continuously over 7 days. Once the pump was removed, glucose exhibited a small decrease and then stayed at the induced level of 127±8 mg/dl (low-dose) and 154±30 mg/dl (high-dose) until the end of the study (336 h). Both drug-treated groups showed highly significant differences in time profiles from the control group (p<0.0001). Glucose induction was dose-dependent (p<0.0001). Insulin concentrations also showed continuous increases from 0.67±0.22 to 1.94±0.67 ng/ml with 0.1 mg/kg/h MPL 7 day infusion, and from 0.51±0.20 to 2.35±1.07 ng/ml with 0.3 mg/kg/h infusion. However, once drug administration stopped at 168 h, plasma insulin immediately dropped back to baseline in both dose groups. Both treated groups showed significantly different time profiles from the control group (p<0.0001). Insulin induction by MPL was not dose-dependent (p = 0.43). The continuous hyperglycemia during and after long-term MPL treatment suggests that irreversible changes had occurred in the glucose regulation system. The fast insulin return to baseline after infusion despite the almost doubled glucose concentration implies possible dysfunctions in glucose-induced insulin secretion. Homeostasis of the biological system was disrupted with chronic dosing.
Figures 5 and 6 show the model fittings of the naive-pooled data using Equations (10–14), and Table 4 lists the parameter estimates. This model represented the final selection after comparing several other possible mechanistic models. Glycemic control by insulin with inhibiting input or stimulating output were both tested. Stimulation of glucose utilization better captured the data and was in agreement with insulin's major actions in peripheral tissues and the possibly secondary action on hepatic glucose production [13]. Corticosteroid action on glucose production versus utilization were both tested. Stimulation of glucose production better described the data and was in agreement with the major actions of corticosteroids in gluconeogenesis. The PD model nicely captures the temporary glucose and insulin induction after short-term MPL treatment, and adequately predicts the continuous hyperglycemia and reversible insulin induction with chronic dosing.
Table 4.
Pharmacodynamic parameters for MPL effects on glucose regulation
| Parameter | Definition (doses) | Estimate | CV% | |
|---|---|---|---|---|
| Glucose dynamics | ||||
|
|
Glucose utilization rate constant | 0.58 | 31 | |
| SG (mg/dl)−1 | Glucose sensitivity | 0.17 | 14 | |
| S max | Maximal stimulation | 0.21 | 12 | |
|
|
Stimulation constant | 6506 | — b | |
|
|
Stimulation constant | 1.05 | 4 | |
|
|
Maximal inhibition | 0.53 | 4 | |
|
|
Inhibition constant | 55.4 | 4 | |
| γ G | Hill factor | 2.72 | 21 | |
| G0,injection (mg/dl) | Baseline glucose (0, 10, 50) | 119, 116, 113 | Fixed | |
| G0,infusion (mg/dl) | Baseline glucose (0, 0.1, 0.3) | 86, 70, 80 | Fixed | |
|
|
Glucose production rate (0, 10, 50) | 68, 67, 65 | — b | |
|
|
Glucose production rate (0, 0.1, 0.3) | 49, 41, 46 | — b | |
| Insulin dynamics | ||||
|
|
Insulin degradation rate constant | 0.075 | 18 | |
| SI (ng/ml)−1 | Insulin sensitivity | 0.011 | 54 | |
| I0,injection (ng/ml) | Baseline insulin (0, 10, 50) | 1.36, 1.00, 1.10 | Fixed | |
| I0,infusion (ng/ml) | Baseline insulin (0, 0.1, 0.3) | 0.88, 0.67, 0.67 | Fixed | |
|
|
Insulin secretion rate (0, 10, 50) | 0.10, 0.075, 0.083 | 18 | |
|
|
Insulin secretion rate (0, 0.1, 0.3) | 0.066, 0.050, 0.050 | 18 | |
Secondary parameter.
Not estimated.
Physiological parameters , SG, , SI, describe the glucose-insulin inter-regulation system at normal status. The efficiency of glucose in stimulating insulin secretion (SG) with a value of 0.17 (mg/dl)−1 implies that insulin production rate would increase 100% when glucose concentrations increase 5.88 mg/dl. Similarly, SI represents the ability of insulin in stimulating glucose utilization. The fast return phase of plasma glucose after short-term induction was governed partly by its endogenous degradation rate , and partly by the effect of insulin. The slow return phase of plasma insulin was controlled by its natural degradation rate .
The Smax, and characterize corticosteroid effects on glucose regulation. The Smax of 0.21 indicates that the maximum achievable stimulation of glucose production rate is 1.21-fold by corticosteroid alone or in combination. The high estimate of 6506 ng/ml reflects the very low potency of endogenous CST for regulating glucose, and was well above the CST concentration range present in our normal rats. Although CST was suppressed by MPL and induced by animal handling, it showed little influence on glucose and insulin concentrations. The high CV% associated with the estimate was due to the limited range of CST concentrations in the present study, insufficient to accurately estimate . The low estimate of 1.05 ng/ml reflects the very high sensitivity of MPL for regulating glucose. Plasma MPL concentrations were maintained above its SC50 value for more than 6 h after injection, and during the entire 7 day infusion. Drug effect was saturated by the high MPL concentration after both 10 and 50 mg/kg i.v. injection, resulting in the lack of dose-dependency of glucose and insulin responses after short-term dosing. The very high potency ratio ξ of 6187 illustrates the large difference between endogenous and exogenous steroids on regulating glucose.
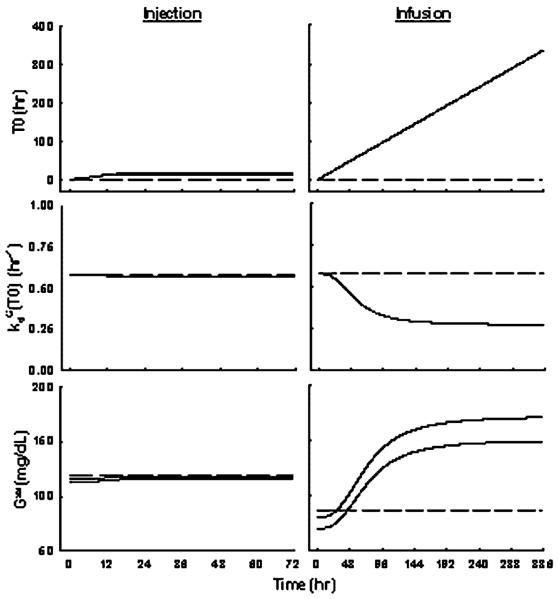
Parameters , and γG control system changes underlying hyperglycemia progression after long-term treatment. The of 0.53 suggests that glucose degradation rate could be inhibited to as low as 0.27 h−1. The high γG estimate of 2.72 indicates a relatively fast system adaptation once was achieved around 2 days after continuous drug exposure. Without these pathological parameters, glucose concentrations would be greatly under-predicted during infusion and would return back to baseline after infusion (data not shown). Figure 7 shows simulations for T0, and Gss in all animal groups. After single-doses, glucose was only temporarily induced (T0 small), which caused very little changes of the system ( and Gss almost remained constant). With long-term treatment, glucose was kept induced resulting in a linear increase in T0. The glucose disposition rate was reduced and slowly approached a nadir after 6 days, which could be explained by saturation/desensitization of transporters or enzymes. This dysfunction in glucose utilization was irreversible, therefore leading to the continued hyperglycemia after drug administration. Since maximum destruction had been achieved, glucose would stay at a new steady-state governed by the balance of its production and the lowered disposition rate. This newly established steady-state works as a new set-point in controlling insulin secretion. Therefore, no further insulin was induced after infusion.
Figure 7.
Simulations of T0, and Gss versus time profiles upon administration of saline, 10 and 50 mg/kg MPL injection (left), or saline, 0.1 and 0.3 mg/kg/h MPL infusion for 7 days (right) using Equations (5–14) with parameters fixed as in Table 4. Broken lines represent control groups, thin solid lines represent low-dose groups, and thick solid lines represent high-dose groups
Discussion
In this study, a mechanistic pharmacodynamic model was developed to jointly describe corticosteroid effects on adrenal suppression and glycemic control in normal rats. The effects of corticosteroids on glucose regulation, the mechanisms controlling glucose homeostasis, and modeling of the carbohydrate system were discussed in detail previously [5]. This report focuses on the implications of differences between ADX and normal animals in response to MPL treatment. All results for ADX rats were described previously [5] unless stated otherwise.
Methylprednisolone exhibited roughly dose-proportional PK in normal rats at present doses. All MPL concentration profiles from all doses and regimens were described with one set of PK parameters, whereas different parameters were required to capture MPL behavior after different doses and regimens in ADX rats. Normal rats appear to have a larger clearance, larger plasma volume of distribution and a longer elimination half-life (1 h) of MPL than ADX rats in these studies. These PK properties produced lower steady-state concentrations during infusion in normal rats. Despite the longer half-life, the ascending part of the MPL concentration profile during infusion was still unavailable, and it was assumed that bioavailability was complete and the absorption rate was much faster than the rate of drug release from the pump because of the high lipophilicity of MPL. Due to the small number of animals in the present study and the between-study (with historical ADX rat data) instead of within-study PK comparison, the difference of MPL pharmacokinetics in normal versus ADX rats may need to be further confirmed.
Control rats maintained constant body weights in the chronic dosing study. These rats underwent jugular vein cannulation, subcutaneous pump implantation (0 h) and removal (168 h), as well as sequential blood sampling over 2 weeks. These surgeries and continuous handling/sampling may be stressful and limit rat growth. Such stress was partially confirmed by the increase of CST concentrations over 2 weeks. Continuous growth was observed in ADX rats (108±4% predose body weight), which may simply be explained by inter-animal variability. System parameters describing weight gain () and weight loss () were similar between normal and ADX rats, which is consistent with the fact that adrenalectomy would not impair growth of rats. The drug had similar sensitivity () in both types of animals, but the maximum capacity () of the catabolic effect of MPL was higher in normal rats. This difference was responsible for the lower nadir in normal animals at the end of 7 days. This implies that adverse effects of MPL at the whole-body level were greater in normal rats than in ADX rats. This drug toxicity was reversible in all animals. Weight redistribution between muscle and fat, as well as multiple adipose tissue regions is expected. Only whole body weights were available in the present study and weight losses were similar to those found previously [8].
Normal animals have functional adrenal glands which produce CST as the endogenous corticosteroid. It is well recognized that these steroid hormones exhibit a circadian rhythm in both animals (CST) and humans (cortisol) because of biorhythmic secretion [14–16]. The assessment of CST secretion relies on the correct measurement of baseline levels. Rats are sensitive to outside disturbances and any stress will induce CST secretion. Stress was reduced in the animals by working in a quiet room and handling them gently. Rats were kept in metabolic cages for frequent sampling during the initial 24 h with minimal handling. The CST biorhythmic baseline obtained from control rats in the initial 24 h is consistent with literature findings [16]. The later increase in baseline CST was likely due to the stress induced by handling animals.
The circadian rhythm of CST in animals (and cortisol in man) is often asymmetric and variable. A single cosine function was not sufficient to describe such a complex pattern. Several methods have been proposed to describe the episodic/circadian nature of endogenous corticosteroids in humans and animals [11]. After testing several models, the Fourier analytical approach was chosen to generate the appropriate circadian harmonic functions. This approach is flexible, accurate and stable over time. An extra complexity of a linearly increased mesor with time after 24 h successfully captured the alteration in baseline, and could be used to describe any changing baseline with biorhythmic properties.
Even though adrenal gland functionality is usually assessed clinically by the ACTH stimulation test [17], cortisol or CST suppression may be used as a PD marker for drug effects. This adverse effect of MPL was quickly reversible after both acute and chronic dosing, which implies that no intrinsic adrenal insufficiency occurred at the current doses.
The adrenal glands provide two major physiological contributions. The adrenal cortex secretes glucocorticoids (which control the metabolism of proteins, carbohydrates and fats) and mineralocorticoids (which reduce sodium and increase potassium excretion). The adrenal medulla, on the other hand, plays a major role in the autonomic nervous system in secreting adrenaline and noradrenaline directly into the circulation upon activation by sympathetic nerve fibers. Adrenaline has a number of important metabolic effects [18]. It stimulates hepatic glucose production by increasing gluconeogenesis and glycogenolysis. It reduces glucose uptake and utilization in skeletal muscle. In addition, adrenaline and noradrenaline can inhibit insulin secretion through their α-adrenergic receptor activation, whereas β-adrenergic receptor activation initiates insulin secretion, reflecting a dual effect of catecholamines on insulin secretion mechanisms [19]. Therefore, adrenalectomy not only eliminated the normal effects of corticosteroids, but also removed the effects of adrenal medulla hormones on glucose regulation.
Normal rats from the current study exhibited higher initial values of glucose (G0) and insulin (I0) than ADX rats. This is comparable to previous findings that adrenalectomy resulted in significantly decreased serum glucose (88% of control) and insulin (23% of control) concentrations in rats [20]. The decreased plasma glucose after adrenalectomy is expected because of the well-known actions of both adrenaline and the corticosteroids on stimulating hepatic glucose production, suppressing glucose uptake/utilization and antagonizing insulin effects in peripheral tissues. This supports our higher glucose degradation () and insulin sensitivity (SI) estimates in ADX rats.
The adrenal medulla hormones can influence insulin secretion from pancreatic β-cells. In mice and rats, adrenalectomy lowered basal insulin secretion moderately. However, the glucose-induced insulin secretion after i.v. injection of 2.8 mmol/kg glucose was also almost doubled in ADX mice [21]. This observation is consistent with our low estimate which represents the basal insulin production, and high SG estimate which represents the ability of glucose to induce insulin secretion in ADX rats. These changes in system characteristics produced the lower initial insulin concentration (I0) and the higher magnitude of insulin induction especially during infusion in ADX rats.
The maximum achievable stimulation of glucose production by corticosteroids (Smax) was comparable in normal and ADX rats. The lower estimate in normal rats implies that MPL exhibited higher sensitivity in regulating glucose under normal conditions. The potency ratio ξ of 6190 describing the relative effect of MPL and CST in regulating glucose was much higher than the reported potency ratio of 10–20 for lymphocyte trafficking [14,15]. This suggests that synthetic corticosteroids are much more potent in causing glucose induction than physiological corticosteroids.
The parameter representing the maximal severity of hyperglycemia progression () was comparable between normal and ADX rats, which implied that similar maximum damage may be produced in the metabolic system. However, the higher estimate and lower γG estimate in normal rats produced a delayed and slower disease progression. These parameters controlled the gradual glucose increase during MPL infusion in normal rats. The low and high γG in ADX rats generated the fast early rise in glucose and the hyperglycemic plateau after 48 h, implying that maximum destruction in glucose uptake/utilization had already been achieved. These pathophysiologic parameters suggest that healthy animals can tolerate glucose toxicity for longer times and trigger irreversible system alterations later.
Although the model successfully described all glucose and insulin dynamics for an array of MPL treatments simultaneously, it was limited by several factors. Some known mechanisms (such as suppression of glucose output by insulin, both the insulin-dependent and insulin-independent pathways of glucose utilization) were left out to avoid overparameterization, assuming they played less important roles in glucose homeostasis. Plasma MPL concentrations instead of its binding to glucocorticoid receptors was used as a driving force for drug effects. Linear stimulation coefficients SG and SI were used due to model complexities, which may limit prediction capability.
In summary, hyperglycemia and hyperinsulinemia evolved after corticosteroid treatment in normal rats. This systemic change was temporary after acute dosing. Long-term treatment was associated with additional complexities which caused irreversible disturbance of the system homeostasis. Normal and ADX animals have different physiological properties of the metabolic system, different responses to drug treatment and different progression to disease state. Experimental results and mathematical characterizations of both types of animals provided more insightful information on the hormonal control of glucose homeostasis. The mechanistic PK/PD model integrating the endogenous and exogenous effects of corticosteroids allows quantitation of drug effects and system controls in the normal metabolic condition.
Acknowledgements
Financial support for this research was provided by Grant GM24211 from the National Institutes of Health. The authors would like to thank Ms Suzette Mis for performing the HPLC assay, and Ms Xiao Tan for technical assistance for glucose and insulin assays in the infusion study.
References
- 1.Baxter JD. Glucocorticoid hormone action. Pharmacol Ther. 1976;2:605–669. doi: 10.1016/0306-039x(76)90010-6. [DOI] [PubMed] [Google Scholar]
- 2.Baxter JD, Forsham PH. Tissue effects of glucocorticoids. Am J Med. 1972;53:573–589. doi: 10.1016/0002-9343(72)90154-4. [DOI] [PubMed] [Google Scholar]
- 3.Wilcke JR, Davis LE. Review of glucocorticoid pharmacology. Vet Clin North Am Small Anim Pract. 1982;12:3–17. doi: 10.1016/s0195-5616(82)50001-0. [DOI] [PubMed] [Google Scholar]
- 4.Pellacani A, Fornengo P, Bruno A, et al. Acute methylprednisolone administration induces a transient alteration of glucose tolerance and pyruvate dehydrogenase in humans. Eur J Clin Invest. 1999;29:861–867. doi: 10.1046/j.1365-2362.1999.00553.x. [DOI] [PubMed] [Google Scholar]
- 5.Jin JY, Jusko WJ. Pharmacodynamics of glucose regulation by methylprednisolone I. Adrenalectomized rats. 2008. In press. companion article. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Haughey DB, Jusko WJ. Analysis of methylprednisolone, methylprednisone and corticosterone for assessment of methylprednisolone disposition in the rat. J Chromatogr. 1988;430:241–248. doi: 10.1016/s0378-4347(00)83159-x. [DOI] [PubMed] [Google Scholar]
- 7.Dayneka NL, Garg V, Jusko WJ. Comparison of four basic models of indirect pharmacodynamic responses. J Pharmacokinet Biopharm. 1993;21:457–478. doi: 10.1007/BF01061691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Ramakrishnan R, DuBois DC, Almon RR, Pyszczynski NA, Jusko WJ. Pharmacodynamics and pharmacogenomics of methylprednisolone during 7-day infusions in rats. J Pharmacol Exp Ther. 2002;300:245–256. doi: 10.1124/jpet.300.1.245. [DOI] [PubMed] [Google Scholar]
- 9.Krzyzanski W. FOURPHARM User's Guide: A Computer Program Applying Fourier Analysis to Biorhythmic Data. Buffalo, NY: 2000. [Google Scholar]
- 10.Krzyzanski W, Chakraborty A, Jusko WJ. Algorithm for application of Fourier analysis for biorhythmic baselines of pharmacodynamic indirect response models. Chronobiol Int. 2000;17:77–93. doi: 10.1081/cbi-100101034. [DOI] [PubMed] [Google Scholar]
- 11.Chakraborty A, Krzyzanski W, Jusko WJ. Mathematical modeling of circadian cortisol concentrations using indirect response models: comparison of several methods. J Pharmacokinet Biopharm. 1999;27:23–43. doi: 10.1023/a:1020678628317. [DOI] [PubMed] [Google Scholar]
- 12.D'Argenio DZ, Schumitzky A. ADAPT II User's Guide: Pharmacokinetic/Pharmacodynamic Systems Analysis Software. BioMedical Simulations Resource; Los Angeles, CA: 1997. [Google Scholar]
- 13.Flakoll PJ, Carlson MG, Cherrington AD. Chapter 14. Physiologic action of insulin. In: LeRoith D, Taylor SI, Olefsky JM, editors. Diabetes Mellitus. A Fundamental and Clinical Text. 2nd edn Lippincott Williams & Wilkins; Philadelphia: 2000. pp. 148–161. [Google Scholar]
- 14.Milad MA, Ludwig EA, Anne S, Middleton E, Jr, Jusko WJ. Pharmacodynamic model for joint exogenous and endogenous corticosteroid suppression of lymphocyte trafficking. J Pharmacokinet Biopharm. 1994;22:469–480. doi: 10.1007/BF02353790. [DOI] [PubMed] [Google Scholar]
- 15.Chow FS, Sharma A, Jusko WJ. Modeling interactions between adrenal suppression and T-helper lymphocyte trafficking during multiple dosing of methylprednisolone. J Pharmacokinet Biopharm. 1999;27:559–575. doi: 10.1023/a:1020974408657. [DOI] [PubMed] [Google Scholar]
- 16.Meno-Tetang GM, Hon YY, Van Wart S, Jusko WJ. Pharmacokinetic and pharmacodynamic interactions between dehydroepiandrosterone and prednisolone in the rat. Drug Metabol Drug Interact. 1999;15:51–70. doi: 10.1515/dmdi.1999.15.1.51. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Membreno L, Irony I, Dere W, Klein R, Biglieri EG, Cobb E. Adrenocortical function in acquired immunodeficiency syndrome. J Clin Endocrinol Metab. 1987;65:482–487. doi: 10.1210/jcem-65-3-482. [DOI] [PubMed] [Google Scholar]
- 18.Lefkowitz RJ, Hoffman BB, Taylor P. Chapter 6. Neurotransmission: the autonomic and somatic motor nervous systems. In: Hardman JG, Limbird LE, Molinoff PB, Ruddon RW, Gilman AG, editors. Goodman & Gilman's The Pharmacological Basis of Therapeutics. 9th edn McGraw-Hill; New York: 1996. [Google Scholar]
- 19.Hoffman BB, Lefkowitz RJ. Chapter 10. Catecholamines, sympathomimetic drugs, and adrenergic receptor antagonists. In: Hardman JG, Limbird LE, Molinoff PB, Ruddon RW, Gilman AG, editors. Goodman & Gilman's The Pharmacological Basis of Therapeutics. 9th edn McGraw-Hill; New York: 1996. [Google Scholar]
- 20.Freedman MR, Stern JS, Reaven GM, Mondon CE. Effect of adrenalectomy on in vivo glucose metabolism in insulin resistant Zucker obese rats. Horm Metab Res. 1986;18:296–298. doi: 10.1055/s-2007-1012300. [DOI] [PubMed] [Google Scholar]
- 21.Ahren B, Lundquist I. Adrenalectomy and chemical sympathectomy by 6-hydroxydopamine. Effects on basal and stimulated insulin secretion. Pflugers Arch. 1981;390:17–21. doi: 10.1007/BF00582705. [DOI] [PubMed] [Google Scholar]