Abstract
Background.
Visuomotor abnormalities are common in aging and age-related disease, yet difficult to quantify. This study investigated the effects of healthy aging, sex, and handedness on the performance of a tracing task. Participants (n = 150, aged 21–95 years, 75 females) used a stylus to follow a moving target around a circle on a tablet computer with their dominant and nondominant hands. Participants also performed the Trail Making Test (a measure of executive function).
Methods.
Deviations from the circular path were computed to derive an “error” time series. For each time series, absolute mean, variance, and complexity index (a proposed measure of system functionality and adaptability) were calculated. Using the moving target and stylus coordinates, the percentage of task time within the target region and the cumulative micropause duration (a measure of motion continuity) were computed.
Results.
All measures showed significant effects of aging (p < .0005). Post hoc age group comparisons showed that with increasing age, the absolute mean and variance of the error increased, complexity index decreased, percentage of time within the target region decreased, and cumulative micropause duration increased. Only complexity index showed a significant difference between dominant versus nondominant hands within each age group (p < .0005). All measures showed relationships to the Trail Making Test (p < .05).
Conclusions.
Measures derived from a tracing task identified performance differences in healthy individuals as a function of age, sex, and handedness. Studies in populations with specific neuromotor syndromes are warranted to test the utility of measures based on the dynamics of tracking a target as a clinical assessment tool.
Key Words: Functional performance, Geriatric assessment, Motor control, Normative aging, Sensory.
Visuomotor abnormalities are common in aging and age-related diseases, yet difficult to quantify. Brief clinical exams of neuromuscular performance focus on qualitative assessments, including obtaining a patient history, assessing the patient’s cognitive status, motor and sensory functions, coordination, and reflexes. Performing these exams requires medical expertise, with the exams rated on scales with coarse gradations and subject to interobserver variability. In addition, assessment of progression over time may lack objectivity and sensitivity. Thus, there is a clinical need to obtain an objective value with sufficiently high resolution quantifying a patients’ neuromotor functionality.
Previous work has shown that clinically important information is encoded in the nonlinear fluctuations of physiological time series (1,2). These fluctuations represent the dynamics of the underlying physiological control systems and the nonlinear interactions between the multiple inherent regulatory mechanisms. For example, fine motor movement variability has been shown to increase with age, specifically with impairments in executive control (3). However, traditional measures of variability (eg, standard deviation, spectral power) may not fully characterize the nonlinear structure of the physiological time series, as the physiological control mechanisms normally operate over many time scales (4). From biological and clinical points of view, complexity is related to adaptability and system function (5–7). One computational tool developed to analyze complex-appearing signals is called multiscale entropy (MSE). This method quantifies the information content of a time series over a range of scales (5,6). Studies have shown that disease and aging are associated with a loss or degradation of complexity, which in turn reflects system adaptability. For example, patients with congestive heart failure or those with atrial fibrillation (5,8), as well as patients with an acute major depressive episode (9) showed a marked reduction in cardiac interbeat interval complexity compared with healthy control participants. Older adults have also shown a reduction in balance complexity compared with younger adults (10).
To assess the integrity of the visuomotor system, we developed a continuous motion-tracing task based on a rotary pursuit model (11,12). We extend this model by defining “microcontrol adaptations” as the real-time error corrections that occur during the task. These microcontrol adaptations may be adjusted by feedforward or feedback control mechanisms and rely on real-time sensory processing. Previous work has shown that age-related motion effects can be attributed to deficits in online sensing and feedforward control (17). Thus, we also examined the percentage of time within the target region (PTTR) to evaluate the accuracy of the user’s imposed control method.
Previous studies of human movement have shown that even continuous motions are composed of quantized submovements (18,19). These submovements were observable after stroke as isolated movement segments that became more overlapped with recovery (19,20) and in babies prior to maturing their reaching strategies (21). The literature contains differing interpretations as to why submovements are generated. Although some studies suggest that the submovements are corrective adjustments (19,22,23), others suggest that the generation of submovements are a compensatory mechanism due to decreased movement smoothness (24). For the task described here, we measured submovement concatenation by recording the micropause timing of the participant’s tracing activity, which was defined as the time when the velocity was zero. Because the tracing task involved a continuous motion, we assumed that pauses were primarily due to delays in concatenation of submovements and thus provided an indication of neurological performance.
Previous arm-reaching studies have shown that although the dominant and nondominant hand had similar end point errors, there were different hand paths to achieve the goal, implying a different neural organization to perform the task (25). Further, adaptive-reaching studies have shown that with aging, there are degradations in interlimb transfer of motion information (ie, initial training with one hand in a new environment would be reflected with increased performance of the other hand) (26). Therefore, in this study, we examined a visuomotor-tracing task where the participant was asked to follow a moving target with dominant and nondominant hand as a surrogate for neurological functionality. We hypothesized that with aging and use of the nondominant hand (a) the absolute mean and variance of the error would increase, (b) the complexity index (CI) would decrease, (c) the PTTR would decrease, and (d) the cumulative micropause duration (CMD) would increase.
Methods
Task Development
Time series suitable for assessing the integrity of neuromotor control require numerous, consecutive data points. Further, because the goal was to examine the fluctuations in the time series, a simple target signal was desired as any complexity found in the fluctuations would be due to the person performing the task with minimal effects of the task itself. We selected a circular-tracing task. Measures derived from tracing a circle have previously been shown to correlate with gross gait and posture measurements in those with Parkinson’s disease (13,15) and attention deficit disorder (14). We hypothesized that this type of task would also provide information useful for assessing the integrity of visuomotor mechanisms in putatively healthy adult participants across a wide range of ages.
Target velocity represents a trade-off between speed and accuracy in task performance, as originally shown by Fitts (16). Faster motions permit less error correction and thus have decreased accuracy with respect to slower ones. The speed of the moving target was selected through pilot testing, with the goal of achieving a speed that was slow enough to allow for microcontrol adaptations (error corrections), but not so slow that the participant would consciously stop and wait for the target to move. These pilot tests led to selecting a speed of 18 deg/s around a circle with a 400-pixel (8.13cm) diameter.
Participants
A total of 152 healthy people provided written consent, and 150 participants completed the study. Two participants were unable to complete the study, one due to the onset of tremors (an exclusion criterion) and the other for not being able to properly follow directions. Procedures were approved by the Harvard Medical School Committee on Human Studies. Participants were recruited if they were between 21 and 95 years of age and were able to follow instructions in English. Fifteen men and 15 women were recruited within five age groups, each spanning 15 years (21–35, 36–50, 51–65, 66–80, and 81–95 years). These age groups were determined a priori based on a power analysis from pilot data. Because this study examined function during a putative healthy baseline, participants were excluded if they had (a) a self-reported or diagnosed neuromotor disorder such as Parkinson’s disease, multiple sclerosis, cerebral palsy, attention deficit hyperactivity disorder, or seizure disorders; (b) a visual handicap that prevented them from seeing the objects on a computer screen; (c) any acute or chronic medical conditions potentially affecting neuromotor control (eg, arthritis in the hand or tremors); (d) regular use of medications that could cause tracking errors or induce a tremor (eg, psychotropic and antidepressant drugs, stimulants, and antiemetics); (e) regular tobacco use, more than two alcoholic beverages per day, or recreational drugs; or (f) more than four cups of coffee (or other caffeinated beverages) per day.
Experimental Protocol
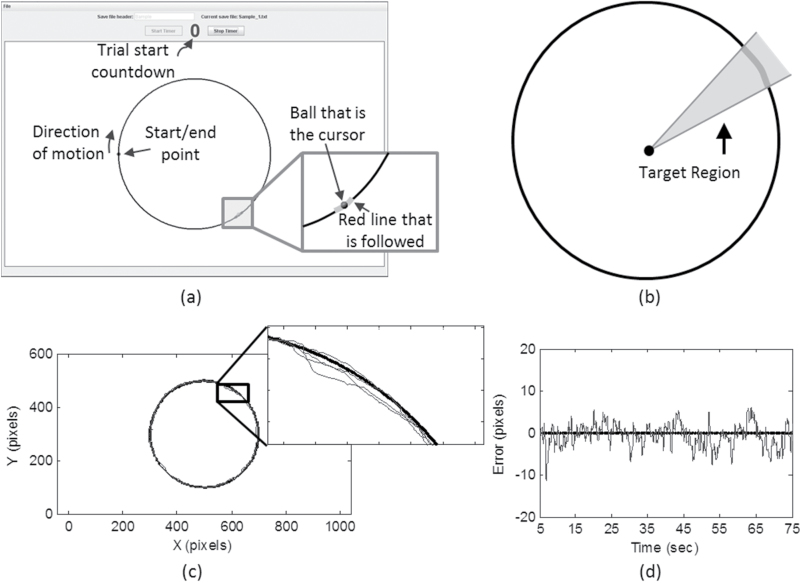
Participants began by responding to a brief health and demographic questionnaire (see Table 2 for summary), followed by a near vision test. Participant handedness was determined through self-report in the questionnaire by asking which hand was primarily used for writing. They then used their dominant hand to perform the Trail Making Test, a standard neuropsychological impairment test, which is sensitive to speed of processing (part A) and rule shifting and sequencing (part B) (27,28). This test is considered a measure of executive control function. Upon completing the Trail Making Test, participants were provided with instructions regarding the tracing task to be performed on a tablet PC (Panasonic Toughbook H1 Field). The tracing task involved following a red line clockwise around a circle four times using a stylus, with the cursor position indicated by a ball (Figure 1a). The software was written in-house in Java. The tablet PC running the software was placed 4 in (10.16cm) from the edge of a table of standard height, with participants allowed to place the chair so they could sit and reach the tablet PC comfortably. Participants performed the task in a predetermined randomized order using their self-reported dominant and nondominant hand. One practice trial was given, followed by 14 experimental trials (7 for each hand). Participants were permitted to take breaks when requested.
Table 2.
Summary of Participant Demographics and Clinical Characteristics
| Parameter | Summary |
|---|---|
| Age | 58±22 y, range 21–95 y |
| Sex | 75 male, 75 female |
| Dominant hand | |
| Right | 129 (86%) |
| Left | 21 (14%) |
| Education | |
| Bachelors | 132 (88%) |
| Advanced degree | 48 (32%) |
| Self-reported general health | |
| Fair | 10 (7%) |
| Good | 32 (21%) |
| Very good or above | 108 (72%) |
| Self-reported activity level | |
| Light daily activity or less | 12 (8%) |
| Light physical exercise | 53 (35%) |
| Moderate exercise or more | 85 (57%) |
Figure 1.
(a) Screenshot of the visuomotor-tracing task. The participants controlled the cursor, represented as a ball, with a stylus. The goal was to stay within the moving red line. (b) Rays are drawn from the center of the circle to the boundaries of the moving target at each time point to define the target region for data analysis (not shown to scale). (c) Sample data for the tracing task and (d) the associated error signal. Pixels were 0.008×0.008 in (0.020×0.020cm).
Data Collection
The tablet computer used had an 8.25×6.125 in (20.96×15.56cm) screen size, with a resolution of 125 ppi, and pixel size of 0.008×0.008 in. (0.020×0.020cm). The cursor was presented as a ball with a 5-pixel radius. The red line that was followed was 22 pixels in length and 6 pixels thick. The circular path was 400 pixels in diameter, with a 2-pixel thick line. The data collection software generated files containing the Cartesian coordinates of both the target and the stylus position over time. The sampling frequency was 31.25 Hz. This value was chosen taking into consideration the speed of the moving target and the pixel size to enhance the likelihood that individual pixels were sampled only once.
Data Processing
As Trial 1 was a practice trial, the analysis described here was performed for Trials 2 through 15 (7 trials for each hand, order randomized). The calculated measures of the tracing task were the absolute mean and variance of the error, the CI of the error signal, the PTTR, and the CMD. These measures are defined below and summarized in Table 1.
Table 1.
Summary of Measures and Abbreviations
| Measure | Abbreviation | Definition |
|---|---|---|
| Absolute mean error | — | Absolute value of the mean of the error signal |
| Variance of the error | — | Variance of the error signal |
| Complexity index | CI | Summation of the sample entropies for scales 1–4 |
| Percentage of time within the target region | PTTR | Percentage of task time that the stylus coordinates were within the target region |
| Cumulative micropause duration | CMD | Summation of the time periods during which the stylus position did not change while performing the task |
If (xc, yc) are the coordinates of the center of the circle and (xs, ys) are the coordinates of the stylus at a recorded time point, then the instantaneous error at that time point is defined as
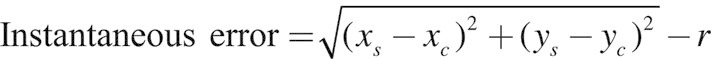 |
(1) |
where r is the radius of the circle (Figure 1c and d). The error time series is then the sequence of instantaneous errors. To account for initiation and termination effects, the first and last quarter circle were removed. Thus, a total of 3.5 revolutions were analyzed. The absolute mean error was also computed.
The CI was calculated using the MSE method, described in detail elsewhere (5). Briefly, the MSE method incorporates three steps: (a) deriving a set of coarse-grained time series that represent a system’s dynamics over different time scales, (b) measuring the information content of each of these coarse-grained time series by using an entropy measure termed sample entropy (SampEn) (26), and (c) integrating the SampEn values over a predefined range of scales to obtain a CI. SampEn is a conditional probability measure quantifying the likelihood that if a sequence of m consecutive data points matches (within a tolerance r) a template sequence of the same length, then the two will still match when their length increases from m to m + 1 data points. Thus, SampEn quantifies the degree of irregularity of a time series. Periodic signals, such as sine waves, are very predictable and therefore have SampEn values that are close to zero. In contrast, uncorrelated random signals are completely unpredictable and consequently have very high SampEn values. (The maximum value of SampEn for a given time series depends on its number of data points.) An element j of the coarse-grained time series y for scale n is calculated according to the equation,
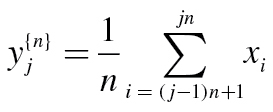 |
(2) |
where xi with 1 ≤ j ≤ N is a data point from the original time series that comprises a total of N data points. The MSE curve was obtained by plotting the SampEn values for each coarse-grained time series as a function of scale. The CI was the area under the MSE curve calculated for a predefined range of scales. For this study, given the available length of the original error time series, we used n = 4 (6). Finally, we note that the MSE method was originally developed for the analysis of stationary time series. Spurious low complexity values can be obtained if the original signals are highly nonstationary. Therefore, before applying the MSE method, the error time series were detrended using a moving average window of 21 data points.
The target region was defined at each of the generated time points by computing the rays from the circle origin to the boundaries of the moving target (Figure 1b). If the cursor, represented by the ball, touched or fell within the target region, the time point was considered within the region. The time increments associated with the cursor in and out of the target region were then summed to determine a total time in the target region, as well as to verify the total task time. The PTTR was then determined by dividing the total time in the region by the total task time.
Micropauses were defined as time intervals during which the position of the stylus did not change, thus
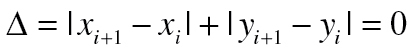 |
(3) |
where (x, y)i and (x, y)i+1 are the stylus coordinates at time i and i + 1, respectively. The CMD is then the summation of the time increments associated with the repeated stylus coordinates. This parameter is limited only when the stylus location is not sampled frequently enough as pauses would be missed. If the data are sampled at higher rates, the CMD would not be affected.
Statistical Analysis
A mixed multifactorial repeated-measures analysis of variance using Systat 12 (SigmaPlot, Chicago, IL) was implemented to analyze the independent effects of age, sex, and handedness over the trials, as well as their interaction on the calculated measures. Age, sex, and handedness (dominant vs nondominant) were treated as between-groups factors, whereas trial was treated as the repeated-measures factor. For the analyses, hand was defined as dominant or nondominant, rather than left or right. The absolute mean and variance of the error, CI, PTTR, and CMD were each compared across age, sex, and handedness. Age was categorized into five groups, with each group spanning 15 years (21–35, 36–50, 51–65, 66–80, and 81–95 years). For these comparisons, significance was set at .05. A post hoc analysis was performed to examine the difference in the five age groups and within group with respect to dominant hand and sex. These comparisons were conducted using the Bonferroni adjusted level of significance.
To quantify possible correlations between the calculated measures with the Trail Making Test, separate linear least squares regressions were performed for each measure with Trails A score, Trails B score, and the difference between Trails B and A scores. The difference between Trails B and A was included so that the executive control task was adjusted for the subject’s speed of performance. For each of the linear least squares regressions, age group, sex, and handedness were used as covariates.
Results
Description of Study Population
A summary of the participant demographics and clinical characteristics is presented in Table 2. Overall participants reported they were in “Very Good” health and had a “Light” level of daily physical activity. Participants in this study had higher education levels than the average population and the Massachusetts population, the state in which the study was conducted (2000U.S. Census).
Effect of Age, Handedness, and Sex on the Calculated Measures
The effects observed were independent of intrasubject variation as trial was included in the analysis as a repeated measure. Within subjects, the absolute mean error, CI, and CMD were significantly related to trial number (p < .0005). Trial was not statistically significantly related to the variance of the error (p = .083) or PTTR (p = .549). For the absolute mean error, post hoc comparisons showed a difference between the first trial and subsequent trials. However, this may be a spurious effect due to the Trial × Handedness effect (p = .002). When post hoc comparisons were made stratified by handedness, there was no significant effect of trial for the dominant hand; however, for the nondominant hand, there was a significant difference between the first and second times the task was performed (p < .0005). There was no significant difference for the nondominant hand for the absolute mean error between the second and subsequent times the task was performed. For CI, there was a significant increase in CI between the first and last performance of the task when post hoc comparisons were made. No clear trends were observable between trials for CMD when post hoc tests were performed. However, the fifth and sixth times the task was performed were found to have significantly lower values than the first time the task was performed. No other trials were significantly different after Bonferroni corrections were applied for the CMD measures.
Effect of age.—
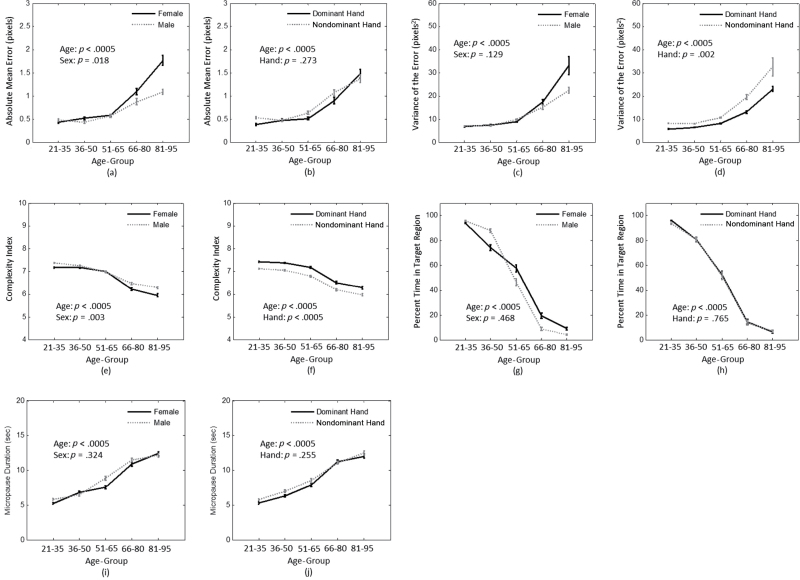
Highly significant differences were seen as a function of age group for all the calculated measures (Figure 2). Overall, increasing age showed increased absolute mean error, increased variance, decreased CI, decreased PTTR, and increased CMD.
Figure 2.
Effect of age group, sex, and hand on (a, b) absolute mean error, (c, d) variance of the error, (e, f) complexity index, (g, h) percentage of time within the target region, and (i, j) cumulative micropause duration. Error bars are the standard error. Reported significance was adjusted for trial number. Pixels were 0.008×0.008 in (0.02×0.02cm).
Effect of handedness.—
The effect of handedness was statistically significant for the error variance (p = .002, Figure 2d) and the CI (p < .005, Figure 2f). The variance of the error (Figure 2d) was significantly different between hand for all groups except the oldest age group (p < .0005), with nondominant hand having a higher variance than dominant hand. CI was the only measure that showed a significant difference between dominant and nondominant hand for all age groups when post hoc comparisons were made (p < .0005). CI was higher for the dominant hand with respect to the nondominant hand. Absolute mean error, CMD, and PTTR showed no effect of handedness.
Effect of sex.—
Although unanticipated, sex effects were observed in the absolute mean error and CI. Further, Age × Sex interactions were found in the absolute mean error (p = .023). There were no Age × Sex × Hand effects or Sex × Hand effects. When post hoc tests were performed, the absolute mean error (Figure 2a) was significantly different between male and female participants only for the oldest age group. Significant sex differences were found for the youngest (21–35 years) and two oldest age groups (66–80, 81–95 years) for the CI (Figure 2e). The variance of the error, CMD, and PTTR showed no effect of sex.
Relationship Between Trail Making Test Scores and Calculated Measures
Table 3 presents the relationship between the calculated measures and the Trail Making Test using a linear least squares regression with age, sex, and handedness as covariates. An increased Trail Making Test score (Trails A, Trails B, and Trails B – Trails A) was related to an increased absolute mean error, increased variance, decreased CI, decreased PTTR, and increased CMD. Although significant relationships were observed, the linear regressions did not explain the majority of variance within the data, with R2 values ranging from 0.212 to 0.416.
Table 3.
Relationship Between the Calculated Measures and the Trail Making Test Using a Linear Least Square Regression Model With Age Group, Gender, and Hand as Covariates
| Absolute Mean Error | Variance of the Error | Complexity Index | Percentage of Time Within the Target Region | Cumulative Micropause Duration | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Coefficient | R2 | Coefficient | R2 | Coefficient | R2 | Coefficient | R2 | Coefficient | R2 | |
| Trails A | 3.44 | 0.348* | 0.269 | 0.416* | –6.75 | 0.375* | –0.05 | 0.329* | 1.21 | 0.377* |
| Trails B | 9.05 | 0.341* | 0.642 | 0.391* | –18.83 | 0.374* | –0.11 | 0.319** | 3.05 | 0.364* |
| Trails B – Trails A | 5.61 | 0.227* | 0.373 | 0.254* | –12.08 | 0.252* | –0.06 | 0.212*** | 1.84 | 0.241* |
Note: *p < .0005, **p < .005, ***p < .05 for the significance of the measure in the model.
Discussion
This study examined the recorded stylus position during a visuomotor-tracing task in a healthy population as a proof of concept for clinical applications. The recorded time series were quantified using the absolute mean and variance of the error, CI, PTTR, and CMD. As a surrogate for neurological impairment, we examined the task performance of the dominant and nondominant hands. We hypothesized that with aging and use of the nondominant hand (a) the absolute mean and variance of the error would increase, (b) CI would decrease, (c) PTTR would decrease, and (d) CMD would increase. To our knowledge, this study is the first to quantify the effects of age, sex, and handedness on the time-series dynamics obtained during a simple rotary pursuit task.
All calculated measures showed significant effects of age. The measures changed across age group as hypothesized: absolute mean and variance of the error increased, CI decreased, PTTR decreased, and CMD increased. These results are consistent with previous studies that have shown decreases in upper extremity motor performance with aging (17,23–26). Although the variance of the error and the CI showed a significant difference between dominant and nondominant hand, only the CI showed a significant difference within each age group when post hoc tests were performed. CI of the error time series was lower for the nondominant hand than the dominant hand. Thus, these data are consistent with a previous arm-reaching study (24) showing no effect of handedness on final position accuracy within age groups. A limitation to the measure of variation is that it only includes information about the time series at one scale, whereas physiological control mechanisms normally operate over many time scales (4). Thus, determining the mean variation for each trial neglects potential differences in microerror kinematics across scales, which was quantified by the CI measure in our study.
A sex effect was observed in the absolute mean error and the CI; however, when post hoc tests were performed, significant sex differences were only found in the oldest age group (81–95 years) for the absolute mean error and for the youngest (21–35 years) and two oldest groups (66–80 and 81–95 years) for the CI. Sex distinctions in the older age groups could be a function of differences in neuromotor performance as male and female participants age (eg, see Ref. (30)), or could result from differences in education level, activity, and social status in these groups as seen in previous studies of cognitive functioning (31).
Because neuromotor control relies on executive function, correlations were assessed between the calculated measures of the visuomotor-tracing task with Trails A, Trails B, and the difference between Trails B and A, which are clinical measures of executive function. Although all calculated measures showed significant relationships with the Trail Making Test when considered separately, the linear regression did not capture the majority of variability within the data. Participants in this study were self-reported to be healthy, active individuals. However, it is important to note that this population was, in general, more educated than the standard U.S. or Massachusetts populations (2000U.S. Census). It is well known that the Trail Making Test has education effects (28). Specifically, Trails A performance is unaffected by education, whereas Trails B is affected. Thus, future work should examine strengthening the model to predict performance by specifically incorporating education, along with other potential confounders.
This tracing task and associated performance metrics have the potential to provide a quantitative assessment in a variety of clinical contexts. However, it is important to note that the task does not have specificity. That is, although a number is obtained that can show the differences in performance between various individuals or conditions, the task does not currently specify the reason for the changes in performance. For the purposes of this study, only a self-reported healthy population was included. By expanding the study to different populations (ie, certain pathologies, drug prescriptions, or interventional therapies), it may be possible to examine the time series for more specific indicators of disease or disability. Given the intrasubject variation of repeated trials on some calculated measures (absolute mean error, CMD, and CI), the optimum number of trials for a clinical test using these measures needs to be determined. Further, this study examined measures obtained during only one visit. In order to determine the intrasubject test–retest reliability across multiple visits, additional studies will be necessary.
Conclusions
Visuomotor abnormalities are common in aging and age-related disease, yet difficult to quantify and use to predict outcomes. The task and calculated measures developed here have the potential to become a quantitative assessment tool, with the ability to compare changes over time to determine how the patient progresses through healing, rehabilitation, and training. This study demonstrated that the calculated measures selected are sensitive to age and handedness, as well as having statistically significant relationships with the Trail Making Test. This task could potentially provide an improved predictor of falls or cognitive decline. The next step for the development of this task into a diagnostic tool is to expand data collection from a healthy population to a diseased or injured population with neuromotor impairments (eg, Parkinson’s disease, cerebral palsy, stroke, multiple sclerosis, concussion, traumatic brain injury, etc.). In this manner, we can assess if the calculated measures can be used to characterize specific pathophysiological conditions, quantitatively assess the progression of aging effects, and possibly determine the impact of therapeutic interventions.
Funding
This work was supported by the Wyss Institute for Biologically Inspired Engineering at Harvard University; the National Institutes of Health (K99/R00 AG030677, AG025037, and R01GM104987); the G. Harold and Leila Y. Mathers Charitable Foundation; and the James S. McDonnell Foundation. Dr. L.A.L. holds the Irving and Edyth S. Usen Chair in Geriatric Medicine at Hebrew SeniorLfe.
Acknowledgments
The authors would like to thank Ms. Marcie Freeman and Mr. Ike Iloputaife for their assistance in collecting data at Hebrew SeniorLife, as well as Mr. James Niemi for his helpful comments during the preparation of this manuscript.
References
- 1. Lipsitz LA, Goldberger AL. Loss of ‘complexity’ and aging. Potential applications of fractals and chaos theory to senescence. JAMA. 1992; 267: 1806–1809 [PubMed] [Google Scholar]
- 2. Goldberger AL, Amaral LA, Hausdorff JM, Ivanov PCh, Peng CK, Stanley HE. Fractal dynamics in physiology: alterations with disease and aging. Proc Natl Acad Sci USA. 2002; 99(Suppl 1):2466–2472 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Krampe RT. Aging, expertise and fine motor movement. Neurosci Biobehav Rev. 2002; 26: 769–776 [DOI] [PubMed] [Google Scholar]
- 4. Goldberger AL. Non-linear dynamics for clinicians: chaos theory, fractals, and complexity at the bedside. Lancet. 1996; 347: 1312–1314 [DOI] [PubMed] [Google Scholar]
- 5. Costa M, Goldberger AL, Peng CK. Multiscale entropy analysis of complex physiologic time series. Phys Rev Lett. 2002; 89: 068102 [DOI] [PubMed] [Google Scholar]
- 6. Costa M, Goldberger AL, Peng CK. Multiscale entropy analysis of biological signals. Phys Rev E. 2005; 71: 021906 [DOI] [PubMed] [Google Scholar]
- 7. Kang H, Costa M, Priplata A, et al. Frailty and the degradation of complex balance dynamics during a dual-task protocol. J Gerontol A Biol Sci Med Sci. 2009; 64: 1304–1311 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Costa MD, Peng CK, Goldberger AL. Multiscale analysis of heart rate dynamics: entropy and time irreversibility measures. Cardiovasc Eng. 2008; 8: 88–93 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Leistedt SJ-J, Linkowski P, Lanquart J-P, et al. Decreased neuroautonomic complexity in men during an acute major depressive episode: analysis of heart rate dynamics. Transl Psychiatry. 2001; 1: e27 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Costa M, Priplata A, Lipsitz L, et al. Noise and poise: enhancement of postural complexity in the elderly with a stochastic resonance-based therapy. Europhys Lett. 2007; 77: 68008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Ammons RB. Acquisition of motor skill: III. Effects of initially distributed practice on rotary pursuit performance. J Exp Psychol. 1950; 40: 777–787 [DOI] [PubMed] [Google Scholar]
- 12. Piper BJ. Age, handedness, and sex contribute to fine motor behavior in children. J Neurosci Methods. 2011; 195: 88–91 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Inzelberg R, Schechtman E, Hocherman S. Visuo-motor coordination deficits and motor impairments in Parkinson’s disease. PLoS ONE. 2008; 3: e3663 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Tirosh E, Perets-Dubrovsky S, Davidovitch M, Hocherman S. Visuomotor tracking related to attention-deficit hyperactivity disorder (ADHD). J Child Neurol. 2006; 21: 503–507 [PubMed] [Google Scholar]
- 15. Hocherman S, Alexandrovsky L, Badarny S, Honigman S. L-DOPA improves visuo-motor coordination in stable Parkinson’s disease patients. Parkinsonism Relat Disord. 1998; 4: 129–136 [DOI] [PubMed] [Google Scholar]
- 16. Fitts PM. The information capacity of the human motor system in controlling the amplitude of movement. J Exp Psychol. 1954; 47: 381–391 [PubMed] [Google Scholar]
- 17. Pohl P, Winstein C, Fisher B. The locus of age-related movement slowing: sensory processing in continuous goal-directed aiming. J Gerontol Psych Sci. 1996; 51B: 94–102 [DOI] [PubMed] [Google Scholar]
- 18. Meyer D, Smith J, Kornblum S, Abrams R, Wright C. Speed accuracy tradeoff in aimed movements: toward a theory of rapid voluntary action. In: Jeannerod M, ed. Attention and Performance XIII: Motor Representation and Control. Hillsdale, NJ: L.E.A. Publishers; 1990; 173–226 [Google Scholar]
- 19. Krebs H, Aisen M, Volpe B, Hogan N. Quantization of continuous arm movements in humans with brain injury. Proc Natl Acad Sci USA. 1999; 96: 4645–4649 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Rohrer B, Fasoli S, Krebs H, et al. Movement smoothness changes during stroke recovery. J Neurosci. 2002; 22: 8297–8304 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. von Hofsten C. Predictive reaching for moving objects by human infants. J Exp Child Psychol. 1980; 30: 369–382 [DOI] [PubMed] [Google Scholar]
- 22. Abrams RA, Pratt J. Rapid aimed limb movements: differential effects of practice on component submovements. J Mot Behav. 1993; 25: 288–298 [DOI] [PubMed] [Google Scholar]
- 23. Ketcham CJ, Seidler RD, Van Gemmert AW, Stelmach GE. Age-related kinematic differences as influenced by task difficulty, target size, and movement amplitude. J Gerontol B Psychol Sci Soc Sci. 2002; 57: P54–P64 [DOI] [PubMed] [Google Scholar]
- 24. Fradet L, Lee G, Dounskaia N. Origins of submovements in movements of elderly adults. J Neuroeng Rehabil. 2008; 5: 28 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Sainburg RL, Kalakanis D. Differences in control of limb dynamics during dominant and nondominant arm reaching. J Neurophysiol. 2000; 83: 2661–2675 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Wang J, Przybyla A, Wuebbenhorst K, Haaland KY, Sainburg RL. Aging reduces asymmetries in interlimb transfer of visuomotor adaptation. Exp Brain Res. 2011; 210: 283–290 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Davies AD. The influence of age on trail making test performance. J Clin Psychol. 1968; 24: 96–98 [DOI] [PubMed] [Google Scholar]
- 28. Tombaugh TN. Trail Making Test A and B: normative data stratified by age and education. Arch Clin Neuropsychol. 2004; 19: 203–214 [DOI] [PubMed] [Google Scholar]
- 29. Richman JS, Moorman JR. Physiological time-series analysis using approximate entropy and sample entropy. Am J Physiol Heart Circ Physiol. 2000; 278: H2039–H2049 [DOI] [PubMed] [Google Scholar]
- 30. Shinohara M, Li S, Kang N, Zatsiorsky VM, Latash ML. Effects of age and gender on finger coordination in MVC and submaximal force-matching tasks. J Appl Physiol. 2003; 94: 259–270 [DOI] [PubMed] [Google Scholar]
- 31. Arbuckle TY, Gold D, Andres D. Cognitive functioning of older people in relation to social and personality variables. Psychol Aging. 1986; 1: 55–62 [DOI] [PubMed] [Google Scholar]