Abstract
Many clinical trials fall short of their accrual goals. This can be avoided with accurate accrual prediction tools. Past researchers provide important methodological alternative models for predicting accrual in clinical trials. One model allows for slow accrual at the start of the study, which eventually reaches a threshold. A simpler model assumes a constant rate of accrual. A comparison has been attempted but we wish to point out some important considerations when comparing these two models. In fact, we can examine the reasonableness of a constant accrual assumption (simpler model) which had data 239 days into a three-year study. We can now update that and report accumulated from the full three years of accrual data and we can demonstrate that constant accrual rate assumption was met in this particular study. We will use this report to frame future research in the area of accrual prediction.
Keywords: prior elicitation, exponential, inverse gamma, Bayesian, sample size
1. Introduction
Zhang and Long (2010) provide an important methodological contribution to the literature for predicting accrual in clinical trials. They accurately describe their effort as an extension of Gajewski, Simon and Carlson (2008). An important parallel result was provided by Anisimov and Fedorov (2007), and was derived and published independently.
The model developed by Zhang and Long allows for slow accrual at the start of the study, which eventually reaches a threshold. The Gajewski et al. model is simpler in that it assumes a constant rate of accrual. Zhang and Long compare their methodology to Gajewski et al., but we wish to extend some important considerations when comparing these two models.
Zhang and Long assert that “in most real trial situations, the constant accrual rate assumption does not hold”. We have found evidence to the contrary. In fact, we can examine the reasonableness of a constant accrual assumption using data cited in Gajewski et al. which had data 239 days into a three-year study. We can now update that and report accumulated from the full three years of accrual data and we can demonstrate that constant accrual rate assumption was met in this particular study. We will use this report to frame future simulations in the area of accrual prediction.
2. Review of Gajewski et al. Model & Bayesian Runs Test
Before reporting the prediction results, we will review the model in Gajewski et al. (constant accrual). We also report here a new Bayesian runs test that we claim is an important diagnostic that should be computed for any accrual problem.
2.1 Review of Model
We wish to predict accrual after accruing m patients. Let w1, w2,…, wm represent the gap in time that each new patient is accrued. The goal of the accrual monitoring process is to develop a model for the yet to be observed waiting times Wm+1, Wm+2,…, Wn, where n is the actual patient accrual at the end of the trial.
We assume that wi|θ ~ exp(1/θ) where exp(·) is the exponential distribution and E(wi) = θ. In Gajewski et al. two priors were proposed: a flat prior and an informative prior. These were respectively θ ~ IG(k = 0,V = 0) and θ ~ IG(k = 175, V = 1.5), where IG(·) is the inverse gamma distribution. The 175 and 1.5 comes from answering two questions: (1) How long will it take to accrue n subjects? (2) On a scale of 1–10, how confident are in your answer to (1)? The answer to (1) provides T and the answer to (2)/10 provides P. In Gajewski et al. we have T =3 years and P=0.5. We arrive at our informative prior since k = nP and V = T P (the flat sets P = 0).
This conjugate prior results in alternative posteriors (flat- and informative-based) θ|w ~ IG(m, tm) and θ|w ~ IG(175 +m,1.5 +tm), where represents the time the last patient was accrued.
2.2. Review of Prediction Algorithm
The overall goal is to predict n with m gap times. First we predict the n − m data Wm+1,…, Wn. To achieve this, first we randomly select θ1 from the posterior distribution and then randomly select waiting time n − m random variables from Wm+1,1,…, Wn,1 from an exponential distribution with parameter θ1. This process is repeated for θ2, θ3, …, θb. The sum of observed and simulated waiting times, S b(n) = w1 + w2 + · · ·+ wm + Wm+1,b + · · · + Wn,b represents b estimates of the total duration of the clinical trial of size n. However, n is the unknown, so we use this process to obtain a posterior predictive sample size (np). Let T represent the time point at which the study ends (for the purposes here T = 3 years). We then compute partial sums S b(m+1), S b(m+2),… until the partial sum exceeds T. The values which represent the largest values where the partial sums do not exceed T, provides a realization of the predictive distribution of sample sizes. Replication of this process provides the posterior distribution nP. In this paper we will use observations in 1/12 year increments to explore the cross validated prediction of the true accrual (n = 265) for T = 3 years of accrual.
2.3. New Bayesian Runs Test
A Bayesian runs test, motivated by (Gelman, 2004, Chapter 6), tests the assumption of independence and identical distribution. This test is performed using all n = 265 gap data points. First, the number of runs of the observed gap data (w1, w2,…, wm) relative to posterior mean (θb) is calculated. This is repeated for posterior predictive gap data (W1,b, …, Wn,b) and posterior mean (θb).
3. Results of Prediction
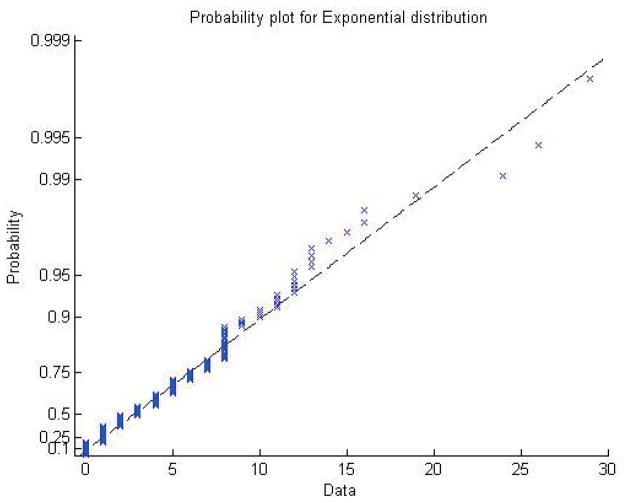
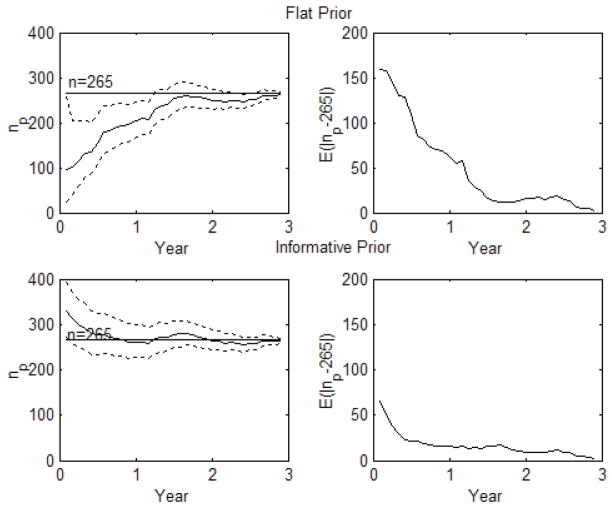
The probability of observed runs larger than predictive runs is 0.3986, suggesting independent and identically distributed gap data. A graphical examination of the accrual data (Figure 1) supports the use of exponential waiting times rather than a more complex waiting time distribution. We evaluate the prediction accuracy using the expected absolute deviation from the true accrual (n = 265), E(|np − 265|). Figure 2 displays the monthly prediction across 36 months using a non-informative prediction and an informative prediction. The first column displays the true three-year accrual (n = 265) and the point estimate with 95% prediction intervals using only the data up to that point. We can see that the informative prior does much better than the flat prior early on. Past the two-year point the flat and informative versions essentially agree. The second column displays the error across time as measured by E(|np − 265|). This can be described in terms of error %= E(|np − 265|)/265. Early in the process (first year) the error for the flat prior is above 20% (20–60%) whereas during that same timeframe the informative prior is always less than 20%. The true a prior defined informative simple prediction model (Exponential) was extremely useful for prediction in this clinical trial.
Figure 1.
Probability plot for Exponential distribution fit of the gap data after three years
Figure 2.
Monthly prediction across 36 months using a non-informative prediction with 95% intervals
4. Direction for Future Research
Our experience is that a constant rate of accrual seems quite reasonable. One difference, perhaps, between our experience and the experience of Zhang and Long is that we work in an academic setting with smaller trials, typically at a single location. We do not know if our experience, or the experience of Zhang and Long hold for most other researchers and suggest that data be collected in a systematic fashion to better understand accrual patterns in most clinical trials.
It is clear that a more complex model can be superior to a simpler model. We are in favor of more complex models in some settings, but a further assessment would note the drawbacks of a more complex model. First, specifying a prior distribution is far more difficult. Important elements in a complex model, such as the number of knots in the cubic spline (Zhang & Long, 2010) are not incorporated at all into the prior distribution, and those elements which are incorporated are too complex for the average researcher to fathom. Second, a more complex model is frequently inefficient with limited data. Limited data, of course, occurs early in the study. We believe that accurate early predictions are very important because small changes to the study at an early stage to improve a sagging accrual rate are easier and more efficient than changes made later in the trial. Third, a simple model of accrual has a closed form solution for the posterior predictive distribution that is intuitively plausible. The mean of the posterior predictive distribution, for example, is simply a weighted average of the data and the prior mean. A closed form solution also means that tracking accrual throughout a clinical trial could be conducted directly by the researcher on a daily or weekly basis, perhaps even on a simple spreadsheet.
Perhaps a compromise between complexity and simplicity is most appropriate. In fact, we are looking at a linear piecewise regression model as an alternative to a complex spline and a compromise between the two approaches. The piecewise approach would allow for slow early accrual rates (both a step and elbow).
Regardless of using simple, complex, or compromise we would like to propose guidance for evaluating the approaches with simulation studies. While it is impossible to conduct a simulation study that covers every possible research scenario, we believe a broad number of conditions need consideration to show scenarios where a simple model would perform well. Here are some suggested conditions:
performance under a constant accrual model. We believe that a simple model will perform well relative to the complex model in settings where a comlex model over fits the data.
performance early in the trial. We believe that a simple model will perform well relative to a complex model when only a small fraction of the accrual data is available. For example, in Zhang and Long, the simulation examined the performance of the model only when 30% and 60% of the accrual data was available. It would be very valuable to see the performance when only 5% or 10% of the accrual data was available.
performance under slow accrual rates. The average threshold accrual rate in the Zhang and Long simulation was 12 patients per day. While this may be normal in large multi-center trials, our experience with smaller academic center trials is that accrual rates of fewer than one person per day is more common. It would be instructive to test the cubic spline model with data where the Poisson counts are mostly zeros and ones.
performance under a weak, but not totally data driven prior. While we suggested an initial approach for getting a prior distribution using a simple question (how confident are you on a scale of 1 to 10), that prior was not intended to be plugged in thoughtlessly. Instead, that initial assessment would be used to examine the behavior of the predictive distribution. Review of that distribution would then lead the researcher to revise the prior accordingly. With a total sample size of 3,000 patients (much larger than the norm in an academic setting), P=0.5 constitutes an extremely strong prior. It says that after accumulating 1,500 patients, the prior and the data should still have equal weight. We would suggest that P=0.1 might be a more reasonable prior with such a large sample size, even when the researchers had strong prior information. In fact, all models need to be testing with a range of informative priors which needs to be balanced between two competing models of different complexity.
5. Conclusion
A simpler model (e.g. Gajewski et al.) can and should be used in many other settings. The availability of both a simple and a complex (e.g. Zhang and Long) model of accrual will allow researchers to choose the approach that best fits their needs. Carefully crafted simulation studies designed to better understand the tradeoffs between simplicity and complexity would be most beneficial.
Acknowledgments
This work was supported in part by DHA Supplementation and Pregnancy Outcomes 1R01 HD047315 (BJG & SEC) and Kansas Frontiers: The Heartland Institute for Clinical and Translational Research CTSA UL1RR033179 (BJG). The contents are solely the responsibility of the authors and do not necessarily represent the official views of the NIH
References
- Anisimov V, Fedorov VD. Modelling, prediction and adaptive adjustment of recruitment in multicen-tre trials. Statistics in Medicine. 2007;26(27):4958–4975. doi: 10.1002/sim.2956. http://dx.doi.org/10.1002/sim.2956. [DOI] [PubMed] [Google Scholar]
- Gelman A, Carlin JB, Stern HS, Rubin DB. Bayesian Data Analysis. 2. Washington DC: Chapman and Hall/CRC; 2004. [Google Scholar]
- Gajewski B, Simon S, Carlson S. Predicting accrual in clinical trials with Bayesian posterior predictive distributions. Statistics in Medicine. 2008;27(13):2328–2340. doi: 10.1002/sim.3128. http://dx.doi.org/10.1002/sim.3128. [DOI] [PubMed] [Google Scholar]
- Zhang X, Long Q. Stochastic modeling and prediction for accrual in clinical trials. Statistics in Medicine. 2010;29(6):649–658. doi: 10.1002/sim.3847. http://dx.doi.org/10.1002/sim.3847. [DOI] [PubMed] [Google Scholar]