Femtosecond Fiber Lasers Based on Dissipative Processes for Nonlinear Microscopy

Abstract

Recent progress in the development of femtosecond-pulse fiber lasers with parameters appropriate for nonlinear microscopy is reviewed. Pulse-shaping in lasers with only normal-dispersion components is briefly described, and the performance of the resulting lasers is summarized. Fiber lasers based on the formation of dissipative solitons now offer performance competitive with that of solid-state lasers, but with the benefits of the fiber medium. Lasers based on self-similar pulse evolution in the gain section of a laser also offer a combination of short pulse duration and high pulse energy that will be attractive for applications in nonlinear bioimaging.

I. Introduction

Optical techniques provide excellent imaging capabilities, with sub-micron spatial resolution, and are non-invasive. An overall goal of biomedical imaging is to obtain diagnostic or functional information about biological structures. The difficulty of acquiring high-resolution images of structures deep in tissue presents a major challenge, however, owing to strong scattering of light. As a consequence, optical imaging has been limited to thin (typically ~0.5 mm) samples or superficial tissue. In contrast, techniques such as ultrasound and magnetic resonance provide images of structures centimeters deep in tissue, with ~100-micron resolution. It is desirable to develop techniques that offer the resolution of optics with the depth-penetration of other techniques.

Since 1990, researchers have found that techniques based on ultrashort light pulses can offer some advantages over traditional approaches to optical imaging. Nonlinear-optical effects can be exploited through the high instantaneous power that can be obtained with an ultrashort pulse of even modest energy, while the average power remains low. The nonlinear microscopy that has had the most extensive impact is 2-photon microscopy [1]. New capabilities for three-dimensional visualization of dynamic cellular processes, microanalytical chemistry, and micropharmacology have become possible with multiphoton excitation. Multiphoton microscopy has been increasingly applied to cell biology and neuroscience [2,3,4]. Near-field enhanced multiphoton excitation [5] and multiphoton endoscopic imaging [6] have emerged, and further broadened the field. Overviews of nonlinear microscopy in the life sciences were written by Konig [7] and by Zipfel et al. [8]. Second-harmonic generation (SHG) imaging was first reported as early as 1978 [9], and the earliest biological investigations used SHG to understand the structure of rat-tail tendon [10]. Three-dimensional images of transparent specimens are produced by third-harmonic generation (THG) imaging [11,12]. High-resolution, nondestructive images of live neurons, their soma, and dendritic spines have been obtained without stains or markers by the use of THG. An important characteristic of all nonlinear microscopies is that the signal is generated only near the focal plane of the microscope objective, owing to the nonlinear dependence of the signal on the exciting fields. This facilitates sectioning, and limits bleaching and damage. Finally, the longer wavelengths generally used for nonlinear excitation (800–1200 nm) scatter less from tissue than the visible wavelengths typically used in confocal microscopy, and this may facilitate deeper imaging.

II. Status of lasers relevant to nonlinear microscopy

A crucial factor in the development of multiphoton fluorescence microscopy was the nearly-simultaneous discovery of Kerrlens modelocking in titanium-doped sapphire lasers [13,14]. Commercial Ti:sapphire lasers became available in the early 1990’s. Other solid-state laser media, such as Nd:glass [15], Yb:glass [16], and Yb: tungstate [17] have been developed in the past decade and find use in applications. For reviews see [17,18]. Without the development of commercial instruments, multiphoton microscopy would have been limited to laboratories of the few researchers who could design and construct femtosecond lasers. Of course, multiphoton and other nonlinear microscopies have grown dramatically and now constitute a significant subfield of microscopy. Raman microscopies [19,20] appear to be on the cusp of dramatic growth, and appropriate short-pulse sources will be needed for that growth to occur. Solid-state modelocked lasers are excellent laboratory tools, but instruments that are even more stable and reliable, more user-friendly, cheaper, and more compact will allow application in a much broader range of settings.

Standard Ti:sapphire lasers generate ~100-fs pulses between 700 and 1000 nm, with pulse energies of 10–20 nJ and average powers of 1–2 W. Picosecond-pulse operation is also possible. The range of wavelengths employed in nonlinear microscopy to date corresponds mainly to the tuning range of Ti:sapphire, supplemented by studies that employed Nd or Yb lasers, which emit near 1050 nm [21]. The knowledge base and technical infrastructure to support multiphoton and harmonic-generation microscopies within this spectral window are reasonably established.

Researchers are exploring a range of excitation wavelengths. Absorption and scattering of light by tissue are major factors in the optimal wavelengths for deep-tissue imaging. The optical properties of tissue vary and are not entirely understood, but some general trends are clear. Absorption by intrinsic molecules such as proteins, NADH, and hemoglobin dominates in the ultraviolet and visible ranges. Absorption by water increases rapidly for wavelengths longer than 1000 nm, and this dominates the absorption of tissue. On the other hand, scattering from tissue structures decreases rapidly at wavelengths longer than 1000 nm [22]. Studies of the optical properties of organs indicate minimal attenuation in the range 1200–1300 nm [23]. Accounting for absorption and scattering, Denk and co-workers [24] conclude that imaging to depths of 2–3 mm will be favorable around 1300 nm. In addition to deeper penetration of the exciting light, reduced attenuation of emitted fluorescence will improve signal collection, which is a serious concern in scattering samples [25].

The range 1000–1300 nm is also important for high-viability imaging of redder dyes and fluorescent proteins [26]. A variety of existing fluorescence indicators can be two-photon excited at wavelengths out to 1300 nm. Examples include indocyanine green (ICG), Cy7, Alexa 750, and red fluorescent proteins.

Solid-state lasers cannot directly reach wavelengths out to 1300 nm that appear to be so promising for deep-tissue imaging. Parametric oscillators pumped by solid-state lasers offer an effective way to reach this range, but they are expensive and complex, and require user expertise. Shared instruments distribute the cost burden among users, but such facilities are not always optimal for time-critical studies of living organisms. Thus, there is great motivation to develop short-pulse lasers for bioimaging that complement and extend the performance of existing instruments, but with robust, turnkey packages.

Fiber lasers offer major practical advantages. Most significantly,

• The waveguide medium avoids the need for careful alignment and ensures good spatial mode quality.

• Fiber laser systems are efficient and can be scaled to high average powers.

• Fiber lasers are naturally compatible with endoscopes and related instrumentation.

• Manufacturing costs benefit from economies of scale of telecommunications components.

Fiber-based femtosecond sources with parameters appropriate for nonlinear microscopies will never require re-alignment, and ultimately should be much cheaper and smaller than solid-state versions. These features will be most important for applications of short pulses outside of research laboratories. For example, there is interest in performing optical-coherence tomography and Raman microscopy in clinical situations. These features have motivated substantial research in the area of short-pulse fiber lasers and amplifiers, and it is not practical to review it all here. Several reviews of the field have been published [27–31]. Despite much progress, short-pulse fiber lasers still have limited impact in nonlinear microscopy, compared to solid-state lasers. This is largely due to the fact that fiber lasers have lagged well behind their solid-state counterparts in the key performance parameters -- pulse energy and duration. Fiber lasers and amplifiers can now generate high average powers, but it is a major challenge to control a short pulse of light owing to nonlinear propagation effects in the fiber.

As a result of recent advances, it is now feasible to design fiber lasers that will compete directly with existing solid-state lasers in nonlinear bioimaging applications. New concepts in pulse propagation allow the generation of energetic ultrashort pulses in fiber, with the added benefit of simplified design. This paper will summarize the main features of two pulse evolutions that occur in lasers with only normal-dispersion components. The all-normal-dispersion lasers counter 25 years of conventional wisdom regarding short-pulse generation. A major advance is the demonstration in 2006 of lasers based on a new kind of pulse, called a dissipative soliton. Dissipative solitons are stable with extremely high energy and peak power, and the absence of anomalous-dispersion segments substantially simplifies the design of lasers at 1000 nm wavelength. In the last year, normal-dispersion lasers have also been shown to support pulses that evolve self-similarly in the gain segment of the laser. Although the self-similar pulses rely critically on dissipative processes for their existence, they are not dissipative solitons. Initial indications are that the self-similar lasers will also offer attractive properties for nonlinear bioimaging.

III. HIGH-ENERGY FEMTOSECOND FIBER LASERS BASED ON DISSIPATIVE SOLITONS

The following capabilities and characteristics are desired in sources for multiphoton microscopy:

• Ideally, the source would be wavelength-tunable over as much of the range 700 to 1300 nm as possible, to overlap and complement existing sources.

• The pulse duration should be ~100 fs or less.

• The pulse repetition rate should be between 10 MHz and 500 MHz for microscopy, to achieve reasonable scan rates. The upper limit of 500 MHz is determined by typical fluorophore lifetimes of a few nanoseconds. For many applications, 10–100 MHz is fine.

• Peak power of 100 kW is desirable, to achieve good signal-to-noise ratios at fast scan rates. This implies a pulse energy of 10 nJ for a 100-fs pulse and an average power of 1 W for a 100-MHz repetition rate. Higher average power allows faster imaging, which helps reduce motion artifacts (breathing, heartbeat, etc.) when imaging animals. Part of the requirement for high energy is that most microscope optics are quite lossy, particularly at infrared wavelengths.

• Fluctuations in the power must be low (~1% or less) and the source should supply a high-quality gaussian beam with good pointing stability.

• The source should be compact and robust, offer turnkey operation, and require little maintenance.

• The technology must be practical and manufacturable.

The workhorse of ultrafast science, including nonlinear microscopy, is the Ti:sapphire oscillator. The 20-nJ and 100-fs pulses generated by a standard commercial Ti:sapphire laser set the standard for performance in nonlinear microscopy. Sources that consist of a fiber oscillator and one or more stages of amplification can reach this combination of pulse energy and duration. An advantage of the oscillator-amplifier configuration is that each stage can be designed for modest performance. On the other hand, amplifiers are fundamentally noisier than oscillators, and in general an oscillator-amplifier system will be more complex and costly than an oscillator. Even a 20-nJ fiber amplifier requires chirped-pulse amplification to avoid excessive nonlinear phase accumulation, e.g. Finally, the gain bandwidth is a greater limitation to the pulse duration from an amplifer than it is to the pulse duration from an oscillator.

In general, a femtosecond laser has segments or components with both normal and anomalous group-velocity dispersion (GVD). The net or average GVD can be normal or anomalous. When the net GVD is anomalous, the pulse-shaping is soliton-like as the nonlinearity balances the GVD in an average sense. Amplitude modulation is needed to initiate a pulse from noise, but the steady-state pulse is determined largely by phase modulations. This is the case in standard Ti:sapphire lasers, e.g. Since the demonstration (in 1984) that prism pairs can provide adjustable anomalous GVD with low loss, virtually all femtosecond lasers have included anomalous-dispersion segments or components. If the peak power is too high, the nonlinear phase cannot be balanced by dispersion, which causes the pulse to break into two (or more) pulses. Excessive nonlinear phase shift is the fundamental limitation to pulse energy in a mode-locked laser. Soliton fiber lasers are limited to ~0.1-nJ pulses, which is 10–100 times lower than the energy of solid-state lasers.

As the net GVD of a laser increases, the maximum stable pulse energy typically increases. Dispersion-managed solitons [32,33] form in lasers with net GVD near zero, and self-similar pulses [34] occur with large normal GVD. These increase the stable pulse energy to ~1 nJ and ~10 nJ, respectively. The self-similar laser just begins to compete with the performance of Ti:sapphire and other solid-state lasers. These pulse energies are for lasers constructed of standard single-mode fibers, which have core diameters of 5–10 micrometers.

In a laser with net normal GVD, solitons will not form. A process that promotes pulse formation when the dispersion is normal is illustrated in Fig. 1. If a frequency-swept (“chirped”) pulse is filtered, both the spectral and temporal wings of the pulse are absorbed, while the center of the pulse is preferentially transmitted. Thus, the pulse is sharpened. This mechanism was first demonstrated experimentally with a Ti:sapphire laser [35]. In 2006 Chong et al. proposed to exploit pulse-shaping based on chirping and filtering in a fiber laser without an anomalous-dispersion segment. The all-normal-dispersion (ANDi) laser indicated schematically in Fig. 2 generated femtosecond pulses with nanojoule energies, and numerical simulations showed that the filtering process indeed dominates the pulse-shaping [36]. The pulses can be dechirped to the transform-limited duration outside the laser, as is done with dispersion-managed solitons and self-similar pulses.

Fig. 1.

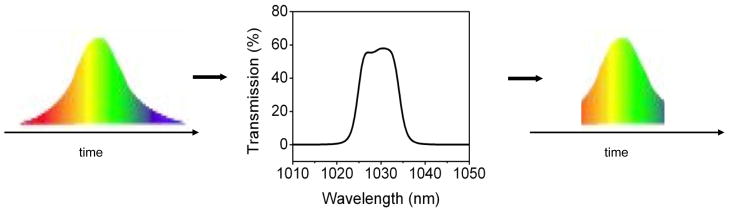
Pulse-shaping by filtering of a highly-chirped pulse.

Fig. 2.

Schematic diagram of normal-dispersion fiber laser. PBS: polarizing beam splitter, QWP: quarter-wave plate, HWP: half-wave plate, WDM: wavelength-division multiplexing coupler.

Established theories of modelocked lasers [37] failed to thoroughly describe the behavior or performance of the ANDi lasers, and this motivated the investigation of alternative models. Optical pulse evolution in the presence of the electronic nonlinearity, GVD, and dissipative processes can be modeled by a complex Ginzburg-Landau equation,

$$\frac{\partial a(z,t)}{\partial z}=ga(z,t)+\left(\frac{1}{\mathrm{\Omega }}-i\frac{D}{2}\right)\frac{{\partial }^{2}a(z,t)}{\partial t^2}+(\alpha +i\gamma ){\mid a(z,t)\mid }^{2}a(z,t)+\delta {\mid a(z,t)\mid }^{4}a(z,t)$$ (1)

with the terms on the right side corresponding to gain, gain dispersion, GVD, saturable absorption, self-phase modulation, and a quintic saturable-absorber term. This equation is sometimes referred to as the cubic-quintic Ginzburg-Landau equation (CQGLE). Renninger et al. found that an exact particular solution of the CQGLE models pulses in the normal-dispersion laser:

$$a(z,t)=\sqrt{\frac{A}{cosh(t/\tau )+B}}{e}^{-i\frac{\beta }{2}ln[cosh(t/\tau )+B]+i\theta z}$$ (2)

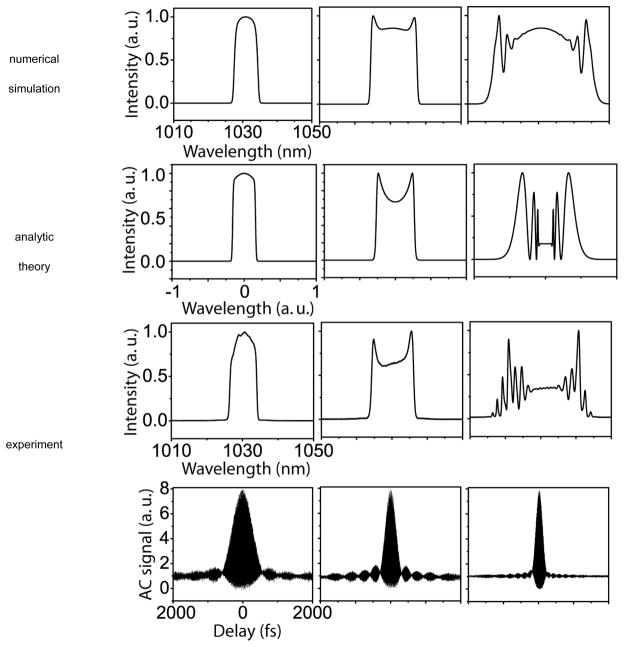
with A, B, τ, β, and θ real constants [38]. The agreement between the analytic theory and experiments is illustrated in Fig. 3. The key parameters in the design of an ANDi laser are the dispersion, which is determined by the fiber length, the filter bandwidth, and the nonlinear phase shift accumulated by the pulse as it traverses the cavity. With fixed fiber length and filter, the nonlinear phase shift can be varied through the pump power, and the corresponding variation of the power spectrum is shown. The analytic solution (Eq. 2) exhibits the qualitative features observed experimentally, with order-of-magnitude quantitative accuracy. The steep sides and “cat-ear” spectra are signatures of normal-dispersion operation. Numerical simulations are performed to refine the quantitative agreement between theory and experiment. Propagation in each segment or component of the laser is modeled by the appropriate terms of the wave equation (Eq. 1), and feedback and output coupling are added. A noise field is placed in the cavity, and the evolution is followed. If the field converges to a steady solution, the parameters are recorded. Numerically-simulated spectra are also shown in Fig. 3. The good agreement between analytic theory, numerical simulations, and experiments is evidence of our understanding of the ANDi lasers. The pulses represented by Eq. 2 balance amplitude and phase modulations, i.e., dissipation is central to their existence. The analytic pulse shape does not depend on position in the cavity (z), so the pulse is referred to as a dissipative soliton. Of course, the analytic model is an approximation, and we know from simulations and experiments that the pulse “breathes” to some extent as it traverses the cavity, with the pulse duration typically varying by a factor of 2 to 4. The analytic form represents some average of the breathing solution.

Fig. 3.

Theoretical spectra (top two rows) and measured spectra (third row). Fourth row: measured pulse autocorrelations. Nonlinear phase increases from left to right.

The dissipative-soliton lasers are promising for photophysical applications such as multiphoton microscopy because they support stable pulses with much higher energies than prior fiber lasers. This can be partially-understood intuitively: the large chirp reduces the peak power by stretching the pulse in the cavity. However, it is equally important that the dissipative solitons can accommodate large nonlinear phase shifts without distortion or splitting. An ordinary soliton accumulates no nonlinear phase; the nonlinearity is cancelled by the dispersive phase at each point in the propagation. A dispersion-managed soliton can accumulate a nonlinear phase shift Φ^NL ~ π/2. Dissipative solitons can be stable with Φ^NL ~ 20π [39], and this underlies pulse energies that are 1–2 orders of magnitude above those of soliton fiber lasers.

Kieu et al. exploited dissipative-soliton formation to demonstrate the first fiber laser to reach the performance of standard commercially-available Ti:sapphire lasers [40]. The laser was constructed according to the schematic of Fig. 1, but with double-clad fiber so that it could be pumped with a high-power laser diode. The construction of such a laser is shown in Fig. 4. The laser generated 80-fs pulses with pulse energies to 30 nJ and average power above 2 W. At the time, this was by far the highest average power for a short-pulse laser with an ordinary single-mode core, as well as the highest pulse energy.

Fig. 4.

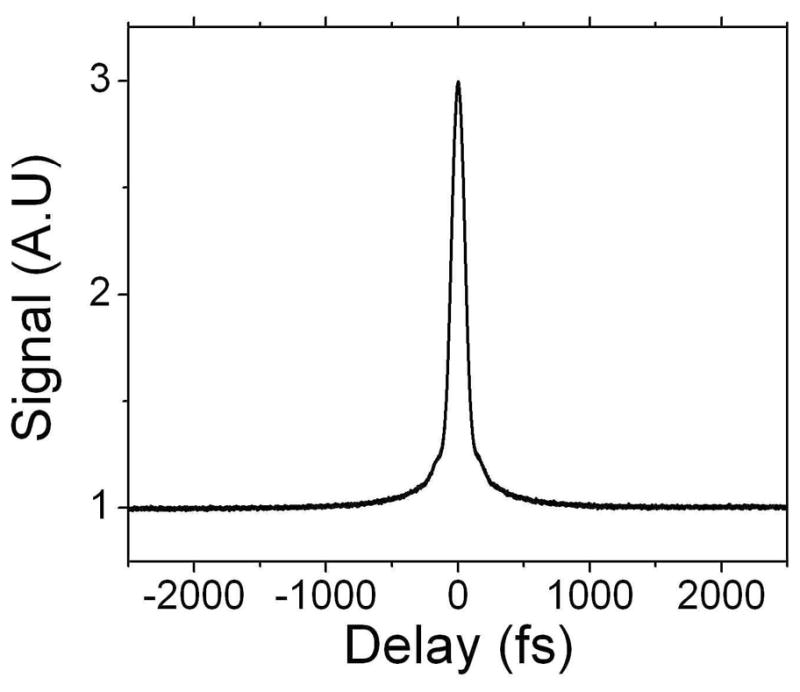
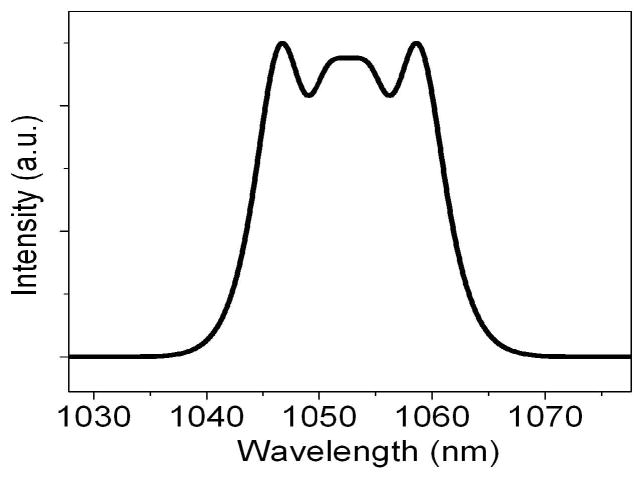
Top: Photograph of dissipative-soliton laser. The pump laser is not shown. Holes in the plate are one inch apart. Bottom: Spectrum (left) and autocorrelation (right) of 80-fs pulse from normal-dispersion laser with double-clad gain segment.

The performance of the dissipative-soliton laser in bioimaging applications is illustrated by images recorded with such a laser in the laboratory of Professor C. Schaffer at Cornell. A craniotomy was performed on an anesthetized mouse to grant optical access to the brain. The transgenic mouse expresses yellow fluorescent protein (YFP) on the Thy-1 promoter (line H), and this promotes YFP expression in a subset of pyramidal neurons in the mouse cortex. In addition to imaging the neurons, vasculature could be visualized by labeling with Texas Red dextran, which was injected intravenously. Some typical images of the mouse cortex at depths up to 900 μm are shown in Fig. 5.

Fig. 5.

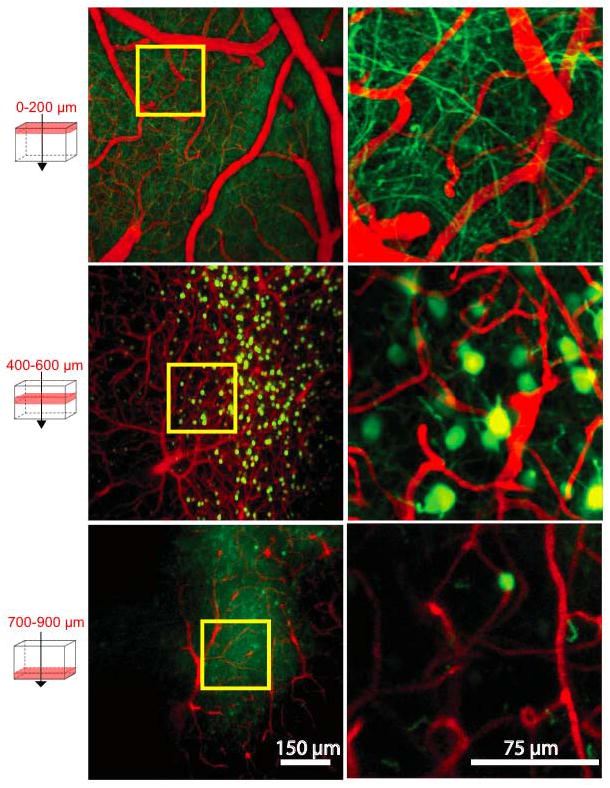
Two-photon fluorescence images recorded with dissipative–soliton laser for excitation. Subprojections of images of mouse cortex containing YFP labeled pyramidal neurons and Texas Red labeled vasculature at various depths below the cortical surface. The top row shows surface vessels and dendritic processes; the middle range shows arterioles, venules and capillaries as well as neuron cell bodies; the bottom row reveals capillaries and the remaining cell bodies as well as axonal processes. Yellow boxes (left) delineate areas of higher magnification (right).

IV. SCALING POWER AND ENERGY IN LARGE-MODE-AREA FIBERS

Although the pulse energy and average power of the dissipative-soliton lasers are quite similar to those of solid-state lasers, some applications will benefit from further increases. The maximum stable pulse energy is proportional to the mode-field area of the fiber, and there are major efforts to develop fibers with larger core areas. Photonic-crystal fibers (PCFs) with 40-micrometer core diameter are commercially available, e.g. Lefrancois et al. built a laser following the design of Kieu [40], but with PCF replacing the ordinary gain fiber [41]. The dissipative-soliton laser with large-mode-area PCF could theoretically achieve 300-nJ pulse energy, which would correspond to 25-W average power. The pulse energy of the PCF laser was limited by the available pump power to 100 nJ, with ~100-fs pulse duration. A peak power of close to 1 MW was achieved, with an average power of 8 W. By use of a rigid photonic-crystal rod with an even larger mode area, 500-nJ pulses were obtained from a dissipative-soliton laser [42].

Lasers constructed with photonic-crystal fiber and photonic-crystal rod sacrifice some of the benefits of optical fiber. They are not directly compatible with standard fusion splicing, and they cannot be coiled tightly on spools. For core diameters below 20 μm, PCF can be spliced to step-index fibers with 0.3–1 dB loss. This is much higher than the loss of a splice between standard fibers, but still tolerable for most fiber lasers. Splicing of large-mode-area PCF to a step-index fiber requires tapering the PCF while minding the microstructure and then fusing with a filamentary splicer. Thus, it is a more specialized procedure. Splicing and handling of PCF will presumably become more routine as the fibers enter a wider range of applications, so designs based on large-mode-area PCF may well become practical in the future.

A standard approach to the design of short-pulse fiber amplifiers is to create a large-area mode by isolating the lowest-order mode of a fiber designed for multimode operation. By coiling the fiber, the higher-order modes are “stripped off” in propagation because they suffer higher loss than the lowest-order mode [43]. The higher-order-mode content can be reduced to levels that allow nearly diffraction-limited beams to be generated. Motivated by the successes in amplifiers, Ding and co-workers performed a study of normal-dispersion lasers constructed with multimode fiber. These workers found that lasers constructed with coiled multimode fiber consistently exhibit multi-pulsing at energies well below those achieved with the photonic-crystal fibers [44]. A simplified model of a laser with two transverse modes is consistent with the experimental observations. A mode-locked laser is evidently very sensitive to the higher-order modes, and this rules out the use of the most practical way to increase the mode area in a laser.

A new class of fiber that offers large mode area while being compatible with standard fiber integration techniques is under development. Chirally-coupled-core fibers suppress higher-order modes by selectively “siphoning” them off through a small secondary core that is wrapped in a helix around the main core [45]. Lefrancois and co-workers showed that the pulse energy in a dissipative-soliton laser constructed with chirally-coupled core fiber scales as expected [46]. This is a significant observation because it shows that the chirally-coupled-core fiber rigorously holds the lowest-order mode. Pulses as short as 100 fs were generated, and longer pulses were generated with energies up to 40 nJ. Therefore, the technologies needed to build femtosecond fiber lasers at the 100-nJ and 10-W level have been demonstrated.

V. WAVELENGTH TUNABILITY

Fiber gain media do not offer the broad wavelength tunability possible with Ti:sapphire. With Yb-doped fiber, femtosecond pulses with center wavelengths between about 1020 and 1080 nm can be generated with reasonable energy. The pulse energies and peak powers achieved by dissipative-soliton lasers with large-mode-area fibers are higher than needed for standard 2-photon fluorescence microscopy, but they may be valuable for some forms of nonlinear imaging. More significantly, these pulse energies would allow efficient nonlinear conversion to other wavelengths, which should enable watt-level sources of femtosecond pulses tunable over the range 700–1300 nm.

The 2-W laser by Kieu et al. [40] can be frequency-doubled to excite a parametric oscillator based on quadratic nonlinear media such as barium borate or lithium niobate. This would yield pulses tunable from 750 to 850 nm and around 1300 nm, e.g., but the benefits of fiber would only be accrued by the oscillator. Fiber-based frequency-conversion stages are desired.

Two processes are natural candidates for fiber-based frequency conversion. Cerenkov radiation and four-wave mixing (4WM). Both Cerenkov radiation and 4WM rely on kinds of phase-matching, which in turn depends on the group-velocity dispersion of the fiber. PCFs allow engineering of the dispersion curves, which is a new degree of freedom in controlling these processes. PCFs can be endlessly single-mode, which implies that all frequencies involved in nonlinear interactions will have good mode overlap, even over a wide range of generated frequencies. Fiber format naturally enhances the interaction length. However, longer interaction lengths eventually tend to favor processes such as stimulated Raman scattering and self-phase modulation, which do not suffer from the group-velocity mismatch that accompanies the interaction of widely-spaced frequencies and which degrades that interaction.

A. Cerenkov Radiation

When an ultrashort pulse is injected into an anomalous dispersion fiber, it forms a higher-order soliton that can split under perturbations. During fission, soliton compression occurs, and this pushes part of the spectral energy into the normal dispersion regime, where dispersive waves form. Phase-matching can resonantly channel the dispersive energy into a narrowband Cerenkov pulse that is so named because it propagates slower than the soliton. Cristiani et al. demonstrated the generation of visible pulses from femtosecond pulses at 800 nm [47]. Tu et al. have demonstrated tunability of the scheme: 150 nm of tunability in the visible is possible by pumping over the 800–1000 nm range with a Ti:Sapphire laser [48]. The pulse energy is modest (~1 nJ) with this scheme, but that will be adequate for some applications. It will be interesting to pursue this approach with a high-energy fiber oscillator, and to determine if fibers can be designed to reach higher-energy and shorter Cerenkov pulses.

B. Four-wave mixing

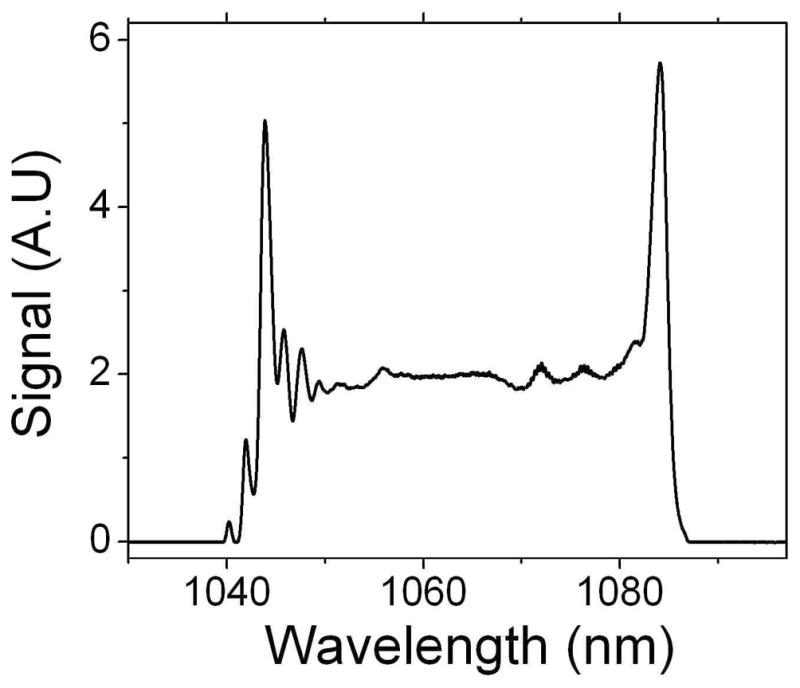
Two pump photons are annihilated, and signal and idler photons are created, in 4WM. In a fiber with normal dispersion, 4WM can be phase-matched by higher-order dispersion in dispersion-engineered media such as PCFs [49]. This produces sidebands that grow narrower and more widely spaced as the pump is shifted away from the zero-dispersion wavelength. The 4WM peak conversion wavelengths as a function of pump wavelength are shown in Fig. 6 for a commercially-available PCF as an example. Tunability from 750 to 850 nm can be achieved by changing the pump wavelength from 1030 to 1050 nm, which is feasible. 4WM exeriments will likely have to be done with short fibers, owing to the group-velocity mismatch between short pulses at different frequencies. In long fibers, stimulated Raman scattering and continuum generation will compete with the desired 4WM process. Thus, there will be tradeoffs between pulse duration and efficiency.

Fig. 6.

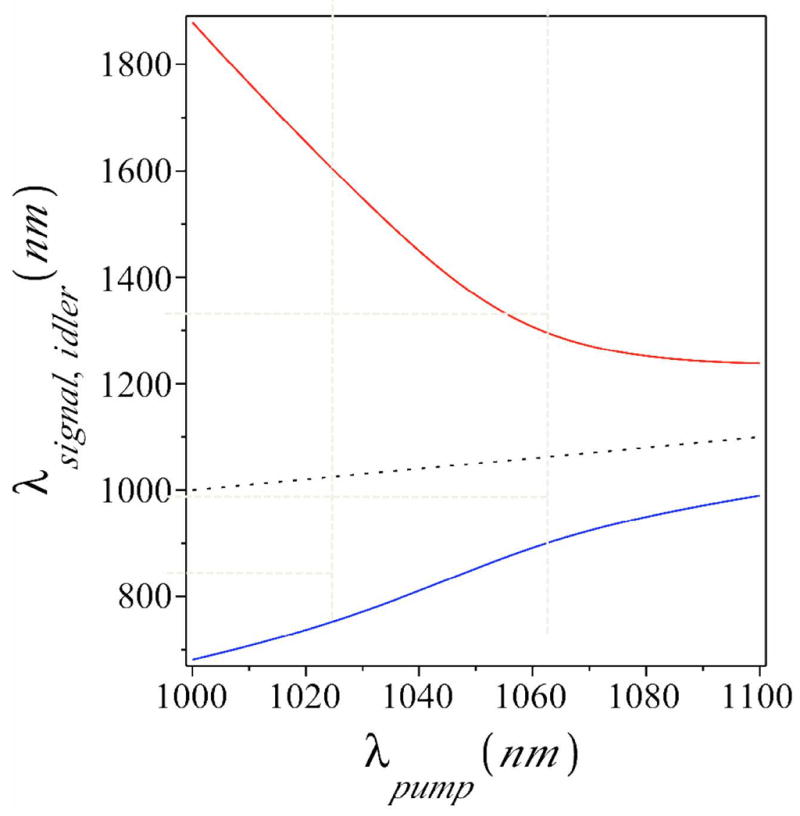
Peak conversion wavelength for 4WM in LMA-5 at 10 kW peak power.

To summarize this section, promising routes to fiber-based wavelength converters for Yb fiber lasers exist based on Cerenkov radiation and four-wave mixing. An all-fiber source of tnable femtosecond pulses would be extremely attractive. However, such sources do not exist currently, and some research will be required to reach the performance levels needed by nonlinear microscopies.

VI. TOWARD ALL-FIBER INSTRUMENTS

The initial demonstrations of new pulse evolutions are performed with experimental arrangements such as the one in Fig. 4 above. Bulk optical components such as beam splitters, filters, and wave plates are employed, to allow variation of the cavity parameters and study trends in the pulse evolution and performance. The setup is intended to be a physics experiment more than a useful instrument. After the desired pulse propagation is established, some effort is made to design and construct all-fiber versions of the lasers. It is worth mentioning that lasers constructed as in Fig. 4 are quite useful laboratory tools. Unattended in an ordinary laboratory environment with temperature fluctuations of a few degrees, they typically operate for many days before requiring minor adjustment. Soliton lasers that are fiber-integrated and even environmentally stable are available commercially. An important task for current and future development will be to create all-fiber, and eventually, environmentally-stable, versions of the normal-dispersion lasers.

The elimination of an anomalous-dispersion segment simplifies the construction of dissipative-soliton lasers. The key components for dissipative-soliton lasers will be the filter and the saturable absorber. A filter can easily be constructed in fiber format, because a fiber coupler is wavelength-dependent. A crucial component in any modelocked laser is a saturable absorber, which is essential to starting and stabilizing the laser. A fiber-format saturable absorber is needed. Semiconductor saturable-absorber mirrors (SESAMs) have found wide success in solid-state lasers [50], and some success in low-energy fiber lasers [51,52]. In our lab we consistently find that SESAMs damage in high-power fiber lasers. Kieu et al. have recently demonstrated fiber-format saturable absorbers based on tapered fiber embedded in carbon nanotubes [53]. The evanescent field interacts with the nanotubes (Fig. 7) over several millimeters of length, so the absorption and any heat are distributed, and this may mitigate problems with damage. Soliton fiber lasers with this kind of saturable absorber and Er (1550 nm) [53] or Tm (1900 nm) [54] gain media have been demonstrated successfully. A dissipative-soliton laser based on Yb-doped fiber generates 230-fs and 3-nJ pulses, for an average power of 150 mW [55]. However, the saturable absorbers for 1000-nm operation decline in performance with operation. The carbon nanotubes apparently photodegrade when excited by 1000-nm light. Thus, there is currently not a reliable fiber-format saturable absorber for Yb-doped fiber lasers. The potential of these lasers for applications can be appreciated from Fig. 8, which shows an all-fiber dissipative-soliton laser. The goal of this direction of research will be to construct integrated, all-fiber devices that retain the performance of the lasers constructed with bulk optical components.

Fig. 7.

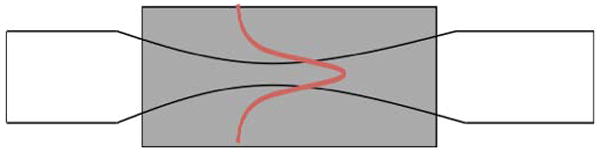
Schematic and photo of a carbon nanotube saturable absorber. The grey area represents the carbon nanotubes.

Fig. 8.

Photograph of dissipative-soliton laser assembled from fiber components. The pump laser is not shown.

A second issue that must be addressed is control of the polarization of the electric field in the laser. A polarization controller (black component at the right in the photo in Fig. 8) stabilizes the initial all-fiber dissipative-soliton laser. The need for this likely arises from birefringence introduced in the fabrication of the fiber filter. Ultimately, it will be desirable to construct the fiber lasers with polarization-maintaining fiber, which would yield instruments that are unaffected by mechanical or thermal perturbations.

The development of a fiber-format saturable absorber that can tolerate high pulse energy (>10 nJ) and average power (1 W) will have major impact, particularly if it can be implemented in polarization-maintaining fiber. Such a component will enable the construction of monolithic, rugged, high-performance lasers that will be very attractive for biophotonics applications.

In some situations an oscillator-amplifier system may be preferable to a high-performance oscillator. Even then, a simple, robust, high-energy oscillator will always be desired as the first stage. The chirped output of a dissipative-soliton laser can simplify a fiber amplifier. Thus, the dissipative-soliton lasers should be attractive in either case.

VII. AMPLIFIER SIMILARITON LASERS

An optical pulse with a parabolic intensity profile and a linear frequency chirp will avoid wave-breaking despite the presence of nonlinearity [56]. Such a pulse evolves in a self-similar fashion; it is always a scaled version of itself. The name “similariton” was coined to convey the particle-like nature of self-similar pulses. Similaritons are of major interest in short-pulse generation and amplification, because they essentially convert nonlinear phase shifts to linear phase shifts. The formation of similaritons was first demonstrated in a single-pass fiber amplifier [57]. Self-similar propagation in passive fiber was exploited by Ilday et al. to demonstrate a high-energy laser with large normal dispersion [34]. Oktem et al. first reported a laser based on self-similar evolution of a pulse in the amplifier [58]. After amplification, the pulse entered an anomalous-dispersion segment, where it became a soliton.

Renninger proposed that the formation of amplifier similaritons might be stabilized by strong spectral filtering in an all-normal-dispersion laser [59]. Such a laser (indicated schematically in Fig. 9) is simply an ANDi cavity with a narrow spectral filter. The filter is implemented with a diffraction grating and a fiber collimator functioning as “spectrometer slit.” Numerical simulations of a simplified cavity that contains only the gain fiber, a saturable absorber based on nonlinear polarization evolution (NPE), and a filter do exhibit stable solutions with the desired evolution. The spectral and temporal profiles of the pulse both broaden in the gain fiber, before being cut drastically in the filter (Fig. 10). The evolution of the spectrum is particularly remarkable: the spectral width expands and contracts (or breathes) by a factor of 5. The output pulse does have a parabolic profile (Fig. 10), while the spectrum has a characteristic structure that lacks the steep sides of the dissipative solitons.

Fig. 9.

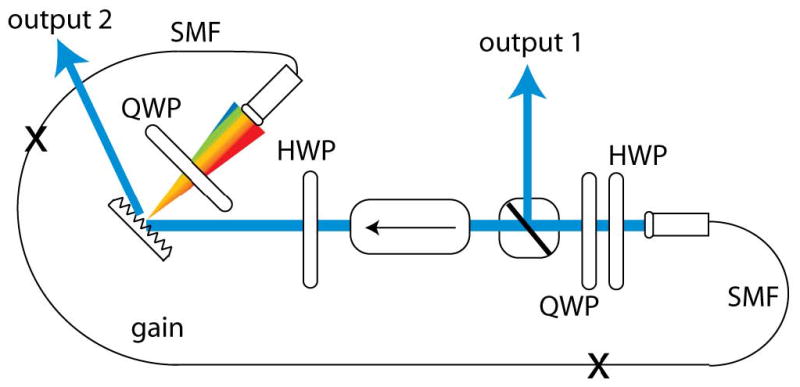
Schematic of laser designed to support self-similar evolution in its amplifier.

Fig. 10.

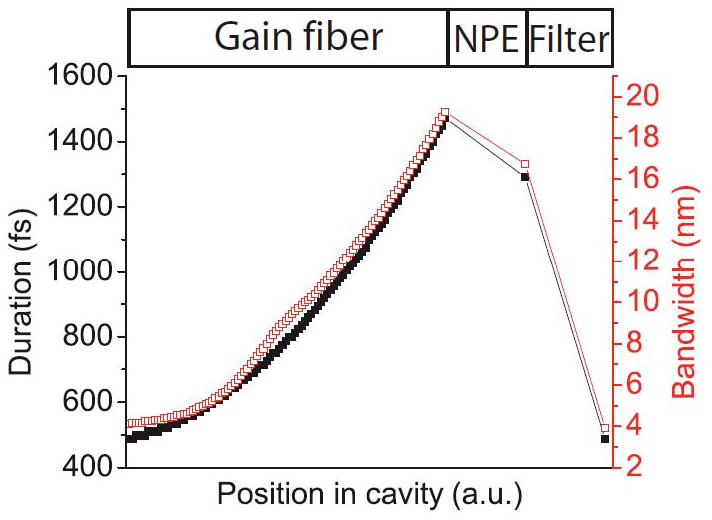
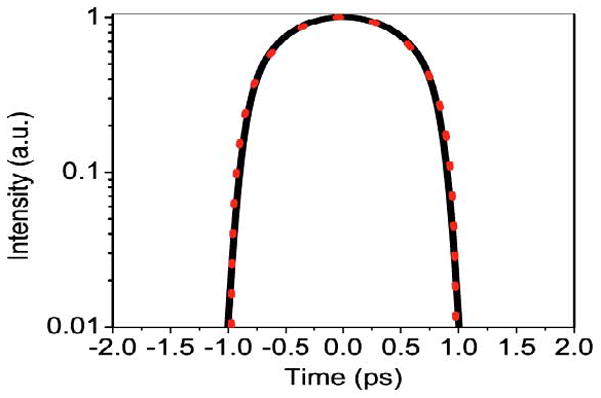
Results of numerical simulations of laser designed to have self-similar pulse evolution in its amplifier. Top: variation of pulse duration and bandwidth in amplifier-similariton laser. Bottom left: Output pulse (line) from simulation, along with parabolic pulse (symbols) for comparison. Bottom right: power spectrum of emitted pulse.

Experiments verify the existence of the amplifier-similariton evolution in an ANDi laser. The output labeled “output 2” in Fig. 8 should be compared to the numerical simulations, which model the pulse that is transmitted by the output coupler (and is thus kept in the cavity at that point). The agreement between theory and experiment (Fig. 11) is very good. In addition to the parabolic pulse in the cavity, the output can be dechirped to produce clean 65-fs pulses.

Fig. 11.

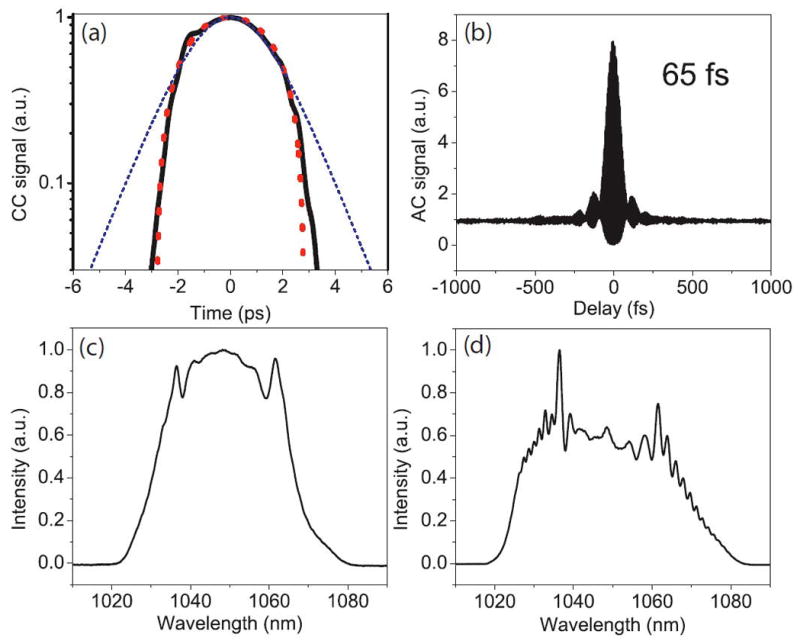
Experimental results that demonstrate formation of amplifier similaritons in the laser. Top: chirped parabolic output pulse and measured power spectrum. Bottom: autocorrelation of pulse from output 1.

The strong spectral and temporal breathing in the amplifier-similariton laser distinguish the pulses from dissipative-solitons, which exhibit only weak breathing. The characteristic power spectra with relatively–smooth shapes contrast with the steep-sided spectra of dissipative solitons. Amplifier similaritons are nonlinear attractors in fiber with gain – an input pulse will asymptotically approach the similariton solution if the fiber is long enough and the input is close enough to the asymptotic solution. The nonlinear attraction in the gain fiber is a remarkable feature. It implies that the pulse can be perturbed significantly in other sections of the laser, and will always be “pulled back” to the desired solution in the gain segment. It will be interesting to see if amplifier-similariton lasers exhibit enhanced stability as a consequence of the nature of the evolution.

The possibility of generating very short, high-energy pulses through similariton evolution is exciting for nonlinear imaging applications. In a first demonstration, Bai et al. constructed an amplifier-similariton laser with double-clad fiber with 10-micrometer signal core. The self-similar evolution was confirmed, and stable pulses with up to 22 nJ were generated by the laser [60]. The pulses were diagnosed and dechirped by the use of multiphoton intrapulse interference phase scan (MIIPS), which yielded 42-fs and 10-nJ pulses. For comparison, it will be very difficult to generate such short, energetic pulses via dissipative-soliton evolution. The resulting 250-kW peak power is among the highest achieved by a femtosecond fiber laser constructed with single-mode fiber, and will be quite attractive for nonlinear microscopy. These early results bode well for the impact of amplifier-similariton lasers in biomedical applications.

VIII. Conclusion

The pulse evolutions that occur in all-normal-dispersion fiber lasers offer a number of attractive features for applications in nonlinear microscopy. Dissipative solitons, which can be thought of intuitively as pulses that balance chirping and filtering, can tolerate unprecedented nonlinear phase shifts, which translate directly into higher stable pulse energies. The dissipative-soliton lasers generate femtosecond pulses with the highest energies from a fiber laser. As a practical point, the dissipative-soliton fiber lasers equal, and even exceed, the energies of available 100-fs Ti:sapphire lasers. Further increases in the stable pulse energy should be expected. In contrast to the nearly-static evolution of dissipative solitons, the formation of similaritons in the amplifier of a laser produces strong spectral and temporal breathing. The use of narrow (<4 nm) spectral filters stabilizes this evolution, which is independent of the global or average cavity parameters. The output of an amplifier-similariton laser has a smooth spectrum, and can be dechirped to a transform-limited pulse with duration below 60 fs. Energetic pulses as short as 42 fs have been produced in initial experiments. Instruments based on these new pulse evolutions will be compact and reliable, with significant commercial potential and ultimately, telecom-grade construction. The high pulse energies available from these new lasers will facilitate the development of fiber-based frequency-conversion stages, which will provide wavelength tuning. We expect such instruments to have major impact in nonlinear microscopy and other biomedical applications of ultrashort pulses.

Biography

Frank W. Wise received a B. S. degree from Princeton University, an M. S. degree from the University of California, Berkeley, and a Ph. D. degree from Cornell University. Since 1989, he has been on the faculty in the Department of Applied Physics at Cornell.