Abstract
Background: No consensus exists about which cutoff point should be applied for serum vitamin B-12 (SB-12) concentrations to define vitamin B-12 status in population-based research.
Objective: The study's aim was to identify whether a change point exists at which the relation between plasma methylmalonic acid (MMA) and SB-12 changes slope to differentiate between inadequate and adequate vitamin B-12 status by using various statistical models.
Design: We used data on adults (≥19 y; n = 12,683) from NHANES 1999–2004—a nationally representative, cross-sectional survey. We evaluated 6 piece-wise polynomial and exponential decay models that used different control levels for known covariates.
Results: The MMA-defined change point for SB-12 varied depending on the statistical model used. A linear-splines model was determined to best fit the data, as determined by the approximate permutation test; 3 slopes relating SB-12 and MMA and resulting in 2 change points and 3 subgroups were shown. The first group (SB-12 <126 pmol/L) was small and had the highest MMA concentration (median: 281 nmol/L; 95% CI: 245, 366 nmol/L; n = 157, 1.2%); many in this group could be considered at high risk of severe deficiency because combined abnormalities of MMA and homocysteine were very frequent and the concentrations themselves were significantly higher. The highest SB-12 group (SB-12 >287 pmol/L; n = 8569, 67.6%) likely had adequate vitamin B-12 status (median MMA: 120 nmol/L; 95% CI: 119, 125 nmol/L). The vitamin B-12 status of the sizable intermediate group (n = 3957, 33%) was difficult to interpret.
Conclusions: The 3 distinct slopes for the relation between SB-12 and MMA challenges the conventional use of one cutoff point for classifying vitamin B-12 status. In epidemiologic research, the use of one cutoff point would fail to separate the small, severely deficient group from the intermediate group that has neither normal nor clearly deficient vitamin B-12 concentrations (ie, unknown vitamin B-12 status). This intermediate group requires further characterization.
INTRODUCTION
Serum vitamin B-12 (SB-12)5 concentrations directly reflect circulating vitamin B-12 concentrations, whereas methylmalonic acid (MMA) accumulates in the absence of adequate vitamin B-12 concentrations and is considered a “functional” indicator of vitamin B-12 status (1, 2). Each of these biomarkers has limitations in sensitivity and specificity. To minimize these limitations, some experts have suggested the use of both a direct measure and a functional measure to assess vitamin B-12 status in population-based studies (3–7). Previously, using this combined biomarker approach with commonly used cutoff points for adults in NHANES, we determined that ∼1% of US adults had both a low SB-12 and a high plasma MMA concentration, which indicated a suboptimal vitamin B-12 status (8).
A critical step in defining a population's vitamin B-12 status is the selection of applicable cutoffs (3). Recently, a roundtable of experts identified uncertainties in the published cutoff points for biomarkers of vitamin B-12 status (7). Indeed, when this group applied different cutoff points that are commonly used in the scientific literature to each biomarker in isolation, the prevalence of low SB-12 concentrations ranged from 3% to 26%, and the prevalence of high MMA concentrations ranged from 2% to 6% (8).
The purpose of the current analysis was to examine whether a change point exists at which the relation between SB-12 and MMA concentrations changes the slope to help differentiate between adequate and inadequate vitamin B-12 status (9, 10). We used various statistical models with data on a large NHANES population after controlling for confounding variables that are known to affect these biomarker measurements but are not related to vitamin B-12 status.
SUBJECTS AND METHODS
NHANES
NHANES is a nationally representative, cross-sectional survey of the noninstitutionalized US population that uses a complex, stratified, multistage probability cluster sampling design. The National Center for Health Statistics of the CDC collects the NHANES data. Survey participants are first interviewed in their homes; at this interview, demographic information, data on dietary supplement use, and some health-related data are collected. Participants then complete a standardized physical examination, 24-h dietary recall, and a blood draw in a mobile examination center ∼1–2 wk later.
Analytic sample
For this study, we combined data from NHANES 1999–2000, 2001–2002, and 2003–2004 (n = 31,126). We excluded data on anyone younger than 19 y (n = 14,942); those with only interview data (ie, lacking mobile examination center data, n = 1160); lactating (n = 145) and pregnant (n = 802) females; and those with missing MMA (n = 928), SB-12 (n = 114), or creatinine (n = 107) data. We also excluded those with SB-12 concentrations greater than the 99th percentile (>1265 pmol/L; range: 25–148,935 pmol/L; n = 135). Extraordinarily high SB-12 concentrations almost always reflect phenomena that are unrelated to vitamin B-12 metabolism or status and can exert substantial influence over the change point, leading to biased models. Finally, we excluded those with an estimated glomerular filtration rate (eGFR) <30 (n = 116) because impaired kidney function increases MMA and vitamin B-12 concentrations independently of vitamin B-12 status (see Supplemental Table 1 under “Supplemental data” in the online issue). The final analytic sample size was 12,683. Written informed consent was obtained from all participants; the survey protocol was approved by the Research Ethics Review Board of the National Center for Health Statistics. Interview and examination response rates for each survey year are publicly available (11).
Biochemical methods
NHANES 1999–2004 measured SB-12 concentrations with the use of the Quantaphase II radioassay (BioRad). Plasma total homocysteine (tHcy) concentrations were measured by using a fluorescence polarization immunoassay reagent kit (Abbott Laboratories) (12) and plasma MMA concentrations by gas chromatography–mass spectrometry after cyclohexanol derivatization of the extracted MMA. NHANES 1999–2000 measured serum creatinine by using the Jaffe method with the Hitachi 917 multichannel analyzer, and NHANES 2001–2004 used the Jaffe rate method (kinetic alkaline picrate) with the Beckman Synchron LX20 modular chemistry analyzer. We adjusted serum creatinine data for NHANES 1999–2000 using the equation 0.147 + 1.013 × uncorrected serum creatinine (mg/dL), as the analytic note recommends (13). High-sensitivity C-reactive protein was measured by latex-enhanced nephelometry on a BN II nephelometer (Dade Behring). Details and documentation for each of these methods and the biomarker coefficients of variations for each survey year are publicly available on the NHANES website (14–16).
Vitamin B-12 exposure
Dietary supplement information was collected via the NHANES Dietary Supplement Questionnaire, which determines each participant's intakes of vitamins, minerals, herbs, and other dietary supplements over the past 30 d. The average daily intake of vitamin B-12 from all supplements was calculated (17). Six participants in our sample had very high intakes of supplemental vitamin B-12; because this might have been a result of the metric in which the dose was provided (mL), we are uncertain whether the data on their intake are reliable. We Winsorized these 6 observations to the next highest value of 3000 μg.
Data on one 24-h dietary recall are available for each participant for 1999–2002 and on two 24-h dietary recalls for 2003–2004. We used the vitamin B-12 intakes from the first 24-h dietary recall from 2003 to 2004; if day 1 24-h dietary recall data were missing but day 2 data were available, we used the day 2 data. We report intake data as means or medians rather than the prevalence of low values because of the inability to correct for within-person variability. Because of limitations in the food-composition databases, estimates of vitamin B-12 intake in 1999–2004 did not account for bioavailability differences between naturally occurring and added vitamin B-12 sources (18). We combined data on the average daily intake of vitamin B-12 from supplemental sources with the daily estimates of vitamin B-12 intake from foods to reflect total vitamin B-12 exposure. Dietary data were available for 12,124 participants.
Statistical models and analysis
We estimated descriptive statistics of the sample by using SAS-Callable Sudaan (version 9.3) and used the examination survey weights to make the estimates reflective of the US adult population. We determined statistical comparisons by using diffvar statements in PROC DESCRIPT. We log transformed any nonnormal variables before statistical comparison. The median MMA concentrations, tHcy concentrations, and dietary vitamin B-12 intakes might be more descriptive of each group than the mean values, because some very high values skewed the means and, thus, their interpretability. ORs of having elevated MMA (>271 nmol/L) or tHcy (>13 nmol/L) were derived via PROC RLOGIST in Sudaan. Statistical significance was set at P < 0.05
All models
To reduce heteroscedasticity and skewness of the distribution, we selected the log-transformed MMA concentration as the dependent variable after examining several possible transformations for both MMA and SB-12. All models were examined with several covariates that were significant predictors of log-MMA in stepwise regression models; the covariates that we examined included eGFR, age, ethnicity, dietary and supplemental intakes of vitamin B-12, use of antibiotics, session of blood collection, hours of fasting, and C-reactive protein concentrations. We examined all models using 3 tiers of adjustment. Tier 1 was unadjusted, tier 2 was minimally adjusted (ie, for eGFR, hours of fasting before the blood draw, and age), and tier 3 was maximally adjusted (ie, for all covariates). We found no appreciable differences in the models based on the tier level of adjustment that we used. We therefore present results using the minimally adjusted models, which controlled only for the most relevant factors. Use of these models maximized the df and therefore enhanced statistical reliability while ensuring that adjustments for the effects of known biological covariates were made.
The first step was to use locally weighted regression or the locally estimated scatterplot smoothing (LOESS) technique. LOESS is an unweighted nonparametric scatterplot of the data to define the optimal shape of the function to summarize the nature of the relation for the 2 biomarkers (19, 20). Once confirmed by the LOESS model, we used 2 broad types of modeling procedures (exponential decay and piece-wise polynomial) to best “mimic” the shape of the function of the relation of SB-12 and log-MMA concentrations. For both of these model types, we accounted for the multistage sampling scheme and sampling weights by using an adaptation of the SVY module in the STATA statistical package (version 12; StataCorp). The change point estimates were first determined for each model type; the 95% CIs around the change point estimates were derived by a bootstrapping technique that accounted for the survey design. The bootstrap method for complex survey data are implemented by the bsweights command in STATA (21).
Exponential model
Exponential models, sometimes called nonlinear exponential or exponential decay models, are ideal for working with biological phenomena because they permit modeling of the nonlinear relation between 2 variables and estimations of the rate of change of one variable (y) as a function of another (x) while confounding factors are accounted for. Specifically, the following model was fit to our data:
where A, B, and C are nonnegative variables to be estimated. Notice that this exponential curve approaches a plateau equal to the variable A for large values of vitamin B-12. Thus, for the exponential model in this analysis, the “no change” point was defined as the smallest value of SB-12 for which log-MMA is not significantly different from its plateau value under the model. Precisely, the variable A was estimated along with the corresponding SE by using the least-squares method. The point of “no-change” was determined as that value of vitamin B-12 for which log MMA, under the model, equals the upper limit of the 95% CI of A. CIs for the “no change” point were calculated by the bias corrected bootstrap approach, accounting for design effects.
Piece-wise polynomial
In the linear-linear model, 2 lines are fit to the data; these 2 lines are connected at the change point or “knot.” We applied 2 additional piece-wise polynomial models to the data. The other “2-phase” models (ie, linear-quadratic and quadratic-quadratic) did not improve the fit compared with the simpler linear-linear model, and we do not discuss them extensively in this report. The linear-splines model draws several smaller lines throughout the data, and these lines are joined in an iterative process to reduce the residual sum of squares; these minimal join points were used to determine the change point for the linear-splines model. The 2-knot approach that we used in this analysis had 3 phases: during phase 1, MMA concentrations declined rapidly with increasing SB-12 concentrations; in phase 2, MMA concentrations decreased much more slowly with increasing SB-12 concentrations; and in phase 3, MMA concentrations no longer changed as a function of SB-12 concentrations.
For all of the piece-wise models, we estimated the regression parameters and change points by performing a grid search (22). Briefly, we divided the vitamin B-12 distribution range into an equally spaced grid. For the one-knot (linear-linear) model, we fitted a piece-wise linear model for each of the grid values. We deemed the grid values resulting in the smallest residual sum of squares to be the best estimator of the change point. We estimated the 2 change points in a 2-knot model in a similar fashion by selecting 2 grid values at a time and fitting a piece-wise linear regression model. The model with the smallest residual sum of squares yielded estimators for the knots and regression parameters. Estimation of change points via the grid process makes use of the residual sum of squares, which in turn uses the sampling weights information but does not use the survey design (ie, primary sampling units and strata) in the estimation. The computer implementation of the grid algorithm requires the specification of the search range. In this analysis, the data were examined for the change point between the 1st and 99th percentiles of the vitamin B-12 distribution.
Model fit
To determine the most robust of “best-fit” model, we tested the selection between the zero-knot (linear regression), one-knot (linear-linear), and 2-knot (linear-splines) models using an approximate permutation test to determine the best model to describe the relation between SB-12 and log-MMA (23). This procedure was used to test whether the 2-knot model is preferred over the zero-knot model. If significant, then compare the 2-knot compared with the one-knot model. The first step in the application of the approximate permutation test is to fit the null model (ie, the zero-knot model) and compute the residuals (observed - expected), followed by randomly permutating these residuals and adding them to predicted value (under the null model). Next, a grid search approach is applied to fit the alternative model (ie, 2-knot model) to the resulting data and compute the residuals. An F-like goodness-of-fit test statistic is constructed by using these 2 sets of residuals. The distribution of this test statistic is approximated by Monte Carlo simulations, and P values are determined from the resulting distribution.
RESULTS
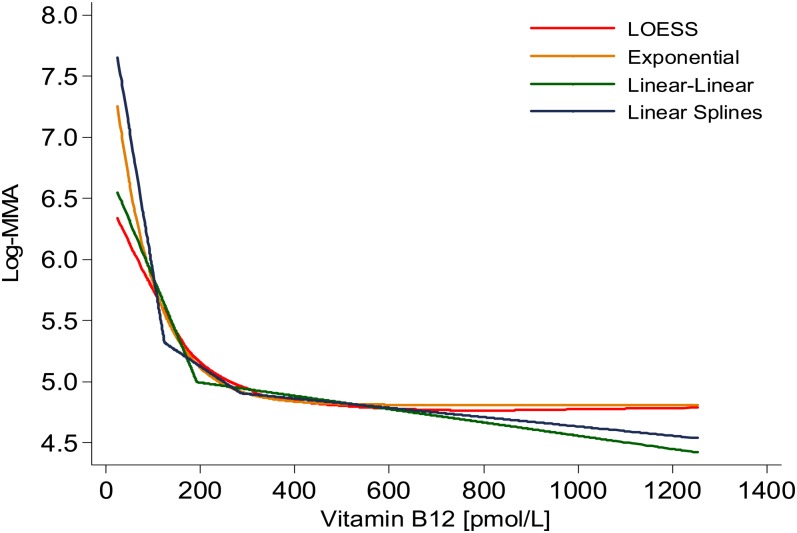
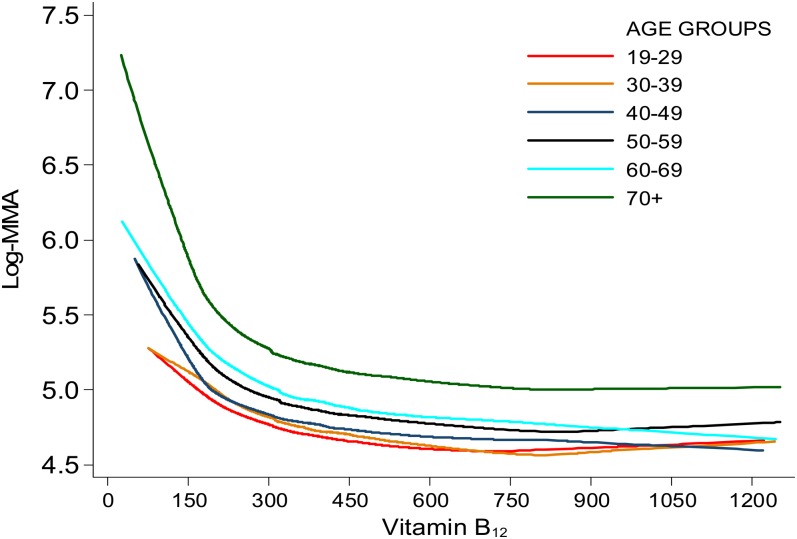
We determined different SB-12 change points by using each model strategy (Table 1). The exponential model with its curvilinear rate of change most closely mimicked the LOESS curve (ie, the curve that describes the scatter of the 2 variables) (Figure 1). Using the LOESS procedure by age group, we observed a similarly shaped curve in the relation between MMA and SB-12 concentrations across age groups, although the curves occurred at higher MMA values for groups with increasing age (Figure 2).
TABLE 1.
Change points derived for serum vitamin B-12 as a function of plasma MMA by using different modeling techniques1
| Change points (95% CIs) | R2 value2 | |
| pmol/L | % | |
| Exponential | 212 (184, 289) | 24.7 |
| Linear-linear | 193 (182, 279) | 24.0 |
| Linear-quadratic | 260 (192, 371) | 22.8 |
| Quadratic-quadratic | 314 (266, 442) | 23.7 |
| Linear splines3 | 126 (117, 182), 287 (253, 434) | 25.1 |
Data from NHANES 1999–2000, 2001–2002, and 2003–2004 (n = 31,126) were combined. Data for participants younger than 19 y (n = 14,942); those with only interview data (n = 1160); lactating (n = 145) and pregnant (n = 802) females; those with missing data on MMA (n = 928), serum vitamin B-12 (n = 114), or creatinine (n = 107) concentrations; those with a serum vitamin B-12 concentration greater than the 99th percentile (>1265 pmol/L; n = 135); and those with a glomerular filtration rate <30 (n = 110) were excluded. The final analytic sample size was 12,683. Age, glomerular filtration rate, and hours of fasting were controlled for before the blood samples were drawn. Other relevant covariates were examined, which were not influential in determining the change point. See supplementary analytic materials under “Supplemental data” in the online issue for details. NHANES assessed serum vitamin B-12 concentrations by using the Quantaphase II radioassay from BioRad and plasma MMA concentrations with gas chromatography–mass spectrometry. MMA, methylmalonic acid.
Defined as the amount of variability in serum vitamin B-12 that is explained by the model; this value is not interpreted as a fit statistic.
The linear-splines (2-knot) model was statistically more robust than was the exponential model (ie, zero-knot; P < 0.001) or the one-knot model (P < 0.001), determined by the approximate permutations test.
FIGURE 1.
LOESS, exponential, linear-linear, and linear-splines models of the relation between serum vitamin B-12 and log-MMA concentrations among US adults aged ≥19 y, 1999–2004. Data from NHANES 1999–2000, 2001–2002, and 2003–2004 (n = 31,126) were combined. Data for participants younger than 19 y (n = 14,942); those with only interview data (n = 1160); lactating (n = 145) and pregnant (n = 802) females; those with missing data on MMA (n = 928), serum vitamin B-12 (n = 114), or creatinine (n = 107) concentrations; those with a serum vitamin B-12 concentration greater than the 99th percentile (>1265 pmol/L; n = 135); and those with a glomerular filtration rate <30 (n = 110) were excluded. The final analytic sample size was 12,683. Age, glomerular filtration rate, and hours of fasting were controlled for before the blood samples were drawn. Other relevant covariates were examined, which were not influential in determining the change point. See supplementary analytic materials under “Supplemental data” in the online issue for details. NHANES assessed serum vitamin B-12 concentrations by using the Quantaphase II radioassay from BioRad and plasma MMA concentrations with gas chromatography–mass spectrometry. LOESS, locally estimated scatterplot smoothing; MMA, methylmalonic acid.
FIGURE 2.
LOESS of the relation between serum vitamin B-12 and log-MMA concentrations by 10-y age groupings among US adults, 1999–2004. Data from NHANES 1999–2000, 2001–2002, and 2003–2004 (n = 31,126) were combined. Data for participants younger than 19 y (n = 14,942); those with only interview data (n = 1160); lactating (n = 145) and pregnant (n = 802) females; those with missing data on MMA (n = 928), serum vitamin B-12 (n = 114), or creatinine (n = 107) concentrations; those with a serum vitamin B-12 concentration greater than the 99th percentile (>1265 pmol/L; n = 135); and those with a glomerular filtration rate <30 (n = 110) were excluded. The final analytic sample size was 12,683. Age, glomerular filtration rate, and hours of fasting were controlled for before the blood samples were drawn. Other relevant covariates were examined, which were not influential in determining the change point. See supplementary analytic materials under “Supplemental data” in the online issue for details. NHANES assessed serum vitamin B-12 concentrations by using the Quantaphase II radioassay from BioRad and plasma MMA concentrations with gas chromatography–mass spectrometry. LOESS, locally estimated scatterplot smoothing; MMA, methylmalonic acid.
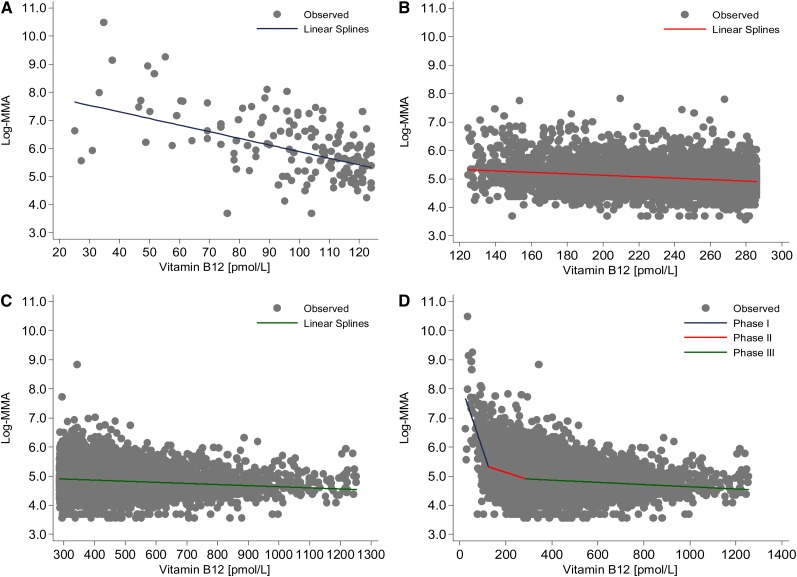
The statistically based approximate permutation test showed that the linear-splines model best fit the data to describe the relation between SB-12 and MMA concentrations better than the exponential model (P < 0.001) or any of the “one-knot” models (P < 0.001) (see Supplemental Figures 1 and 2 under “Supplemental data” in the online issue). The slope of the relation between MMA and SB-12 concentrations was significantly different for each of the groups that we created by the linear-splines model (Figure 3; see Supplemental Table 2 under “Supplemental data” in the online issue). By using the cutoff points that we derived from the linear-splines model for SB-12 concentrations (Table 1), we examined 3 groups of adults by serum vitamin B-12 concentration: group 1, <126; group 2, 126–287, and group 3, >287 pmol/L (Table 2). Group 1 had a high risk of vitamin B-12 deficiency and represented a very small proportion of adults in the United States. In addition, group 1 had the highest MMA and tHcy concentrations. The group with the highest SB-12 concentrations, group 3, had the lowest MMA and tHcy concentrations. NHANES participants in the middle group (126–287 pmol/L), group 2, had intermediate median MMA (148 nmol/L) and tHcy (9 μmol/L) concentrations, although their values for these 2 biomarkers were closer to those of the highest SB-12 group (120 nmol/L and 8 μmol/L, respectively) than to those of the lowest SB-12 group (281 nmol/L and 12 μmol/L, respectively). When compared with group 3, both group 1 and group 2 had a significantly increased odds of having an elevated MMA or tHcy concentration: group 1 compared with group 3 [MMA OR: 32.1 (95% CI: 21.6, 47.8); tHcy OR: 18.5 (95% CI: 13.9, 24.5)], group 2 compared with group 3 [MMA OR: 3.5 (95% CI: 2.9, 4.3); tHcy OR: 3.1 (95% CI: 2.7, 3.6)]. We observed no differences between the groups in creatinine, eGFR, or C-reactive protein concentrations (data not shown).
FIGURE 3.
The linear-splines model of the relation between serum vitamin B-12 and log-MMA concentrations among US adults, 1999–2004. Data from NHANES 1999–2000, 2001–2002, and 2003–2004 (n = 31,126) were combined. Data for participants younger than 19 y (n = 14,942); those with only interview data (n = 1160); lactating (n = 145) and pregnant (n = 802) females; those with missing data on MMA (n = 928), serum vitamin B-12 (n = 114), or creatinine (n = 107) concentrations; those with a serum vitamin B-12 concentration greater than the 99th percentile (>1265 pmol/L; n = 135); and those with a glomerular filtration rate <30 (n = 110) were excluded. The final analytic sample size was 12,683. Age, glomerular filtration rate, and hours of fasting were controlled for before the blood samples were drawn. Other relevant covariates were examined, which were not influential in determining the change point. See supplementary analytic materials under “Supplemental data” in the online issue for details. NHANES assessed serum vitamin B-12 concentrations by using the Quantaphase II radioassay from BioRad and plasma MMA concentrations with gas chromatography–mass spectrometry. A: The shape of the linear-splines model for NHANES participants with a serum vitamin B-12 concentration <126 pmol/L. B: Data points for participants with a serum B-12 concentration of 126–287 pmol/L. C: Data points for participants with a serum vitamin B-12 concentration >287 pmol/L. D: The overall shape of the linear-splines model for all data points. MMA, methylmalonic acid.
TABLE 2.
Demographic, biochemical, and dietary variables by change points determined with the linear-splines approach among US adults, 1999–20041
| Serum vitamin B-12 concentrations |
|||
| <126 pmol/L(n = 157) | 126–287 pmol/L(n = 3957) | >287 pmol/L(n = 8569) | |
| Percentage of sample (%) | 1 | 33 | 66 |
| Demographic characteristics2 | |||
| Age (y) | 53 ± 1a,3 | 45 ± 0.3b | 46 ± 0.3c |
| ≥60 y (%) | 37 ± 4a | 21 ± 1b | 23 ± 1c |
| Male (%) | 37 ± 5a | 48 ± 1b | 51 ± 1c |
| Non-Hispanic white (%) | 81 ± 4a | 76 ± 2a | 70 ± 2b |
| Non-Hispanic black (%) | 6 ± 2a | 7 ± 1a | 12 ± 1b |
| Mexican American (%) | 5 ± 1a | 6 ± 1a | 8 ± 1b |
| Biochemical variables4 | |||
| Plasma MMA (nmol/L) | 719 ± 113a | 176 ± 2b | 137 ± 2c |
| Median (nmol/L) | 281 (245, 366) | 148 (140, 153) | 120 (119, 125) |
| Plasma tHcy (μmol/L) | 17 ± 2a | 10 ± 0.1b | 8 ± 0.1c |
| Median (μmol/L) | 12 (10.9, 13.1) | 9 (8.5, 8.8) | 8 (7.6, 7.8) |
| Dietary components | |||
| Vitamin B-12 from food sources (μg/d) | 4.7 ± 0.5 | 4.7 ± 0.2 | 5.5 ± 0.1 |
| Median (μg/d) | 3.1 (2.5, 3.6) | 3.4 (3.3, 3.6) | 4.1 (3.9, 4.3) |
| Vitamin B-12 from dietary supplements (μg/d)5 | 10.3 ± 1.5a | 38.8 ± 9.1b | 75.4 ± 13.1c |
| Median (μg/d) | 5.9 (5.6, 8.0) | 6.0 (5.9, 6.0) | 9.9 (8.8, 11.8) |
| Percentage using vitamin B-12 supplements (%) | 24 ± 4a | 24 ± 1a | 45 ± 1b |
| Total vitamin B-12 intake (μg/d) | 7.2 ± 0.7a | 14.4 ± 2.3b | 39.6 ± 6.2c |
| Median (μg/d) | 3.7 (3.3, 5.9) | 4.5 (4.3, 4.8) | 7.7 (7.6, 7.8) |
Data from NHANES 1999–2000, 2001–2002, and 2003–2004 (n = 31,126) were combined. Data for participants younger than 19 y (n = 14,942); those with only interview data (n = 1160); lactating (n = 145) and pregnant (n = 802) females; those with missing data on MMA (n = 928), serum vitamin B-12 (n = 114), or creatinine (n = 107) concentrations; those with a serum vitamin B-12 concentration greater than the 99th percentile (>1265 pmol/L; n = 135); and those with a glomerular filtration rate <30 (n = 110) were excluded. The final analytic sample size was 12,683. 95% CIs in parentheses. Values in a row with different superscript letters are significantly different, P ≤ 0.05 [determined by a diffvar statement in PROC DESCIPT (SAS-callable Sudann)]. MMA, methylmalonic acid; tHcy, total homocysteine.
Percentages do not add up to 100 because data for the “other” racial-ethnic group are not presented.
Mean ± SE (all such values).
NHANES assessed serum vitamin B-12 concentrations by using the Quantaphase II radioassay from BioRad, plasma MMA concentrations by using gas chromatography–mass spectrometry, and plasma homocysteine concentrations by using a fluorescence polarization immunoassay reagent kit from Abbott Laboratories.
Estimates are for users of dietary supplements only; the total is for users and nonusers of supplements combined.
Group 1 members tended to be older, and female members of group 3 were more likely to be non-Hispanic black or Mexican American. Group 2 is a group of people whose age and sex profiles were significantly different from those of both the lowest and highest SB-12 groups and more closely resembled those of group 3. Racial-ethnic characteristics did not differ significantly between groups 2 and 1; however, the highest proportion of non-Hispanic whites was in group 1, and the highest proportion of non-Hispanic blacks was in group 3.
We observed no differences between the 3 SB-12 groups in vitamin B-12 intakes from foods alone, and the intakes from food sources appeared to be adequate with mean and median intakes above the Estimated Average Requirements of 2.0 μg/d (18). However, intakes from dietary supplements differed significantly, ranging from a mean (±SE) of 10.3 ± 1.5 μg/d in the group 1 to 75.4 ± 13.1 μg/d in group 3. Thus, differences in total intakes between groups were due almost exclusively to differences in supplement use.
DISCUSSION
With the use of various statistical models, we quantified the complex relation between SB-12 and plasma MMA concentrations. The best-fit model produced 3 different and independent slopes for the relation between SB-12 and MMA concentrations and yielded 2 points of change. This strategy thereby identified 3 subsets of the adult US population along the continuum of vitamin B-12 status that has been previously described by others in the field (4–7). However, our work is the first to use a statistical model that specifically identifies an intermediate group of people based on 2 cutoff points. Previous epidemiologic researchers would have classified these people as having either deficient or sufficient vitamin B-12 status, but neither of these classifications seem appropriate for this group.
Group 1 was small (representing ∼1% of US adults) but included several individuals with severe vitamin B-12 deficiency and the highest MMA and tHcy concentrations of any of the 3 groups we identified. Their downward slope between MMA and SB-12 concentrations was steep across a fairly narrow range of SB-12 concentrations. Group 3 (∼68% of US adults) had optimal vitamin B-12 status and this group had almost a flat trajectory for the relation between vitamin B-12 and MMA concentrations across a very wide range of SB-12 values (Figure 3C). Group 2, the remaining third (31%) of US adults, had SB-12 concentrations between the 2 change points. The members of group 2 had a vitamin B-12 status that is arguably much more difficult to interpret than the status of the other 2 groups. The increase in MMA in group 2 for a given SB-12 value was smaller than that of group 1 and larger than that of group 3 (Figure 3C).The median MMA and tHcy concentrations of group 2 were not much higher than those of group 3, but the odds of having elevations in these functional indicators was 3-fold [MMA OR: 3.5 (95% CI: 2.9, 4.3); tHcy OR: 3.1 (95% CI: 2.7, 3.6)].
The demographic data gave a mixed picture of group 2, the age and sex profiles of which were similar to those of group 3 and whose racial-ethnic profiles were similar to those of group 1. It is unknown to what extent individuals in this middle group were likely to progress to the more obvious vitamin B-12 deficiency in group 1, which individuals were simply experiencing a mild or temporary period of vitamin B-12 deficiency, and which individuals had reduced SB-12 for reasons unrelated to vitamin B-12 deficiency [eg, polymorphisms within the FUT2 gene and mutations within the TCN1 gene that alter SB-12 without altering MMA or tHcy concentrations (24, 25)]. Previous studies have found elevated concentrations of functional biomarkers (MMA and/or tHcy) in cases in which SB-12 concentrations were within the normal range (3, 9, 26). Although several observational studies have suggested that vitamin B-12 concentrations in the low-normal range are associated with cognitive function or decline and impaired nervous system function (as reviewed in reference 10), these results require confirmation in clinical trials (7).
The second unique finding of this study was that, although each of the models produced the expected curvilinear relation between MMA and SB-12 concentrations, each model also produced different points of change for SB-12 concentrations. Thus, the derived change point is model dependent. This finding could explain some of the differences in change point concentrations between published studies whose authors relied primarily on a single statistical model approach without explaining why they chose the model they used (9, 27). For example, Vogiatzoglou et al (27) used a segmented linear regression to identify a change point of 334 pmol/L for SB-12 as a function of MMA concentration in the Hordaland Homocysteine Study in Norway; because the authors did not specify how many linear segments they used in this study, a comparison of data from this study to our data are not possible. Conversely, the differences in change point are smaller in our study than in the results of Selhub et al (9), who used a linear-linear model that is similar to one of the models we tested (Table 1). Selhub et al found a change point of 150 pmol/L in an NHANES III sample, whereas we found a change point of 194 pmol/L using the same model in an NHANES 1999–2004 sample. Because of differences in the survey years, the ages of the subjects, changes in MMA assay methods, and use of different exclusion criteria and covariates, a more thorough comparison of these 2 studies cannot be achieved. Our linear-splines model suggested that using only one cutoff point to define status in survey data often leads to inappropriately dividing members of the intermediate group into sufficient and deficient groups. Furthermore, the use of traditional groupings (eg, quartiles or centiles) in epidemiologic research often hides the small, but clearly deficient, group by combining its members with persons in the more “intermediate” group. Both of these practices led to misclassification.
The 3-phase approach that we used is appealing not only because of its superior ability to identify subgroups but also because of its biological plausibility. The underlying pathophysiologic causes and known health risks in the deficient and intermediate groups might have been different (3). The utility of the linear-splines framework to understand vitamin B-12 status needs to be confirmed in other population-based surveys and is probably not practical for clinical applications in which a single cutoff point is used.
This analysis had some limitations. Age affected the relation between MMA and SB-12 concentrations in our analyses. The NHANES data were cross-sectional, and the survey assessed the relations between SB-12 and MMA concentrations at a single point in time. We examined several but not all types of statistical models. Because the major determinants of MMA are largely unknown (27), we probably missed some key covariates. Finally, the gold-standard approach for identifying cutoff points is the randomized clinical trial or repletion study. No data from such studies are currently available, and the statistical approach that we used is at best an interim approach pending the availability of such data. A common problem in understanding vitamin B-12 status in any population is that both SB-12 and MMA concentrations vary by age independently of vitamin B-12 status (9, 22). For this reason, we recognized that the cutoff points that we derived might not be optimal for different age subgroups or populations (3).
Given the negative cognitive and other health consequences that can result from clinical vitamin B-12 deficiency, it is critical to accurately monitor the vitamin B-12 status among all age groups, especially among the oldest groups. This study highlights the difficulty (in the absence of clinical trials) of defining the vitamin B-12 status of the population and underscores the uncertainty regarding interpretations of the available data from NHANES to estimate the population prevalence of vitamin B-12 deficiency. These data also show the need for caution when selecting a statistical modeling approach to derive cutoff points. Epidemiologic applications will benefit from the recognition of the variability among statistical models and the need to critically evaluate how best to integrate statistical, biological, and practical considerations when selecting change points for assessing vitamin B-12 status.
Supplementary Material
Acknowledgments
The authors’ responsibilities were as follows—RLB, RC, RG, CMP, CTS, and EAY: contributed to the concept development and manuscript preparation, designed the research, and wrote the manuscript; RAD-A: completed the statistical modeling of the data with consultation from AC; and all authors: read and approved the final version of the manuscript. RC has submitted a patent application for work related to transcobalamin I deficiency and its genetic aspects. None of the other authors had a personal or financial conflict of interest.
Footnotes
Abbreviations used: eGFR, estimated glomerular filtration rate; LOESS, locally estimated scatterplot smoothing; MMA, methylmalonic acid; SB-12, serum vitamin B-12; tHcy, total homocysteine.
REFERENCES
- 1.Pennypacker LC, Allen RH, Kelly JP, Matthews LM, Grigsby J, Kaye K, Lindenbaum J, Stabler SP. High prevalence of cobalamin deficiency in elderly outpatients. J Am Geriatr Soc 1992;40:1197–204. [PubMed] [Google Scholar]
- 2.Green R, Miller JW. Vitamin B12 deficiency is the dominant nutritional cause of hyperhomocysteinemia in a folic acid-fortified population. Clin Chem Lab Med 2005;43:1048–51. [DOI] [PubMed] [Google Scholar]
- 3.Carmel R. Biomarkers of cobalamin (vitamin B-12) status in the epidemiologic setting:a critical overview of context, applications, and performance characteristics of cobalamin, methylmalonic acid, and holotranscobalamin II. Am J Clin Nutr 2011;94:348S–58S. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Miller JW, Garrod MG, Rockwood AL, Kushnir MM, Allen LH, Haan MN, Green R. Measurement of total vitamin B12 and holotranscobalamin, singly and in combination, in screening for metabolic vitamin B12 deficiency. Clin Chem 2006;52:278–85. [DOI] [PubMed] [Google Scholar]
- 5.Clarke R, Refsum H, Birks J, Evans JG, Johnston C, Sherliker P, Ueland PM, Schneede J, McPartlin J, Nexo E, et al. Screening for vitamin B-12 and folate deficiency in older persons. Am J Clin Nutr 2003;77:1241–7. [DOI] [PubMed] [Google Scholar]
- 6.Lloyd-Wright Z, Hvas AM, Moller J, Sanders TA, Nexo E. Holotranscobalamin as an indicator of dietary vitamin B12 deficiency. Clin Chem 2003;49:2076–8. [DOI] [PubMed] [Google Scholar]
- 7.Yetley EA, Pfeiffer CP, Phinney KW, Bailey RL, Blackmore S, Bock JL, Brody LC, Carmel R, Curtin R, Durazo-Arvizu RA, et al. Biomarkers of vitamin B-12 status in NHANES: a roundtable summary. Am J Clin Nutr 2011;94:313S–21S. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Bailey RL, Carmel R, Green R, Pfeiffer CM, Cogswell ME, Osterloh JD, Sempos CT, Yetley EA. Monitoring of vitamin B-12 nutritional status in the United States by using plasma methylmalonic acid and serum vitamin B-12. Am J Clin Nutr 2011;94:552–61. [DOI] [PMC free article] [PubMed]
- 9.Selhub J, Jacques PF, Dallal G, Choumenkovitch S, Rogers G. The use of blood concentrations of vitamins and their respective functional indicators to define folate and vitamin B12 status. Food Nutr Bull 2008;29:S67–73. [DOI] [PubMed] [Google Scholar]
- 10.Smith AD, Refsum H. Do we need to reconsider the desirable blood level of vitamin B12? J Int Med 2012;271:179–82. [DOI] [PubMed]
- 11.National Center for Health Statistics. Response rates & CPS population totals, National Health and Nutrition Examination Survey. Available from: http://www.cdc.gov/nchs/nhanes/nhanes_cps_totals.htm (cited 1 April 2010).
- 12.Pfeiffer CM, Osterloh JD, Kennedy-Stephenson J, Picciano MF, Yetley EA, Rader JI, Johnson CL. Trends in circulating concentrations of total homocysteine among US adolescents and adults: findings from the 1991-1994 and 1999-2004 National Health and Nutrition Examination Surveys. Clin Chem 2008;54:801–13. [DOI] [PubMed] [Google Scholar]
- 13.Selvin E, Manzi J, Stevens LA, Van Lente F, Lacher DA, Levey AS, Coresh J. Calibration of serum creatinine in the National Health and Nutrition Examination Surveys (NHANES) 1988-1994, 1999-2004. Am J Kidney Dis 2007;50:918–26. [DOI] [PubMed] [Google Scholar]
- 14.National Center for Health Statistics. Available from: http://www.cdc.gov/nchs/nhanes/lab99_00.htm. National Health and Nutrition Examination Survey Laboratory Methods, 1999-2000 (cited 1 April 2010).
- 15.National Center for Health Statistics. Available from: http://www.cdc.gov/nchs/nhanes/nhanes2001-2002/lab01_02.htm. National Health and Nutrition Examination Survey Laboratory Methods, 2001-2002 (cited 1 April 2010).
- 16.National Center for Health Statistics. Available from: http://www.cdc.gov/nchs/nhanes/nhanes2003-2004/lab03_04.htm. National Health and Nutrition Examination Survey Laboratory Methods, 2003-2004 (cited 1 April 2010).
- 17.Bailey RL, Dodd KW, Gahche JJ, Dwyer JT, McDowell MA, Yetley EA, Sempos CA, Burt VL, Radimer KL, Picciano MF. Total folate and folic acid intake from foods and dietary supplements in the United States: 2003-2006. Am J Clin Nutr 2010;91:231–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Food and Nutrition Board. Dietary reference intakes for thiamin, riboflavin, niacin, vitamin B6, folate, vitamin B12, pantothenic acid, biotin, and choline. Washington, DC: National Academy Press, 1998. [PubMed] [Google Scholar]
- 19.Cleveland W. Robust locally weighted regression and smoothing scatterplots. J Am Stat Assoc 1979;74:829–36. [Google Scholar]
- 20.Cleveland W, Devlin S. Locally-weighted regression: an approach to regression analysis by local fitting. J Am Stat Assoc 1988;83:596–610. [Google Scholar]
- 21.Kolenikov S. Resampling variance estimation for complex survey data. Stata J 2010;10:165–99.
- 22.Lerman PM. Fitting segmented regression models by grid search. Appl Stat 1980;29:77–84. [Google Scholar]
- 23.Kim HJ, Fay MP, Feuer EJ, Midthune DN. Permutation tests for joinpoint regression with applications to cancer rates. Stat Med 2000;19:335–51. [DOI] [PubMed] [Google Scholar]
- 24.Oussalah A, Besseau C, Chery C, Jeannesson E, Gueant-Rodriguez RM, Anello G, Bosco P, Elia M, Romano A, Bronowicki JP, et al. Helicobacter pylori serologic status has no influence on the association between fucosyltransferase 2 polymorphism (FUT2 461 G->A) and vitamin B-12 in Europe and West Africa. Am J Clin Nutr 2010;95:514–21. [DOI] [PubMed]
- 25.Carmel R, Parker J, Kelman Z. Genomic mutations associated with mild and severe deficiencies of transcobalamin I (haptocorrin) that cause mildly and severely low serum cobalamin levels. Br J Haematol 2009;147:386–91. [DOI] [PubMed] [Google Scholar]
- 26.Refsum H, Nurk E, Smith AD, Ueland PM, Gjesdal CG, Bjelland I, Tverdal A, Tell GS, Nygard O, Vollset SE. The Hordaland Homocysteine Study: a community-based study of homocysteine, its determinants, and associations with disease. J Nutr 2006;136:1731S–40S. [DOI] [PubMed] [Google Scholar]
- 27.Vogiatzoglou A, Oulhaj A, Smith AD, Nurk E, Drevon CA, Ueland PM, Vollset SE, Tell GS, Refsum H. Determinants of plasma methylmalonic acid in a large population: implications for assessment of vitamin B12 status. Clin Chem 2009;55:2198–206. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.