Decay of Motor Memories in the Absence of Error

Abstract

When motor commands are accompanied by an unexpected outcome, the resulting error induces changes in subsequent commands. However, when errors are artificially eliminated, changes in motor commands are not sustained but show decay. Why does the adaptation-induced change in motor output decay in the absence of error? A prominent idea is that decay reflects the stability of the memory. We show results that challenge this idea and instead suggest that motor output decays because the brain actively disengages a component of the memory. Humans adapted their reaching movements to a perturbation and were then introduced to a long period of trials in which errors were absent (error-clamp). We found that, in some subjects, motor output did not decay at the onset of the error-clamp block but a few trials later. We manipulated the kinematics of movements in the error-clamp block and found that, as movements became more similar to subjects' natural movements in the perturbation block, the lag to decay onset became longer and eventually reached hundreds of trials. Furthermore, when there was decay in the motor output, the endpoint of decay was not zero but a fraction of the motor memory that was last acquired. Therefore, adaptation to a perturbation installed two distinct kinds of memories: (1) one that was disengaged when the brain detected a change in the task and (2) one that persisted despite it. Motor memories showed little decay in the absence of error if the brain was prevented from detecting a change in task conditions.

Introduction

When motor commands produce unexpected results, the brain changes the commands on the subsequent trial (Thoroughman and Shadmehr, 2000). For example, when one reaches while holding an object that has novel dynamics (Shadmehr and Mussa-Ivaldi, 1994), the sensory consequences of motor commands are different from expected. This prediction error alters the motor commands on the subsequent trial, and the accumulation of this error-dependent learning, combined with repetition of the motor commands (Huang et al., 2011), produces a motor memory that can be recalled months later (Shadmehr and Brashers-Krug, 1997). The ability to protect and recall a memory can be strengthened by altering the perturbation schedule, amount of repetition, or type of feedback (Huang et al., 2011; Pekny et al., 2011; Shmuelof et al., 2012). Paradoxically, in one condition, the motor memory appears transient: if training is followed by a block of error-clamp (EC) trials, trials in which errors are artificially eliminated, the motor output decays. That is, error produces a change in motor output, but absence of error also produces a change. The change in motor output in the absence of error has been taken as evidence that error-dependent adaptation produces a motor memory that is inherently labile, exhibiting decay (Cheng and Sabes, 2006; Smith et al., 2006; Criscimagna-Hemminger and Shadmehr, 2008; Joiner and Smith, 2008; Zarahn et al., 2008; Galea et al., 2011). How is it that recently acquired motor memories exhibit decay in the absence of error over tens of trials yet have long-term stability as exhibited by recall months later?

An important clue is an observation that was made by Scheidt et al. (2000). Subjects learned to compensate for a perturbation and were then exposed to EC trials. In most healthy subjects, in the absence of error, the motor output decayed at the very onset of the EC block, exhibiting zero lag (Scheidt et al., 2000, their Fig. 5B). However, on rare occasions, motor output showed no decay for tens of trials: in one subject, there was a 60 trial lag (Scheidt et al., 2000, their Fig. 5C). Therefore, absence of error is not a sufficient condition for decay of motor output. Rather, the trial at which the decay begins may be probabilistic.

Figure 5.

Lag to decay in shooting movements with constant EC trials in experiment 2. A, Time course of the change in adaptation index in EC trials for two example subjects. Both subjects were in group 2.2. A delayed exponential was fit to the data. B, Distribution of lags to the start of the decay for all subjects.

The aim of our study was to better understand why motor output decays in the absence of error. In our first experiment, we explored the question of the steady state (or endpoint) to which motor output decays. We found that this endpoint was never zero but always a fraction of the motor memory that was last acquired. In our sample of subjects, we also observed an occasional instance in which the decay started not at the beginning of the EC block but after a lag. In our second and third experiments, we explored conditions that changed this lag. We found that the lag could be extended, sometimes indefinitely, by closely matching the statistics of movements in the EC trials to the preceding training trials. These results suggest that motor memories do not passively decay in the absence of error but are actively disengaged because the brain detects a change in the task.

Materials and Methods

Fifty-five healthy right-handed subjects with no known neurological impairment participated in this study (aged 23.1 ± 4.6 years, 31 females). All subjects were naive to our apparatus, the paradigm, and the purpose of the experiment. This work was approved by the Johns Hopkins University School of Medicine Institutional Review Board.

Subjects grasped the handle of a two-link robotic manipulandum with their right hand and made reaching or shooting movements, described below, for ∼60 min. A screen covered the hand; veridical visual feedback (3-mm-diameter cursor) was provided throughout the experiment. Subjects were permitted short breaks at defined points in the experiment. Position, velocity, and force at the handle were recorded at a rate of 200 Hz. During some trials, participants experienced a viscous curl field f = kBẋ (Fig. 1A), where f is force on the hand, k is a constant describing the field strength, B is a viscosity matrix describing a counterclockwise curl field, $B=\left[\begin{array}{cc}0& -15\\ 15& 0\end{array}\right]\text{N}·\text{s}/\text{m}$, and ẋ is the hand velocity vector. In some trials, subjects experienced an error-clamp (Fig. 1A) in which the movement was constrained to the line between the start position and an endpoint (usually the target, except in experiment 3; see below) by a stiff, one-dimensional spring (spring coefficient, 6 kN/m; damping coefficient, 250 Ns/m) (Scheidt et al., 2000). In these trials, we were able to record the compensatory forces exerted by the subject onto the walls of the channel formed by the spring. We placed EC trials with 20% probability randomly throughout each experiment.

Figure 1.

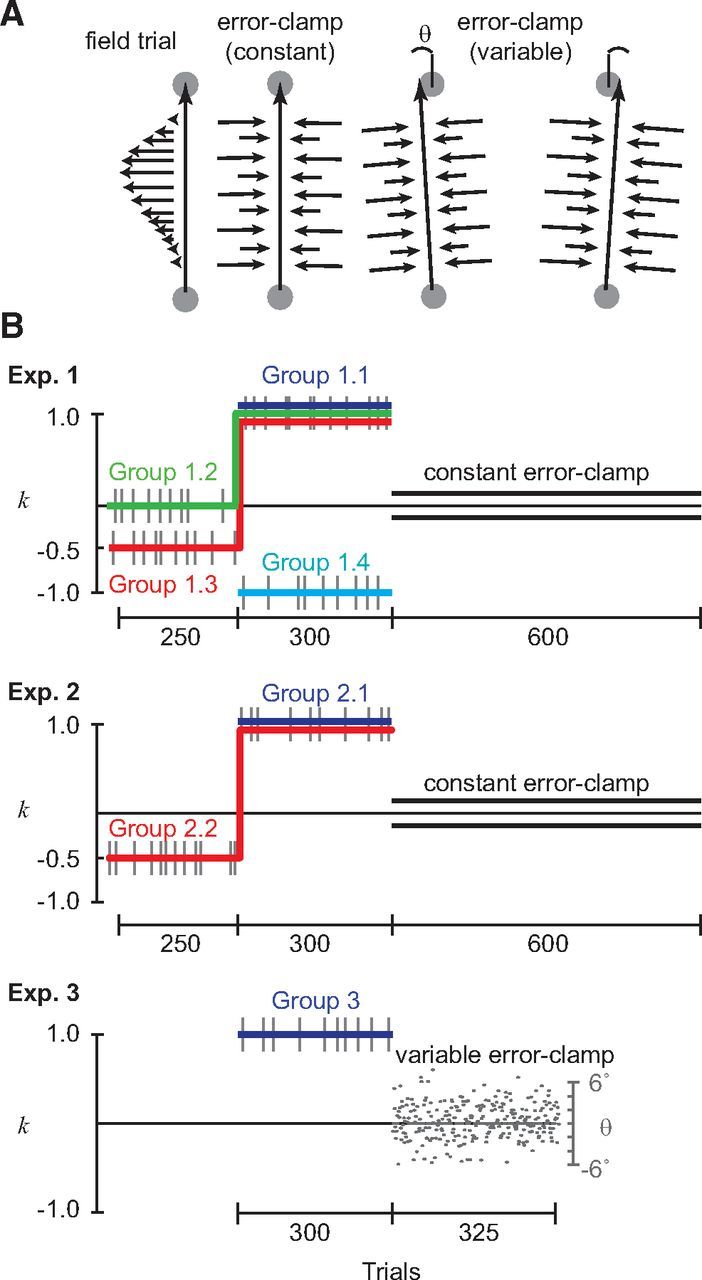
Experimental paradigm. A, Participants experienced three types of trials. In FF trials, participants experienced a viscous curl field f = kBẋ, where f is force on the hand, k is a constant describing the field strength, B is a viscosity matrix describing a counterclockwise curl field, and ẋ is the hand velocity. In error-clamp trials, movements were constrained to a straight line by a stiff one-dimensional spring. Constant EC trials constrained movements in a line to the target. In variable EC trials, the movement endpoint was a random variable θ that matched the natural variability in subjects' movement (Shmuelof et al., 2011). B, In experiment 1, subjects made point-to-point reaching movements. In experiments 2 and 3, subjects made shooting movements through and past the target. k indicates the field strength. Constant EC trials (thin gray lines) were interspersed randomly with 20% probability through the experiment. θ (gray points) indicates the movement endpoint in variable EC trials. Black parallel lines indicate constant EC trials.

Our aim was to understand why motor output decays in EC trials. To answer this question, we began with a series of experiments in which we varied the history of the training (experiment 1). We followed up with another series of experiments (experiments 2 and 3) in which we tested the hypothesis that the decay occurs only if the brain detects a change from the force-field (FF) trials to error-clamp (EC) trials.

Experiment 1: reaching with constant error-clamp.

In experiment 1, our aim was to determine the effect of the history of training on the rate, endpoint, and lag of the decay in motor output in the EC trials. Participants (n = 24) made point-to-point reaching movements from a 1-cm-diameter starting circle at approximately midline of the body to a 1-cm-diameter target 10 cm away. The start circle was visible throughout the experiment. Subjects were instructed to move “rapidly and accurately” to the target once the target appeared and an auditory cue was played. Once the hand stopped at the target, feedback was provided. If the movement took too long (>550 ms), the target turned blue. If the movement was too brief (<450 ms), the target turned red. Subjects received a point and an “explosion” of the target for movements between 450 and 550 ms. Auditory feedback was also provided: a 2000 Hz tone indicated success, and a 200 Hz tone indicated failure. After each trial, the target was removed and the robot returned the subject's hand from the target to the start position.

Four groups of subjects participated in this experiment (Fig. 1B). Group 1.1 (n = 6) trained only in field k = 1 (counterclockwise field, 300 trials) without baseline training in null. Group 1.2 (n = 6) trained in null (k = 0, 250 trials), followed by 300 trials of k = 1 field training. Group 1.3 (n = 6) trained in k = −0.5 (250 trials), followed by 300 trials of training in k = 1. Group 1.4 (n = 6) trained only in field k = −1, without training in null. After completion of training in field, all subjects completed 600 EC trials.

Experiments 2: shooting with constant error-clamp.

To test the hypothesis that change detection may be a critical component of decay of motor memories in EC trials, we tried to make the differences between movements in FF trials and EC trials less pronounced. In experiment 2, subjects (n = 12) were asked to “shoot through and past” the target into a virtual pillow positioned beyond the target. The cursor was turned off once the subject moved past the target. The goal duration was 150–250 ms. Feedback for movements that were too fast, too slow, or correct was identical to the reaching task in experiment 1. If subjects struck the virtual pillow in the appropriate time but missed the target, the target turned pink, a 500 Hz tone was played, and the trial was considered unsuccessful. Group 2.1 (n = 6) trained only in field k = 1 (300 trials) without baseline training in null. Group 2.2 (n = 6) trained in k = −0.5 (250 trials), followed by 300 trials of training in k = 1. After completion of training in field, all subjects completed 600 EC trials.

Experiments 3: shooting with variable error-clamp.

In experiment 3, we attempted to make the transition from the FF to the EC block more difficult to detect by making the EC trials have a variability that matched the variability of FF trials. Subjects (n = 19) trained only in field k = 1 (300 trials) without baseline training in null. This was followed by a block of variable EC trials (325 trials). In these trials, as in constant EC trials, the movement was constrained to a line by a stiff one-dimensional spring between the start position and an endpoint (Fig. 1A). The variable error-clamps were designed so that the endpoint of a given EC trial was a random variable θ with a distribution that matched the natural variability of the endpoint of subjects' movements (Fig. 1C) (Shmuelof et al., 2011). The distribution of this random variable was selected based on the distribution of the movement endpoints of subjects in experiment 2 at the end of training. The angular deviation θ was drawn from a normal distribution with the following mean and variance: θ ∼ N(−0.2°, 2.6°). Note that the small non-zero bias in the mean angular deviation of these EC trials is equivalent to a 0.03 cm lateral deviation to the right at the end of the movement, well within the target width of 1 cm (5.7°). As in experiments 1 and 2, EC trials directly to the target were interspersed with 20% probability throughout the experiment.

Adaptation index.

We quantified performance via an adaptation index during EC trials (Smith et al., 2006). The lateral force produced during an EC trial was regressed onto the ideal compensatory force profile for a counterclockwise field with k = 1. The adaptation index was zero if the forces were uncorrelated and one if they were perfectly correlated. For example, perfect compensation for a counterclockwise field (k = 1) results in an adaptation index of 1; perfect compensation for the weak clockwise field (k = −0.5) results in an adaptation index of −0.5.

Decay of force in EC trials.

In all experiments, we assessed whether subjects reduced their motor output immediately on entering the block of EC trials or with a lag. The adaptation index of subjects in the last 50 trials of training and during the final EC block were fit using a nonlinear least-squares fit to a lagged exponential decay f(τ):

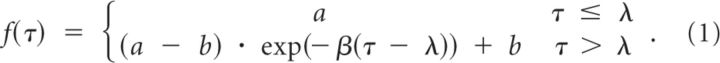In Equation 1, τ is the trial number in the EC block, a is adaptation index the subject achieved in FF trials, b is the endpoint of the decay, β is the rate of decay, and λ is the lag:

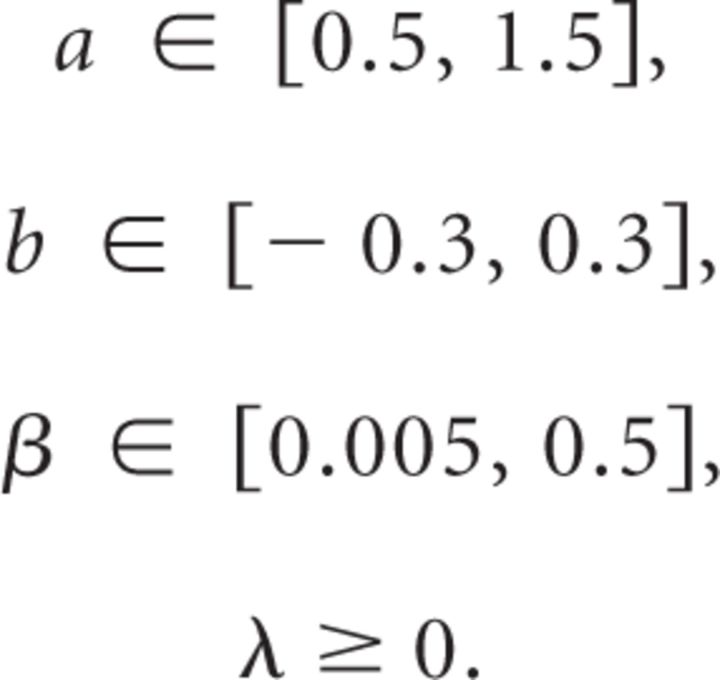Predictions of two-state model.

We compared our results with the predictions of a two-state model, in which motor output is the sum of two internal states: (1) one that shows high sensitivity to error but forgets quickly, termed the “fast” state, and (2) another that shows low sensitivity to error but forgets slowly, termed the “slow” state (Smith et al., 2006). On trial n, the motor output is x⁽ⁿ⁾, resulting in error e⁽ⁿ⁾. This error produces an update of the states as follows:

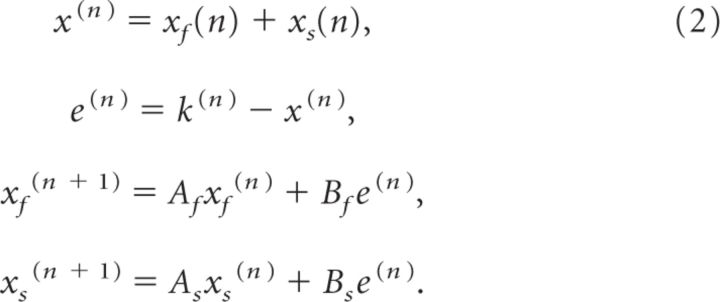In Equation 2, x_f and x_s are the fast and slow states, respectively, k⁽ⁿ⁾ is the perturbation, and e⁽ⁿ⁾ is the error on trial n. The learning rates are 0 < B_s < B_f < 1, and the rates of forgetting are 0 < A_f < A_s < 1. The learning and forgetting rates were identified using a nonlinear least-squares fit of predicted motor output to the adaptation index in EC trials during field training. These parameters were used to predict behavior in the EC block. Constant EC trials were simulated as having an error e⁽ⁿ⁾ = 0. To simulate performance in variable EC trials, we computed the relationship between error, e⁽ⁿ⁾, and angular deviation, θ⁽ⁿ⁾. We calculated, for the first 50 trials of experiment 3, the linear relationship between the error in EC trials, that is, the difference between the field strength k and the measured adaptation index in that trial, and the endpoint angular deviation in the subsequent FF trial. A variable EC trial with deviation θ⁽ⁿ⁾ was simulated as having an error e⁽ⁿ⁾ = cθ⁽ⁿ⁾, where c is the slope of the line.

Statistics.

All statistical analyses were conducted using MATLAB (R2012a; MathWorks) or SPSS (version 21; IBM). Unless otherwise indicated, we used Student's t test, ANOVA, and repeated-measures ANOVA with Greenhouse–Geisser correction when Mauchly's test of sphericity failed. One-tailed tests were used when indicated when there was an a priori expectation of a directional effect.

Results

Effect of history of training on rate and endpoint of decay

We began by asking whether the decay of motor output that typically takes place in EC trials is influenced by initial training in a null field. In all previous publications of which we are aware, volunteers were initially trained in a null or baseline condition in which reaches were performed without a perturbation. We wondered whether this pretraining affected the motor output in the EC block. If so, training subjects with a different baseline, or without baseline training, might change the endpoint of the decay.

To answer this question, we compared performance of two groups of subjects. Group 1.1 trained for 300 trials in a counterclockwise field (Fig. 1B) but received no previous training in the null field (i.e., field was at full strength from the very first trial). In contrast, group 1.2 trained for 250 trials in a null field and was then exposed to the field (Fig. 1B). Both groups experienced a block of EC trials after field training. Our measure of motor output was an adaptation index, which quantified force produced in EC trials as a function of ideal forces needed to compensate for a counterclockwise force field. To assess performance, we considered the mean adaptation index at the end of field training (trials 500–550) and in the final 50 EC trials in the experiment (trials 1100–1150). We found that, by end of field training, performance in the two groups was comparable (Fig. 2A,B; adaptation index: mean ± SEM, group 1.1, 0.93 ± 0.04; group 1.2, 0.86 ± 0.03; two-tailed t test, p = 0.17). The motor outputs decayed rapidly over the course of ∼75 EC trials (Fig. 2C) but showed no additional decay over the next 500 trials (Fig. 2B). The decay endpoints were similar in the two groups (group 1.1, 0.21 ± 0.05; group 1.2, 0.26 ± 0.03; p = 0.41). Furthermore, after 600 EC trials, the motor outputs in both groups were still significantly greater than zero (one-tailed t test, group 1.1, p = 0.005; group 1.2, p = 2e-4). Therefore, motor output decayed in the EC trials whether or not subjects were exposed to the null field. The decay endpoint was not zero but a fraction of the motor output attained during training.

Figure 2.

Learning and decay in reaching movements in experiment 1. Motor output was quantified via an adaptation index. The adaptation index represents the linear regression of the ideal compensatory force profile onto the actual force profile measured in EC trials. Time course of the change in the adaptation index during baseline training and adaptation (A) and in final EC trials (B). C, Initial decay. Data are mean ± SEM across all subjects.

To further investigate the factors that contributed to the decay endpoint, we recruited a new group. Group 1.3 first trained in a clockwise field and then in a counterclockwise field (Fig. 1B). Subjects learned to compensate for the counterclockwise field as well as subjects in groups 1.1 and 1.2 (adaptation index: mean ± SEM, group 1.3, 0.89 ± 0.01; ANOVA, effect of group on training, p = 0.25). However, in EC trials, the motor output of group 1.3 declined somewhat faster than groups 1.1 and 1.2 (repeated-measures ANOVA for trials 550–625, significant within-subject interaction effect between group × trial number, p = 0.02) but had an endpoint that was similar to the two other groups (adaptation index: mean ± SEM, group 1.3, 0.28 ± 0.07; ANOVA, effect of group on endpoint, p = 0.57). This suggested that no matter which sequence of fields subjects trained in, decay endpoint was always a fraction of the last field to which they had been exposed.

To check the validity of this conclusion, we recruited a new group and tested them in a field opposite to all previous groups. Group 1.4 never trained in a null field and was only exposed to a clockwise field (Fig. 1B). In EC trials, the motor output of group 1.4 also declined (Fig. 2B). Like other groups, the decay endpoint for group 1.4 was a fraction of the motor output learned in the last set of FF trials (adaptation index: mean ± SEM, group 1.4, −0.19 ± 0.09; one-tailed t test, p = 0.04). We conducted an ANOVA to determine the effect of baseline (clockwise, null, or none) and training (clockwise or counterclockwise) on the decay endpoint in these four groups. There was a significant effect of training (p = 3e-4) but no effect of baseline (p = 0.67).

If subjects are reducing their motor output in EC trials to minimize the effort of their movements (Emken et al., 2007) or because a motor memory is passively being forgotten from trial to trial (Smith et al., 2006), we would expect decay endpoints to be zero. In contrast, our results show that decay endpoint is a non-zero fraction of the last motor output learned during training. Furthermore, our results show that, whereas the rate of decay depends on the sequence of fields that have been learned, the decay endpoint depends only on the final field that was learned.

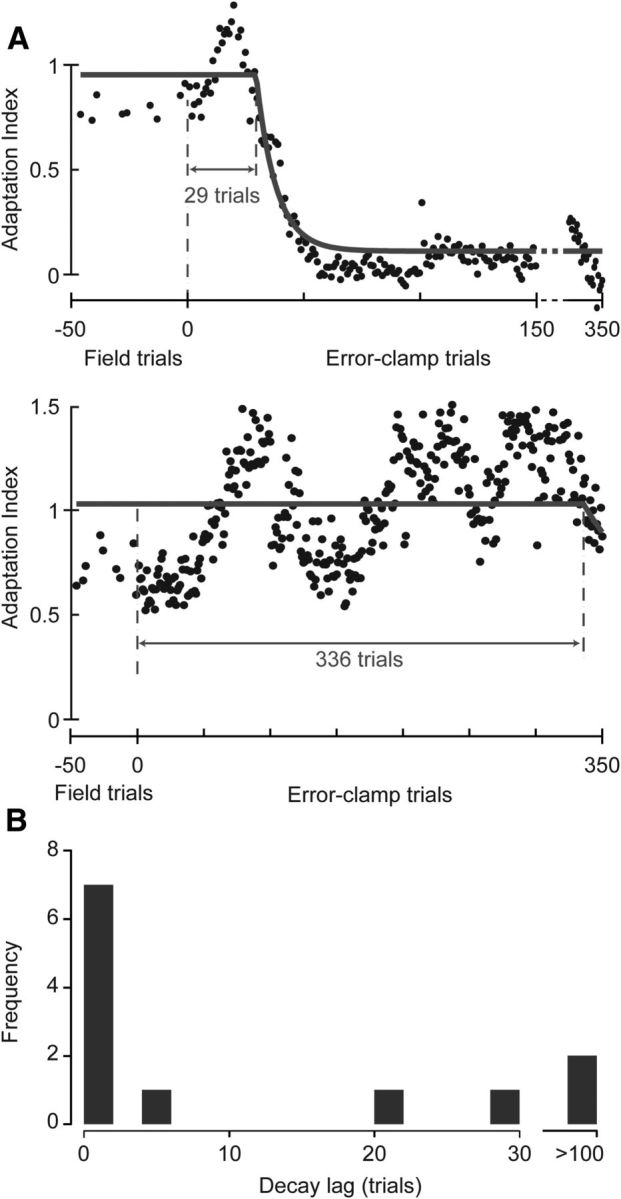
A lag to the start of the decay

In closely inspecting our data, we noticed that some subjects did not show a decay of their motor output at the onset of the EC trials. Rather, there were some subjects who displayed a lag to the start of the decay, as shown by the data from two subjects in Figure 3A. To quantify this pattern, for each subject, we fit a delayed exponential (Eq. 1) to the final 50 trials of adaptation and the 600 trials of the EC trials and estimated their lag λ (in units of trials). Across subjects, λ is a random variable with the distribution shown in Figure 3B. We found that, on average, there was a small but significant lag of 4.8 ± 1.3 trials (mean ± SEM; one-tailed t test, p = 7e-4). The lag was not different between groups (ANOVA, effect of group on delay, p = 0.98).

Figure 3.

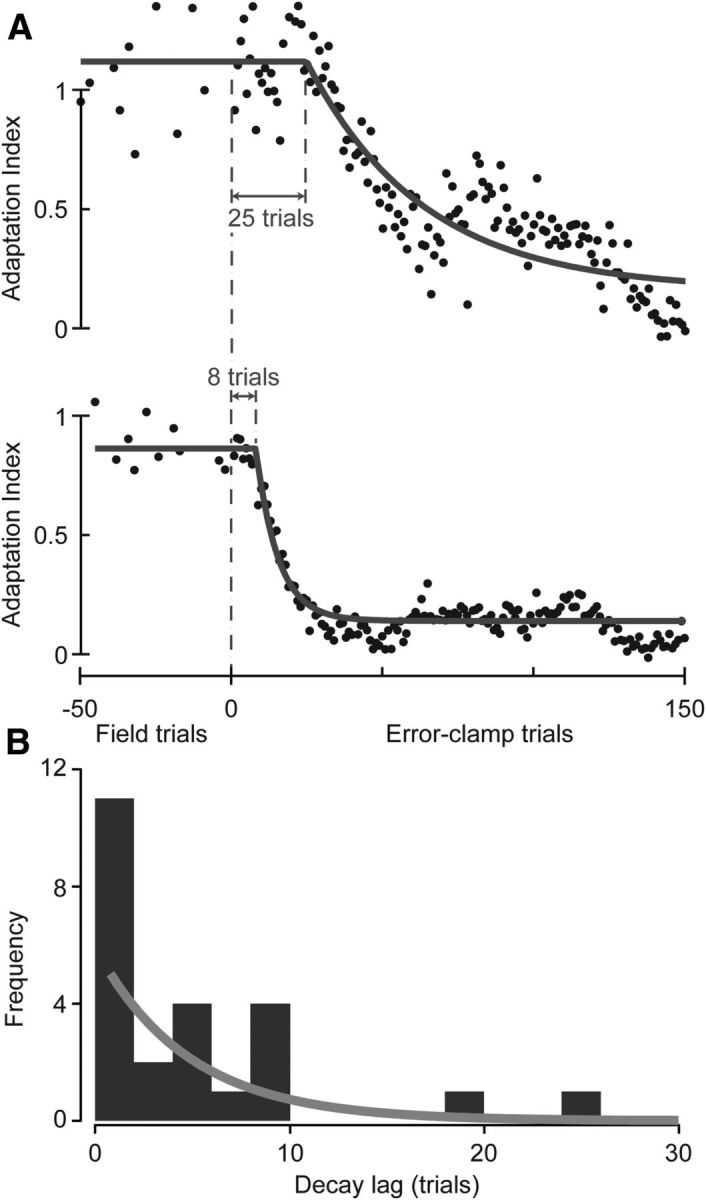
Lag to decay in reaching movements in experiment 1. A, Time course of the change in adaptation index in EC trials for two example subjects (top, group 1.7; bottom, group 1.1). A delayed exponential was fit to the data. B, Distribution of lags to the start of the decay for all subjects. The distribution was well fit by an exponential function (gray).

We next wanted to assess the distribution of the lags in this experiment. If the initiation of decay is a probabilistic event occurring independently on a trial-to-trial basis, we would expect the distribution of lags to be exponential. We computed the maximum likelihood fit of the decay lag λ to normal, Poisson, gamma, and exponential probability distributions and used the Akaike information criterion (AIC) to assess the relative quality of the fits. To fit a Poisson distribution, the lags were rounded to the nearest integer. To fit a gamma distribution, which has a probability of zero at zero, the distribution of the first trial of decay (i.e., lag plus one) was used. We found that the decay lag λ was best fit by an exponential probability distribution $P\left(\lambda \right)=\frac{1}{\beta }\exp \left(-\frac{\lambda }{\beta }\right)$, resulting in β = 4.8 trials (AIC: exponential, 125; normal, 160; Poisson, 238; gamma, 136). The 95% confidence interval of β was [3.3, 7.5] trials (goodness-of-fit log-likelihood of −62), further confirming that the mean of the distribution of the lags is quite likely to be greater than zero.

The data from experiment 1 (Fig. 3B) hinted that the start of the decay may be a probabilistic event: for many subjects, the decay started at the first EC trial, but for others started a few trials later. To explain this probabilistic behavior, we hypothesized that the decay of motor output may have been initiated when the brain detected a change from the FF to the EC trials.

To better understand what may be changing between these two block of trials, we quantified performance of each subject at the end of the FF trials (last 20 trials) and at the beginning of the EC trials (first 20 trials). The data are summarized for each subject in the left column of Figure 4. We found that, when subjects transitioned from field to EC trials in experiment 1, the EC trials made the movements artificially more straight (deviation of trajectories from a straight line: mean ± SEM, FF, 18 ± 2 cm²; EC, 0.15 ± 0.02 cm²; one-tailed t test of FF vs EC, p = 3e-7; Fig. 4A), more similar from trial to trial (intertrial correlation of velocity time series: FF, 0.41 ± 0.03; EC, 0.56 ± 0.03; p = 2e-4; Fig. 4B), more successful in terms of acquiring reward (probability of reward: FF, 0.43 ± 0.04; EC, 0.81 ± 0.02; p = 1e-9; Fig. 4C), and shorter in duration because of a need to make fewer corrections (movement duration: FF, 577 ± 13 ms; EC, 479 ± 12 ms; p = 1e-7; Fig. 4D). Therefore, at the onset of the EC block, there was a significant change in movement kinematics. It seems reasonable that the motor system detected some of these changes. We hypothesized that, if detection of these changes is partly responsible for the non-zero lag that we observed in the initiation of decay, then reducing the differences between FF and EC trials should increase the lag. We pursued this idea in experiments 2 and 3.

Figure 4.

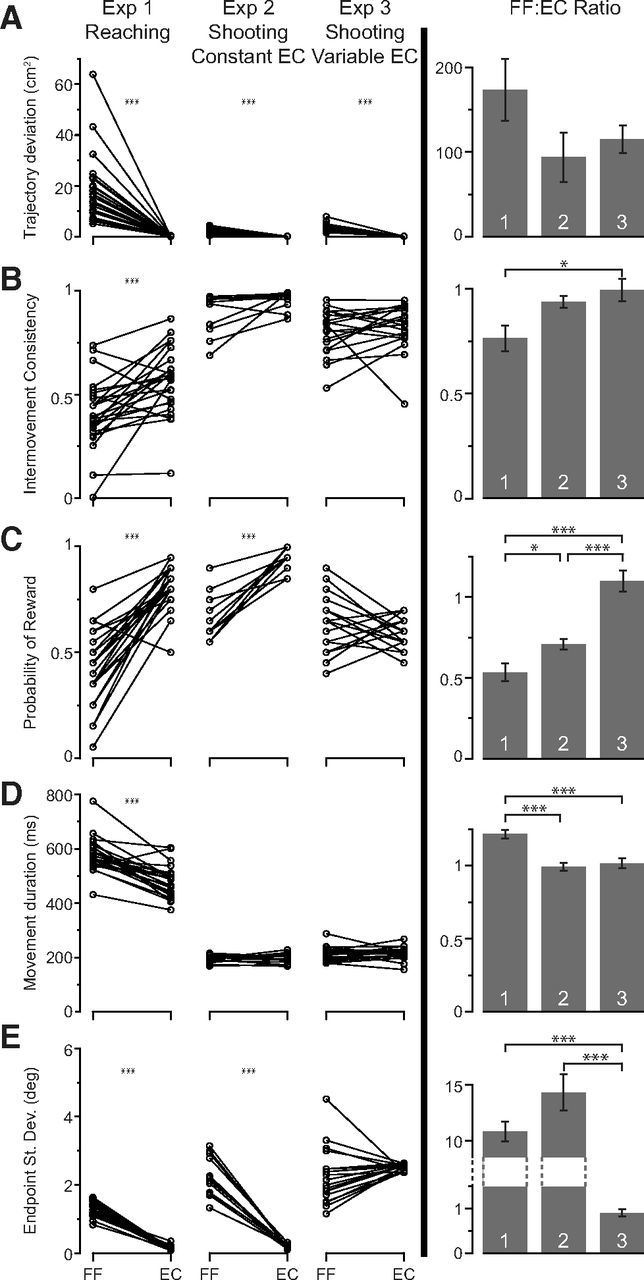
Change in behavior between the end of the FF trials (last 20 trials) and the beginning of the EC trials (first 20 trials). A, Trajectory deviation: sum of the squared deviation of each point in the trajectory from the straight line connecting the start to end positions. B, Intermovement consistency: correlation between the velocity time series from one trial to the next (Shadmehr and Mussa-Ivaldi, 1994). C, Probability of reward. D, Movement duration. E, Endpoint angle: the angle between the line from start to the target and the line connecting the start and end positions. Left column, The change in task parameters for reaching movements in experiment 1, shooting movements with constant error clamp in experiment 2, and shooting movements with variable error clamp in experiment 3. Lines are the mean (A–D) or SD (E) of the measure for each subject. One-tailed t test that consistency and reward increase, and deviation, duration, and endpoint variability decrease, in EC trials. Right column, The ratio of the value of each measure in FF trials to its value in EC trials (FF:EC ratio). A ratio of 1 indicates no change. Data are mean ± SEM across all subjects. One-tailed t test that FF:EC ratios of consistency and reward increase, and deviation, duration, and endpoint variability decrease, in later experiments. *p < 0.05, ***p < 0.001.

Increasing the lag

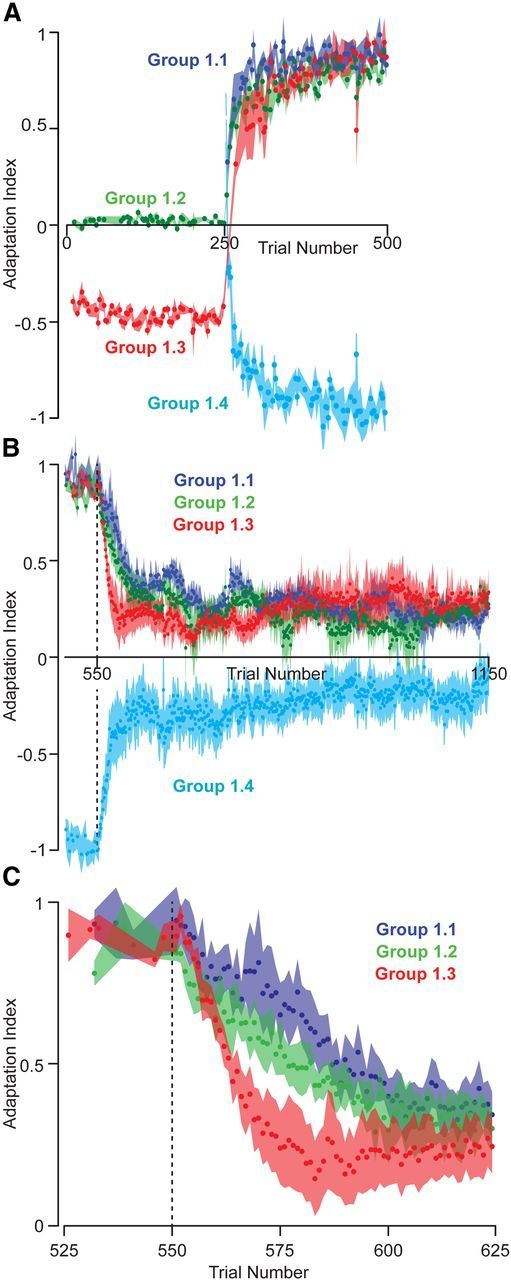
In experiment 2 (Fig. 1B), we asked subjects to make a shooting movement so that the hand went through and past the target and then hit a virtual pillow. In this paradigm, they did not have to correct their movements or stop at the target. Our logic was that, because a shooting movement to a target at a given distance is shorter in duration and is straighter than a reaching movement to the same target, in the shooting task performance at the end of the adaptation block might be more similar to the EC block, making it harder for the brain to detect a change. Indeed, we found that performance measures in the two blocks of trials were now more similar. The data for the shooting task are summarized for the last 20 FF trials and the first 20 EC trials in column labeled Exp. 2 in Figure 4. To quantify the change in performance from the end of FF trials to start of EC trials, we computed the ratio of the value of each measure in the FF trials to its value in EC trials (FF:EC ratio; Fig. 4, right column). We found that the change in performance from FF trials to EC trials was less pronounced in most measures in the shooting task compared with the reaching task (one tailed t test, straightness, p = 0.08; consistency, p = 0.03; reward, p = 0.02; movement time, p = 1e-5). Therefore, in the shooting paradigm (experiment 2), movements in the FF and EC blocks of trials were more similar than the reaching movements in the same two blocks of trials (experiment 1). Did this increased similarity affect the decay lags?

We quantified the lag to decay of motor output in the shooting experiment (experiment 2). Data from two subjects are shown in Figure 5A. In one of these subjects, we see a lag of 25 trials, whereas in the other subject, the motor output shows no decay for >300 trials. Interestingly, most subjects, including those who show decay in motor output, did not report observing any changes in the dynamics of the manipulandum when asked after the experiment was complete. However, when asked about her perceptions of the experiment, the latter subject (Fig. 5A, bottom) reported noticing that the manipulandum was pushing her to the left and then began to make her movements straight, but she showed no evidence of decay. Together, these suggest that explicit awareness of the change in the task may be independent of the detection of a change by the motor system.

The distribution of lags for the entire population of subjects in experiment 2 is shown in Figure 5B. We fit the data in Figure 5B to an exponential probability distribution, $P\left(\lambda \right)=\frac{1}{\beta }\exp \left(-\frac{\lambda }{\beta }\right)$, and found that β = 44 trials (95% confidence interval of [27, 86] trials, goodness-of-fit log-likelihood of −57). In comparing the lag distributions in experiment 1 and experiment 2, we find that the mean lag is significantly greater in experiment 2 than in experiment 1 (mean ± SEM, experiment 2, 44.3 ± 28.8 trials; one-tailed t test, p = 0.03). Furthermore, we find that the mean of the lag distribution β has increased by an order of magnitude, and the 95% confidence intervals are well separated. In summary, as we increased the similarity between the movements in the FF and EC blocks of trials, we found an increase in the decay lags.

To pursue this idea further, we considered an experiment (experiment 3) in which we attempted to delay the decay indefinitely by making the characteristics of movements in the error clamp more closely match the statistics of movements that subjects produced at the end of training in the FF trials. To do so, we focused on two variables: (1) probability of success, a variable that was shown previously by Pekny et al. (2011) to act as a cue for the brain to detect a change in the properties of the task, and (2) the trial-to-trial variance of movements. In the column marked Exp. 2 in Figure 4, we see that probability of reward increased significantly from the end of FF trials to start of the EC block (one-tailed t test, p = 2e-6). Similarly, the SD of movement endpoints decreased significantly during these two periods (one-tailed t test, p = 5e-8). In experiment 3, we attempted to make these two measures more similar in the FF and EC trials. To achieve this goal, we introduced trial-to-trial variance in the EC trials that matched the variance of movement endpoints at the end of training in the FF trials.

In the final FF trials of experiment 2, subjects on average had a movement endpoint 0.2° to the right of center of the target (target was 5.7° in width), with an average within-subject SD of 2.6°. In experiment 3, we again considered shooting movements, but we varied the endpoint of the line to which subjects were constrained in the EC trials to match the variability of movement endpoints of subjects in the final FF trials of experiment 2. The resulting movements are summarized in the column marked experiment 3 in Figure 4. We found that endpoint SD, movement duration, probability of reward, and intermovement consistency were now similar at the end of the FF block and the beginning of the EC block (FF:EC ratio significantly different from 1; two-tailed t test, p = 0.21, p = 0.65, p = 0.15, and p = 0.93 respectively). Therefore, by making the EC trials slightly variable in experiment 3, we were better able to match the statistics of FF and EC trials.

Interestingly, a large fraction of subjects in experiment 3 showed no appreciable decay in their motor output, even after 100 or more EC trials. Data from two of these subjects are shown in Figure 6A. As a population, we observed a mean decay lag of 96.1 ± 27 trials (mean ± SEM) (Fig. 6B). Eight of the 19 subjects in this group had a lag of >100 trials. Indeed, as a group, there was no evidence of decay in the EC trials (Fig. 6C). The lack of decay cannot be attributable to the small bias in the endpoint distribution of the movements in the EC block: the bias in the mean angular deviation of these EC trials is equivalent to a 0.3 mm lateral deviation to the right at the end of the movement, well within the target width of 1 cm. Compensation of this bias by the subject would require 0.21 N of force to the left at the end of the movement. Subjects instead maintain a force of 6.7 ± 1.0 N to the right (mean ± SEM, EC trials 100–120) in the final 50 ms of their movement in EC trials.

Figure 6.

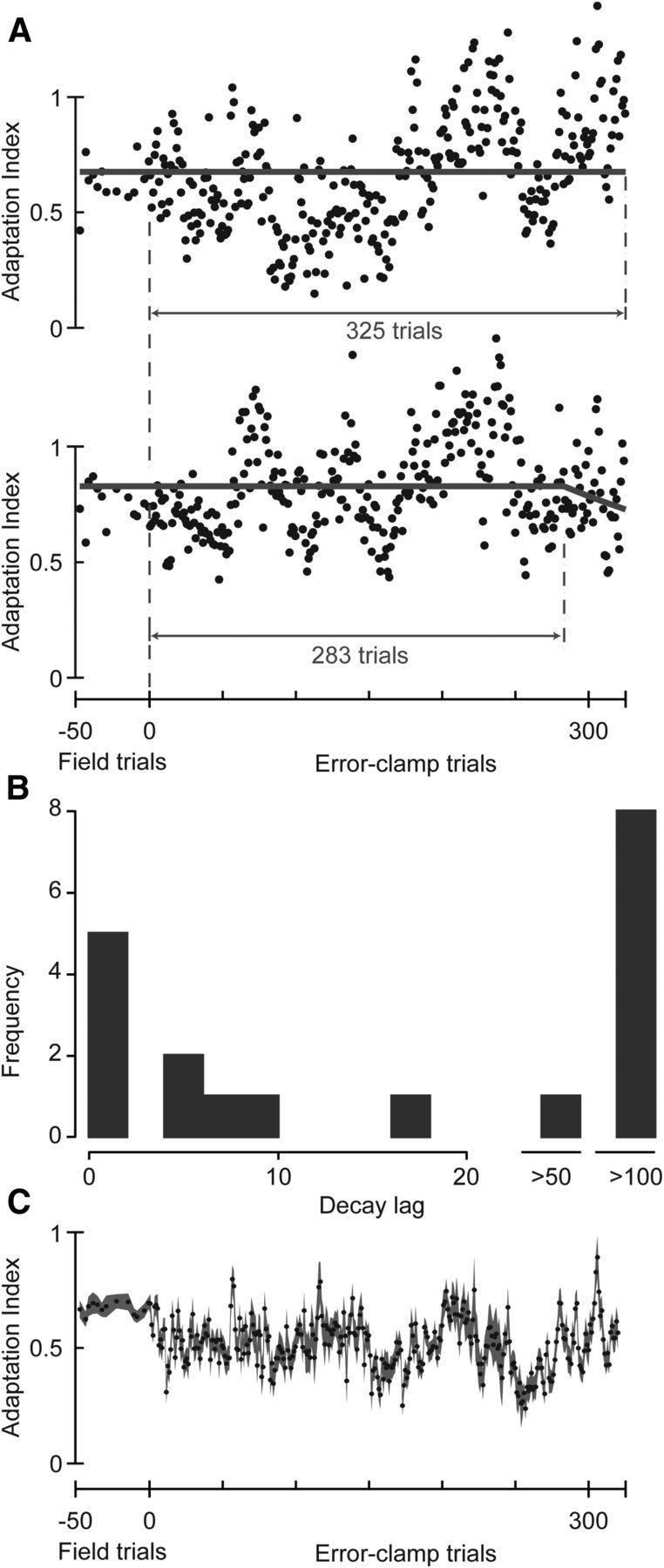
Lag to decay in shooting movements with variable EC trials in experiment 3. A, Time course of the change in adaptation index in EC trials for two example subjects. Both subjects were in group 3.1. A delayed exponential was fit to the data. B, Distribution of lags to the start of the decay for all subjects. C, Time course of the change in adaptation index in EC trials for all subjects. Data are mean ± SEM across subjects.

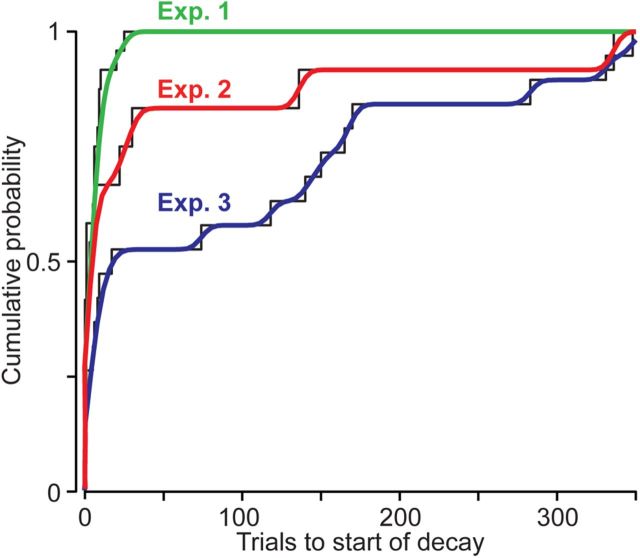
One way to compare the decay lags in the various experiments is to consider the cumulative probability distribution of lags in each experiment (Fig. 7). These distributions allow us to estimate at what trial we can say with some reasonable certainty that the decay will have started in most subjects. As we moved from reaching to shooting, the decay lag (with 75% certainty) in the EC block shifted from six trials in experiment 1 to 22 trials in experiment 2. When we made the EC trials more closely resemble FF trials, the decay lag shifted (with 75% certainty) from 22 trials in experiment 2 to 165 trials in experiment 3. Of course, at 95% certainty, these numbers are even farther apart. Therefore, the start of decay in motor output is a probabilistic event that can be manipulated by altering the properties of EC trials.

Figure 7.

Cumulative probability distribution of the lag to decay in experiments 1–3. An estimated cumulative probability density estimate for each experiment (in color) is overlaid on the data (black).

Predicting the lag of an individual

We next considered whether the changes in movement kinematics from the FF to EC trials can be used to predict the lag to decay for individual subjects. For each experiment, we used a multiple linear regression model, with the FF:EC ratio of each subject's straightness, consistency, reward, movement time, and endpoint variability as predictors of their lag. We also included the mean and variability of the adaptation index at the end of field training as additional predictors and a constant term. For each experiment, the value of these parameters did not linearly predict the lag to decay (experiment 1: R² = 0.17, F test, p = 0.854; experiment 2: R² = 0.62, F test, p = 0.556; experiment 3: R² = 0.22, F test, p = 0.856). This suggests that the motor system of different subjects may be weighing these parameters differently, so a single linear model for all subjects is not appropriate. Alternatively, other, related parameters may be driving the process of change detection, or these parameters may have a nonlinear effect.

Predictions of two-state model

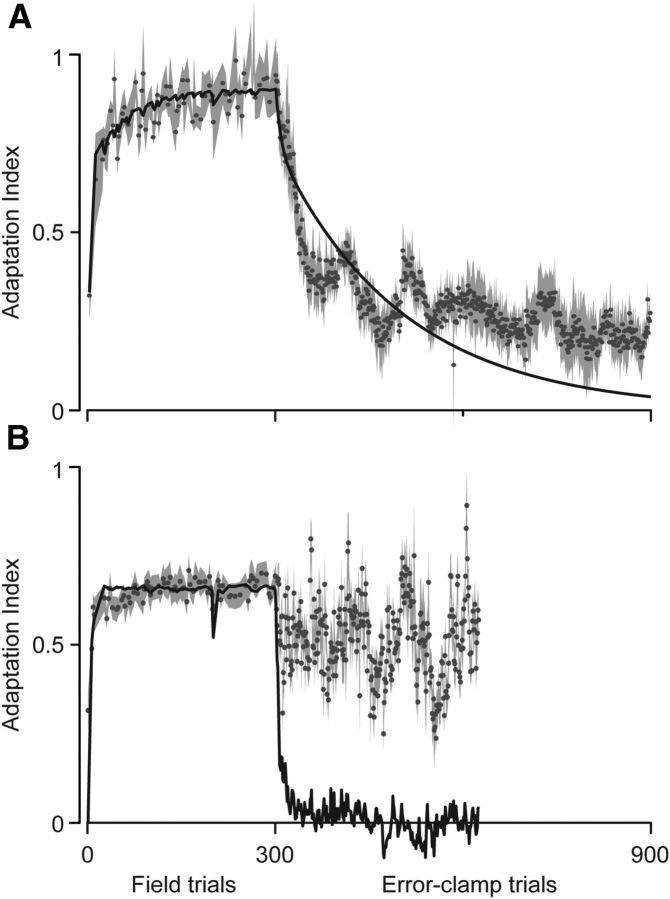
We compared our results to the predictions of a two-state model that we previously proposed to describe the process of adaptation (Smith et al., 2006). This model has been successful in fitting performance during adaptation trials in several previous experiments (Kording et al., 2007; Ethier et al., 2008; Joiner and Smith, 2008; Keisler and Shadmehr, 2010; Sing and Smith, 2010). Furthermore, for these experiments, the two-state model is equivalent to the multiple-context model proposed by Lee and Schweighofer (2009) in which large errors signal a contextual switch for the slow state. This is because, in some of our groups, subjects did not receive baseline training and accordingly were exposed to only one context, because no large errors are presented in EC trials to signal a contextual switch. We were interested in determining the extent to which these models could account for the data during EC trials.

We fit the two-state model to subjects' performance during FF trials in experiment 1.1 and used the parameters to predict subjects' behavior in EC trials. The results are shown in Figure 8A. The two-state model fits the FF trial data well (A_f = 0.876, B_f = 0.315, A_s = 0.995, B_s = 0.056, R² = 0.68 for trials 1–300). It also appears to provide a good prediction of the behavior in EC trials (R² = 0.71 for trials 301–900). However, there are two fundamental differences between the predictions of the model and the actual data. First, the model predicts that the decay in motor output will always begin at the onset of the EC block, whereas the data suggest that the initiation of decay is a probabilistic event that depends on the similarity between movements in these two blocks of trials. Second, in the model, the endpoint of the decay is zero, whereas in the data, the endpoint is a fraction of the motor commands that were produced in the FF trials. This suggests that, if decay is attributable to de-instantiation of motor memory, it is only effective for a component of that memory and not its entirety.

Figure 8.

Predictions of the two-state model for experiment 1.1 (A) and experiment 3.1 (B). The model (black line) was fit to the behavior during field training for each experiment and used to predict behavior on the 600 constant (A) or 325 variable (B) EC trials. Data (gray) are the time course of the change in the adaptation index, mean ± SEM across all subjects.

Finally, we fit the model to subjects' performance during FF trials in experiment 3.1 and used the parameters to predict subjects' behavior in the variable EC block (Fig. 8B). Again, the model fits the field data well (A_f = 0.432, B_f = 0.422, A_s = 0.938, B_s = 0.199, R² = 0.69 for trials 1–300). However, the two-state model does not predict the lack of decay in variable EC trials (R² = 0.07 for trials 301–625). Rather, in the variable EC block, the model predicts rapid decay of motor output to zero.

Discussion

A few hundred movements with a novel tool can produce a motor memory that can persist for days, weeks, or months after training (Shadmehr and Brashers-Krug, 1997; Joiner and Smith, 2008). However, motor memories have been considered inherently transient; that is, in the absence of an error signal, the motor output that was acquired during training decays immediately and automatically. This decay has been attributed to a number of possible processes, including trial-to-trial forgetting (Smith et al., 2006; Criscimagna-Hemminger and Shadmehr, 2008; Joiner and Smith, 2008; Galea et al., 2011) and optimization of effort (Emken et al., 2007; Ganesh et al., 2010). Our results challenge these views and suggest that decay is not forgetting or optimization in the absence of error but a reflection of de-instantiation of a component of motor memory.

We considered a standard reach task in a force field and made three observations. First, decay of motor output in EC trials was not to zero but to an endpoint that was a non-zero fraction of the motor output in the last field subjects trained in. This observation was independent of the long-term history of training. Second, the rate of decay was biased by the history of training, because previous training in null or the opposite field accelerated the rates of decay. Third, there was a lag to the initiation of decay. The lag was a probabilistic variable that differed among subjects: occasionally, a subject would show little or no decay for many EC trials and then initiate decay. We were able to extend this lag significantly by making EC trials more closely resemble FF trials during learning.

Our results challenge three assumptions in current models of motor learning. The first assumption is that decay or removal of a memory in absence of error is an inherent part of motor memories, often attributed to a process of forgetting (Cheng and Sabes, 2006; Smith et al., 2006; Kording et al., 2007; Zarahn et al., 2008). Although others have shown that reinforced memories persist and can be recalled later (Pekny et al., 2011; Shmuelof et al., 2012), our results suggest for the first time that the reduction in motor output in EC trials is tied to a probabilistic event that depends on change detection in the parameters of the task. Once a change is detected, decay follows, suggesting that decay is a form of de-instantiation and not an inherent part of the acquired memory, i.e., decay is an active process that is initiated after an event is detected. We speculate that, when the motor system detects a change in the parameters of the task, it de-instantiates part of the motor memory, which behaviorally masquerades as decay.

Second, our results are inconsistent with the assumption that decay is attributable to minimization of effort, a hypothesis proposed by Emken et al. (2007). In this case, one would expect the endpoint of decay to be independent of the training schedule. Here, we found that the endpoint of decay was a non-zero fraction of the last field subjects learned. For example, subjects who most recently trained in a counterclockwise field maintained a significant component of their recently learned motor output for 600 trials, although the training was only for 300 trials, whereas subjects who most recently trained in a clockwise field maintained a significant component in the opposite direction.

Third, our results suggest that retention of a motor memory, as assayed in movements in the absence of error, consists of not one but multiple processes: (1) a process that detects a change in context, behaviorally assayed via the decay lag; (2) a process that de-instantiates a component of the memory, behaviorally assayed via the rate of decay; and (3) a component of the memory that appears immune to this process of de-instantiation, behaviorally assayed via the endpoint of decay.

We interpret our results as follows. Motor memories consist of multiple components: (1) one component that can be easily de-instantiated as task parameters change and (2) another component that is resistant to de-instantiation, expressed as decay endpoint. A recent brain stimulation study suggests a role for the primary motor cortex (M1) in the persistent component of motor memory, i.e., the endpoint of decay. Galea et al. (2011) trained subjects in a visuomotor rotation task. After subjects learned to compensate for the visual perturbation, they made movements in a series of trials in which no visual feedback was presented, akin to EC trials in force field learning. Galea et al. (2011) applied transcranial direct current stimulation (tDCS) to M1 and found that the stimulation had no effect on rates of acquisition compared with a sham group. However, M1 tDCS significantly elevated the endpoint of the decay. This suggests a role for M1 in the persistent component of memories, assayed by the endpoint, at least for a visuomotor rotation task. Because M1 has been shown to be involved in use-dependent plasticity (Bütefisch et al., 2004), it is plausible this memory may develop in M1 through repetition and reinforcement.

Recently, Huang et al. (2011) suggested that learning to compensate for a perturbation installs a motor memory that may have three components: (1) a forward model that associates motor commands with their sensory consequences and learns from prediction errors (Izawa et al., 2012; Schaefer et al., 2012); (2) a bias in motor output that develops because of repetition of the motor commands (Diedrichsen et al., 2010; Verstynen and Sabes, 2011); and (3) a reinforcement-dependent bias that develops because of reward-dependent association between stimuli and the resulting motor commands (Huang et al., 2011; Izawa et al., 2012; Shmuelof et al., 2012). One may speculate that the decay endpoint in our data is the motor output that is being expressed by one of these processes, perhaps the process that learns from repetition and/or reinforcement.

We observed that the rate of decay was modulated by the history of training (experiment 1). Pekny et al. (2011) demonstrated that, in EC trials, when a change was inserted by manipulating reward feedback, previous motor memories were transiently recalled. The magnitude of recall was comparable with the magnitude of the persistent component of memory in that work. We speculate that the persistent component of memories is briefly recalled when a change is detected, resulting in the changes in rates of decay. Alternatively, Huang and Shadmehr (2009) showed that the statistics of the history of training played a role in the subsequent rate of decay in EC trials. Although this finding cannot explain the recall of memory in the study by Pekny et al. (2011), in our work, it may be that groups 1.2 and 1.3 have experienced larger errors than group 1.1 and so decay faster. Once a change is detected, a combination of recall of previous memories and sensitivity to task statistics likely play a role in the process of de-instantiation.

We hypothesized that the similarity between FF and EC trials was a key factor in detecting a change and indeed showed that, by making these trials more similar, the lag to decay could be extended. However, one limitation of our work is that, using a linear model, we could not explain why a given subject produced their particular lag in a given experiment. That is, although our interpretations are likely true in a probabilistic sense, we have not shown that subjects who show greater lag in a given experiment are also those whose movements are more similar in the field and EC blocks. It is possible that individual subjects weigh different kinematic and task factors differently, and so a single model across subjects is not appropriate, or these or other parameters may have an nonlinear effect. This question would benefit from additional exploration in future work.

We also observed that, in experiment 2 and experiment 3, subjects had trial-to-trial variability in their behavior during the EC block before the onset of decay. In experiment 3, this may be, in part, a result of learning from the errors presented in the variable EC trials. However, learning from error cannot explain the variability seen in the constant EC trials in experiment 2, because no errors are presented. The low frequency of that variability in experiment 2 suggests the behavior is not simply noise in the motor output. Subjects may be exploring their environment, or the variability may be a manifestation of the instability of the component of the motor memory that will be de-instantiated.

In summary, we offer evidence that adaptation installs two distinct types of motor memory: (1) one that is actively de-instantiated during detection of change in the environment and (2) one that persists despite that detection.