Enthalpic Barriers Dominate the Folding and Unfolding of the Human Cu,Zn Superoxide Dismutase Monomer

Abstract

The rate-limiting step in the formation of the native dimeric state of human Cu, Zn superoxide dismutase (SOD1) is a very slow monomer folding reaction that governs the lifetime of its unfolded state. Mutations at dozens of sites in SOD1 are known to cause a fatal motor neuron disease, amyotrophic lateral sclerosis, and recent experiments implicate the unfolded state as a source of soluble oligomers and histologically observable aggregates thought to be responsible for toxicity. To determine the thermodynamic properties of the transition state ensemble (TSE) limiting the folding of this high contact order β-sandwich motif, a combined thermal/urea denaturation thermodynamic/kinetic analysis was performed. The barriers to folding and unfolding are dominated by the activation enthalpy at 298 K and neutral pH; the activation entropy is favorable and reduces the barrier height for both reactions. The absence of secondary structure formation or large-scale chain collapse prior to crossing the barrier for folding led to the conclusion that dehydration of nonpolar surfaces in the TSE is responsible for the large and positive activation enthalpy. Although the activation entropy favors the folding reaction, the transition from the unfolded state to the native state is entropically disfavored at 298 K. The opposing entropic contributions to the free energies of the TSE and the native state during folding provide insights into structural properties of the TSE. The results also imply a crucial role for water in governing the productive folding reaction and enhancing the propensity for the aggregation of SOD1.

INTRODUCTION

Landscape Theory proposes that unfolded proteins access their native conformations by a random search over a funnel-shaped energy surface that progressively constraints the conformational entropy.¹ Experimental evidence consistent with an important role for the loss in chain entropy during folding can be found in the inverse correlation of the logarithm of the folding rate constants of dozens of small two-state folders with the contact order, a metric related to the proportion of short- and long-range contacts in the native conformation.² Proteins with a higher fraction of long-range contacts tend to fold more slowly, implying a more convoluted search process. However, the considerable variation in the folding rate constants for proteins with similar motifs but different sequences and the systematic differences in the rate constants between motifs (α, β, α/β) shows that the chain entropy penalty in folding can be significantly modulated by the sequence and the motif.³

Counterbalancing almost precisely the chain entropy penalty in folding is the gain in solvent entropy when water is released from the backbone and freed from constraints imposed by exposure to nonpolar side chains in the unfolded state. The maximum in the stability, i.e., the maximum free energy of folding, for many globular proteins occurs in the range from 5–25 °C.⁴ The entropy change for the folding reaction at the temperature of maximum stability is, from standard thermodynamic relationships, equal to zero: ${\left(\frac{\partial \mathrm{\Delta }{G}^0}{\partial T}\right)}_P=-\mathrm{\Delta }S=0$.⁵ Thus, although large and opposing contributions to the entropy are involved, the free energy of folding is dominated by enthalpic contributions for most proteins near room temperature. To reconcile these potentially conflicting kinetic and thermodynamic views of the forces driving folding reactions, it is useful to consider the thermodynamic properties of the transition state ensemble (TSE) that separates the native and unfolded states.

The thermodynamic properties of TSEs may also have profound clinical implications, a case in point being dimeric human superoxide dismutase. Dozens of mutations in the SOD1 gene lead to the formation of soluble oligomeric and/or histologically-observable aggregates of SOD1 protein which are potential sources of toxicity in amyotrophic lateral sclerosis (ALS),⁶ an invariably fatal motor neuron disease (see http://alsod.iop.kcl.ac.uk/ for a complete list of known mutations). Although the exact nature of the toxic species remains controversial,^9–13 a candidate of recent interest is the monomeric unfolded state. Metal loss has been implicated as a preliminary step in the aggregation pathway and the existence of disease variants with WT-like stability in the metal-free state¹⁶ suggests that apo-SOD1 is inherently aggregation prone. Furthermore, several of the most widely studied SOD1 mutations dramatically increase the population of the unfolded state, especially in the absence of metals,^17–19 and the concentration of the unfolded state has been shown to be directly correlated with the rate of aggregation in vitro.²⁰ Given the possibility that the unfolded state may be responsible for nucleating the aggregation reaction of ALS-variants., the thermodynamic properties of the TSE that governs its lifetime become relevant to disease.

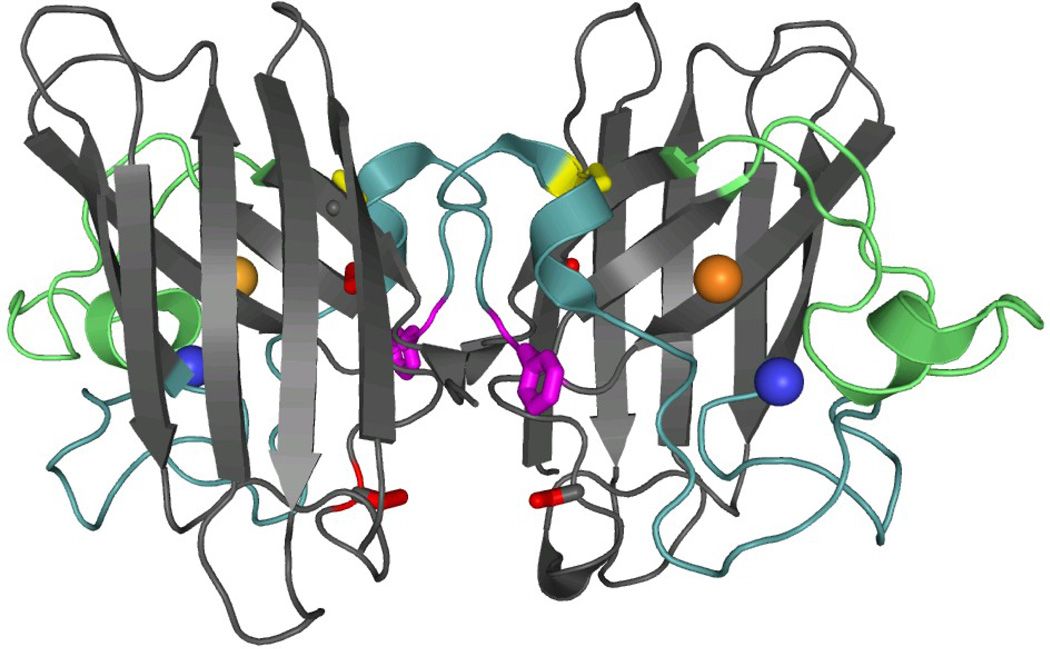
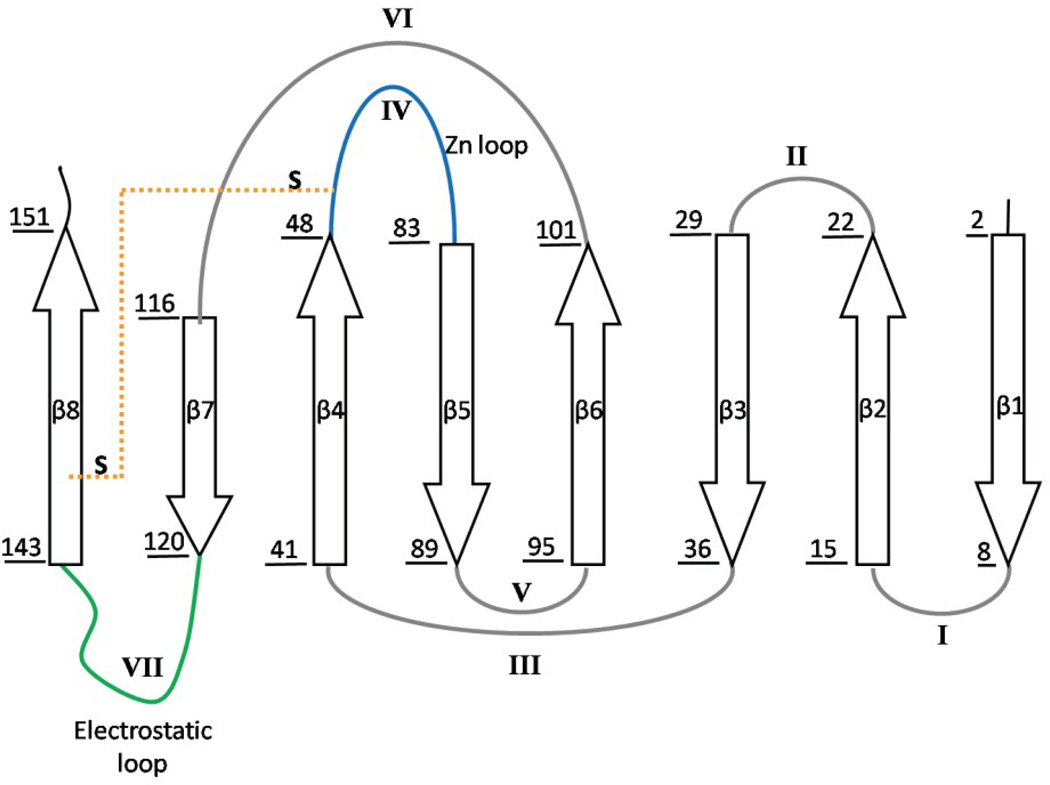
SOD1 is primarily a cytosolic protein responsible for the dismutation of the highly reactive superoxide anion (O_2⁻) into peroxide and oxygen. The protein is a homodimer with one catalytic copper ion and one structural zinc ion bound to each subunit (Figure 1A). The fold can be described as a β-sandwich, with eight anti-parallel β-strands supporting two large loops that dock on the surface of the protein (Figure 1B). Loop IV, the Zn binding loop, plays an important role in stabilizing the native conformation in the presence of Zn, and Loop VII, the electrostatic loop, guides the substrate to the active site.⁹ In the absence of the metals, as in the present study, these loops have been shown to be intrinsically disordered by NMR spectroscopy²⁴ and x-ray crystallography.²⁵ Each subunit also features an intramolecular disulfide bond between C57 and C146 that links Loop IV and β8.

Figure 1. Crystal structure and topology of SOD1.

A) SOD1 is a dimeric β-sandwich protein consisting of eight anti-parallel β-stands supporting two catalytic loops (PDB: 2C9V). The electrostatic loop is depicted in green, while the Zn-binding loop is depicted in cyan. Each monomeric subunit also contains a Zn (blue sphere) and Cu ion (orange sphere), which were not present for this study, as well as an intramolecular disulfide bond (yellow). The free cysteines, C6/C111 (red), were replaced with alanine and serine respectively. Additionally, a pair of glutamic acid residues was introduced in the dimer interface, replacing F50/G51 (violet), in order to obtain the obligate monomer, mSOD1*. B) The topology of SOD1 has the immunoglobulin fold. It is made up of two β-sheetsconsisting of strands β1β2β3β6 and β5β4β7β8, and contains a Greek-key motif. The loops have been labeled with sequential Roman numerals.

The folding mechanism of SOD1 can be best described as a three-state reaction,^26–28 2U⇆2M⇆N₂, in which the rate-limiting monomer folding reaction from the unfolded state, U, to the folded state, M, is followed by the rapid self-association to form the dimeric native state, N₂. Previous studies on a stable monomer variant (herein referred to as mSOD1*, see Introduction to Results) have found that the folding reaction is well described by a two-state process. Relevant to the activation free energy barrier for the folding of the monomer, the native conformation of SOD1 is dominated by nonlocal interactions that would be expected to raise the magnitude of the entropic contribution and further enhance the propensity for aggregation by increasing the lifetime of the unfolded state. Mutational analysis of the side chains that stabilize the TSE in the absence of Zn revealed key roles for residues in β1, β2, β3, β4 and β7; with the exception of β1, the TSE involves the interior β-strands of the β-sandwich (Figure 1).²⁹ Post-translational modifications that enhance the connectivity of SOD1 also accelerate refolding. Although the disulfide bond only accelerates the folding reaction by 2-fold,¹⁹ the pre-organization of the Zn binding loop,³⁰ or possibly the Cu binding site,³¹ by Zn speeds the folding by ~100-fold.³⁰ A comprehensive analysis of the thermodynamic properties of the TSE for mSOD1* revealed that the unfolding and refolding reactions are dominated by the activation enthalpy at 298 K. However, unlike the slightly unfavorable entropy difference for folding between the unfolded and native states at this temperature, the activation entropy for folding favors the formation of the TSE. Thus, the enthalpy/entropy compensation evolves during folding so as to enhance the formation of the TSE for SOD1 and speed the formation of the native conformation. Although the barrier for the folding reaction is dominated by the activation enthalpy, the activation entropy and the attendant chain entropy penalty modulate the barrier. The long lifetime of the U state for SOD1 reflects both the inherently more complex search process for a TSE dominated by long-range interactions and, we propose, the necessity to simultaneously dehydrate a large nonpolar surface to reach the TSE. The long lifetime would also increase the opportunity for both WT and ALS-variants to aggregate prior to folding.

RESULTS

Monomeric SOD1

To avoid complications related to the dimer association/dissociation reactions in wild-type SOD1, a stable monomeric version of SOD1 was created by replacing two nonpolar interface residues with glutamic acid, F50E/G51E (Figure 1A).³² To preclude disulfide scrambling in the unfolded state, the two natural cysteines at positions 6 and 111 were replaced with alanine and serine, respectively, C6A/C111S.³³ The removal of the free cysteines, combined with the absence of methionine residues in the protein, also reduces the possibility of increased oxidative damage associated with folding experiments above room temperature. The quadruple mutant, C6A/F50E/G51E/C111S, is designated as mSOD1*. All experiments were performed on mSOD1* where the native disulfide bond between C57 and C146 was intact. The disulfide-containing species was chosen to enable measurement of the folding properties over a temperature range sufficient to insure the accuracy of the extracted thermodynamic parameters. Because the structures of oxidized and reduced SOD1 are very similar by NMR³⁴ and the presence of the disulfide bond only accelerates the refolding reaction by 2-fold,¹⁹ we presume that the results for the oxidized protein will be pertinent to its reduced counterpart.

Thermodynamic properties of the mSOD1* folding reaction

Free Energy Change

To provide a framework for the thermodynamic analysis of the TSE, we investigated the thermodynamic properties of the equilibrium unfolding transition between the M and U states of mSOD1*. The strategy involved performing reversible urea titrations at a series of temperatures between 285 and 313 K (Figures S1A and S1B) and fitting the ellipticity changes at 215–240 nm to a two-state model that assumes a linear dependence of the free energy of folding on the denaturant concentration.³⁰ The change in ellipticity at 230 nm, chosen to avoid the absorbance of light by urea at the typical minimum for β-sandwich proteins, 216–218 nm, reveal a cooperative unfolding transition (Figure S1). It has previously been shown that the amplitude of the small positive band at 230 nm reflects the integrity of the native conformation for mSOD1*.²⁷ The free energy of folding in the absence of urea as a function of temperature is shown in Figure 2A.

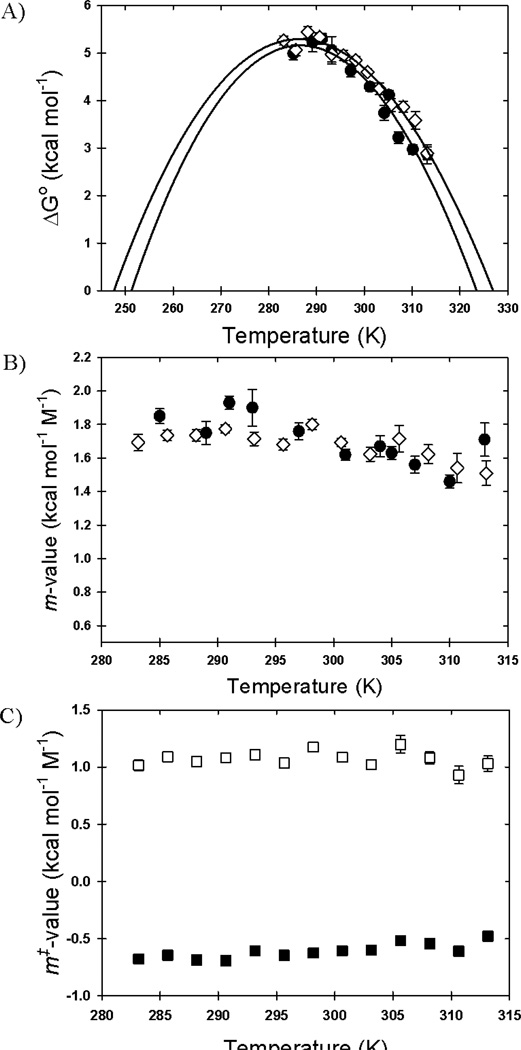
Figure 2. Temperature dependence of the ΔG⁰, m-values and m^‡-values.

A) The free energy of folding in the absence of denaturant and B) the m-values of folding are shown as a function of temperature as derived from kinetic (open diamonds) and equilibrium (filled circles) experiments. C) The refolding (open squares), and unfolding (filled squares) kinetic m^‡-values are shown as a function of temperature. The error bars represent the standard deviation of the fit. The solid linesin panel A represent the best fit to the Gibbs-Helmholtz equation (Equation 1).

The stability increases from 5.26 kcal mol⁻¹ at 285 K to a maximum value of 5.45 kcal mol⁻¹ at ~291 K and then decreases to 2.9 kcal mol⁻¹ at 313 K. This behavior is typical of globular proteins and reflects the interplay between enthalpic, entropic, and heat capacity changes accompanying unfolding reactions.⁴ Within the estimated errors, the m-values change little across this temperature range (Figure 2B), implying that the buried surface area changes are not sensitive to temperature. By inference, the heat capacity change, proportional to the change in buried surface area,³⁵ is also independent of temperature across this range.

Enthalpy and Heat Capacity Changes

To extract the enthalpy and heat capacity changes for unfolding, the dependence of the free energy of unfolding on the temperature for a two-state process can be described by the modified Gibbs-Helmholtz equation:

$$\mathrm{\Delta }{G}^0(T)=\mathrm{\Delta }{H}_m(1-\frac{T}{T_m})-\mathrm{\Delta }{C_p}^0((T_m-T)+T\mathrm{l}\mathrm{n}(\frac{T}{T_m}))$$ (1)

where T_m corresponds to the melting temperature, ΔH_m correspond the enthalpy of unfolding at the melting temperature and ΔC_p⁰ is the heat capacity change upon unfolding at the standard state. The fit of the data in Figure 2A to Equation 1, with the assumption of a temperature-independent heat capacity change and interpolating to the standard state, yields a ΔH⁰ of 31.2±4.3 kcal mol⁻¹ and a ΔC_p⁰ of 2.27±0.69 kcal mol⁻¹ K⁻¹ for the unfolding of the M state to the U state at 298 K (Table 1). By carrying out a secondary calculation, the entropy change at the standard state can be calculated: ΔS⁰ = (ΔH⁰ − ΔG⁰)/T⁰ = 89±14 cal mol⁻¹ K⁻¹ (Table 1).

Table 1.

Thermodynamic parameters of folding and the transition state ensemble of mSOD1* at 298 K and pH 7.2.^a

	ΔH0 (kcal mol−1)	ΔS0 (cal mol−1 K−1)	−TΔS0 (kcal mol−1 K−1)	ΔCp0 (kcal mol−1 K−1)	ΔG0 (kcal mol−1)
M⇆U: Equilibrium	31.2 ± 4.3	89±14	−26.5±4.5	2.27 ± 0.69	4.64±0.14b
M⇆U: Kinetics	28.0 ± 1.9	78±6	−23.3±1.8	1.93 ± 0.27	4.84±0.08c
	ΔH0‡ (kcal mol−1)	ΔS0‡ (cal mol−1 K−1)	−TΔS0‡ (kcal mol−1 K−1)	ΔCp0‡ (kcal mol−1 K−1)	ΔG0‡ (kcal mol−1)
U→TSE	16.7±0.6	12±2	−3.6±0.6	−0.85±0.12	13.1±0.1d
N→TSE	45.6±1.7	93±6	−27.7±1.8	1.06±0.37	18.0±0.1d
M⇆Ue	28.9±1.8	81±7	−24.1±2.1	1.91±0.39	4.9±0.1

^aThe thermodynamic parameters were calculated by fitting the observed stabilities or folding rates as a function of temperature, in the absence of denaturant, unless otherwise stated. B) The choice of prefactor in the Kramers formalism was k_a = 5×10⁸ s⁻¹.

^bCalculated from the interpolation of the equilibrium stability measurements.

^cCalculated from the interpolation of the kinetic stability measurements.

^dCalculated from the kinetic data at 298 K.

^e$\mathrm{\Delta }{H}^0=\mathrm{\Delta }{H}_u^{0^{‡}}-\mathrm{\Delta }{H}_f^{0^{‡}},\mathrm{\Delta }{S}^0=\mathrm{\Delta }{S}_u^{0^{‡}}-\mathrm{\Delta }{S}_f^{0^{‡}},\mathrm{\Delta }{C}_p^0=\mathrm{\Delta }{C_p}_u^{0^{‡}}-\mathrm{\Delta }{C_p}_f^{0^{‡}},\mathrm{\Delta }{G}^0=\mathrm{\Delta }{G}_u^{0^{‡}}-\mathrm{\Delta }{G}_f^{0^{‡}}$

For a two-state reaction, the thermodynamic properties can also be extracted from kinetic folding experiments and are expected to match those from the equilibrium experiments. Urea-induced kinetic folding and unfolding experiments were performed on mSOD1* at 2.5 K intervals between 283 K and 313 K. As observed previously, the folding and unfolding circular dichroism (CD) traces were well described by single exponential relaxation kinetics without any change in ellipticity in the dead time of the experiment, ~5 s (Figure S2). Plots of the relaxation times at a given temperature as a function of the final denaturant concentration, the chevron plot, are shown in Figure 3. The reciprocals of the relaxation times, the observed rate constants, were fit to an exponential dependence of the unfolding and refolding rate constants on the denaturant concentration:

$$k_{\mathit{\text{obs}}}=k_f^0{e}^{-{m_f}^{‡}[\mathit{\text{urea}}]/RT}+k_u^0{e}^{-{m_u}^{‡}[\mathit{\text{urea}}]/RT}$$ (2)

Where k_obs is the observed rate constant at a given denaturant concentration, [urea], and temperature, T, $k_f^0$ and $k_u^0$ are the folding and unfolding rate constants in the absence of denaturant, and m_f^‡ and m_u^‡ are the denaturant dependence of the folding and unfolding rate constants, respectively. The best fit values for $k_f^0,k_u^0$, m_f^‡, and m_u^‡ as a function of temperature are tabulated in Table S1.

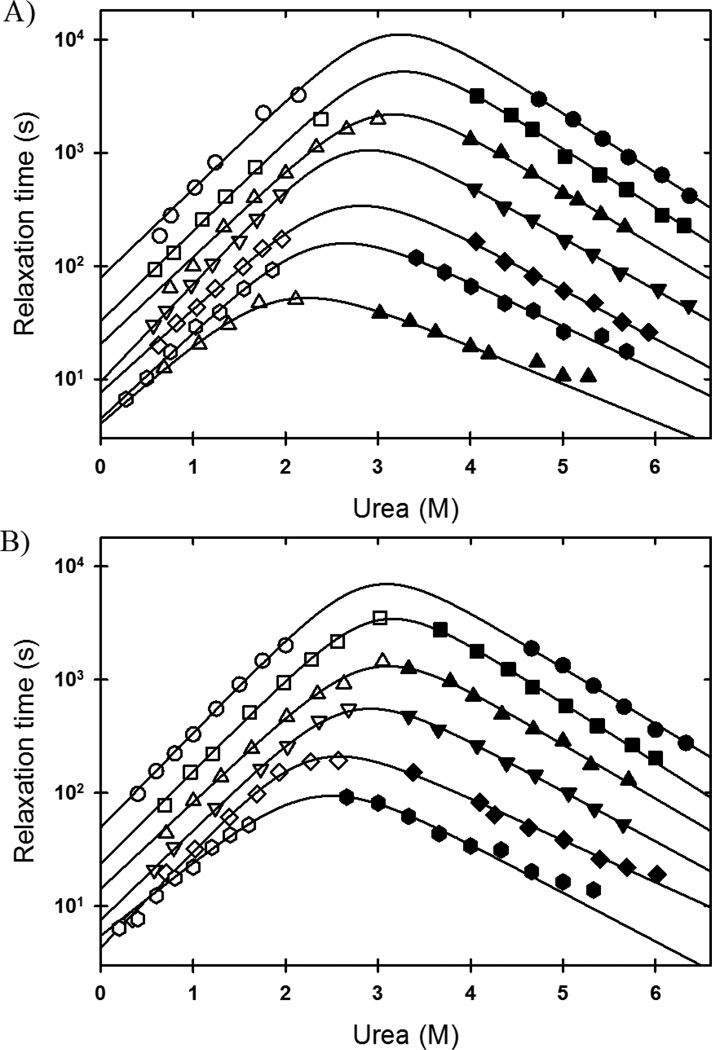
Figure 3. Temperature dependence of mSOD1* folding kinetics.

The folding (open symbols) and unfolding (filled symbols) relaxation times of mSOD1*, as a function of denaturant concentration, are shown at every 5 K. A) 283 K (circles), 288 K (squares), 293 K (up triangle), 298 K (down triangle), 303 K (diamond), 308 K (hexagon), and 313 K (up triangle). B) 285.5 K (circles), 290.5 K (squares), 295.5 K (up triangle), 300.5 K (down triangle), 305.5 K (diamond), and 310.5 K (hexagon).

The temperature dependence of the stability can be calculated from the rate constants in the absence of denaturant via ΔG⁰ = − RTln (k_u / k_f), and the temperature dependence of the equilibrium m-value, m_eq, can be determined from the kinetic m^‡-values by m_eq = m_r^‡ − m_u^‡. The very good agreement between the stabilities (Figure 2A) and m-values (Figure 2B) determined from the equilibrium and kinetic experiments support the choice of the two-state model and lends credence to the parameters extracted from the fits of the data. As above, the enthalpy and the heat capacity change between the M and U states for mSOD1* can be extracted from the temperature dependence of the stability calculated from the kinetic folding data using the Gibbs-Helmholtz equation (Equation 1). The estimates of ΔH⁰ and ΔC_p⁰ at 298 K, 28.0±1.9 kcal mol⁻¹ and 1.93±0.27 kcal mol⁻¹K⁻¹ (Table 1), are in very good agreement with the values derived from the equilibrium experiments and are of higher precision. The larger uncertainties in ΔC_p⁰ and ΔH⁰ obtained from the analysis of equilibrium experiments reflect the low intrinsic stability of mSOD1* and, as a consequence, the diminished native baseline regions at higher temperatures. The magnitude of the errors from the equilibrium experiment is also exacerbated by the limited temperature range accessible below the temperature of maximum stability (Figure 2A). The temperature of maximum stability for mSOD1* (δΔG/δT = 0), calculated from the more reliable parameters extracted from the kinetic analysis, is 291 K.

Thermodynamic properties of the TSE for mSOD1*

The temperature dependence of the unfolding and refolding rate constants can also be used to calculate the thermodynamic properties of the TSE. From transition state theory:

$$k_{\mathit{\text{obs}}}=k_a·\text{exp}\left(\frac{-\mathrm{\Delta }{G}^{0^{‡}}}{RT}\right)=k_a·\text{exp}\left(\frac{-\mathrm{\Delta }{H}^{0^{‡}}}{RT}\right)·\text{exp}\left(\frac{\mathrm{\Delta }{S}^{0^{‡}}}{R}\right)$$ (3)

where k_a is the prefactor, T is the absolute temperature, R is the gas constant and ΔS^0‡ and ΔH^0‡, are the change in activation entropy and activation enthalpy, respectively, at standard state. When the effects of the heat capacity change, $\mathrm{\Delta }{C}_p^{0^{‡}}$, on the activation enthalpy and activation entropy are also considered:

$$\mathrm{\Delta }{H}^{0^{‡}}=\mathrm{\Delta }{H}^{0^{‡}}(T_0)+\mathrm{\Delta }{C}_p^{0^{‡}}·(T-T_0)$$ (4)

$$\mathrm{\Delta }{S}^{0^{‡}}=\mathrm{\Delta }{S}^{0^{‡}}(T_0)+\mathrm{\Delta }{C}_p^{0^{‡}}·\mathrm{l}\mathrm{n}\left(\frac{T}{T_0}\right)$$ (5)

The rate constants in the absence of denaturant at a given temperature can be parameterized from Equation 3 as:

$$\mathrm{l}\mathrm{n}\left(\frac{k}{T}\right)=\frac{\mathrm{\Delta }{S}^{0^{‡}}-\mathrm{\Delta }{C}_p^{0^{‡}}}{R}+\mathrm{l}\mathrm{n}\left(\frac{k_a}{T}\right)+\left(\frac{T}{T^0}\right)\frac{\mathrm{\Delta }{C}_p^{0^{‡}}-\frac{\mathrm{\Delta }{H}^{0^{‡}}}{T^0}}{R}-\frac{\mathrm{\Delta }{C}_p^{0^{‡}}}{R}\mathrm{l}\mathrm{n}\frac{T}{T^0}$$ (6)

where T⁰ is the reference temperature, 298 K. The value for k_a, 5×10⁸s⁻¹, was chosen based on experiments performed on peptide models. The fits of the temperature dependence of the folding and unfolding rate constants, in the absence of denaturant, to Equation 6 are shown in Figures 4A and 4B.

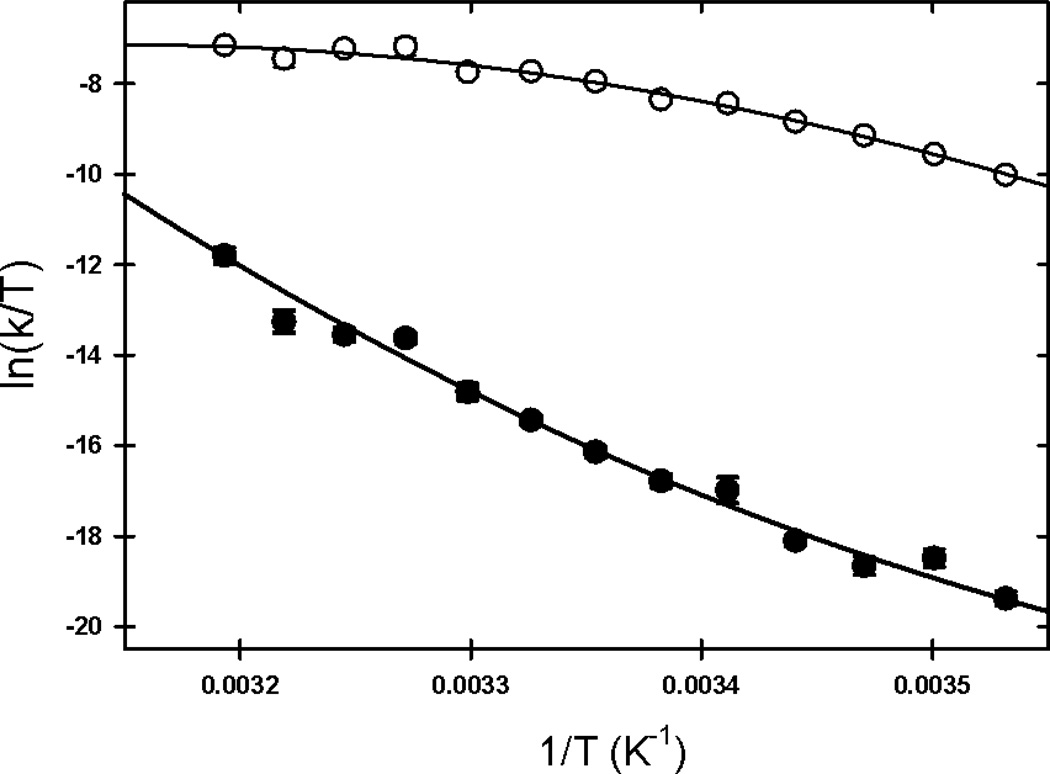
Figure 4. Fit of the kinetic data to the Kramers model.

The natural log of the folding (open circles) and unfolding (filled circles) rate constants divided by the temperature were plotted as a function of the inverse of the temperature and fit to the Kramers model as described in the Results to obtain the thermodynamic parameters of the transition state, ΔS^0‡, ΔH^0‡ and $\mathrm{\Delta }{C}_p^{0^{‡}}$ (Table 1).

The activation free energy for folding, ΔG^0‡, 13.1±0.1 kcal mol⁻¹, is primarily dictated by the activation enthalpy, ΔH^0‡, 16.7±0.6 kcal mol⁻¹ (Table 1). Interestingly, the activation entropy contribution favors access to the TSE by lowering the activation free energy by 3.6 kcal mol⁻¹. The barrier for the unfolding reaction is also dominated by the activation enthalpy, 45.6±1.7 kcal mol⁻¹. Similar to folding, the activation entropy favors access to the TSE by decreasing the activation free energy by 27.7±1.8 kcal mol⁻¹ at 298 K. The equilibrium enthalpy, entropy, heat capacity, and free energy changes between the M and U states can also be calculated from the difference of the activation counterparts, $\mathrm{\Delta }{H}^0=\mathrm{\Delta }{H}_u^{0^{‡}}-\mathrm{\Delta }{H}_f^{0^{‡}},\mathrm{\Delta }{S}^0=\mathrm{\Delta }{S}_u^{0^{‡}}-\mathrm{\Delta }{S}_f^{0^{‡}},\mathrm{\Delta }{C}_p^0=\mathrm{\Delta }{C_p}_u^{0^{‡}}-\mathrm{\Delta }{C_p}_f^{0^{‡}},\mathrm{\Delta }{G}^0=\mathrm{\Delta }{G}_u^{0^{‡}}-\mathrm{\Delta }{G}_f^{0^{‡}}$ (Table 1). These parameters are of similar or greater precision and within the ranges estimated from the equilibrium experiments (Table 1). Using these parameters, one finds that the free energy of unfolding (M→U) is 4.9±0.1 kcal mol⁻¹, the enthalpy of unfolding is 28.9±1.8 kcal mol⁻¹, and the entropy of unfolding is 81±7 cal mol⁻¹ K⁻¹ at 298K. Above the temperature of maximum stability, the entropy change disfavors the folding of globular proteins.

Position of the TSE on folding reaction coordinates

Insights into the relative position of the TSE on folding reaction coordinates, with respect to the native and unfolded states, can be obtained by comparing the ratio of the m_f^‡-value and the $\mathrm{\Delta }{C_p}_f^{0^{‡}}$ to the m-value and the $\mathrm{\Delta }{C}_p^0$ for the M⇆U reaction. The α-parameter is defined as:

$$\alpha =\frac{X_{U\to M}^{‡}}{X_{U\to M}^{‡}-X_{M\to U}^{‡}}$$ (7)

where X^‡ is either the m^‡ or the $\mathrm{\Delta }{C}_p^{0^{‡}}$ value. An α-value near 1 suggests a very native-like transition state, whereas an α-value near zero suggests an unfolded-like transition state. The α-values obtained from the m_f^‡-value and the $\mathrm{\Delta }{C_p}_f^{0^{‡}}$-value are 0.65±0.02 and 0.44±0.11, respectively. The differing α values reflect the fact that m-value is sensitive to the total change in buried surface area,³⁵ while $\mathrm{\Delta }{C}_p^{0^{‡}}$ is positive for the exposure of nonpolar surface area to water and negative for exposure of polar surfaces to water. Although the burial of nonpolar surface dominates the change in the heat capacity when the U state accesses the TSE (Table 1), the rank order of these α-values demonstrates that the burial of polar surface area modulates position of the TSE for these two different views of the folding reaction coordinate.

DISCUSSION

The refolding relaxation time of mSOD1* at the standard state, τ ~ 9.5 s, is much slower than folding reactions observed for many other two-state proteins, which can fold in milliseconds or even microseconds.⁴² The potential relationship between the slow folding reaction and propensity for a toxic aggregation reaction motivated a study of the thermodynamic properties of the transition state ensemble separating the folded and unfolded states of this β-sandwich protein.

Enthalpy-controlled barriers for folding and unfolding

The greater conformational entropy cost required to access the TSE for mSOD1* does not account for its slow folding reaction. A combined thermal-urea denaturation analysis of the reversible unfolding of mSOD1* revealed that, in the absence of denaturant, the barriers for both folding and unfolding are dominated by the activation enthalpy (Figure 5 and Table 1). For the unfolding reaction, this observation implies that the disruption of secondary and tertiary structure required to access the TSE outweighs the gain in entropy from those segments of mSOD1* that become unstructured. The expected gain in entropy from main chain and side chain dynamics, however, is mitigated by the loss in entropy when nonpolar surface is exposed to solvent in the TSE. The observation that 56% of the heat capacity gain for the M⇆U reaction occurs in the M→TSE step (Table 1) is consistent with the exposure of extensive nonpolar surface to water. Large enthalpic barriers, i.e., high Arrhenius activation energies, for unfolding have been observed for many monomeric and dimeric proteins (see Liu & Chan, JMB 2005 and references therein),⁴³ demonstrating that escape from the native thermodynamic state involves the substantial disruption of structure in a variety of motifs.

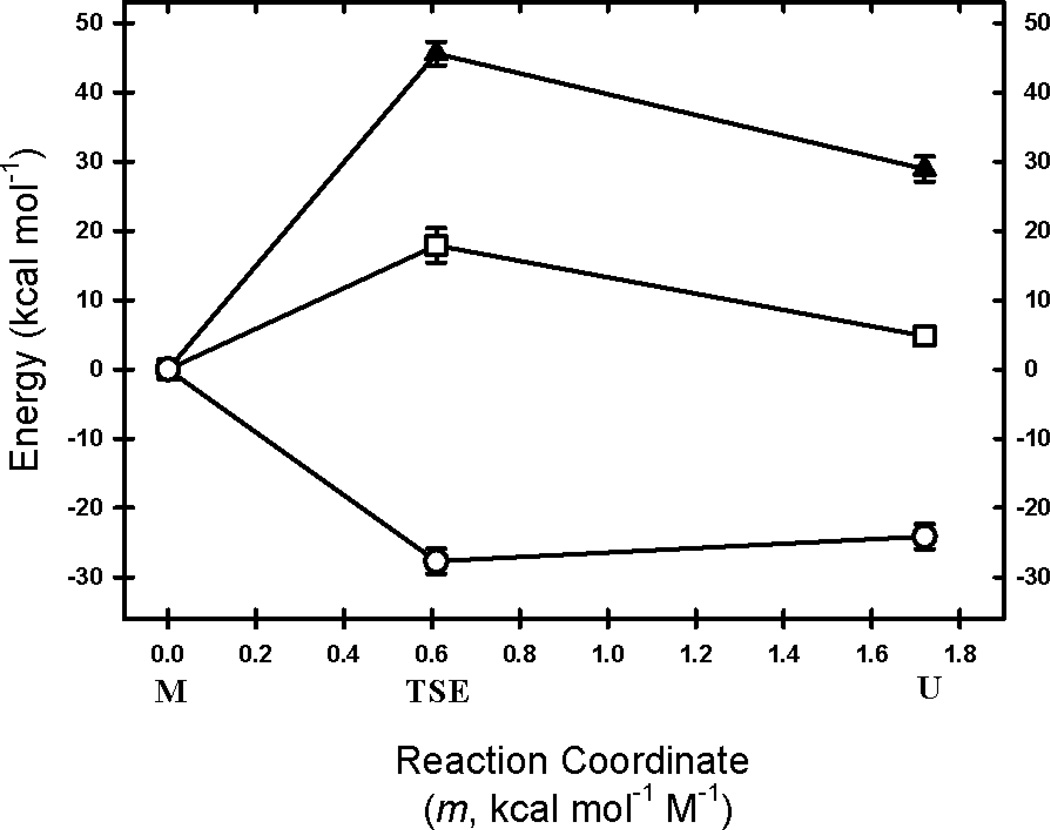
Figure 5. Reaction Coordinate Diagram for mSOD1*.

The enthalpic, ΔH⁰, (filled triangle) and entropic, −TΔS⁰ (open circle) contributions to the free energies (open square) of the M, TSE, and U states at the standard state of 298 K and using the M state as the reference state are shown. The placement of the TSE and U states relative to M was based on m^‡-values and m-values extracted from the kinetic folding data analysis.

The significant enthalpic barrier for the folding of mSOD1*, 16.7±0.6 kcal mol⁻¹, rules out biased chain diffusion through solvent, predicted by Landscape Theory, and its expected 4.5 kcal mol⁻¹ activation energy as the source. The excellent fit of both the equilibrium and the kinetic data to a two-state model implies that transient or stable intermediates are not measurably populated during the folding reaction. The absence of intermediates is also supported by the full recovery of the native ellipticity in the sole kinetic phase (Figure S2) and by the lack of a large-scale collapse of the unfolded chain by small angle x-ray scattering.²⁷ The presence of small, localized, and non-native clusters of side chains in the nominally unfolded state under native conditions cannot be ruled out by these experiments. However, the disruption of non-native nonpolar contacts would be exothermic and expected to lower the enthalpic barrier, as would the stabilizing hydrogen bonds presumably formed between the β-strands in the TSE.^44–46 These results imply that neither the disruption of hydrogen bonding networks in partially-folded states or van der Waals-stabilized hydrophobic clusters of nonpolar side chains in the unfolded state ensemble can explain the enthalpic barrier for folding. What then could be the source of the enthalpic barrier?

The α-values calculated from the m-value analysis and the $\mathrm{\Delta }{C}_p^0$ analysis, 0.65 and 0.44, respectively, shows that a substantial fraction of the nonpolar surface area is buried in the TSE. Studies on model compounds have revealed that the exposure of nonpolar side chains to water is accompanied by negative changes in both enthalpy and entropy and large positive changes in the heat capacity. Therefore, the most likely source of the enthalpic barrier is the dehydration of nonpolar surfaces required to form the TSE. A similar conclusion was reached for the TSE of the association reaction for the dimeric core domain of the Trp repressor,⁴⁸ as well as the TSE in the two-state folding reactions of cold shock protein from B. subtillis⁴⁹ and lysine motif domain from E. coli.⁵⁰ Supporting this view are the results of theoretical analyses by Chan and colleagues in which the cooperativity of folding and the associated enthalpy changes can be explained as a consequence of the cooperative desolvation of hydrophobic surfaces for a large set of proteins. Thus, the dehydration required to form compact structures stabilized by weak van der Waals interactions between carbon-based moieties in the TSE would be expected to yield positive changes in the activation enthalpy for folding.

Enthalpy-entropy compensation and folding

The well-known small magnitude of the folding free energy of many proteins is a consequence of large and opposing changes in the enthalpy and entropy of the reaction. Enthalpy-entropy compensation has been the subject of discussion for many years, but a satisfactory molecular explanation has been elusive.^53–58 Although the enthalpy change dominates the stability and the refolding barrier of mSOD1* at 298 K, the entropic contributions differentially modulate the free energies of the TSE and the native state in an informative fashion. The observation that the TSE, relative to the unfolded state, is entropically favored while the native state is disfavored offers insights into the interplay between chain organization, side chain packing and dehydration that differentiate the TSE and the native state.

Crystal structures of globular proteins invariably show well-organized main chains stabilized by networks of hydrogen bonds, side chains constrained in strongly preferred rotamer positions, and tight side chain packing reminiscent of organic solids; water is largely absent in the interior. The net decrease in entropy when the unfolded state is converted to the folded state for mSOD1* at 298 K shows that the penalty incurred by constraints on the main chain and side chains is greater than the gain in entropy from the release of water. By contrast, the favorable entropy change observed as the unfolded state accesses the TSE implies that the gain from solvent release exceeds the penalty paid for organizing segments of the main chain and bringing at least a fraction of the side chains into contact. Mutational analysis of mSOD1* found that only a few nonpolar side chains in β1 (Cys6), β2 (Ile18), β3 (Ile35), and β7 (Leu117) play a major role in defining the free energy of the TSE; the contribution of neighboring side chains diminish with the distance from this cluster.²⁹

The picture that emerges from the present thermodynamic study and the mutational analysis is a TSE in which local and distant segments of the chain coalesce into a structure of varying packing density. Presumably, the more tightly packed regions exclude water from their interiors as a consequence of constraining their main chains and side chains. The more loosely packed regions, however, exclude or at least reduce their exposure to water while retaining a dynamic character for main chains and side chains. The entropy gain from the release of water exceeds the entropic cost of bringing several local and distant segments of the unfolded chain together in the TSE. The conversion of the TSE to the native state, however, requires a further entropic cost for ordering the main chains and side chains that is not entirely compensated for by the release of water. As a result, the activation entropy change favors the formation of the TSE but the equilibrium entropy change disfavors the formation of the native state at 298 K. The entropy-enthalpy compensation observed for SOD1 folding is compellingly similar to explicit solvent simulations of the association of polyalanine and polyleucine helices, where the desolvation of the hydrophobic helix-helix contact area is also the sole contributor to the enthalpic barrier of association.⁵⁹ To the extent that the TSE involves the docking of preformed elements of secondary structure, this transient “steric dewetting”⁵⁹ would amplify the enthalpic and entropic consequences of the hydrophobic effect for the large surface area buried in this TSE.

Is the slow folding of mSOD1* unusual?

The refolding relaxation time of mSOD1*, ~10 seconds at 298 K and neutral pH, is four orders-of-magnitude slower than predicted for a relative contact order of 0.13 (based on PDB:1RK7) in the original formulation of the metric² and 10-fold slower in using the subsequently-proposed absolute contact order (ACO), 20.6.⁶⁰ A recent re-analysis of the correlation between folding rates and topological complexity by Istomin and colleagues has shown that differentiating proteins by secondary structure content, all-α, all-β, and mixed-α/β, leads to much improved correlations.³ Indeed, when considering only all-β proteins, the folding rate constant for mSOD1* lies within the expected range for its ACO (Figure S3).

This latter reappraisal of folding rate constants and contact order points to distinct differences between all β-proteins and those that are wholly or in part helical. One might speculate that, unlike α-helices, β-strands are only stable in association with one or more partners. The probability that a pair of nascent β-strand segments would simultaneously be in the proper format to form an anti-parallel β-hairpin is very likely to be smaller than the same opportunity for a pair of α-helices. The probability of assembling at least five β-strands to create the TSE for mSOD1* would be corresponding diminished and, therefore, an inherently slow reaction compared to all-α or mixed-α/β proteins of the same contact order. This problem would only be compounded by a preponderance of nonlocal interactions in this high contact order protein.

Slow folding of SOD1 monomers and ALS

A potentially deleterious consequence of the high enthalpic barrier for mSOD1* is the predisposition towards aggregation of the long-lived unfolded state and, thereby, a role in toxicity for ALS. Following synthesis on the ribosome, wild-type SOD1 spontaneously folds to an immature monomeric species that lacks an intact intra-molecular disulfide bond. Interestingly, an intact disulfide bond only accelerates the folding reaction by a factor of ~2, showing that its presence in the disulfide-containing species does not differentially affect the free energies of the TSE and unfolded states to a major extent.¹⁹ A number of ALS-variants remain unfolded after synthesis and only achieve the mature native dimeric form after the formation of the disulfide bond and the addition of zinc and copper. When the significantly increased population of the unfolded state for these variants is combined with the intrinsically slow folding reaction for SOD1, the potential for self-association and, eventually, large-scale aggregation is enhanced. Thus, perturbations of the biophysical properties of protein folding reactions by amino acid replacements can have devastating pathological consequences.

MATERIALS AND METHODS

Protein purification

Recombinant mSOD1* was expressed in BL21-Gold (DE3) cells (Stratagene^®, Inc. Cedar Creek, TX) and purified according to the procedure previously described.³⁰ Protein mass and purity were determined by LC-ESI mass spectrometry. Protein concentrations were determined by absorbance measurements performed on a Jasco UV-580 UV/V is spectrophotometer (Jasco Inc., Easton, MD) using an extinction coefficient of 5,400 M⁻¹ cm⁻¹ at 280 nm.

Kinetics analysis of folding

The unfolding and refolding kinetics were all initiated by manual mixing with a dead time of ~3 seconds and monitored by CD utilizing a Jasco J-810 CD spectrophotometer (Jasco Inc., Easton, MD). The data were collected at 230 nm in a 1 cm² cuvette with continual mixing and a total volume of 1.9 mL. The standard buffer for all experiments was 20 mM HEPES, 1 mM EDTA, pH 7.2 at 293 K. Refolding jumps were initiated from 5 M urea while unfolding jumps were initiated from the absence of denaturant. The final denaturant concentration for each kinetic point was determined by index of refraction measurements. The final concentration of protein for all experiments was 5–15 µM. Individual kinetic traces were fit independently using Savuka 6.2, in-house software utilizing the Marquardt-Levenberg non-linear least squares algorithm.⁶² The relaxation kinetics were well described by a single exponential.

Equilibrium analysis of folding

The urea induced unfolding curves of 15 µM mSOD1* were monitored from 215–240 nm in a 0.2 cm path length quartz cuvette using a scan rate of 20 nm min⁻¹, a response time of 8 s. The samples were prepared from concentration-matched stocks of folded protein in buffer and unfolded protein at 6 M urea and mixed precisely using a Hamilton Microlab 500 titrator. The samples were incubated in a water bath at the appropriate temperature overnight, and the final denaturant concentrations were determined by refractive index after the CD spectra were measured. The titration data were fit to a two-state model, assuming a linear dependence of the free energy of folding on the urea concentration.²⁷

Supplementary Material

02. Figure S1. Equilibrium titrations with varying temperature.

The urea titrations of mSOD1* at ten temperatures are shown with the best-fit line to a two-state model (solid lines). A) 285 K (circles), 291 K (squares), 297 K (up triangle), 304 K (diamond), and 310 K (down triangle). B) 289 K (circles), 294 K (squares), 301 K (up triangle), 307 K (diamond), and 313 K (down triangle). The monotonic temperature dependence of the unfolded baseline may reflect the dissociation of urea from the backbone in the unfolded chain. All experiments were performed at pH 7.2.

03. Figure S2. Initial amplitudes in kinetic refolding and unfolding experiments measured by CD.

The initial ellipticities for the refolding (open squares) and unfolding (open triangles) kinetic phases agree closely with the extrapolated folded (dashed line) and unfolded (dotted line) baselines of the equilibrium titration (filled circles) at 293 K.

04. Figure S3. Folding rate constants and topology.

The natural log of the refolding rate is plotted as a function of the absolute contact order determined from the structure of the protein. Symbols represent a combination of all-β (gray squares), all-α (open circles), and mixtures of α/β topologies (open triangles). The filled square represents mSOD1*. The dashed line is a linear fit of the data for all-β proteins while the solid line is a linear fit of the data for all-α proteins. The data for proteins other than SOD1 was adapted from Istomin et al.³

Statement for broader audience.

This work evaluates the energetic contributions from entropy and enthalpy to the folding of the human superoxide dismutase monomer, variants of which are involved in familial cases of amyotrophic lateral sclerosis. These studies were performed to understand the molecular basis of the unusually slow folding reaction that may predispose the protein to form toxic aggregates and cause disease. The results reveal insights into the role of the solvent in controlling the folding reactions of globular proteins.

Highlights.

• The slow folding reaction of SOD1 has profound implications for ALS.

• The unfolding and refolding reactions of SOD1 are dominated by enthalpic barriers.

• Favorable entropic contributions to the TSE accelerate refolding.

• Dehydration required to reach the TSE is the likely cause of the enthalpic barrier.

Abbreviations and symbols

ACO

Absolute contact order

ALS

Amyotrophic lateral sclerosis

CD

circular dichroism

mSOD1*

C6A/F50E/G51E/C111S SOD1

SOD1

Human copper, zinc superoxide dismutase

TSE

Transition state ensemble