Abstract
Objective
Clinical trials are unlikely to ever be launched for many Comparative Effectiveness Research (CER) questions. Inferences from hypothetical randomized trials may however be emulated with marginal structural modeling (MSM) using observational data but success in adjusting for time-dependent confounding and selection bias typically relies on parametric modeling assumptions. If these assumptions are violated, inferences from MSM may be inaccurate. In this article, we motivate the application of a data-adaptive estimation approach called Super Learning to avoid reliance on arbitrary parametric assumptions in CER.
Study Design and Setting
Using the electronic health records data from adults with new onset type 2 diabetes, we implemented MSM with inverse probability weighting estimation to evaluate the effect of three oral anti-diabetic therapies on the worsening of glomerular filtration rate.
Results
Inferences from IPW estimation were noticeably sensitive to the parametric assumptions about the associations between both the exposure and censoring processes and the main suspected source of confounding, i.e., time-dependent measurements of hemoglobin A1c. Super Learning was successfully implemented to harness flexible confounding and selection bias adjustment from existing machine learning algorithms.
Conclusion
Erroneous IPW inference about clinical effectiveness due to arbitrary and incorrect modeling decisions may be avoided with Super Learning.
Keywords: super learning, marginal structural model, inverse probability weighting, comparative effectiveness research, time-dependent confounding, selection bias
1. Introduction
In 2006, the American Diabetes Association changed its recommendations for the treatment of patients with type 2 diabetes mellitus (T2DM). The longstanding recommendation to begin pharmacotherapy only after a trial of lifestyle modification that failed to lower A1c to <7% was replaced with the new guideline for immediate prescription of metformin at detection of diabetes, regardless of A1c level. Authors of the new recommendation indicated that it reflects consensus rather than solid evidence.
In addition, adverse events linked to the use of thiazolidinediones [1] and inhaled insulin raised concerns over the long-term safety and effectiveness of agents used to control glycemia in T2DM patients. While most experts interpret existing data as strongly supporting the safety and effectiveness of metformin, there is less confidence in the long-term safety and effectiveness of sulfonylurea and the use of metformin and sulfonylurea in combination.
Using the electronic health records (EHRs) from patients of four sites of the HMO Research Network (HMORN) Consortium [2], we assembled a large retrospective cohort study of adults with new onset T2DM to evaluate the effect of immediate versus delayed initial monotherapy or bitherapy with metformin and sulfonylurea on the risk of several clinical outcomes. We investigated these effects using marginal structural modeling (MSM) based on inverse probability weighting (IPW) estimation for the purpose of properly accounting for the time-dependent confounding and informative selection bias that often arise in observational cohort analyses.
Here, our principal goal is twofold: 1) to illustrate the potential for incorrect inference resulting from inadequate parametric adjustment for confounding and informative censoring using MSM in Comparative Effectiveness Research (CER) and 2) to illustrate the practical impact of and motivation for data-adaptive estimation with Super Learning (SL) in MSM. SL is a prediction algorithm, grounded in theroretical results, that builds an optimal weighted combination of predictors from a user-specified library of existing prediction methods using cross-validation. In addition, we illustrate the application of IPW estimation with a time-varying polychotomous (non-binary) exposure. All illustrations are based on results for one survival outcome, the worsening of glomerular filtration rate (GFR).
2. An observational, multi-center retrospective cohort study
We searched the entire adult membership of four participating HMORN health plans for enrollees meeting the eligibility criteria described in Appendix A. We enrolled each patient at the earliest date between 1 January 2006 and 30 June 2009 on which all criteria were met. As in a clinical trial, these eligibility criteria were devised to identify adults for whom the CER question is relevant, i.e., adults with new onset T2DM defined based on one elevated A1c measurement (>6.5%) or two elevated measurements from fasting (>126 mg/dl) or random (>200 mg/dl) plasma glucose tests within a two-year period. We excluded members whose life expectancy was limited by selected co-morbid conditions. These criteria identified a cohort of 51,430 patients from which members with an observed or imputed baseline A1c≥8% were excluded. All n = 36, 020 patients from the resulting cohort were followed up from study entry until the earliest of 30 June 2010, plan disenrollment, or death.
3. Analytic Approach
3.1. Motivation for MSM
To address the CER question, we aim to emulate inferences from an ideal randomized experiment with observational data [3]. In the hypothetical trial of interest, patients from the study cohort described above would be randomized to one of several treatment arms corresponding with: i) no T2DM pharmacotherapy, ii) initiation of metformin monotherapy (met) at study entry, iii) initiation of sulfonylurea monotherapy (sul) at study entry, iv) initiation of bitherapy with metformin and sulfonylurea (met+sul) at study entry, v) met initiation at 6 months post study entry, vi) sul initiation at 6 months post study entry, vii) met+sul initiation at 6 months post study entry, viii) met initiation at 12 months post study entry, etc. This trial is ideal in the sense that 1) patients would remain uncensored for the duration of the trial (2 years), and 2) patients in arm i) would comply with the assigned lack of therapy while patients in all other arms would comply with the assigned treatment regimen until at least the assigned time of treatment initiation. In each arm, patients’ GFR would be monitored to detect evidence of first GFR worsening after study entry. The corresponding survival curve in each arm would be contrasted at 2 years. More specifically, the cumulative risk differences between any two treatment interventions in this trial are the comparative effectiveness measures that we wish to evaluate with observational data.
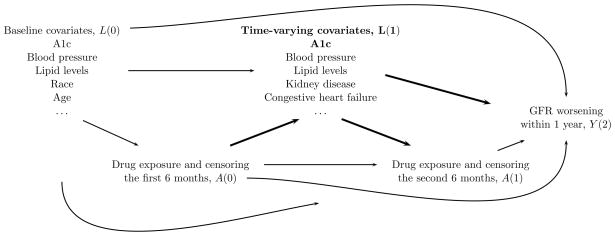
Standard modeling approaches are known [4, 5] to be inadequate to handle time-dependent confounding and selection bias [6] as they rely on conditioning of time-varying covariates which are also often expected to lie on a causal pathway of interest between one of variables defining the exposure groups of interest and the outcome. Figure 1 illustrates such a scenario with a causal diagram [7, 8] of a subset of measurements collected over one year for each patient in this study. MSM with IPW estimation can permit adequate adjustment for such time-varying covariates also on a causal pathway between early therapy exposure and the outcome and can directly emulate inference for the intention-to-treat (ITT) effects of interest [9, 10, 11] in this study1.
Figure 1.
Directed acyclic graph that represents plausible causal relationships between a subset of the variables collected on any given patient in the first year of this study. Standard modeling approaches are not adequate to account for time-varying covariates such as L(1) (e.g. A1c is both a mediator of the effect of early treatment decisions A(0) on the outcome Y(2) and a confounder of the effect of subsequent treatment decision A(1) on the outcome Y(2)).
3.2. Data structure
The observed data on each patient in this study consist of exposure, outcome, and confounding variable measurements made at 180-day intervals until each patient’s end of follow-up. Patient follow-up ended at the earliest of the time to GFR worsening or the time to a censoring event. The longest follow-up time was approximately 4 years and the median follow-up time was about 1.5 years. Censoring events included administrative end of study, health plan disenrollment, death, or insufficient GFR monitoring. GFR worsening was defined as moving from a lower number renal function stage at baseline to a higher number stage based on any single follow-up GFR measurement. Renal function was classified as stage 1 (estimated GFR [eGFR] ≥ 90 ml/min/1.73 m2), stage 2 (eGFR 60–89), stage 3a (eGFR 45–59), stage 3b (eGFR 30–44), stage 4 (eGFR 15–29), and stage 5 (eGFR<15). Insufficient GFR monitoring was defined as a gap between consecutive GFR measurement that exceeded 360 days (two 180-day intervals); the censoring date was set as the beginning date of the third 180-day interval. Each patient’s exposure to an intensified DM treatment during each 180-day follow-up interval was categorized in 6 levels: 1) No T2DM pharmacotherapy, 2) met, 3) sul, 4) met+sul, 5) other T2DM pharmacotherapies, and 6) undetermined. The exposures were characterized with the first five levels until and at the 180-day interval at which the patient initiated a first line pharmacotherapy. The exposures were not determined (level 6) thereafter because such information is irrelevant for the investigation of the ITT effect of interest in this analysis. Each patient’s covariate (e.g., A1c measurements) and outcome (indicator of GFR worsening) at each 180-day follow-up interval were defined from measurements assumed not to be affected by the exposure at that time interval of thereafter. Details about the approach implemented for mapping EHR data into this coarsened exposure, covariate and outcome data for each patient was described elsewhere [12, Appendix E]. A formal presentation of the observed data structure on which is based the MSM analysis reported here is given in Appendix B for the purpose of allowing a detailed description of our application of IPW estimation with a polychotomous (non-binary) exposure.
3.3. Assumptions
Success in emulating causal inferences from the hypothetical randomized trial of interest using observational data with the MSM approach described below relies on assumptions [5, 13, 14, 15, 16, 17] including:
No unmeasured confounders assumption
This assumption is not testable with data alone but may be motivated based on a causal directed acyclic graph (DAG) such as the one in Figure 1. For example in this analysis, this assumption would hold if all risk factors for the outcome that also affect censoring and the decision to initiate a particular therapy were included in the observed covariate process. Appendix C describes the time-independent and time-varying covariates selected for confounding and selection bias adjustment in this analysis.
Positivity assumption (a.k.a. Experimental Treatment Assignment assumption)
Patient’s censoring status and exposure to the therapies of interest at any given 180-day interval should not be determined deterministically based on past observed covariates.
3.4. Road map of the MSM approach
The road map of the analytic approach starts with the specification of a MSM for representing the hazards in each arm of the hypothetical trial of interest. The assumed logistic MSM in this analysis is described in Appendix D.
The second step consists in estimating the unknown components of the numerators and denominators of stabilized weights (Appendix D and [18, 19, 20]). The numerators of the weights were estimated non-parametrically. We describe the estimation approaches considered for the denominators in the next section.
The third step consists in fitting the logistic marginal structural model by standard weighted logistic regression with follow-up data from each patient pooled over time and where only the person-time observations under the treatment regimens of interest (i.e., corresponding with the treatment interventions in the hypothetical arms of interest) contribute to the regression. Each person-time observation is weighted using the estimated stabilized weights.
The fourth step consists in analytically mapping the estimates of the hazards into the estimates of the survival curves of interest [21] using the formula linking discrete-time hazards to survival probabilities (Appendix D).
For the fifth and final step, the estimates of the survival curves are contrasted. In this study, differences of survival at two years are of interest. Using the delta method [22] and the influence curve [23, 24] of the IPW estimator of the MSM coefficients, we analytically derived asymptotically conservative inference (confidence intervals and p-values) for these cumulative risk differences.
4. Motivation for Super Learning
The success of the MSM approach described above relies on not only the assumptions of positivity and no unmeasured confounders but also on the consistent estimation of the denominators of the stabilized weights. Their estimation has typically relied on parametric models (maximum likelihood estimation). The latter assumption then corresponds to correct model specification.
We implemented two such estimation strategies which are respectively based on: i) 11 logistic models with main terms for each explanatory variable considered and no interaction terms, and ii) the same 11 logistic models except that the two terms for the latest A1c and change in A1c levels were replaced by main terms for 10 dummy variables2 indicating whether the continuous values for A1c and change in A1c levels were elements of given intervals. We refer to these strategies as estimation approaches with linear and nonlinear adjustment for A1c. In both approaches, each of the 11 models is used to estimate a distinct component of the denominators of the stabilized weights. Appendix E describes these components and explains why the following 11 models are sufficient for estimating the denominators of the stabilized weights: 8 models for predicting each of the 4 types of therapy initiation during the first 180 days (E.6) and after the first 180 days (E.7), 3 models for predicting censoring due to disenrollment from the health plan (E.3), death (E.4), and artificial censoring for insufficient GFR monitoring (E.5) (we assumed that censoring due to administrative end of study was uninformative). The explanatory variables considered in this analysis were all time-independent covariates, the last measurement of time-varying covariates (Appendix C), and the variable indexing the 180-day follow-up intervals. In addition, past pharmacotherapy initiation was included as an explanatory variable for the 3 models predicting censoring and the latest change in A1c was included as an explanatory variable for the 8 models predicting pharmacotherapy initiation.
As is the case above, the parametric models adopted for estimating the denominators of the stabilized weights in practice do not typically reflect true subject-matter knowledge. To avoid erroneous inference [25, 26] due to arbitrary model specifications, data-adaptive estimation of the stabilized weights has been proposed but is still implemented rarely in practice [27, 28, 29, 30, 31]. Consistent IPW estimation then relies on judicious selection of a machine learning algorithm also known as ’learner’. Several learners are potential candidates for estimating the different components of the denominators of the stabilized weights (e.g., [32, 33, 34, 35, 36, 37, 38, 39, 40, 41]). Akin to the selection of a parametric model, the selection of a learner does not typically reflect real subject-matter knowledge about the relative suitability of the different learners available, since “in practice it is generally impossible to know a priori which learner will perform best for a given prediction problem and data set” [42].
To hedge against erroneous inference due to arbitrary selection of a learner, SL [42] may be implemented [43] to combine predicted values from a library of various candidate learners (that includes the arbitrary learner that would have been guessed otherwise) through a weighted average. The selection of the optimal combination of the candidate learners is based on cross-validation [44, 45, 46, 47] to protect against over-fitting such that the resulting learner (called ’super learner’) performs asymptotically as well (in terms of mean error) or better than any of the candidate learners considered. If the arbitrary learners that would have been guessed is based on a parametric model and happens to be correct then using SL instead of the correctly guessed learner only comes at a price of increase in prediction variability.
For this analysis, we implemented [48] 11 super learners as alternatives to the 11 logistic models described earlier for estimating the denominators of the stabilized weights. Each super learner is defined based on 7 candidate learners: i) 5 learners defined by logistic models with only main terms for the most predictive explanatory variables identified by a significant p value in univariate regressions with 5 significance levels, and ii) two polychotomous regression learners based on the most predictive explanatory variables identified by a significant p value in univariate regressions with two significance levels. Only the continuous A1c and change in A1c measurements were considered as explanatory variables for SL, i.e., the dummy variables defined earlier for non-linear adjustment for A1c were not considered. Appendix F describes the details of the implementation of the super learners considered in this analysis.
5. Results
Of the n = 34, 468 patients in the study cohort, 15.7% experienced worsening of GFR during follow-up. Among the patients who did not experience worsening of GFR during follow-up, 73.6% were followed until the end of the study period, and 16.7%, 1.2%, and 8.5% were lost to follow-up due to health plan disenrollment, death, and insufficient GFR monitoring, respectively. Of all patients in the cohort, 28.2% initiated pharmacotherapy for T2DM during follow-up. Of the patients initiating therapy, 7,021 (72.3%) did so within the first 180 days. Across the entire study period, a total of 9,714 patients initiated therapy, with 7192 (74%), 981 (10.1%), and 950 (9.8%) initiating treatment with met, sul, and met+sul, respectively.
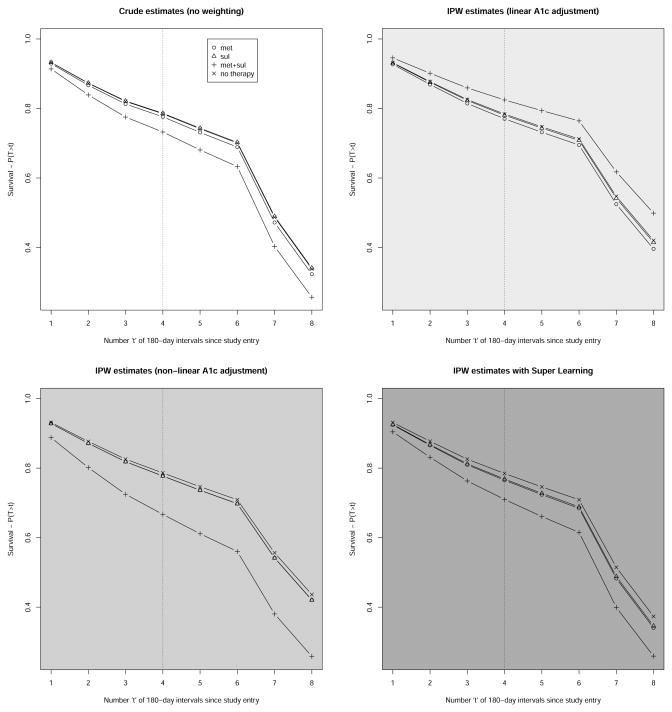
We only report results obtained by contrasting estimates of the counter-factual survival curves under no therapy or three ITT therapy regimens (met, sul, met+sul) initiated in the first 180 days of follow-up. Figure 2 represents four estimates of these survival curves: 1) crude estimates corresponding with IPW estimates based on weights equal to 1, 2) IPW estimates based on weights estimated using 11 logistic models with linear adjustment for A1c, 3) IPW estimates based on weights estimated using 11 logistic models with nonlinear adjustment for A1c, and 4) IPW estimates based on weights estimated with 11 super learners whose compositions are described in Table 2. The relative predictive power of each learner that composes the 11 super learners are described in Table 3. For each of these estimates, Table 1 provides inferences about the cumulative risk differences at two years. Depending on the weight estimation approach employed, the 98th and 99th percentiles of the stabilized weights ranged approximately 18–24 and 37–46, respectively. Stabilized weights were truncated at 50 to improve the performance of the three IPW estimators considered [49, 50, 51].
Figure 2.
Four estimates of the counterfactual survival curves under four therapy regimens corresponding with continuous absence of T2DM pharmacotherapy exposure and therapy initiation with monotherapy or bitherapy with metformin and sulfonylurea during the first 180 days of follow-up. The top left graph represents crude estimates corresponding with IPW estimation based on stabilized weights equal to 1. The top right graph represents IPW estimates based on linear adjustment for A1c. The bottom left graph represents IPW estimates based on non-linear adjustment for A1c. The bottom right graph represents IPW estimates based on SL. The dotted vertical line indicates the 2-year mark post study entry when the four survival probabilitities of interest are compared.
Table 2.
Weighted combination (%) of the 7 candidate learners that define the 11 Super Learners for estimating the denominators of the IPW weights. Each candidate learner is defined by a type of algorithm (’glm’ or ’polyclass’) and a subset of explanatory variables identified by univariate regressions based on a particular significance level (p-value).
| Learner | glm | glm | glm | glm | glm | polyclass | polyclass |
|---|---|---|---|---|---|---|---|
|
| |||||||
| Subset of explanatory variables | p≤1e-30 | p≤1e-10 | p≤1e-5 | p≤0.1 | p≤1 | p≤1e-30 | p≤1 |
| met initiation at t=0 | 0 | 0 | 0 | 8.3 | 6 | 9.8 | 76 |
| sul initiation at t=0 | 0 | 0 | 0 | 0 | 14 | 35 | 50 |
| met+sul initiation at t=0 | 13 | 0 | 4.9 | 0 | 28 | 0.37 | 53 |
| other therapy initiation at t=0 | 0 | 0 | 0 | 2.3 | 34 | 0 | 64 |
| met initiation at t>0 | 0 | 0 | 0 | 0 | 0 | 16 | 84 |
| sul initiation at t>0 | 0 | 0 | 0 | 0 | 5.2 | 59 | 36 |
| met+sul initiation at t>0 | 0 | 0 | 0 | 0 | 9.8 | 19 | 71 |
| other therapy initiation at t>0 | 0 | 0 | 0 | 14 | 24 | 30 | 32 |
| censoring by health plan disenrollment | 0 | 0 | 0 | 0 | 32 | 40 | 28 |
| censoring by death | 0 | 0 | 54 | 3.1 | 7 | 0 | 36 |
| insufficient GFR monitoring | 0 | 0 | 0 | 0 | 0 | 0 | 100 |
Table 3.
Cross-validated risks of the 7 candidate learners that define the 11 Super Learners for estimating the denominators of the IPW weights. Each candidate learner is defined by a type of algorithm (’glm’ or ’polyclass’) and a subset of explanatory variables identified by univariate regressions based on a particular significance level (p-value).
| Learner | glm | glm | glm | glm | glm | polyclass | polyclass |
|---|---|---|---|---|---|---|---|
|
| |||||||
| Subset of explanatory variables | p≤1e-30 | p≤1e-10 | p≤1e-5 | p≤0.1 | p≤1 | p≤1e-30 | p≤1 |
| met initiation at t=0 | 0.13159 | 0.1305 | 0.13046 | 0.1303 | 0.13027 | 0.12903 | 0.12759 |
| sul initiation at t=0 | 0.02852 | 0.0285 | 0.02847 | 0.02839 | 0.02834 | 0.0279 | 0.02781 |
| met+sul initiation at t=0 | 0.02663 | 0.02641 | 0.02629 | 0.02627 | 0.02627 | 0.02661 | 0.02617 |
| other therapy initiation at t=0 | 0.01971 | 0.01837 | 0.01839 | 0.01756 | 0.01741 | 0.01962 | 0.01691 |
| met initiation at t>0 | 0.04005 | 0.04001 | 0.03996 | 0.03981 | 0.03982 | 0.03179 | 0.0316 |
| sul initiation at t>0 | 7.86e-03 | 7.87e-03 | 7.86e-03 | 7.86e-03 | 7.85e-03 | 7.15e-03 | 7.2e-03 |
| met+sul initiation at t>0 | 5.33e-03 | 5.34e-03 | 5.27e-03 | 5.27e-03 | 5.24e-03 | 4.65e-03 | 4.6e-03 |
| other therapy initiation at t>0 | 2.29e-03 | 2.29e-03 | 2.28e-03 | 2.28e-03 | 2.29e-03 | 2.28e-03 | 2.28e-03 |
| censoring by health plan disenrollment | 0.04918 | 0.04917 | 0.04916 | 0.04914 | 0.04914 | 0.04909 | 0.04908 |
| censoring by death | 3.86e-03 | 3.84e-03 | 3.84e-03 | 3.85e-03 | 3.86e-03 | 3.9e-03 | 3.88e-03 |
| insufficient GFR monitoring | 0.02717 | 0.02631 | 0.02623 | 0.02608 | 0.02601 | 0.02589 | 0.02088 |
Table 1.
Crude and stabilized, truncated IPW estimates of the (cumulative) risk differences (RDs) for GFR worsening at 2 years. Each cell describes estimates of the risk difference between two exposure groups identified by the row and column labels. SE and p stand for standard error and p-value, respectively. The 95% confidence intervals are provided in parentheses next to the point estimates.
| RD = row minus column | met+sul | sul | met | ||
|---|---|---|---|---|---|
| no therapy | crude |
−0.0524 (−0.0844; −0.0204) SE=0.0163, p=0 |
0.0016 (−0.0271;0.0302) SE=0.0146, p=0.91 |
−0.0088 (−0.0216;0.0039) SE=0.0065, p=0.17 |
|
| linear A1c |
0.0406 (−0.0096;0.0907) SE=0.0256, p=0.11 |
−0.0033 (−0.0371;0.0305) SE=0.0172, p=0.85 |
−0.0137 (−0.0335;0.006) SE=0.0101, p=0.17 |
||
| non-linear A1c |
−0.1192 (−0.1962; −0.0423) SE=0.0393, p=0 |
−0.009 (−0.0459;0.0279) SE=0.0188, p=0.63 |
−0.0087 (−0.0287;0.0114) SE=0.0102, p=0.4 |
||
| super learning |
−0.0747 (−0.1451; −0.0044) SE=0.0359, p=0.04 |
−0.016 (−0.0528;0.0208) SE=0.0188, p=0.39 |
−0.0194 (−0.0419;0.003) SE=0.0115, p=0.09 |
||
|
| |||||
| met | crude | −0.0436 (−0.0767; −0.0104) SE=0.0169, p=0.01 |
0.0104 (−0.0195;0.0404) SE=0.0153, p=0.5 |
||
| linear A1c | 0.0543 (0.0021;0.1066) SE=0.0267, p=0.04 |
0.0105 (−0.0257;0.0467) SE=0.0185, p=0.57 |
|||
| non-linear A1c | −0.1105 (−0.1885; −0.0326) SE=0.0397, p=0.01 |
−3e−04 (−0.0383;0.0377) SE=0.0194, p=0.99 |
|||
| super learning | −0.0553 (−0.1276;0.0171) SE=0.0369, p=0.13 |
0.0034 (−0.0365;0.0433) SE=0.0204, p=0.87 |
|||
|
| |||||
| sul | crude | −0.054 (−0.0959; −0.0121) SE=0.0214, p=0.01 |
|||
| linear A1c | 0.0438 (−0.0151;0.1028) SE=0.0301, p=0.15 |
||||
| non-linear A1c | −0.1102 (−0.1939; −0.0266) SE=0.0427, p=0.01 |
||||
| super learning | −0.0587 (−0.1363;0.0188) SE=0.0396, p=0.14 |
||||
6. Discussion
The results of this analysis illustrate the sensitivity of IPW inferences to the strategy adopted for estimating the denominator of the stabilized weights. In particular, the three IPW inferences about the risk difference between the ’no therapy’ and ’met+sul’ exposure groups (bold text in Table 1) is striking.
While results from randomized trials are not available in this study to serve as surrogate gold standards to formally evaluate the accuracy of inferences derived from the three estimation strategies for the stabilized weights, it is worth noting that almost all 11 arbitrary specified logistic models with linear A1c adjustment for estimating the denominators of the stabilized weights had higher cross-validated residual sum of squares (not reported) than their 11 counterparts based on non-linear A1c adjustment. This observation provides support for favoring inferences based on IPW estimation with nonlinear A1c adjustment which are overall concordant with inferences based on IPW estimation with SL.
Even though the 11 super learners could not make use of the dummy variables that permitted ’manual’ non-linear adjustment for A1c, the SL algorithm appears3 to be successful in automating flexible (i.e., non-linear) adjustment for A1c in this analysis using a polyclass learner.
This report illustrates that differences between results from trials and advanced analytic methods such as MSM with IPW estimation in observational studies may not necessarily reflect real differences between efficacy and effectiveness but biased estimates of effectiveness due to arbitrary and incorrect parametric modeling decisions. This report also demonstrates the feasibility of SL estimation in a study based on large healthcare databases for the purpose of automating flexible confounding/selection bias adjustment from existing machine learning algorithms and hedging against incorrect inferences that may otherwise arise from arbitrary parametric assumptions.
What is new?
Inferences from marginal structural modeling based on inverse probability weighting estimation and electronic health records data are sensitive to parametric decisions for modeling the treatment and right-censoring mechanisms.
Super Learning can successfully harness flexible confounding and selection bias adjustment from existing machine learning algorithms.
Erroneous inference about clinical effectiveness due to arbitrary and incorrect parametric assumptions may be avoided with Super Learning.
Appendix A. Inclusion/Exclusion criteria
Inclusion
Age > 18 years, < 80 years, and currently enrolled in health plan from one of the following four sites: Kaiser Permanente of Northern California, Northwest, Hawaii, or Colorado,
-
Cohort Entry: At initial detection of diabetes by one or more of following noted between 1/1/2006 and 6/30/2009:
two elevated FPGs (>126 mg/dl) within 2 year period; or
two elevated RPGs (>200 mg/dl) within 2 year period: or
one elevated FPG and one elevated RPG within 2 year period; or
one elevated A1c (>6.5%)
>2 years continuous (no gap > 2 months) health plan enrollment before cohort entry
At least one BMI recording prior to or within 1 month after cohort entry.
Pharmacy benefit at time of initial detection and throughout follow-up, and no gap in benefit coverage > 2 months in 2 years before cohort entry
Exclusions
Any anti-diabetic medication (including metformin) at any time prior to cohort entry
Any prior diagnosis of diabetes mellitus† at any point prior to cohort entry
Most recent serum creatinine (prior to or within 3 months following cohort entry) > 1.5 mg/dL in men, or > 1.4 mg/dL in women
Diagnosis in prior 2 years of any of the following: active cancer other than non-melanoma skin cancer; endstage renal disease or chronic kidney disease; hepatic failure or dementia (from inpatient or outpatient records), or a hospitalization within past year for congestive heart failure.
Any evidence (diagnoses, laboratory test, procedure) of pregnancy in the 15 months before cohort entry‡
630–639 Ectopic or molar pregnancy; other pregnancy with abortive outcome
640–649 Complications mainly related to pregnancy
650–659 Normal delivery, other indications for care in pregnancy, labor, delivery
660–669 Complications occurring mainly in the course of labor and delivery
670–677 Complications of the puerperium
678–679 Other Maternal and Fetal Complications
V22 Normal Pregnancy
V23 Supervision of high-risk pregnancy
81025 Urine pregnancy test: Positive
84702 Serum pregnancy test quantitative
94703 Serum pregnancy test - qualitative
Appendix B. Data structure
The observed data on any given patient in this study consist of the collected measurements on exposure, outcome, and confounding variables over time (every 180 days) until the patient’s end of follow-up. The time when the patient’s follow-up ends is denoted by T̃ and is defined as the earliest of the time to failure (i.e., GFR worsening) denoted by T or the time to a right-censoring event denoted by C. Renal function was classified as stage 1 when estimated GFR (eGFR) was ≥ 90 ml/min/1.73 m2, stage 2 for eGFR 60–89, stage 3a for eGFR 45–59, stage 3b for eGFR 30–44, stage 4 for eGFR 15–29, and stage 5 for eGFR<15. GFR worsening was defined as movement from any lower numbered stage at baseline to any higher numbered stage based on a single follow-up GFR measurement. Patients were artificially right-censored the first time there was a gap longer than two 180-day intervals between two consecutive GFR measurements. The artificial censoring event was set at the third 180-day period of such a gap. When T̃ = C, the type of right-censoring event experienced by the patient is denoted by Γ with possible values 1, 2, 3, or 4 to represent end of follow-up by administrative end of study, disenrollment from the health plan, death, or insufficient GFR monitoring, respectively. The indicator that the follow-up time T̃ is equal to the failure time T is denoted by Δ = I(T̃ = T). At each time point t = 0, …, T̃, the patient’s exposure to an intensified DM treatment is represented by the variable A1(t), and the patient’s right-censoring status is denoted by the indicator variable A2(t) = I(C ≥ t). The combination A(t) = (A1(t), A2(t)) is referred to as the action at time t. The treatment variable A1(t) is polychotomous with 6 possible levels 0 through 5 to represent 1) no T2DM pharmacotherapy, 2) met, 3) sul, 4) met+sul, 5) other T2DM pharmacotherapies, and 6) undetermined, respectively. The exposures were characterized with values 0 and 4 until and at the 180-day interval at which the patient initiated a first line pharmacotherapy. The exposures were not determined therafter, i.e. characterized with value 5, because such information is irrelevant for the investigation of the ITT effect of interest. At each time point t = 0, …, T̃, covariates (e.g., A1c measurements) are denoted by the multi-dimensional variable L(t) and defined as measurements that occur before A(t) or are otherwise assumed not to be affected by the actions at time t or thereafter, (A(t), A(t + 1), …). For each time point t = 0, …, T̃ + 1, the outcome (i.e., the indicator of past failure) is denoted by Y(t) = I(T ≤ t−1) and is an element of the covariates at time t, L(t). By definition, the outcome is thus 0 for t = 0, …, T̃, missing at t = T̃ + 1 if Δ = 0 and 1 at t = T̃ + 1 if Δ = 1. To simplify notation, we use overbars to denote covariate and exposure histories, e.g., a patient’s exposure history through time t is denoted by Ā(t) = (A(0), …, A(t)). Following the MSM framework [18], we approached the observed data in this study as realizations of n independent and identically distributed copies of O = (T̃, Δ, (1 − Δ)Γ, L̄(T̃), Ā(T̃), ΔY(T̃ + 1)) denoted by Oi for i = 1, …, n where n = 34, 4684 represents the sample size. The approach implemented for mapping EHR data into the coarsened observed data Oi for each patient i was described elsewhere [12, Appendix E]. The longest observed follow-up time was maxi=1,…,n T̃i = 7 (≈ 4 years) and the median follow-up time was about 1.5 years.
Appendix C. Covariates considered in the analysis
The following time-independent covariates were considered for confounding and selection bias adjustment: age at study (years), sex (male/female), median neighborhood household income in the patients census block, prospective DxCG risk scores based on baseline diagnoses and prescriptions [52], race (white, black, asian, pacific islander, native american, hispanic, unknown), baseline eGFR (≥90,60–89,45–59,30–44,15–29, <15), study site (Kaiser Permanente of Northern California, Northwest, Hawaii, or Colorado), and reason for study entry (FPG only, RPG only, A1c only, FPG and RPG, multiple reasons).
In addition, the following time-varying covariates were considered for confounding and selection bias adjustment: history of arrhythmia, history of coronary heart disease, history of congestive heart failure, history of cerebrovascular disease, history of peripheral arterial disease, body mass index, hemoglobin A1c, lipoprotein values (LDL and HDL, triglyceride), blood pressure values (SBP and DBP), and albuminuria level (Microalbumin/Creatinine Ratio <30, 30–300, >300).
Appendix D. Details of the MSM approach
We assumed the following logistic MSM m(t, ā1(t−1)|β) for the discrete-time counterfactual hazards P(Yā(t−1)(t) = 1|Yā(t−1)(t − 1) = 0) where β = (βj)j=0,…,8 is a 9-dimensional coefficient and the subscript notation Yā(t−1) is used to represent the counterfactual outcomes of interest (where ā2(t−1) = 0) [12, Appendix B]:
This MSM was fitted by standard weighted logistic regression with weights defined by:
The resulting estimates of the coefficients β of the logistic MSM are denoted by βn and were used to derive estimates of the counterfactual survival curves of interest, Pn(Tā1(t) > t), based on the formula linking discrete-time hazards to survival probabilities:
Appendix E. Decomposition of the denominator of the stabilized weights
The three strategies considered for estimating the denominators of the stabilized weights in this report are based on the following probability factorization using the chain rule:
since A(t) = (A1(t), A2(t)). Given that only the person-time observations collected before censoring can contribute to the fitting of the MSM, only the following two conditional probabilities need to be estimated:
| (E.1) |
and
| (E.2) |
For clarity, (Y(t) = 0, Ā2(t−1) = 0, L̄(t), Ā1(t−1)) and (Y(t) = 0, L̄(t), Ā1(t−1) = 0, Ā2(t) = 0) are denoted below by
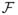 (t) and
(t) and
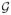 (t), respectively.
(t), respectively.
The conditional probability E.1 can be factorized using the chain rule and information about the different types of possible censoring events: P(A2(t) = 0|
 (t)) = [1 − P(I(A2(t) = 1, Γ = 1) = 1|
(t)) = [1 − P(I(A2(t) = 1, Γ = 1) = 1|
 (t))] × [1 − P(I(A2(t) = 1, Γ = 2) = 1|
(t))] × [1 − P(I(A2(t) = 1, Γ = 2) = 1|
 (t), I(A2(t) = 1, Γ = 1) = 0)] × [1 − P(I(A2(t) = 1, Γ = 3) = 1|
(t), I(A2(t) = 1, Γ = 1) = 0)] × [1 − P(I(A2(t) = 1, Γ = 3) = 1|
 (t), I(A2(t) = 1, Γ = 1) = 0, I(A2(t) = 1, Γ = 2) = 0)] × [1 − P(I(A2(t) = 1, Γ = 4) = 1|
(t), I(A2(t) = 1, Γ = 1) = 0, I(A2(t) = 1, Γ = 2) = 0)] × [1 − P(I(A2(t) = 1, Γ = 4) = 1|
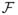 (t), I(A2(t) = 1, Γ = 1) = 0, I(A2(t) = 1, Γ = 2) = 0, I(A2(t) = 1, Γ = 3) = 0)]
(t), I(A2(t) = 1, Γ = 1) = 0, I(A2(t) = 1, Γ = 2) = 0, I(A2(t) = 1, Γ = 3) = 0)]
since A2(t) = 0 is equivalent to (I(A2(t) = 1, Γ = 1) = 0, …, I(A2(t) = 1, Γ = 4) = 0) where I(A2(t) = 1, Γ = j) is the indicator of censoring by an event of type Γ = j. The first probability on the right-hand side of the previous equality may be ignored from the definition of the denominator of the weights (and thus does not need to be estimated) if one assumes that censoring due to administrative end of study is not informative, i.e., P(I(A2(t) = 1, Γ = 1) = 1|
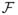 (t)) is only a function of time t.
(t)) is only a function of time t.
Thus, the only three conditional probabilities of censoring that need to be estimated to estimate the stabilized weights are:
| (E.3) |
| (E.4) |
| (E.5) |
Given that the effects of interest in this analysis are ITT effects, the conditional probability E.2 is 1 at all time points t following the time point when a treatment was initiated since P(A1(t) = 5|Y(t) = 0, L̄(t), Ā1(t−1) ≠ 0, Ā2(t) = 0) = 1. Thus, only the following conditional probability needs to be estimated: P(A1(t)|
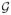 (t)). Using the chain rule, this probability can be factorized as: P(A1(t)|
(t)). Using the chain rule, this probability can be factorized as: P(A1(t)|
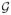 (t)) = P(I(A1(t) = 1)|
(t)) = P(I(A1(t) = 1)|
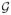 (t)) × P(I(A1(t) = 2)|
(t)) × P(I(A1(t) = 2)|
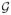 (t), I(A1(t) = 1)) × P(I(A1(t) = 3)|
(t), I(A1(t) = 1)) × P(I(A1(t) = 3)|
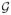 (t), I(A1(t) = 1), I(A1(t) = 2)) × P(I(A1(t) = 4)|
(t), I(A1(t) = 1), I(A1(t) = 2)) × P(I(A1(t) = 4)|
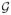 (t), I(A1(t) = 1), I(A1(t) = 2), I(A1(t) = 3)) since A1(t) can be equivalently coded with the following four dummy variables which each indicates treatment with one of the four therapies of interest (met, sul, met+sul, other): (I(A1(t) = 1), I(A1(t) = 2), I(A1(t) = 3), I(A1(t) = 4)). Note that the last three conditional probabilities on the right-hand side of the previous equality are equal to 1 when, respectively, I(A1(t) = 1) = 1, I(A1(t) = 1) = 1 or I(A1(t) = 2) = 1, and I(A1(t) = 1) = 1 or I(A1(t) = 2) = 1 or I(A1(t) = 3) = 1. Thus, the only four conditional probabilities that need to be estimated to estimate component E.2 are: P(I(A1(t) = 1) = 1|
(t), I(A1(t) = 1), I(A1(t) = 2), I(A1(t) = 3)) since A1(t) can be equivalently coded with the following four dummy variables which each indicates treatment with one of the four therapies of interest (met, sul, met+sul, other): (I(A1(t) = 1), I(A1(t) = 2), I(A1(t) = 3), I(A1(t) = 4)). Note that the last three conditional probabilities on the right-hand side of the previous equality are equal to 1 when, respectively, I(A1(t) = 1) = 1, I(A1(t) = 1) = 1 or I(A1(t) = 2) = 1, and I(A1(t) = 1) = 1 or I(A1(t) = 2) = 1 or I(A1(t) = 3) = 1. Thus, the only four conditional probabilities that need to be estimated to estimate component E.2 are: P(I(A1(t) = 1) = 1|
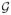 (t)); P(I(A1(t) = 2) = 1|
(t)); P(I(A1(t) = 2) = 1|
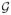 (t), I(A1(t) = 1) = 0); P(I(A1(t) = 3) = 1|
(t), I(A1(t) = 1) = 0); P(I(A1(t) = 3) = 1|
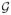 (t), I(A1(t) = 1) = 0, I(A1(t) = 2) = 0); and P(I(A1(t) = 4) = 1|
(t), I(A1(t) = 1) = 0, I(A1(t) = 2) = 0); and P(I(A1(t) = 4) = 1|
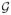 (t), I(A1(t) = 1) = 0, I(A1(t) = 2) = 0, I(A1(t) = 3) = 0). These probabilities may be equivalently written as:
(t), I(A1(t) = 1) = 0, I(A1(t) = 2) = 0, I(A1(t) = 3) = 0). These probabilities may be equivalently written as:
| (E.6) |
| (E.7) |
Appendix F. Super Learner implementation
The Super Learner considered in this analysis was implemented with the SuperLearner R package [48] as described here. All routines referenced below are included in the R package with the exception of the R routine SL.polyclass given below.
The 5 candidate learners based on logistic regression were implemented by the SL.glm routine using the template screening routine screen.glmP to define 5 nested subsets of explanatory variables based on the following 5 significance levels: α = 1e-30, 1e-10, 1e-5, 0.1.
The two candidate learners based on polychotomous regression were implemented by the SL.polyclass routine using the template screening routine screen.glmP to define 2 nested subsets of explanatory variables based on the following 2 significance levels: α =1e-30 and 1.
SL.polyclass <- function(Y.temp, X.temp, newX.temp, family, obsWeights, …){
cat(“\nUsing SL.polyclass”)
tryCatch(require(polspline), warning = function(…) {
stop(“you have selected polyclass as a library algorithm but do not have
the polspline package installed”)
})
if (family$family == “gaussian”) {
stop(“the outcome must be categorical”)
}
if (family$family == “binomial”) {
fit.polyclass <- polyclass(Y.temp, X.temp, penalty = log(length(Y.temp)),
weight = obsWeights)
out <- ppolyclass(cov = newX.temp, fit = fit.polyclass)[, 2]
fit <- list(fit = fit.polyclass)
}
foo <- list(out = out, fit = fit)
class(foo$fit) <- c(“SL.polymars”)
return(foo)
}
The R routine above implements the polyclass learner [38] based on the Bayesian Information Criterion (BIC) as the model selection criterion. To improve computing speed, this learner was favored over the SL.polymars routine that is available by default in the SuperLearner R package but that relies on cross-validation for model selection.
Footnotes
These effects are referred to as ITT effects because their interpretation is similar to the interpretation of conventional ITT effects in the sense that, in the hypothetical trial of interest, patients adhere to the assigned treatment regimen up to and at the assigned time of treatment initiation and may be non-adherent (by discontinuing or changing pharmacotherapy) thereafter.
I(A1c<6%), I(6%≤A1c<6.5%), I(7%≤A1c<7.5%), I(7.5%≤A1c<8%), I(A1c≥8%), I(A1c change<−1%), I(−1%≤A1c change<−0.5%), I(−0.5%≤A1c change<0%), I(0.5%≤A1c change<1%), I(A1c change≥1%) where I(·) denotes indicator variables.
from the concordance of the results from IPW estimation with SL and that from IPW estimation with non-linear adjustment for A1c.
1, 552 patients were excluded from the study cohort in the GFR analysis due to missing GFR measurements at baseline.
ICD-9-CM codes 249, 250.x, 357.2, 366.41, 362.0x, 443.81, 648.0x
Note: A patient with prior evidence of pregnancy may enter the cohort only if the date of initial detection is at least 15 months following first evidence of most recent pregnancy (i.e., allow 9 months following first evidence of pregnancy plus 6 months post-partum). To identify pregnancy, the following ICD-9 codes or CPT-4 codes were used:
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Nissen SE, Wolski K. Effect of rosiglitazone on the risk of myocardial infarction and death from cardiovascular causes. N Engl J Med. 2007;356:2457–2471. doi: 10.1056/NEJMoa072761. [DOI] [PubMed] [Google Scholar]
- 2.Vogt TM, Elston-Lafata J, Tolsma D, Greene SM. The role of research in integrated healthcare systems: the HMO Research Network. Am J Manag Care. 2004;10:643–8. [PubMed] [Google Scholar]
- 3.Hernan MA. With great data comes great responsibility: publishing comparative effectiveness research in epidemiology. Epidemiology. 2011;22:290–291. doi: 10.1097/EDE.0b013e3182114039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Rosenbaum PR. The consequence of adjustment for a concomitant variable that has been affected by the treatment, Journal of the Royal Statistical Society, Series A. General. 1984;147:656–66. [Google Scholar]
- 5.Robins JM. Association, causation and marginal structural models. Synthese. 1999;121:151–179. [Google Scholar]
- 6.Hernan MA, Hernandez-Diaz S, Robins JM. A structural approach to selection bias. Epidemiology. 2004;15:615–625. doi: 10.1097/01.ede.0000135174.63482.43. [DOI] [PubMed] [Google Scholar]
- 7.Greenland S, Pearl J, Robins JM. Causal diagrams for epidemiologic research. Epidemiology. 1999;10:37–48. [PubMed] [Google Scholar]
- 8.Pearl J. Causality: Models, Reasoning, and Inference. 2. Cambridge University Press; Cambridge: 2009. [Google Scholar]
- 9.Cole SR, Hernan MA, Robins JM, Anastos K, Chmiel J, Detels R, Ervin C, Feldman J, Greenblatt R, Kingsley L, Lai S, Young M, Cohen M, Munoz A. Effect of highly active antiretroviral therapy on time to acquired immunodeficiency syndrome or death using marginal structural models. Am J Epidemiol. 2003;158:687–694. doi: 10.1093/aje/kwg206. [DOI] [PubMed] [Google Scholar]
- 10.Hernan MA, Lanoy E, Costagliola D, Robins JM. Comparison of dynamic treatment regimes via inverse probability weighting. Basic Clin Pharmacol Toxicol. 2006;98:237–242. doi: 10.1111/j.1742-7843.2006.pto_329.x. [DOI] [PubMed] [Google Scholar]
- 11.Hernan MA, Hernandez-Diaz S. Beyond the intention-to-treat in comparative effectiveness research. Clinical Trials. 2011 doi: 10.1177/1740774511420743. [Epub ahead of print] [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Neugebauer R, Fireman B, Roy JA, O’Connor PJ, Selby JV. Dynamic marginal structural modeling to evaluate the comparative effectiveness of more or less aggressive treatment intensification strategies in adults with type 2 diabetes. Pharmacoepidemiol Drug Saf. 2012;21(Suppl 2):99–113. doi: 10.1002/pds.3253. [DOI] [PubMed] [Google Scholar]
- 13.Neugebauer R, van der Laan M. Why prefer double robust estimates. Journal of Statistical Planning and Inference. 2005;129:405–26. [Google Scholar]
- 14.Neugebauer R, van der Laan MJ. Nonparametric causal effects based on marginal structural models. Journal of Statistical Planning and Inference. 2007;137:419–434. [Google Scholar]
- 15.Pearl J. On the consistency rule in causal inference: axiom, definition, assumption, or theorem? Epidemiology. 2010;21:872–875. doi: 10.1097/EDE.0b013e3181f5d3fd. [DOI] [PubMed] [Google Scholar]
- 16.VanderWeele TJ. Concerning the consistency assumption in causal inference. Epidemiology. 2009;20:880–883. doi: 10.1097/EDE.0b013e3181bd5638. [DOI] [PubMed] [Google Scholar]
- 17.Pearl J. Causal inference in statistics: an overview. Stat Surv. 2009;3:96–146. [Google Scholar]
- 18.Robins J. Marginal Structural Models. 1997 Proceedings of the American Statistical Association, Section on Bayesian Statistical Science; pp. 1–10. [Google Scholar]
- 19.Hernan MA, Brumback BA, Robins JM. Estimating the causal effect of zidovudine on CD4 count with a marginal structural model for repeated measures. Statistics in Medicine. 2002;21:1689–1709. doi: 10.1002/sim.1144. [DOI] [PubMed] [Google Scholar]
- 20.Robins JM, Hernan MA, Brumback B. Marginal structural models and causal inference in epidemiology. Epidemiology. 2000;11:550–560. doi: 10.1097/00001648-200009000-00011. [DOI] [PubMed] [Google Scholar]
- 21.Hernan MA. The hazards of hazard ratios. Epidemiology. 2010;21:13–15. doi: 10.1097/EDE.0b013e3181c1ea43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.van der Vaart AW. Asymptotic Statistics. Cambridge University Press; 1998. [Google Scholar]
- 23.van der Laan MJ, Robins JM. Unified methods for censored longitudinal data and causality. Springer; New York: 2003. [Google Scholar]
- 24.Tsiatis A. Semiparametric Theory and Missing Data. Springer; New York: 2006. [Google Scholar]
- 25.Kang JDY, Schafer JL. Demystifying Double Robustness: A Comparison of Alternative Strategies for Estimating a Population Mean from Incomplete Data. Statistical Science. 2007;22:523–539. doi: 10.1214/07-STS227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Robins J, Sued M, Lei-Gomez Q, Rotnitzky A. Comment: Performance of Double-Robust Estimators When ”Inverse Probability” Weights are Highly Variable. Statistical Science. 2007;22:544–559. [Google Scholar]
- 27.McCaffrey DF, Ridgeway G, Morral AR. Propensity score estimation with boosted regression for evaluating causal effects in observational studies. Psychol Methods. 2004;9:403–425. doi: 10.1037/1082-989X.9.4.403. [DOI] [PubMed] [Google Scholar]
- 28.Petersen ML, Wang Y, van der Laan MJ, Guzman D, Riley E, Bangsberg DR. Pillbox organizers are associated with improved adherence to HIV antiretroviral therapy and viral suppression: a marginal structural model analysis. Clin Infect Dis. 2007;45:908–915. doi: 10.1086/521250. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Lippman SA, Shade SB, Hubbard AE. Inverse probability weighting in sexually transmitted infection/human immunodeficiency virus prevention research: methods for evaluating social and community interventions. Sex Transm Dis. 2010;37:512–518. doi: 10.1097/OLQ.0b013e3181d73feb. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Westreich D, Lessler J, Funk MJ. Propensity score estimation: neural networks, support vector machines, decision trees (CART), and meta-classifiers as alternatives to logistic regression. J Clin Epidemiol. 2010;63:826–833. doi: 10.1016/j.jclinepi.2009.11.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Lee BK, Lessler J, Stuart EA. Improving propensity score weighting using machine learning. Stat Med. 2010;29:337–346. doi: 10.1002/sim.3782. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Breiman L. Random forests. Machine Learning. 2001;45:5–32. [Google Scholar]
- 33.Efron B, Hastie T, Johnstone I, Tibshirani R. Least angle regression. Annals of Statistics. 2004;32:407–499. [Google Scholar]
- 34.Ruczinski I, Kooperberg C, LeBlanc M. Logic regression. Journal of Computational and Graphical Statistics. 2003;12:475–511. [Google Scholar]
- 35.Breiman L, Friedman JH, Olshen RA, Stone CJ. Classification and Regression Trees. Wadsworth & Brooks/Cole; Monterey: 1984. [Google Scholar]
- 36.Hoerl A, Kennard R. Ridge regression: Biased estimation for nonorthogonal problems. Technometrics. 1970;12:55–67. [Google Scholar]
- 37.Friedman J. Multivariate adaptive regression splines. Annals of Statistics. 1991;19:1–141. [Google Scholar]
- 38.Kooperberg C, Bose S, Stone CJ. Polychotomous Regression. Journal of the American Statistical Association. 1997;92:117–127. [Google Scholar]
- 39.Sinisi SE, van der Laan MJ. Deletion/substitution/addition algorithm in learning with applications in genomics. Stat Appl Genet Mol Biol. 2004;3:Article18. doi: 10.2202/1544-6115.1069. [DOI] [PubMed] [Google Scholar]
- 40.Schneeweiss S, Rassen JA, Glynn RJ, Avorn J, Mogun H, Brookhart MA. High-dimensional propensity score adjustment in studies of treatment effects using health care claims data. Epidemiology. 2009;20:512–522. doi: 10.1097/EDE.0b013e3181a663cc. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Ridgeway G, McCaffrey DF. Comment: Demystifying Double Robustness: A Comparison of Alternative Strategies for Estimating a Population Mean from Incomplete Data. Statistical Science. 2007;22:540–543. doi: 10.1214/07-STS227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.van der Laan M, Polley E, Hubbard A. Super learner, Statistical Applications in Genetics and Molecular Biology. 2007;6 doi: 10.2202/1544-6115.1309. [DOI] [PubMed] [Google Scholar]
- 43.Neugebauer R, Chandra M, Paredes A, Graham D, McCloskey C, Go A. A Marginal Structural Modeling Approach with Super Learning for a Study on Oral Bisphosphonate Therapy and Atrial Fibrillation. Journal of Causal Inference Accepted. 2012 [Google Scholar]
- 44.Dudoit S, van der Laan M. Asymptotics of cross-validated risk estimation in estimator selection and performance assessment. Statistical Methodology. 2005;2:131–154. [Google Scholar]
- 45.van der Laan M, Dudoit S, Keles S. Asymptotic optimality of likelihood-based cross-validation. Statistical Applications in Genetics and Molecular Biology. 2004;3 doi: 10.2202/1544-6115.1036. [DOI] [PubMed] [Google Scholar]
- 46.van der Vaart A, Dudoit S, van der Laan M. Oracle inequalities for multi-fold cross-validation. Statistics and Decisions. 2006;24:351–371. [Google Scholar]
- 47.van der Laan M, Dudoit S, van der Vaart A. The cross-validated adaptive epsilon-net estimator. Statistics and Decisions. 2006;24:373–395. [Google Scholar]
- 48.Polley EC. SuperLearner R package (version 1.1-18) 2011 https://github.com/ecpolley/SuperLearner.
- 49.Cole SR, Hernan MA. Constructing inverse probability weights for marginal structural models. Am J Epidemiol. 2008;168:656–664. doi: 10.1093/aje/kwn164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Bembom O, van der Laan MJ. Technical Report 230. Division of Biostatistics; UC Berkeley: 2008. Data-adaptive selection of the truncation level for Inverse-Probability-of-Treatment-Weighted estimators. [Google Scholar]
- 51.Petersen ML, Porter KE, Gruber S, Wang Y, van der Laan MJ. Diagnosing and responding to violations in the positivity assumption. Stat Methods Med Res. 2012;21:31–54. doi: 10.1177/0962280210386207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.DxCG Inc. Risk Smart®Models and Methodologies Guide. DxCG Inc; Boston, MA: 2002. [Google Scholar]