Erythropoietin-Stimulating Agents and Survival in End-Stage Renal Disease: Comparison of Payment Policy Analysis, Instrumental Variables, and Multiple Imputation of Potential Outcomes

Abstract

Objective

To compare the assumptions and estimands across three approaches to estimating the effect of erythropoietin-stimulating agents (ESAs) on mortality.

Study Design and Setting

Using data from the Renal Management Information System, we conducted two analyses utilizing a change to bundled payment that we hypothesized mimicked random assignment to ESA (pre-post, difference-in-difference, and instrumental variable analyses). A third analysis was based on multiply imputing potential outcomes using propensity scores.

Results

There were 311,087 recipients of ESAs and 13,095 non-recipients. In the pre-post comparison, we identified no clear relationship between bundled payment (measured by calendar time) and the incidence of death within six months (risk difference -1.5%; 95% CI - 7.0% to 4.0%). In the instrumental variable analysis, the risk of mortality was similar among ESA recipients (risk difference -0.9%; 95% CI -2.1 to 0.3). In the multiple imputation analysis, we observed a 4.2% (95% CI 3.4% to 4.9%) absolute reduction in mortality risk with use of ESAs, but closer to the null for patients with baseline hematocrit >36%.

Conclusion

Methods emanating from different disciplines often rely on different assumptions, but can be informative about a similar causal contrast. The implications of these distinct approaches are discussed.

INTRODUCTION

The estimation of causal effects from non-experimental studies is a venture common to many empirical disciplines. As a result, multiple procedures for estimation of causal effects have been developed [1-3], emanating from different intellectual traditions and relying on different assumptions. The recent emphasis on comparative effectiveness research has promoted interdisciplinary sharing of methods and perspectives [4], including those from econometrics, statistics, health services research, and epidemiology [5]. However, researchers may be unfamiliar with the appropriate assumptions and estimands produced by a particular analytic technique.

For example, in cohort studies where the treatment groups are matched on propensity score, differences in outcomes are typically interpretable as the effect of the treatment on the treated [6]. However, an instrumental variable analysis employed in the same dataset and with the same exposure specification will, under certain assumptions, produce an estimate of the local-average treatment effect (LATE), local to just those patients whose treatment choice was affected by the instrument (the “compliers”) [7]. The different analyses also carry distinct assumptions that make them suitable for different applications. In certain circumstances, evaluation of policies may provide some information about the effect of a treatment whose use is influenced by the policy [8], resulting in comparability between the policy effect and the effect of a treatment affected by the policy.

The purpose of this paper is to present a case study in which the authors compared three methods for estimating the effect of a class of anemia treatments, erythropoietin-stimulating agents (ESAs), on mortality among patients with end-stage renal disease (ESRD). ESAs are recombinant glycoprotein hormones that mimic endogenous erythropoietin and treat anemia associated with chronic kidney disease [9]. The first two methods have an econometric legacy and leverage a Medicare payment policy change that reduced use of ESAs for patients with high hematocrit. The third technique multiply imputes counterfactual outcomes (mortality) within levels of the propensity score, allowing a more specific person-level analysis [10].

METHODS

Policy Context for Econometric Analyses

Until December 31, 2010, Medicare reimbursed hemodialysis providers separately for each dose of ESAs administered, so that each dose resulted in additional revenue and profit for the provider. Effective January 1, 2011, Medicare introduced an “expanded bundled” payment of a fixed sum for hemodialysis treatments, including the administration of ESAs, so that providers can no longer earn more revenue by increasing their use of ESAs [11]. The Medicare program simultaneously introduced financial penalties that reduced payments to hemodialysis providers with low performance on a composite measure of three quality indicators. Three-quarters of this composite score was based on the proportion of ESRD patients with hematocrit between 30% and 36%. Over 95% of providers adopted the new payment model immediately [11].

These changes in payment occurred within the context of findings that treating patients with ESAs to higher hemoglobin targets is associated with an increased risk of adverse effects, including death [12-15]. The Food and Drug Administration (FDA) issued a black-box warning cautioning providers to not to exceed hemogloblin levels of 12 g/dL with ESA treatment [16], and recently the FDA issued a new guideline suggesting that ESAs be used only to reduce the frequency of transfusions [17]. As a result, after Medicare implemented bundled payment for ESRD services, use of ESAs at the encounter level among patients with hematocrit > 36% immediately declined by 7 to 14 percentage points [18].

We viewed Medicare's payment policy change and the resulting reduction in use of ESAs as an opportunity to identify the effect of ESA use on the rate of mortality at the patient level. We hypothesized that a comparison of patients initially exposed to ESAs before bundled payment to those initially exposed after the change in payment policy would mimic random assignment to ESA treatment for patients with an initial hematocrit of >36% and form the basis for an instrumental variable analysis [7].

Data Source and Study Population

We obtained data from the Renal Management Information System (REMIS) on all ESRD patients undergoing hemodialysis between January 1, 2007 and December 31, 2011 through the Centers for Medicare and Medicaid Services (http://www.cms.gov/Research-Statistics-Data-and-Systems/Files-for-Order/IdentifiableDataFiles/RenalManagementInformationSystem.html). REMIS data include information on specific hemodialysis encounters, including each patient's baseline hematocrit (for patients beginning dialysis), a binary variable indicating whether patients received ESA (recorded one to three times quarterly), and demographic and clinical data. We restricted the study population to patients beginning hemodialysis.

The three analyses presented in this paper used different timeframes. Because Analyses 1 and 2 relied on the policy change, it was necessary to narrow the window of study to around the time of the policy change (the year before and after). Analysis 3 had no such requirement and was able to accommodate all of the data (from 2007−2011).

Outcome and Covariates

Date of death was collected from provider report on the CMS 2746 Death Notification Form and linkage to the Medicare enrollment file, as listed in the REMIS data.

Additional covariates included age, sex, race, albumin level at time of entry into ESRD, hematocrit level at time of entry into ESRD, body mass index (BMI), time since entering the ESRD program, and the presence or absence of a range of comorbid conditions assessed at the time of entry into the ESRD program. Because we performed these analyses for expository purposes, patients with missing values of body mass index, age, sex, albumin, and initial hematocrit were excluded from the analyses, and the results are subject to the assumption that these data were missing completely at random [19].

Analysis 1: Comparison of Mortality Pre-post Bundling of Payment for ESRD using a Difference-in-Differences Analysis

Because the introduction of bundled payments reduced prescribing of ESA therapy mainly among patients with a hematocrit level >36%, we estimated the risk of 180-day mortality in this population in the post-bundling period relative to the pre-bundling period. We also estimated the differential temporal change in the use of ESAs across hematocrit levels (≤36% and >36%) and risk of mortality. If bundled payment policy affected only the use of ESAs (i.e., there were no changes in the population covariates between the two periods) and the effect of the policy on patients with hematocrit ≤36% is negligible, then this method provides an estimate of the average effect of bundled payment on mortality, mediated by use of ESAs for those patients whose hematocrit is >36% and who do not receive ESA because of the new policy. That is, any increase or reduction in mortality would be attributable to the effect of bundled payment on use of ESAs.

The analysis took the form:

$$Mor{t}_i={\beta }_0+{\beta }_1{T}_i+{\beta }_2{D}_i+{\beta }_3{T}_i{D}_i+{\mathbf{x}}_i{\beta }_4+u_i$$

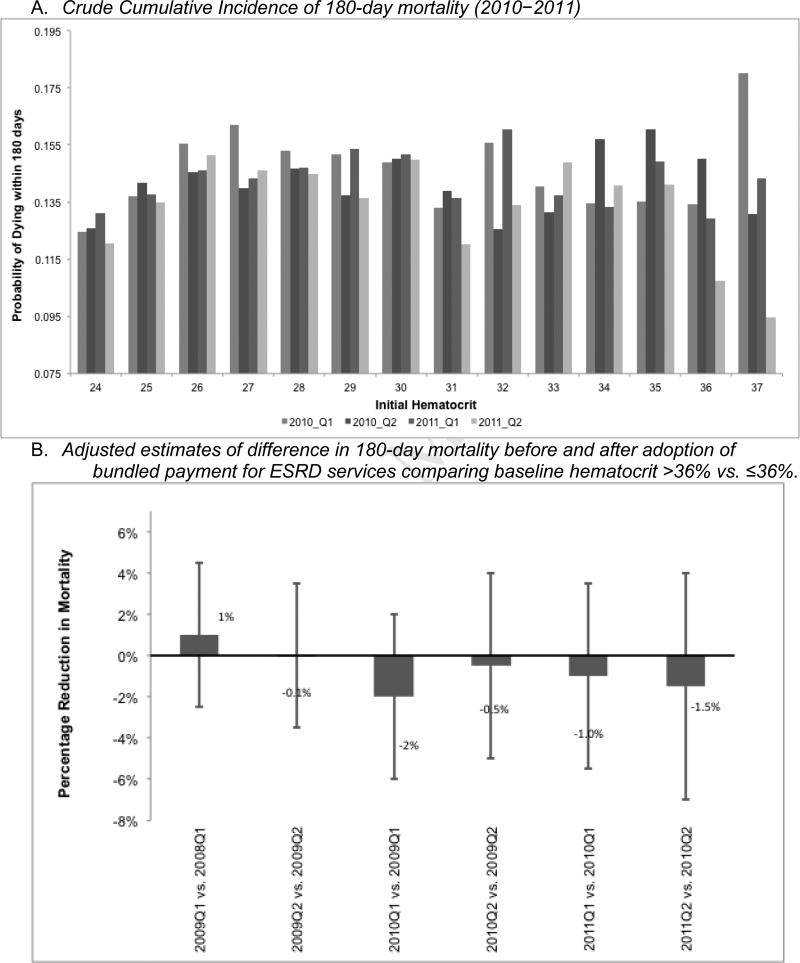
Where T=1 for patients who began hemodialysis in the first quarter of 2011 (post-bundling) and T=0 for patients who began hemodialysis during the first quarter of 2010 (pre-bundling), Mort_i=1 if patient who began hemodialysis in period T died within 180 days of beginning hemodialysis, D_i is a dummy variable=1 if the patient's initial hematocrit was >36%, x is a vector of patient characteristics, and u_i is an identically, independently, and normally distributed error term. The coefficient of interest, β₃, plotted in Figure 2, Panel B, is the difference in the differences in the risk of 180-day mortality before and after bundling (first differences) between patients with hematocrit >36% versus ≤36% (second difference).

Figure 2.

Crude and adjusted cumulative incidence of 180-day mortality following first hemodialysis treatment by date of first dialysis treatment (proxy for exposure to erythropoietin-stimulating agents), Renal Management Information System, 2008–2011

Ideally, this analysis would have been restricted to treatment facilities that opted into the bundled payment system (as 95% of facilities did), because only those facilities were affected by the policy change. However, the data did not include an indicator of which facilities opted for bundled payment.

Analysis 2: Instrumental Variable Analysis

In the second analysis, we identified recipients of ESAs whose baseline hematocrit was >36% and whose first hemodialysis treatment occurred in the first half of the year preceding or the six months following the change in payment policy, creating a variable, Z, assumed to be an instrument corresponding with the date of first ESA exposure. We classified ESA exposure, T, as a binary, time-fixed measure of exposure status upon entry into REMIS. Specifically, each recipient was classified as exposed if he or she received ESA during the first recorded hemodialysis visit.

We then conducted a two-stage least-squares analysis in which we regressed the ESA-treatment variable on the time block of first hemodialysis (the proposed instrument) and patient covariates:

$$T_i={\beta }_0+{\beta }_1{Z}_i+X_i{\beta }_2+e_i^1$$

where T_i is ESA exposure status for patient i, Z_i is the instrumental variable for patient i (time block of first hemodialysis treatment), X represents measured patient covariates, and e_i¹ is a randomly distributed error term. In stage two, we fit a model of the form

$$Y_i={\alpha }_0+{\alpha }_1{\widehat{T}}_i+X_i{\alpha }_2+e_i^2$$

where Y_i was mortality, T̂_i was the predicted value of ESA exposure given the proposed instrumental variable from the first model, α₁ provides an estimate of the risk difference of mortality corresponding with ESA use at baseline, and e_i² is a randomly distributed error term.

Analysis 3: Multiple Imputation of Potential Outcomes

In this analysis, we estimated the causal effect of treatment with ESAs on 180-day mortality relative to non-treatment using a broader set of data (2007–2011). This analysis operationalized the Rubin Causal Modeling framework,[1] in which a causal effect of a binary treatment with ESAs (W) on mortality (Y) for person i (i = 1,...,N) is defined by a comparison of two “potential” outcomes, Y_i(1) and Y_i(0), only one of which is observed for each patient (the unobserved outcome is counterfactual and represents the experience of the same patient had he or she received the alternative treatment). These potential outcomes are the outcomes for each person under the two possible levels of exposure W: W_i = 1 indicates baseline exposure to ESA, and W_i = 0 indicates the control level (non-exposure), where Y_i(1) and Y_i(0) would be realized under the active and control treatment conditions, respectively.

We compared the effect of receiving ESA during any hemodialysis encounter (W_i=1) vs. never receiving ESA (W_i=0) at any hemodialysis encounter after hemodialysis initiation. Follow-up began at the initiation of hemodialysis. Approximately 92% of ESA recipients received ESA at the time of the first recorded hemodialysis treatment, making this measure of exposure comparable to the baseline measure used in Analysis 2 and also making it unlikely that bias resulted from the misclassification of unexposed, immortal time prior to treatment or selection bias [20-22].

Because only one potential outcome is observed for each patient, we cannot directly estimate the causal effect for person i. Instead we must observe multiple people, some exposed to ESAs (W_i = 1) and others unexposed (W_i = 0), and consider their covariates, X_i, which we assumed were unaffected by W_i. We accounted for the covariates (X_i) using estimated propensity scores for each person [23].

We implemented a novel methodology for imputing the missing counterfactual outcomes and estimating the treatment effect. First, we estimated the propensity scores using an algorithm described in Imbens and Rubin [24]. Patients for whom no person in the opposing exposure group had a similar estimated propensity score were excluded [25]. Second, we partitioned the patients into 10 equal size strata based on their estimated propensity score. We then compared the distributions of the covariates and all second order interactions of the covariates in the treatment and control groups in each stratum. If the stratum-specific distributions of covariates and interactions in the treatment and comparison group differed, we went back to the first step. We iterated between the first two steps until the distributions of the covariates in the treatment and control groups in each stratum were similar.

Third, we estimated the response surfaces (distribution of Y(W) | X) using two separate regression spline models. The knots of the spline were placed at the boundaries of strata from the Step 2. Fourth, we use the estimated response surfaces from the third step to multiply impute the missing potential outcome. For the patients in the comparison group we imputed Y_i(1) and for patients in the ESA group we imputed the Y_i(0).

Imputing the missing potential outcomes only once cannot adequately account for the uncertainty of the response surfaces or the uncertainty in the missing potential outcomes [19, 26]. Using multiple imputation with Rubin's combining rule [26] results in intervals that take into account the additional variability due to the missing potential outcomes and unknown parameters, and typically provides approximately valid statistical procedures. Lastly we estimated the average difference in 180-day mortality among strata of the initial hematocrit level. Note that the initial hematocrit value was included in the propensity score model. Complete description and theoretical justification for this procedure can be found in recent publications [10, 26, 27].

RESULTS

Characteristics of Recipientsand Non-recipients of ESAs

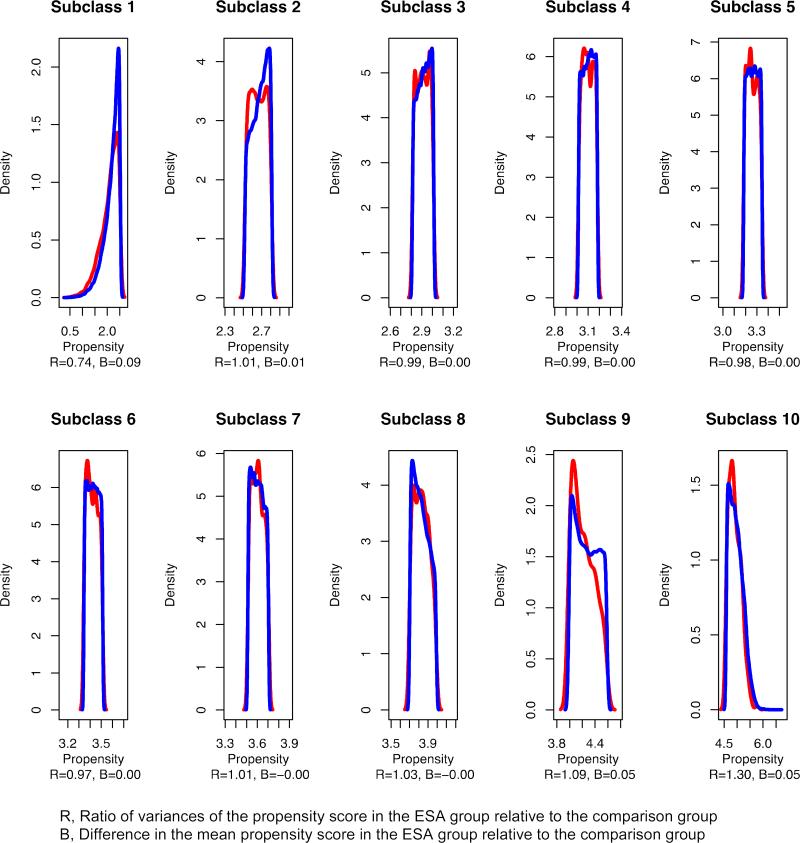
There were 311,087 recipients of ESAs between 2007 and 2011 and 13,095 non-recipients (Table 1). With respect to Analyses 1 and 2, most, but not all covariates were balanced across the time periods defined before and after the adoption of the bundling payment policy (Table 2, first stage) [18]. For example, the mean age and albumin levels were appreciably higher in the post-bundling period. There was a similar distribution of the estimated propensity score across exposure categories within deciles of the estimated propensity score after removal 2 ESA recipients (from 13,093) and 158 non-recipients (from 310,929) for whom there was no person in the opposing exposure group with a similar propensity score (Figure 1).

Table 1.

Distribution of baseline covariates for users and non-users of erythropoietin-stimulating agents, Renal Management Information System, 2007–2011^*

	Users N=311,087	Non-users N=13,095
	%	%
Men	44.6	43.0
Age (years), mean	66.4	61.2
Race
Black	27.7	31.8
White	67.0	61.2
Other	5.3	7.0
Initial albumin level, g/dL
0–1	0.2	0.2
1–2	5.8	5.3
2–3	30.7	27.0
3–4	37.2	40.0
5–6	5.9	8.5
Initial hematocrit, mean %	29.7	29.1
Year of first hemodialysis treatment
2007	23.7	7.7
2008	23.3	20.0
2009	22.3	23.1
2010	21.0	29.6
2011	9.7	19.6
Initial hemodialysis time >4 hours	1.0	1.4
Fistula or graft used at initial hemodialysis	17.1	24.1
Fistula used at initial hemodialysis	13.7	20.6
Catheter used at initial hemodialysis	82.2	75.4
Diagnoses
Diabetes	46.5	43.4
Hypertension	30.2	31.0
Body mass index, mean	28.8	29.3
Obesity	36.7	39.7
Congestive heart failure	36.2	28.0
Ischemic heart disease	23.8	18.5
Myocardial infarction	19.6	15.6
Hypertension	13.6	13.7
Tobacco use	6.1	6.5

^*This table represents the study population and exposure definition used in Analysis 3.

Table 2.

Estimated difference in risk of mortality comparing use of erythropoietin-stimulating agents to non-use using the bundled payment policy as an instrumental variable, Renal Management Information System, 2010–2011

First stage: Difference in prevalence of covariates and receipt of ESAs
	Change (Z=1)–(Z=0)a
ESA use, overall	-1.5%***
Men	0.001
Age (years)	0.27*
Race
Black	0.005
White	0.002
Other	-0.006
Initial albumin level, mean g/dL	0.012*
Initial hematocrit, mean %	-0.32*
Initial hemodialysis time > 4 hours	0.02
Fistula used at initial hemodialysis	0.004
Catheter used at initial hemodialysis	0.003
Diagnoses
Diabetes	-0.004
Hypertension	0.003
Body Mass Index, mean kg/m2	0.007
Congestive heart failure	-0.002
Ischemic heart disease	-0.001
Myocardial infarction	-0.002
Tobacco use	-0.003*
First Stage F-Statistic on Instrumental Variable	12.62
Second Stage: Estimate of ESA effect	Adjustedb 180-day risk of death (95% CI)
Receipt of ESAs	-0.9 (-2.1–0.3)

ESAs, erythropoietin-stimulating agents

^***significant at 1% level

**significant at 5% level

^*significant at 10% level

^aZ=1 if patient began hemodialysis between January 1, 2011 and June 30, 2011 and Z=0 if patient began hemodialysis between January 1, 2010 and June 30, 2010.

^bEstimated coefficient from two-stage least-squares regression model after adjusting for covariates shown the first stage.

Figure 1.

Distribution of propensity score in each decile, Renal Management Information System, 2007–2011

Analysis 1: Pre-post Comparison

Figure 2, Panel A shows a comparison of the 180-day mortality risk among patients whose first hemodialysis treatment was before or after the adoption of the bundled-payment policy, by first hematocrit level. Because current treatment guidelines and treatment quality incentive parameters [28] suggest that the dose of ESAs should be reduced if the patient's hematocrit exceeds 36%, we would expect that any effect of bundled payment on mortality would be stronger at higher levels of hematocrit. In these data, we see no clear relationship between bundled payment (measured by calendar time) and the incidence of death. The increased variability in the rate of death at higher hematocrit levels is ascribable to a smaller sample size. The mean hematocrit at first hemodialysis treatment was approximately 29%. The results also show no differences in the rate of mortality before and after the adoption of bundled payment among patients with hematocrit >36% (Figure 2, Panel B).

Analysis 2: Instrumental Variable Analysis

Overall, patients who began hemodialysis in the first half of 2011 were approximately 1.5% less likely to receive ESAs than their counterparts who began hemodialysis in the first half of 2010 (Table 2), suggesting that time relative to implementation of bundled payment is a weak potential instrument [29]. Although the summary statistics in Table 2 suggest that the proposed instrument is not highly correlated with many of the covariates used in the model, there still exists a correlation with age, initial albumin level, and initial hematocrit. This information suggests the possibility of some correlation between the instrumental variable and important unmeasured covariates. Under the assumption that we have a valid instrumental variable, the risk difference of 180-day mortality associated with receipt of ESAs was -0.9 (95% CI -2.1–0.3), but the interval estimate is consistent with no difference in the risk of mortality. The point estimate is interpretable as a non-significant protective effect of ESAs.

Analysis 3: Multiple Imputation of Potential Outcomes

After multiple imputation of counterfactual outcomes for recipients and non-recipients, we observed reductions of approximately three to five percent in the risk of mortality among recipients of ESAs across nearly all baseline levels of hematocrit (Figure 3). The average decrease in absolute risk comparing ESAs to non-use across levels of hematocrit was 4.2% (95% CI 3.4%–4.9%). There was no clear effect of ESAs on mortality at hematocrit levels of 40% and above, but the confidence intervals in these strata were wide.

Figure 3.

Differences in the cumulative incidence of mortality comparing users of erythropoietin-stimulating agents to non-users by initial hematocrit, Renal Management Information System, 2007–2011

DISCUSSION

We present three analyses that could be used to estimate different types of causal effects. The results from each approach are somewhat different, though qualitatively similar in showing little or no effect of ESAs on the risk of mortality for patients with higher levels of hematocrit. The specific estimands differ, as do the required assumptions for causal inference in each case. Below we discuss each of the assumptions and interpretation of each analysis in reverse order.

Analysis 3

Analysis 3 is likely most familiar to investigators in comparative effectiveness research. The values from this analysis are interpretable as estimates of the effect of initial treatment with ESAs among the full population of patients receiving hemodialysis, and in this case are comparable to the effect among the treated (96% of patients received treatment).

Analysis 3 requires assumptions that are common to many non-experimental methods in comparative effectiveness research, most importantly the assumption of no unmeasured confounding. The other assumptions required for the estimates from Analysis 3 to reflect a causal effect are Rubin's Stable Unit Treatment Value Assumption (SUTVA) and that each patient has a positive probability of receiving ESAs [34].

Analysis 2

In Analysis 2, the estimand produced is unclear. With instrumental variable analysis, estimating average treatment effects for the population under study requires sometimes untenable assumptions that affect the estimand produced [30, 31]. Indeed, the correlation between the proposed instrument and observed covariates suggests that our use of “time” as an instrumental variable is flawed to an unknown degree, and highlights the fundamental problem of instrumental variable analysis: finding a valid instrument. Moreover, in the presence of a heterogeneous treatment effect (i.e., where the treatment effect is not equal for each subject), interpreting the treatment effect as an average effect (e.g., among the treated) is unwarranted.

A commonly employed assumption for the estimation of causal effects from instrumental variables in the presence of heterogeneity is monotonicity [7, 31]. In Analysis 2, the presence of the bundled payment policy was treated as an instrumental variable, taking the value of 1 if a patient entered hemodialysis in the six months following the introduction of bundled payments and zero if the patient entered hemodialysis in the same months during the previous year. In this case, monotonicity states that the probability of use of ESAs among patients with baseline hematocrit >36% must be uniformly lower after bundled payment relative to before bundled payment. Under this assumption, the analysis identifies the causal effect of treatment with ESAs on the risk of mortality among patients whose exposure to ESAs was influenced by the bundled payment policy—the “compliers” with bundled payment [7]. Whether this method identifies a causal effect under the formality of the Rubin Causal Model requires additional assumptions about changes in care over the time before and after bundled payment.

The comparability of this treatment effect with the average treatment effect estimated in Analysis 3 (i.e., among the treated) is not immediately clear. Neither is it immediately clear what subset of the study population makes up the “compliers” (although methods have been developed that involve identification of the “compliers” to whom the estimated LATE applies), making it difficult to know how applicable the estimate is to the target population [32].

With Analysis 2, the instrumental variable approach aims to identify the causal effect without the assumption of no unmeasured confounding, but relies on other strong assumptions including SUTVA. In addition to the assumptions regarding treatment effect heterogeneity, for a causal interpretation of Analysis 2, we must assume that: (1) the instrumental variable (bundled payment) has a causal effect on the use of ESAs (or is a surrogate for such an instrument), (2) bundled payment affects mortality only through its effect on use of ESAs, and (3) the effect of bundled payment on mortality is not associated with unmeasured patient characteristics [7, 30, 35]. Violations of these assumptions can result in bias. For instance, assumption (2) would be violated if the bundled-payment policy increased use of iron or blood transfusions and these interventions affected mortality [35]. The magnitude of this bias can be large with even small violations of assumption (2) if the instrumental variable has a weak association with the exposure (as in the case here) [36].

Analysis 2 also assumes that there is no treatment effect heterogeneity by hematocrit level. If there is heterogeneity, then the interpretability of the estimand is again complicated because it applies only to the “compliers.” Moreover, because there is only a weak correlation between bundled payment and person-level use of ESAs, bundled payment is a weak proxy for exposure to ESAs. Thus, in this analysis actual exposure to ESAs is misclassified, and produces an estimate of the effect of bundled payment on mortality [18] instead of the explicit effect of ESA receipt on mortality.

Analysis 1

In Analysis 1, we estimated changes in mortality after transitioning from fee-for-service payment for ESAs administered during hemodialysis to a fixed-sum, bundled hemodialysis payment that includes use of ESAs—that is, Analysis 1 involved estimating the policy effect [18].

For an interpretation that Analysis 1 estimates the causal effect of ESA receipt (rather than the policy), assumptions (2) and (3) from Analysis 2 are required plus the assumption that the bundled payment policy strongly affects use of ESAs among patients whose hematocrit is >36, but not at all among patients whose hematocrit is ≤36%.

Comparing the Approaches

These three analyses require different assumptions, and therefore have different strengths and weaknesses for certain applications. To be sure, it is best to start with a carefully designed causal question [37]. However, in the reality of public health, clinical and policy decision-makers often need information on treatment effectiveness well before the ideal study can be implemented, arguing for the availability of a range of methods that could be applied to the available data.

It is important to note that comparability of these methods is hard to evaluate when there is appreciable effect heterogeneity. In the presence of effect modification, the estimates from the three analyses could be startlingly different, because they apply to different subsets of the population, even if they are unbiased [33].

Notably, however, the results of the three analyses for patients with an initial hematocrit of >36% are not dissimilar, and while all three findings rely on untested assumptions, their qualitative similarity (despite their different analytic assumptions) provides information about the robustness of the findings that would be missing if only a single analysis had been performed.

More general limitations of these analyses deserve mention. First, misclassification of exposure, outcome, and covariates are possible in the REMIS data. Of particular importance is exposure misclassification, because our time-fixed, binary measures of ESA use do not capture the complex time-dependent nature of ESA use in common practice [38]. This point is particularly salient for readers who are interested in the clinical implications of our work. We did not intend for our analyses to directly inform clinical practice. Instead, we used this topic as an example for comparing different methodological approaches. ESAs are used in a more nuanced way than this paper captures. They are not prescribed in a binary way—treat always or never treat—but instead their use involves careful tracking of treatment response and regular dosage adjustments. This paper does not address these issues.

Second, because the data are left censored, it is difficult to characterize patients as new or prevalent users of ESAs or to identify the true baseline value of hematocrit. Third, none of the analyses presented accounted for time-dependent confounding. Indeed, all of the analyses make the assumption that the steps taken to address confounding—that is, covariate measurement and propensity scoring in Analysis 3 and the instrumental variable in Analyses 1 and 2—are sufficient. Our exposure measures are time-fixed, and similarly, we do not explicitly address time-dependent confounding. Fourth, because the rate of mortality is high in patients beginning dialysis, loss to follow-up remains a concern. Fifth, we did not exclude patients with polycystic kidney disease (PKD), who typically do not need ESAs, and whose inclusion may weaken the instrumental variables. Patients with PKD would be expected to account for ≤ 10% of the study population [39]. Each of these assumptions has been discussed in the literature on pharmacoepidemiology and comparative effectiveness research [40, 41].

Additionally, the proposed instrumental variable was weakly correlated with person-level use of ESAs, whereas it is more strongly associated with encounter-level use of ESAs [18]. Thus, it appears that physicians have reduced the intensity of within-patient ESA use but have not reduced the number of patients who receive ESA.

In summary, applied researchers from different backgrounds bring different approaches to inferring the causal effect of a treatment in non-experimental studies. Although not always feasible, each study should have clear aims based not on the analytical procedure that the researcher intends to use, but rather on the scientific question at hand. Once the aims of the research are clearly defined, an appropriate method should be chosen with care, and only after checking whether the assumptions made by this method can be defended by the available data. It is true that some of the assumptions made are unverifiable, but researchers should attempt to examine whether the data available refute the analytic assumptions and apply substantive expertise and sensitivity analyses to evaluate whether the assumptions for causal inference in a given application are defensible.

What is new?

• The recent emphasis on comparative effectiveness research has promoted interdisciplinary sharing of methods, including those from econometrics, statistics, health services research, and epidemiology.

• We present three analyses that could be used to estimate different types of causal effects of erythropoietin-stimulating agents (ESAs) on mortality, including a pre-post, difference-in-difference comparison of a bundled payment policy that reduced prescribing of ESAs, an instrumental variable analysis derived from the bundled payment policy, and an analysis that involved imputation of counterfactual outcomes within levels of the propensity score.

• The specific estimands that we estimated differ, as do the required assumptions for causal inference in each analysis.

• The three analyses have different strengths and weaknesses for certain applications.

• Researchers from different disciplines in comparative effectiveness research should work together to develop the most appropriate design and analysis for the causal question of interest.