Abstract
Cancer is a leading cause of morbidity and mortality in many countries. Solid tumors generally initiate at one particular site called the primary tumor, but eventually disseminate and form new colonies in other organs. The development of such metastases greatly diminishes the potential for a cure of patients and is thought to represent the final stage of the multi-stage progression of human cancer. The concept of early metastatic dissemination, however, postulates that cancer cell spread might arise early during the development of a tumor. It is important to know whether metastases are present at diagnosis since this determines treatment strategies and outcome. In this paper, we design a stochastic mathematical model of the evolution of tumor metastases in an expanding cancer cell population. We calculate the probability of metastasis at a given time during tumor evolution, the expected number of metastatic sites, and the total number of cancer cells as well as metastasized cells. Furthermore, we investigate the effect of drug administration and tumor resection on these quantities and predict the survival time of cancer patients. The model presented in this paper allows us to determine the probability and number of metastases at diagnosis and to identify the optimum treatment strategy to maximally prolong survival of cancer patients.
Keywords: Stochastic dynamics, Cancer modeling, Branching processes
1. Introduction
Tumor metastases arise when cancer cells leave the primary tumor site and form new colonies elsewhere (Sahai, 2007). Before metastatic dissemination occurs, tumors can cause symptoms due to localized growth but are often clinically undetectable. Diagnosis frequently occurs when distant metastases interfere with the normal functioning of organs and lead to more severe symptoms. The development of metastases greatly decreases the chances of successful therapy of the tumor by chemotherapy or surgery, and represents the main cause of mortality in cancer patients.
The process of metastasis formation requires multiple steps: first, cell motility is initiated, followed by the invasion of cells into the extracellular matrix and intravasation into blood vessels; metastasizing cells then transit in the bloodstream, extravasate from the blood vessels, and initiate colonies in distant organs (Sahai, 2007). Metastases are a common occurrence in cancer patients, with about 70% of patients with advanced breast or prostate cancer suffering from bone metastases (Roodman, 2004) and 85% of patients with pancreatic tumors carrying liver metastases (Hess et al., 2006). Distant metastases are also often responsible for recurrence of the disease after initially successful therapy. A recent study reporting 25 year follow-up data determined that about 65% of breast cancers recurred up to 20 years after treatment (Fisher et al., 2002).
Since the observation that the injection of mice with rat embryo cells transfected with the RAS oncogene leads to a large number of metastatic nodules (Pozzatti et al., 1986), the genetic profile of metastatic tumors has been the topic of intense investigations. In 2000, the NM23 gene was shown to suppress the in vivo metastatic abilities of various types of tumor cells (Yoshida et al., 2000). Another metastasis suppressor gene, KAI1, functions in cell–cell interactions and was demonstrated to decrease both invasiveness and motility of cells in vitro (Yoshida et al., 2000). MKK4, which phosphorylates JNK and p38, reduces the in vivo rate of spontaneous metastasis formation in melanoma and breast cancer (Yoshida et al., 1999). Conversely to inactivation of genes that suppress the formation of metastases, there are also genes that lead to increased metastatic frequency if activated or overexpressed. For example, the activation of Twist or PDGFR signaling promotes the metastatic ability of cells (Yang et al., 2004; Jechlinger et al., 2006). These alterations, together with activation of RAS (Pozzatti et al., 1986), MYC (Wyllie et al., 1987), and ERBB2/NEU (Yu and Hung, 1991), serve as examples for situations in which a single genetic change is sufficient to confer metastatic potential to cells.
Metastasis formation has been considered as a late stage of tumorigenesis (Hanahan and Weinberg, 2000) because the metastatic process requires multiple steps, which may be acquired only once the tumor has reached an advanced stage and a large cell number. However, a different concept proposes that metastasis formation is an early event in tumorigenesis (Bernards and Weinberg, 2002) and that dissemination of premalignant cells may be driven by the alteration of particular proto-oncogenes, which occurs early during tumor development (Hüsemann et al., 2008; Podsypanina et al., 2008). This hypothesis suggests that many patients may harbor metastases or micrometastases at diagnosis. It is of clinical importance to estimate the frequency and size of such metastases when the tumor is first detected since their existence influences diagnosis, prognosis and treatment choices.
Mathematical models of metastasis formation have contributed to the understanding of this aspect of the disease. Bosl et al. (1983) developed a logistic regression model of metastatic testicular cancer and predicted the prognoses of patients utilizing several clinical characteristics, such as serum values of tumor markers and the total number of metastatic sites. Panetta (1996) designed a competition model between tumor and normal cells during periodically pulsed chemotherapy and investigated parameter regions in which a tumor recurs due to the presence of a small number of metastatic cells. Thames et al. (1999) developed a mathematical model, which they used to investigate the correlation between a delay of surgery for breast cancer patients and the risk of distant metastases. These authors found that a delay of surgery increases the risk of dissemination by 1–4% per month. Wodarz and Anton-Culver (2005) studied the dynamical interactions between a primary tumor and its metastatic sites and investigated the growth of metastatic tumors in cases in which the dissemination from the primary tumor occurs early. The dynamics of metastases arising from a primary tumor of constant size was investigated by Iwasa and colleagues; these authors calculated the expected number of metastatic cells over time in situations in which a single mutation (Michor et al., 2005) or two mutations (Michor and Iwasa, 2006) are necessary to confer metastatic abilities to a cell. In both cases, they found that the ability to metastasize is likely a property of most if not all cells in the primary tumor. Dingli et al. (2007) subsequently examined a branching process model of tumor metastases and investigated the effect of the export of metastatic cells from the primary site on the growth of the primary tumor.
In this paper, we design and analyze a stochastic mathematical model of the evolution of tumor metastases in an expanding cancer cell population. We calculate the probability of metastasis and the total number of cancer cells as well as of metastasized cells at a particular time during tumorigenesis. Furthermore, we investigate the effect of drug administration and tumor resection on these quantities and predict the survival time of cancer patients. Here we concentrate on situations in which the tumor cell population exhibits robust clonal expansion, i.e. in which the growth rate of tumor cells is significantly larger than the death rate; situations in which growth and death rates are of similar magnitude have been discussed elsewhere (Michor et al., 2006; Michor and Iwasa, 2006; Dingli et al., 2007). The model presented in this paper allows us to determine the probability and number of metastases at diagnosis and to identify the optimum treatment strategy to maximally prolong survival in cancer patients.
2. The model
2.1. The stochastic process
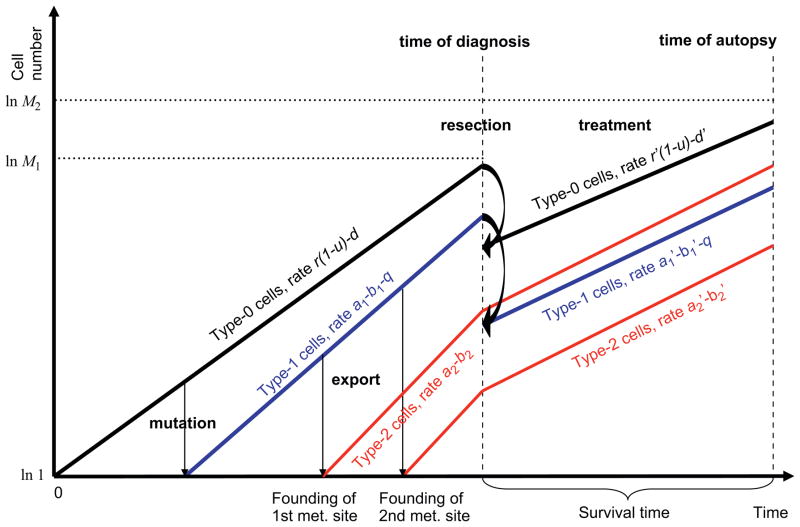
Consider the exponential expansion of cancer cells starting from a single cell that has not yet evolved the ability to metastasize. The cells follow a stochastic process: during each elementary time step, a cell is chosen proportional to fitness for reproduction, death, or export from the primary tumor to establish a metastatic colony elsewhere. Time is measured in numbers of cell divisions. Cells that have not yet evolved the ability to metastasize are called type-0 cells. These cells divide at rate r and die at rate d per time unit. We consider situations in which metastatic ability is a consequence of a single genetic or epigenetic change that occurs with probability u per cell division. Cells carrying such an (epi)genetic change are called type-1 cells. These cells divide at rate a1 and die at rate b1 per time unit. Once a type-1 cell has been produced, it has a certain probability of being exported from the primary tumor to attempt the establishment of metastases elsewhere. The integrated rate of leaving the primary site and founding a new colony at a distant site is denoted by q (Fig. 1). The relative fitness of type-1 cells as compared to type-0 cells is given by α1 = (a1 − b1 − q)/(r − d) since an increased rate of export, q, contributes to the loss of cells from the primary tumor and hence leads to a selective disadvantage of type-1 cells. If α1 = 1, then the fitness of type-1 cells is neutral as compared to type-0 cells and the metastasis-enabling mutation does not confer an advantage or disadvantage to a cell in the primary tumor. If α1 > 1—either through an increased growth rate or a decreased death rate of type-1 cells, then the mutation confers an advantage to those cells; and if α1 < 1—either through a decreased growth rate, an increased death rate or a sufficiently large rate of export of type-1 cells from the primary tumor, then the mutation confers a disadvantage to the cells. Once a type-1 cell has emigrated to a distant site, it may initiate exponential growth with division rate a2 and death rate b2 per time unit; such metastasized cells are referred to as type-2 cells (Fig. 1). The relative fitness of type-2 cells as compared to type-1 cells is given by α2 = (a2 − b2)/(a1 − b1 − q). Again, if α2 = 1, then the fitness of type-2 cells is neutral, if α2 > 1, it is advantageous, and if α2 < 1, it is disadvantageous as compared to the fitness of type-1 cells in the primary tumor. The total number of tumor cells (including all three types) at diagnosis is denoted by M1, and the total number of tumor cells at autopsy is given by M2. Here diagnosis refers to the initial detection of the tumor when the patient is first admitted to the hospital, and autopsy refers to the time after the death of the patient when the tumor is resected and the cause of death determined. We assume that all three cell types contribute to the size at diagnosis since in rare cases, metastatic disease with unknown primary is diagnosed, in which case only type-2 cells can be detected.
Fig. 1.
Schematic illustration of the model. We consider three different types of tumor cells: type-0 cells reside in the primary tumor and have not yet evolved the ability to metastasize. These cells divide and die at rates r and d per time unit and produce cells that have the ability to metastasize at rate u per cell division. These cells are called type-1 cells, also reside in the primary tumor, and divide and die at rates a1 and b1 per time unit. Type-1 cells may be exported to found distant metastases at rate q per time unit. Once exported, these cells are called type-2 cells. Each export event establishes a new metastatic colony in which type-2 cells proliferate and die at rates a2 and b2 per time unit. Initially, there is one type-0 cell which initiates clonal expansion. The clone may produce type-1 and -2 cells. When the total number of all cell types reaches M1, the tumor is diagnosed and treatment in the form of chemotherapy (assumed to reduce growth rates or increase death rates by factors γ or η) and/or surgery (assumed to reduce the primary tumor by a factor ε) initiates. Here r′ = r(1 − γ), , d′ = d(1+η), and . When the total number of all cell types reaches M2, patients die.
Once the tumor has been diagnosed with a population size of M1, there are four options: (i) there may be only palliative treatment due to the advanced age of the patient, the advanced stage of the tumor, or other factors; (ii) the patient may undergo surgery, which removes a fraction ε of the primary tumor; (iii) the patient may receive chemotherapy, which reduces the growth rate and/or increases the death rate of all cells by factors of γ and η; or (iv) the patient may undergo surgery followed by chemotherapy (Fig. 1). This stochastic mathematical model serves to investigate the probability that patients harbor metastases at a particular time during tumorigenesis, the total number of cancer cells, the effect of chemotherapy and tumor resection on these quantities, and the survival time of cancer patients.
2.2. Computer simulations
We perform exact computer simulations of the stochastic process. There are three types of cells: type-0, -1, and -2 cells. Their respective numbers are denoted by x, y, and zi; the latter specifies the number of cells in the i-th metastatic site. A change in x, y, and zi can occur by cell division (possibly with mutation), cell death, or export from the primary site. Each time an export event occurs, a new metastatic colony is established. The number of sites where tumor cells can found metastases is denoted by I. Initially, there is one type-0 cell, x=1, and no type-1 or type-2 cells, y = zi = 0 for all i ∈ I.
The stochastic simulation is performed by determining the probabilities of all possible events—the production and death of a type-0, -1 or -2 cell and the export of a type-1 cell to found a new metastatic site. The chance of each event occurring is proportional to its rate normalized by the sum of the rates of all possible events, given by . The timing of the first event is given by a negative exponential distribution with mean 1/Γ. The process is continued either until all cells go extinct, x = y = Σi zi = 0, or until the total cell number reaches the final size, x + y + Σi zi = M1 at diagnosis or x + y + Σi zi = M2 at autopsy.
The transition probabilities between states of the stochastic process are determined as follows. The number of type-0 cells increases if a type-0 cell divides without mutating. Hence the probability that the number of type-0 cells increases by one is given by
| (1a) |
The number of type-1 cells increases by mutation of a type-0 cell or by division of a type-1 cell. The probability that the number of type-1 cells increases by one is given by
| (1b) |
Export of a type-1 cell to a new metastatic site (j∈I) increases the number of metastatic sites by one and decreases the number of type-1 cells by one,
| (1c) |
The probability that the number of type-2 cells increases by one in the i-th metastatic site is given by
| (1d) |
The probabilities that the numbers of type-0, -1, and -2 cells decrease by one are given by
| (1e) |
For each parameter set, we perform many independent runs of the stochastic process to account for random fluctuations, and count the fraction of runs that reach the final size, M1 or M2, and have produced at least one type-2 cell. We also record the number of metastatic sites with non-zero cell numbers, the total number of type-2 cells in those sites, and the time between diagnosis and autopsy.
2.3. Analytical approximations
We have derived analytical approximations for three quantities: (i) the probability of having at least one metastatic site at diagnosis and at autopsy in dependence of the treatment options; (ii) the expected number of metastatic sites at diagnosis and at autopsy; and (iii) the expected total number of cells in all metastatic sites at diagnosis and at autopsy. In the following, we outline the derivations of these quantities.
2.3.1. Three quantities at diagnosis
(i) The probability of metastasis at diagnosis
The probability that at least one metastatic site exists at diagnosis is given by
| (2) |
Here β = (1 − (b1 + q)/a1)u/(1 − d/r). The time between the emergence of a type-1 cell from x type-0 cells and when the total number of type-0 and -1 cells reaches M1 is denoted by τx and is given by xe(r−d)τx)+e(a1−b1−q)τx = M1. See Appendix A for details of the derivation.
(ii) The expected number of metastatic sites at diagnosis
The expected number of metastatic sites produced by a type-1 lineage that arises when there are x type-0 cells is given by e(a1−b1−q)q(1 − b2/a2)/(a1 − b1 − q) (see Appendix A). Hence the expected number of metastatic sites at diagnosis conditional on metastases having emerged is given by
| (3) |
(iii) The expected total number of cells in all metastatic sites at diagnosis
As described in Appendix B, the expected total number of cells in all metastatic sites at diagnosis conditional to metastases having emerged is given by
| (4) |
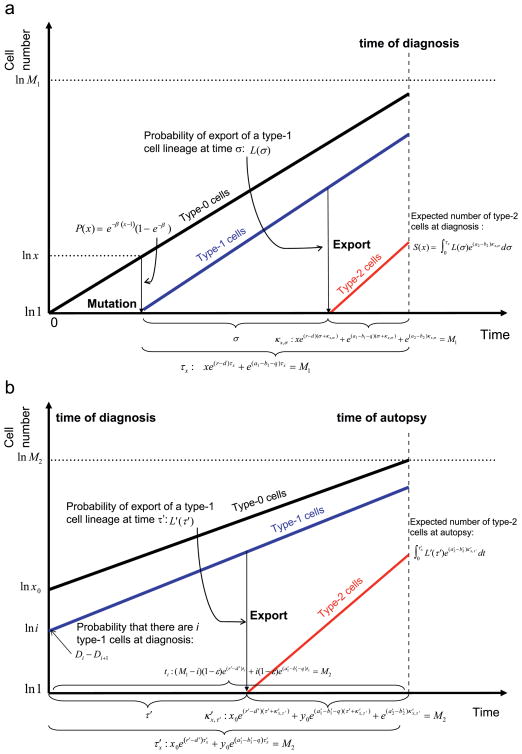
Here the probability that a type-1 cell emerges when there are x type-0 cells is given by P(x) = e−β(x−1)(1 − e−β), and the expected number of type-2 cells at diagnosis emerging from such a type-1 lineage is given by . Here L(σ) = exp[−e(a1−b1−q)σ − 1)q(1 − b2/a2)/(a1 − b1 − q)](1 − exp[−qe(a1−b1−q)σ (1 − b2/a2)]) represents the probability that the first successful lineage of type-2 cells emerges at time σ. The parameter κx,σ denotes the amount of time between the emergence of a type-2 cell and the time of diagnosis, i.e. the time when the total number of type-0, -1, and -2 cells reaches M1, under the condition that a type-1 cell emerges when the number of type-0 cells is x; this quantity is given by xe(r−d)(σ+κx,σ) + e(a1−b1−q)(σ+κx,σ) + e(a2−b2)κx,σ = M1. The mathematical approach is outlined in Fig. 2a. Note that the expression P(x) decreases with x; intuitively, when the number of type-0 cells becomes very large, the length of time during which there are exactly x such cells becomes very short. Therefore the expected number of mutations occurring when there are x type-0 cells is approximately independent of x and is given by u/(1 − d/r) (Iwasa et al., 2006). Furthermore, here we focus on the first successful mutation occurring and hence the probability of mutation decreases with x because the case is excluded in which the mutation arises before the population of type-0 cells has reached x. See Appendix B for details of the derivation.
Fig. 2.
Schematic illustration of the analytical approximations. The figure shows the mathematical expressions used for the derivation of the analytical approximation. (a) Schema of the derivation of the three quantities at diagnosis. We first consider the probability that a type-1 cell arises when there are x type-0 cells, P(x). Next we consider the probability and expected number of export events of type-1 cells during τx (these quantities except τx and P(x) are not shown). In order to obtain the total number of metastatic cells, the probability of export at time σ is calculated as L(σ). The length of time between export and diagnosis is expressed as κx,σ. The number of type-2 cells after this time is deterministically calculated. (b) Schema of the derivation of the three quantities at autopsy. We first consider the probability that there are i type-1 cells at diagnosis, Di − Di+1. Then the probability and the expected number of export events of type-1 cells until autopsy are calculated (these quantities except ti, which represents the amount of time between diagnosis and autopsy, are not shown). The derivation of the approximation for the case in which there are no type-1 cells at diagnosis is not shown for simplicity. In order to obtain the total number of metastatic cells, the probability of export at time τ′ after the diagnosis is calculated as L′(τ′), where the lineage of type-1 cells emerged when there were x type-0 cell. The length of time between export and autopsy is expressed as κ′x,τ′. The number of type-2 cells after this time is deterministically calculated. The case where type-2 cells exist at the time of diagnosis is not shown. The black line represents the growth of type-0 cells, the blue line that of type-1 cells, and the red line that of type-2 cells.
2.3.2. Three quantities at autopsy
Let us now calculate these quantities at the time of autopsy. If a patient does not receive any treatment—for reasons of morbidity, advanced age or other factors—then the three quantities are given by Eqs. (2)–(4) in which M1 is replaced by M2. If treatment such as surgery or chemotherapy is administered, then the analytical expressions are altered as outlined below. Assume that chemotherapy reduces the growth rates of all types of tumor cells by a factor γ and increases the death rate of all types of tumor cells by a factor η such that these rates during therapy are given by r′ = r(1 − γ), d′ = d(1+η), , and . Furthermore, assume that tumor resection reduces the number of cancer cells at the primary site (type-0 and -1 cells) by a factor ε. If both surgery and chemotherapy are administered, then both effects apply.
(i) The probability of metastasis at autopsy with treatment
For the derivation of this quantity, we first consider the probability distribution of type-1 cells at diagnosis since the number of type-1 cells influences the probability of the emergence of a type-2 cell. The probability that the number of type-1 cells exceeds i at diagnosis is given by
Here ki = ln(M1 − i)/(r(1 − u) − d) and hi = ln i/(a1 − b1 − q) for i≥1. The expression ki − hi represents the amount of time during which type-0 cells can accumulate mutations such that the number of type-1 cells reaches frequency i at diagnosis. If ki − hi is less than 0, then Di = 0. The non-extinction probability of a type-1 lineage is given by (1 − (b1 + q)/a1). Then the probability that there are i type-1 cells at diagnosis is given by Di − Di+1 (Fig. 2b).
After diagnosis, the dynamics of type-0 cells (xa) and type-1 cells (ya) are deterministically given by
| (5) |
The initial condition of the number of type-0 and -1 cells at diagnosis is given by xa(0) = (M1 − i)(1 − ε) and ya(0) = i(1 − ε), respectively; we have ε > 0 when considering a patient undergoing surgery. We can then obtain the number of type-1 cells at a given time after diagnosis explicitly, and with that quantity, we calculate the probability of metastasis emerging until autopsy, B(i, ti), as outlined in Appendix C. The time between diagnosis and autopsy, ti, is given by . Hence the probability of metastasis at autopsy when the number of type-1 cells is i≥1 at diagnosis is given by
Let us now consider the case in which there is no type-1 cell present at diagnosis. According to Iwasa et al. (2006), the probability of no mutation at diagnosis is given by
Recall that the relative fitness of type-1 cells as compared to type-0 cells is denoted by α1 = (a1 − b1 − q)/(r − d). Then the probability of metastasis at autopsy given that the metastasis-enabling mutation has not emerged before diagnosis is given by
| (6) |
Here the terms in the summation are the same as in Eq. (2), where represents the length of time between the emergence of the first successful type-1 cell and autopsy, and is given by since the only difference between this case and the probability of metastasis at diagnosis (Eq. (2)) is the initial condition. Taken together, the probability of metastasis at autopsy is given by
| (7) |
See Appendix C for details of the derivation.
(ii) The expected number of metastatic sites at autopsy with treatment
The expected number of metastatic sites at autopsy under the condition that there are i type-1 cells at diagnosis is given by A(i,ti) in Appendix C. Then the expected number of metastatic sites at autopsy with treatment is given by
| (8) |
Here the expected number of metastatic sites at autopsy given that the metastasis-enabling mutation has not emerged before diagnosis is denoted by Ea2. See Appendix C for details of the derivation.
(iii) The expected total number of cells in all metastatic sites at autopsy with treatment
The expected number of type-2 cells at autopsy with treatment is given by
| (9) |
Here the expected number of type-2 cells at autopsy conditional on the existence of such cells at diagnosis is given by
where t′ is calculated by , and the expected number of type-2 cells at autopsy conditional on the absence of such cells at diagnosis is given by
See Appendix D for details of the derivation.
3. Results
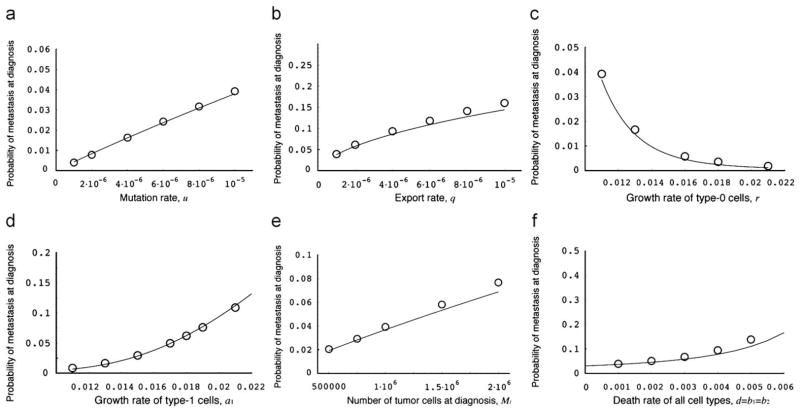
Let us now investigate the parameter dependence of each quantity. The probability of metastasis at diagnosis and at autopsy without treatment is shown in Fig. 3. The analytical approximation, Eq. (2), accurately predicts the results of the exact stochastic computer simulations. An increase of the mutation rate and of the rate of export of type-1 cells from the primary tumor increases the probability of metastasis at diagnosis (Fig. 3a and b). The probability of metastasis at diagnosis decreases with an increasing growth rate of type-0 cells because a quickly growing tumor has a lower chance of accumulating mutations and developing the ability to metastasize (Fig. 3c). This effect arises because a faster growing tumor undergoes a smaller number of cell divisions (and a smaller number of cell deaths) than a tumor that grows more slowly; since the probability of metastases is directly related to the number of cell divisions, a faster growing tumor has a lower risk of metastases. An enhanced division rate of type-1 cells increases the probability of metastasis at diagnosis (Fig. 3d). The division rate of type-2 cells does not affect the probability of metastasis to a large extent (data not shown) because once metastatic colonies have been established, type-2 cells do not go extinct as long as the division rate is sufficiently larger than the death rate. As the number of tumor cells at diagnosis and the death rate increase, the probability of metastasis at diagnosis also increases (Fig. 3e and f).
Fig. 3.
The probability of metastasis at diagnosis. The figure shows the dependence of the probability of metastasis at diagnosis on various parameters. The curves indicate the predictions of the analytical approximation, Eq. (2), while the circles indicate the results of the direct computer simulation, system (1). Parameter values are M1 = 1 000 000, r = 0.011, a1 = 0.016, a2 = 0.021, d = b1 = b2 = 0.001, u = 10−5, and q = 10−6.
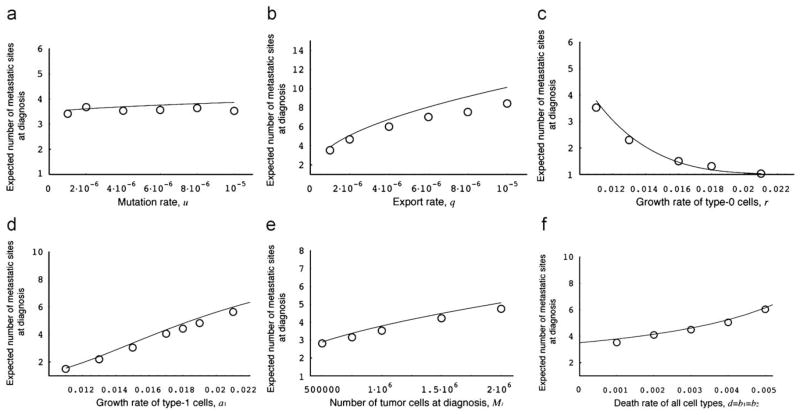
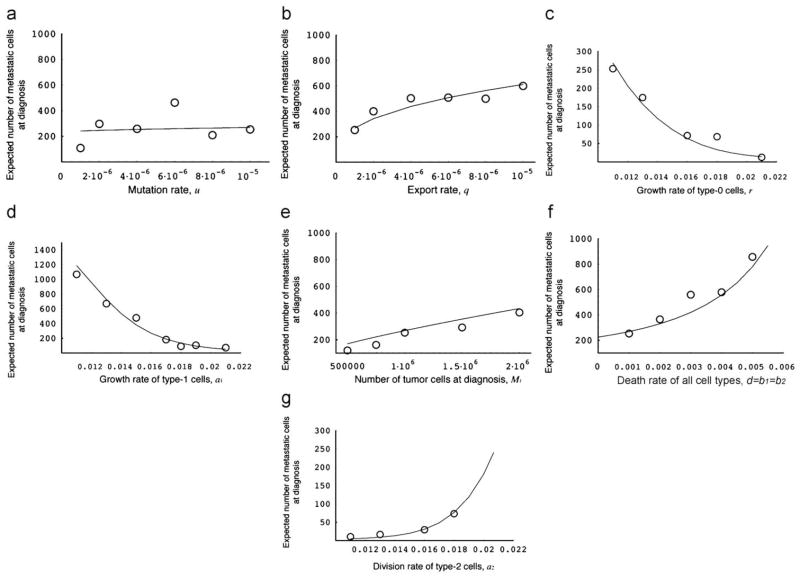
Let us next investigate the parameter dependence of the expected number of metastatic sites at diagnosis and at autopsy without treatment conditional to metastatic cells being present (Fig. 4). The parameter dependence of this quantity is similar to that of the probability of metastasis (Fig. 3), apart from the effect of the mutation rate (Fig. 4a). Unlike the probability of metastasis, the expected number of metastatic sites is not appreciably affected by changes in the mutation rate.
Fig. 4.
The expected number of metastatic sites at diagnosis. The figure shows the dependence of the expected number of metastatic sites at diagnosis on various parameters. The curves indicate the predictions of the analytical approximation, Eq. (3), while the circles indicate the results of the direct computer simulation, system (1). Parameter values are M1 = 1 000 000, r = 0.011, a1 = 0.016, a2 = 0.021, d = b1 = b2 = 0.001, u = 10−5, and q = 10−6.
The parameter dependence of the number of metastatic cells at diagnosis conditional to metastases having emerged is shown in Fig. 5. Again, the dependence is very similar to that of the expected number of metastatic sites (Fig. 4), apart from the effect of the division rate of type-1 cells (Fig. 5d). A large division rate of type-1 cells increases the probability of metastasis and the expected number of metastatic sites at diagnosis but decreases the expected total number of metastatic cells. This effect emerges because a large division rate of type-1 cells increases the number of type-1 cells present at diagnosis, which leads to a high probability of metastasis and a large expected number of metastatic sites. However, metastatic cells cannot reach large frequencies until diagnosis because the population size of diagnosis is quickly reached due to the large growth rate of type-1 cells. A large division rate of metastatic cells, however, does result in large numbers of metastatic cells at diagnosis (Fig. 5g).
Fig. 5.
The expected total number of metastatic cells at diagnosis. The figure shows the dependence of the expected total number of metastatic cells at diagnosis on various parameters. The curves indicate the predictions of the analytical approximation, Eq. (4), while the circles indicate the results of the direct computer simulation, system (1). Parameter values are M1 = 1 000 000, r = 0.011, a1 = 0.016, a2 = 0.021, d = b1 = b2 = 0.001, u = 10−5, and q = 10−6.
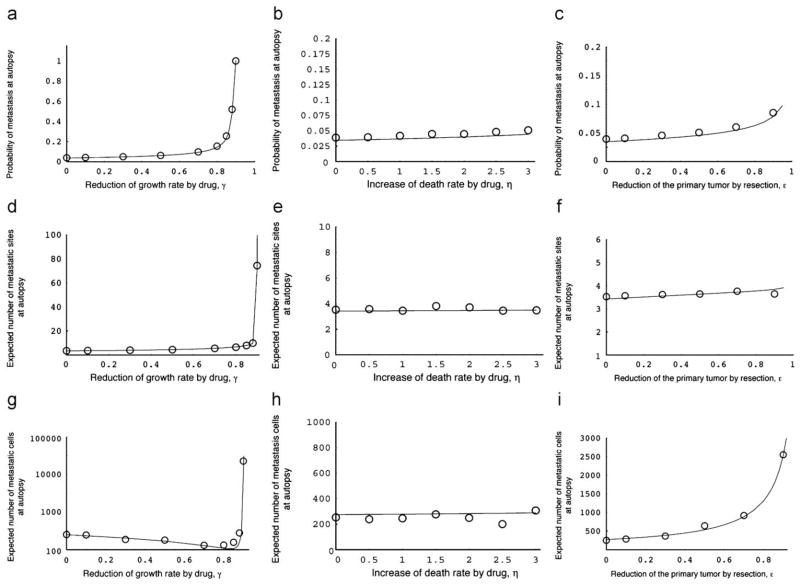
Let us now consider the effects of chemotherapy and resection. Figs. 6a–c show the probability of metastasis at autopsy when chemotherapy is initiated at diagnosis (Fig. 6a and b) or the primary tumor is resected at diagnosis (Fig. 6c). Interestingly, both treatment options increase the probability of metastasis since they prolong the survival time (i.e. time until autopsy); this delay leads to an increase in the eventual probability of metastasis. Drugs which increase the death rate of tumor cells do not significantly alter the probability of metastasis, the number of metastatic sites and the number of metastatic cells at autopsy (Fig. 6b, e, h).
Fig. 6.
Three quantities at autopsy with treatment. (a)–(c) The panels show the dependence of the probability of metastasis at autopsy on the two treatment strategies. The curves indicate the predictions of the analytical approximations, Eq. (7), while the circles indicate the results of the direct computer simulation, system (1). Parameter values are (a) M1 = 250 000, M2 = 1 000 000, r = 0.011, a1 = 0.016, a2 = 0.021, d = b1 = b2 = 0.001, u = 10−5, q = 10−6, and ε = η = 0.0; (b) ε = γ = 0.0; and (c) γ = η = 0.0. (d)–(f) The panels show the dependence of the expected number of metastatic sites at autopsy on the two treatment strategies. The curves indicate the predictions of the analytical approximations, Eq. (8), while the circles indicate the results of the direct computer simulations, system (1). Parameter values are as above. (e)–(g) The panels show the dependence of the expected total number of metastatic cells at autopsy on the two treatment strategies. The curves indicate the predictions of the analytical approximations, Eq. (9), while the circles indicate the results of the direct computer simulations, system (1). Parameter values are as above.
The expected number of metastatic sites conditional to metastasis at autopsy when chemotherapy or resection is administered is shown in Figs. 6d–f. The parameter dependence is similar to that of the probability of metastasis at autopsy. Interestingly, the expected number of metastatic sites at autopsy is almost independent of the effect of resection (Fig. 6f). This observation implies that most metastatic sites are founded before diagnosis.
Lastly, the number of metastatic cells at autopsy with drug administration or resection (conditional to metastasis) is shown in Figs. 6g–i. Interestingly, the number of metastatic cells first decreases with an increasing effect of drug administration on the growth rate, but then drastically increases when γ is sufficiently large (Fig. 6g). When the administration of chemotherapy leads to small reductions in the growth rate of tumor cells, then this effect on the growth of type-2 cells leads to smaller numbers of metastatic cells (see Fig. 5g). As the effect of chemotherapy increases, the survival time of patients is enhanced and the relative fitness of type-2 cells as compared to the other types increases; this change in relative fitness leads to the sudden rise of the expected number of type-2 cells at autopsy in Fig. 6g. A large efficacy of resection increases the number of metastatic cells because the reduction of the primary tumor by a large amount prolongs the survival of the patient, which in turn increases the number of metastatic cells.
3.1. The expected survival time
At the time of diagnosis, the expected survival time of a patient is important information since it might influence treatment choices. Therefore, let us now derive this quantity by setting the sum of all tumor cell types at autopsy equal to M2. For mathematical simplicity, we assume that the number of type-2 cells at diagnosis is small and neglect it in the derivation of the survival time. The numbers of type-0 and -1 cells at diagnosis depend on the time at which the first successful type-1 lineage emerges. If this event occurs when there are x type-0 cells, then the number of type-1 cells at diagnosis is given by e(a1−b1−q)τx, where τx is calculated from xe(r−d)τx + e(a1−b1−q)τx = M1; the probability that a successful type-1 cell emerges when there are x, where type-0 cells is given by P(x) = e−(x− 1)β(1 − e−β), where β = u(1 − (b1 + q)/a1)/(1 − d/r). See Appendix A for the details of the derivation. After diagnosis and resection, the expected number of type-0 and -1 cells are respectively given by (1 − ε)(M1 − e(a1−b1−q)τx) and (1 − ε)e(a1−b1−q)τx. Both cell types grow exponentially until autopsy. Therefore, the expected time at which the total number of cancer cells reaches M2 under the condition that the first successful type-1 cell emerged when there were x type-0 cells is given by
| (10) |
Here the amount of time between the emergence of a type-1 lineage from x type-0 cells and diagnosis is given by τx and the amount of time between diagnosis and autopsy is given by Tx.
Moreover, there is a possibility that no mutation occurs until diagnosis (i.e., there are only type-0 cells present at diagnosis). This probability is calculated as G in Eq. (C.8) in Appendix C. Assuming that type-0 cells are dominant in the population until autopsy and increase exponentially, the expected time until autopsy, T0, is given by
| (11) |
Taken together, we obtain the expected survival time as
| (12) |
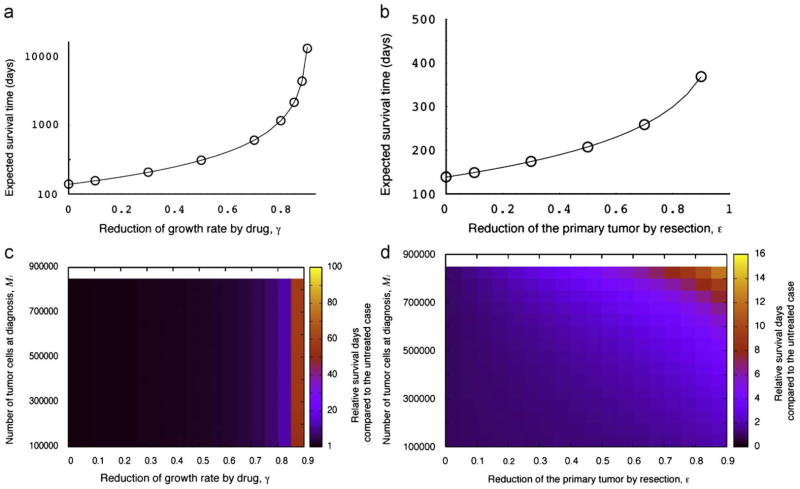
Fig. 7a and b show the dependence of the expected survival time on either treatment strategy. As expected, the survival time increases drastically with the efficacy of the drug (Fig. 7a). Furthermore, the more efficiently the resection of the primary tumor is done, the longer the expected time of survival becomes (Fig. 7b). We also investigate the relative survival benefit conferred by either treatment option as compared to the untreated case (Fig. 7c and d). The effect of drug administration is independent of the size of the tumor at diagnosis, M1, while an increased efficiency of resection prolongs the survival time nonlinearly when the tumor is large at diagnosis. Furthermore, we perform a comprehensive investigation of the combination of the two treatment strategies (Fig. 8). The colors in the panels indicate the relative survival time of a patient who receives either or both treatment options compared to the untreated case (γ = ε = 0). As the effect of treatment increases, the survival time increases as well.
Fig. 7.
The survival time after diagnosis with treatment. Panels (a) and (b) show the dependence of the survival time after diagnosis on the two treatment strategies. The curves indicate the predictions of the analytical approximation, Eq. (12), while the circles indicate the results of the direct computer simulation, system (1). Panels (c) and (d) show the relative survival time compared the untreated case (γ = ε = 0.0). Parameter values are (a) and (c) M1 = 250 000, M2 = 1 000 000, r = 0.011, a1 = 0.016, a2 = 0.021, d = b1 = b2 = 0.001, u = 10−5, q = 10−6; and ε = 0.0; and (b) and (d) γ = 0.0.
Fig. 8.
The relative survival time of a patient after diagnosis with treatment compared to the untreated case. The expected survival time is calculated from Eq. (12). Parameter values are M2 = 1 000 000, r = 0.011, a1 = 0.016, a2 = 0.021, d = b1 = b2 = 0.001, u = 10−5, and q = 10−6.
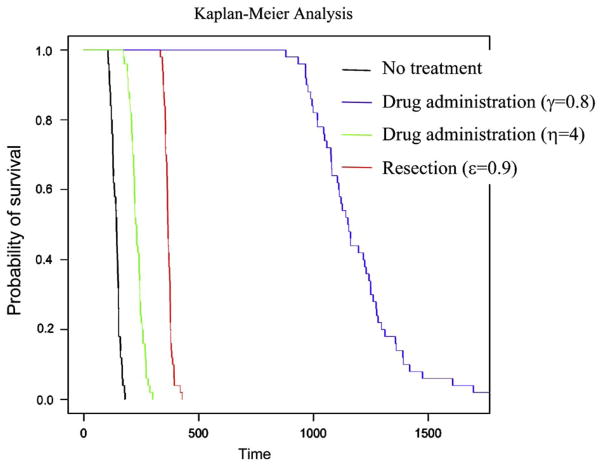
Furthermore, we perform a Kaplan–Meier analysis of survival by using the simulation, system (1). Fig. 9 shows the effect of different treatment choices on survival. We assume that the number of tumor cells at diagnosis is given by a normal distribution and the number at autopsy is constant. We simulate the survival time of 50 patients with respect to each treatment option (Fig. 9). Using this particular parameter set, we find that the treatment choice reducing the growth rate of tumor cells is the most effective option to prolong survival of patients.
Fig. 9.
Kaplan–Meier analysis. The figure shows the probability of survival depending on the treatment option. We performed 50 runs of the exact simulation (system 1) and recorded the survival time after diagnosis for each patient. The black line represents the survival probability over time without any treatment; the blue line with administration of a drug that reduces the growth rate of tumor cells; the green line with administration of a drug that increases the death rate of tumor cells; and the red line with tumor resection. The tumor size at diagnosis is given by a normal distribution with mean value 250,000 and standard deviation 50,000. Parameter values are M2 = 1 000 000, r = 0.011, a1 = 0.016, a2 = 0.021, d = b1 = b2 = 0.001, u = 10−5, and q = 10−6.
4. Discussion
In this paper, we have investigated the evolutionary dynamics of metastases emerging from an expanding cancer cell population. We have derived analytical approximations of several quantities, such as the probability of metastasis at diagnosis and autopsy, the expected number of metastatic colonies, and the expected total number of metastatic sites. We found our approximations to be in good agreement with the exact stochastic computer simulation of the process.
The predictions of our model significantly depend on various parameter values. The probability of metastasis at diagnosis is large when: (i) the mutation rate conferring metastatic capabilities to cells is large (Fig. 3a); (ii) the rate of export of metastasis-enabled cells is high (Fig. 3b); (iii) the relative division rate of tumor cells that have evolved the ability to metastasize (type-1 cells) is large (Fig. 3c and d); (iv) the number of tumor cells at diagnosis is large (Fig. 3e); and (v) the death rate of tumor cells is high (Fig. 3f). The expected number of metastatic sites conditional to having metastases is large when: (i) the rate of export is high (Fig. 4b); (ii) the relative division rate of type-1 cells is large (Fig. 4c and d); (iii) the number of tumor cells at diagnosis is large (Fig. 4e); and (iv) the death rate is high (Fig. 4f). The mutation rate does not affect the number of metastatic sites at diagnosis to a large extent (Fig. 4a). The parameter dependence of the total number of metastatic cells is almost the same as that of the number of metastatic sites (Fig. 5). Interestingly, an increase of the division rate of type-1 cells increases the probability of metastasis and the number of metastatic sites, but decreases the total number of metastatic cells. This effect arises because a rapid expansion of type-1 cells increases the proportion of type-1 cells in the total population and the rate at which new metastatic sites are founded, but decreases the time during which type-2 cells can increase in abundance. The results that small numbers of tumor cells at diagnosis decrease the risk of metastasis (Figs. 3e, 4e, and 5e) are consistent with the finding that early detection of tumors reduces the risk of recurrence after therapy (Dawson et al., 1998). We have also obtained accurate predictions (as tested with direct computer simulations) of the survival period after diagnosis with or without treatment (Fig. 7). As expected, the administration of treatments (chemotherapy and/or resection of the primary tumor) increases the survival time (Figs. 7 and 8). If the number of tumor cells at diagnosis and the effect of chemotherapy are small, resection of a large fraction of the primary tumor is needed to prolong survival effectively (Fig. 8a). If the number of tumor cells at diagnosis is small and the effect of chemotherapy is large, then resection of the tumor does not affect the survival time noticeably (Fig. 8a–c). Hence as long as the number of tumor cells at diagnosis is large, resection of the primary tumor is very effective to prolong survival (Fig. 8d). We also performed a Kaplan–Meier analysis to visualize the effect of particular treatment options (Fig. 9).
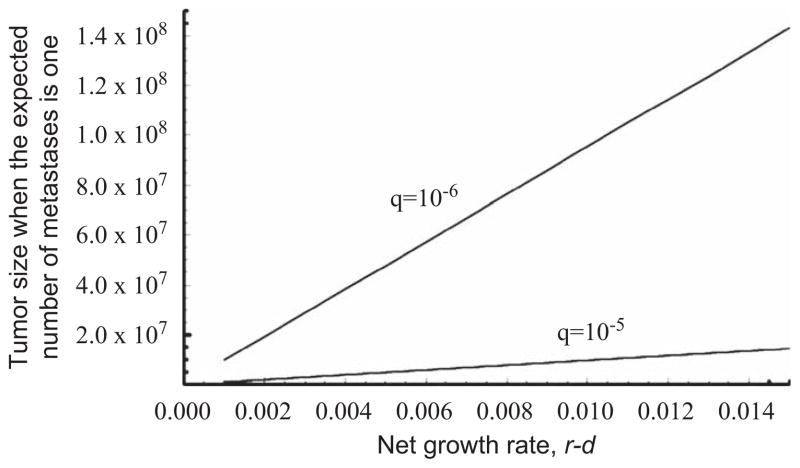
One of the questions arising in metastasis research pertains to the time at which dissemination of metastatic cells first occurs (Bernards and Weinberg, 2002). Using Eq. (3), we determine the number of tumor cells at the time when metastasis first emerges, i.e. when the expected number of metastatic sites is one (Fig. 10). If the tumor expands slowly, then the first metastasis likely arises when a small number of tumor cells are present. When the rate of metastasis, q, is high, then a small number of tumor cells is sufficient to lead to successful establishment of metastatic sites.
Fig. 10.
Tumor size at the time of the first metastatic dissemination. The figure shows the tumor size when the expected number of metastatic sites is one. Parameter values are d = b1 = b2 = 0.001 and u = 10−5. Growth rates vary between r = a1 = a2 = 0.002 and r = a1 = a2 = 0.016. Results using two values for the rate of metastatic dissemination, q, are shown.
The estimation of parameter values needed for the model is complicated by the fact that quantitative studies into growth and death rates, export probabilities, and mutation frequencies of cancer cells are still rare. One important consideration pertains to the cell type of interest for our calculations; if all cells in a tumor may accumulate a mutation leading to enhanced metastatic propensity, then the numbers of cells at diagnosis and autopsy (M1 and M2) are given by the total tumor burden at that time. However, it could be that only tumor stem cells have the required characteristics of self-renewal and evolvability (Dick, 2008) and hence are the only cells that can accumulate mutations leading to metastasis-enabled cells. Let us consider chronic myeloid leukemia (CML) as a particular example. CML is diagnosed once the number of tumor cells approximately equals the number of healthy cells and hence the total number of tumor cells at diagnosis is about 1012. The number of tumor stem cells at that time has been estimated at about 100,000 cells (Holyoake et al., 1999). Hence, if all tumor cells may accumulate mutations leading to metastases, then the population size at diagnosis is around M1 = 1012 while it is approximately M1 = 105 if only tumor stem cells may accumulate such changes. Similar considerations apply for the estimation of mutation rates, which may differ between cell types (Cairns, 1975), and the rate of export of cells and their survival in the bloodstream.
Not only different cell types, but also cancer types influence the dynamics of growth and metastatic progression. While about 40% of breast cancer patients relapse and develop metastatic disease, only 10% of prostate cancer patients do so (American Cancer Society). Pancreatic cancer is a notoriously invasive cancer type in that approximately 80% of patients present with unresectable disease due to the presence of metastases or local extension (El Kamar et al., 2003). As a comparison, only 21% of breast cancer patients present with metastases at diagnosis (Cazzaniga et al., 2006). As shown in Fig. 7d, our results imply that tumor resection effectively prolongs survival when the tumor is large. However, many cancer patients cannot undergo surgery to remove the primary tumor since metastatic dissemination has already occurred before diagnosis. Therefore, prevention of invasion as well as early detection can prolong survival in patients.
Interdisciplinary studies utilizing theory, experiments and clinical findings provide qualitative and quantitative insights into complex phenomena such as the development of tumor metastases. In this study, we have determined the probability that metastatic dissemination has already occurred before diagnosis of the tumor. If supplied with the right parameter values derived from experimental and clinical investigations, our theory is able to predict the metastatic profile of cancer patients. This knowledge is useful for the estimation of the number of undetectable metastatic sites at diagnosis—it has been shown that disseminated tumor cells can exist in distant organs at the time of diagnosis of the primary tumor (Riethdorf et al., 2008) and premalignant cells are able to initiate metastatic dissemination (Husemann et al., 2008; Podsypanina et al., 2008). We have also investigated how treatment options such as chemotherapy and surgical resection of the primary tumor modulate the survival time of patients, and have identified treatment strategies that are able to effectively prolong survival in dependence of the primary tumor size at diagnosis.
In future studies, it will be important to (i) determine the parameter values needed to inform the model and identify the optimum treatment strategies, (ii) consider the necessity of multiple mutations to confer metastatic abilities to cells, (iii) investigate the effect of competition among different cell types, and (iv) model spatially explicit situations arising in metastasis development, in which the rates of leaving a primary site via the steps of intravasation into blood vessels, transition in the blood stream, extravasation from blood vessels, and founding a new colony at a distant site are expressed separately.
Acknowledgments
The authors would like to thank Christine Iacobuzio-Donahue, Mithat Gonen, and the Michor lab for discussion and comments. Support from the Japan Society for Promotion of Science of H.H. is gratefully acknowledged. F.M. is a Leon Levy Foundation Young Investigator.
Appendix A. The probability of metastasis at diagnosis
Let P(x) be the probability that the first successful lineage of type-1 cells arises when there are x type-0 cells. This probability can be written as the product of the probability that no successful type-1 cell lineage arises when there are 1, 2, 3, …, x−1 type-0 cells, and the probability that a successful type-1 cell lineage is created when there are exactly x type-0 cells. We assume that the number of type-1 cells created when there are x type-0 cells follows a Poisson distribution with mean Rx. A fraction of these newly produced cells survive the initial stochastic fluctuations and give rise to an exponentially growing lineage. The surviving fraction is given by ω = 1 − (b1 + q)/a1, the non-extinction probability. Hence we have . Iwasa et al. (2006) show that the expected number of type-1 cells arising when there are x type-0 cells is given by Rx = u/(1 − d/r), which is independent of x. With β = ω · Rx = (1 − (b1 + q)/a1) · u/(1 − d/r), we have P(x) = e− (x−1)/β (1 − e−β) (Haeno et al., 2007). The derivation of P(x) is outlined in Fig. 2a.
Next we consider the probability that a surviving type-2 cell is created within a lineage starting from one type-1 cell. Let y be the number of type-1 cells present when the total cell population reaches size M1, and let N be the mean number of export events that occur while type-1 cells increase from 1 to y cells. The per capita rate of increase of type-1 cells is given by a1 − b1 − q, and the per capita rate of export events is given by q. Hence we have (a1 − b1 − q)/q = (y − 1)/N. With y ≫ 1, this expression becomes N = yq/(a1 − b1 − q). Hence the probability that at least one cell of the lineage establishes a new metastatic site is given by Q(x) = 1 − exp[−qy(1 − b2/a2)/(a1 − b1 − q)] where y = exp[(a1 − b1 − q)τx]. The expression τx denotes the amount of time between the emergence of a successful type-1 cell and when the total number of type-0 and -1 cells reaches M1, and (1 − b2/a2) is the probability of non-extinction of the new type-2 lineage. If y≫1, we have
| (A.1) |
Here x exp[(r − d)τx] is the number of type-0 cells at diagnosis, exp[(a1 − b1 − q)τx] is the number of type-1 cells at diagnosis, and their sum equals M1. Note that we neglect the number of type-2 cells at diagnosis in this derivation. Eq. (A.1) is a transcendental equation and has to be solved numerically to obtain τx. Then the probability of metastasis at diagnosis is given by in the main text.
Appendix B. The expected total number of cells in all metastatic sites at diagnosis
Let us consider the number of type 2-cells once the population reaches its final size, M1, by using a deterministic approximation. Note that we have already derived the probability that at least one type-2 cell exists at the time of diagnosis, Pd, and the amount of time between the emergence of the first type-1 cell and diagnosis, τx; in the derivation of the latter quantity, we neglected the number of type-2 cells for mathematical simplicity. Let us now consider the probability that a type-2 cell emerges at time σ after the appearance of a type-1 cell. The probability that the first successful lineage of type-2 cells emerges at time σ is given by
| (B.1) |
Here the probability that no metastases have emerged until time σ is given by leading to the first term in Eq. (B.1), while the probability that the successful metastatic site arises at time σ is given by 1 − exp[qe(a1−b1−q)σ (1 − b2/a2)]. The number of type-1 cells at time σ after the emergence of their clone is expressed as e(a1−b1−q)σ and the probability of non-extinction of the newly emerged type-2 lineage is given by (1 − b2/a2). Once a type-2 cell has emerged, it gives rise to a lineage which increases exponentially until diagnosis. The amount of time between the emergence of the first successful type-2 cell (which was produced from a lineage of type-1 cells that arose when there were x type-0 cells) and diagnosis is denoted by κx,σ, which is given by xe(r−d)(σ+κx,σ) + e(a1−b1−q)(σ+κx,σ) + e(a2−b2)κx,σ= M1. Type-1 cells may be exported from the primary tumor during the time period of length τx. Hence the expected total number of cells in all metastatic sites at diagnosis is given by Eq. (4) in the main text, . The mathematical approach is outlined in Fig. 2a.
Appendix C. The probability of metastasis at autopsy with treatment
Let us first consider the probability distribution of the number of type-1 cells at diagnosis; this quantity is needed to derive the probability of metastasis at autopsy because the stochasticity in the number of type-1 cells at diagnosis cannot be neglected. Let i be the number of type-1 cells at diagnosis, and let hi be the time it takes from the appearance of the first successful type-1 cell until diagnosis. Assuming that type-1 cells increase exponentially in abundance, we have hi = ln i/(a1 − b1 − q) for i≥1. If there are i type-1 cells at diagnosis, then we can calculate the amount of time for the type-0 cell lineage to increase from the first cell until diagnosis as ki = ln(M1 − i)/(r(1 − u) − d). The probability that the number of type-1 cells at diagnosis exceeds i is equivalent to the probability that a type-1 cell emerges during the time period ki − hi and is given by
| (C.1) |
Here (1 − (b1 + q)/a1) represents the non-extinction probability for a type-1 cell lineage. In particular, the probability that the number of type-1 cells is larger than one is given by
| (C.2) |
Eq. (C.2) represents the deterministic approximation of the probability that at least one mutated cell exists at time k1. The probability that there are i type-1 cells at diagnosis is given by Di − Di +1 (Fig. 2b).
Let us now consider the dynamics of tumor cells during treatment. Since the numbers of type-0 and -1 cells at diagnosis are expected to be large, we can approximate their dynamics with a deterministic model. Denote the number of type-0 and -1 cells after diagnosis by xa and ya. Then we have
| (C.3) |
With the initial condition xa(0) = (M1 − i)(1 − ε) and ya(0) = i(1 − ε), we have
| (C.4) |
Then the expected total number of mutational events until time ti is given by
| (C.5) |
Assuming a Poisson distribution of the mutational events, the probability of metastasis at time ti after diagnosis, starting from i type-1 cells at diagnosis, is given by
| (C.6) |
The time period between diagnosis and autopsy, ti, is given by (Fig. 2b). When considering all possibilities for the number of type-1 cells at diagnosis, we obtain the probability of metastasis at autopsy as
| (C.7) |
Let us now consider the case in which there is no type-1 cell at diagnosis, i=0. According to Iwasa et al. (2006), the probability that there is no type-1 cell at diagnosis is given by
| (C.8) |
To calculate the probability of metastasis at autopsy for the case in which there are no type-1 cells at diagnosis, we utilize the derivation of the probability of metastasis at diagnosis (Appendix A), since the situation at autopsy differs from the situation at diagnosis in the initial number of type-0 cells only. Let us first consider the expected number of type-1 cells arising when there are x type-0 cells; this number is given by where fx(t) is the probability that there are x type-0 cells at time t after diagnosis. We consider a Markov chain of the number of type-0 cells with division rate r′ and death rate d′ and approximate the number of cells at diagnosis, M1, as the reflecting boundary condition; i.e. the number of type-0 cells cannot become less than M1. Then we have
| (C.9a) |
where x = M1 + 1, M1 + 2; …, M2 − 2. Furthermore, we have
| (C.9b) |
| (C.9c) |
In Eq. (C.9b), we assume that M1 represents the reflecting boundary condition and therefore, we neglect cell death occurring when there are M1 cells. The initial condition is given by fM1 (0) = 1, and fx(0) = 0 for x = M1 + 1, M1 + 2, …, M2 − 1. With , we have
| (C.10a) |
| (C.10b) |
| (C.10c) |
Eq. (C.10b) becomes gM1+1 − gM1 = gM1(r′ − d′)/d′ − 1/d′ and then Eq. (C.10a) becomes gx+1 − gx = (r′/d′)x−M1 (gM1 (r′ − d′)/d′ − 1/d′). Hence gx = gM1 (r′ − d′)x−M1 + (1 − (r′ − d′)x−M1)/(r′ − d′). From Eq. (C.10c), we have gM1 ≈ 1/(r′ − d′). We further have gx ≈ 1/(r′ − d′) for x = M1 + 1, M1 + 2, …, M2 − 2. Using these results, we have . The non-extinction probability of a type-1 lineage is given by and the probability of metastases arising from such a type-1 lineage is given by . Here and , which represents the length of time between the emergence of the first successful type-1 cell and autopsy, is given by . Taken together, the probability of metastasis at autopsy given that there is no type-1 cell at diagnosis is given by Eq. (6) in the main text.
Finally the probability of metastasis at autopsy with treatment is given by Eq. (7) in the main text. The expected number of metastatic sites at autopsy with treatment given that there is no type-1 cell at diagnosis is given by
Appendix D. The expected total number of cells in all metastatic sites at autopsy with treatment
Let us now consider the expected number of type-2 cells once the total number of all cell types reaches M2 at autopsy. Note that we have already derived the probability that at least one type-2 cell exists at autopsy, Pa. Let us first consider the case in which the first successful type-2 lineage emerges before diagnosis. The probability that the first surviving type-2 cell lineage arises at time σ from a type-1 cell lineage that emerged when there were x type-0 cells is given by L(σ) in Eq. (B.1). Once a type-2 cell has emerged, its lineage will increase exponentially in abundance until diagnosis. The amount of time between the emergence of a type-2 cell and diagnosis is given by κxσ and is derived numerically from xe(r−d)(σ+κx,σ + e(a1−b1−q)(t+κx,σ) + e(a2−b2)κx,σ = M1. Right after diagnosis and resection, the expected numbers of type-0, -1, and -2 cells are given by x0 =(1 − ε)xe(r−d)(σ+κx,σ), y0 = (1 − ε)e(a1−b1−q)(σ+κx,σ), and z0 = e(a2−b2)κx,σ, respectively. Here the factor (1 − ε) represents the effect of resection of the primary tumor. After diagnosis we approximate the dynamics of the number of type-2 cells, za, deterministically as
| (D.1) |
The number of type-2 cells at autopsy is then given by . Here t′ is calculated by . Hence the expected number of type-2 cells at autopsy in the situation in which type-2 cells have emerged before diagnosis is given by
| (D.2) |
Here P(x) represents the probability that the first successful type-1 cell emerges when there are x type-0 cells (see Appendix A.)
Let us next consider the case in which the first successful type-2 cell does not emerge before diagnosis, but does arise between diagnosis and autopsy. Under the condition that a type-1 cell lineage emerges when there are x type-0 cells but does not metastasize until diagnosis, the numbers of type-0, -1, and -2 cells at diagnosis are given by x0 = (1 − ε)xe(r−d)τx, y0 = (1 − ε) e(a1−b1−q)τx, and z0 = 0. Here τx is calculated from xe(r−d)τx + e(a1−b1−q)τx = M1. Then the probability that the first surviving type-2 cell emerges at time τ′ after diagnosis is given by
| (D.3) |
Here the first term on the right-hand side represents the probability that no type-2 cell emerges until time τ′, while the second term represents the probability that the first type-2 cell emerges at time τ′ after diagnosis. Once a type-2 cell has emerged, its lineage increases exponentially in abundance until autopsy. The amount of time between the emergence of the first type-2 cell and autopsy is given by κ′x,τ′ and is numerically obtained from . Then the expected number of type-2 cells at autopsy in the case in which there are no type-2 cells present at diagnosis is given by
| (D.4) |
Here the factor represents the probability that there are no type-2 cells present at diagnosis, and is obtained from . Finally, expected number of type-2 cells at autopsy is given by Eq. (9) in the text. A schematic illustration of the derivation of each quantity is shown in Fig. 2b.
References
- Bernards R, Weinberg RA. A progression puzzle. Nature. 2002;418:823. doi: 10.1038/418823a. [DOI] [PubMed] [Google Scholar]
- Bosl GJ, Geller NL, Cirrincione C, CityVogelzang NJ, Kennedy BJ, Whitmore WF, Jr, Vugrin D, Scher H, Nisselbaum J, Golbey RB. Cancer Res. 1983;43:3403–3407. [PubMed] [Google Scholar]
- Cairns J. Mutation selection and the natural history of cancer. Nature. 1975;255:197–200. doi: 10.1038/255197a0. [DOI] [PubMed] [Google Scholar]
- Cazzaniga ME, Dogliotti L, Cascinu S, Barni S, Labianca R, Chiara S, Conte PF, Gasparini G, Pasetto L, Torri V. Diagnosis, management and clinical outcome of bone metastases in breast cancer patients: results from a prospective, multicenter study. Oncology. 2006;71:281–374. doi: 10.1159/000107772. [DOI] [PubMed] [Google Scholar]
- Dawson LA, Chow E, Goss PE. Evolving perspectives in contralateral breast cancer. Eur J Cancer. 1998;34:2000–2009. doi: 10.1016/s0959-8049(98)00208-1. [DOI] [PubMed] [Google Scholar]
- Dick JE. Stem cell concepts renew cancer research. Blood. 2008;112:4793–4807. doi: 10.1182/blood-2008-08-077941. [DOI] [PubMed] [Google Scholar]
- Dingli D, Michor F, Antal T, Pacheco JM. The emergence of tumor metastases. Cancer Biol Ther. 2007;6:383–390. doi: 10.4161/cbt.6.3.3720. [DOI] [PubMed] [Google Scholar]
- El Kamar FG, Grossbard ML, Kozuch PS. Metastatic pancreatic cancer: emerging strategies in chemotherapy and palliative care. The Oncologist. 2003;8:18–34. doi: 10.1634/theoncologist.8-1-18. [DOI] [PubMed] [Google Scholar]
- Fisher B, Anderson S, Bryant J, Margolese RG, Deutsch M, Fisher ER, Jeong JH, Wolmark N. Twenty-year follow-up of a randomized trial comparing total mastectomy, lumpectomy, and lumpectomy plus irradiation for the treatment of invasive breast cancer. N Engl J Med. 2002;347:1233–1241. doi: 10.1056/NEJMoa022152. [DOI] [PubMed] [Google Scholar]
- Haeno H, Iwasa Y, Michor F. The evolution of two mutations during clonal expansion. Genetics. 2007;177:2209–2221. doi: 10.1534/genetics.107.078915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hanahan D, Weinberg RA. The hallmarks of cancer. Cell. 2000;100:57–70. doi: 10.1016/s0092-8674(00)81683-9. [DOI] [PubMed] [Google Scholar]
- Hess KR, Varadhachary GR, CityplaceTaylor SH, Raber MN, Lenzi R, Abbruzzese JL. Metastatic patterns in adenocarcinoma. Cancer. 2006;106:1624–1633. doi: 10.1002/cncr.21778. [DOI] [PubMed] [Google Scholar]
- Holyoake T, Jiang X, Eaves C, Eaves A. Isolation of a highly quiescent subpopulation of primitive leukemic cells in chronic myeloid leukemia. Blood. 1999;94:2056–2064. [PubMed] [Google Scholar]
- Hüsemann Y, Geigl JB, Schubert F, Musiani P, Meyer M, Burghart E, Forni G, Eils R, Fehm T, Riethmüller G, CityKlein CA. Systemic spread is an early step in breast cancer. Cancer Cell. 2008;13:58–68. doi: 10.1016/j.ccr.2007.12.003. [DOI] [PubMed] [Google Scholar]
- Iwasa Y, Nowak MA, Michor F. Evolution of resistance during clonal expansion. Genetics. 2006;172:2557–2566. doi: 10.1534/genetics.105.049791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jechlinger M, Sommer A, Moriggl R, Seither P, Kraut N, Capodiecci P, Donovan M, Cordon-Cardo C, Beug H, Grünert S. Autocrine PDGFR signaling promotes mammary cancer metastasis. J Clin Invest. 2006;116:1561–1570. doi: 10.1172/JCI24652. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Michor F, Hughes TP, Iwasa Y, Branford S, Shah NP, Sawyers CL, Nowak MA. Dynamics of chronic myeloid leukemia. Nature. 2005;435:1267–1270. doi: 10.1038/nature03669. [DOI] [PubMed] [Google Scholar]
- Michor F, Nowak MA, Iwasa Y. Stochastic dynamics of metastasis formation. J Theor Biol. 2006;240:521–530. doi: 10.1016/j.jtbi.2005.10.021. [DOI] [PubMed] [Google Scholar]
- Michor F, Iwasa Y. Dynamics of metastasis suppressor gene inactivation. J Theor Biol. 2006;241:676–689. doi: 10.1016/j.jtbi.2006.01.006. [DOI] [PubMed] [Google Scholar]
- Panetta JC. A mathematical model of periodically pulsed chemotherapy: tumor recurrence and metastasis in a competitive environment. Bull Math Biol. 1996;58:425–447. doi: 10.1007/BF02460591. [DOI] [PubMed] [Google Scholar]
- Podsypanina K, Du YCN, Jechlinger M, Beverly LJ, Hambardzumyan D, Varmus H. Seeding and propagation of untransformed mouse mammary cells in the lung. Science. 2008;321:1841–1844. doi: 10.1126/science.1161621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pozzatti R, Muschel R, Williams J, Padmanabhan R, Howard B, Liotta L, Khoury G. Primary rat embryo cells transformed by one or two oncogenes show different metastatic potentials. Science. 1986;232:223–227. doi: 10.1126/science.3456644. [DOI] [PubMed] [Google Scholar]
- Riethdorf S, Wikman H, Pantel K. Review: biological relevance of disseminated tumor cells in cancer patients. Int J Cancer. 2008;123:1991–2006. doi: 10.1002/ijc.23825. [DOI] [PubMed] [Google Scholar]
- Roodman GD. Mechanisms of bone metastasis. N Engl J Med. 2004;350:1655–1664. doi: 10.1056/NEJMra030831. [DOI] [PubMed] [Google Scholar]
- Sahai E. Illuminating the metastasis process. Nat Rev Cancer. 2007;7:737–749. doi: 10.1038/nrc2229. [DOI] [PubMed] [Google Scholar]
- placeThames HD, Buchholz TA, Smith CD. Frequency of first metastatic events in breast cancer: implications for sequencing of systematic and local-regional treatment. J Clin Oncol. 1999;17:2649–2658. doi: 10.1200/JCO.1999.17.9.2649. [DOI] [PubMed] [Google Scholar]
- Wyllie AH, Rose KA, Morris RG, Steel CM, Foster E, Spandidos DA. Rodent fibroblast tumors expressing human myc and ras genes: growth, metastasis and endogenous oncogene expression. Br J Cancer. 1987;56 (3):251–259. doi: 10.1038/bjc.1987.186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang J, CityMani SA, Donaher JL, Ramaswamy S, Itzykson RA, Come C, Savagner P, Gitelman I, CityplaceRichardson A, Weinberg RA. Twist, a master regulator of morphogenesis, plays an essential role in tumor metastasis. Cell. 2004;117:927–939. doi: 10.1016/j.cell.2004.06.006. [DOI] [PubMed] [Google Scholar]
- Yoshida BA, Dubauskas Z, Chekmareva MA, Christiano TR, Stadler WM, Rinker-Schaeffer CW. Mitogen-activated protein kinase kinase 4/stress-activated protein/Erk kinase 1 (MKK4/SEK1), a prostate cancer metastasis suppressor gene encoded by human chromosome 17. Cancer Res. 1999;59:5483–5487. [PubMed] [Google Scholar]
- Yoshida BA, Sokoloff MM, Welch DR, Rinker-Schaeffer CW. Metastasis-suppressor genes: a review and perspective on an emerging field. J Natl Cancer Inst. 2000;92:1717–1730. doi: 10.1093/jnci/92.21.1717. [DOI] [PubMed] [Google Scholar]
- Yu DH, Hung MC. Expression of activated rat neu oncogene is sufficient to induce experimental metastasis in 3t3 cells. Oncogene. 1991;6:1991–1996. [PubMed] [Google Scholar]