Design and Estimation for Evaluating Principal Surrogate Markers in Vaccine Trials

Summary

In vaccine research, immune biomarkers that can reliably predict a vaccine’s effect on the clinical endpoint (i.e., surrogate markers) are important tools for guiding vaccine development. This paper addresses issues on optimizing two-phase sampling study design for evaluating surrogate markers in a principal surrogate framework, motivated by the design of a future HIV vaccine trial. To address the problem of missing potential outcomes in a standard trial design, novel trial designs have been proposed that utilize baseline predictors of the immune response biomarker(s) and/or augment the trial by vaccinating uninfected placebo recipients at the end of the trial and measuring their immune biomarkers. However, inefficient use of the augmented information can lead to counterintuitive results on the precision of estimation. To remedy this problem, we propose a pseudo-score type estimator suitable for the augmented design and characterize its asymptotic properties. This estimator has superior performance compared with existing estimators and allows calculation of analytical variances useful for guiding study design. Based on the new estimator we investigate in detail the problem of optimizing the sampling scheme of a biomarker in a vaccine efficacy trial for efficiently estimating its surrogate effect, as characterized by the vaccine efficacy curve (a causal effect predictiveness curve) and by the predicted overall vaccine efficacy using the biomarker.

1. Introduction

Development of effective vaccines for preventing infectious diseases such as HIV/AIDS is a challenging task due to the complexity of the human immune system. In a randomized trial, identification of immune biomarkers measured after immunization that are associated with a vaccine’s protective effect can be very useful in guiding the vaccine’s development (Plotkin, 2010). The research in this manuscript is motivated by the need to evaluate immune responses as potential surrogate markers for HIV infection in HIV vaccine efficacy trials now being planned. Among various frameworks proposed for evaluating surrogate markers in biomedical research (Joffe and Greene, 2009; Buyse et al., 2000; Burzykowski et al., 2005; Lin et al., 1997; Freedman et al., 1992; Li et al., 2010, 2011; Prentice, 1989; Daniels and Hughes, 1997; Robins and Greenland, 1992), we use the principal surrogate framework (Frangakis and Rubin, 2002), which is particularly advantageous for the motivating HIV application as has been discussed in previous work including Gilbert et al. (2011b).

Study design and characteristics play an important role in principal surrogate evaluation. Principal surrogate estimands are defined conditional on an individual’s potential biomarker values given vaccine or placebo, and thus are generally not identifiable from observed data in standard randomized trial designs. Gilbert and Hudgens (2008), Wolfson and Gilbert (2010) and others have focused on the special case, common in HIV vaccine trials, where there is no variability in the immune biomarker values of placebo recipients. In this setting estimands of surrogate effects are defined conditional on vaccine-induced immune responses only. Two of such estimands we focus on in this paper are the vaccine efficacy curve (also called the “principal effect” curve (Frangakis and Rubin, 2002) or the “causal effect predictiveness” curve (Gilbert and Hudgens, 2008)) and the predicted overall vaccine efficacy. However, even in this relatively simple setting, these principal surrogate estimands of interest remain nonidentifiable in standard vaccine trials.

Realizing the limitation of a standard trial design for immune surrogate evaluation, Follmann (2006) proposed two ways to enhance the study design using baseline immunogenicity predictors (BIPs) and an approach he termed “closeout placebo vaccination” (CPV). The BIP strategy develops an imputation model for unobserved immune biomarkers based on the observed relationship between baseline covariates and biomarker values. However, this approach only identifies th principal surrogate estimands under strong, untestable assumptions made on the risk model (Gilbert and Hudgens, 2008). A more direct solution for the missing data problem is CPV, which augments the design by vaccinating uninfected placebo recipients at the end of the trial and measuring their subsequent biomarker values. The values are then treated as if they had been recorded from subjects assigned to vaccine at the beginning of the trial (Follmann, 2006). Under certain assumptions such as equal early clinical risk and time constancy as will be detailed in the paper, the inclusion of the CPV component allows nonparametric estimation of disease risks under each assignment of vaccine or placebo, which makes the evaluation of risk model assumptions possible.

Despite its appealing potential to increase identifiability, little research has been done to ascertain the gains in estimation efficiency which may be possible using CPV. What estimation method to use in this novel design and how to optimize the sampling of immune biomarkers for better efficiency in evaluating their surrogate effects are important questions remaining to be addressed and are the major focus of this paper. The research for this paper was motivated by the planning of a future HIV vaccine efficacy trial in South Africa, detailed in Gilbert et al. (2011a), where the primary objective is to evaluate the vaccine efficacy to prevent HIV infection of multiple prime-boost vaccine regimens versus a shared placebo group, with assessment of immune surrogates as a secondary objective. The CPV design was examined for its capacity in immune surrogates evaluation in the trial planning. As we will show later in Section 2.2, the additional information generated by the augmented component, if not used efficiently, can lead to counter-intuitive results regarding the estimation precision. We propose and investigate a pseudo-score type estimator particularly suitable for the augmented design. Based on this estimator we investigate in detail the problem of optimizing the biomarker sampling scheme to efficiently estimate surrogate effects in HIV vaccine trials. Beyond vaccine trials this research has application to surrogate endpoint evaluation in general clinical trials for which an augmented design akin to CPV is feasible.

In Section 2, we introduce the setting for evaluating principal surrogates, describe the utility of the vaccine efficacy curve and the predicted overall vaccine efficacy for quantifying surrogate effects in HIV vaccine trials, and briefly review problems in applying existing estimation methods to the augmented design. We then propose a new estimator as a solution for the augmented design and examine its asymptotic properties. In Section 3, we evaluate the finite-sample performance of the proposed estimator and compare its performance with alternative estimators. In Section 4 we study optimal sampling schemes for estimating principal surrogate effects in the motivating HIV application using the proposed estimator. Finally we end the paper with a discussion.

2. Method

We consider a two-arm randomized trial. Let Z be the binary treatment indicator, 0 for placebo and 1 for active treatment (vaccination). Let W be baseline covariates such as demographics and laboratory measurements. We focus on discrete W in this manuscript, but note that the methods we describe can be generalized to accommodate continuous W by incorporating nonparametric smoothing techniques. Let S be the candidate surrogate of interest measured on the continuous scale at fixed time τ after randomization. Here we consider a univariate marker, but the estimation method we propose could be easily extended to allow for more than one marker. Let Y denote the binary clinical endpoint of interest, 0 for non-diseased and 1 for diseased. Acknowledging the possibility that Y occurs before S is measured, let Y^τ be the indicator of whether disease develops before τ. S is only measurable if Y^τ = 0; if Y^τ = 1, then S is undefined. We further incorporate the potential outcomes framework. Let S(z), Y^τ(z), Y(z) be the corresponding potential outcomes under treatment assignment z, for z = 0, 1. If Y^τ(z) = 1, S(z) is undefined and we set S(z) = *. We also consider a possible CPV component. At the end of the trial followup period, some fraction of placebo recipients who are uninfected at study closeout are vaccinated and the immune biomarker S_c at time τ after vaccination is measured; the proportion of the uninfected placebo recipients selected for closeout vaccination can range from 0 to 1.

Following the notation in Follmann (2006), we call the design with no CPV the BIP-only design (the design with baseline predictors W only), and the design with non-zero CPV component the BIP + CPV design. The setting we consider is a two-phase sampling design. In the first phase, information about Y, Z, and W are collected for every trial participant. In the second phase, S(1) or S_c is measured in a subcohort of study participants selected according to a random mechanism. We let δ to indicate the availability of S(1) or S_c.

Frangakis and Rubin (2002) proposed characterizing the principal surrogate effect of a marker based on comparison between the risk of Y(1) and Y(0) conditional on S(1) and S(0). In HIV vaccine trials, only subjects without previous infection with the pathogen under study are enrolled such that S(0) = 0; the characterization of surrogate value simplifies to comparison between risk₍₀₎{S(1)} = P{Y(0) = 1|S(1), Y^τ(0) = Y^τ(1) = 0} and risk₍₁₎{S(1)} = P{Y(1) = 1|S(1), Y^τ(0) = Y^τ(1) = 0}, namely the marginal causal effect predictiveness curve (CEP) as proposed in Gilbert and Hudgens (2008) with CEP{S(1)} = h [risk₍₁₎{S(1)}, risk₍₀₎{S(1)}] for a pre-specified contrast function h.

For a rare disease like HIV, one natural choice of CEP function is the vaccine efficacy (VE) as a function of S(1):

$$VE\{S(1)\}=1-\frac{{\mathit{risk}}_{(1)}\{S(1)\}}{{\mathit{risk}}_{(0)}\{S(1)\}},$$ (1)

the percent reduction in infection rate for the subgroup of vaccine recipients with immune response S(1) compared to if they had not been vaccinated. The vaccine efficacy curve (curve of VE(s) versus s) tells us the range of vaccine efficacies we can achieve with respect to HIV infection corresponding to varying levels of vaccine-induced immune response. For a desired vaccine efficacy level, the corresponding immune response level helps set the target for refining the vaccine in follow-up phase I/II studies. A useful surrogate will have strong effect modification in the sense of large variability in VE{S(1)} and thus there is potential to achieve a large vaccine efficacy by increasing the immune responses. Examples of vaccine efficacy curves for two biomarkers with the same S(1) distribution are displayed in Figure 1(a) with the steeper curve (marker 1) corresponding to a more useful surrogate. In general, the x-coordinates of these curves can be brought to the same scale through a cumulative distribution function (CDF) transformation to facilitate comparison between curves.

Figure 1.

(a) Vaccine efficacy curves: VE{S(1)} versus S(1). The grey horizontal line is the vaccine efficacy in the population defined as 1 − P(Y = 1|Z = 1)/P(Y = 1|Z = 0). (b) Plot of VE^new(Δ) versus Δ (the location shift in immune response for the refined vaccine versus original vaccine), under the assumption that P [Y = 1|Z = z, S(1) = s] = Φ(β₀ + β₁z + β₂s + β₃sz) and P[Y = 1|Z^new = z, S(1) = s] = Φ {β₀ + β₁ + β₂s + β₃(s + Δ)}.

After we refine a vaccine to achieve certain immune response levels in phase I/II trials, the next step is to determine whether the refined vaccine has large enough predicted vaccine efficacy in a future licensure trial, based on the change in immune responses we observe in phase I/II studies through the refinement. The quality of this prediction depends on the surrogacy of the biomarker identified in the current trial as well as the ‘bridging’ assumption regarding the relationship between the vaccine effect on immune response and the vaccine effect on infection rate. For example, suppose the risk of HIV infection given S(1) and Z in the current trial can be modeled with risk₍₁₎{S(1)} = Φ{β₀ + β₁Z + β₂S(1) + β₃ZS(1)} with Φ the CDF of N(0,1), and the refined vaccine leads to a location-shift Δ in immune response distribution relative to the original vaccine. For a valid bridging surrogate, Follmann (2006) models the HIV infection rate conditional on S(1), the immune response induced by the original vaccine, and the treatment assignment Z^new in the future trial with risk_(z^New){S(1)} = Φ [β₀ + β₁Z^new + β₂S(1) + β₃{S(1) + Δ}Z^new]. Then the predicted overall efficacy of the refined vaccine on Y is

$$\begin{array}{l}V{E}^{\mathit{new}}(\mathrm{\Delta })=1-\frac{P(Y=1\mid Z^{\mathit{new}}=1)}{P(Y=1\mid Z^{\mathit{new}}=0)}\\ =1-\frac{\int \mathrm{\Phi }\{{\beta }_0+{\beta }_1+{\beta }_{2}s+{\beta }_3(s_1+\mathrm{\Delta })\}dF(s_1)}{\int \mathrm{\Phi }({\beta }_0+{\beta }_2{s}_1)dF(s_1)},\end{array}$$ (2)

with F{S(1)} the distribution of S(1). This model will be used later in our simulation studies and study design. In Figure 1(b), we show the curves of VE^new(Δ) as a function of Δ corresponding to the same two markers whose vaccine efficacy curves are displayed in Figure 1(a). Note that the same location shift in the better surrogate marker (marker 1) corresponds to a higher predicted overall vaccine efficacy.

We next consider the estimation of VE{S(1)} and VE^New(Δ), by first estimating the disease risk conditional on S(1) and Z. We make the following assumptions.

2.1 Identifiability Assumptions

• (A1)SUTVA and Consistency: {S(1), S(0), Y^τ(1), Y^τ(0), Y(1), Y(0)} of one subject is independent of the treatment assignments of other subjects, and given the treatment a subject actually received, a subject’s potential outcomes equal the observed outcomes.
• (A2) Ignorable Treatment Assignments: Z ⊥ W, S(1), S(0), Y^τ(1), Y^τ(0), Y(1), Y(0).
• (A3)Equal Early Clinical Risk : Y^τ(1) = Y^τ(0) for all subjects.

  Assumptions (A1)–(A3) have been made in earlier literature (Gilbert and Hudgens, 2008; Hudgens and Gilbert, 2009; Huang and Gilbert, 2011). Basically, (A1) is plausible in trials where participants do not interact with one another and (A2) is ensured by randomization. As discussed in Wolfson and Gilbert (2010), (A3) is plausible if relatively few clinical events happen before the biomarker is measured. (A3) implies that the risk of Y conditional on Z = z, W, S(1), S(0) and Y^τ(0) = Y^τ(1) = 0 can be identified based on the subset of subjects assigned Z = z who are observed to have the marker measured at time τ (i.e., Y^τ = 0), with additional identifiability assumptions needed as given below. Henceforth we simplify the notation and drop the conditioning of all probabilities on Y^τ(1) = Y^τ(0) = Y ^τ = 0.

  Motivated by the design of HIV vaccine trials where S(0) = 0 for all subjects, we focus on risk models conditional on S(1) only, which is the one most relevant to vaccine development. In general when S(0) varies, risk conditional on S(1) has the interpretation of risk conditional on S(1) and S(0) averaged over the conditional distribution of S(0) and is still useful for vaccine development (Wolfson and Gilbert, 2010). Next, in assumption (A4) we posit generalized linear models for risk conditional on Z, S(1), and W.

• (A4)The risk of Y conditional on Z, S(1) and W can be modeled with a parametric function: risk_(z) {S(1), W} ≡ P{Y(z) = 1|S(1), W} = g {β; S(1), Z, W}, with g a pre-specified link function and β a finite-dimensional parameter.

  Based on the standard trial design, (A1)–(A4) and the observed data identify risk₍₀₎ and risk₍₁₎. But since S(1) is unobserved for all subjects in the placebo arm (Z = 0), one cannot fully test the appropriateness of the model assumption (A4) as pointed out in Gilbert and Hudgens (2008). This issue is resolved with the addition of the CPV component, together with the assumptions (A5) and (A6) below.

• (A5)Time-constancy of immune response: For uninfected placebo recipients, S(1) = S^true + U₁, and S_c = S ^true + U₂, for some underlying S ^true and i.i.d. measurement error U₁, U₂.
• (A6)No placebo subjects uninfected at closeout have an infection over the next τ time-units. Under (A5) and (A6), S_c can be used to substitute S(1) for these subjects sampled in CPV. The addition of the CPV component makes (A4) fully testable by allowing non-parametric estimation of the risk model, as sketched in Web Supplementary Appendix A. Henceforth we simplify the notation and use S to indicate a measurement of vaccine-induced immune response which can be obtained either during standard trial period or during CPV. Let N be the number of trial participants. The observed data are N iid copies O_i = (Z_i, W_i, δ_i, δ_iS_i, Y_i)′, i = 1, ···, N. Finally, we state two assumptions about the sampling probability of S (either S(1) or S_c) required for validity of the pseudo-score estimators described later in Section 2.3.
• (A7)∫ P(δ = 1|y, Z, W)dy > 0 for every Z, W level.
• (A8)∫ P(δ = 1|y, z, W )dydz > 0 for every W level.

2.2 Existing Methods and the Motivating Example

Under the two-phase sampling design described above, the vaccine-induced immune response S is missing at random (MAR) because it is determined completely by design. The MAR assumption allows identification of the risk model in (A4) based on observed likelihood

$$\begin{array}{l}ℒ=\prod _{{\delta }_i=1}P(Y_i\mid Z_i,W_i,S_i)\prod _{{\delta }_i=0}P(Y_i\mid Z_i,W_i)\\ =\prod _{{\delta }_i=1}P(Y_i\mid Z_i,W_i,S_i)\prod _{{\delta }_i=0}\int P(Y_i\mid Z_i,W_i,s)dF(s\mid Z_i,W_i),\end{array}$$ (3)

where F(S|Z, W) is the CDF of S conditional on Z, W.

Earlier work for identifying risk model parameters in evaluating principal surrogate markers was based on an estimated likelihood approach (Pepe and Fleming, 1991) that maximizes an estimated version of the likelihood (3). Specifically, estimation is performed in two steps. In the first step, F(S|Z, W) is estimated; and then in the second step, its estimator F̂(S|Z, W) is substituted into (3) and β is estimated as the maximizer of the resulting estimated likelihood. Approaches to estimating F(S|Z, W) vary along the spectrum from nonparametric to parametric (Gilbert and Hudgens, 2008; Qin et al., 2008; Hudgens and Gilbert, 2009; Huang and Gilbert, 2011). These methods work for both the BIP-only and the BIP+CPV designs. For both designs, the estimation in the first step is achieved using vaccine recipients with S measured given that F(S|Z = 1, W) = F(S|Z = 0, W) = F(S|W) as ensured by the randomization assumption (A2). When sampling of S depends on other phase-I variables such as the response Y, inverse probability weighting (IPW) (Horvitz and Thompson, 1952) can be implemented to correct for biased sampling (Gilbert et al., 2011a; Huang and Gilbert, 2011). Note that in a BIP+CPV design, even if all CPV samples contribute a full conditional likelihood term P(Y|Z, W, S) to the estimated likelihood, they cannot be used for estimating F(S|W). The fact that all infected placebo recipients have zero sampling probability for S prevents the application of IPW to the whole S sample in estimating F(S|W).

In our motivating design of the South Africa HIV vaccine trial, Gilbert et al. (2011a) considered incorporating the CPV component into the trial design and examined power for detecting principal surrogates using a parametric estimated likelihood approach. They examined two-phase case-control sampling using either a BIP-only or a BIP+CPV design where cases and controls were sampled at 1:5 ratio within the vaccine arm and controls ten times that of the number of cases in placebo arm were included in CPV. A surprising finding was that in some scenarios where W had a strong correlation with S, the BIP-only design was more powerful than the BIP+CPV design for testing an interaction effect between S and Z (Table 7 of Gilbert et al. (2011a)).

Here we investigate in further detail this seemingly counter-intuitive result of decreased efficiency caused by adding the CPV component. We compare variances of the risk model parameter estimators between the BIP-only design and the BIP+CPV design with varying ratios of CPV sampling. As shown in Web Supplementary Figure 1, the efficiency loss of the BIP+CPV design relative to the BIP-only design becomes more severe as the proportion of uninfected placebo recipients selected for closeout vaccination increases. In contrast, as also shown in Web Supplementary Figure 1, if we enter the ‘true’ F(S|W) into the observed likelihood (3), then the BIP+CPV design is more efficient than the BIP-only design and the efficiency gain increases in general with a higher CPV sampling fraction, as expected. These results suggest that the decreased efficiency caused by CPV sampling is due to the fact that two different sets of “validation data” are used in the two steps of the estimated likelihood procedure: the CPV component is included in the validation set in maximizing the likelihood but not in the estimation of the conditional distribution of S. This will be further demonstrated in Section 3.

To use the CPV component more efficiently, we need an estimation method that removes the incompatibility in the use of validation sets as present in the estimated likelihood methods. In the next section, we propose a pseudo-score type estimator as a solution, building upon the original work by Chatterjee et al. (2003).

2.3 The Pseudo-Score Estimator for Principal Surrogates Evaluation

The score equation of the observed likelihood (3) is

$$\frac{\partial l(\beta ,F)}{\partial \beta }=\sum _{{\delta }_i=1}{U}_{\beta }(Y_i\mid S_i,Z_i,W_i)+\sum _{{\delta }_j=0}\frac{\int U_{\beta }(Y_j\mid s,Z_j,W_j)P(Y_j\mid s,Z_j,W_j)dF(s\mid Z_j,W_j)}{\int P(Y_j\mid s,Z_j,W_j)dF(s\mid Z_j,W_j)}=0,$$ (4)

with U_β(Y|S, Z, W) = ∂log P(Y|S, Z, W)/∂β. Equation (4) can be further written into the following parsimonious form incorporating the randomization assumption (A2)

$$\sum _{{\delta }_i=1}{U}_{\beta }(Y_i\mid S_i,Z_i,W_i)+\sum _{{\delta }_j=0}\frac{\int U_{\beta }(Y_j\mid s,Z_j,W_j)P(Y_j\mid s,Z_j,W_j)dF(s\mid W_j)}{\int P(Y_j\mid s,Z_j,W_j)dF(s\mid W_j)}=0.$$ (5)

According to Bayes’ theorem, we have

$$dF(S\mid W)=\frac{dF(S\mid W,\delta =1)P(\delta =1\mid W)}{P(\delta =1\mid S,W)}.$$ (6)

Substituting the right hand side of (6) for its left hand side into (5) we arrive at a pseudo-score

$$\sum _{{\delta }_i=1}{U}_{\beta }(Y_i\mid S_i,Z_i,W_i)+\sum _{{\delta }_j=0}\frac{\int U_{\beta }(Y_j\mid s,Z_j,W_j)\frac{P(Y_j\mid s,Z_j,W_j)}{P(\delta =1\mid s,W_j)}dF(s\mid W_j,\delta =1)}{\int \frac{P(Y_j\mid s,Z_j,W_j)}{P(\delta =1\mid s,W_j)}dF(s\mid W_j,\delta =1)}.$$ (7)

We propose to estimate the pseudo-score (7) by first estimating the distribution of S conditional on W based on S measured in the second phase sample, and then estimating the sampling probability of S conditional on S and W. The latter can be estimated as the sampling probability of S conditional on all covariates and Y together averaged over the joint distribution of Y and Z conditional on S and W. That is, P(δ = 1|S, W) = ∫∫ P(δ = 1|y, z, S, W)P(y, z|S, W)dydz = ∫∫ P(δ = 1|y, z, W)P(y|S, z, W)P(z)dydz. The corresponding pseudo-score estimator is defined as the solution to (7). Note this proposed estimator is an extended version of an original pseudo-score estimator proposed by Chatterjee et al. (2003). We call the original pseudo-score estimator the PSO estimator and the proposed new estimator the PSN estimator. Both estimators transforms the task of estimating the conditional distribution of S in the population into the task of estimating the conditional distribution of S in the sample; PSN requires estimation of F(S|W, δ = 1) while PSO requires estimation of F(S|W, Z, δ = 1) (details provided in Web Supplementary Appendix B). Note that both PSN and PSO allow incorporation of the CPV component into estimation of the distribution of S conditional on W or Z and W, and can be applied to a design with non-zero CPV component. The PSO estimator does not, however, apply to a BIP-only design since F(S|Z = 0, W, δ = 1) is undefined. In other words, given that risk_(z)(S, W) > 0 almost surely, validity of PSO requires the sampling probability of S being greater than zero for every Z, S, W level (assumption (A7)); in contrast, the PSN relaxes this requirement to the weaker requirement (A8) that the sampling probability of S exceeds zero for every S, W level and hence is applicable to both the BIP-only and the BIP+CPV designs.

To obtain the PSN estimator, for each unique value w of W, we estimate F(s|w, δ = 1) empirically with Σ_δi=1I(S_i ≤ s, W_i = w)/Σ_δi=1I(W_i = w). An Expectation-Maximization (EM) algorithm can be employed to estimate the risk model parameters β:

1. Start with an initial value of β;

2. For a subject i with δ_i = 1, use its observed data. For a subject with δ_i = 0, construct a set of filled-in data with length equal to the number of observations in V_Wi, where V_Wi is the set of validation subjects with δ = 1 and W = W_i. Specifically, for each j ∈ V_Wi, we construct a new observation {Y_i, S_j, Z_i, W_i}.

3. For each filled-in observation {Y_i, S_j, Z_i, W_i}, j ∈ V_Wi, calculate an associated weight,

   $$\frac{\widehat{P}(Y_i\mid S_j,Z_i,W_i)/\widehat{P}(\delta =1\mid S_j,W_i)}{{\sum }_{j\in V_{W_i}}\widehat{P}(Y_i\mid S_j,Z_i,W_i)/\widehat{P}(\delta =1\mid S_j,W_i)},$$

   which is an estimate of the density of S_j conditional on Y_i, Z_i, W_i, where $\widehat{P}(\delta =1\mid S_j,W_i)={\sum }_{z=0}^1{\sum }_{y=0}^1\widehat{P}(\delta =1\mid y,z,W_i)\widehat{P}(y\mid S_j,z,W_i)P(z)$, with P̂(δ = 1|y, z, W_i) a consistent estimate of P(δ = 1|y, z, W_i) and P̂(y|S_j, z, W_i) obtained based on the current β estimate.

4. Fit a weighted GLM to the augmented dataset and obtain a new estimate of β.

5. Repeat steps (II) to (IV) until convergence.

Suppose the sampling probability of S conditional on Y, Z, and W can be modeled with P(δ = 1|Y, Z, W) = π(Y, Z, W; α) for some parameter α. We substitute α with its maximum likelihood estimator (MLE) α̂ to obtain P̂(δ = 1|y, z, w) for computing the pseudo-score (7). For example, in the simulation studies described next where the sampling probability of S depends on Y and Z only, we apply a saturated model for the sampling probability of S with π = {π(Y, Z)} = {π(0, 0), π(0, 1), π(1, 0), π(1, 1)}, such that MLE of π(y, z) equals the observed sampling fractions in the category defined by Y = y and Z = z. Under regularity conditions specified in Web Supplementary Appendix C, the PSN estimator β̂ can be shown to be consistent and asymptotically normally distributed. Theorem 1 in Web Supplementary Appendix C describes the asymptotic distribution of β̂ with a proof sketched. In our simulation and design studies, we consider a risk model P{Y = 1|S(1), Z, W} = Φ{β₀ + β₁Z + β₂S(1) + β₃S(1)Z}. Based on risk model parameter estimators β̂₀, β̂₁, β̂₂, β̂₃, we estimate VE{S(1)} with $\widehat{VE}\{S(1)\}=1-\mathrm{\Phi }\{{\widehat{\beta }}_0+{\widehat{\beta }}_1+{\widehat{\beta }}_{2}S(1)+{\widehat{\beta }}_{3}S(1)\}/\mathrm{\Phi }\{{\widehat{\beta }}_0+{\widehat{\beta }}_{2}S(1)\}$, and estimate VE^New(Δ) with ${\widehat{VE}}^{\mathit{New}}(\mathrm{\Delta })=1-\int \{{\widehat{\beta }}_0+{\widehat{\beta }}_1+{\widehat{\beta }}_2{s}_1+{\widehat{\beta }}_3(s_1+\mathrm{\Delta })\}dF(s_1)/\int ({\widehat{\beta }}_0+{\widehat{\beta }}_{2}s)dF(s_1)$ with pre-specified F(s₁). Asymptotic normality of $\widehat{VE}\{S(1)\}$ and ${\widehat{VE}}^{\mathit{new}}(\mathrm{\Delta })$ follow from Theorem 1. Their asymptotic variances can be derived based on the Delta method: $var\left[\widehat{VE}\{S(1)\}\right]={\left[\partial VE\{S(1)\}/\partial \beta {\mid }_{\widehat{\beta }}\right]}^{T}var(\widehat{\beta })\left[\partial VE\{S(1)\}/\partial \beta {\mid }_{\widehat{\beta }}\right]$ and $var\left\{{\widehat{VE}}^{\mathit{new}}(\mathrm{\Delta })\right\}={\{\partial V{E}^{\mathit{new}}(\mathrm{\Delta })/\partial \beta {\mid }_{\widehat{\beta }}\}}^{T}var(\widehat{\beta })\{\partial V{E}^{\mathit{new}}(\mathrm{\Delta })/\partial \beta {\mid }_{\widehat{\beta }}\}$.

3. Simulation Study

In this section, we evaluate the finite-sample performance of the PSN estimator and compare it with the estimated likelihood estimator (EL) (Gilbert et al., 2011a). In addition, we study two other alternatives: the original pseudo-score estimator PSO, and a variant pseudo-score estimator (PSV) where we transform the task of estimating F(S|W) into the task of estimating F(S|W, Z = 1, δ = 1). Details about the derivation of PSV are provided in Web Supplementary Appendix B. PSV is included as the closest pseudo-score analogue of EL from the perspective that both estimators include the CPV component in the validation set for likelihood maximization but not for estimation of the conditional distribution of S.

Our simulation settings are chosen to reflect the characteristics of a typical HIV vaccine trial. We simulate S from a normal distribution with mean 3 and variance 1, and simulate a categorical W with four levels derived from discretizing a normal variable correlated with S (with correlation ρ = 0.5) by quartiles. We assume a probit risk model of the binary outcome Y conditional on S, Z and W : P(Y = 1|S, Z, W) = Φ(β₀ + β₁Z + β₂S + β₃SZ). The risk model parameters are chosen such that the probability of infection is 0.12 and 0.06 in the Z = 0 and Z = 1 arms, respectively.

Consider a two-phase sampling design. In phase 1, N = 4, 000 subjects are randomized in a 1:1 ratio to vaccine (Z = 1) and placebo (Z = 0). In this phase, W, Z, and Y are observed. In phase 2, stratified Bernoulli sampling of S is conducted as follows: All cases (infected) in the vaccine arm have S measured, and a portion of controls (uninfected) in the vaccine arm or placebo arm (the CPV component) have S measured. The performance of different estimators are compared as a function of two study design parameters: γ_V, the average ratio of sampled controls to cases in the vaccine arm; and γ_P, the average ratio of sampled controls in the placebo arm to cases in the vaccine arm. For each scenario, results are based on 5,000 Monte-Carlo simulations. Note that EL, PSN, and PSV apply to both the BIP-only and the BIP+CPV designs, whereas PSO applies only to the BIP+CPV design. When using EL, PSN or PSV, we can think of the BIP-only design as a special case of the BIP+CPV design with γ_P = 0, and PSN and PSV are equivalent when γ_P = 0. We evaluate performance for estimating β₀, β₁, β₂, β₃, estimating VE{S(1)} using formulae (1) for S(1) corresponding to the 90^th percentile of the distribution, and estimating VE^New(Δ) using formulae (2) with F{S(1)} specified to be N(3,1) for a Δ value corresponding to VE^New(Δ) = 0.75.

First, we present efficiency of the proposed PSN estimator relative to the EL estimator for various combinations of γ_V and γ_P (Table 1). The PSN estimator in general is more efficient than the EL estimator for either the BIP-only (γ_P = 0) or the BIP+CPV (γ_P > 0) design. In particular, dramatic efficiency gains can be achieved when γ_P is equal to or larger than γ_V.

Table 1.

Efficiency of PSN relative to EL

Relative Efficiencya
γV	γP	β0	β1	β2	β3	VE{S(1)}	VENew(Δ)
1	0	1.05	1.08	1.05	1.07	1.08	1.06
1	1	1.03	1.17	1.04	1.18	1.36	1.22
5	0	1.00	1.00	1.00	1.00	0.99	0.99
5	5	1.03	1.07	1.04	1.08	1.08	1.08
10	0	1.00	1.00	1.00	1.00	1.00	1.00
10	10	1.07	1.07	1.08	1.07	1.07	1.08
16.62b	0	1.00	1.00	1.00	1.00	1.00	1.00
16.62b	15.5c	1.07	1.05	1.08	1.05	1.04	1.06
1	2	1.06	1.30	1.08	1.32	1.72	1.43
2	5	1.15	1.32	1.18	1.32	1.44	1.40
1	10	2.23	2.75	2.33	2.76	10.73	3.87
5	10	1.17	1.22	1.19	1.22	1.24	1.26

^aefficiency of PSN relative to EL = var(EL)/var(PSN)

^bγ_V = 16.62 corresponds to sampling all uninfected vaccinees

^cγ_P = 15.5 corresponds to sampling all uninfected placebo recipients

We then evaluate the finite-sample performance of the proposed PSN estimator. For different γ_V and γ_P values, Table 2 provides bias, standard deviation, and coverage of 95% Wald confidence intervals based on asymptotic variance estimates. The PSN estimator has minimal biases in all settings. A larger number of S sampled in particular among vaccinees leads to smaller variance. The 95% Wald confidence intervals based on standard error estimates from analytical formulas have accurate coverage in general.

Table 2.

Finite-Sample Performance of the PSN Estimator.

	γV	γP	Expected $n_0^a$	β1	β2	β3	β4	VE{S(1)}	VENew(Δ)
Bias	1	0	120	−0.0045	0.0049	−0.0003	−0.0012	−0.0157	−0.0231
	1	1	240	−0.0030	0.0065	−0.0008	−0.0018	−0.0140	−0.0212
	5	0	600	−0.0001	−0.0004	−0.0015	0.0001	−0.0131	−0.0199
	5	5	1200	−0.0020	0.0032	−0.0010	−0.0009	−0.0125	−0.0190
	1	10	1320	−0.0032	0.0045	−0.0008	−0.0012	−0.0136	−0.0206
	10	1	1320	0.0001	0.0007	−0.0016	−0.0002	−0.0125	−0.0191
	10	10	2400	−0.0017	0.0021	−0.0010	−0.0007	−0.0113	−0.0172
	16.62b	0	1994	0.0009	−0.0036	−0.0019	0.0012	−0.0134	−0.0202
	16.62b	15.5c	3854	−0.0013	0.0010	−0.0010	−0.0004	−0.0107	−0.0162
SD	1	0	120	0.244	0.304	0.085	0.106	0.101	0.131
	1	1	240	0.236	0.295	0.082	0.103	0.097	0.126
	5	0	600	0.238	0.279	0.082	0.097	0.089	0.118
	5	5	1200	0.225	0.275	0.078	0.096	0.089	0.117
	1	10	1320	0.227	0.289	0.079	0.101	0.093	0.123
	10	1	1320	0.232	0.272	0.080	0.095	0.087	0.116
	10	10	2400	0.216	0.261	0.075	0.091	0.084	0.111
	16.62b	0	1994	0.237	0.274	0.082	0.095	0.087	0.117
	16.62b	15.5c	3854	0.208	0.249	0.072	0.087	0.082	0.106
Coveraged	1	0	120	96.0	95.1	95.7	95.5	96.1	96.6
	1	1	240	95.5	94.9	95.7	95.3	96.4	96.9
	5	0	600	95.4	95.5	95.4	95.5	96.6	96.8
	5	5	1200	94.8	94.5	95.2	95.0	96.2	96.7
	1	10	1320	94.8	94.8	94.8	94.9	96.4	96.8
	10	1	1320	95.3	94.9	95.4	95.2	96.2	96.9
	10	10	2400	94.8	94.9	94.9	94.9	96.3	96.9
	16.62b	0	1994	95.3	95.3	95.4	95.6	96.7	97.0
	16.62b	15.5c	3854	95.1	94.9	95.3	94.9	96.3	96.8

^aExpected n₀: expected number of uninfected subjects with S(1) or S_c sampled

^bγ_V = 16.62 corresponds to sampling all uninfected vaccinees

^cγ_P = 15.5 corresponds to sampling all uninfected placebo recipients

^dCoverage of 95% Wald confidence interval using variance estimate based on analytical formula, assuming parameter estimates are normally distributed for β₁, β₂, β₃, β₄ and assuming logit transformed parameter estimates are normally distributed for VE{S(1)} and VE^New(Δ)

For comparison among various alternative estimators, Web Supplementary Figure 2 shows the empirical variance of β₃ estimators as a function of γ_V using a BIP-only or a BIP+CPV design (with γ_P = 10). The patterns for estimating other quantities are fairly similar and results are omitted. Corresponding results as a function of γ_P when γ_V is fixed at 5 are displayed in Web Supplementary Figure 3. When γ_V is small compared to γ_P, the EL and PSV estimators based on BIP+CPV can have much larger variance compared to EL based on BIP-only. These two estimators are the only ones with differential use of the CPV component between the two steps of estimation, consistent with our conjecture about the reason for efficiency loss observed with EL in the BIP+CPV design. This issue is fixed by using PSN or PSO. Based on PSN, for example, increasing the sampling rate of the CPV component (i.e. increasing γ_P) can lead to a substantial efficiency gain (up to 16% in our setting) compared to the BIP-only design (Supplementary Figure 2(b)). Also PSN can have a substantial efficiency gain relative to PSO in a BIP+CPV design (up to 15% in our setting in Supplementary Figures 2(b),3(b)).

4. Optimal two-phase biomarker sampling design for estimating the vaccine efficacy curve and predicting the population-average vaccine efficacy

In practice, given limited resources for measuring immune biomarkers, an important decision is how to best allocate resources to maximize efficiency in estimating surrogate effects. In this section, we use the PSN estimator to help determine the optimal two-phase sampling scheme for efficient estimation of VE{S(1)} and VE^new(Δ). Again consider a two-phase sampling setting where S is randomly sampled from infected vaccinees, uninfected vaccinees or uninfected placebo recipients (the CPV component) separately. For a rare disease like HIV infection, typically we sample all infected vaccinees available in the trial. The question is then how to divide the sampling of uninfected subjects between the vaccine and placebo arms given a fixed overall case-control sampling ratio. In other words how to choose γ_V and γ_P when their sum is bounded from above. The asymptotic variances for the PSN estimator derived in Section 2.3 can be used to guide the sampling design.

Before examining the sampling under fixed cost, we first examine the efficiency change when varying one of γ_V and γ_P while holding the other constant. In Web Supplementary Figure 4(a), we explore the efficiency gain for estimating various quantities as γ_V increases relative to γ_V = 1, holding γ_P = 0, using the same numerical setting as in Section 3. Corresponding results for increasing γ_P with γ_V fixed at 1 are shown in Web Supplementary Figure 4(b). Relative to the BIP-only design with 1:1 case-control sampling ratio, further increases in γ_V have larger impact on estimating the main effect of Z(β₁) and the interaction between Z and S(1) (β₃) compared to the intercept (β₀) and the main effect of S(1) (β₂). The impact on estimating VE{S(1)} and VE^new(Δ) is in-between. When fixing γ_V = 1 but increasing the sampling of the CPV component, the pattern is reversed: increases in γ_P have largest impact on estimating β₀ and β₂.

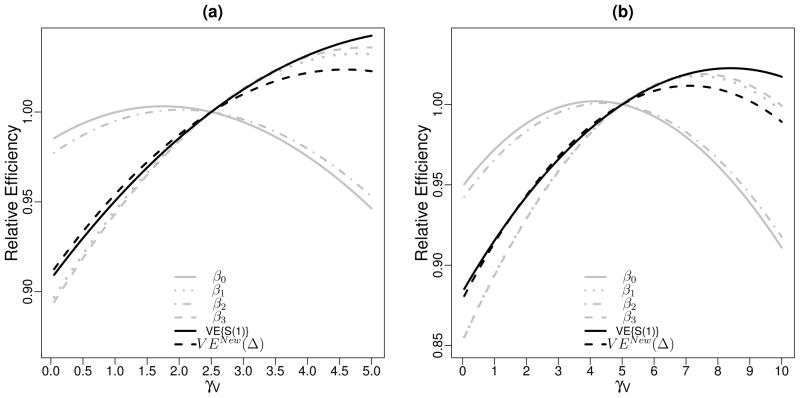
Moreover, given fixed cost for marker sampling, defined as Cost ≡ γ_V + γ_P, we evaluate the efficiency of study designs with various allocations of γ_V and γ_P. Figure 2 shows the asymptotic efficiency relative to the design with equal γ_V and γ_P. The pattern is similar when Cost is fixed at different levels. In general, a design with larger γ_P is more efficient for estimating β₀ and β₂, whereas a design with larger γ_V is optimal for estimating β₁, β₃, VE{S(1)} and VE^new(Δ). The last two quantities are of clinical interest and most relevant in guiding our study design.

Figure 2.

Efficiency of estimators for various designs as γ_V varies from 1 to Cost − 1 relative to the design with γ_V = γ_P, given fixed Cost = γ_V + γ_P, for (a) Cost = 5 and (b) Cost = 10, given ρ = 0.5. Relative Efficiency presented is equal to (variance at γ_V = γ_P = Cost/2)/(variance at various γ_V and γ_P = Cost − γ_V).

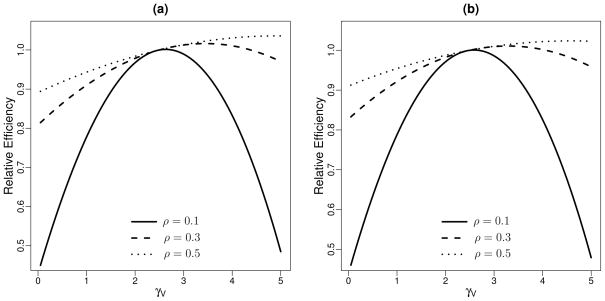
Finally, we examined the impact of the strength of the baseline predictor W in terms of its correlation with S on the optimal sampling scheme. Given Cost = 5 and for various linear correlations ρ, Figure 3 shows the asymptotic efficiency of different designs relative to the design with equal γ_V and γ_P for estimating VE(S) and VE^new(Δ). For each measure, it appears that the optimal γ_V tends to increase with increased correlation. In other words, when the baseline predictor is highly predictive of the biomarker, less efficiency is gained by incorporating information from CPV.

Figure 3.

Efficiency of estimators for various designs as γ_V varies from 1 to Cost−1 relative to the design with γ_V = γ_P, given fixed Cost = γ_V + γ_P = 5 for different linear correlations ρ, for estimating (a) VE{S(1)} and (b) VE^New(Δ). Relative Efficiency presented is equal to (variance at γ_V = γ_P = Cost/2)/(variance at various γ_V and γ_P = Cost − γ_V ).

5. Discussion

In this paper we investigated an estimation procedure and sampling scheme for evaluating surrogate markers in an augmented vaccine trial design (the CPV design) where uninfected placebo recipients are vaccinated at study closeout and have their immune responses measured. Motivated by the observation that incorporating closeout vaccination data into existing estimation procedures results in increased estimation error, we proposed a new pseudo-score type estimator appropriate for the CPV design. Besides providing a more efficient use of the augmented data, a contribution of our research to the surrogate marker problem is the derivation of an analytic variance estimator which was not achieved with existing estimated likelihood-based methods where inference relies solely on bootstrap resampling. Compared to the original pseudo-score estimator in the literature, our proposed estimator is more efficient since it exploits the marker-treatment independence intrinsic in randomized trials. It can also be applied to both standard and augmented trial designs.

The asymptotic variance developed for the proposed estimator is valuable for guiding the immune biomarker sampling scheme. We examined the question of optimally dividing biomarker samples between the CPV component and the uninfected vaccinees for efficient estimation of the vaccine efficacy curve and the predicted overall vaccine effect, given fixed total cost of measuring immune responses. In practice, there are other costs researchers will want to take into consideration, e.g., the additional cost of vaccination and follow-up associated with the CPV component. The example in this paper based on equal cost between uninfected vaccine and placebo recipients can be easily extended to allow for different costs between the two kinds of samples. At the same time, because the BIP+CPV design provides a way to test the modeling assumption (A4) that is unverifiable from the BIP-only design, in practice one might prefer to collect ample samples from both the vaccine and placebo arms to ensure model testing ability, as long as the sacrifice in efficiency compared to the optimal scheme is relatively small. All these considerations should be evaluated on a case-by-case basis. The examples studied in this manuscript suggest that a design that samples slightly larger numbers of uninfected vaccinees than placebo recipients are preferred for estimating the vaccine efficacy curve and predicting the vaccine’s overall effect on HIV infection.

The model we studied in this manuscript is the risk conditional on treatment Z, baseline covariate W, and the potential biomarker value given assignment to vaccine S(1). This is equivalent to the model which further conditions on the potential biomarker value given assignment to placebo S(0), for the case where S(0) is constant as in our motivating HIV application. In cases where subjects have had previous exposure to similar pathogens such that S(0) has variability, baseline biomarker measures might be used to substitute for S(0) under a time-constancy assumption that biomarkers measured at baseline reflect the biomarker value that would have been measured at time τ, if assigned to placebo. The technique we used in this manuscript can then be directly applied by treating S(0) as a part of W. This generalization implies the method has potential broad applicability for surrogate endpoint evaluation in many types of clinical trials.

The pseudo-score estimator derived in this manuscript applies when the baseline predictor W is available from every trial participant. Future research is warranted to extend the estimator to more general setting where a subset of W is sampled from the trial cohort and to evaluate the sampling scheme of W with respect to the efficiency of estimation.

Finally, the essence of our proposed modification of the pseudo-score estimator in randomized trials has a much more general implication in the modeling and estimation of disease risk. Since baseline covariates included for adjustment in the risk model are not always strongly correlated with the immune biomarker to be useful for its prediction, implementation of some model selection for a parsimonious subset of W’s in predicting the vaccine-induced immune response S(1) could potentially increase efficiency. This is currently under investigation.

Web Supplementary Appendix

Web Appendices referenced in Sections 2–4 are available with this paper at the Biometrics website on Wiley Online Library.