Rogue taxa phenomenon: a biological companion to simulation analysis

Abstract

To provide a baseline biological comparison to simulation study predictions about the frequency of rogue taxa effects, we evaluated the frequency of a rogue taxa effect using viral data sets which differed in diversity. Using a quartet-tree framework, we measured the frequency of a rogue taxa effect in three data sets of increasing genetic variability (within viral serotype, between viral serotype, and between viral family) to test whether the rogue taxa was correlated with the mean sequence diversity of the respective data sets. We found a slight increase in the percentage of rogues as nucleotide diversity increased. Even though the number of rogues increased with diversity, the distribution of the types of rogues (friendly, crazy, or evil) did not depend on the diversity and in the case of the order-level data set the net rogue effect was slightly positive. This study, assessing frequency of the rogue taxa effect using biological data, indicated that simulation studies may over-predict the prevalence of the rogue taxa effect. Further investigations are necessary to understand which types of data sets are susceptible to a negative rogue effect and thus merit the removal of taxa from large phylogenetic reconstructions.

1. Introduction

Rogue taxa change the evolutionary relationships among sets of taxa when included in a phylogeny. Their effect, often the result of long branch attraction, is generally assumed to be negative and often rogues are eliminated from phylogenetic studies to avoid misinterpreting evolutionary relationships. Such an approach was used by Thomson and Shaffer (2010) in a recent phylogenetic study of existing turtles. Rogue taxa were identified using an instability index, allowing these taxa to be removed before analysis of the robustness of the phylogeny (Thomson and Shaffer, 2010). Similarly, Trautwein et al. (2011) pruned rogue taxa and improved phylogenetic resolution in a bee fly study. Although removal is often recommended (see Baurain et al., 2007), there have been few mathematical analyses in which the rogue taxa effect has been analyzed. As phylogenetic data sets grow in terms of taxon number, evaluating the rogue effect may be increasingly important.

Cueto and Matson provided a framework for such analysis using polyhedral geometrics to make predictions about the frequency of a rogue taxa effect (2011). They found that the rogue taxa effect was common when the added taxa were chosen without reference to the original tree (arbitrarily) and that the effect worsened as the number of taxa increased (Cueto and Matson, 2011). Their study indicated that 29% of four taxa phylogenies would be reconstructed differently had a fifth taxa been added. These percentages increased to 50% for five taxa trees and 62% for six taxa trees (Cueto and Matson, 2011). However, Cueto and Matson point out that their estimated rogue frequencies may have been greater given the use of random branch lengths (2011).

To provide a baseline biological comparison to this study, we used a quartet-tree framework and evaluated the frequency of a rogue taxa effect using viral data sets which differed in diversity. While not intended as a critique of previous studies, this work provides an in vivo benchmark for the frequency of the rogue taxa phenomenon. We also sought to find a relationship between the diversity of the data set and the frequency of the rogue taxa phenomenon. Such a relationship could help determine which types of data sets should be carefully analyzed for potential rogue effects.

In similar work to Cueto and Matson (2011), Eikmeyer et al. estimated how frequently the rapid neighbor joining (NJ) algorithm obtained the same solution as the more time consuming Balanced Minimum Evolution (BME) method whose solution NJ is designed to approximate (2008). Their study found that for five taxa trees NJ and BME reconstructed the same tree for 98% of four taxa data samples (Eikenmeyer et al., 2008). Our data set was also used to provide an in vivo benchmark for this result.

2. Materials and Methods

We measured the frequency of a rogue taxa effect in three data sets of increasing genetic variability (within viral serotype, between viral serotype, and between viral family) to test whether the rogue taxa was correlated with the mean sequence diversity of the respective data sets and to measure how frequently the NJ and BME methods obtained the same phylogenetic solution. A rogue taxa effect described the case for which the addition of a supplementary taxon in phylogenetic reconstruction changes the predicted relationship among the existing taxa. We chose taxa from within individual serotypes (A, Asia-1, C, O, SAT1-3) of foot-and-mouth disease virus (FMDV), between FMDV serotypes, and between the families (Bornaviridae, Filoviridae, Paramyxovridae, and Rhabdoviridae) in the viral order Mononegavirales. Mean sequence diversity, calculated in Mega 5.0 (Tamura et al., 2011), ranged from 0.065 ± 0.002 (serotype C; Table 1) to 0.191± 0.003 for between FMDV serotypes to 0.597 ± 0.002 for the order Mononegavirales. In addition to measuring the frequency of the rogue taxa effect, we also classified the effects by whether adding the supplementary taxon caused a correct topology to become in error (evil rogue), recovered the predicted topology from one in error (friendly rogue), or caused a different incorrect topology from one already in error (crazy rogue). A χ² test of independence was used to test whether the distribution of the types of rogues depended on nucleotide diversity. R² was calculated to determine whether the frequency of rogues increased with nucleotide diversity.

Table 1.

Summary of nucleotide diversity and rogue taxa effect for within FMDV serotypes

Serotype (Effective sample size*)	Nucleotide Diversity	Number of rogues (%)
A (88)	0.144 ± 0.003	5 (5.7%)
Asia 1 (97)	0.124 ± 0.003	9 (9.3%)
C (100)	0.065 ± 0.002	0 (0)
O (100)	0.110 ± 0.002	0 (0)
SAT (100)	0.135 ± 0.002	1 (1.0%)
Average	0.117 ± 0.003	12 (2.4%)

^*Two Asia 1 sequences were later identified as clones and any group of five containing those was eliminated. Additional subsets of the A sequences were also identified as identical. Groups of five were eliminated if any of these identical sequences were members of the group.

FMDV is a single-stranded, positive sense RNA virus and a member of the viral family Picornaviridae. There are seven recognized serotypes of FMDV (A, Asia 1, C, O, and SAT1-3). Four phylogenetic studies using complete genomic sequences of FMDV sequences have been published (Carillo et al., 2005, Cooke and Westover, 2008, Lewis-Rogers et al., 2008, and Yoon et al., 2011). The most recent, (Yoon et al., 2011) using a Bayesian coalescent approach to estimate the robustness of the topology, showed O - Asia 1 and A -C as pairs of sister-group relationships, with SAT1-3 depicted as a single clade. This topology was used as the predicted ‘correct’ FMDV phylogeny in the current experiment. Non-identical sequences from 183 complete FMDV genomes were included in this analysis (details in Supplementary Data 1).

Members of the Mononegavirales are enveloped viruses with a genome consisting of a non-segmented negative-sense RNA molecule varying from approximately 9-12 kb in size. Many members of the order such as Measles virus (MeV), Rinderpest virus (RPV), Borna disease virus (BDV), Ebola virus (EV), and Rabies (RV) are well known human and animal pathogens. Members of the order belong to four recognized families: Bornaviradae, Filoviridae, Paramyxoviridae, and Rhabdoviridae. Five proteins common to all families: glycoprotein (G), the matrix protein (M), the nucleoprotein or nucleocapsid protein (N), the phosphoprotein (P), and the RNA polymerase protein (L) common to all families were collected from complete Mononegavirales genomes for consideration in the study (details in Supplementary Data 2). The G-protein gene codes for a structural and non-structural component. We included only the structural component, which is responsible for receptor binding and membrane fusion with host cells (Takada et al., 1997).

All nucleotide sequences used in this study were collected, translated, and aligned the CLUSTAL W program (Thompson et al., 1994) implemented in MEGA 5.0 (Tamura et al., 2011). A recent phylogenetic treatment conducted using polymerase (L) and nucleocapsid (N) proteins showing significant support for sister-group relationships between Paramyxoviridae-Rhabdoviridae and Filoviridae-Bornaviridae clades (Mihindukulasuriya et al., 2009) was used to predict ‘correct’ topologies for the current experiment.

A random number generator (Mathematica 8.0; Wolfram Research, 2010) was used to construct data sets for each sample. For each of the five within FMDV serotype data sets, 100 random subsets of order five were chosen from the entire sample. A base tree was constructed using the first four elements of the subset. A second tree, including the fifth element, was constructed to test for the rogue effect. For the between FMDV serotype data set, 400 random subsets of order five were chosen so that each serotype was represented exactly once in every subset. A base tree was constructed using the first four taxa, and the remaining fifth taxon was added in a second tree to test for the rogue effect. For the between Mononegavirales family data set, 400 random subsets were chosen such that one taxa from each family was used to construct the four taxa base three, while the fifth taxa was drawn at random from the entire sample to construct the second five taxa tree to test for the rogue effect.

Phylogenies were constructed using the balanced minimum evolution (BME) method (Rzhetsky and Nei, 1987) and the neighbor-joining (NJ) method (Saitou and Nei, 1987) using uncorrected p distances, implemented in MEGA 5.0 program (Tamura et al., 2011). Four taxa BME and NJ phylogenies were computed and we evaluated whether the BME and NJ phylogenies exhibited the same labeled unrooted tree topologies. Then the fifth taxon was added and both phylogenies were computed again. We scored whether the BME and NJ trees were similar, whether there was a rogue effect, and if so whether the effect was friendly, evil, or crazy as described above.

3. Results

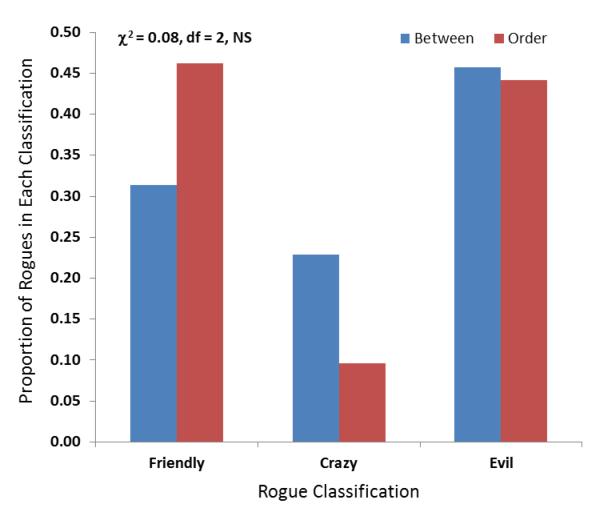
Phylogenies constructed NJ and BME yielded identically labeled unrooted-tree topologies in all reconstructions. There was an increase in the percentage of rogues as nucleotide diversity increased; from 2.4% within the serotype-level data set to 13.2% within the order-level data set. However, this result was not statistically significant (R²=0.89). Even though the number of rogues increased with diversity, the distribution of the types of rogues (friendly, crazy, or evil) did not depend on the diversity (χ² = 0.08, df=2, NS; Fig. 1) and in the case of the order-level data set the net rogue effect was slightly positive (Table 2). Accuracy of quartet and quintet reconstructions was similar within each of the two data sets tested, and greater accuracy was obtained for the order-level data set compared to the between serotype data set (Table 2).

Figure 1.

Distribution of rogue types (χ²= 0.08, df =2, NS) in the between FMDV serotype (blue) and within Mononegavirales order (red).

Table 2.

Summary statistics for the between FMDV serotype and within Mononegavirales order analyses

	Between Serotype	Within Order
Effective data points*	392*	394**
Number of rogues	35	52
Percentage of rogues	8.9	13.2
Initial correct quartets	277	317
Initial quartet accuracy	0.706	0.805
Correct quartets based on quintet trees	272	318
Accuracy of quartets based on quintets	0.694	0.807
Net rogue effect	−0.018	0.003
Quintet-Quartet Accuracy	0.731	0.860

^*One A sequence was later identified as clones and any group of five containing those was eliminated.

^**Three Bornaviridae sequence was later identified as clones and any group containing those was eliminated. Three sets of Paramyxoviridae clones were eliminated when they were found in groups as well.

4. Discussion

In the BME method, distance measures that correct for multiple hits at the same sites are used, and a topology showing the smallest value of the sum of all branches (S) is chosen as an estimate of the correct tree. However, the construction of a minimum evolution tree is time-consuming because, in principle, the S values for all topologies must be evaluated. The number of possible topologies (unrooted trees) rapidly increases with the number of taxa so it becomes very difficult to examine all topologies. In this case, one may use the NJ method. The NJ method computes the shortest pair-wise distances between two taxa and joins them until the entire tree is constructed. It has been shown in (Eickmeyer et al., 2008) that for 5-trees the NJ algorithm will construct the BME tree 98.06% of the time under the assumption that all distance matrices are equally likely. In our reconstructions, NJ and BME methods yielded identical trees in all cases. This suggests that NJ may do a better job of solving the BME problem for in vivo datasets then the combinatorial model of Eickmeyer et al. (2008) theoretically predicts.

The rogue taxa phenomenon is thought to be especially problematic for super-phylogenies and rogues are often removed from data sets in order to resolve relationships. Yet, there have been few explicit measurements of the effects. Cueto and Matson’s experiments demonstrated the rogue taxa effect was common when the added taxa were sampled and added arbitrarily (2011). In this study, using viral sequences, we found far fewer cases of a rogue taxa effect (≤ 13.2%). While this effect increased with sequence diversity, the numbers of different types of rogues did not differ with increasing diversity (Fig. 1). In fact, we found that it was just about as likely to be a ‘friendly’ effect as an ‘evil’ one. Therefore, although identification and removal of rogue taxa from large data sets may be one strategy for providing more robust tree scores, further investigation is necessary to make sure that the ones being removed are really responsible for negative interpretation of evolutionary relationships. Perhaps, helpful or ‘friendly’ sequences are among those removed. In addition, if we assume that a friendly rogue amends a previously wrong topology by correcting for long branch attraction, then additional taxon sampling becomes increasingly important particularly for genomic-scale data sets.

We believe that simulation studies should continue to play an important role in understanding phylogenetic phenomenon. They are important for analysis as the correct biological reconstruction can be difficult or impossible to reconstruct with 100% accuracy. However simulation studies are limited by definition to imposed mathematical assumptions which only partially reflect the complexity of life. We believe this small in vivo companion can help provide biologists with a benchmark for viewing simulation data.

Highlights.

• We evaluated the frequency of a rogue taxa effect using viral data sets which differed in diversity.

• Our results showed a slight increase in the percentage of rogues as nucleotide diversity increased.

• However, the distribution of the types of rogues (friendly, crazy, or evil) did not depend on the diversity.

• In the case of the order-level data set (greatest diversity) the net rogue effect was slightly positive.