Stochastic Cardiac Pacing Increases Ventricular Electrical Stability—A Computational Study

Abstract

The ventricular tissue is activated in a stochastic rather than in a deterministic rhythm due to the inherent heart rate variability (HRV). Low HRV is a known predictor for arrhythmia events and traditionally is attributed to autonomic nervous system tone damage. Yet, there is no model that directly assesses the antiarrhythmic effect of pacing stochasticity per se. One-dimensional (1D) and two-dimensional (2D) human ventricular tissues were modeled, and both deterministic and stochastic pacing protocols were applied. Action potential duration restitution (APDR) and conduction velocity restitution (CVR) curves were generated and analyzed, and the propensity and characteristics of action potential duration (APD) alternans were investigated. In the 1D model, pacing stochasticity was found to sustain a moderating effect on the APDR curve by reducing its slope, rendering the tissue less arrhythmogenic. Moreover, stochasticity was found to be a significant antagonist to the development of concordant APD alternans. These effects were generally amplified with increased variability in the pacing cycle intervals. In addition, in the 2D tissue configuration, stochastic pacing exerted a protective antiarrhythmic effect by reducing the spatial APD heterogeneity and converting discordant APD alternans to concordant ones. These results suggest that high cardiac pacing stochasticity is likely to reduce the risk of cardiac arrhythmias in patients.

Introduction

The physiological activation rate of the cardiac ventricular tissue varies stochastically even under constant environmental conditions. These variations are a consequence of the heart rate variability (HRV), which relates to the physiologically normal rate variations in the sinoatrial node impulse formation. A low HRV standard deviation (SD) was found to be a predictor for pathological cardiac conditions, such as lethal arrhythmic events in postmyocardial infarction patients (1–6). More recently, it was reported that a reduction in heart-rate complexity characterizes patients with heart failure who are prone to develop malignant ventricular arrhythmia (7,8). Traditionally, the ability of HRV to predict arrhythmia events has been attributed to the fact that during arrhythmias the balance between sympathetic and parasympathetic tones is impaired, and a low HRV merely reflects this autonomic tone damage (1–5,9). This explanation is supported by the fact that HRV is a product of both sympathetic and parasympathetic inputs to the heart (6,9,10). However, in the ventricles, autonomic nervous system innervation is less dominant than in the atria, and tissue remodeling due to impaired sympathetic and parasympathetic tones does not seem to provide a full mechanism for increased arrhythmogeneity. Currently, there is no concrete model that directly relates activation rate stochasticity per se to abnormal electrical conduction properties in the cardiac ventricular tissue and to arrhythmogenic dynamic properties.

It is well known that the potentially fatal transition from cardiac tachycardia to cardiac arrhythmias and fibrillation is attributed to wavebreaks and the formation of reentrant waves (11). In many scenarios, wavebreaks are correlated with the appearance of preceding action potential duration (APD) alternans at high activation rates, which render the cardiac substrate functionally heterogeneous (12–14). There are two types of APD alternans: spatially concordant and spatially discordant. In spatially concordant alternans, the APD sequentially alternates between long and short in a similar pattern throughout the tissue, so that for a specific activation wave the APD is either short or long in all locations. Spatially discordant alternans indicate a condition in which spatial synchronization does not exist, so in some tissue regions the APD alternates between long and short, whereas in other regions the alterations are inverted between short and long for the same activation wave. Although both types of alternans indicate tissue instability, spatially discordant alternans are considered more arrhythmogenic (15) due to the increased heterogeneity of the spatial APD distribution. When a premature or ectopic beat is initiated in the presence of a sufficiently large spatial APD heterogeneity, a wavebreak can be elicited, resulting in a reentry that may lead to fibrillatory activity (15). A common method to assess the likelihood of the appearance of APD alternans and wavebreaks is to construct APD restitution (APDR) curves, which plot the dependency of the APD on its preceding diastolic interval (DI) (16–18). In particular, an APDR slope >1 is considered to be a risk factor for alternans and wavebreaks (16). In the presence of small DI perturbations, the APD value changes according to the APDR curve. If the APDR slope is <1 this difference will eventually decay with iterations, but if the slope is >1 this difference will produce large changes of the APD that will be amplified in the next iteration, a process that may end in a conduction block and wavebreak (19). One way to establish the APDR curve is to employ a dynamic pacing protocol, which was previously found to be more reliable than the standard S1-S2 pacing protocol for predicting arrhythmia risk factors (20,21). In addition to the APDR, conduction velocity restitution (CVR) curves, which plot the dependency of a pulse’s conduction velocity on its preceding DI, are commonly established to assess arrhythmogeneity. Steeper CVR slopes usually indicate on increased propensity to develop wavebreaks.

Stochastic pacing was employed in previous studies mainly as a new method to investigate cardiac memory; however, its effect on stability was not explored (22,23). To the best of our knowledge, thus far only deterministic changes of the cardiac activation rate have been investigated in the context of tissue stability and arrhythmogeneity. Banville et al. (24) showed in isolated pig hearts that an abrupt shortening of the cycle length acted to damp down alternans by accordingly changing the APDR curve, and hence had an antiarrhythmic effect explained by short-term memory. Weinberg and Tung (25) applied repetitive cycle length oscillations (CLOs) and studied the occurrences and pattern of alternans. They concluded that, depending on the specific conditions, CLO pacing can either initiate ventricular fibrillation (VF) due to the induction of spatially discordant alternans or have an antiarrhythmic effect. However, they did not apply pacing stochasticity in their study, and did not discuss possible mechanisms. In a preliminary study from our laboratory, we demonstrated that the addition of stochasticity to the pacing sequence in a one-dimensional (1D) atrial cable model decreased the APD for a similar preceding DI, effectively lowering the APDR curve (26), in agreement with the work of Chernyak et al. (27). A theoretical explanation derived from control and switched systems theory was proposed (26).

In this work, we studied the influence of pacing stochasticity on cardiac tissue arrhythmogeneity in 1D and two-dimensional (2D) ventricular models. We show that increased stochastic variations in the pacing sequence are antiarrhythmic in terms of reduced APDR slope and the elimination of discordant APD alternans. These effects render the tissue more electrophysiologically uniform, thereby preventing wavebreak and potential arrhythmogenesis. These results may offer a novel strategy for arrhythmia management, for example, by adding stochasticity to pacing schemes in patients carrying implanted pacemakers.

Materials and Methods

Geometrical and biophysical model

We simulated ventricular electrical propagation using two geometrical configurations: a 10-mm-long cable and a 10 ×10 mm 2D tissue. Transmembrane voltages were calculated by solving the following reaction-diffusion partial differential equation for myocytes, assuming the monodomain formalism and tissue isotropy:

$$\frac{\partial \text{V}}{\partial \text{t}}=-\frac{\left({\text{I}}_{\text{ion}}+{\text{I}}_{\text{stim}}\right)}{C_m}+\nabla \cdot \left(\text{D}\text{∇}\text{V}\right),$$ (1)

where V [mV] is the transmembrane voltage; C_m = 2 μF/cm² is the membrane capacitance per unit area; I_stim and I_ion [μA/cm²] are the external stimulation and membrane ionic currents, respectively; and D [mm²/ms] is the diffusion coefficient originating from the electrotonic coupling among myocytes. We set D = 0.04 mm²/ms so that a mean planar wave conduction velocity of 0.4 m/s was achieved. The ten Tusscher and Panfilov (17) kinetic model for human ventricular myocytes was employed for the calculation of I_ion. A spatial resolution of Δx = 0.1 mm was employed, resulting in 100 computational cells along the cable and 100 × 100 cells in the 2D tissue. Equation 1 was numerically solved using Euler integration with a temporal resolution of Δt = 7.5 μs, and a standard three-point central finite-difference approximation for the diffusion term. Resting membrane conditions were set as initial conditions for all simulations. Kinetic model parameters were set to fit APD restitution with a maximum slope of 1.8 along with standard sodium current dynamics, by using the following values as in ten Tusscher and Panfilov (17): G_Kr = 0.172 nS/pF, G_Ks = 0.441 nS/pF, G_pCa = 0.8666 nS/pF, G_pK = 0.00219 nS/pF, τ_f,inact = × 2, and τ_j fast, where G_kr, G_Ks, G_pCa, and G_pK are the maximal I_Kr, I_Ks, I_pCa, and I_pK conductances, respectively, τ_f,inact is the calcium f-gate time constant for positive voltages, and τ_j fast (standard) is the j-gate time constant.

Stochastic pacing

In this work, we focused on the significance of stochasticity in cardiac pacing. We therefore performed a comparison between deterministic and stochastic pacings. Stochastic pacing sequences were constructed by setting the cycle length (CL) between two stimulation pulses as

$$\text{CL}=\text{BCL}+\text{G}\left(0\text{,}\text{σ}\right),$$ (2)

where BCL (ms) is the mean (deterministic) basic cycle length, and G(0, σ) is a Gaussian distribution with zero mean and an SD of σ (ms), so that increased pacing stochastic variability could be modeled by increasing σ. Deterministic pacing (i.e., without pacing stochastic variability) was simply modeled by setting σ = 0 in Eq. 2.

Construction of APDR and CVR curves

We constructed restitution curves by using the cable model and applying the following dynamic restitution pacing protocol: A series of 50 stimuli were initially applied with a BCL of 800 ms, after which sequential sets of 50 stimuli were applied with gradually decreasing BCL between sets. The gradual decrease was done in steps of 50 ms for BCL > 400 ms, in steps of 10 ms for 400 ≥ BCL > 330 ms, and in steps of 2 ms for BCL ≤ 330 ms (16,17,28). APDR curves were generated by plotting the APD of the last pulse in each set with a certain BCL against its preceding DI. For this purpose, APDs were measured at 90% repolarization (APD90), and the rest of the cycle length was defined as the DI. Measurements were taken from the 80th cell along the cable to avoid boundary artifacts (29). CVR curves were obtained by plotting the conduction velocity of the last pulse in each set with a certain BCL against the same DI values used for constructing the APDR curves (29). Conduction velocities were measured from the difference in activation times (taken at $max\left(\partial \text{V/}\partial \text{t}\right)$) between the 80th and 20th cells. Pacing stochasticity was modeled as described above. Thirty random pacing sequences were generated using Eq. 2 for each value of σ to account for statistical variability, and the restitution curves were established from the pooled measurements. APDR and CVR slopes were estimated by employing linear regression within a relatively narrow range of BCLs so that the curves could be approximated as linear.

Simulating discordant APD alternans

One way to induce spatially discordant APD alternans in a simulation environment is to apply spatial ionic heterogeneity (15). In the 2D simulations, we employed heterogeneity in the potassium-channels conductance in a manner similar to the model of Qu et al. (13):

$$G_K\left(\text{x},\text{y}\right)={\overline{\text{G}}}_K\cdot \left(\alpha +\beta \sqrt{\frac{\left({\left(x-L_x\right)}^2+{\left(y-L_y\right)}^2\right)}{\left(L_x^2+L_y^2\right)}}\right)$$ (3)

where (x,y) are the planar coordinates, (L_x,L_y) are the tissue dimensions, ${\overline{\text{G}}}_{\text{K}}$ is the maximal potassium-channels conductance (of either the rapid or slow K+ channel), α = 1.2, and β = 0.8. This specific heterogeneity pattern yields an ionic heterogeneity similar to that seen in guinea pig ventricles (30). Pacing stimulations were applied at (x,y) = (0,0). Since discordant alternans appear only at high pacing rates, the tissue was first paced at a BCL = 300 ms for 40 beats to allow for accommodation, and then the pacing rate was increased to a BCL = 245 ms for an additional 65 beats. Without added stochasticity, this pacing protocol resulted in the appearance of discordant APD alternans during the high-rate pacing phase with BCL = 245 ms.

Quantifying APD spatial heterogeneity

The effect of stochastic pacing on the spatial APD heterogeneity was measured as the maximal APD SD for all beats during the high-rate pacing, Σ (13):

$$\text{Σ}={\max }_{1\le \text{beat}\le 65}\left\{\sqrt{\frac{1}{N}\sum _{i=1}^N{\left(AP{D}_i-\overline{APD}\right)}^2}\right\}$$ (4)

where N = 10,000 is the total cell number in the tissue, APD_i is the APD of the ith cell, and $\overline{APD}$ is the average APD of the cells within the tissue. Greater values of Σ indicate a higher degree of APD spatial heterogeneity, which is known to correlate with a higher risk of arrhythmias (13,15). In contrast, lower Σ values indicate a reduced vulnerability to arrhythmia.

Statistical analysis

Differences in APDR and CVR slopes between deterministic and random pacing were evaluated by analysis of covariance (ANCOVA). One-sample Student’s t-tests were used to compare 2D APD heterogeneity between stochastic and deterministic pacings. Statistical significance was defined as p < 0.05.

Results

Effect of stochastic pacing on the APDR curve

We investigated the ventricular restitution properties by using the cable model and applying both deterministic and random pacing protocols. The deterministic APDR curve is shown in Fig. 1 a, demonstrating a typical APD restitution curve. The APDR slope (Fig. 1 a, inset) was equal to one at DI ∼ 100 ms, which corresponded to a BCL ∼ 330 ms. For stochastic pacing, the SD σ in Eq. 2 was set between 1 and 6 ms in steps of 1 ms, yielding a physiological range of cycle length variability for a target BCL of ∼330 ms (31). For each value of σ, N = 30 random pacing sequences were generated, and the corresponding APDR was established from the pooled results. The slope of the stochastic APDR at DI ∼ 100 ms was then estimated by performing a linear regression analysis for all data points residing within a narrow DI range from 80 to 110 ms, for which the APDR curve was approximately linear. As an example, Fig. 1 b shows the results obtained for σ = 0 (deterministic) and σ = 5 ms. The deterministic APDR curve had a slope of ∼1.2, whereas the curve corresponding to random pacing exhibited a statistically significant lower slope of ∼0.94 (R² > 0.98). The results obtained for all values of σ are summarized in Fig. 1 c, demonstrating a monotonic exponential decrease in the APDR slope as a function of σ. For all cases of random pacing, the obtained APDR slopes were significantly lower than when deterministic pacing was applied (p < 0.05), and for random pacing with σ ≥ 2, the slopes were <1. The results suggest that by adding randomness to the pacing sequence, the slope of the APDR curve is reduced, effectively moderating (or flattening) the APDR curve. This effect potentially can contribute to the heart’s immunity against arrhythmogenic factors, e.g., wavebreaks and the appearance of alternans that commonly occur with steep restitution properties. Both will be demonstrated in the following sections.

Figure 1.

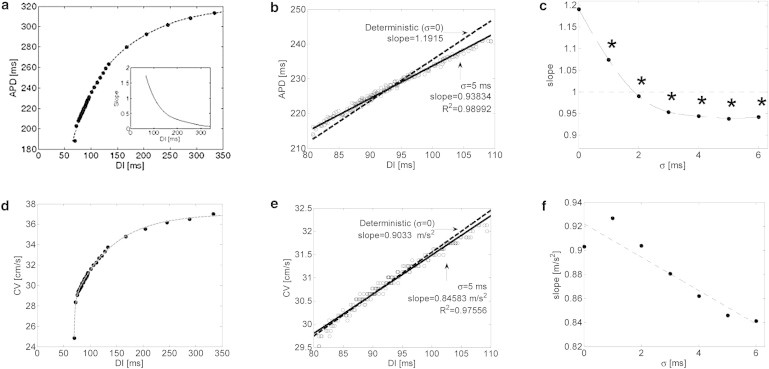
(a–f) Dynamic APD (a–c) and CV (d–f) restitution curves. (a) Deterministic APDR curve. Inset: APDR slope as a function of DI. (b) Linear regression for the APDR curves using data points included within a narrow mean BCL range. Deterministic and stochastic pacings with σ = 5 ms are marked by dashed and solid lines, respectively. Stochastic data points were pooled from N = 30 random pacing sequences. (c) APDR slope as a function of stochastic pacing SD σ. σ = 0 marks deterministic pacing. ^∗p < 0.05 compared with the deterministic case using ANCOVA. (d) Deterministic CV restitution curve. (e) Linear regression for the CV restitution curves using data points included within the same narrow range as in panel b. Deterministic and stochastic pacings with σ = 5 ms are marked by dashed and solid lines, respectively. Stochastic data points were pooled from N = 30 random pacing sequences. (f) CV restitution slope as a function of stochastic pacing SD σ.

Effect of stochastic pacing on the CVR curve

Fig. 1 d shows the deterministic CVR curve obtained using the same pacing protocol employed for the APDR curve. Fig. 1 e shows narrow segments of both deterministic (σ = 0) and stochastic (σ = 5 ms) CVR curves for the same DI range as in Fig. 1 b. In this case, the added pacing stochasticity resulted in a small reduction of the CVR slope from 0.90 to 0.85 m/s². In general, increased stochasticity standard variation tended to monotonically reduce the CVR slope (Fig. 1 f); however, this effect was minor and was not found to be statistically significant for any value of σ (p > 0.2).

Manifestation of APD alternans in the cable model

In addition to large APDR slopes, the appearance of APD alternans at high pacing rhythms is a known arrhythmogenic factor. With deterministic pacing, significant and persistent APD alternans appeared at a pacing BCL < 295.5 ms. Consequently, we employed a modified dynamic pacing protocol in which pacing up to a BCL = 330 ms was performed as described in the previous section, followed by the target BCL of 295 ms. A typical example of alternans appearance is shown in Fig. 2 a. The APD is plotted as a function of the beat number for both deterministic pacing (in black) and for one sequence of random pacing with the same mean BCL and σ = 1.5 ms (in red). The significant suppression of large APD alternans with stochastic pacing in this case is clearly demonstrated. Short segments of electrical activity are shown in Fig. 2 b, demonstrating the existence of APD alternans during the deterministic pacing (top) and their suppression during the corresponding time frame of stochastic pacing (bottom). For σ = 1.5 ms, such a significant suppression of APD alternans amplitude (defined as a decrease of >50% in alternans magnitude in comparison with the deterministic case) occurred in ∼25% of stochastic pacing sequences (8 cases out of N = 30), suggesting increased immunity against arrhythmogenic events. In the rest of the cases, however, the SD of the APD amplitude was similar to that observed with deterministic pacing (as shown in the example in Fig. 2 c). The percentages of sequences in which pacing stochasticity significantly suppressed the magnitude of the APD alternans are summarized in Fig. 3 for σ = 0–1.8 ms. From Fig. 3 it is apparent that with increasing σ, the likelihood that stochasticity would suppress APD alternans increased. This monotonous pattern was consistent up to σ = 2 ms, above which 2:1 conduction blocks started to occur. It should be noted that the physiological activation rate variability range for a similar mean BCL, as in this case, agrees with σ ∼ 1–2 ms (32), suggesting that the antiarrhythmic effect of stochasticity in suppressing APD alternans is within the physiological range.

Figure 2.

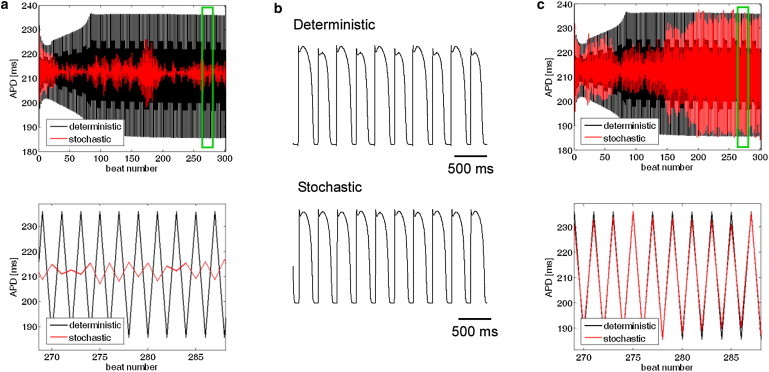
Effect of stochastic pacing on concordant alternans. (a) APD as a function of beat number for a mean BCL = 295 ms. Black and red graphs correspond to deterministic and stochastic (with σ = 1.5 ms) pacings, respectively. The bottom panel shows a short segment corresponding to the time interval marked by the green box. (b) Membrane voltage during deterministic (top) and stochastic (bottom) pacings for the last 10 beats from panel a. Significant alternans appeared during deterministic pacing and were significantly diminished with pacing stochasticity. (c) One case in which APD alternans during stochastic pacing exhibited amplitude similar to that observed during deterministic pacing. Panel organization as in panel a.

Figure 3.

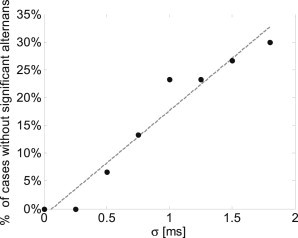
Percentage of simulations in which stochastic pacing significantly diminished the appearance of concordant alternans as a function of pacing variability σ (N = 30); mean BCL = 295 ms.

Manifestation of spatially discordant APD alternans

Although the appearance of concordant alternans as demonstrated in the previous 1D cable model marks the initiation of conduction irregularity and potential deterioration into arrhythmia, a stronger predictor for wavebreaks and arrhythmogenic conduction is the appearance of spatially discordant alternans. Discordant alternans appeared in the 2D simulations using the deterministic pacing protocol with a target BCL = 245 ms as described in Materials and Methods. Fig. 4 a depicts the APD as a function of the beat number during the 65 beats deterministic pacing phase with a BCL of 245 ms. The gray and black graphs correspond to the two locations at (0,0) and (10,10) mm, respectively. A transition from concordant to discordant APD alternans phase was observed at beat 33. The transmembrane voltage recordings at the same locations are presented in Fig. 4 b and clearly show the discordant alternans pattern during this final pacing phase. When stochastic pacing was applied to the same tissue model and with the same pacing protocol, the propensity for discordant alternans was significantly diminished. A representative example is given in Fig. 4, c and d, in which the results of one typical sequence of stochastic pacing with σ = 3.5 ms are given. In comparison with Fig. 4, a and b, the results in Fig. 4, c and d, demonstrate that pacing stochasticity resulted in a generally reduced magnitude of concordant alternans and, more importantly, succeeded in completely avoiding the transition from concordant to discordant alternans. This is further illustrated in Fig. 5, where the spatial profiles of the APD relating to two sequential beats (45 (gray) and 46 (black)) along the main diagonal of the tissue (from (0,0) to (10,10) mm) are shown. For deterministic pacing (solid lines), the two profiles intersect at ∼7 mm along the diagonal, indicating a spatial inversion from a long-short-long to a short-long-short alternans pattern, i.e., the existence of discordant alternans. On the other hand, the two profiles corresponding to the stochastic pacing (dotted lines) are parallel along the diagonal, indicating the sole existence of concordant alternans. The spatial APD distributions for beats 45 and 46 are shown in Fig. 6. Deterministic pacing (Fig. 6, a and b) yielded a highly heterogenic APD distribution. Whereas for beat 45 the gradient was generally oriented from (0,0) to (10,10) mm, for beat 46 it was oriented oppositely from (10,10) mm to (0,0), again indicating the occurrence of discordant alternans. The nodal line, indicating all locations where the pattern of alternans is inverted from long-short-long to short-long-short (i.e., where the APD values for beats 45 and 46 match) is marked in white. In contrast, stochastic pacing yielded a significantly more uniform APD distribution, as shown in Fig. 6, c and d, and concordant alternans pattern with similar gradient orientation for the two beats. We finally quantified the degree of APD heterogeneity for deterministic pacing and for stochastic pacing with added standard variation σ between 0.5 and 3.5 ms (N = 30 for each value of σ). Examination of the spatial APD histograms for each beat consistently showed Gaussian distributions (a typical example is shown in Fig. 7 a), validating our choice of the APD spatial SD, Σ (defined in Eq. 4), as a single measure of heterogeneity. The results for the APD spatial SD, Σ, are summarized in Fig. 7 b in the form of a box plot, where the median, 25th, and 75th percentile (box) and the total range (dotted bar) are shown. Increasing stochasticity degree σ resulted in a statistically significant decrease in the median Σ, as well as in a decrease in the 25 and 75 percentile values. On the other hand, the maximal Σ value changed only slightly. These effects suggest an improved uniformity in the spatial APD distribution as stochasticity increases, which in turn predicts improved immunity against arrhythmogenesis.

Figure 4.

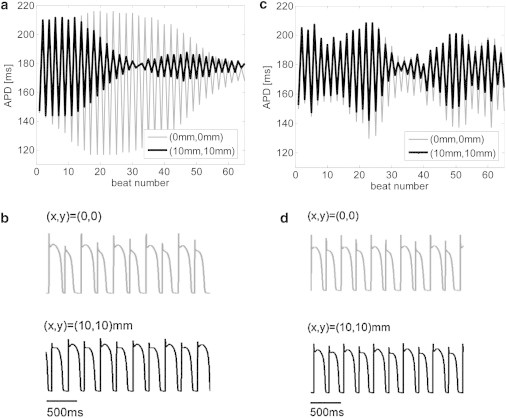
(a–d) Discordant APD alternans in 2D simulations during deterministic (a and b) and stochastic (c and d) pacings. (a) APD as a function of the beat number during the deterministic pacing phase with the target BCL = 245 ms. Traces at two locations, (x,y) = (0,0) and (10,10) mm, are shown in gray and black, respectively. A transition from concordant to discordant alternans can be seen at beat 33. (b) Short segments of membrane voltage during deterministic pacing after beat 33 clearly illustrate the appearance of discordant alternans. (c and d) A typical case in which stochastic pacing (with σ = 3.5 ms) diminished the transition from concordant to discordant alternans in 2D simulations. Panels are organized as in a and b.

Figure 5.

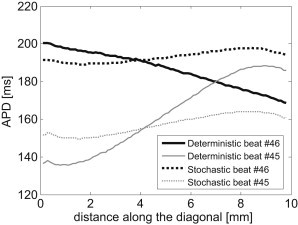
APD as a function of the distance along the diagonal x = y for beats 45 (gray) and 46 (black) of the simulations presented in Fig. 4. The two traces cross in deterministic pacing (solid lines), further illustrating the existence of discordant alternans. In contrast, the traces corresponding to stochastic pacing (dotted lines) are parallel, and concordant alternans do not transform into discordant ones.

Figure 6.

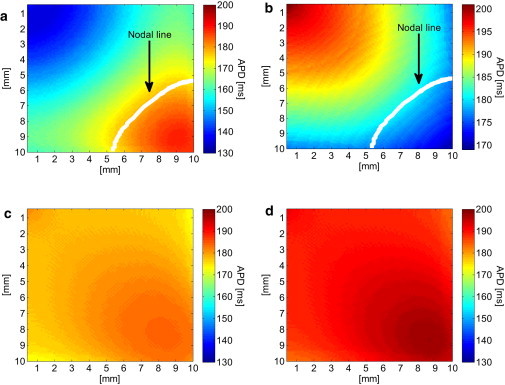
Spatial APD distribution during deterministic (a and b) and stochastic (c and d) pacings, for the two successive beats 45 (a and c) and 46 (b and d). In the deterministic case, the nodal line was found and is marked in white. In the stochastic case, the nodal line was not found.

Figure 7.

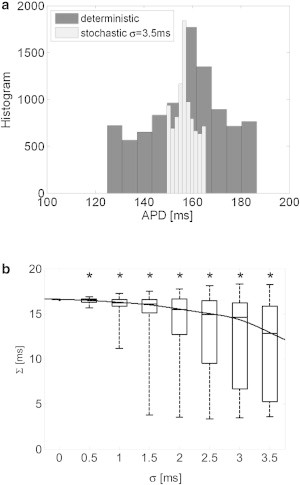
APD heterogeneity. (a) Typical examples of spatial APD histograms for deterministic and stochastic pacings (σ = 3.5 ms), each for the beat with the highest SD (out of 65 beats). Both histograms exhibit Gaussian-like distribution. The mean correlation coefficient of the best Gaussian fits for all values of σ was R² = 0.88 ± 0.02. (b) Quantification of the APD spatial heterogeneity, ∑, as defined in Eq. 4 as a function of the stochastic pacing SD σ (N = 30). Target pacing BCL is 245 ms. The graph marks the median, 25th, and 75th percentiles (box) and the total range (dashed bar) of the ∑ values. The line corresponding to the best-fit curve for the median values is also shown. ^∗p < 0.05 compared with the deterministic case.

Manifestation of wavebreaks

The appearance of spatially discordant alternans and high levels of APD spatial heterogeneity are considered proarrhythmic due to their ability to induce a wavebreak in the presence of premature stimulation (15). In the previous section, the positive effect of stochastic pacing on both the propensity for discordant alternans and the APD spatial heterogeneity was demonstrated. Here we show how this positive effect translates into a diminished likelihood of wavebreak initiation. The 2D tissue was paced using a protocol similar to that described in the previous section, with the exception that during the last pacing phase (with BCL = 245 ms), a premature stimulation was given with a fixed coupling interval of 165 ms after beat 39. During deterministic pacing, this protocol resulted in a wavebreak of the premature beat and initiation of a figure-of-eight reentry, as shown in the transmembrane voltage map in Fig. 8 a. When stochastic pacing was applied with σ = 3.5 ms, the same pacing protocol resulted in a wavebreak of the premature beat and figure-of-eight reentry in only eight (∼27%) of the cases (N = 30). In the rest of the 22 cases, the premature beat either managed to pass without breaking (n = 4 cases, an example is shown in Fig. 8 b) or was completely blocked without the initiation of an activation wave at all (n = 18 cases, an example is shown in Fig. 8, c and d).

Figure 8.

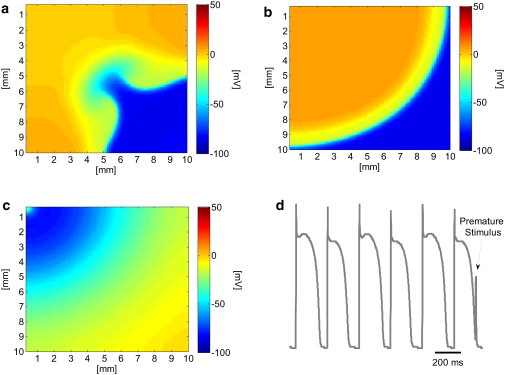
Transmembrane voltage distribution after a premature stimulation. (a) Deterministic pacing: the premature beat wave breaks and a figure-eight reentry pattern is initiated. (b) Stochastic pacing (σ = 3.5 ms): an example in which the premature beat is conducted without a wavebreak. (c) Stochastic pacing (σ = 3.5 ms): an example in which the premature beat is fully blocked. (d) Transmembrane voltage recording at the stimulation site (x,y) = (0,0) demonstrating the block of the premature beat at the origin.

Fig. 9 summarizes the effect of stochastic pacing on the conduction pattern of the premature beat as a function of stochastic pacing SD, σ. For each value of σ, N = 30 random pacing sequences were applied. As σ increased, the premature beat was less likely to undergo a wavebreak. This result is in line with Fig. 7 b, as the reduced APD spatial heterogeneity suggests a reduced likelihood for wavebreaks. In addition, when σ increased, the premature beat was more likely to be fully blocked. This is also a positive outcome since premature beats (e.g., arising from ectopic activity) are arrhythmogenic at very high activation rates.

Figure 9.

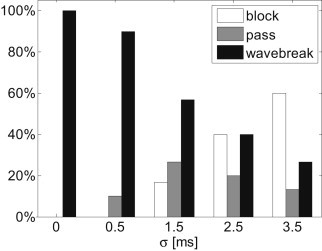
Premature beat conduction patterns for deterministic (σ = 0) and stochastic pacings (N = 30). As σ increases, the propensity for wavebreaks decreases.

Discussion

Low variability in cardiac activation rate was clinically found to be a major predictor for cardiac arrhythmogenic events. In this work, we aimed to characterize the effects of stochastic cardiac pacing on the ventricular tissue arrhythmogenic predictors of restitution slopes and APD alternans. Our major findings are as follows: 1), Pacing stochasticity sustains a significant moderating effect on the dynamic APDR curve by reducing its slope. This effect is stronger with larger pacing variability (σ in Eq. 2). Similarly, pacing stochasticity tends to moderate the CVR curve by reducing its slope, although this effect was minor and was not found to be statistically significant. 2), Random pacing suppresses the occurrence of concordant APD alternans. The higher the σ, the stronger is the suppression that is achieved. 3), Stochastic pacing reduces APD spatial heterogeneity and tends to reduce the propensity for spatially discordant alternans. 4), Stochastic pacing reduces the propensity for wavebreak initiation. The higher the variance of the stochastic pacing, the lower is the likelihood that wavebreak will occur.

Our results are in line with clinical evidence regarding the importance of HRV for protection against arrhythmogenesis. We have shown in both 1D cable and 2D tissue configurations that when stochasticity per se is added to the ventricular pacing protocol, tissue arrhythmogeneity indicators improve, suggesting that cardiac immunity against arrhythmias increases. This was shown on three stability markers: the slope of the APD restitution curve, the propensity for concordant and discordant APD alternans, and the spatial heterogeneity of the APD. Our results did not show a significant effect of pacing stochasticity on the slope of the CVR curve, although a small trend of reduced slope with increased stochasticity was observed. Nevertheless, in contrast to steep APDR slopes, steep CVR slopes are not considered a prerequisite for wavebreak initiation in all scenarios (13). Finally, we demonstrated the influence of stochastic pacing on wavebreak, showing its reduced likelihood to occur for high pacing stochasticity. The moderating effect of rate stochastic variations correlates well with the clinically established protective effect of HRV. Although this study is purely theoretical and is based on computational models and analysis, some experimental support for the proposed effect of stochastic pacing can be found in the literature. Wu and Patwardhan (22) introduced stochastic pacing as a new pacing protocol for establishing APDR curves. Their experiments, conducted on isolated right ventricular endocardial tissue from dogs, showed that a uniform stochastic pacing resulted in shallower APDR slope in comparison with both dynamic and S1-S2 pacing protocols. In addition, Toal et al. (33) assessed experimental APDR curves during the early stages of VF in humans, during which time the ventricular activation sequence is in principle stochastic. They found that during the early stages of VF, the slope of the APDR was very shallow (<1) for small DI values, where the slope is expected to be steep (>1).

Stochastic pacing is associated with modifications of short-term cardiac memory (22,23), and it is possible that stochastic pacing tends to reduce or eliminate short-term memory due to the lack of pacing-rhythm stability. Experiments conducted on isolated rabbit hearts have shown that reduced short-term cardiac memory sustains effects similar to those established in this work, i.e., elimination of concordant and discordant APD alternans (34). Other investigators have proposed random stimulation protocols to investigate short-term cardiac memory. Wu and Patwardhan (22) employed oscillatory, random, and linear pacing to establish APDR curves. They showed that the differences in the resulting curves were attributed to the memory effect (22). However, although they established the APDR for stochastic pacing, the authors did not investigate the antiarrhythmic role of random pacing as a stabilizer of electrical activity. Dai and Keener (23) presented a method that uses stochastic cycle pacing to investigate the relationship between APD bifurcation and restitution to cardiac memory. However, in that study too, pacing stochasticity was introduced solely as a new means of establishing APDR curves that reflect cardiac memory, and the effect of stochastic pacing on stability properties of the cardiac electrical activity was not studied. To the best of our knowledge, our study shows for the first time that increased stochasticity in ventricular pacing is directly linked to a decreasing APDR slope and a tendency to eliminate APD alternans (discordant and/or concordant). These results may imply that the stochasticity essence of HRV per se works to provide the heart with a protective mechanism against arrhythmogenesis, and a better recovery potential once tachypacing is initiated. A plausible alternative mechanism that might explain the protective role of pacing stochasticity relates to the established stabilizing effect of additive random noise on Markovian models, as known from switching and control systems theory (26).

Several limitations in our study should be noted. We modeled pacing stochasticity using a Gaussian distribution. However, ventricular activation variations that arise from HRV are more complex. In the frequency domain, the physiological HRV presents four main frequency ranges: ultralow (≤0.003 Hz), very low (0.003–0.04 Hz), low (0.04–0.015 Hz), and high (0.15–0.4 Hz) (6). This broad range of frequencies indicates a random characteristic and chaos that are often ascribed to HRV (35–37). In this study, we employed a basic, simple, random pacing model that allowed us to study the most basic role of pacing stochasticity in stabilizing the ventricular electrical activity. A more physiological HRV model should be employed in future works. Additionally, we employed the ionic kinetics model of normal human ventricular cardiac myocytes. Further research should be conducted to extend the simulations to cardiac models relating to the existence of heart failure. Finally, the presented model did not include tissue remodeling due to an impaired balance of the autonomic nerve system, which can be a source of pacing variability (38–41). Instead, we chose to uncouple pacing variability and possible membrane remodeling to gain insights into the specific role of heart-rate stochasticity in arrhythmia immunity.

In conclusion, our study provides novel (to our knowledge) insights regarding the mechanisms by which stochastic ventricular activation contributes to cardiac arrhythmia immunity via modulation of arrhythmogenic factors such as the APDR slope and APD alternans propensity. We correlate our results with clinical evidence indicating that low HRV is a risk predictor for arrhythmia. The results of this study may find clinical application in improving the design of artificial pacemakers. We suggest that by adding specific stochasticity to the programmed pacing sequence, the stability of cardiac electrical conduction can be improved to reduce the initiation of arrhythmia events originating from conduction blocks or wavebreaks.