Quantitative Analysis of Three-Dimensional Fluorescence Localization Microscopy Data

Abstract

Identifying the three-dimensional molecular organization of subcellular organelles in intact cells has been challenging to date. Here we present an analysis approach for three-dimensional localization microscopy that can not only identify subcellular objects below the diffraction limit but also quantify their shape and volume. This approach is particularly useful to map the topography of the plasma membrane and measure protein distribution within an undulating membrane.

Single molecule localization microscopy (SMLM) (1–3) is a superresolution fluorescence microscopy technique that produces coordinate data for single molecule localizations with a precision of tens of nanometers in live and fixed cells. These methods have mainly been performed with total internal reflectance fluorescence microscopy and therefore have generated two-dimensional molecular coordinates. Such two-dimensional data sets have revealed nanosized clusters of membrane proteins at the cell surface (4–7). This was achieved with analysis routines based on pair-correlation analysis (8), Ripley’s K function (9), and related techniques. While three-dimensional localization microscopy techniques such as biplane imaging (10), astigmatic spot analysis (11), and depth-encoding point-spread functions (12) have now been developed, quantitative analysis approaches of three-dimensional coordinate patterns have not.

Here, we describe an approach based on Getis and Franklin's local point pattern analysis to quantitatively analyze three-dimensional subcellular structures and map plasma membrane topography. The latter can also be used to account for topography-induced clustering of membrane proteins in an undulating membrane. To illustrate the approach, we generated three-dimensional SMLM data of the membrane dye DiI and the protein Linker for Activation of T cells (LAT) fused to the photoswitchable fluorescent protein mEos2 in T cells. It has been previously shown that LAT resides within the plasma membrane as well as membrane-proximal vesicles (5,13). The data were acquired using the biplane SMLM technique and highly inclined and laminated optical sheet illumination (14). Three-dimensional molecular coordinates were calculated by fitting a three-dimensional theoretical point-spread-function to the acquired data.

As previously described for two-dimensional SMLM data analysis (5), Ripley’s K-function is calculated according to Eq. 1 where V is the analyzed volume, n is the total number of points, and r is the radius of a sphere (a circle for the two-dimensional case) centered on each point. The value K(r) is thus a measure of how many points are encircled within a sphere of radius r:

$$\begin{array}{l}K\left(r\right)=V\sum _{i=1}^n\sum _{j=1}^n\left({\delta }_{ij}/n^2\right);\hfill \\ {\delta }_{ij}=1ifd\left(\text{point}i,\text{point}j\right)<r,0\text{else}.\hfill \end{array}$$ (1)

For completely spatially random (CSR) data, K(r) scales with the volume of the sphere. We therefore linearize the K-function such that it scales with radius (the L-function) using:

$$L\left(r\right)={\left(\frac{3K\left(r\right)}{4\pi }\right)}^{1/3}.$$ (2)

The value of L(r)−r is then zero for the CSR case. Values of L(r)−r above zero indicate clustering at the length scale, r.

Next we used the related Getis and Franklin's local point pattern analysis to generate a clustering value (L(r) at r = 50 nm; L(50)) for each point, j, based on the local three-dimensional molecular density. This was calculated using:

$$\begin{array}{l}{L}_j\left(50\right)={\left(\left(\frac{3V}{4\pi }\right)\sum _{i=1}^n\left(\frac{{\delta }_{ij}}{n}\right)\right)}^{1/3};\hfill \\ {\delta }_{ij}=1ifd\left(\text{point}i,\text{point}j\right)<50,0\text{else}.\hfill \end{array}$$ (3)

These values can then be interpolated such that every voxel in a volume is assigned a cluster value based on the number of encircled points, relative to the expected CSR case. This allows construction of isosurfaces where all points on the surface have an identical L(50) value. A high threshold imparts a strict criterion for cluster detection compared to a lower one, and this allows users to, for example, determine the efficiency of sequestration into clusters by quantifying the cluster number and size as a function of the threshold.

To illustrate the identification of subcellular structures, Lat-mEos2 was imaged by three-dimensional SMLM in activated T cells at the immunological synapse (Fig. 1 A). Three-dimensional projections of isosurfaces (for L(50) = 200) clearly identified intracellular LAT vesicles at varying depths within the synapse (Fig. 1, B and C). Cluster statistics were extracted from this data set to quantify the distribution of clusters in the z direction as well as the volume and sphericity of the LAT objects themselves (Fig. 1, D–F).

Figure 1.

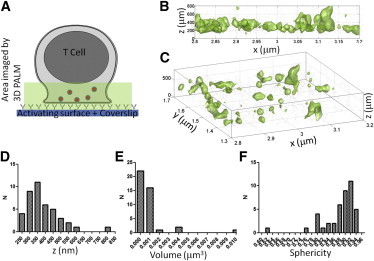
Identification of subcellular objects in three dimensions by isosurface rendering of molecular distribution. (A) Schematic of a T cell synapse formed against an activating coverslip where subsynaptic LAT vesicles (red dots) can be imaged with three-dimensional SMLM. (B and C) Isosurfaces, shown in x,z view (B) and as projection (C), identify T cell vesicles as LAT objects with L(50) > 200 (Eq. 3). (D–F) Distribution of LAT objects in z direction (D), volume (E), and sphericity (F) of LAT objects in T cells.

Membrane undulations can cause clustering artifacts when the distribution of membrane proteins is recorded as a two-dimensional projection (15) (Fig. 2 A), as is the case in two-dimensional SMLM under total internal reflectance fluorescence illumination. To illustrate a solution to this problem, we obtained three-dimensional SMLM data sets of the membrane dye DiI (16) in resting T cells adhered onto nonactivating coverslips. With appropriately short labeling times to prevent dye internalization, it can be assumed that all DiI molecules reside in the plasma membrane. In this case, as is the case for plasma membrane proteins, neither two-dimensional nor three-dimensional analysis is appropriate, as it is a priori known the points must be derived from a two-dimensional membrane folded in three-dimensional space. To correct for membrane undulations, the plasma membrane topography must first be mapped so that molecular coordinates of membrane molecules can be appropriately corrected in two-dimensional projections. The position of the plasma membrane in three dimensions, i.e., the membrane topography, was determined by averaging the z position of all DiI molecules within a 100-nm radius in x-y at each point. The averaged z-position of DiI molecules was then displayed as a map, which exhibits a smooth, undulating profile (Fig. 2 B). The selection of this radius determines the accuracy of the assigned z position but also causes smoothing of the membrane profile.

Figure 2.

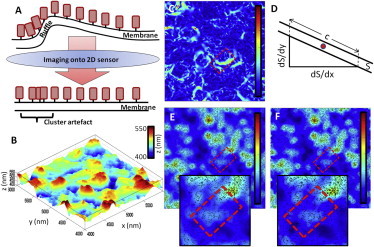
Mapping of membrane topography and correction of molecular distributions in undulating membranes. (A) Two-dimensional projections can cause cluster artifacts, for example in membrane ruffles. Molecules (red rectangles) in the upper image are equally spaced along the membrane but appear as clusters in two-dimensional projections in areas with high gradient. (B) Three-dimensional membrane topography of a 2 × 2 μm plasma membrane area of a resting T cell obtained from averaged z positions of DiI molecules. Note that membrane undulation is ∼100 nm. (C) Map of membrane gradient, corresponding to the topography map shown in panel B, with an area of high gradient highlighted (dashed red box). (D) Correction of the circle radii in the Getis and Franklin cluster map calculations to account for projection artifacts. (E and F) Cluster map of data shown in panel C before (E) and after (F) correction for membrane gradient. Boxes in panels C, E, and F highlight the regions with high membrane gradient.

Next, the gradient at the position of each DiI molecule was determined and interpolated into a gradient map (Fig. 2 C). Here, blue represents horizontal, i.e., flat membrane areas, whereas red regions indicate areas of high gradient. The information from the gradient map was then used to ensure that the two-dimensional circles in the Getis and Franklin cluster map calculations each correspond to an identical area of membrane, hence accounting for two-dimensional projection artifacts. To do this, the size of the circle (r) used to calculate the L value for each molecule was modified using Eq. 4, where c is calculated for the surface, S, using Eq. 5:

$$r\left(\text{corr}\right)=\frac{r\left(\text{uncorr}\right)}{{\left(1+c^2\right)}^{1/4}},$$ (4)

$$c={\left({\left(\frac{\partial S}{\partial x}\right)}^2+{\left(\frac{\partial S}{\partial y}\right)}^2\right)}^{1/2}.$$ (5)

This operation is shown schematically in Fig. 2. The comparison of Getis and Franklin cluster maps before (Fig. 2 E) and after (Fig. 2 F) correction for the gradient shows that cluster values for DiI molecules were substantially reduced by up to 5–10% at sites where the plasma membrane had a high gradient (area highlighted in red box), and where the two-dimensional projection of three-dimensional structures caused an overestimation of clustering.

In conclusion, we demonstrated that three-dimensional superresolution localization microscopy data can be used to identify and quantify subcellular structures. The approach has the distinct advantage that subcellular structures are solely identified by the distribution of the fluorescent marker so that no a priori knowledge of the structure is necessary. How precisely the subcellular structures are identified only depends on how efficiently the fluorescent maker is recruited to the structure, and hence does not depend on the resolution limits of optical microscopy. We applied the methods to two very different structures in T cells: small intracellular vesicles and the undulating plasma membrane. Importantly, the topography of plasma membrane can also be used to correct clustering artifacts in two-dimensional projections, which may be useful for distribution analysis within membranes.

Methods

Linker for Activation of T cells (LAT) fused to the photoswitchable fluorescent protein mEos2 was expressed in the Jurkat T cell line. T cells were activated using coverslips coated with anti-CD3 and anti-CD28 antibodies (eBioscience, San Diego, CA) and imaged after 2 min of activation. To quantify plasma membrane topography, T cells were stained with 500 nM DiI (Invitrogen, Carlsbad, CA) for 5 min and fixed in 4% paraformaldehyde. DiI samples were imaged in a PBS buffer containing 25 mM HEPES, 25 mM glucose, 5% (v/v) glycerol, 50 μg/mL glucose oxidase, 10 mg/mL horseradish peroxidase, and 10 mM cysteamine.

Data were acquired with biplane SMLM under highly inclined and laminated optical sheet illumination on an ELYRA PS-1 SMLM microscope (Carl Zeiss, Jena, Germany) with a ×100, 1.46 NA objective; focal plane offset for biplane SMLM was 372 nm. For mEos2 imaging, 405-nm laser light was used for conversion to the red form and a 561-nm laser used for imaging. For DiI, 561 nm was used for imaging and 405 nm used to recover the molecules from the dark state.

Raw fluorescence intensity images were analyzed with the software Zen 2010D (Zeiss MicroImaging, Carl Zeiss). After Gaussian and Laplace filtering, events were judged to have originated from single molecules when I − M > 6S, where I is event intensity, M is mean image intensity, and S is the standard deviation of image intensity. The center of each point-spread function was then calculated by fitting to a three-dimensional theoretical point-spread function. Multiple localizations of fluorophores were corrected with an off-gap, as previously described in the literature (5,17).

For the generation of cluster maps, L(r) values at a spatial scale of 50 nm (L(50)) were computed for each point (j) individually. Once each molecule had been assigned a value for L(50), a quantitative, pseudo-colored cluster heat map was interpolated on a resolution grid of 10 nm in x, y, and z (MATLAB, The MathWorks, Natick, MA). Isosurfaces were generated at an L(50) value of >200 from which cluster statistics (number, size, shape, molecules per cluster, etc.) were extracted.