ENteric Immunity SImulator: A Tool for In Silico Study of Gastroenteric Infections

Abstract

Clinical symptoms of microbial infection of the gastrointestinal (GI) tract are often exacerbated by inflammation induced pathology. Identifying novel avenues for treating and preventing such pathologies is necessary and complicated by the complexity of interacting immune pathways in the gut, where effector and inflammatory immune cells are regulated by anti-inflammatory or regulatory cells. Here we present new advances in the development of the ENteric Immunity SImulator (ENISI), a simulator of GI immune mechanisms in response to resident commensal bacteria as well as invading pathogens and the effect on the development of intestinal lesions. ENISI is a tool for identifying potential treatment strategies that reduce inflammation-induced damage and, at the same time, ensure pathogen removal by allowing one to test plausibility of in vitro observed behavior as explanations for observations in vivo, propose behaviors not yet tested in vitro that could explain these tissue-level observations, and conduct low-cost, preliminary experiments of proposed interventions/treatments. An example of such application is shown in which we simulate dysentery resulting from Brachyispira hyodysenteriae infection and identify aspects of the host immune pathways that lead to continued inflammation-induced tissue damage even after pathogen elimination.

I. Introduction

Enteric diseases are diseases of the gastrointestinal (GI) tract. These diseases are often caused by ingestion of harmful microbes in food and water. When these harmful microbes enter the GI tract, immune and intestinal epithelial cells trigger an inflammatory response that eliminates the microbe, but may also cause host tissue damage. This collateral damage sometimes has significant impact on disease pathogenesis.

The GI tract is constantly exposed to foreign antigens, most of which are innocuous. To avoid constant tissue-damaging hyperinflammation, this inflammatory response must be regulated. Immune regulation is carried out by the regulatory, or anti-inflammatory immune response triggered by factors such as host tissue damage or commensal gut microflora. In the gut mucosa, immune cells of regulatory and inflammatory responses remain in constant competition with regulatory phenotypes generally predominating [1], [2]. To develop effective and safe host-targeted therapeutics against GI infections, it is critical to understand more completely the mechanisms of immune regulation to pathogens such as pathogenic strains of Escherichia coli or Helicobacter pylori.

In this paper, we present new advances in the development of the ENteric Immunity SImulator (ENISI), a modeling environment for studying the inflammatory and regulatory immune responses in the gut. ENISI is an agent-based simulator whereby bacteria and immune cells are represented as agents, which can move through tissue sites and engage in context-dependent interactions with the nearby agents. The formal model of ENISI can be represented as a co-evolving graphical discrete dynamical system where a time varying graph represents the dynamic contact network of bacteria and immune cell interactions. The interactions are represented in a probabilistic timed transition system capable of handling time and contact dependent stochastic transitions.

With ENISI, immunologists can test and generate hypotheses for enteric disease pathology and propose interventions through experimental infections of an in silico gut. Simulation outcomes given different experimental conditions allow observation of in silico behaviors that are not readily seen through in vitro or in vivo techniques. This information can then be used to better understand immunological mechanisms and to generate novel treatment strategies that can be tested in the laboratory.

A. Mucosal Inflammatory and Regulatory Immune Pathways

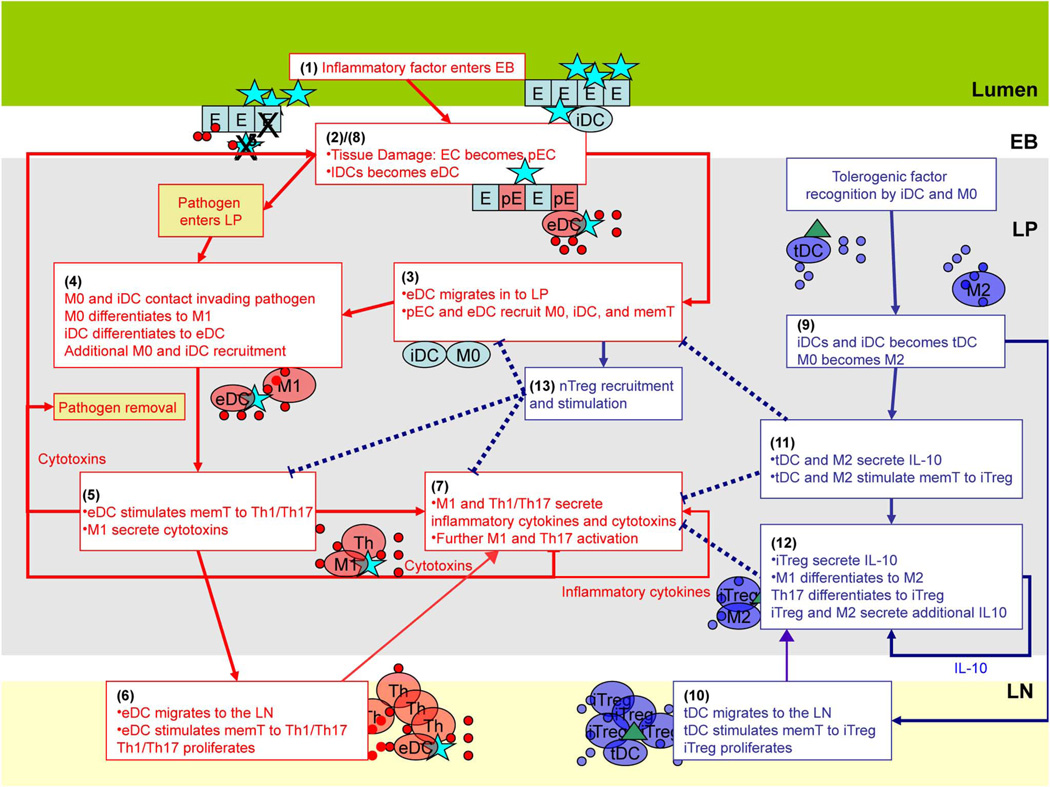
In this section we describe the inflammatory and regulatory immune pathways encoded in ENISI as shown in Fig. 1. In the figure, the red lines represent the inflammatory pathways and the blue lines represent regulatory pathways.

Fig. 1.

Illustration of sequential events in the inflammatory (red arrows) and regulatory (blue arrows) pathways described in the text. Dashed lines indicate events that inhibit the occurrence of another event.

In mammals, the immune system associated with the gut mucosa can be divided into four functional compartments: i) the lumen; ii) the lamina propria (LP); iii) the epithelial barrier (EB); and iv) the gastric or mesenteric lymph node (LN). The lumen corresponds to the external environment, contains ingested food and foreign microbes, and houses gut microflora.

The lamina propria is a tissue site separated from the lumen by the epithelial barrier and occupied by the immune cells. The epithelial barrier is a monolayer of cells that divides the lumen and LP. The gastric lymph node is the primary site of T cell activation.

The events taking place during an inflammatory immune response (red lines) are as follows, with numbers corresponding to those labeling events depicted in Fig. 1: 1) A pathogen, such as foreign bacteria, enters the lumen and contacts the EB. 2) Intestinal epithelial cells (EC) switch to a pro-inflammatory phenotype (pEC) either in response to damage caused by the pathogen or by mere recognition of the pathogen. The pEC phenotype secretes microbicides and various signaling chemicals (cytokines and chemokines) and may become permeable allowing pathogen entry into the LP [3]. At the same time, immature “sampling” dendritic cells (iDCLumen), which are associated with EB and contact microbes in the lumen, internalize the pathogen and mature to effector phenotype (eDC) that migrate into the LP and present components of the pathogen (antigen) on their surfaces. 3) Chemicals secreted by damaged epithelial cells and eDC recruit resting macrophages (M0) and dendritic cells (iDC). 4) These macrophages and dendritic cells may then contact and internalize the invading pathogen. This leads to maturation of iDC to an eDC phenotype and differentiation of macrophages to an inflammatory M1 phenotype. 5) Mature, antigen-presenting eDC goes on to recruit resting CD4+ T cells (restingT) to the LP and secrete cytokines that induce T cell differentiation to a pro-inflammatory Th1 or Th17 phenotype upon antigen recognition [2]. These stimulated T cells enter a transient state of proliferation, each giving rise to approximately 500 daughter cells of the same phenotype. M1 goes on to secrete cytotoxic proteases and radicals that kill surrounding microbes as well host epithelial cells. 6) Presenting effector dendritic cells then migrate to the LN and to contact resting memory and naive T cells, stimulating them to a Th1 or Th17 phenotype. The inflammatory T cells mature here before migrating to the LP site to contribute to the inflammatory response at the infection site. 7) At the infection site in the LP Th1/Th17 cells secrete cytotoxins and cytokines that enhance secretion of inflammatory factors by surrounding T cells as well as induce additional macrophages to a M1 phenotype and T cells to a Th17 phenotype. 8) The epithelial cells damaged by factors derived from Th1, Th17, and M1 then respond by secreting additional inflammatory cytokines resulting in more immune cell recruitment along with openings in the epithelial barrier that can allow direct pathogen entry into the LP at which point recruited M0 and iDC are activated to inflammatory phenotypes. This completes a positive, inflammatory feedback loop. Inflammation generally dissipates when pathogen is eliminated and direct immune cell stimulation ceases.

The anti-inflammatory regulatory pathway is composed of the following events: Dendritic cells and macrophages contact a tolerogenic factor such as self-antigen or commensal bacteria that reside in the lumen or has invaded the LP through the damaged epithelium. 9) Upon internalization of the commensal or self-antigen, dendritic cells differentiate to a tolerogenic phenotype (tDC) and macrophages differentiate to an M2 phenotype. 10) Like eDC, tDC migrates to the LN where it contacts and stimulates T cells to an iTreg phenotype, which go on to the infection site in the LP. 11) M2 and tDC go on to secrete anti-inflammatory cytokines such as IL-10. IL-10 reduces inflammatory cytokine and cytotoxin production in surrounding immune cells, dampening the inflammatory loop. They also present the tolerance-inducing antigen to CD4+ T cells inducing their differentiation to T-regulatory cells (iTreg). 12) iTreg goes on to secrete additional IL-10. The increase in environmental IL-10 induces differentiation of macrophages of the inflammatory M1 phenotype to the regulatory M2 phenotype and T cells of the Th17 phenotype to the iTreg phenotype [1]. This promotes further IL-10 production and stimulation of T cells to iTreg closing a positive anti-inflammatory feedback loop. 13) Another regulatory pathway involves natural T-regulatory cells (nTreg). These are T cells in the LP that are pre-destined to be regulatory cells independent of the phenotype of the presenting dendritic cell (eDC or tDC) or macrophage. nTreg may have a reduced proliferation capacity compared to conventional T cells. Like iTreg, nTreg secretes IL-10 promoting further M2 creation. In addition, nTreg binds eDC and inhibits their recruitment and stimulation of resting T cells to inflammatory phenotypes [4]. Certain genetic predispositions or immune dysfunctions can result in an inflammatory pathway being initiated by commensal bacteria strains [5].

II. Our Contributions and Related Works

Here we present a new version of the ENteric Immunity SImulator (ENISI), an agent-based simulator of the inflammatory and regulatory immune pathways initiated by microbe-immune cell interactions in the gut. With ENISI, immunologists can test and generate hypotheses for enteric disease pathology and propose interventions through experimental infection of an in silico gut. ENISI is a unique contribution to the field of immunological tools as an agent-based model for simulating the mucosal immune system. Key features include: i) a very detailed representation of various regulatory and effector cell types and their interactions; ii) easy to use scripting language for interacting with the simulation; iii) scalable parallel algorithms and implementations. We discuss this in further details below.

ENISI has been designed for high performance computing architectures from the beginning. We have decomposed the problem appropriately and represented interactions amongst constituent elements. ENISI allows us to represent complex interactions and migration of 10⁶ individual cells over a simulated 3-month period within 1 h. We believe that with additional effort ENISI can be scaled to represent 10⁸ cells. ENISI is designed so that over time simulation specific parameters as well as representation of individual components (cells as well as pathogens) can be controlled by scientists who are not computing experts. This is done by using a simple scripting language to assign parameter values that conform to one’s knowledge and assumptions of the experimental scenario they wish to simulate. Simulation outcomes given different experimental conditions allow observation of in silico behaviors that are not readily seen through in vitro or in vivo techniques. This information can then be used to generate novel treatment strategies that can be tested in the laboratory.

It is important to point out that ENISI is a collaborative effort between experimental immunologists, modelers and computer scientists. As pointed out in a number of earlier publications, we believe this is important as it has allowed us to develop parsimonious representations that on one hand capture important biological details so as to render the system useful and at the same time are computationally efficient, thereby enabling the study of the system at an appropriate scale. Finally ENISI is based on a rigorous mathematical framework; the coevolving discrete dynamical systems framework allows us to formally represent individual entities and their interactions. One advantage of this formalization is that it makes specification transparent, making assumptions explicit. We believe that this will lead to improved comparative studies between various agent-based models.

The application of a high performance computing oriented agent-based model such as ENISI to study the mucosal immune responses in the gastrointestinal tract is also novel in that it is the first simulation of its kind to study this problem. Specifically, ENISI models the general architecture of the gut mucosal immune system, including the lumen, its inductive sites (i.e., lymph nodes) and its effector sites (lamina propria and epithelium). ENISI models at the cellular level the regulatory and effector networks involved in maintaining gut homeostasis, including explicit representation of subsets of T cells, macrophages, dendritic cells (DC), epithelial cells, and their interactions. The explicit representation of M1 or classically activated versus M2 or alternatively activated macrophages, regulatory versus effector CD4+ T cells subsets, and effector versus tolerogenic DC is a novel and important feature of ENISI. The integration of systems level cellular interactions with immunological processes of relevance to host response against microbes and tissue homeostasis such as differentiation, proliferation and movement with tissue level phenotype can be performed in ENISI with a very detailed level of resolution.

A. Related Works

Various models of mucosal infection captured the aspects of inflammatory and regulatory immune pathways [6]–[9]. These models have provided insight into mechanisms of clinical symptoms as well as pathogen persistence. The ENISI model is unique in its scope and approach. The model incorporates regulatory mechanisms of both adaptive and innate immunity, multi-location migration of cells, and cross talk between antigen-presenting cells and T-cells. It is an agent-based model which explicitly represents each participating cell of the immune pathway, their movement across compartments, proliferation when appropriate and their differentiation. This facilitates mapping of model parameter specifications and predictions to laboratory techniques such as flow cytometry that manipulate specific cell populations.

Mathematical models have been employed to capture the dynamics of immune system. Most of the models are based on differential equations. Ordinary differential equation (ODE) has been used to model immune cells in [10]–[16]. ODEs are used because of its availability of extensive literature, relatively simpler mathematical analysis and computational efficiency. Delay differential equation (DDE) has been used to capture the delayed responses of biological systems in [17], [18]. Partial differential equation (PDE) is also used in [15] and [19] which considers cell age and location. These models are deterministic and do not capture the stochastic behavior of cells. A stochastic differential equation (SDE) model was also proposed in [20]. agent based model (ABM) provides an alternative approach to model the immune systems with a population of distinct interacting agents representing cells with appropriate set of rules. See [21] and [22] for a detailed and comprehensive discussion on this topic.

Over the past 20 years, various agent based models have been developed in the literature to represent artificial immune systems. This includes: AbAIS (Agent-based Artificial IS) [23], CAFISS [24], ImmSim [25], ImmSim3 [26], C-ImmSim [27], ParImm [27], ImmunoGrid [28], Simmune [29], SIS [30]. An excellent survey of these models can be found in [21], [22], and [31]; we refer the reader to these papers for a detailed discussion. As argued in [30] and [31], SIS and ImmSim are based on two somewhat different philosophies of how in silico immune systems can be developed. Rhapsody [32], [33], NFSim [34], and that developed by [35] translate graphical models into executable code to run simulations. In [36] the authors showed an agent-based implementation of the immune system with simplified deterministic rules. These simulators place an emphasis on rules governing cell-cell contacts and signaling interactions allowing one to enter complicated functions for these mechanisms. Therefore, they provide the useful capability of incorporating complex mathematical models for receptor-ligand interactions and phenotypic differentiation into cell contact networks. However, the scalability of these implementation algorithms in terms of system complexity and the number of individuals in a network is unclear. For example, Rhapsody has been shown to simulate a maximum of 10⁴ individuals efficiently [32], [33]. As an agent-based model, a key aspect of ENISI is a procedural and interactive (a.k.a. mechanistic, algorithmic, executable) view of the underlying systems. This agent-based approach allows incorporation of spatial effects and randomness of cell-cell and cell-bacteria contact.

In contrast to sequential models, the work on developing parallel agent-based models for immune system modeling is quite sparse. C-ImmSim [27] and Immunogrid are two well-known parallel simulators for modeling immune system that can scale to reasonably large system sizes. SIS is also supposed to scale to large systems, but details about this scaling are not clear from the published work. Both are discrete in space and time and use an underlying geometry to represent spatial interactions. The scaling and parallel efficiency achieved by ENISI is one of its distinguishing features.

III. ENISI

ENISI encodes immune pathways as an agent-based model representing individual cells that participate and interact with other cells. The individual cells are distributed spatially to four locations. Locations are further divided into many discrete patches called sublocations. An individual cell’s schedule is assigned by their initial state (cell type). Within a location, cells move randomly between sublocations at short time intervals throughout the scheduled duration in the location. This represents random movement and produces a dynamic contact network. The random movement, which does not favor movement to adjacent sublocations, follows an assumption that cells are moving at a much faster rate than the time periods for sublocation update (30 min) and, therefore, the probability of an individual having traveled far from the current sublocation is the same for it having ended up in a nearby sublocation after the 30 min interval.

A. Formalization of ENISI

The underlying formal mathematical model for ENISI is a co-evolving graphical discrete dynamical system (CGDDS) framework. CGDDS is a time varying network model which captures the co-evolution of immune systems, the inflammation/regulation dynamics, and individual cellular behavior. CGDDS is described in more details in [37]. We will extend the mathematical model to capture the cellular interactions that occurs with the movement of immune cells and bacteria. Here we provide an informal description of the mathematical model. For a comprehensive description please refer to [38].

An extended co-evolving graphical discrete dynamical system ((Cℊ𝒟𝒟S)) over a given domain 𝔻 of state values is a triple (G_t, ℱ, W) where G_t is a time varying graph, ℱ is a set of state transition functions and is an update scheme. In the rest of the paper, we will assume that nodes are updated synchronously.The components of CGDDS can be described as follows:

The dynamic network G_t(V_t, E_t) is a graph where vertices and edges can change with time. For the sake of simplicity we will ignore time index which will be clear from the context. The set of vertices V = {υ₁, υ₂, … υ_n} represents the set of immune cells or bacteria. Also let S = {S₁, S₂,…S_m} ∈ 𝔻 be a set of all possible states (phenotypes) that the cells can take. We also define s^t(υ) ∈ S as the state of any vertex υ ∈ V at time t.

The interactions between vertices of the graph are based on spatial proximity. As cells move through the locations their contacts are changed which results in the addition or deletion of edges which are the basis of network change. The details of the movement model are described subsequently.

For each vertex (cell) υ,g denotes the edge modification function that takes as input the state of the vertex s^t(υ) at time t and returns the set of edges that υ will be adjacent to in a given time period. In other words, g captures the time varying edges at t + 1 in the graph.

We will now discuss how cell state transitions occur. For each vertex υ ∈ V let f be the function representing state transition.The function f takes as input the state of the vertex at time t, the states of other vertices of the edges incident on υ and results the state υ at time t + 1 as output.If vertices υ₁, υ₂,…, υ_k are adjacent to vertex υ we can define the state transition function for υ as

$$s^{t+1}(v)=f(s^t(v),s^t(v_1),s^t(v_2),\mathrm{\dots },s^t(v_k))$$

This function may also be stochastic. At any time t, the configuration ξ(t) of a CGDDS is defined as a vector (s^t(υ₁), (s ^t(υ₂),…, s^t(υ_n)), the states of all vertices. The time evolution of a CGDDS is represented by the sequence of successive configuration changes of the dynamic network. In the following discussion, we will describe several approximations that render this computation efficiently.

Algorithm 1.

Pseudocode describing ENISI execution as formalized using CGDDS

for t = 0 to T do

Compute the interaction graph Gt using function g.

for each vertex υ do

Compute st (υ) using state update function f

Algorithm 1 describes the dynamics of ENISI as formalized using extended CGDDS. Note that the state update for each cell is performed synchronously. That is, the network and state updates are realized only after all nodes have finished executing the relevant transition functions.

B. Modeling Immune System Using CGDDS

We now describe how we can model the immune system and its interaction with the bacteria in the gut using extended CGDDS described above.

The dynamic network

As mentioned earlier, the vertices of our dynamic network represents immune cells and bacteria (called as agents). Each cell has one of many states (phenotypes). A list of cell phenotypes is given in Table I.

TABLE I.

Model States

State	Description	Initial No. of Cells
Phenotypes
memT	Resting CD4+ memory T cell	1·103
Th	Active CD4+ T helper cell	0
iTreg	Induced T regulatory cell	0
nTreg	Active natural T regulatory cell	0
mem_nTreg	Resting natural T regulatory cell	0
iDCs	Immature ’sampling’ DC in the superficial LP with access to the Lumen	1000
iDCLP	Immature dendritic cell in the LP	1000
eDC	Effector dendritic cell in the LP	0
tDC	Tolerogenic dendritic cell in the LP	0
eDCL	Effector sDC in the lumen	0
tDCL	Tolerogenic sDC dendritic cell in the lumen	0
DC Anergic	Anergic dendritic cell	0
M0	Undifferentiated macrophage	1·103
Ml	Activated inflammatory macrophage	0
M12	M2 recently transitioned from Ml	0
M21	Ml recently transitioned from M2	0
M2	Activated regulatory macrophage	0
EC	Healthy epithelial cell	104 [40]
pEC	Damaged or pro-inflammatory epithelial Cell	0
MASource	monocytes: MA precursor	105
DCSource	monocytes: DC precursor	105
Mem T Source	memory T cell in blood	104
ThSource	Potential child cell from a proliferating Th	5·105
iTregSource	Potential child cell from a proliferating iTreg	5·105
Locations
B_lumen	Commensal bacterium in the lumen	1000
Bf_lumen	Foreign bacterium in the lumen	30
B_LP	Commensal bacterium in the LP	0
Bf_LP	Foreign bacterium in the LP	0
Death
Edead	Killed epithelial cell	0
B_dead	Killed commensal bacterium	0
Bf_dead	Killed foreign bacterium	0

There are four tissue sites: i) lumen; ii) epithelial barrier; iii) lamina propria; and iv) lymph node. These are called locations in ENISI. Each of the tissues is divided into small spatial patches called sublocations. Spatially proximal cells are connected by edges. The length scale, the maximum distance between cells that allows for the likelihood of interaction is parameterized to capture the relevant biology. All agents within a sublocation are deemed close enough enabling them to interact with each other. These interactions can change the state of the cells. The dynamic graph is a result of these individual agents moving through the tissue location as discussed earlier. In the current implementation, the agents move randomly through these patches.

All cell-types and bacteria, with the exception of epithelial cells, can change sublocations every 30 real minutes. The movement of the cells from one sublocation to another sublocation is random. The location for each agent is governed by its current state and the time that has elapsed in that state. Location changes can happen only after 6 h of real time. The system updates itself synchronously every 6 h, as described further in subsequent sections.

Interactions and Update Function

E_t represents set of contacts between any two agents at time t. In immune systems cells interact with other cells and bacteria which lead to effector or regulatory responses depending on the execution of the pathway. For simplicity, certain interactions are best represented as modification of cell states as they are affected by concentration of certain chemicals. This view allows in effect a “mass action” like interaction. In general there are three kinds of interactions—i) interaction between a cell and a bacteria; ii) interaction between two cells; and iii) interaction between a cell and a group of cells.

A convenient way to represent a local update function is to use an appropriate automaton. Here we use probabilistic timed transition systems (PTTS) to represent the time evolution of the cell states. In PTTS each state has an id, a set of attributes values, a dwell time distribution, and one or more labeled sets of weighted transitions to other states. The label on the transition sets is used to select the appropriate set of transitions. The attributes of a state describe the features possessed by a cell that is in that state. Once a cell enters a state, the amount of time that it will remain in that state is drawn from the dwell time distribution.

Each cell in the system consists of a set of automata, a set of attributes, a set of schedules (one of which is active at any time), and a scenario, represented by a set of triggers and associated actions. For efficiency, there is only one copy of each automata, and each cell records its current state and its next automatic transition time. In our implementation we consider two types of interactions: i) pairwise interactions including cell-cell and cell-bacteria interactions and ii) group-agent interaction. Each such interaction results in a potential state change and is further described below.

Pairwise interaction

In cell-cell interaction the outcome is determined by a pairwise state transition function between two cells. Though a cell may come into contact with many adjacent cells, only one will interact with it. For each state s^t(u) of individual cell u, there is a set of Interactor states I_s^t(u) such that if a neighbor v of u is in a state s^t(v) ∈ I_s^t(u), u may interact with υ and possibly transition states. Table II lists all states along with their interactor states. Some cell phenotypes exhibit similarity in how they interact with other cells. For example,iDCLP and M0 is grouped into one set as they show similar behavior. We assign each group with an id. A list of the groups is given in Table III. In ENISI each group is mapped with one or more interactor groups for the sake of performance. For example, state transition for cells in group 1 (iDCLP, M0) is induced by cells in group 5 (TolB_LP,CommB_LP) or cells in group 9 (TolB_lumen, CommB lumen).

TABLE II.

Cell States and Their Interactor States

States	Interactor States
iDCLP, M0	CommB_LP, TolB_LP TolB_lumen, CommB_lumen
eDCL	nTreg
memT	eDCL Ml, M21,
CommB_LP, TolB_LP	iDCLP, M0
pEC	Th, Ml, M21
DC source, memT Source M Asource	eDCL, pEC, Ml, M21
TolB_lumen, CommB_lumen	iDCLP, M0, pEC, Edead
mem_nTreg	eDCL, Ml, M21 M12, M2, tDCL, tDC
Ml, M21	nTreg, M12, M2 tDC, tDCL iTreg
M12, M2	eDCL, Th, pEC, M1, M21
EC	eDCL, Th, Ml, M21, Th CommB, TolB
memT	M12, M2, tDCL, tDC
InfB	iDCLP, M0, pEC, Ml
Thsource	ThProlif
iTregsource	iTregProlif
nTregsource	nTregProlif
CommB, TolB	pEC, Ml

TABLE III.

State Groups and Their Interactor Group Identifier

States	Interactor Group Id
iDCLP, eDC, M0	1
eDCL	2
memT	3
Th	4
CommB_LP, TolB_LP	5
pEC	6
DCsource, memT Source, M Asource	7
Edead	8
CommB_lumen, TolB_lumen	9
mem_nTreg	10
nTreg	11
Ml, M21	12
M2, M12	13
tDC, tDCL	14
EC	15
iTreg	16
memT	17
ThSource	23
iTregSource	27
iTregProlif	28
nTregProlif	29
nTregSource	30
CommB, TolB	32
Ml	33

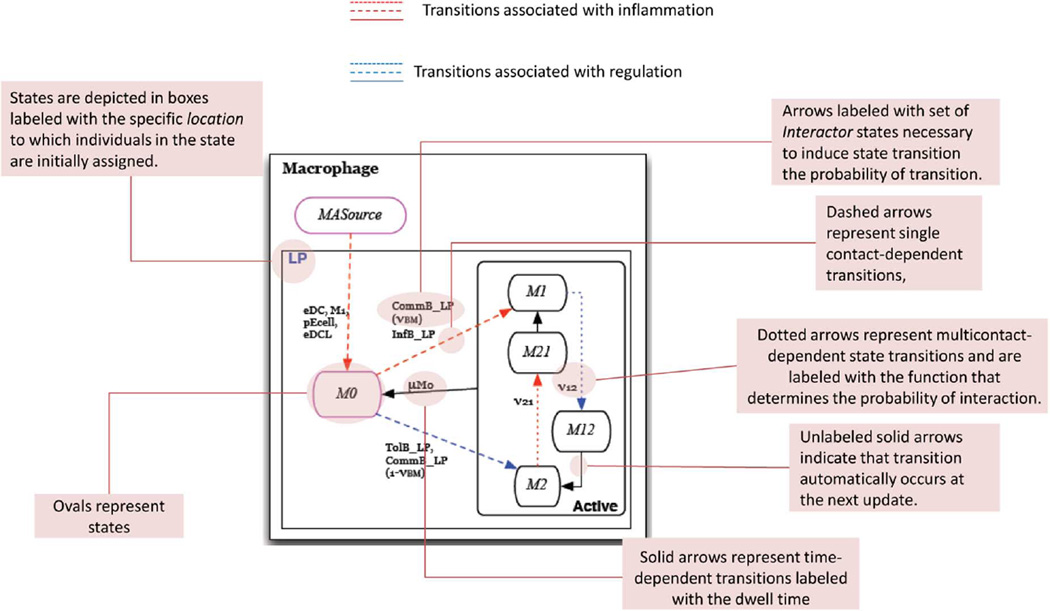
If a cell u ∈ V interacts with cells υ₁, υ₂, … υ_k, then there are k pairwise transition functions. In our implementation we choose one transition with a prespecified probability and apply the PTTS to get the final outcome. Future extensions will consider more sophisticated schemes inspired by work on chemical reactions and Gillispe’s algorithm [39] and its extensions. The automata in Fig. 2 provide pictorial details of the possible cell-cell interactions and the resulting change of cell states.

Fig. 2. State chart description.

A labeled state chart depiction of the Macrophage automaton.

Group-agent interaction: In group-agent interaction the outcome of a cell is dependent on all of the interacting neighbor cells. There are two groups of cells that can interact with a cell, activators and inhibitors. The probability that a transition will take place is defined by the probability

$$p={\left(\frac{aA}{aA+iI}\right)}^y$$ 1

A is the total number of neighbors in a state that induces a state change (activators) and I is the total number of neighbors in a state that inhibits a state change (inhibitors). The variables a, i, and y are model parameters.

During a single 6 h period, an agent can undergo no more than one state change. This can be caused by either a pairwise interaction or a group-agent interaction. In the event more than one such interaction is feasible, the earliest interaction is chosen. Not all of the interaction may lead to a state change. This depends on the current state of the agent. The rationale for this decision is discussed later and this issue needs further investigation.

This contact-dependent transition may explicitly represent contact-dependent cell differentiation, such as the stimulation of resting T cells by dendritic cells, which requires surface-surface contact. Transitions may also implicitly represent differentiation induced by cytokines secreted by surrounding cells, as is the case for a M1 → M2 transition, which is a function of the cytokine concentrations in the local environment. Upon a change of state, the individual may or may not be assigned to a new location.

Each event of the immune pathway is then defined by a specific state transition s_i → x, where x ∈ S. for example, tissue damage occurs when one cell represented by an epithelial cell automaton makes the transition EC → pEcell. A specific health outcome is a stable configuration of the system, ξ_s, following contact between one of the bacteria automata and one of the immune cell automata.

C. Approximations to the Biological Model

The contact-dependency of state transitions in the graphical framework, as well as the need for computational efficiency, require a number of approximations to the biological model. The CGDDS model stipulates that for a state change in one individual to be induced by another individual, the individuals must be colocated. Hence, the model cannot explicitly include induction of state-transitions across location barriers as may occur when chemokines secreted by a cell in the LP influence migration of cells in the blood. To reduce complexity, individuals are not newly created or removed from the contact network G following the start of the simulation. Rather, biological processes that require these functions are either not included or represented in an indirect fashion. For example, the model does not include the constitutive flow of resting immune cells in and out of tissue. Nor do we represent bacterial replication.

Given these model approximations, we describe how the following biological functions are represented in the ENISI implementation: i) bacterial death; ii) lymphocyte recruitment;iii) T cell proliferation; and iv) T cell death. A description of each state referred to in italics is given in Table I.

1. Bacterial death: As computational scaling is a constraint, only those bacteria in contact with the epithelial border are represented. Given this simplification, bacteria in the lumen do not explicitly “die.” Rather, it is assumed that when one commensal bacterium is removed, another bacterium immediately takes its place due to the high concentration in the outer lumen. Therefore, an individual tolerogenic bacterium or commensal bacterium in the lumen is not explicitly removed when it interacts with a den-dritic cell and phagocytosis occurs. Only the den dritic cell changes states from iDCLumen → eDCL In addition, to conserve the number of individuals in the system, we allow bacteria cells in lamina propria that are killed by immune cells move back to the lumen.

2. Cell recruitment: A key function of pro-inflammatory epithelial cells, M1, and eDC is secretion of factors that recruit resting T cells as well as resting DC and macrophage precursors, called monocytes, from the blood to the inflamed LP tissue. Recruitment, therefore, requires that one individual occupying the M ASource, DCSource or TSource state undergo a state transition to M0, iDCLP ,or restingT in the LP, triggered by the transition of another individual from M0 → M1 or iDCLP → eDC. The model stipulates that any state transition dependent on the state of another individual be contact-dependent and defined as an explicit interaction. Hence, the function of recruitment of monocyte and memory T cells in the blood by M1 and eDC in the LP is represented as follows: MA Source, DCSource, and TSource states represent cells that are initially in the blood and do not interact with cells in the LP until they are “recruited” to the tissue site by individuals in the eDC, M1, eDCLumen, and pECell states. In the model, cells occupying MASource, DCSource or Tsource states are present in the LP, but do not interact with other cells. Upon contact with cells in one of the recruiting states (eDC, M1, eDCLumen, or pECell) the contacted monocyte or memory T cell transitions to an M0, iDC, or restingT state. The number of memory T cells and monocytes recruited by each M1 and eDC are determined by the parameters ∈_r and ∈_t (Table IV), are the average number of monocytes or memory T cells a M1 or eDC contacts in each sublocation of the LP.

3. T cell proliferation: The current software requires that all individuals in the entire simulation be defined initially by a state and a location. Hence, all nascent T cells that may spawn from a proliferating T cell are anticipated and predefined with the inactive states ThSource or iTregSource and are assigned to the LP and LN locations. When an individual is in one of the proliferating states, ThProlif, or iTregProlif, it may interact with and induce the source cells to its corresponding phenotype. For example, when an individual enters the Th1Prolif state it contacts individuals in the ThSource state. Contacted individuals then transition from ThSource → Th. Proliferation by individuals in the iTregProlif state is represented in the same manner. Hence, the average number of daughter cells from one proliferating T cell in the LP p_T or the number from a T cell in the LN p_t (Table IV), is determined by the average number of ThSource a ThProlif contacts and is set by the initial number of individuals in the ThSource state.

4. T cell death: In the true mucosa, when T cells are no longer active, a fraction revert to a resting memory T cell state and the rest undergo programmed cell death. To conserve the number of represented individuals in the model,when individual T cells undergo programmed cell death they do not enter a dead state. Rather, they replenish the ThSource, and iTregSource population pools.

TABLE IV.

Parameter Values

Symbol	Parameter	Value
Birth/death
µE	Turnover time of epithelial cells	12hrs [40]
µT	Time a T cell remains active	5days [47]
µM0	Time a macrophage remains active	75 days
µd	Time a dendritic cell remains active	1 day [43]
µdL	Time a sDC remains active	1 day [43]
µce	Probability that pEcell is killed by Inflammatory factors
pT	Average number of daughter cells produced by a proliferating T cell	500 [49]
pTr	Average number of daughter cells produced by a proliferating nTreg	0
Migration
∈r	Average number of monocytes recruited by a single eDC, Ml, or pEcell	10
∈t	Average number of resting T cells recruited by a single eDC, Ml, or pEcell	10
βP	Probability that bacteria will enter the lumen upon contact with a pEcell	1
Contact/interactions
αT	Probability of memory T cell stimulation	1
αTr	Probability of memory nTreg stimulation	1
νT	fraction of active T cells that become memory T cells	0.1 [50]
ν 12	Probability that M1 switches to M 2	${\left(\frac{a_{1}R}{a_{1}R+i_{1}N}\right)}^{y_1}$
ν21	Probability that M2 switches to M1	${\left(\frac{a_{2}N}{i_{2}R+a_{2}N}\right)}^{y_2}$
a 1	co-efficient of ν 12 for activators	1
i 1	co-efficient of ν 12 for inhibitors	1
Y 1	exponent of ν 12	4
a 2	co-efficient of ν 21 for activators	1
i 2	co-efficient of ν 21 for inhibitors	4
y 2	exponent of ν 21
υνBM	probability that microfloral bacteria induces inflammatory phenotype in macrophages	0
νBD	probability that microfloral bacteria induces inflammatory phenotype in dendritic cells	0
νBs	probability that microfloral bacteria induces inflammatory phenotype in ‘sampling’ dendritic cells	0
νEC	Probability that EC transitions to pEcell upon contact with inflammatory factors	0.05
νEB	Probability that EC is damaged by microbial toxins	1 [51]

Users may modify rules to set experimental conditions by specifying any of the following features of the system: i) Infection specifics: dose and timing of pathogen entry; ii) Experimental host phenotypes: parameters governing interactions between specific phenotypes to represent changes in cytokine and cytokine-receptor expression; iii) Host immunological set-point: initial immune cell populations present at the time of infection; and iv) Strain-specific functions of bacteria: specifications of interaction conditions and consequences for commensal bacteria and tolerogenic bacteria that mimic those attributed to experimental strains. Rules are specified using a simple scripting language described in [38].

D. State Transition Functions

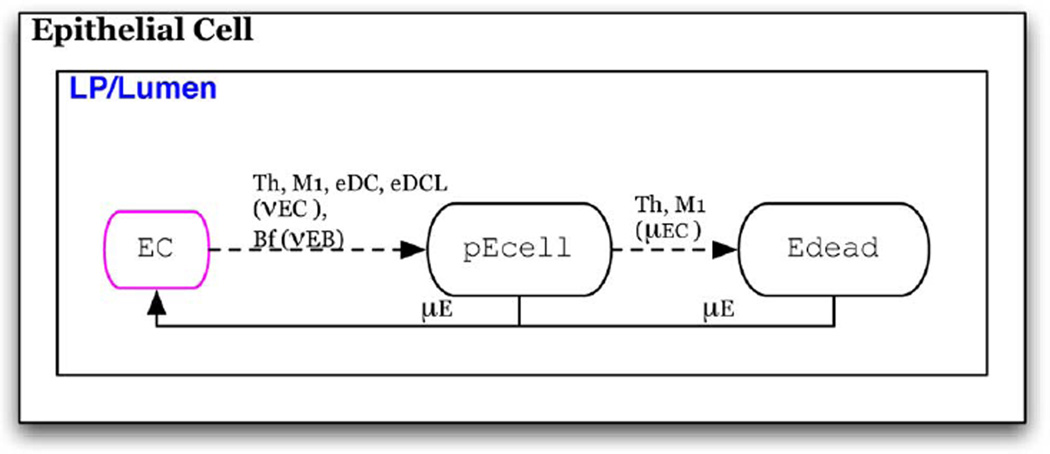
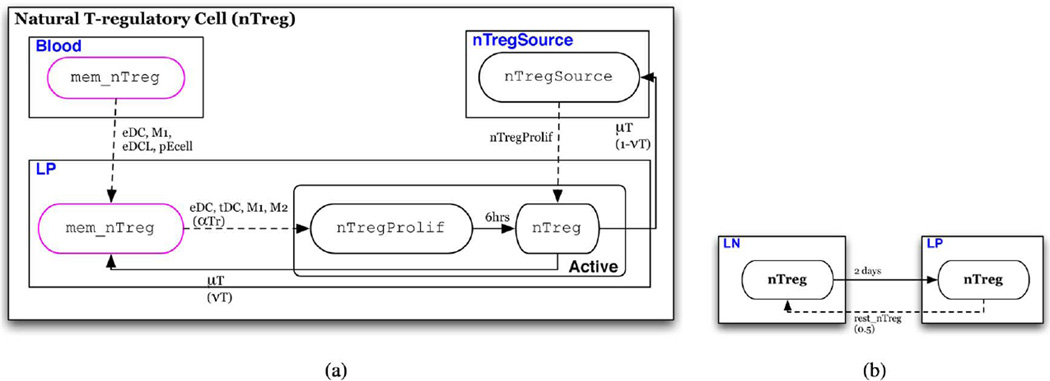
In this section we describe the state transition functions and conditions for schedule changes (intertissue migration). State transition conditions of each of the eight cell-type specific automata are depicted in a state chart like formalism in Figs. 3–9(a) [41]. In these depictions, red arrows indicate transitions that represent events in the inflammatory pathway and blue arrows indicate transitions that represent those of the regulatory pathway. Ovals represent states of the automaton. Solid arrows represent time-dependent transitions labeled with the time in one state before transitioning to another. The dashed arrows represent single contact-dependent transitions, labeled with the set of Interactor states necessary to induce state transition and, in parenthesis, the probability of transition upon interaction. The default probability is 1. Dotted arrows represent multicontact-dependent state transitions and are labeled with the function that determines the probability of interaction. Unlabeled solid arrows indicate that transition automatically occurs at the next update. States outlined in pink indicate the initial state that determines which automaton a cell will be. States are depicted in boxes labeled with blue text that indicate the specific Location to which individuals in the state are initially assigned. An illustrative description of this state chart like formalism is given in Fig. 2. Parameters are listed in Table IV and are referenced in the following descriptions.

Fig. 3. Epithelial cell automaton.

Individuals initially assigned the EC phenotype.

Fig. 9. nTreg automaton.

(a) Automaton for nTreg; individuals initially assigned the rest_ntreg or rest_nTreg Source phenotype (b) conditions for schedule reassignment of nTreg.

Schedule changes are depicted for cell-types that migrate in Figs. 4(b), 4(d), 4(f), 6(b), 7(b), 8(b), and 9(b). In these figures dashed arrows represent schedule reassignment triggered by entry into a specific state and are labeled with the specific state that triggers the reassignment. Solid arrows represent schedule reassignments that occur after specified time period in a state. These arrows are labeled by the state which must be occupied and, in parenthesis, the amount of time in the state at which reassignment occurs.

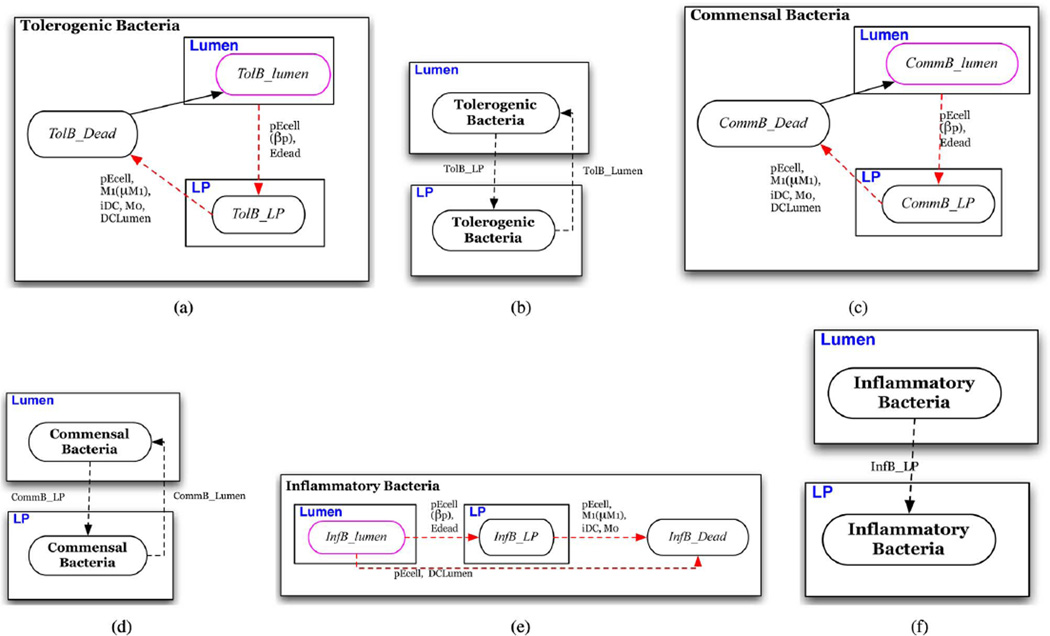
Fig. 4. Bacteria automata.

(a) Automaton for tolerogenic commensal bacteria; individuals initially assigned the TolB_lumen phenotype. (b) Conditions for schedule reassignment of tolerogenic bacterium. (c) Automaton for general commensal bacteria; individuals initially assigned the CommB_lumen phenotype. (d) Conditions for schedule reassignment of a commensal bacterium. (e) Automaton for foreign bacteria (pathogen); individuals initially assigned the InfB_lumen phenotype. (f) Conditions for schedule reassignment of an inflammatory bacterium.

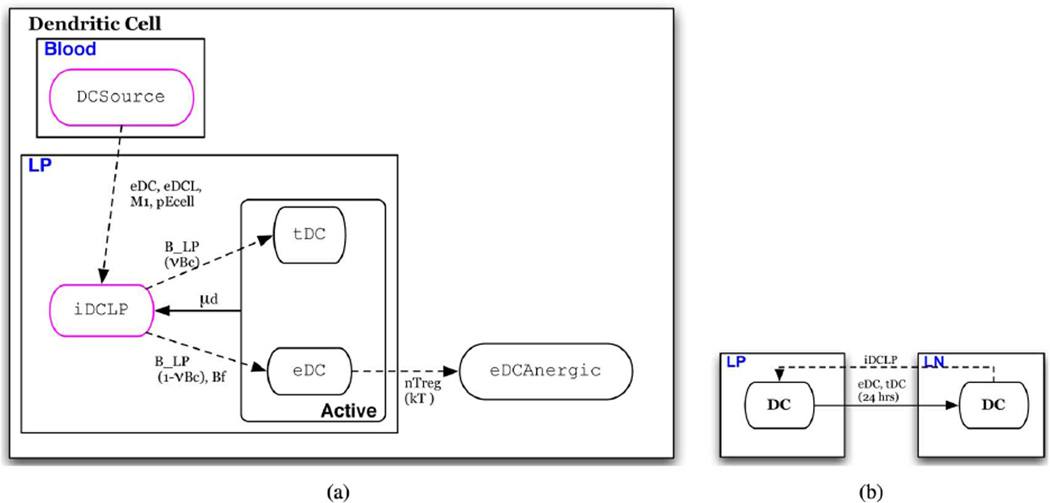
Fig. 6. Dendritic cell automaton.

(a) Automaton for dendritic cells; individuals initially assigned the iDCLP or DCSource phenotype. (b) Conditions for schedule reassignment of dendritic cells

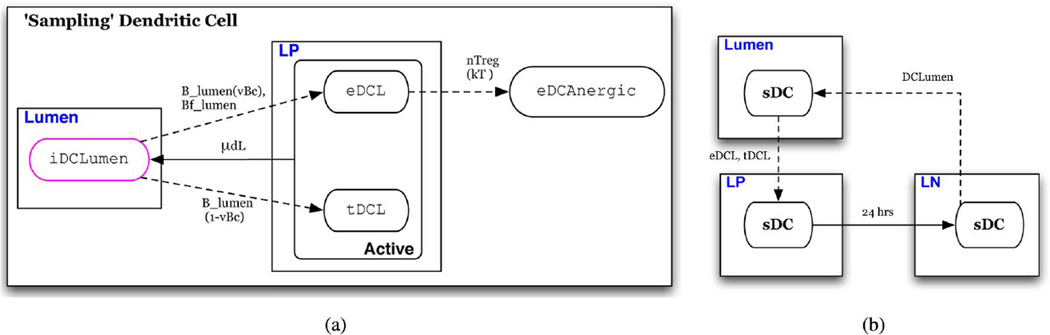
Fig. 7. ‘Sampling’ dendritic cell automaton.

(a) Automaton for commensal bacteria; individuals initially assigned the iDClumen phenotype (b) conditions for schedule reassignment of “sampling dendritic cells.”

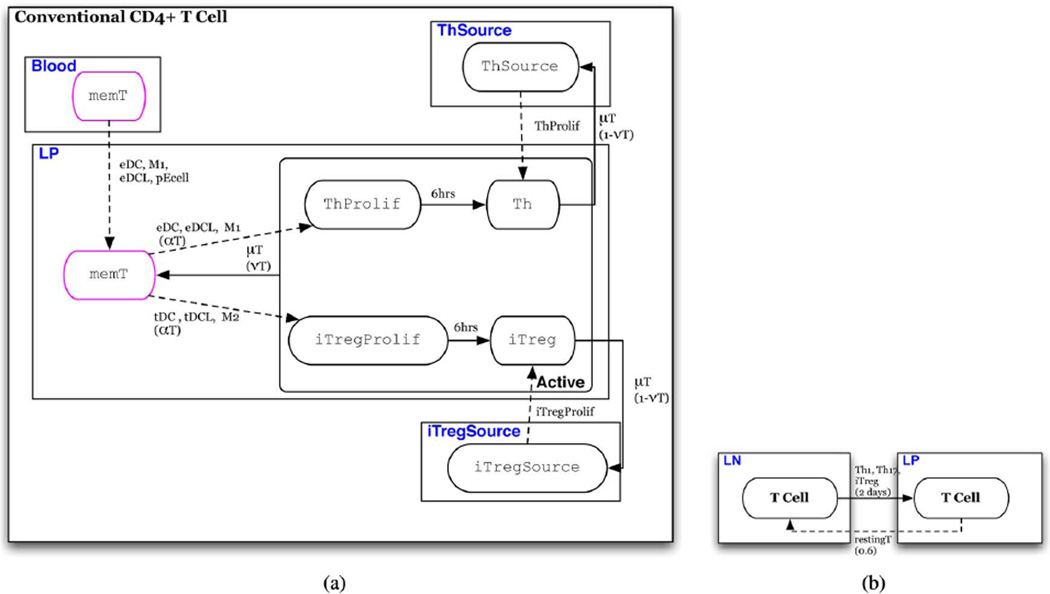
Fig. 8. T cell automaton.

(a) Automaton for T cells; individuals initially assigned the restingT or TSource phenotype. (b) Conditions for schedule reassignment of conventional CD4+ T cells.

Epithelial Cells (Fig. 3)

This population composes the epithelial barrier (EB). These cells are static and do not change sublocations or migrate to other tissues. Initially in the healthy EC state, the cell transitions to a damaged, proinflammatory state, pEcell, with the probability of v_EC upon contact with inflammatory immune cells, individuals in states Th, M1, or eDC. This represents secretion of cytokines, such as IL-6 and IL-17, that induce the NF_KBpathway in epithelial cells which leads to secretion of various pro-inflammatory mediators [3], [42] as well as cytotoxins secreted by M1 that damage epithelial cells. This transition also occurs in the presence of foreign or commensal bacteria that can induce epithelial damage with a probability of α v_EB, which will be specific to the bacterial strains that foreign bacterium and commensal bacterium are meant to represent.

Upon continued exposure to Th and M1, the damaged epithelial cell may transition to Edead state representing death of the epithelial cell that can occur with continued exposure to cytotoxic factors secreted by these inflammatory cells. In the Edeead state epithelial cells no longer secrete pro-inflammatory cytokines. From the pEcell and Edead states, the epithelial cell transitions to a healthy state after a time period of µ_E representing constitutive turnover that allows replacement of dead and inflammatory epithelial cells with healthy ones [40].

Bacteria (Fig. 4)

The model only represents individual bacterium that are in direct contact with the epithelial barrier (EB). There are three general types of bacteria represented: A tolerogenic bacterium that induces regulatory tDC and M2 phenotypes in antigen-presenting cells, an inflammatory bacterium that represents a general pathogen and induces an inflammatory M1 or eDC phenotype in antigen-presenting cells, and a general commensal bacterium that may have inflammatory and tolerogenic properties depending on user specifications. These may represent different strains present in the microbiota and are described below. Each may represent a single species of interest or a composite population within a population characteristics implicitly represented by parameter values. In general, all bacteria are initially present in the lumen. From the lumen, individuals may migrate to the LP represented by a state transition upon contact with Edead} or pEcell that triggers a schedule reassignment to the LP [Fig. 4(b), 4(d), 4(f)]. These transitions represent contact with either an epithelial cell made permeable by cytokine-induced damage or a hole in the epithelial barrier due to epithelial death. Individual bacterium in either location may be killed by microbicidal factors secreted by neighbors in the pEcell and M1 states as well as phagocytosis by resting macrophage (M0) and dendritic cells (iDCLP, iDCLumen) upon contact.

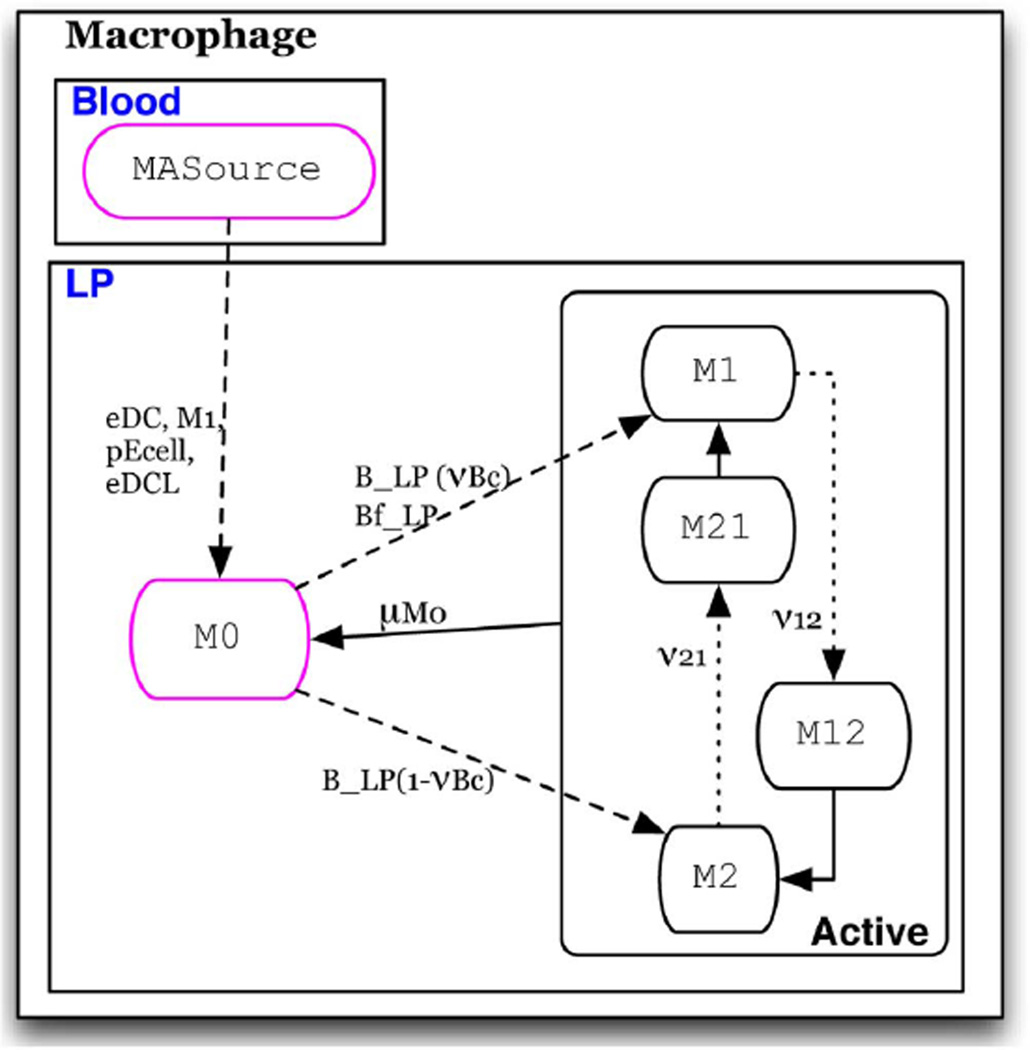
Macrophages (Fig. 5)

Fig. 5. Macrophage automaton.

Individuals initially assigned the M0 or MASource phenotype.

Macrophages occupy the LP where they move randomly and are initially in a resting M0 state. Individuals transition from the M0 state to M1 when in contact with inflammatory bacteria in the LP and to M2 when in contact with tolerogenic bacteria. Upon contact with neighbors that are a commensal bacterium, M0 transitions to M1 with a probability of v_BM, representing the percent of microbiota that is recognized as foreign and M2 state with the probability of 1 – v_BM. It is well established that macrophages may switch phenotypes as the cytokine ratio changes in the environment [1]. M2 may switch to M1 in the presence of inflammatory cytokines such as IFNϒ and TNFα. Conversely, M1 may switch to M2 when in the presence of the regulatory cytokine IL-10. In the model, these switches occur with a probability proportional to the number of inflammatory cytokine-secreting cells, N, and IL-10 secreting cells, R, in the shared sublocation. In ENISI transitions M1 → M2 and M2 → M1 are realized as group-cell interaction.

In the case of no cytokine stimulus, i.e., no contact with individual immune cells in either inflammatory or regulatory states, an activated macrophage will revert back to a resting state after a specified period of time, µ_M0. To represent monocyte recruitment, individuals initially in the inactive M ASource state transition to M0 when in contact with individuals in the pEcell, M1, or eDC states.

Dendritic Cells (Fig. 6)

Dendritic cells are initially in a resting, immature state in the LP (iDCLP)[Fig. 6(a)] These may be referred to as LP dendritic cells and are distinct from the “sampling” dendritic cells associated with the EB [2], [5]. The state transition model is similar to that of macrophages. An individual in the iDCLP state transitions to an inflammatory effector DC (eDC) upon contact with commensal bacteria with the probability of v_BD or when in contact with inflammatory bacteria. Alternatively, it transitions to a tolerogenic DC state (tDC) when in contact with commensal bacteria with a probability of 1 – _VBD, or when in contact with tolerogenic bacteria. In the mature states, tDC or eDC , the dendritic cell remains in the LP for 24 h before migrating to the LN [Fig. 6(b)]. The individual remains in one of these mature states for a time period µ_d before dying [43]. The model represents this removal by reversion to the iDCLP state, recycling the individual to replenish the immature dendritic cell pool from an assumed unlimited monocyte pool [Fig. 6(a)]. Upon transition to the iDCLP state, it is reassigned back to the LP [Fig. 6(b)]. Upon contact with neighbors in the active nTreg state, eDC is rendered anergic at a probability of k_T , transitioning to the eDCanergic state,where it is incapable of stimulating T cells [9]. To represent recruitment, DCSource transitions to iDC when in contact with individuals in the pEcell, M1, or eDC states.

Sampling” Dendritic Cells (sDC, Fig. 7)

sDC represents a dendritic cell that resides in the superficial LP, in association with the EB, where extensions of its cellular body breach the EB to contact and “sample” microbes in the lumen. These dendritic cells are believed to be a distinct phenotype from LP dendritic cells described above [3], [5]. This is represented by assigning resting sDC to the lumen represented by the iDCLumen state. It can be seen that the state transition path from iDCLumen is similar to that for LP dendritic cells. Those in the mature states tDCL and eDCL are assigned to the LP [Fig. 7(b)] and carry out the same functions and behaviors as those in the eDC and tDC states, respectively. However, the parameters governing lifespan and predisposition towards effector or tolerogenic phenotypes following antigen recognition may differ [5]. As a simplification, the default model assumes the same lifespan and probabilities of differentiation upon antigen recognition as LP dendritic cells. These assumptions may be revisited at a later date or modified by the user. As with LP dendritic cells, “sampling” dendritic cells in the mature state are assigned to the LN after 24 h. Upon reentry into the iDCLumen state, they are reassigned to the lumen.

Conventional CD4+ T cells (Fig. 8)

To conserve the number of individuals, the model only represents T cells that specifically recognize and are stimulated by products of the strains represented by the bacteria automata in the model. A T cell is initially in a restingT state that represents either a naive or memory T cell [Fig. 8(a)]. This resting T cell population is divided among the LP and LN locations with the majority, 60%, in the LN. The state TSource are resting T cell precursors and transition to the restingT state upon contact with chemoattractant secreting individuals in the eDC, eDCL, M1, and pECell states.An individual in the restingT state will transition to an active inflammatory Th when in contact with neighbors in the eDC,eDCL, or M1 state.

Alternatively, it may transition to an active iTreg when in contact with neighbors in the tDC, tDCL or M2 state. This rule represents the fact that T cell phenotype depends on the cytokines secreted by the APC during antigen recognition by the T cell receptor [44]. In either case, activation occurs with a probability of αT The value of αT represents the probability that the antigen presented by a specific APC is recognized by the receptor of the contacted T cell. Upon stimulation, the T cell enters a proliferation state, ThProlif or iTregProlif, for approximately 12 h [45]. In this state the cell can induce transition of source cells (ThSource, iTregSource) to a Th or iTreg state giving rise to a new population of active T cells of its same phenotype as described in Section III-C. The value pT is the average number of daughter T cells produced by one proliferating T cell in the LP, presumably from a stimulated effector memory T cell, and p_t is the average number of daughter T cells produced by one proliferating T cell in the LN, presumably from a stimulated central memory T cell or naive T cell. From this state, the individual T cell transitions to a non-proliferating active state, Th1 or iTreg. T cells that are activated in the LN are reassigned to the LP after a maturation period of 2 days [46].

T cells remain in an active state for a period µ_T after which a fraction, v_T, become memory T cells and may be re-stimulated by an APC, i.e. individuals in the M1, M2, tDC, or eDC states. Memory T cells remain in the LP with a probability of 0.4, representing effector memory T cells, or migrate to the LN with a probability of 0.6, representing central memory T cell. This fraction is based on a study in mice that showed 60% of CD8+ memory T cells created in response to lymphocytic choriomeningitis virus were CD62l+, a marker for a central memory as opposed to an effector memory T cell [47]. Such in vivo data was not found for CD4+ T cells specifically. Those that do not become memory T cells, undergo programmed cell death represented by reversion to its associated source state, ThSource or iTregSource, which are equally distributed among the LP and LN locations [Fig. 8(b)].

Natural T-regulatory Cells (nTreg) (Fig. 9)

Natural T-regulatory cells follow a very similar path to conventional T cells [Fig. 9(a)]. The primary difference is that an activated nTreg has only one, regulatory phenotype regardless of the state of the antigen presenting macrophage or dendritic cell. nTreg proliferate upon stimulation giving rise to p_Tr daughter cells. Whether memory nTreg actually proliferate upon stimulation in vivo is still not clear [48]. Hence, the value of p_Tr may be assigned according to the assumption one wishes to make regarding nTreg proliferation capacity following antigen recognition. Upon contact with neighbors in the M1, M2, eDC, or tDC state an individual in the rest_nTreg state transitions to the active nTreg state with a probability of α_Tr, potentially different from that of conventional CD4+ T cells. However, in the default model α_Tr = α_T. Migration of nTreg is similar to that of conventional T cells in that nTreg actived in the LN migrate to the LP after a maturation period of 2 days and memory nTreg are distributed between the LP and LN [Fig. 9(b)].

E. Parameter Estimation

There are three types of parameters that control whether an individual will occupy a specific state s on day d given that it is in state x on the previous day. These are i) the dwell time in state s, ii) the probability p_xs that an individual in state x will differentiate to state s, and iii) the constant factors of the group-cell interaction. Table IV lists the parameters of the ENISI model for a mouse gut. We have assigned the parameter values from the literature when definite measurements are available. Most dwell times are available in the literature. Due to representational differences between the observed biological information and ENISI we have done specific conversion of the measurement units. When direct information regarding specific parameters were not available we have used values with basic assumptions of the model. For example, ENISI simulates the cells which recognize and react to bacteria represented by their automata. Therefore, the parameter α_T is set at 1 as all T cells represented have receptors specific to the bacteria present. Similarly, macrophages are longer-lived and remain in active state by setting µ_M0 with the length of the simulation. For the single contact transition function we have set the default probability p=1.0 where no direct references were found. Adetailed description of biological assumptions can be found in [38]. There are certain parameters whose value is estimated to represent specific experimental conditions. For example, parameters related to bacterial automata are meant to represent a specific strain or family of strains. Such parameters need to be fit to experimental data for the specific strain to be represented.

IV. Implementation

ENISI is a parallel simulation framework that is designed to run on high performance computing (HPC) clusters. The ENISI framework is based on distributed computing model and implemented in C++ using the message passing interface (MPI).

There are three main components of the computation structure: cells as agents, locations, and message brokers. We assume a distributed parallel system which have N cores or processing elements (PEs). The processing is done in the following manner:

Partitioning

Cells and locations are partitioned into N groups denoted by C ₁, C ₂, …, C_N and L ₁, L ₂, …, L_N re- spectively. Currently, we use round-robin distribution to achieve uniform load balancing and simpler data management. Each PE also creates a copy of the message broker, denoted by MB ₁, MB ₂, …, MB_N. Each PE then executes the ENISI algorithm (described below) on its local data set (C_i, L_i).

Computing Visit Data

The first phase of the algorithm consists of computing a set of visits for each individual, Ci for the cycle according to the assigned schedule. A lightweight “copy” of each cell (called a visit message) is then sent to each location (which may be on a different PE) via the local message broker.

Computing Interactions

Each location receives the visit messages and forms a serial discrete event simulation (DES) by collecting the messages into a time-ordered list of arrive and depart events. Using this data, each location computes interactions for each individual at that location.

Collecting Interaction Messages

At the end of each cycle, interaction messages for each cell on a PE are merged, processed and the resulting state of each individual automaton is updated according to its type-specific transition function. If an individual c_j received a message it then transitions from its current state s_j to the next state in its automaton, x, with the probability p_sjx. This synchronous update at the end of each cycle assumes that any changes in behavior that result from the state transition do not take place until the next cycle. As each cycle represents six simulation hours, the synchronous update assumes a 6 h delay between a cell receiving the signal to differentiate and actual expression of cytokines or movement-mediating factors, such as integrins, that will affect subsequent movement, contacts, and effects on neighboring cells.

A pseudocode version of the algorithm is show below as Algorithm 2. All the PEs in the system are synchronized after each simulation phase above. This guarantees that each location has received all the data required to form a DES and each cell has all the data needed to compute its new state.

Algorithm 2.

A pseudocode description of the parallel version of the ENISI algorithm

initialize

partition data across PEs partition for t = 0 to Tincreasing by ∆t do

foreach cell cj∈ Ci do

Send visits to location PEs;

computeVisits (j, t to + ∆t);

sendVisits (MBi);

Visits ← MBi. retrieveMessages();

synchronize();

foreach location lk ∈ Li do

compose a serial DES;

makeEvents(k, Visits);

turn visit data into events;

computeInteractions (k);

Process Events;

sendOutcomes (MBi);

MBi. retrieveMessages();

synchronize();

foreach cj ∈ Ci

combine outcomes of multiple interactions;     updateState (cj);

V. Example Application: Explanation of B. hyodysenteriae Associated Pathogenesis

B. hyodysenteriae infection is characterized by severe dysentery in which epithelial lining is damaged and bacteria is detected in the LP resulting in fever and bloody diarrhea. Associated with infection is the phenomenon that, following B. hyodysenteriae-induced epithelial damage, normally tolerogenic commensal bacteria is able to induce an inflammatory response allowing persistent tissue damage [52].

Here we demonstrate an application of ENISI by simulating a typical inflammatory response to B. hyodysenteriae, an experimental model for acute immunopathological colonic inflammation. We then turn to examples of simulation output to identify a key pathway by which chronic inflammation may persist with continued epithelial cell damage following B. hyododysenteriae elimination.

Simulations with ENISI provide visual outputs in two formats; i) a plot of the total number of individuals in each state in each location over time and ii) a report of the number of individuals in each state that interact with an individual in a user-specified state s_i ∈ S and induce the state change s_i → x over a user-specified time period during the simulation. These counts may then be represented in a number of graphical formats.

In this demonstration, we seek to identify pathways that lead to two different health outcomes following infection, complete recovery and chronic inflammation. In this model we considered three locations for the gut: lumen, epithelial barrier, and lamina propria. Let ${\kappa }_s^t$ be the number of individuals in state s at time t and ${\kappa }_{[s,u]}^t$ be the number of individuals in state sor u at time . Complete recovery is a configuration in which ${\kappa }_{[B_{LP},B{f}_{LP},pEcell,Edead]}^t=0$ and ${\kappa }_{[Th,M1,eDC,eDCL]}^t<r$, where r is a threshold value, t > t_{Bf_dead}, and t_{Bf_dead} is the time at which the last cell enters the Bf_dead state. Chronic inflammation is a configuration in which ${\kappa }_{[B\_LP,pEcell,Edead]}^t\ge 1$ and ${\kappa }_{[Th,M1,eDC,eDCL]}^t\ge r$, where r = 1.

Parameter values for this demonstration are listed in Table IV and were assigned according to published observations of interactions between bacteria of the Brachyspira genus and immune cells or were fit to cell population dynamics reported in animal infection models [52], [53]. Parameter space was reduced by simplifying assumptions. For example, commensal strains represented do not induce an inflammatory response leading to the assignment v_BM = v_BD = v_Bs = 0. For a more detailed explanation of parameter estimation and assumptions, refer to [38].

Table I gives the number of individuals initially assigned to each of the states to represent an immunologically inactive system at the time of infection.

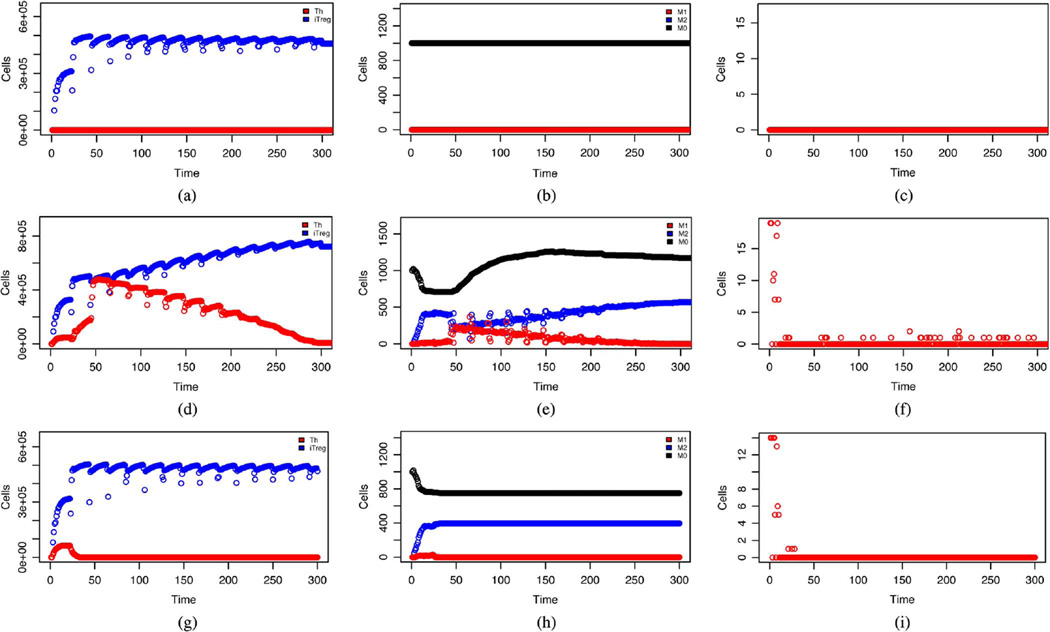
Fig. 10 shows simulated dynamics of certain cell populations over a period of 300 cycles (75 days) under different infection scenarios. The top panel shows expected behavior in a pathogen-free mucosa following population of the lumen by commensal bacteria [3], [5]. Specifically, immune activation occurs indicated by elevated k_tDC (not shown) and K_iTreg [Fig. 10(a)]. However, there is no inflammatory response nor damaged epithelial cells [Fig. 10(c)]. This inhibits bacterial invasion in to the LP and macrophages remain unstimulated [Fig. 10(b)]. The middle panel shows the system response to the addition of 30 individuals in the Bf_lumen state, representing B. hyodysenteriae, on days 1, 2, and 3. The dynamics observed are in agreement with those seen experimentally in pig infections [52], [53] and generally expected with three distinct phases; i) the acute inflammation (days 1–6) marked by an increase in k_eDC (not shown) and k_Th [Fig. 10(d)], followed by epithelial damage [Fig. 10(f)] that is shortly followed by bacterial invasion in to the LP (not shown). At this time macrophages are stimulated and we see k_M1 [Fig. 10(e)] rise in conjunction with k_Th [Fig. 10(d)] along with increased monocyte recruitment and transient reduction in M2 [Fig. 10(e)]; ii) the decline of inflammation (days 7–50) in which clinical signs of epithelial damage and bacterial invasion to the LP subside after 1 week [Fig. 10(f)] as the number of inflammatory T cells continues to rise, along with M1, before declining after 2 weeks. This decline occurs in conjunction with pathogen elimination; iii) the chronic phase (days 51–75) is marked by continued low level epithelial damage [Fig. 10(f)] along with bacterial presence in the LP (not shown). In this phase foreign bacteria has already been removed.

Fig. 10.

Dynamics of cell populations over a period of 75 days. Top: no pathogen present, Middle: following infection with B. hyodysenteriae, Bottom: following infection with B. hyodysenteriae without M1 mediated T cell stimulation. The x-axis is labelled in time units of 6 h. (a) T cells. (b) Macrophages. (c) Damaged epithelial cells. (d) T cells. (e) Macrophages. (f) Damaged epithelial cells. (g) T cells. (h) Macrophages. (i) Damaged epithelial cells.

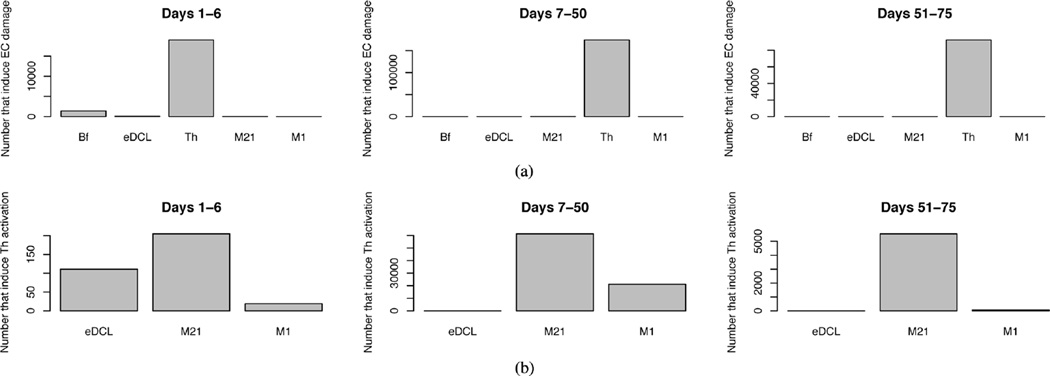
To identify the source of this continued epithelial damage we observed the states of those neighbors that induce the transition EC → pEcell for all epithelial cells that undergo this transition during the three phases of infection. In Fig. 11(a), it can be seen that at all stages of infection, it is individuals occupying the Th state that are inducing the most epithelial damage. In Fig. 11(b) we report the states of neighbors that induce the transition memT → Th showing clearly that, in the chronic phase, it is individuals in the transient state M21, an intermediate state between M2 and M1, that are solely responsible for Th stimulation. In this phase, only tolerogenic commensal bacteria is present to activate macrophages. To further demonstrate that it is stimulation of Th by macrophages that drives tissue damage, simulated infections were repeated in the absence of the ability of M1 to induce state change in neighbors of the memT state, allowing T cell stimulation to occur only through contact with eDC. The result is the dynamics shown in the bottom panel of Fig. 10. In this hypothetical scenario there is a weaker, more rapidly subsiding inflammatory response as “sampling” dendritic cells stimulate T cells. However, dendritic cell activation is short lived and once the pathogen is removed eDCL is quickly removed. The reduced k_Th during the acute inflammation phase results in less epithelial damage as well as lower inflammatory cytokine concentrations reducing the frequency of M2 → M1 transitions. This allows a tolerogenic environment to persist.

Fig. 11.

(a) Histogram of the number of individuals in each state that interact with an epithelial cell and induce the transition EC → pEcell. (b) Histogram of the number of individuals in each state that interact with a T cell and induce the transition memT → Th

The conclusion of this simple demonstration is that residual tissue damage following B. hyodysenteriae infection occurs through Th1/Th17-mediated cytotoxicity which is stimulated by M1 that has recently transitioned from the M2 phenotype. The presence of M1 is due to two parallel consequences of pathogen presence; i) the increase of the Th1/Th17 population that leads to increase of M1-inducing inflammatory cytokines in the tissue, and ii) increased damage of the epithelial layer which allows invasion of commensal bacteria. The implication is that commensal bacteria, which directly induces a tolerogenic response, is indirectly responsible for maintaining immunopathological chronic inflammation via macrophage stimulation once the environmental concentration of inflammatory cytokines reaches above a certain threshold. Further work will needs to be done to improve the computational model. For instance, current version of ENISI does not consider the age of the cell population. This affects the phenotypic transitions and result in some cases in periodic oscillations. Future versions of ENISI will take these limitations into account.

VI. Concluding Remarks

The ENISI is an extension of EpiSimdemics which is known to scale for massive networks approaching real world systems. Large scale network models are particularly important for immune simulators to reproduce a true cellular dynamics of a in vivo system where cell concentrations can reach 10⁸/mL [54]. For instance, extrapolating the results of the dynamics of a small sample might not represent the simulation of entire organ. To do so is to ignore the nonlinear and complex nature of the cell interactions and dynamics by making the assumption of uniform mixing of cellular and molecular components which defeats the purpose of an agent-based approach.

ENISI is an in silico system designed to simulate mucosal immune responses in the gut. Currently we can create a simulation specification using scripting language. A user-friendly graphical user interface is also available at http://www.modelingimmunity.org/modeling/enisi/enisi-job-submission-system/. Currently ENISI is being extended in a number of important directions. This includes: i) chemokine-dependent movement; ii) representing and studying specific bacterial species such as Helicobacter pylori and Escherichia coli; iii) refinement of effector T cell populations into separate Th1 and Th17 types; iv) better representation of cellular movement and cellular affinity so as to be able to show emergent phenomenon such as mucosal lesions; and v) further scaling to represent individuals on a modest compute cluster.