Abstract
Purpose
Recent work has shown that solid-state 1H and 31P MRI can provide detailed insight into bone matrix and mineral properties, thereby potentially enabling differentiation of osteoporosis from osteomalacia. However, 31P MRI of bone mineral is hampered by unfavorable relaxation properties. Hence, accurate knowledge of these properties is critical to optimizing MRI of bone phosphorus.
Methods
In this work, 31P MRI signal-to-noise ratio (SNR) was predicted on the basis of T1 and T2* (effective transverse relaxation time) measured in lamb bone at six field strengths (1.5 – 11.7 T) and subsequently verified by 3-D ultra-short echo-time and zero echo-time imaging. Further, T1 was measured in deuterium-exchanged bone and partially demineralized bone.
Results
31P T2* was found to decrease from 220.3 ± 4.3 μs to 98.0 ± 1.4 μs from 1.5 to 11.7 T, and T1 to increase from 12.8 ± 0.5 s to 97.3 ± 6.4 s. Deuteron substitution of exchangeable water showed that 76% of the 31P longitudinal relaxation rate is due to 1H-31P dipolar interactions. Lastly, hypomineralization was found to decrease T1, which may have implications for 31P MRI based mineralization density quantification.
Conclusion
Despite the steep decrease in the T2*/T1 ratio, SNR should increase with field strength as Bo0.4 for sample-dominated noise and as Bo1.1 for coil-dominated noise. This was confirmed by imaging experiments.
Keywords: 31P MRI, bone mineral, relaxation, mineralization, signal-to-noise ratio
Introduction
Bone mineral is a nanocrystalline, non-stoichiometric, highly substituted calcium apatite (1), most closely resembling calcium hydroxyapatite (Ca10(OH)2(PO4)6) (2,3) and carbonatoapatite type B (4-8), in which some phosphate ions are substituted by carbonate. Phosphorus-31 (31P) has spin I=½ and 100% natural abundance, and as a major component of bone mineral, it therefore should be ideally suited for quantitative evaluation of bone mineral.
Prior 31P NMR studies of bone mineral by magic-angle spinning (MAS) and cross-polarization (CP) from 1H (9-13) have detected the presence of a protonated phosphate group (HPO42−) having an isotropic chemical shift similar to that in octacalcium phosphate (Ca8(HPO4)2(PO4)4·5H2O), and chemical shift anisotropy similar to brushite (CaHPO4·2H2O). Wu, et al. argued that this makes HPO42− in bone mineral uniquely different from any such groups in synthetic models of bone mineral (13). Using 2-D 1H-31P heteronuclear correlation spectroscopy, Cho, et al. determined that bone mineral is also severely deficient in hydroxyl (OH−) groups, having approximately 21% of the OH− content of stoichiometric hydroxyapatite (14).
More recent work has shown that solid-state 1H and 31P MRI have the potential to quantify bone matrix and mineral densities, thereby providing information that is not available using current x-ray based clinical methods, but may enable differentiation of osteoporosis from osteomalacia. 31P NMR (15) and MRI (16-18) have shown substantial potential for quantification of bone mineral density, and 31P MRI of bone mineral has been proven feasible in vivo (19,20).
However, magnetic resonance imaging of solid-state phosphorus in bone is greatly complicated by unfavorable relaxation parameters. Greater net magnetization and higher Larmor frequency at higher magnetic fields generally increase signal strength, but prolonged T1 (longitudinal relaxation time) and reduced T2* (effective transverse relaxation time) as field strength increases may outweigh possible gains. Several groups have measured T1 and T2* of bone mineral 31P (15,17,20,21) under various conditions and selected field strengths, but no systematic study across field strengths has so far been performed.
The purpose of this work was to predict the dependence of bone mineral phosphorus signal-to-noise ratio (SNR) on static magnetic field strength and level of bone mineralization to aid in the design of an in vivo MRI protocol for measurement of bone mineral density. To accomplish this goal, the 31P T1 and T2* relaxation times were measured using NMR in unmodified, deuterium-exchanged, and partially demineralized lamb tibial cortical bone samples at six magnetic field strengths ranging from 1.5 T to 11.7 T using comparable transmit/receive radiofrequency (RF) coils. Relaxation times of unmodified bones were then used to predict the theoretically achievable image SNR at each field strength, and these predictions were compared with SNR measured in ultra-short echo-time (UTE) and zero echo-time (ZTE) images. Finally, the mechanisms responsible for longitudinal relaxation and the effect of demineralization on bone mineral 31P T1 were evaluated using measurements in deuterium-exchanged and partially demineralized bone, respectively.
Methods
Specimens
Lamb tibiae were obtained fresh from a local butcher, cleaned of soft tissue, marrow, and periosteum, wrapped in saline-soaked gauze and aluminum foil, and kept frozen at −20 °C until specimens were cut. Five cylindrical specimens of the tibial cortex (4 mm diameter, 10 mm length) were sectioned such that the specimen axis was parallel to the osteonal axis, and then scanned to determine the dependence of T1 and T2* relaxation times of bone mineral phosphorus on static magnetic field strengths. These specimens were later subjected to deuterium exchange to investigate the mechanisms responsible for longitudinal relaxation. A sixth, larger cylindrical cortical specimen (7 mm diameter, 30 mm length) was sectioned from a lamb tibia and imaged for comparison with predicted SNR trends. An additional five samples of cortical bone, weighing 300 mg each, were ground from the lamb tibiae in a mortar and pestle under liquid nitrogen. The resulting powders were used to measure the effect of partial demineralization on the relaxation times of bone mineral phosphorus. The initial T1s of bone powders (84.97 ± 1.57 μs) were similar to those of intact bone specimens (82.97 ± 2.18 μs), though a slight but statistically significant decrease in T1 was observed upon addition of saline (79.91 ± 2.44 μs). All specimens were stored in saline until the time of scanning. Intact specimens were gently blotted dry before scanning in a sealed vessel to prevent dehydration. Powder specimens were mixed with saline to facilitate transfer into 5 mm NMR tubes, centrifuged, the supernatant removed, and the precipitate scanned. All data were acquired at room temperature.
MRI Scanners and RF Coils
Experiments were performed on the following scanners: 1.5T, 3T, and 7T whole-body MRI scanners (Siemens, Erlangen, Germany); a 4.7T horizontal-bore animal MRI scanner (Varian, Palo Alto, CA); a 9.4T vertical-bore NMR spectrometer and micro-imaging system (Bruker, Billerica, MA); and a 11.7T vertical-bore NMR spectrometer (Varian, Palo Alto, CA).
For all except the 9.4T and 11.7T systems, a standardized set of transmit/receive (T/R) RF coils were constructed and used (1 cm diameter, 3 cm length, 10 turns per cm, shown in Figure 1). Each coil incorporated two interleaved solenoids connected in parallel, each with 5 turns per cm, to reduce the accumulation of phase along the electrical length of the coil. These coils were designed to have sensitivity and homogeneity properties similar to high-resolution NMR probes used in spectrometers. At 9.4 T and 11.7 T, vendor-supplied RF/gradient probes with one gradient axis (for spoiling) were used.
Figure 1.
Example standardized RF coil used at field strengths from 1.5 T to 7 T. Coils are transmit/receive parallel dual-conductor solenoids.
T1 Measurements
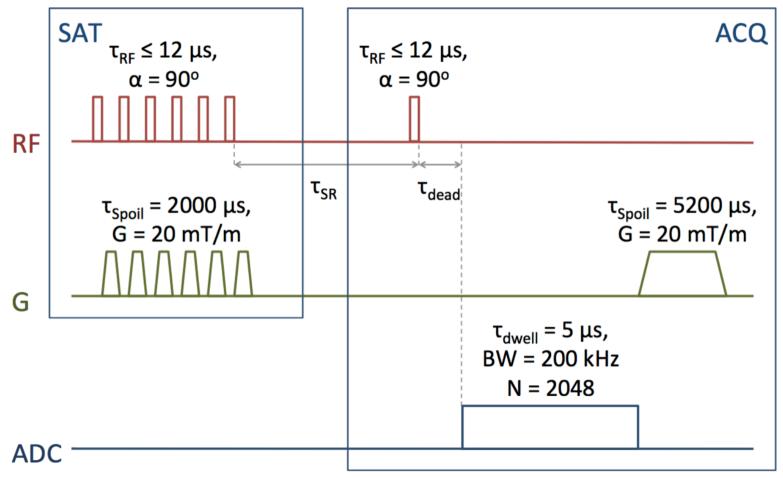
As T2* approaches the duration of an RF pulse, spins experience relaxation during the pulse and are rotated by less than the nominal flip angle, α=ω1TRF. To minimize the duration of RF excitation pulses relative to T2*, saturation-recovery rather than inversion-recovery was used for T1 measurements. A series of six 90-degree rectangular RF saturation pulses were applied, each followed by a spoiler gradient (duration = 2 ms, amplitude = 20 mT/m). Bloch equation simulations show that six repetitions of the saturation pulse-spoiler series saturates longitudinal magnetization to 0.1% of initial magnetization in the presence of a flip angle error of ±20%, and 0.0015% in the presence of a flip angle error of ±10%. After a saturation-recovery time (tSR) following the final saturation pulse, a 90-degree rectangular RF excitation pulse was applied, and free-induction decay (FID) acquisition was begun 20 μs after the end of this pulse. Transmit/receive dead time was taken into account during reconstruction by dropping points acquired before T/R switching was completed (a typical dead time is 40 μs). All 90-degree pulses were identical within each sequence, and RF pulse durations at 1.5, 3, 4.7, 7, 9.4, and 11.7 T were 20, 10, 12, 10, 7, and 12 μs, respectively. 2048 complex points were read out at a dwell time of 5 μs. After acquisition, a final spoiler gradient (duration = 5.2 ms, amplitude = 20 mT/m) was applied. TR was minimized for each repetition, leaving only 1 ms before the first saturation pulse and 1 ms after the final spoiler gradient. This sequence is diagrammed in Figure 2.
Figure 2.
Saturation-recovery pulse sequence used for bulk T1 relaxation time measurements.
T1s were calculated by non-linear least squares fitting of peak amplitudes (processing details are given below) to Eq. 1, where a, b, and T1 are fitted parameters:
| [1] |
T2* Measurements
T2* was measured using a pulse-acquire FID acquisition module identical to that of the saturation-recovery sequence used for T1 measurements. For fully mineralized bone experiments, this sequence was implemented separately from the saturation-recovery sequence. For deuterium exchange and partial demineralization measurements, the FID acquisition after the longest tSR was taken from the saturation-recovery data.
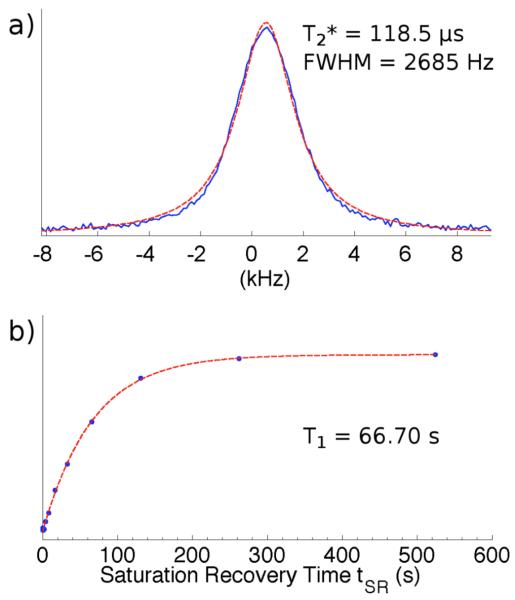
The resulting spectra (processing details are given below) fit a Lorentzian better than a Gaussian function; the quality of fit is shown in Figure 3. T2* was calculated from the full width at half maximum (FWHM) of the fitted Lorentzian:
| [2] |
Figure 3.
Sample 31P relaxation analysis data in specimen of lamb cortical bone at 7 T: a) lineshape (solid line) with Lorentzian fit (dashed line); b) saturation recovery data (points) with exponential fit (dashed line).
Multiple Fields and SNR Estimation
Each fully hydrated solid bone specimen was gently blotted dry and placed into a 5 mm sealed plastic tube (1.5 T - 7 T) or glass NMR tube (9.4 T, 11.7 T), and T1 and T2* measurements were performed. To estimate achievable spectral SNR, measured relaxation times were incorporated into a signal equation (22) which was modified to account for loss of phase coherence during the RF pulse and to include frequency-dependent sample-dominated and coil-dominated noise terms:
| [3] |
and
| [4] |
where
| [5] |
and
| [6] |
describe the response of transverse and longitudinal magnetization, respectively, to a square, on-resonance RF pulse of nominal flip angle α and duration TRF (23). These equations represent purely coil- or sample-dominated noise cases; in practice, actual noise dominance falls between these two extremes, and so these equations represent the upper and lower bounds of expected experimental conditions.
The duration of the RF pulse is much less than T2*, so fxy ≈ sin(α) and fz ≈ cos(α) and the Ernst angle equation, cos(α) = exp(-TR/T1), is therefore valid. The optimal flip angle, calculated using TR = 250 ms and the measured T1, was used as the nominal flip angle at each field strength, and a 10 μs RF pulse duration was assumed. SNR was estimated using dead times (tdead) ranging from 0 to 400 μs. SNR at each dead time was normalized to the value at 1.5 T to allow for comparison across field strengths and fitted to an empirically chosen power law, y = aB0b.
Deuterium Exchange
To determine the contribution of 1H-31P dipolar interaction to the longitudinal relaxation rate (R1 = T1−1) of bone mineral phosphorus, relaxation measurements were repeated on the intact bone specimens at 3 T and 7 T after deuterium oxide (D2O) exchange. The solid bone specimens were thoroughly blotted dry, immersed in 3 mL of D2O saline (a 25-fold volume excess) at 4 °C for 72 h, and scanned upon removal from the solution. The fraction of longitudinal relaxation rate attributed to 1H-31P heteronuclear dipolar interaction was quantified as
| [7] |
which follows from the ratio of the strengths of 1H and 2H dipolar coupling (given by the direct dipole-dipole spin Hamiltonian) (24):
| [8] |
where I1H = ½, I2H = 1, γ1H = 42.58 MHz/T, and γ2H = 6.54 MHz/T are the spin quantum numbers and gyromagnetic ratios of the two nuclei (25).
Partial Demineralization
A solid piece of lamb tibial cortical bone was immersed in liquid nitrogen and ground to powder with a pestle in a mortar. Five 300 mg portions of the powdered samples were measured and combined with 1.2 mL of saline, transferred to 5 mm NMR tubes, centrifuged to settle the powder, and the supernatant removed. Relaxation measurements of the precipitate were performed at 9.4 T, and the powder slurries were then transferred back to storage vials.
The slurries were again centrifuged and the saline supernatant was drawn off and saved. 1.2 mL of 1% ethylenediaminetetraacetic acid (EDTA) solution was added to each sample, and the samples were agitated and left at room temperature for three days to allow partial demineralization to occur. After three days, the samples were centrifuged and the EDTA solution was drawn off, saved, and replaced with 1.2 mL of fresh 1% EDTA solution. The samples were again agitated and left for another three days at room temperature, centrifuged, and the EDTA solution again drawn off and saved. The powders were rinsed with three 1.2 mL changes of water to remove any remaining EDTA and liberated phosphates. In each rinse cycle, water was added, the samples were thoroughly agitated, centrifuged, and the rinse water drawn off and saved. Thereafter, the precipitates were combined with 1.2 mL saline, transferred to 5 mm NMR tubes, and centrifuged. Relaxation measurements were performed on the precipitates at 9.4 T, and the saline and powder slurries transferred back to storage vials. All saline, phosphorus-containing EDTA solution, and rinse water which had been in contact with the bone powders was combined, lyophilized, and redissolved in 0.5 mL of water. The resulting solutions were scanned with a calibrated methylene diphosphonate (MDP) capillary using high-resolution 31P NMR to quantify the amount of phosphorus removed from each sample (number of dummy scans = 4, number of scans = 50, flip angle = 90 degrees, number of points = 65536, bandwidth = 13021 Hz, TR = 47.5 s).
The cycle comprising removal of saline to re-addition of saline, relaxation measurement, and high-resolution 31P NMR spectroscopy, was repeated two more times for a total of three levels of demineralization. Subsequently, 7 mL of 1.23M HCl was added to each powder specimen to dissolve all remaining bone mineral. After two days at room temperature, 10 mL of water and 1 mL of D2O was added to each sample, and high-resolution 31P NMR spectra were run to quantify the amount of phosphorus remaining in each sample of bone powder after the final round of EDTA demineralization. The sum of this amount and the amount of phosphorus removed during all rounds of partial demineralization is the total amount of bone mineral phosphorus initially present in the bone. The degree of demineralization after each round was quantified as the concentration of phosphorus in the saline, EDTA, and rinse liquids divided by this sum.
Spectroscopy Processing Details
Two signal averages were used for deuterium exchange measurements at 7 T, and four for all other measurements. Data were Fourier transformed and automatically phase-corrected based on peak symmetry. All reconstruction and processing were performed using custom scripts programmed in MATLAB (MathWorks, Natick, MA).
Imaging
To test predicted SNR behavior, a sixth, larger bone sample was imaged using two forms of radial pulse sequences: 3-D ramp-sampled UTE (26) and 3-D ZTE (27-31), so called in order to specify whether gradients are ramped up before or after RF excitation, respectively (32). These imaging sequences, shown in Figure 4, were implemented in SequenceTree (33) at 1.5 T, 3 T, and 7 T using the custom-built solenoidal RF coils described earlier. These clinical scanners all have maximum gradient amplitude of 40 mT/m and slew rate of 180 T/m/s.
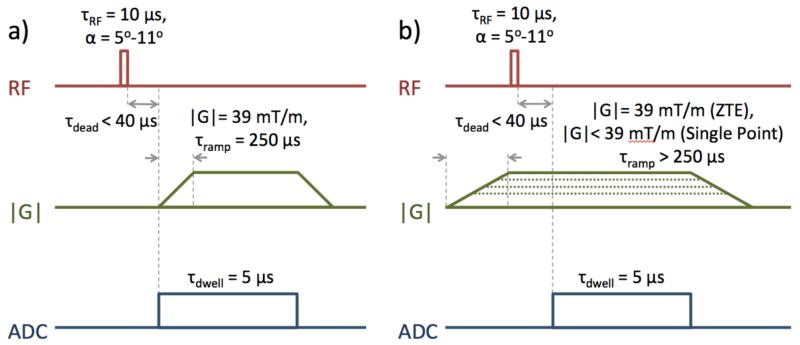
Figure 4.
Imaging pulse sequences used for SNR comparisons to predicted trends: a) ramp-sampled ultra-short echo time (UTE), and b) zero echo time (ZTE) PETRA, with single-point sampling of k-space center.
The UTE imaging sequence started with a 20 μs rectangular RF pulse followed 40 μs later by FID readout begun simultaneously with gradient ramp-up. The gradient direction was varied for each repetition to acquire center-out k-space half-projections distributed uniformly within a sphere using the method described by Wong and Roos (34). This simultaneous readout and gradient ramp-up allows acquisition of the central region of k-space, and the resulting non-uniform sampling density was corrected for during reconstruction. A flip angle equal to the Ernst angle was used at each field strength: 11.3, 7.9, and 5.0 degrees at 1.5 T, 3 T, and 7 T, respectively. Other acquisition parameters were: TR = 250 ms, number of points per readout N = 153, dwell time = 5 μs, number of projections = 5000, field of view (FOV) = 310 mm in all dimensions, gradient ramp time = 250 μs, gradient amplitude = 38.69 mT/m, and number of averages = 1.
The ZTE imaging sequence also begins with a 20 μs rectangular RF pulse, though this pulse is applied after gradients have stabilized at their constant maximum value. The gradient direction was again adjusted for each repetition to acquire the same distribution of center-out k-space half-projections as the UTE sequence. TR, dwell time, number and arrangement of projections, FOV, gradient amplitude, and number of averages were also identical to the UTE sequence described above, and the number of points per projection was N = 128. Because the gradient was already ramped up to full strength before excitation, the same portion of k-space is sampled as the 153-point UTE readout begun simultaneously with gradient ramp-up. Due to receiver dead time, FID readout was begun 40 μs after the end of the RF pulse. During this delay between excitation and beginning of readout, several k-space points are lost. These points were recovered after the main ZTE acquisition using the pointwise encoding time reduction with radial acquisition (PETRA) method (35), which involves single-point acquisition on Cartesian coordinates within a central sphere of k-space. Each single-point acquisition occurs at an echo time of 40 μs. This central Cartesian region was merged with the surrounding radial region during reconstruction.
Data from both UTE and ZTE sequences were re-mapped to a 256 × 256 × 256 point Cartesian coordinate grid. To compensate for non-uniform sampling density, the weight assigned to each k-space point during re-gridding was chosen according to the k-space ‘volume’ occupied by that point (26). Data were Fourier transformed using the non-equispaced fast Fourier transform (NFFT) C subroutine library (36). The reconstructed voxel resolution was 1.21 × 1.21 × 1.21 mm3; however, actual resolution is reduced from its nominal value by point spread function (PSF) blurring due to broad spectral line width.
The signal-to-noise ratio of each image was calculated by dividing the mean signal intensity within a volume of interest (VOI) drawn within the center of the bone sample to the mean signal intensity within a VOI drawn in a region of background noise.
Results
Relaxation Times and SNR
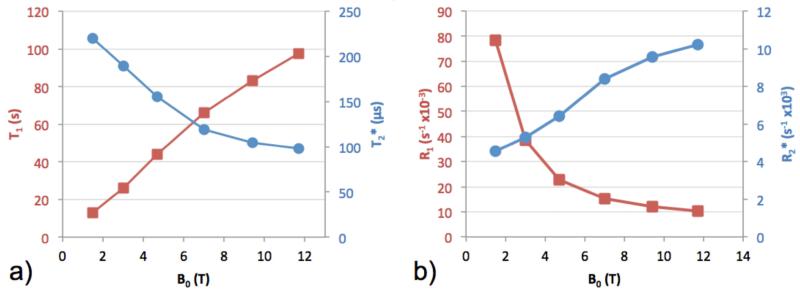
T1 was found to increase monotonically with field strength from 12.8 ± 0.5 s to 97.3 ± 6.4 s (mean ± standard deviation), and T2* to decrease from 220.3 ± 4.3 μs to 98.0 ± 1.4 μs. These results are shown in Figure 5. Fitted parameters a and b in Eq. 1 were observed to be approximately equal, indicating effective saturation.
Figure 5.
31P (a) T1 (squares) and T2* (circles) relaxation times and (b) R1 (squares) and R2* (circles) relaxation rates of bone mineral phosphorus in fully hydrated solid bone samples at six field strengths. Lines connecting points are a visual guide only, and do not represent data or predictions. Error bars are included, but do not extend beyond markers.
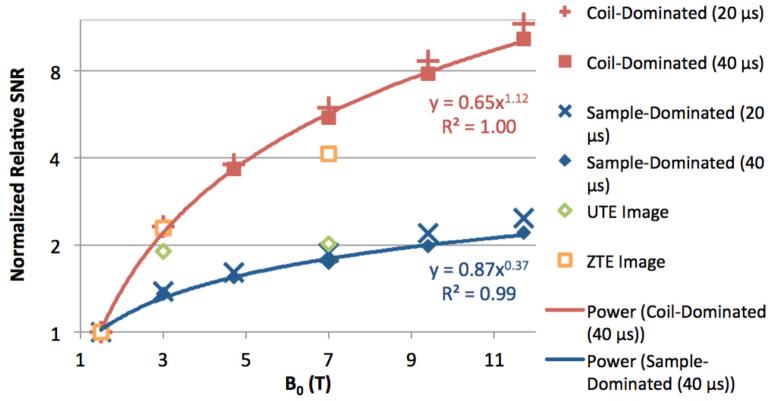
Predicted spectral SNR for both coil- and sample-dominated noise was normalized to their respective values at 1.5 T to facilitate comparison of field strength dependence between noise scenarios (Figure 6). Before normalization, predicted coil-dominated SNR is greater than sample-dominated SNR by a factor of 11.5 at 1.5 T. In each noise scenario, the field dependence is shown for both a realistic receiver dead time of 40 μs in UTE and ZTE imaging sequences reported in literature (in UTE and ZTE, echo time TE is more accurately described as receiver dead time, as no actual echo is created in these sequences). A clear SNR dependence on field strength is lost at tdead = 320 μs for coil-dominated noise, and tdead = 130 μs for sample-dominated noise. For tdead = 40 μs, SNR is predicted to increase as Bo0.4 for sample-dominated noise and Bo1.1 for coil-dominated noise.
Figure 6.
Predicted (solid markers) relative bone mineral 31P SNR based on measured relaxation times at multiple field strengths at tdead = 20 and 40 μs, normalized to the value at 1.5 T for each condition, and power fits (solid lines) at tdead = 40 μs. Relative SNR trends calculated from actual UTE and ZTE imaging acquisitions (open markers), also normalized to the value at 1.5 T for each condition.
Deuterium Exchange and Partial Demineralization
Replacement of exchangeable 1H atoms with 2H caused a substantial increase in T1, but only a very small, albeit significant, increase in T2*, as shown in Table 1. Eq. 7 suggests that 78.6 ± 2.0% of R1 is due to 1H-31P heteronuclear dipolar interaction at 3 T, and 74.3 ± 2.1% of R1 at 7 T. At each stage of partial demineralization, T1 decreased significantly while T2* showed no dependence on level of mineralization (Table 2).
Table 1.
Bone mineral phosphorus relaxation times in solid bone samples before and after D2O exchange
| B0 | Condition | T1 (s) | T2* (μs) | R1 (s−1×10−3) | R2* (s−1×10−3) |
|---|---|---|---|---|---|
| 3 T | Unmodified | 26.0 ± 1.4 | 189 ± 2.2 | 38.5 ± 2.0 | 5.29 ± 0.06 |
| D2O-Exchanged | 99.0 ± 10.5 | 203 ± 2.1 | 10.2 ± 1.0 | 4.92 ± 0.05 | |
|
| |||||
| 7 T | Unmodified | 66.0 ± 0.8 | 119 ± 0.4 | 15.2 ± 0.2 | 8.40 ± 0.03 |
| D2O-Exchanged | 218 ± 15 | 121 ± 1.0 | 4.6 ± 0.3 | 8.30 ± 0.07 | |
Table 2.
Bone mineral phosphorus relaxation times at 9.4 T in bone powder samples before and after three stages of demineralization
| % Mineralization | T1 (s) | T2* (μs) | R1 (s−1×10−3) | R2* (s−1×103) |
|---|---|---|---|---|
| 100.0 ± 0.0 | 79.9 ± 2.4 | 91.1 ± 0.3 | 12.5 ± 0.4 | 11.0 ± 0.03 |
| 97.4 ± 0.1 | 71.7 ± 1.6 | 91.8 ± 0.4 | 13.9 ± 0.3 | 10.9 ± 0.05 |
| 94.3 ± 0.4 | 68.5 ± 0.7 | 90.3 ± 0.5 | 14.6 ± 0.1 | 11.1 ± 0.06 |
| 92.0 ± 0.6 | 65.5 ± 1.2 | 91.7 ± 0.2 | 15.3 ± 0.3 | 10.9 ± 0.03 |
Imaging
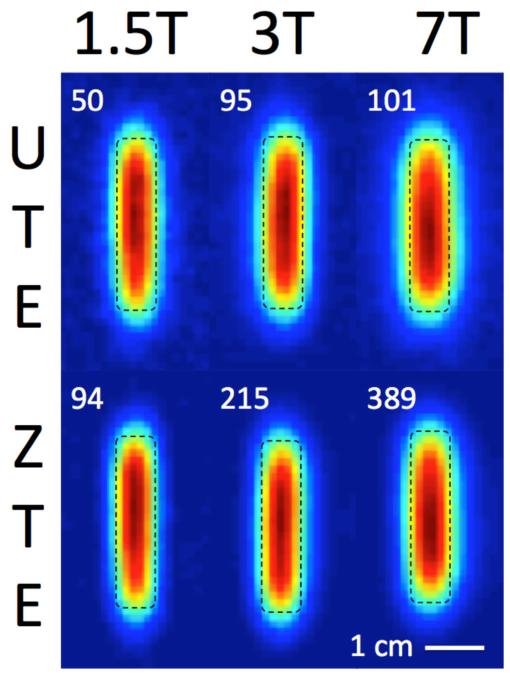
UTE and ZTE images of a cylindrical sample of lamb tibial cortical bone (7 mm diameter, 30 mm length) acquired at 1.5 T, 3 T, and 7 T are shown in Figure 7. Quality factor ratios (Qloaded/Qunloaded), which describe noise dominance, were 0.92, 0.74, and 0.21, respectively. Noise is therefore predominantly coil-dominated at 1.5 T and 3 T, and sample-dominated at 7 T. Image SNR is displayed in each panel of Figure 7, and relative SNR trends, normalized to the value at 1.5 T, are displayed within Figure 6. These trends roughly follow the coil-dominated SNR predictions for 1.5 T and 3 T, but diverge at 7 T.
Figure 7.
UTE and ZTE images (1.21 mm isotropic voxel resolution) of a longitudinal section through the center of a cylindrical solid cortical bone specimen (7 mm diameter, 30 mm length) at 1.5 T, 3 T, and 7 T, with SNR values. Specimen dimensions are indicated with a dashed line.
Discussion
The main objective of this study was to evaluate the dependence of SNR in solid-state 31P imaging on static magnetic field strength, with the expectation that the findings will have implications on the choice of field strength for in vivo 31P MRI studies of bone mineral. Although previous work has cast doubt on the notion that increasing field strength will yield a greater SNR (17,20,37), these prior studies were performed on different sets of bone specimens using disparate hardware and scanning parameters and, therefore, are not able to provide conclusive evidence to support or reject this hypothesis. Wu, et al. previously reported 31P T1s of 7 s, 19.8 ± 0.5 s, and 40 s in human cortical bone at 1.5 T (37), lamb cortical bone at 2.0 T (31), and dry rabbit cortical bone at 4.7 T (38), respectively, although the measurement of 51.1 s at 4.7 T by Cao, et al. (15) in fully hydrated rat cortical bone is more relevant to the present study. Robson, et al. (20) also measured a T1 of 8.6 ± 3.0 s in human cortical bone in vivo at 1.5 T. Anumula, et al. (17) found a value 54.1 ± 2.7 s for T1 in whole rabbit bone ex vivo at 9.4 T. Wu, et al. also reported 31P T2* of 199 μs and 143 μs at 1.5 T and 2.0 T, respectively. These values are similar to those found by Robson, et al. (207 ± 12 μs at 1.5 T), but are considerably larger than Anumula’s, et al. at 9.4 T (92.8 ± 7.5 μs). In addition to field strength, bone mineral 31P T1 is affected by the concentration of nearby 1H nuclei, which in turn could depend on species, age, porosity, and hydration state of the bone. Subtle differences in the composition of bone mineral, which is known to vary with age (12), may also affect measured relaxation times.
The present study employed standardized RF coils, acquisition parameters, and analysis, and measurements were performed on a single set of cortical bone specimens from the same species and anatomical location. Our results generally support the field strength behavior implied in these prior studies, although differences in the state of bone specimens have a considerable effect on relaxation times (for example, 31P T1s of dry rabbit cortical bone and hydrated rat cortical bone at 4.7 T differ by 28%).
Dipolar coupling involving protons, which is independent of B0, and chemical shift anisotropy, especially of the fraction of 31P in the form of HPO42− (104-128 ppm (13)), as well as induced local gradients arising from the difference in magnetic susceptibility between bone and water, both being linearly dependent on B0, contribute to the effective transverse relaxation rate (R2*) (Figure 5b). The near-absence of motional averaging of these interactions in bone mineral leads to extremely short 31P T2*, although the fact that the line shape fits best to a Lorentzian (rather than exhibiting a powder pattern) likely means that negligible motional averaging of chemical shift anisotropy does occur. This restricted motion also means that dipolar interactions with nearby 1H and 31P nuclei contain very little power at the 31P Larmor frequency, leading to a very long 31P T1. While a sharp increase in 31P T1 at high field would not be expected for a small, rapidly tumbling biomolecule such as ATP (1.42 ± 0.21 s, 1.35 s, and 1.24 s at 4 T, 7 T, and 9.4 T, respectively (39-41)), it is reasonable to expect such an increase in a solid due to the long rotational correlation time (42).
Based on the measurements presented in this study, we can conclude that although the relaxation properties of bone phosphorus do become significantly less favorable at higher field strengths, as long as RF pulse duration and receiver dead time are adequately short relative to T2* (TRF < 20 μs, Tdead < 40 μs), and k-space is traversed rapidly (tdwell ≈ 5 μs, G > 30 mT/m), then SNR can be expected to increase with B0 for both sample-dominated and coil-dominated noise.
Solid-state projection imaging pulse sequences implemented on clinical hardware with transmit/receive extremity coils already commonly meet such requirements for pulse duration, dead time, and bandwidth. It is important to note that Eqs. 3 and 4 predict spectral SNR, and do not include the effect of k-space apodization due to T2* decay during readout. Particularly in UTE where central k-space is traversed slowly during gradient ramping, the low-spatial-frequency signals are attenuated resulting in an SNR penalty (43).
Coil sensitivity and therefore SNR varies inversely with solenoid coil diameter, provided the length-to-diameter ratio is constant (44), so a significant decrease in SNR is expected with a larger solenoid receive coil. Birdcage coils, whose sensitivity is less than a solenoid of the same size, would entail a further SNR decrease. The predicted SNR trends should apply for a single RF coil arrangement, provided RF excitation at all field strengths can be accomplished by transmit pulses of equal duration, while still operating within limits on specific absorption rate (SAR) of RF power.
The predicted SNR behavior is supported by SNR calculated from images acquired at three field strengths (Figure 6). Mirroring findings by Weiger, et al. (43), the ZTE imaging pulse sequence was found to achieve higher SNR than its UTE counterpart at all field strengths (88%, 126%, and 285% at 1.5 T, 3 T, and 7 T, respectively). A possible explanation for this observation is that ZTE traverses k-space much more quickly than UTE (45) and, with PETRA, uses single-point acquisition to sample the central portion of k-space with a uniform, short delay time after excitation (46). Specifically, in ZTE, the time taken to reach k = 30 m−1, measured from the center of the RF pulse to arrival at that point, is 40 μs, while in UTE, the time taken to reach the same spatial frequency is much longer, approximately 190 μs, during which much more T2* signal decay would occur. This loss in relative SNR efficiency for UTE is exacerbated at elevated B0 due to shortened T2*. Noise also becomes sample-dominated at 7 T with a quality factor ratio of 0.21, causing image SNR for both sequences to fall below the predicted coil-dominated SNR trend.
While increasing static field strength does offer an SNR advantage, other important factors in MRI may become more problematic at high field. For example, as field strength increases and T2* decreases (spectral line width increases), PSF blurring will increase, further limiting intrinsic resolution. The FWHM of the PSF, with the gyromagnetic ratio expressed in MHz/T is given by Eq. 9:
| [9] |
At a gradient strength of 40 mT/m, the width of the PSF can be expected to increase from ~2.1 mm at 1.5 T to ~3.9 mm at 7 T. This effect is qualitatively visible in both UTE and ZTE images in Figure 7. Lastly, SAR increases quadratically with frequency, and could become a limiting factor at high field strengths.
While this work proposes that 31P SNR in cortical bone improves with field strength, the SNR of bone phosphorus is still several orders of magnitude lower than for 1H imaging of bone water. Assuming a T1 of 223 ms and T2* of 390 μs for bone water at 3 T (47), TR of 250 ms, flip angle equal to the Ernst angle at this T1 and TR, pulse duration of 10 μs, receiver dead time of 30 μs, and equal spin density, coil-dominated predicted SNR (Eqs. 3-6) is 55 times higher for 1H than for 31P of equal spin density. Intrinsic resolution, which depends on gyromagnetic ratio as well as T2*, is also finer in bone 1H imaging, achieving a point spread function FWHM of 0.48 mm at 40 mT/m gradient amplitude as opposed to 2.44 mm in 31P imaging.
Due to the different architecture of RF coils between the 1.5T – 7T scanners (solenoids) and the 9.4T – 11.7T scanners (saddle), the cylindrical axis of the sample must be orthogonal to the main magnetic field at 1.5 T – 7 T and parallel to the main magnetic field at 9.4 T and 11.7 T. Due to the incoherent macroscopic organization of bone mineral (48), we did not expect relaxation properties to depend on orientation with respect to B0, as does the collagen water proton signal (49,50). A cursory examination of relaxation times of bone specimens oriented parallel and perpendicular to the main magnetic field did not reveal a significant dependence.
It has been postulated that bone mineralization, and therefore demineralization, proceed under conservation of total bone volume (51). This means that as mineral is lost, it is replaced by water. Deuterium exchange has shown that 1H-31P dipolar interaction is the principal mechanism for T1 relaxation of phosphorus in bone. Thus, as suggested by Eq. 10 below, as demineralization progresses, the pool of water protons, N, contributing to 31P relaxation increases:
| [10] |
Although the number of protons, N, increases with distance, it is also possible that these additional water protons may be too far from the remaining 31P nuclei to contribute appreciably to relaxation; however, because the remaining mineral crystals are smaller after partial demineralization, the proportion of 31P nuclei at the surface of these crystals is increased (i.e. the surface-to-volume ratio of the crystals is greater after demineralization), also leading to an increase in longitudinal relaxation via a decrease in the average distance, r, between 31P and 1H nuclei. Because of the significant shortening of T1 at relatively modest levels of demineralization, use of a single, general value for T1 of bone mineral 31P across different subjects for eventual bone mineral density quantification may affect the accuracy of such an examination.
While the experimentally observed gains in SNR with field strength are in fair agreement with predictions, the gains in larger objects such as the human extremities are likely more modest. Even using an extremity coil, noise will presumably be sample-dominated, and so the in vivo SNR gain, illustrated in the sample-dominated SNR predictions in Figure 6, will likely not exceed a factor of two across the range of clinical field strengths. Lastly, besides diminishing SNR returns with increasing field strength, other criteria, including increased PSF blurring, must be taken into consideration when choosing a field strength for 31P imaging of mineralized tissues.
Conclusions
In spite of the steep increase in bone mineral 31P T1 and decrease in T2*, SNR is predicted to increase modestly with field strength. These predictions are supported as well by solid-state 31P imaging. This work also shows that 1H-31P dipolar interaction is the dominant longitudinal relaxation mechanism and that T1 is reduced with decreasing level of mineralization of bone. The results have implications on MRI-based studies of bone mineralization.
Acknowledgements
This work was supported in part by NIH R01 AR50068, NIH T32 EB009384, NIH F31 AG042289, the Howard Hughes Medical Institute International Student Research Fellowship (CL), and the University of Pennsylvania Institute for Translational Medicine and Therapeutics. This work was also supported in part by the National Center for Research Resources Grant UL1RR024134, and is now at the National Center for Advancing Translational Sciences Grant UL1TR000003. The content is solely the responsibility of the authors and does not necessarily represent the official views of the NIH.
The authors would like to thank Dr. Thomas J. Connick for his advice and substantial assistance in the design of RF coils and implementation of transmit/receive interfaces at 1.5 T, 3 T, and 7 T, and Dr. Stephen Pickup for implementing the FID and saturation-recovery pulse sequences on the Varian 4.7T and 11.7T systems.
List of Abbreviations
- 31P
31-Phosphorus
- SNR
signal-to-noise ratio
- T2*
effective transverse relaxation time
- T1
longitudinal relaxation time
- 3-D
three-dimensional
- MAS
magic angle spinning
- UTE
ultra-short echo time imaging
- ZTE
zero echo time imaging
- RF
radiofrequency
- B0
static magnetic field strength
- ω1
Larmor precession frequency in rotating frame of applied radiofrequency magnetic field
- TRF
time duration of radiofrequency pulse
- tSR
saturation-recovery time
- FID
free-induction decay
- FWHM
full width at half maximum
- tdead
transmit/receive switch dead time
- D2O
deuterium oxide
- R1
longitudinal relaxation rate
- EDTA
ethylenediamenetetraacetic acid
- MDP
methylene diphosphonate
- FOV
field of view
- PETRA
pointwise encoding time reduction with radial acquisition
- PSF
point spread function
- VOI
volume of interest
- Q
radiofrequency coil quality factor
- SAR
specific absorption rate of radiofrequency power
References
- 1.Levy M. Chemische untersuchungen über osteomalacische knochen. Z Physiol Chem. 1894;19:239–270. [Google Scholar]
- 2.DeJong W. La substance minérale dans les os. Rec Trav Chim. 1926;45:445–448. [Google Scholar]
- 3.Roseberry H, Hastings A, Morse J. X-ray analysis of bone and teeth. J Biol Chem. 1931;90:395–409. [Google Scholar]
- 4.Kaflak A, Chmielewski D, Gorecki A, Kolodziejski W. Kinetics of 1H --> 31P cross-polarization in human trabecular bone. Solid State Nucl Magn Reson. 1998;10(4):191–195. doi: 10.1016/s0926-2040(97)00085-4. [DOI] [PubMed] [Google Scholar]
- 5.Kaflak A, Chmielewski D, Gorecki A, Slosarczyk A, Kolodziejski W. Efficiency of 1H --> 31P NMR cross-polarization in bone apatite and its mineral standards. Solid State Nucl Magn Reson. 2006;29(4):345–348. doi: 10.1016/j.ssnmr.2005.11.005. DOI: 10.1016/j.ssnmr.2005.11.005. [DOI] [PubMed] [Google Scholar]
- 6.Kaflak A, Kolodziejski W. Phosphorus-31 spin-lattice NMR relaxation in bone apatite and its mineral standards. Solid State Nucl Magn Reson. 2007;31(4):174–183. doi: 10.1016/j.ssnmr.2007.04.005. DOI: 10.1016/j.ssnmr.2007.04.005. [DOI] [PubMed] [Google Scholar]
- 7.Kaflak A, Kolodziejski W. Kinetics of 1H --> 31P NMR cross-polarization in bone apatite and its mineral standards. Magn Reson Chem. 2008;46(4):335–341. doi: 10.1002/mrc.2207. DOI: 10.1002/mrc.2207. [DOI] [PubMed] [Google Scholar]
- 8.Kaflak-Hachulska A, Samoson A, Kolodziejski W. 1H MAS and 1H --> 31P CP/MAS NMR study of human bone mineral. Calcif Tissue Int. 2003;73(5):476–486. doi: 10.1007/s00223-002-2111-5. DOI: 10.1007/s00223-002-2111-5. [DOI] [PubMed] [Google Scholar]
- 9.Herzfeld J, Roufosse A, Haberkorn RA, Griffin RG, Glimcher MJ. Magic angle sample spinning in inhomogeneously broadened biological systems. Philos Trans R Soc Lond Ser B-Biol Sci. 1980;289(1037):459–469. doi: 10.1098/rstb.1980.0064. DOI: 10.1098/rstb.1980.0064. [DOI] [PubMed] [Google Scholar]
- 10.Rothwell WP, Waugh JS, Yesinowski JP. High-Resolution Variable-Temperature P-31 NMR of Solid Calcium Phosphates. J Am Chem Soc. 1980;102(8):2637–2643. DOI: 10.1021/ja00528a020. [Google Scholar]
- 11.Roufosse AH, Aue WP, Roberts JE, Glimcher MJ, Griffin RG. Investigation of the mineral phases of bone by solid state phosphorus-31 magic angle sample spinning nuclear magnetic resonance. Biochemistry. 1984;23(25):6115–6120. doi: 10.1021/bi00320a033. DOI: 10.1021/bi00320a033. [DOI] [PubMed] [Google Scholar]
- 12.Roberts JE, Bonar LC, Griffin RG, Glimcher MJ. Characterization of very young mineral phases of bone by solid-state phosphorus-31 magic angle sample spinning nuclear magnetic resonance and x-ray diffraction. Calcif Tissue Int. 1992;50(1):42–48. doi: 10.1007/BF00297296. DOI: 10.1007/bf00297296. [DOI] [PubMed] [Google Scholar]
- 13.Wu Y, Glimcher MJ, Rey C, Ackerman JL. A unique protonated phosphate group in bone mineral not present in synthetic calcium phosphates. Identification by phosphorus-31 solid state NMR spectroscopy. J Mol Biol. 1994;244(4):423–435. doi: 10.1006/jmbi.1994.1740. DOI: 10.1006/jmbi.1994.1740. [DOI] [PubMed] [Google Scholar]
- 14.Cho G, Wu Y, Ackerman JL. Detection of hydroxyl ions in bone mineral by solid-state NMR spectroscopy. Science. 2003;300(5622):1123–1127. doi: 10.1126/science.1078470. DOI: 10.1126/science.1078470. [DOI] [PubMed] [Google Scholar]
- 15.Cao H, Nazarian A, Ackerman JL, Snyder BD, Rosenberg AE, Nazarian RM, Hrovat MI, Dai G, Mintzopoulos D, Wu Y. Quantitative (31)P NMR spectroscopy and (1)H MRI measurements of bone mineral and matrix density differentiate metabolic bone diseases in rat models. Bone. 2010;46(6):1582–1590. doi: 10.1016/j.bone.2010.02.020. DOI: 10.1016/j.bone.2010.02.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Anumula S, Magland J, Wehrli SL, Ong H, Song HK, Wehrli FW. Multi-modality study of the compositional and mechanical implications of hypomineralization in a rabbit model of osteomalacia. Bone. 2008;42(2):405–413. doi: 10.1016/j.bone.2007.10.011. DOI: 10.1016/j.bone.2007.10.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Anumula S, Magland J, Wehrli SL, Zhang H, Ong H, Song HK, Wehrli FW. Measurement of phosphorus content in normal and osteomalacic rabbit bone by solid-state 3D radial imaging. Magn Reson Med. 2006;56(5):946–952. doi: 10.1002/mrm.21050. DOI: 10.1002/mrm.21050. [DOI] [PubMed] [Google Scholar]
- 18.Anumula S, Wehrli SL, Magland J, Wright AC, Wehrli FW. Ultra-short echo-time MRI detects changes in bone mineralization and water content in OVX rat bone in response to alendronate treatment. Bone. 2010;46(5):1391–1399. doi: 10.1016/j.bone.2010.01.372. DOI: 10.1016/j.bone.2010.01.372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Wu Y, Reese TG, Cao H, Hrovat MI, Toddes SP, Lemdiasov RA, Ackerman JL. Bone mineral imaged in vivo by 31P solid state MRI of human wrists. J Magn Reson Imaging. 2011;34(3):623–633. doi: 10.1002/jmri.22637. DOI: 10.1002/jmri.22637. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Robson MD, Gatehouse PD, Bydder GM, Neubauer S. Human imaging of phosphorus in cortical and trabecular bone in vivo. Magn Reson Med. 2004;51(5):888–892. doi: 10.1002/mrm.20055. DOI: 10.1002/mrm.20055. [DOI] [PubMed] [Google Scholar]
- 21.Ackerman JL, Wu Y, Reese TG, Cao H, Hrovat MI, Toddes SP, Lemdiasov RA. In Vivo 31P Solid State MRI of Human Wrists: Short-T2 MRI Using the Scanner 1H Channel; Proceedings of the 19th Annual Meeting of the International Society for Magnetic Resonance in Medicine; Montreal, QC. 2011. Abstract nr 427. [Google Scholar]
- 22.Techawiboonwong A, Song HK, Wehrli FW. In vivo MRI of submillisecond T(2) species with two-dimensional and three-dimensional radial sequences and applications to the measurement of cortical bone water. NMR Biomed. 2008;21(1):59–70. doi: 10.1002/nbm.1179. DOI: 10.1002/nbm.1179. [DOI] [PubMed] [Google Scholar]
- 23.Sussman MS, Pauly JM, Wright GA. Design of practical T2-selective RF excitation (TELEX) pulses. Magn Reson Med. 1998;40(6):890–899. doi: 10.1002/mrm.1910400615. [DOI] [PubMed] [Google Scholar]
- 24.Abragam A. In: The Principles of Nuclear Magnetism. Marshall WC, Wilkinson DH, editors. Oxford University Press; Oxford: 1961. pp. 294–297. [Google Scholar]
- 25.Bernstein MA, King KF, Zhou XJ. Handbook of MRI Pulse Sequences. Elsevier Academic Press; Burlington, MA: 2004. p. 960. [Google Scholar]
- 26.Glover GH, Pauly JM, Bradshaw KM. B-11 imaging with a 3-dimensional reconstruction method. Journal of Magnetic Resonance Imaging. 1992;2(1):47–52. doi: 10.1002/jmri.1880020109. DOI: 10.1002/jmri.1880020109. [DOI] [PubMed] [Google Scholar]
- 27.Hafner S. Fast imaging in liquids and solids with the back-projection low angle shot (BLAST) technique. Magnetic Resonance Imaging. 1994;12(7):1047–1051. doi: 10.1016/0730-725x(94)91236-p. DOI: 10.1016/0730-725x(94)91236-p. [DOI] [PubMed] [Google Scholar]
- 28.Kuethe DO, Caprihan A, Fukushima E, Waggoner RA. Imaging lungs using inert fluorinated gases. Magnetic Resonance in Medicine. 1998;39(1):85–88. doi: 10.1002/mrm.1910390114. DOI: 10.1002/mrm.1910390114. [DOI] [PubMed] [Google Scholar]
- 29.Madio DP, Gach HM, Lowe IJ. Ultra-fast velocity imaging in stenotically produced turbulent jets using RUFIS. Magnetic Resonance in Medicine. 1998;39(4):574–580. doi: 10.1002/mrm.1910390410. DOI: 10.1002/mrm.1910390410. [DOI] [PubMed] [Google Scholar]
- 30.Madio DP, Lowe IJ. Ultra-fast imaging using low flip angles and FIDs. Magnetic Resonance in Medicine. 1995;34(4):525–529. doi: 10.1002/mrm.1910340407. DOI: 10.1002/mrm.1910340407. [DOI] [PubMed] [Google Scholar]
- 31.Wu Y, Ackerman JL, Chesler DA, Li J, Neer RM, Wang J, Glimcher MJ. Evaluation of bone mineral density using three-dimensional solid state phosphorus-31 NMR projection imaging. Calcif Tissue Int. 1998;62(6):512–518. doi: 10.1007/s002239900471. [DOI] [PubMed] [Google Scholar]
- 32.Weiger M, Pruessmann KP, Hennel F. MRI with Zero Echo Time: Hard versus Sweep Pulse Excitation. Magnetic Resonance in Medicine. 2011;66(2):379–389. doi: 10.1002/mrm.22799. DOI: 10.1002/mrm.22799. [DOI] [PubMed] [Google Scholar]
- 33.Magland J. SequenceTree. 4.2.1; 2009.
- 34.Wong STS, Roos MS. A strategy for sampling on a sphere applied to 3D selective RF pulse design. Magnetic Resonance in Medicine. 1994;32(6):778–784. doi: 10.1002/mrm.1910320614. DOI: 10.1002/mrm.1910320614. [DOI] [PubMed] [Google Scholar]
- 35.Grodzki DM, Jakob PM, Heismann B. Ultrashort echo time imaging using pointwise encoding time reduction with radial acquisition (PETRA) Magn Reson Med. 2012;67(2):510–518. doi: 10.1002/mrm.23017. DOI: 10.1002/mrm.23017. [DOI] [PubMed] [Google Scholar]
- 36.Keiner J, Kunis S, Potts D. NFFT: Chemnitz University of Technology.
- 37.Wu Y, Ackerman JL, Chesler DA, Wang J, Glimcher MJ. In Vivo Solid State 31P MRI of Human Tibia at 1.5T; Proceedings of the 7th Annual Meeting of the International Society for Magnetic Resonance in Medicine; 1999. [Google Scholar]
- 38.Wu Y, Chesler DA, Glimcher MJ, Garrido L, Wang J, Jiang HJ, Ackerman JL. Multinuclear solid-state three-dimensional MRI of bone and synthetic calcium phosphates. Proc Natl Acad Sci U S A. 1999;96(4):1574–1578. doi: 10.1073/pnas.96.4.1574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Du F, Zhu XH, Qiao H, Zhang X, Chen W. Efficient in vivo 31P magnetization transfer approach for noninvasively determining multiple kinetic parameters and metabolic fluxes of ATP metabolism in the human brain. Magn Reson Med. 2007;57(1):103–114. doi: 10.1002/mrm.21107. DOI: 10.1002/mrm.21107. [DOI] [PubMed] [Google Scholar]
- 40.Du F, Zhu XH, Zhang Y, Friedman M, Zhang N, Ugurbil K, Chen W. Tightly coupled brain activity and cerebral ATP metabolic rate. Proceedings of the National Academy of Sciences of the United States of America. 2008;105(17):6409–6414. doi: 10.1073/pnas.0710766105. DOI: 10.1073/pnas.0710766105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Du F, Cooper A, Lukas SE, Cohen BM, Ongur D. Magnetic Resonance Imaging. 2012. Creatine kinase and ATP synthase reaction rates in human frontal lobe measured by (31)P magnetization transfer spectroscopy at 4T. DOI: 10.1016/j.mri.2012.06.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Bloembergen N, Purcell EM, Pound RV. Relaxation effects in nuclear magnetic resonance absorption. Physical Review. 1948;73(7):679–712. DOI: 10.1103/PhysRev.73.679. [Google Scholar]
- 43.Weiger M, Pruessmann KP, Bracher AK, Kohler S, Lehmann V, Wolfram U, Hennel F, Rasche V. High-resolution ZTE imaging of human teeth. NMR Biomed. 2012;25(10):1144–1151. doi: 10.1002/nbm.2783. DOI: 10.1002/nbm.2783. [DOI] [PubMed] [Google Scholar]
- 44.Peck TL, Magin RL, Lauterbur PC. Design and analysis of microcoils for NMR microscopy. J Magn Reson B. 1995;108(2):114–124. doi: 10.1006/jmrb.1995.1112. [DOI] [PubMed] [Google Scholar]
- 45.Weiger M, Pruessmann KP. MRI with Zero Echo Time. In: Grant DM, Harris RK, editors. Encyclopedia of Magnetic Resonance. John Wiley; Chichester: 2012. [Google Scholar]
- 46.Grodzki DM, Jakob PM, Heismann B. Ultrashort echo time imaging using pointwise encoding time reduction with radial acquisition (PETRA) Magn Reson Med. 2011 doi: 10.1002/mrm.23017. DOI: 10.1002/mrm.23017. [DOI] [PubMed] [Google Scholar]
- 47.Du J, Carl M, Bydder M, Takahashi A, Chung CB, Bydder GM. Qualitative and quantitative ultrashort echo time (UTE) imaging of cortical bone. J Magn Reson. 2010;207(2):304–311. doi: 10.1016/j.jmr.2010.09.013. DOI: 10.1016/j.jmr.2010.09.013. [DOI] [PubMed] [Google Scholar]
- 48.Rho JY, Kuhn-Spearing L, Zioupos P. Mechanical properties and the hierarchical structure of bone. Med Eng Phys. 1998;20(2):92–102. doi: 10.1016/s1350-4533(98)00007-1. DOI: 10.1016/s1350-4533(98)00007-1. [DOI] [PubMed] [Google Scholar]
- 49.Fullerton GD, Rahal A. Collagen structure: the molecular source of the tendon magic angle effect. J Magn Reson Imaging. 2007;25(2):345–361. doi: 10.1002/jmri.20808. DOI: 10.1002/jmri.20808. [DOI] [PubMed] [Google Scholar]
- 50.Ong HH, Wright AC, Wehrli FW. Deuterium nuclear magnetic resonance unambiguously quantifies pore and collagen-bound water in cortical bone. J Bone Miner Res. 2012 doi: 10.1002/jbmr.1709. DOI: 10.1002/jbmr.1709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Robinson RA, Elliott SR. The water content of bone. I. The mass of water, inorganic crystals, organic matrix, and CO2 space components in a unit volume of the dog bone. J Bone Joint Surg Am. 1957;39-A(1):167–188. [PubMed] [Google Scholar]