FEATURE RANKING BASED NESTED SUPPORT VECTOR MACHINE ENSEMBLE FOR MEDICAL IMAGE CLASSIFICATION

Abstract

This paper presents a method for classification of structural magnetic resonance images (MRI) of the brain. An ensemble of linear support vector machine classifiers (SVMs) is used for classifying a subject as either patient or normal control. Image voxels are first ranked based on the voxel wise t-statistics between the voxel intensity values and class labels. Then voxel subsets are selected based on the rank value using a forward feature selection scheme. Finally, an SVM classifier is trained on each subset of image voxels. The class label of a test subject is calculated by combining individual decisions of the SVM classifiers using a voting mechanism. The method is applied for classifying patients with neurological diseases such as Alzheimer’s disease (AD) and autism spectrum disorder (ASD). The results on both datasets demonstrate superior performance as compared to two state of the art methods for medical image classification.

1. INTRODUCTION

Neurological diseases such as autism spectrum disorder (ASD) and Alzheimer’s disease (AD) are an ever growing health burden in the United States. Early detection of these diseases can significantly improve prognosis. However, diagnosis of these diseases is based on clinical evaluation, history and neuropsychological tests; clinical evaluation is subjective and neuropsychological tests do not always have a high accuracy for detecting early stages of disease. Magnetic resonance imaging (MRI) offers the possibility of an objective and quantitative strategy for early diagnosis of these diseases. Nevertheless, crunching the large amount of information presented by voxels in an MR image into a binary clinical diagnosis is extremely challenging. Hence, in recent years, a substantial research effort has been directed at the development of high dimensional classification methods to discriminate between patients and normal controls using MR scans.

A detailed review of recent methods used for MR image classification is given in [1]. Most methods use a supervised classification framework. In this framework: a) training images with known labels are aligned to a common space, b) discriminative features are extracted, c) an SVM classifier is trained on these features. Extracted features may simply be voxel intensity values from the whole brain [2], a smaller set of values from selected voxels[2], or features calculated from regions of interest (ROIs)[3]. These ROIs are either predefined or learned from the data.

One major challenge of medical image classification is the very high dimensionality of the image domain. A typical MRI scan of the brain includes several millions of measurements on respective image voxels. Furthermore, depending on the type of the disease, pathology might cause subtle changes in specific brain ROIs (e.g. atrophy of the hippocampus), on the whole brain (e.g. atrophy of the gray matter), or even both together. In order to obtain high classification performance on different datasets, a classifier should be trained on features that capture different patterns of structural degeneration, going from very localized to completely global.

With this aim, we extend and improve upon the supervised classification framework by using two established concepts of machine learning, a) ensemble learning, and b) feature ranking.

Ensemble learning [4] involves training multiple classifiers on different feature sets. Prediction is done by combining the decisions of all classifiers on the test data. In this way, one aims to obtain a classifier that overperforms each individual classifier. SVM ensembles have been shown to have improved performance over single SVMs [5, 6], and a more robust performance on unbalanced datasets [6].

Feature ranking focuses on ordering features based on their relevance to classification. In [7] it was shown that training on a diverse set of features decreases the probability of generalization error in ensemble of classifiers. In this work, we use a feature ranking strategy as a first step for constructing nested feature subsets. The features with the highest ranking are grouped in the first feature subset. Each subsequent subset extends the previous one by adding less discriminative features, until all features are included. Each SVM classifier in the ensemble is trained on one of these feature vectors.

The method is applied for classifying two different neurological diseases: Alzheimer’s disease (AD) and autism spectrum disease (ASD). The results on both datasets demonstrate superior performance as compared to two state of the art methods [2, 3] for medical image classification.

2. METHOD

Our method consists of two steps: 1) Generation of nested feature subsets, 2) Training and testing using SVM ensemble classifiers.

2.1. Generation of nested feature subsets

Feature selection has been an active research area in applications that involve very high dimensional data. Selection of a subset of relevant features from the available data before applying a learning model could avoid overfitting and improve the generalization ability of the final classifier. Also, feature selection allows a better understanding and visualization of the data and the learned model. Selection of the optimal feature set for a classification task is a NP-hard problem and is only feasible for datasets with low dimensionality. For high dimensional data, a practical alternative is the univariate feature ranking. In this technique, a score is calculated for each feature based on its relevance to the specific classification problem, independently from the others. The features are then ranked by the assigned score from highest to lowest.

In this work, we used Welch’s t-test for ranking individual image voxels in order of their discriminative power with respect to class labels. Let $\mathbf{I}={\{{\mathbf{I}}_i^{yi}\in R^n\}}_{i=1}^m$ be a set of m training images with known class labels y_i ∈ {+1, −1}, aligned to a common template space. For each voxel x_j, j ∈ {1,…,n}, a t-score is calculated, defined as:

$$t_j=\frac{|{\overline{X}}_{j,+1}-{\overline{X}}_{j,-1}|}{\sqrt{\frac{s_{j,+1}^2}{N+1}+\frac{s_{j,-1}^2}{N-1}}}$$ (1)

where X̄_j,+1 and X̄_j,−1 are the mean intensities, $s_{j,+1}^2\text{and}{s}_{j,-1}^2$ are the variances of intensities, and N₊₁, N₋₁ are the number of samples in the respective classes.

The voxels are ordered by the calculated t-score, from most significant to least significant, and a rank value r_j is assigned to each voxel.

K nested feature sets f_k, k = {1,…,K} are selected from image voxels based on the rank values:

$$f_k=\underset{j=1}{\overset{\lfloor n{(\frac{k}{K})}^{\alpha }\rfloor }{\cup }}{x}_{r_j}$$ (2)

where α is a parameter that describes the rate of increase in number of voxels added to subsequent nested subsets.

The feature sets are constructed so that the voxels with the highest t-score are selected first. Voxels with lower t-score are added incrementally to form multiple sets of features. This process continues until all voxels in the image are selected in a final feature set (Figure 1). This method of feature selection ensures that each feature set is a subset of the subsequent set, and hence constitutes a nested forward feature selection scheme. In this scheme, voxels with the highest ranking are included in all feature sets and voxels with the lowest ranking are only included in one feature set that contains all voxels. This nested fashion of feature selection enforces an implicit weighting of voxels as features.

Fig. 1.

Nested subsets generated using feature ranking. Red indicates higher ranked voxels.

2.2. SVM Ensemble

An SVM constructs a hyperplane in a high-dimensional space that separates training samples with the largest distance to the nearest samples. It has been shown, both theoretically and practically, that this hyperplane minimizes the generalization error of the classifier. SVMs were first applied to medical image classification in [3] after being successfully applied on classification problems in various domains.

We briefly describe the theory behind the SVM next. Let the imaging data and the associated class labels of m subjects be defined by (I_i, y_i), i ∈ {1,…,m}, I_i ∈ Rⁿ, y_i ∈ {−1, +1}. Here I_i is a n-dimensional point representing an image containing n voxels. The linear SVM attempts to find w ∈ Rⁿ and b ∈ R such that:

$$\underset{\mathbf{w},b}{\text{min}}\frac{1}{2}{\Vert \mathbf{w}\Vert }^2+C\sum _{i=1}^m{\xi }_i$$ (3)

subj. to

$$y_i({\mathbf{w}}^T{\mathbf{I}}_i+b)\ge 1-{\xi }_i{\xi }_i\ge 0,i=1,\dots ,m$$

where ξ_i are slack variables. Here w and b define the hyperplane that separates the two classes with the maximum margin.

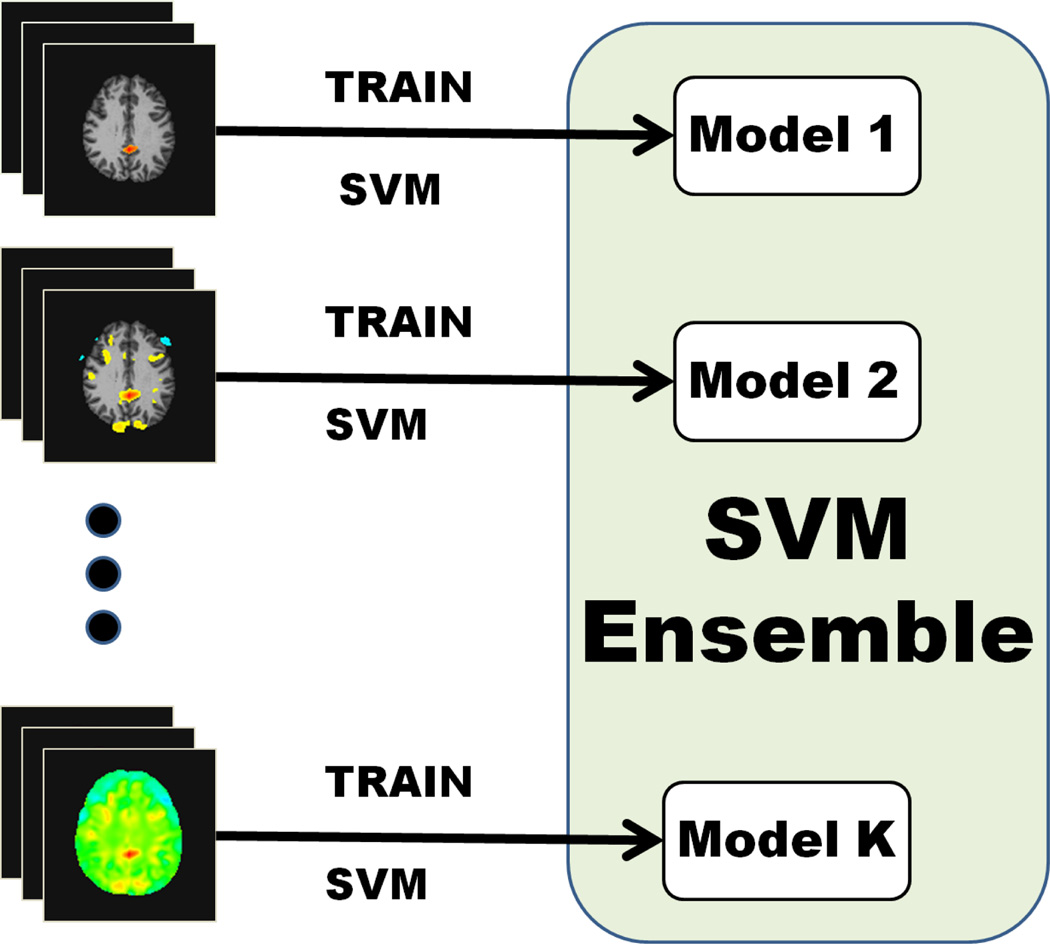
We construct an SVM ensemble model by training an individual SVM on each nested feature set f_k. The ensemble methodology is particularly adapted herein for combining many feature sets with different dimensionalities that we extracted from the data. Also training SVM ensembles and then applying an aggregation strategy such as majority voting is known to improve classification accuracy compared to a single SVM [5].

The ensemble model consists of the hyperplane normal vectors w_k and intercepts b_k, k ∈ {1,…, K} that were learned by each individual SVM classifier (Figure 2).

Fig. 2.

Training of the SVM ensemble.

2.3. Testing using the SVM ensemble

To apply the SVM ensemble on a new test image, K feature sets ${\mathbf{I}}_{f_k}^{\mathit{\text{test}}},k\in \{1,\dots ,K\}$ are first extracted from the test data. These sets include voxels that were used as features for training each SVM classifier. Each SVM model is applied on the respective feature set from the test image to predict a classification score:

$$y_k^{\mathit{\text{pred}}}={\mathbf{w}}_k^T{\mathbf{I}}_{f_k}^{\mathit{\text{test}}}+b_k$$ (4)

The prediction score obtained from all SVMs are combined using simple voting to determine the class label of the test image:

$$y_{\mathit{\text{test}}}=\mathit{\text{sgn}}(\frac{1}{K}\sum _{k=1}^K{y}_k^{\mathit{\text{pred}}})$$ (5)

3. EXPERIMENTAL RESULTS

3.1. Data sources

The method is applied on two independent datasets. Alzheimer’s disease data was obtained from the Alzheimer’s Disease Neuroimaging Initiative (ADNI). The MR scans were all T1-weighted, acquired sagittally using volumetric 3D MPRAGE with 1.25 × 1.25 mm in plane spatial resolution and 1.2 mm thick sagittal slices. All images were acquired on a 1.5 T scanner. 268 different age matched subjects were preprocessed and used for the classification task. The autism data was accessed with permission from Childrens Hospital of Philadelphia (CHOP). There were scans of a total of 131 different male subjects (81 ASD / 50 controls). The images were T1 MR scans. Compared to AD dataset, these subjects represented a more heterogeneous and unbalanced population. The mean age of ASD subjects were 11.83 and standard deviation was 2.98. The mean age of controls was 16.71 and standard deviation 7.23. A large age variance hints at the wide spectrum of structural differences that is evident in the brains of these subjects.

3.2. Preprocessing

The preprocessing protocol includes skull removal using the BET algorithm [8] and bias field removal using N3 [9]. Images are then nonlinearly registered to a common template using HAMMER [10]. Instead of directly using voxel intensities, voxelwise tissue density maps for gray matter (GM), white matter (WM) and ventricles (VN) are extracted for each individual brain using the method described in [11]. These tissue density maps give a quantitative representation of the spatial distribution of brain tissues on a common space, and thus they are ideal to be used as features for classification of neurodegenerative diseases.

3.3. Experiments

We generated K = 20 nested feature subsets with linearly increasing dimensions, by using the algorithm described in 2.1. with α = 1. In order to evaluate the performance at variable threshold values of the classifier, Receiver Operating Characteristic (ROC) curves are created. Area Under the Curve (AUC) scores are calculated from the ROC curves. Also, classification accuracy, sensitivity and specificity values are calculated for the optimal cut-off threshold value in the ROC curves of the respective methods.

The classification performance of the proposed method is compared to two state of the art methods that both use SVM for classification, COMPARE [3] and Kloppel’s [2]. Kloppel’s method trains a linear SVM using segmented brain’s voxel intensities as features. On the other hand, COMPARE executes internal leave-one-out cross validation to determine the most discriminative regions of interest after a watershed segmentation has been applied. These features are then trained using a linear SVM. According to the comparative evaluation results reported in [1, 2], Kloppel’s method and COMPARE both obtained competitive scores in the classification of AD data. We also applied an SVM classifier that trains only on f₁, in order to show that the SVM ensemble improves classification accuracy compared to a single SVM trained on the features with the highest ranking. The same protocols for training, testing and validation are used in all experiments.

For the AD dataset, GM, WM and VN tissue density maps are used for training and testing. In experiments with AD, 132 subjects were used for training (58 AD / 74 NC) and 136 were used for testing (58 AD / 74 NC). For the ASD dataset, only GM and WM maps are used. This is in agreement with [12] which shows that in autism significant volumetric differences were mostly observed in GM and WM. The ASD dataset contained 81 ASD / 50 NC. Due to the limited number of subjects in ASD dataset we report leave-one-out cross validation accuracy instead of test accuracy.

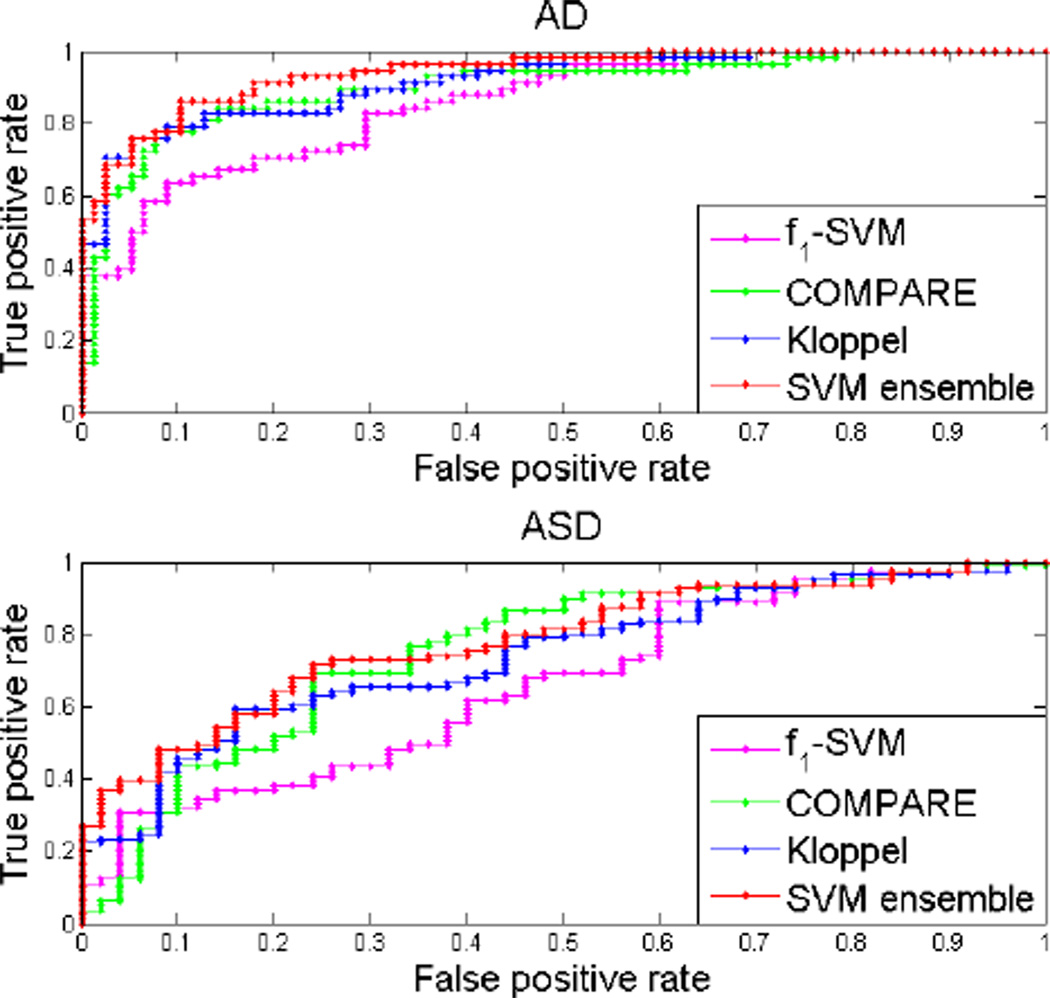
Our method outperformed both COMPARE and Kloppel’s method in the classification of both datasets in terms of AUC score, accuracy, specificity and sensitivity. It also had better scores than single SVM on f₁. Note that AUC is better at quantifying classifier performance than accuracy because it has higher statistical consistency [13]. The quantitative results for our method, Kloppel’s method and COMPARE are presented in table 1. The ROC curves corresponding these methods as well as SVM trained on f₁ is shown in figure 3.

Table 1.

AUC, accuracy, sensitivity(SENS), specificity(SPEC) of classification by our method, Kloppel’s method and COMPARE on the two datasets.

Data	Method	AUC	ACC %	SENS %	SPEC %
AD	Our’s	0.941	88.23	86.21	89.74
	Kloppel’s	0.918	85.29	82.76	87.18
	COMPARE	0.903	84.56	84.48	85.90
	f1-SVM	0.859	78.42	70.69	82.05
ASD	Our’s	0.783	73.28	71.60	76.00
	Kloppel’s	0.741	67.93	65.43	72.00
	COMPARE	0.755	70.99	69.14	76.00
	f1-SVM	0.663	60.30	60.00	60.49

Fig. 3.

ROC curves for the classification by our method, Kloppel’s method, COMPARE and SVM trained on f₁ on the two datasets.

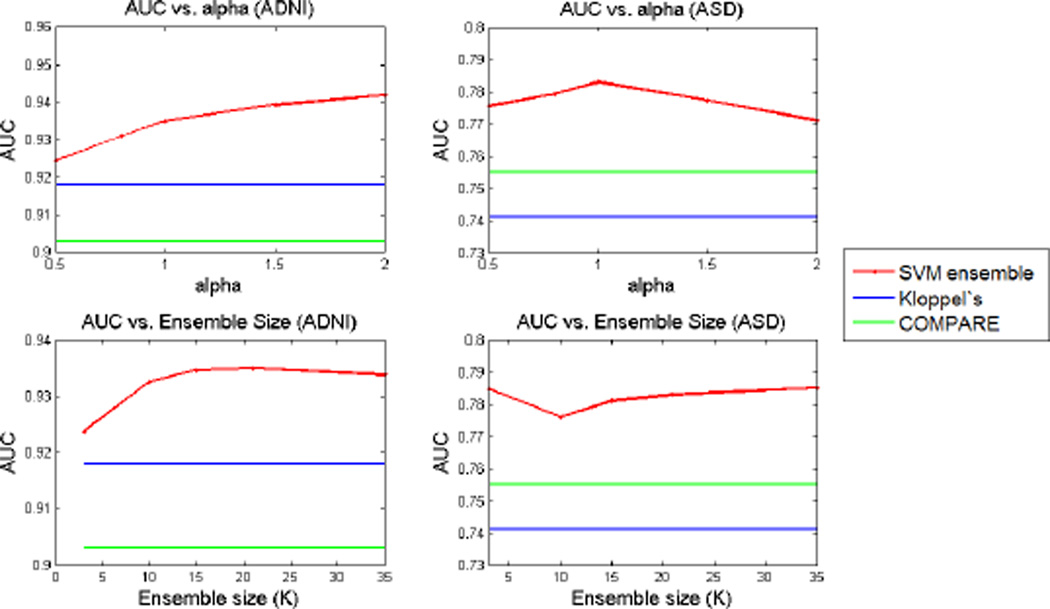
Our method has two parameters α and K, which are used in combination to define the number and dimensionality of the feature sets that are used in the SVM ensemble. We evaluated the robustness of the method to the variation of these parameters. To explore the sensitivity of the method to the choice of α we fixed K = 20 and applied the classification for α values varying in a range from 0.5 to 2. Similarly, we applied the method for fixed α = 1 and K varying between 3 and 35. AUC values for classification of both datasets are computed for all different parameter values. Figure 4 shows the variation of AUC scores for variable values of α and K. These results confirm that the method is robust to variation of these two parameters in a wide range.

Fig. 4.

AUC results for variable α and K values.

4. DISCUSSION

Specifically, on the ASD data we observed a more significant increase in the classification performance compared to Kloppel’s method. The implicit weighting of smaller but statistically more significant features in feature selection emphasizes the respective regions in training of the classifiers. Selecting smaller regions as features may fare better with a disorder such as autism which exhibits a localized pathological structure.

We used a feature selection strategy based on ranking individual voxels by their discriminative power. This strategy could be enhanced by ranking clusters of voxels instead of individual ones. In [7], it has been demonstrated that employing a diverse set of feature subsets in ensembles reduces the generalization error. Hence, it may be beneficial to investigate further methods to generate feature subsets.

In addition, other feature selection approaches or ensemble aggregation strategies may be incorporated into the proposed framework in the future. Boosting, bagging or weighted voting strategies may be used to combine the individual classifiers to improve the classification performance.

5. CONCLUSION

We presented a novel model for medical image classification using feature ranking and SVM ensemble classifiers. We showed that aggregating classifiers trained on nested feature sets attained better classification performance than classifiers trained on a single feature set. Furthermore, our method consistently outperformed two state of the art methods for medical image classification on two different clinical datasets.