Abstract
Optical antennas have been utilized to tailor the emission properties of nanoscale emitters in terms of the intensity, directivity and polarization. In this letter, we further explore the capability of beam steering via the use a spiral plasmonic structure as a transmitting antenna. According to both numerical simulation and experimental observations, the beaming direction can be steered through introducing a displacement of the feeding point to the spiral antenna from the geometrical center. For a 3-turn Archimedes' spiral antenna, experimental results show that steering angles of 3° and 7° are obtainable when the excitation location is transversally shifted from the center by a displacement of 200 nm and 500 nm, respectively. Furthermore, the emitted photons carry spin angular momentum determined by the chirality of the spiral optical antenna. A steerable nanoscale spin photon source may find important applications in single molecule sensing, quantum optical information processing and integrated photonic circuits.
Similar to their radio frequency (RF) counterparts, optical antennas are designed to efficiently convert free space electromagnetic radiation to localized energy in optical frequency, and vice versa1. Subwavelength metallic structures become increasingly accessible with the rapid development of modern nanofabrication techniques, assisting the rapid expansion of the research in optical antennas. Despite the differences between optical antennas and the conventional antennas used in the RF and microwave regime, the basic principles of classical antenna design have been demonstrated to be still effective in the optical regime2,3. Depending on their roles played in the process of energy exchange, the optical antennas can be generally classified into two categories: receiving antenna and transmitting antenna. Receiving antenna is designed to detect the incident electromagnetic wave and concentrate it into localized energy for further processing. For optical antennas using noble metals, the coupling between optical field and surface plasmon polaritons (SPPs) offers an efficient way to design a metallic receiving antenna that can localize the energy with a small region well beyond the diffraction limit. By matching the modes between excitation and the optical antenna, the incident field can be efficiently captured by the antenna at a certain resonance condition, which gives rise to an extremely strong localized electromagnetic field due to the surface plasmon resonance. Various types of receiving antenna have been developed to manipulate and control the optical radiation at a subwavelength scale, for instance nanowires, nanoparticles, bull's eyes, spirals, bowties, tips4,5,6,7,8,9,10, and so on.
Besides the receiving antenna, transmitting antenna has also attracted attention in recent years due to its capability of tailoring the properties of photons emitted from nanoscale emitters. In reciprocal to a receiving antenna, a transmitting antenna is designed to efficiently convert the localized feeding energy to free space propagating optical radiation. Through controlling the optical resonance in the vicinity of emitters, the properties of emitted photons from the emitters can be engineered. For example, a controlled enhancement of single-molecule fluorescence can be achieved by coupling a single molecule to a single sphere gold nanoparticle acting as a transmitting antenna11. In addition, directional emission offered by transmitting antenna is very useful for the applications requiring high angular sensitivity, such as light-emitting devices, molecule sensing, and unidirectional fluorescence molecular sources. As a classical antenna in RF and microwave regimes, Yagi-Uda antenna structure has been experimentally demonstrated with good performance as a transmitting antenna in the optical regime. Linearly polarized beam with highly directional far-field emission can be realized from an array of Yagi-Uda optical antenna2,12. Besides the Yagi-Uda antenna, a practical transmitting antenna consists of single nanoaperture surrounded by shallow grooves in gold film has been demonstrated to significantly enhance the fluorescence count rates per molecule with high emission directivity13. Through tuning the groove-nanoaperture distance, the fluorescence directivity can be controlled as a result of the interference phenomenon14.
It is desirable to by able to achieve comprehensive control of the emitted photons properties with transmitting antenna beyond intensity and directivity. For example, additional polarization control of the emitted photons has been proved feasible by the use of a cross resonant optical antenna15 or a spiral optical antenna. As a receiving antenna, the focusing properties of spiral structure show strong dependence on the spin of optical excitation16,17,18. Reversely, if the spiral structure is used as a transmitting antenna, both spin and orbital angular momentum can be imprinted to the emitted photons through coupling nanoscale emitters to a spiral optical antenna. When the pitch of spiral equals to the surface plasmon polariton wavelength, a highly directional circularly polarized emission can be realized in the far field19,20. The spin carried by the emitted photons is determined by the chirality of the spiral antenna that converts the emission of nano emitters into the far field. Increasing number of turns for the spiral leads to even narrower angular width and higher brightness of the emission. More interestingly, for spiral pitch of m·λspp with m being an integer number larger than 1, the emitted photons will carry not only spin angular momentum (SAM) but also orbital angular momentum (OAM)21. The intrinsic SAM is associated with the polarization helicity, where σ± = ±1 correspond to the right and left handed circular polarizations (RHC and LHC), respectively. Besides beaming photons with specific polarization states at a prescribed (fixed) direction, capability of dynamically steering the emission direction of these photons in a controllable manner is highly desirable with many potential applications. In this letter, we demonstrate such a beam steering function of directional photon emissions through introducing displacements to the feed point of a transmitting spiral antenna. Unlike the electrical feed used in RF antennas, the feed point displacement and the proposed beam steering concept can be easily implemented in optical antennas due to the non-contact nature of optical feeding. First we introduce the beam steering concept with a simple analytical model. Then finite element method electromagnetic simulation is performed to confirm the analytical model. Experiments are designed and conducted to verify this beam steering concept. In the experiment, fluorescence emission from uniformly distributed quantum dots deposited on the spiral antenna is adopted as feed to the spiral antenna. Radially polarized beam is used to locally excite the quantum dots to establish longitudinally polarized feed to the antenna. The displacement of the feed point is realized by precisely moving the spiral antenna with respect to the fixed focal spot of the excitation. Experimental results demonstrate that the direction of the photons emitted from the quantum dots can be dynamically steered while maintaining the high directivity and polarization properties of the emission.
Results
Physical mechanisms
The proposed spiral structure is a right-hand Archimedes' spiral (RHS) slot etched into a thin metal film. In its local cylindrical coordinates, the RHS structure can be described as
where 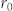 is a constant that represents the distance from the geometrical center to the innermost slot, the pitch of spiral is defined by λspp which is the wavelength of SPPs on the metal/air interface, and θ is the azimuthal angle. The feed to the antenna is simulated by an electric dipole located on the metal/air interface with oscillating direction normal to the spiral surface. SPPs excited by the oscillating electric dipole propagate to the spiral slot and are guided through the slot opening to the other side of the spiral, then re-radiate into the free space after transmitting through the glass substrate. An analytical model for a single turn spiral has been built to provide more insight into the beaming properties of the spiral antenna. When the electric dipole is located at the geometrical center, the electric field at an observation point (z, ρ, ϕ) in the far field can be described in the cylindrical coordinates as21:
is a constant that represents the distance from the geometrical center to the innermost slot, the pitch of spiral is defined by λspp which is the wavelength of SPPs on the metal/air interface, and θ is the azimuthal angle. The feed to the antenna is simulated by an electric dipole located on the metal/air interface with oscillating direction normal to the spiral surface. SPPs excited by the oscillating electric dipole propagate to the spiral slot and are guided through the slot opening to the other side of the spiral, then re-radiate into the free space after transmitting through the glass substrate. An analytical model for a single turn spiral has been built to provide more insight into the beaming properties of the spiral antenna. When the electric dipole is located at the geometrical center, the electric field at an observation point (z, ρ, ϕ) in the far field can be described in the cylindrical coordinates as21:
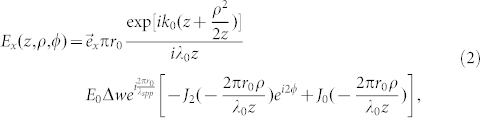 |
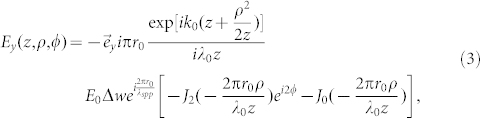 |
where r0 is a constant, λspp is the wavelength of SPPs on the metal/air interface, Δw is the slit width, λ0 is the emission wavelength of the electric dipole and k0 = 2π/λ0 is its wavevector in air.
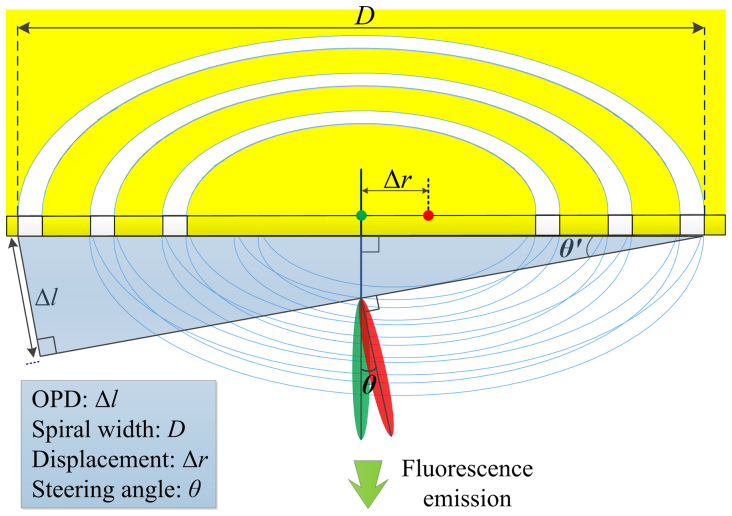
It can be seen that both the x and y components have two terms and the total electric field is a superposition of two different modes proportional to 0th and 2nd order Bessel functions. The main lobe of the far field is given by the 0th order Bessel function and the polarization is RHC. As far as the main lobe is concerned, spiral plasmonic antenna with specifically designed pitch can be used to generate photons with both spin angular momentum and orbital angular momentum states. More derivation details and discussions could be found in ref 21. The underline physics of the beam steering concept using a spiral plasmonic antenna can be understood with a simple model illustrated in Figure 1. Please note that a cut-through of the structure is shown and the spiral structure is represented as the thin blue lines. The evanescent field radiated by the oscillating electric dipole excites SPPs waves on the metal/air interface and propagate towards the spiral slot. When the dipole is placed at the origin of the spiral structure (location of the dipole and its corresponding emission pattern are sketched by the red dot and the red ellipse in Figure 1, respectively), both simulation and experiment have demonstrated the generation of directional emission normal to the surface19,20 due to the nonaxisymmetrical shape of the spiral structure. In this case, the corresponding optical path difference (OPD) from the edges of the device is assumed to be zero so that there is no tilt of the overall wavefront emitted from the device. If the electric dipole is displaced away from the geometrical center with a displacement of Δr, the OPD from the edges of the device is no longer zero so that a tilt of the overall wavefront will develop and the emission peak will shift from the normal direction accordingly (the dipole and corresponding emission pattern are sketched by the green dot and green ellipse in Figure 1, respectively). The steering angle defined as the angle between the normal direction and the direction of the emission peak (shown in Figure 1 as θ) can be estimated with a simple OPD calculation. According to the principles of similar triangles, the steering angle θ = θ′ = sin−1(Δl/D), where D is the width of the spiral antenna along the direction of the displacement and Δl is the OPD between locations across the device. The OPD can be calculated as Δl = 2Δr × kspp/k0, where kspp is the wave vectors of the SPPs on the metal/air interface, and k0 is the wavevector of the optical emission field in free space. This simple analysis enables the estimation of the steering angle of the far-field emission, which increases linearly with larger displacement Δr. For a 3-turn spiral antenna with pitch of λspp and r0 of 3 μm, the steering angle θ are calculated to be 2.7° and 6.7° for the displacement Δr of 200 nm and 500 nm, respectively.
Figure 1. Schematic diagram for the steering angle calculation.
The green and red dots stand for the nanoscale emitters with different locations. The color-filled ellipses represent the corresponding far-field emission patterns.
FEM simulation
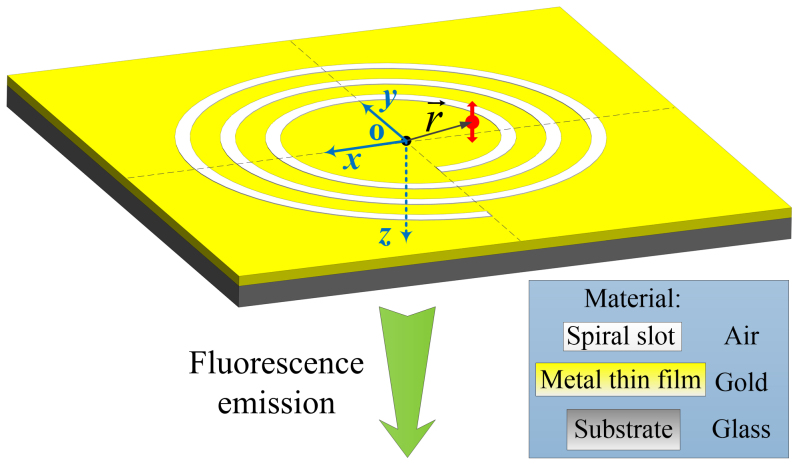
Although the analytical model above provides valuable insights into the steering characteristics of the proposed dipole coupled plasmonic spiral antenna, it only provides a rough estimation because some effects, such as the propagation loss and the effects of the transverse components of SPPs, are ignored in the derivation. In order to take these effects into consideration, an adequate three-dimensional geometry has been modeled using finite element method (COMSOL). As shown in Figure 2, the modeled structure consists of a 3-turn spiral structure with slot width of 200 nm and r0 of 3 μm and pitch of λspp etched through a 150 nm gold film (n = 0.197 + i3.0908) on a glass substrate (n = 1.5). An electric dipole is placed 5 nm above the spiral surface, and the location of dipole from the origin is indicated by the vector 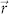 (shown in Figure 2). The electric dipole oscillates normally to the spiral surface and its emission wavelength is chosen to be 633 nm in the model. Postprocessing available in COMSOL is used to calculate the far-field distributions emitted from the spiral antenna into the half space that is to the other side of the dipole source (emission direction indicated by the green arrow in Figure 2). Simulation results of far-field intensity distributions for different
(shown in Figure 2). The electric dipole oscillates normally to the spiral surface and its emission wavelength is chosen to be 633 nm in the model. Postprocessing available in COMSOL is used to calculate the far-field distributions emitted from the spiral antenna into the half space that is to the other side of the dipole source (emission direction indicated by the green arrow in Figure 2). Simulation results of far-field intensity distributions for different 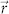 are shown in Figure 3. Figure 3a shows the far-field intensity distribution when
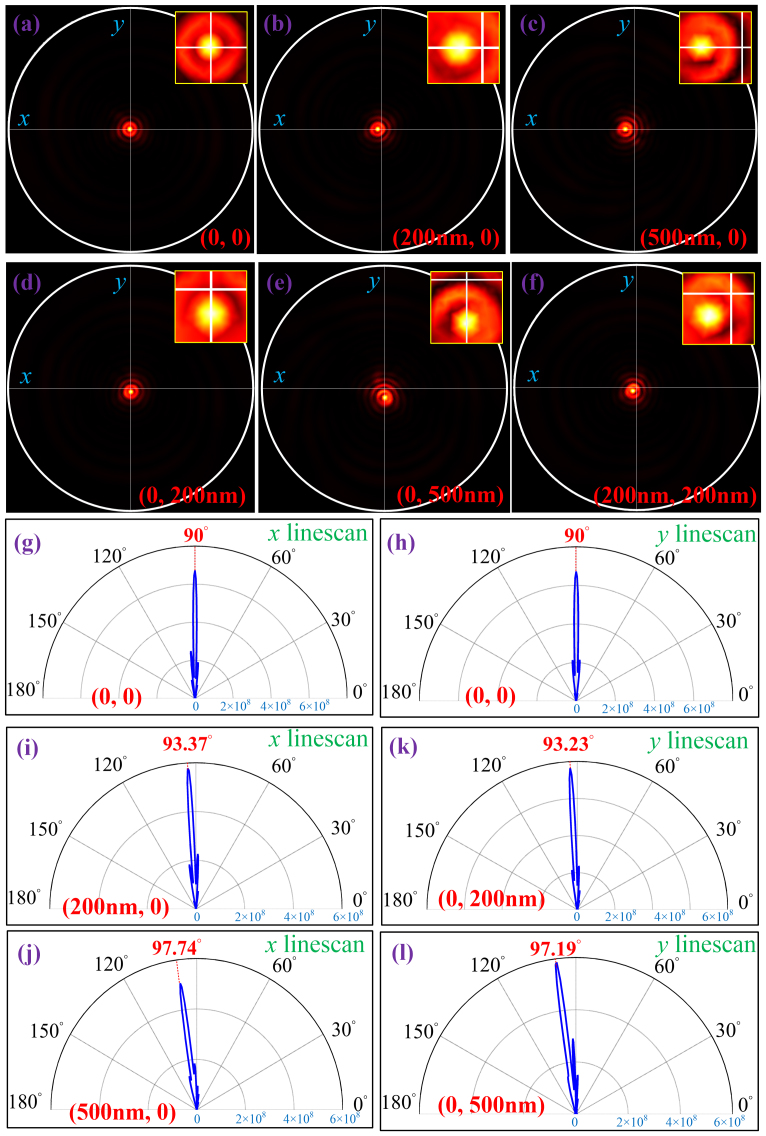
are shown in Figure 3. Figure 3a shows the far-field intensity distribution when 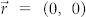 , namely the electric dipole is placed at the geometrical center. The corresponding angular radiations are shown in Figure 3b, c, there is a clear peak centered at 90°, which means the emission is normal to the spiral surface. The emission pattern is highly directional, with a full-width-half-maximal (FWHM) of 3.3° and 3.6° in x-z and y-z planes, respectively. According to the theoretical predictions, the emission peak will shift from the normal direction when the dipole is moved away from the geometrical center. Figure 3b, c show the far-field intensity distributions for electric dipole with x-directional displacement (along x axis) of 200 nm and 500 nm, respectively. The emission pattern maintains the solid bright spot profile, while the emission peak is no longer normal to the spiral surface, which can be clearly seen from the angular radiation patterns shown in Figure 3i, j. For the case of
, namely the electric dipole is placed at the geometrical center. The corresponding angular radiations are shown in Figure 3b, c, there is a clear peak centered at 90°, which means the emission is normal to the spiral surface. The emission pattern is highly directional, with a full-width-half-maximal (FWHM) of 3.3° and 3.6° in x-z and y-z planes, respectively. According to the theoretical predictions, the emission peak will shift from the normal direction when the dipole is moved away from the geometrical center. Figure 3b, c show the far-field intensity distributions for electric dipole with x-directional displacement (along x axis) of 200 nm and 500 nm, respectively. The emission pattern maintains the solid bright spot profile, while the emission peak is no longer normal to the spiral surface, which can be clearly seen from the angular radiation patterns shown in Figure 3i, j. For the case of 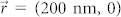 , the steering angle is 3.4° along the x direction. Same as the definition used in the simple theoretical model, the steering angle is defined as the angle between the direction that is normal to the spiral surface (90° in the polar plots) and the corresponding polar angle of the emission peak. When the x-directional displacement of the dipole increases up to 500 nm, the steering angle also becomes larger (7.7°). In addition, the emission patterns do not severely deteriorate and the angular widths are almost invariable. Similar simulation results were obtained for electric dipole with y-directional displacement. In this case, the steering angles are 3.2° and 7.2° for
, the steering angle is 3.4° along the x direction. Same as the definition used in the simple theoretical model, the steering angle is defined as the angle between the direction that is normal to the spiral surface (90° in the polar plots) and the corresponding polar angle of the emission peak. When the x-directional displacement of the dipole increases up to 500 nm, the steering angle also becomes larger (7.7°). In addition, the emission patterns do not severely deteriorate and the angular widths are almost invariable. Similar simulation results were obtained for electric dipole with y-directional displacement. In this case, the steering angles are 3.2° and 7.2° for 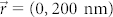 and (0, 500 nm), respectively. These results agree very well with the predictions given by the simple analytical model described above. More general condition is also studied when the displacement of the dipole occurs on both axes. Figure 3f show the emission pattern when
and (0, 500 nm), respectively. These results agree very well with the predictions given by the simple analytical model described above. More general condition is also studied when the displacement of the dipole occurs on both axes. Figure 3f show the emission pattern when 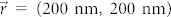 , in this case the steering direction of the emission peak is 45° with respect to the x direction. In summary, these numerical simulations confirm that the angular position of the emission depends on the displacement vector
, in this case the steering direction of the emission peak is 45° with respect to the x direction. In summary, these numerical simulations confirm that the angular position of the emission depends on the displacement vector 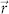 , which can be explored for beam steering applications.
, which can be explored for beam steering applications.
Figure 2. Diagram of the spiral plasmonic antenna structure used in the numerical simulation.
An oscillating electric dipole is located 5 nm above the spiral surface. The oscillating direction of the dipole is illustrated by the red arrow. The displacement of the dipole from the geometrical center of the spiral is denoted by the vector 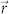 . The spiral antenna re-radiates the emission from the electric dipole into the free space on the other side of the dipole source after transmitting through the supporting glass substrate. The direction of far-field emission is indicated by the green arrow.
. The spiral antenna re-radiates the emission from the electric dipole into the free space on the other side of the dipole source after transmitting through the supporting glass substrate. The direction of far-field emission is indicated by the green arrow.
Figure 3. Numerical simulation results for a 3-turn spiral plasmonic antenna structure with different displacement 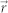 .
.
For 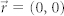 : (a) intensity distribution, (g, h) line-scans in the x-z and y-z planes. For
: (a) intensity distribution, (g, h) line-scans in the x-z and y-z planes. For 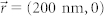 and (500 nm, 0): (b, c) intensity distributions, (i, j) line-scans in the x-z plane. For
and (500 nm, 0): (b, c) intensity distributions, (i, j) line-scans in the x-z plane. For 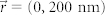 and (0, 500 nm): (d, e) intensity distribution, (k, l) line-scans in the y-z plane. (f) Intensity distribution for
and (0, 500 nm): (d, e) intensity distribution, (k, l) line-scans in the y-z plane. (f) Intensity distribution for 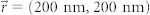 . Zoom-in of the intensity distributions are shown as the insets for better visualization of the emission peak. The white circles shown in (a)–(f) represent the maximum collection angular range for an objective lens with NA = 0.8.
. Zoom-in of the intensity distributions are shown as the insets for better visualization of the emission peak. The white circles shown in (a)–(f) represent the maximum collection angular range for an objective lens with NA = 0.8.
Experimental design to control the direction of fluorescence emission
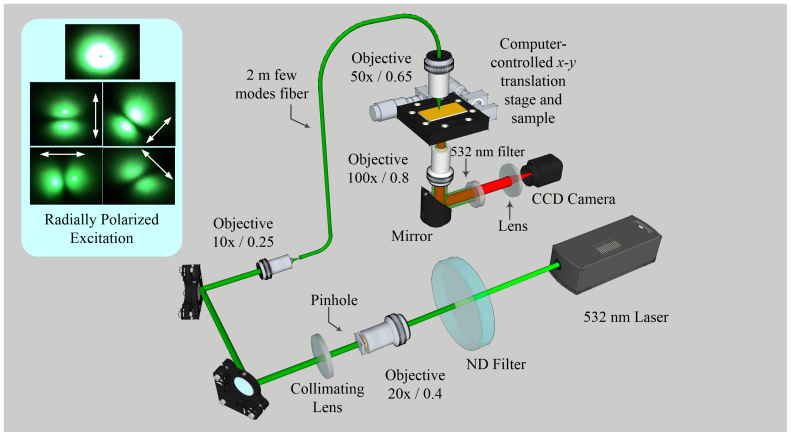
Experiment has been designed and conducted to demonstrate the proposed beam steering concept. Quantum dots were adopted as the nanoscale emitters to excite the spiral antenna. Fluorescent Qdots (R) 625 ITK carboxyl quantum dots from Invitrogen were used due to its excellent stability and lifetime. The peak emission (625 nm) wavelength of this kind of quantum dots is very close to the simulated wavelength above (633 nm). In the simulations, a critical requirement to realize the desired far-field emission characteristics is the orientation of dipole oscillation, which should be normal to the spiral surface. It can be fulfilled with a radially polarized excitation source due to its strong longitudinal electric component. More discussion about the necessity of radially polarized excitation can be found in ref. 20. The diagram of the experimental setup is shown in Figure 4. The radially polarized beam was generated through coupling laser beam into a few-mode optical fiber22. The optical excitation wavelength is chosen to be at 532 nm. The quantum dots were diluted in isopropyl alcohol with volume ratio 1:10. A droplet of the diluted quantum dots solution is carefully dripped on the spiral surface and dried in air. An objective lens (Mitutoyo M Plan Apo NIR HR 50 ×/0.65) with numerical aperture (NA) of 0.65 was used to tightly focus the radially polarized beam coming out from the fiber end onto the gold/air interface of the spiral antenna. Although the NA of this lens is not high enough to provide a dominating longitudinal electric component in the excitation, the far-field emission is still dominated by the longitudinal excitation (with a calculated FWHM spot size of 370 nm.), because it has been reported that the excitation efficiency of longitudinal components is about 12 times higher than transverse components20. The spiral sample is placed on an x-y translation stage that connected to a computer, through which the motion of the stage can be precisely controlled. According to the simulation results, the steering angle of the emission peak depends on the displacement vector of excitation location, i.e., the feed point to the spiral antenna. In the experiment, this is realized by moving the sample to specific location while keep the excitation beam fixed so that quantum dots in different areas within the spiral antenna are excited. It should be noted that, different from the ideal single point excitation used in the simulation, all the quantum dots within the illumination spot are excited in the experiment, leading to a broader peak emission angular width. However, the centroid of the far-field emission pattern is determined by the center of the illumination spot and the steering performance is still given by the displacement of the center of the illumination spot with respect to the geometric center of the spiral antenna. A CCD camera (not shown in the setup diagram) was used to capture the images reflecting from the gold/air interface of the spiral, which was helpful to determine the positions of both illumination spot and the spiral antenna. An inverted objective lens (Nikon LU Plan 100 ×/0.8) with an NA of 0.8 below the x-y translation stage was used to collect the emission from the glass side of the sample. The focal plane of this objective lens was adjusted to the glass/air interface of the sample and its position was kept unchanged during the experiment. A 532 nm notch filter was placed after the inverted objective lens to filter out the excitation wavelength. The red fluorescence signals are slightly focused by a lens and then collected by another CCD camera (all the fluorescence images shown in this manuscript are collected by this CCD camera). The inset of Figure 4 shows the donut pattern of the generated radially polarized beam. To confirm the radial polarization distribution, radiation patterns passing through a linear polarizer oriented at different angles are also captured and shown as inset of Figure 4.
Figure 4. Experimental configuration.
Inset: radially polarized excitation beam generated at the end of fiber, and pictures of the beam after it passes through a linear polarizer orientated at different angles shown by the white arrows (adapted from [17]).
Images of the beam steering phenomenon
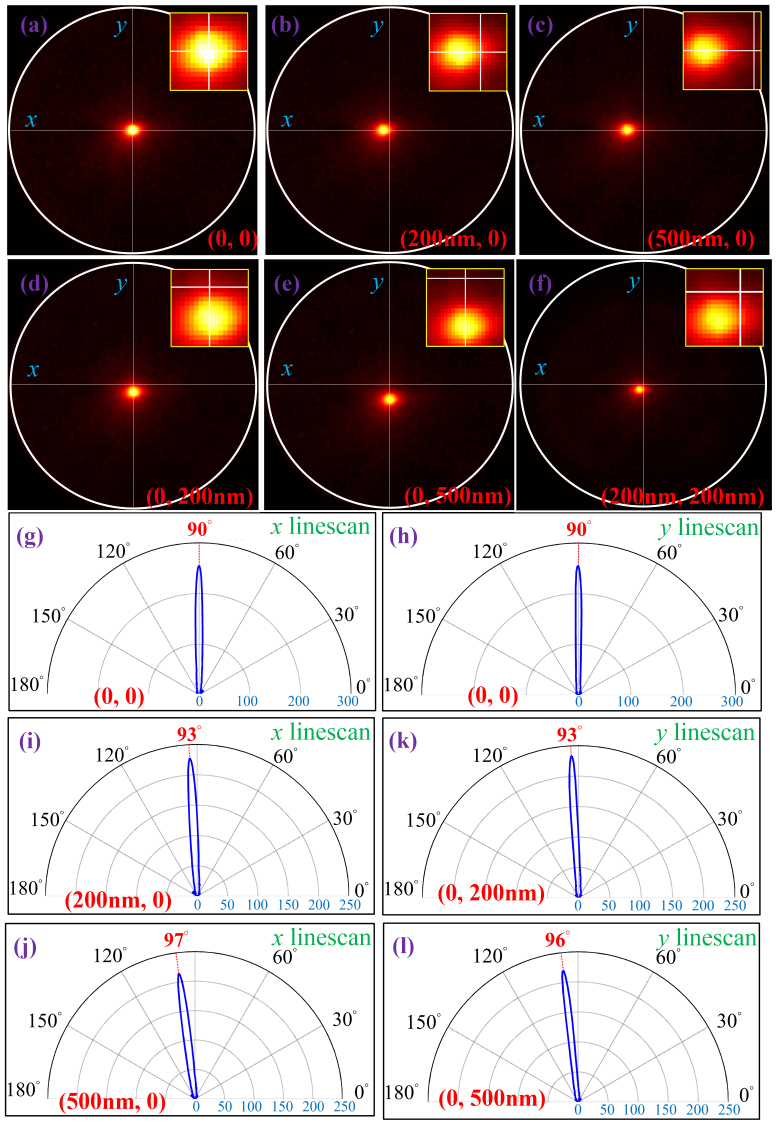
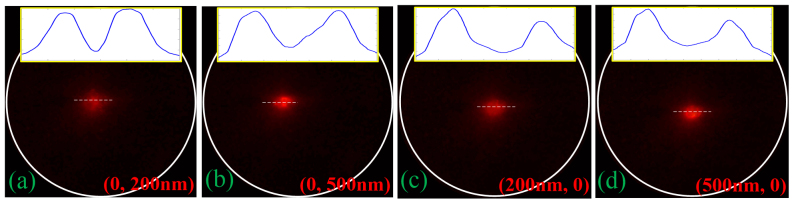
The collected fluorescence signals are shown in Figure 5. At first the focused radially polarized beam is aligned with the geometrical center of the spiral antenna. In this case a bright fluorescence spot centered at the optical axis is observed on the CCD camera (shown in Figure 5a). The radius of outermost white circle represents the maximum collection angle of the inverted objective of 53°. The line-scans through the center of the emission are shown in Figure 5g, h. The emission pattern is highly directional, with FWHM of 6.4° and 5° along x and y directions, respectively. With the computer-controlled x-y stage, the sample can be shifted or scanned along the x or y directions at a designated distance or speed. Figure 5b, c show the collected fluorescence intensity distributions for the x-directional displacement of 200 nm and 500 nm, respectively. Clearly, the radiation field maintains the solid spot pattern, while an x-directional shift of the emission peak is observed. The line-scan of fluorescence emission patterns along x axis are shown in Figure 5i, j. It can be clearly seen that the steering angle depends on the displacement of the feed to the antenna, and larger displacement leads to a larger steering angle. The steering angles are about 3° and 7° for the x-directional displacements of 200 nm and 500 nm, respectively. Figure 5d, e, k, l show the emission patterns and corresponding line-scans along the y direction when the sample is moved along y direction by 200 nm and 500 nm. In this case, the emission is shift along y direction and the steering angles are 3° and 6° for the y-directional displacement of 200 nm and 500 nm, respectively. For the case of displacement on both axes, a similar phenomenon is observed and confirms the numerical simulation results. Figure 5f shows the collected fluorescence emission distribution for quantum dots with displacement of 200 nm on both x and y direction. It can be seen that the emission peak is in the third quadrant. Two movie clips were captured to illustrate the beam steering phenomenon of the spiral antenna (please refer to the videos and the supplementary information). These movies show the collected fluorescence signals when the sample was scanned along x or y direction within a range of 500 nm around the geometrical center. With the displacement increases, the emission peak further shifts from the normal direction, the peak intensity of the emission decreases slightly while the angular width of the emission remains nearly the same.
Figure 5. Fluorescence intensity distributions in the back focal plane of a NA = 0.8 objective lens.
For 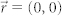 : (a) intensity distribution, (g, h) line-scans in the x-z and y-z planes. For
: (a) intensity distribution, (g, h) line-scans in the x-z and y-z planes. For 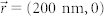 and (500 nm, 0): (b, c) intensity distribution, (i, j) line-scans in the x-z plane. For
and (500 nm, 0): (b, c) intensity distribution, (i, j) line-scans in the x-z plane. For 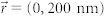 and (0, 500 nm): (d, e) intensity distribution, (k, l) line-scans in the y-z plane. (f) Emission pattern for
and (0, 500 nm): (d, e) intensity distribution, (k, l) line-scans in the y-z plane. (f) Emission pattern for 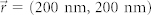 . Zoom-in of the intensity distributions are shown as the insets for better visualization of the emission peak. The white circles shown in (a)-(f) represent the maximum collection angular range for an objective lens with NA = 0.8.
. Zoom-in of the intensity distributions are shown as the insets for better visualization of the emission peak. The white circles shown in (a)-(f) represent the maximum collection angular range for an objective lens with NA = 0.8.
Polarization control of the photons
It has been demonstrated both theoretically and experimentally that the fluorescence emission carries polarization property essentially determined by the handedness of the spiral antenna. For a RHS structure, the polarization state of the radiation emission should be RHC. To explore the influence of beam steering phenomenon to the polarization of emitted photons, a circular polarization analyzer composed of a quarter-wave plate followed by a linear polarizer is placed behind the collection objective lens. The angle between the fast axis of the quarter-wave plate and the linear polarizer is set to 45°. The emission patterns after the LHC polarizer are shown in Figure 6. The intensity of radiation emission passing through a LHC polarizer is greatly reduced and a dark hole is observed in the center of the radiation pattern (see insets of Figure 6). On the other hand, for a RHC polarizer, the emission pattern does not change much and a bright central spot is still observed (not shown). This is the manifestation of RHC polarization carried by the emitted photons. Circular polarization ratio defined as I1/I2 is introduced to evaluate the purity of RHC polarization, where I1 and I2 are the fluorescence intensities in the center of the emission patterns after the right and left circular polarization analyzer respectively. For x-directional displacements of 200 nm and 500 nm, extinction ratios of 8 and 7 have been achieved for RHS structure with 3 turns. On the other hand, extinction ratios of 7.5 and 7 are obtained for y-directional displacements of 200 nm and 500 nm, respectively.
Figure 6. Images of emission patterns filtered by a LHC polarization analyzer that is composed of a quarter-wave plate and a linear polarizer.
(a) 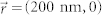 , (b)
, (b) 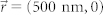 , (c)
, (c) 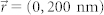 , (d)
, (d) 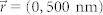 . Linescans through the centers of the emission patterns are shown in the insets. The dips in the center demonstrate the suppression of the LHC polarization emission.
. Linescans through the centers of the emission patterns are shown in the insets. The dips in the center demonstrate the suppression of the LHC polarization emission.
Discussion
In conclusions, we demonstrated the feasibility of beam steering of the emission from nanoscale emitters coupled to a spiral optical antenna through introducing a displacement to the feed point of the antenna. As oppose to the electrical feed in RF antenna, the non-contact nature of an optical feeding enables the introduction of feed point displacement and the proposed beam steering concept. It is found that the steering angle strongly depends on the position of the feed, with larger displacement leading to higher steering angle. Experimental results also reveal that the far field emission intensity distribution and the spin states of the emitted photons remain nearly unchanged with the steered emission angular direction. Although the beam steering concept is demonstrated with the use of a translational stage, there are existing technologies that can be adapted to develop a chip scale beam steering devices for integrated devices and systems. For example, it has been reported that optical force in an integrated photonic circuit can be used to drive nanoscale mechanical devices23,24. Such mechanism can be utilized to introduce the feed point shift required in our beam steering concept, enabling a much more integrated and compact device design. A steerable nanoscale photon source with high brightness, high directivity as well as prescribed spin demonstrated in this work may have great potential for the applications in single molecule sensing, quantum optical information processing and integrated photonics circuits.
Methods
Sample preparation
A 150 nm gold film was deposited onto a glass substrate by e-beam evaporation. This thickness was chosen to prevent far field direct transmission of the laser through the gold film. Right handed Archimedes' spiral slot with 3-turn was fabricated with focused ion beam (FIB) milling (FEI dual beam SEM-FIB NOVA 200 Nanolab system). The parameters of spiral were chosen to be the same as the numerical simulation. The FIB was used with an acceleration voltage of 30 kV and a very small ion current of 28 pA to obtain the smallest possible beam diameter (21 nm), thus to guarantee minimal redeposition of Ga in the cut regions and highly vertical sidewalls.
Angular distribution determination
In the experiment, the fluorescence emission coming through the glass substrate is collected at the Fourier plane (k-space) of an infinite conjugate objective lens with NA of 0.8. First, we collect the fluorescence signals coming from a glass substrate without the spiral structure, the image contains a single disk with its radius representing the maximum collection angle of the objective lens, which is calculated to be θmax = sin−1(NA)≅53°. Then the glass substrate is replaced by the spiral antenna sample. With the help of a top CCD camera and ND filters, the geometrical center of the spiral can be aligned with the central peak of the illumination through carefully adjusting the x-y translation stage. In this case, the far-field emission pattern contains a bright spot centered on the optical axis with a weak background that covers the entire NA. The radius of the white circle (Rmax) representing the maximum collection angle of the objective lens is used as a reference. The angular distributions of the measured far-field emission patterns can be determined by the distances (R) to the center of this circle using the conversion relationship between the far-field emission angle θ and the spatial position in the back focal plane as θ = sin−1(NA·R/Rmax) = sin−1(0.8R/Rmax).
Author Contributions
Q. Z., G. R. and R. L. N. designed the experiments, G. R. performed the experiments, D. C. A fabricated the sample, G. R. wrote the paper with the help of Q. Z. All authors reviewed the manuscript.
Supplementary Material
scanning along x direction
scanning along y direction
Supplementary Information
Acknowledgments
D. Abeysinghe, R. Nelson and Q. Zhan acknowledge the support of the US Air Force Research Laboratory's (Materials and Manufacturing Directorate) Metamaterials Program.
References
- Stutzman W. L. & Thiele G. A. Antenna theory and design. Wiley: New York, 1998. [Google Scholar]
- Kosako T., Kadoya Y. & Hofmann H. F. Directional Control of Light by a Nano-Optical Yagi-Uda Antenna. Nature Photon. 4, 312–315 (2010). [Google Scholar]
- Novotny L. & Van Hulst N. Antennas for light. Nat. Photon. 5, 83–90 (2011). [Google Scholar]
- Cao L., Park J. S., Fan P., Clemens B. & Brongersma M. L. Resonant Germanium Nanoantenna Photodetectors. Nano Lett. 10, 1229–1233 (2010). [DOI] [PubMed] [Google Scholar]
- Knight M. W. et al. Nanoparticle-Mediated Coupling of Light into a Nanowire. Nano Lett. 7, 2346–2350 (2007). [DOI] [PubMed] [Google Scholar]
- Chen W., Abeysinghe D. C., Nelson R. L. & Zhan Q. Plasmonic Lens Made of Multiple Concentric Metallic Rings under Radially Polarized Illumination. Nano Lett. 9, 4320–4325 (2009). [DOI] [PubMed] [Google Scholar]
- Chen W., Abeysinghe D. C., Nelson R. L. & Zhan Q. Experimental Confirmation of Miniature Spiral Plasmonic Lens as a Circular Polarization Analyzer. Nano Lett. 10, 2075–2079 (2010). [DOI] [PubMed] [Google Scholar]
- Grober R. D., Schoelkopf R. J. & Prober D. E. Optical antenna: Towards a unity efficiency near-field optical probe. Appl. Phys. Lett. 70, 1354 (1997). [Google Scholar]
- Zou Y., Steinvurzel P., Yang T. & Crozier K. B. Surface plasmon resonances of optical antenna atomic force microscope tips. Appl. Phys. Lett. 94, 171107 (2009). [Google Scholar]
- Yu N. et al. F. Plasmonics for laser beam shaping. IEEE Trans. Nanotechnol. 9, 11–29 (2010). [Google Scholar]
- Kuhn S., Hakanson U., Rogobete L. & Sandoghdar V. Enhancement of single-molecule fluorescence using a gold nanoparticle as an optical nanoantenna. Phys. Rev. Lett. 97, 017402 (2006). [DOI] [PubMed] [Google Scholar]
- Curto A. G. et al. Unidirectional Emission of a Quantum Dot Coupled to a Nanoantenna. Science 329, 930–932 (2010). [DOI] [PubMed] [Google Scholar]
- Aouani H. et al. Bright Unidirectional Fluorescence Emission of Molecules in a Nanoaperture with Plasmonic Corrugations. Nano Lett. 11, 637–644 (2011). [DOI] [PubMed] [Google Scholar]
- Aouani H. et al. J. Plasmonic Antennas for Directional Sorting of Fluorescence Emission. Nano Lett. 11, 2400–2406 (2011). [DOI] [PubMed] [Google Scholar]
- Biagioni P., Huang J. S., Duo L., Finazzi M. & Hecht B. Cross resonant optical antenna. Phys. Rev. Lett. 102, 256801 (2009). [DOI] [PubMed] [Google Scholar]
- Yang S., Chen W., Nelson R. L. & Zhan Q. Miniature circular polarization analyzer with spiral plasmonic lens. Opt. Lett. 34, 3047–3049 (2009). [DOI] [PubMed] [Google Scholar]
- Wu Z., Chen W., Abeysinghe D. C., Nelson R. L. & Zhan Q. Two-photon fluorescence characterization of spiral plasmonic lenses as circular polarization analyzers. Opt. Lett. 35, 1755–1757 (2010). [DOI] [PubMed] [Google Scholar]
- Chen W., Abeysinghe D. C., Nelson R. L. & Zhan Q. Experimental Confirmation of Miniature Spiral Plasmonic Lens as a Circular Polarization Analyzer. Nano Lett. 10, 2075–2079 (2010). [DOI] [PubMed] [Google Scholar]
- Rui G., Nelson R. L. & Zhan Q. Circularly polarized unidirectional emission via a coupled plasmonic spiral antenna. Opt. Lett. 36, 4533–4535 (2011). [DOI] [PubMed] [Google Scholar]
- Rui G., Chen W., Abeysinghe D. C., Nelson R. L. & Zhan Q. Beaming circularly polarized photons from quantum dots coupled with plasmonic spiral antenna. Opt. Express 20, 19297–19304 (2012). [DOI] [PubMed] [Google Scholar]
- Rui G., Nelson R. L. & Zhan Q. Beaming photons with spin and orbital angular momentum via a dipole-coupled plasmonic spiral antenna. Opt. Express 20, 18819–18826 (2012). [DOI] [PubMed] [Google Scholar]
- Chen W. & Zhan Q. Realization of an evanescent Bessel beam via surface plasmon interference excited by a radially polarized beam. Opt. Lett. 34, 722–724 (2009). [DOI] [PubMed] [Google Scholar]
- Li M. et al. Harnessing optical forces in integrated photonic circuits. Nature. 456, 480–484 (2008). [DOI] [PubMed] [Google Scholar]
- Li M., Pernice W. H. P. & Tang H. X. Broadband all-photonic transduction of nanocantilevers. Nature. 4, 377–382 (2009). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
scanning along x direction
scanning along y direction
Supplementary Information