Enhanced Open-Circuit Voltage of PbS Nanocrystal Quantum Dot Solar Cells

Abstract

Nanocrystal quantum dots (QD) show great promise toward improving solar cell efficiencies through the use of quantum confinement to tune absorbance across the solar spectrum and enable multi-exciton generation. Despite this remarkable potential for high photocurrent generation, the achievable open-circuit voltage (V_oc) is fundamentally limited due to non-radiative recombination processes in QD solar cells. Here we report the highest open-circuit voltages to date for colloidal QD based solar cells under one sun illumination. This V_oc of 692 ± 7 mV for 1.4 eV PbS QDs is a result of improved passivation of the defective QD surface, demonstrating 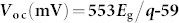as a function of the QD bandgap (E_g). Comparing experimental V_oc variation with the theoretical upper-limit obtained from one diode modeling of the cells with different E_g, these results clearly demonstrate that there is a tremendous opportunity for improvement of V_oc to values greater than 1 V by using smaller QDs in QD solar cells.

Solution processability coupled with potential for multiple exciton generation processes¹,²,³,⁴,⁵ makes nanocrystal quantum dots (QD) promising candidates for third generation low-cost and high-efficiency photovoltaics. In particular, sequential layer-by-layer assemblies of lead chalcogenide QDs (e. g., PbS⁶, PbSe⁷, and PbSSe⁸) have been demonstrated as an excellent photoactive absorber layer. For example, PbSe QD films with a bandgap (E_g) of ~ 1.0 eV have yielded a remarkably high short-circuit current density (J_sc) of ~ 24 mA/cm²¹, which is comparable to a J_sc of 24.4 mA/cm² for a nanocrystalline Si absorber⁹. Similarly, thin-films of PbS QDs with a band gap of ~ 1.5 eV have also shown high J_sc values of ~ 18 mA/cm²,¹⁰ which is greater than the J_sc of 16.75 mA/cm² obtained for amorphous Si solar cells¹¹.

Despite these remarkable J_sc values¹,⁷, the overall power conversion efficiency of these devices has been limited largely due to low open-circuit voltages (V_oc), regardless of the type of junctions used¹². Generally this is understood to be due to Fermi level pinning at the mid-gap states⁷,¹³, which are formed by a large number of surface states¹⁴,¹⁵ associated with defects on the QD surface. As a result, the barrier height between the metal and the QDs has been relatively invariant for metals with differing work functions⁷. This makes it difficult to create large barriers at the metal-QD Schottky junction or implement an ohmic contact to the QDs using high work function metals (e. g., Au)¹⁶.

We have fabricated Schottky junction solar cells with the highest open-circuit voltages ever reported for colloidal QD based solar cells by improving the passivation of the PbS QD surface and metal-QD interface with LiF passivation. By fitting the measured dark J–V characteristics of the solar cells with different QD sizes and therefore different bandgaps, we extract various diode parameters including the saturation current and examine the effect of quantum confinement on the dark J–V characteristics. Combining these results with the experimental device performance under one-sun illumination, we predict that it is possible to increase the V_oc value to over 1 V with smaller QDs.

Results

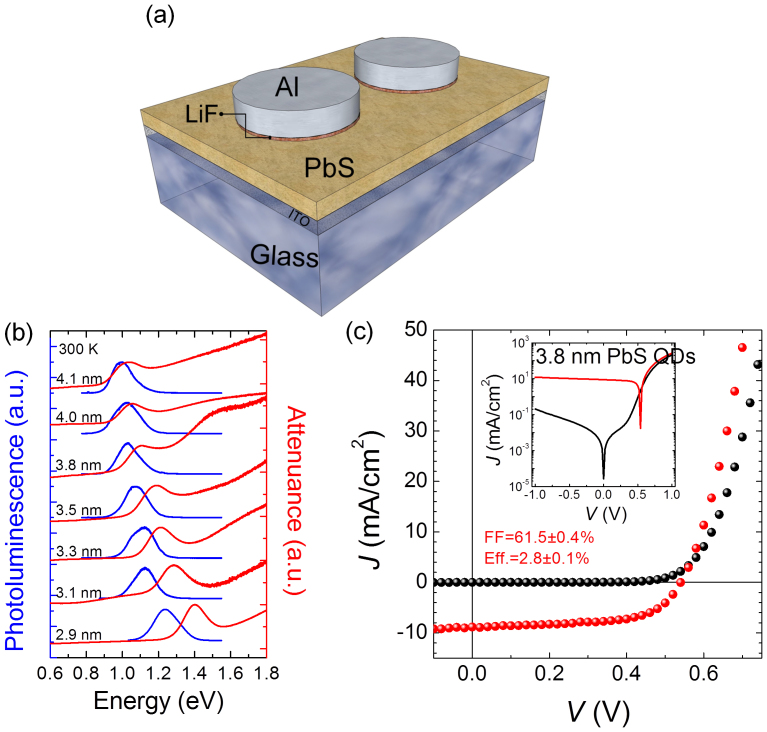
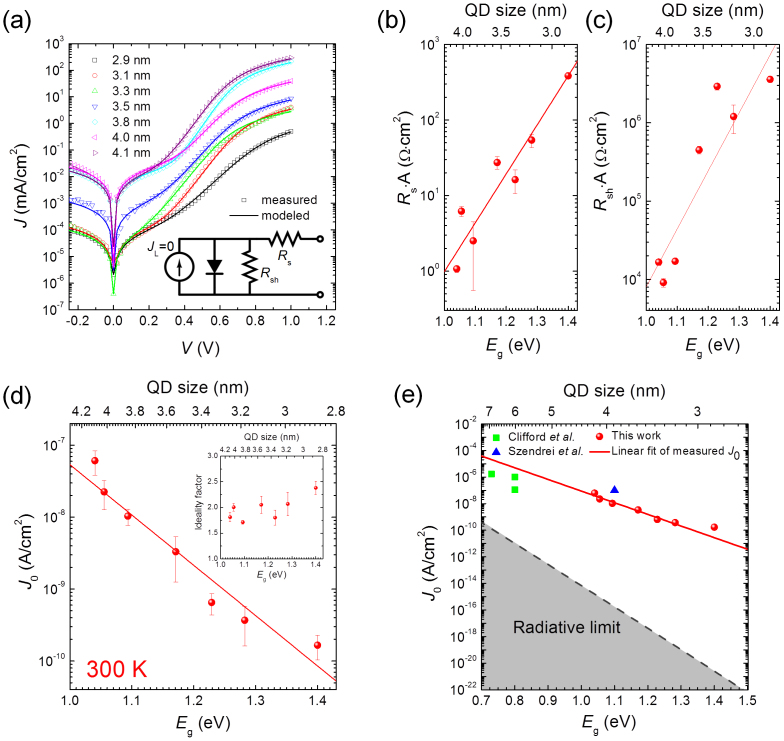
Several Schottky junction solar cells were fabricated (Fig 1a) using PbS nanocrystal QD films spin coated on commercial indium-tin oxide (ITO) glass. The Schottky junction was formed by evaporation of a LiF (1 nm)/Al (100 nm) contact defined by a shadowmask. Full details of the device fabrication are described in Methods. The PbS nanocrystals were oleic acid (OA) capped and synthesized following the procedure developed by Hines and Scholes (see Methods for full details of the synthesis and characterization)¹⁷. The bandgap of the absorber layer was controlled by changing the diameter of the PbS QDs, and the energy bandgap was determined through room-temperature photoluminescence (PL) and attenuance spectra (see Fig. 1b). As-synthesized QDs showed a well-defined first-exciton attenuance energy ranging from 1.0 eV to 1.4 eV (4.1 nm to 2.9 nm).

Figure 1. Surface barrier solar cells based on semiconducting PbS quantum dots and quantum confinement effects.

(a) Schematic of metal-PbS QD Schottky junction solar cells (ITO/PbS QDs/LiF/Al). (b) Room-temperature photoluminescence (PL) and attenuance spectra of films assembled with OA-PbS QD with different sizes as estimated using the empirical equation by Moreels et al¹⁸. The size of QDs estimated here is in good agreement with the results obtained from TEM size distribution statistics (see Supplementary information for details). (c) Representative J–V characteristics of QD solar cells in air under AM 1.5 G filtered spectral illumination (100 mW/cm²) with very high FF of > 60%. The inset shows the J–V curve in semi-logarithm scale.

Representative J−V characteristics under illumination and in the dark are shown in Fig. 1c. The highest power conversion efficiency of 2.8 ± 0.1% was obtained with a very high FF of ~ 61.5 ± 0.4%, V_oc = 545 ± 9 mV, and J_sc = 8.6 ± 0.3 mA/cm² under AM 1.5 G filtered spectral illumination (100 mW/cm²) for devices with 1.1 eV PbS QD absorber layers.

The J−V characteristics of devices with different bandgaps of QDs were measured under one sun in air. The V_oc values were then plotted as a function of the QD bandgap energy as illustrated in Fig. 2, and were shown to increase linearly with QD bandgap energy (E_g) as 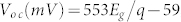, where q is the elementary electric charge (e). In addition to the linear fit, literature V_oc values are plotted in Figure 2 for comparison. These literature values were obtained from QD solar cells based on p-type PbS QDs and employing three different types of junctions; (1) metal-QD Schottky junction⁶,¹⁹,²⁰,²¹,²²,²³; (2) p–n heterojunction using n-type wide bandgap metal oxides such as TiO₂ or ZnO¹²,²⁴,²⁵,²⁶,²⁷, or n-type organic materials (C60 and PCBM)²⁸,²⁹; and (3) a recently introduced p-n homojunction using n-doped PbS QDs³⁰. We obtained a V_oc of 692 ± 7 mV from cells based on 2.9 nm PbS QDs (1.4 eV) under AM 1.5 G filtered spectral illumination (100 mW/cm²), which is, to the best of our knowledge, the highest V_oc ever demonstrated from a colloidal QD based solar cell. In addition, for a given nanocrystal diameter, all of the V_oc values reported in Figure 2 are the highest reported for any device geometry. All solar cell performance data is summarized in Table I.

Figure 2. PbS quantum dot solar cells with high open-circuit voltages.

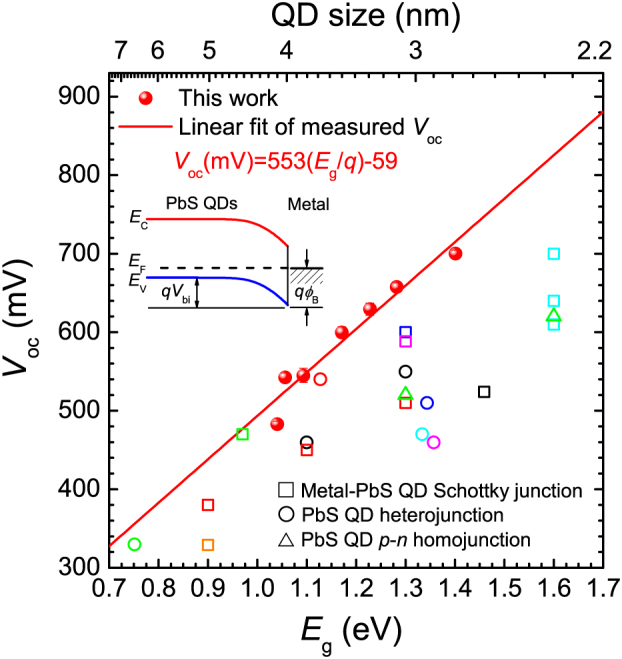
Experimentally measured open-circuit voltage (V_oc) as a function of bandgap (E_g) in PbS QD solar cells under 1 sun in air (closed circle). A linear fit to measured V_oc values yields 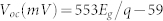, where q is the electronic charge (e). In addition to the linear fit, previously reported literature V_oc values are also plotted for comparison. These literature values were obtained from QD solar cells based on p-type PbS QDs employing three different types of junctions; (1) metal-QD Schottky junction (open circle)⁶,¹⁹,²⁰,²¹,²²,²³; (2) p–n heterojunction using n-type wide bandgap metal oxides such as TiO₂ or ZnO¹²,²⁴,²⁵,²⁶,²⁷, or n-type organic materials (C60 and PCBM)²⁸,²⁹ (open square); and (3) a recently introduced p–n homojunction using n-doped PbS QDs (closed triangle)³⁰. The inset illustrates the energy-band diagram of the metal-p-type semiconductor junction at thermal equilibrium.

Table 1. Performance data for metal-PbS QD Schottky junction solar cells (ITO/PbS QDs/LiF/Al) in the dark and under AM 1.5 G filtered spectral illumination (100 mW/cm²).

d	t	Jsc	Voc	FF	Eff.	J0	Rs·A	Rsh·A
(nm)	(nm)	(mA/cm2)	(mV)	(%)	(%)	(A/cm2)	(Ω·cm2)	(Ω·cm2)
2.9	148	5.7 ± 0.5	692 ± 7	34.9 ± 2.8	1.4 ± 0.1	(1.7 ± 0.7) × 10−10	383 ± 4.2	(3.6 ± 0.2) × 106
3.1	151	6.7 ± 0.8	657 ± 6	45.4 ± 0.9	2.1 ± 0.1	(3.7 ± 2.1) × 10−10	54 ± 11	(1.2 ± 0.1) × 106
3.3	198	8.6 ± 0.8	629 ± 8	48.4 ± 1.8	2.6 ± 0.2	(6.6 ± 2.1) × 10−10	16 ± 5.7	(2.9 ± 0.3) × 106
3.5	164	7.2 ± 0.5	602 ± 7	45.8 ± 1.4	2.0 ± 0.3	(3.3 ± 2.1) × 10−9	27 ± 5.2	(4.5 ± 0.4) × 105
3.8	136	8.6 ± 0.3	545 ± 9	61.5 ± 0.4	2.8 ± 0.1	(1.0 ± 0.3) × 10−8	2.5 ± 1.9	(1.7 ± 0.1) × 104
4.0	115	8.3 ± 0.3	542 ± 5	48.6 ± 1.1	2.2 ± 0.2	(2.2 ± 0.9) × 10−8	6.2 ± 0.1	(1.0 ± 0.1) × 104
4.1	148	8.4 ± 0.7	483 ± 3	59.7 ± 1.3	2.5 ± 0.3	(5.1 ± 0.8) × 10−8	1.0 ± 0.1	(1.6 ± 0.4) × 104

In general, the fundamental process determining V_oc is recombination, and the dark saturation current can be considered a direct measure of the recombination in the device. The relationship between dark saturation current and V_oc is inferred from the ideal diode equation under illumination³¹,

where J₀ is the dark saturation current density (A/cm²), J_sc is the short circuit current density (A/cm²), and n is the ideality factor. Assuming that the J_sc is voltage independent and J_sc ≫ J₀, the V_oc is then given by setting J to 0,

From equation (2), V_oc is proportion to ln(J_sc/J₀), and therefore J₀ needs to be as small as possible to maximize V_oc. For this reason, we measured J–V curves (symbols) in the dark for devices (ITO/PbS QDs/LiF/Al) using different sizes of PbS QDs, plotted as symbols in Fig. 3a. An increase in the forward dark current density was observed with increasing size, suggesting that hole injection could be enhanced due to reduction in the Schottky barrier height. This result is consistent with recent observations of the variation in barrier height between Ag and PbS QDs, showing that the barrier height increased for smaller QDs¹⁶. To investigate the variation in saturation current, series resistance, and shunt resistance by quantum confinement, the dark current density of the QD solar cell was fit by a one diode model including both series and shunt resistances;

where J₀ is the dark saturation current density (A/cm²), R_s is the series resistance (Ω), R_sh is the shunt resistance (Ω), A is the device area (cm²), and n is the ideality factor. This transcendental equation is solved iteratively using Newton's method to give the current density at a given bias voltage. Measured J–V data in the dark is fitted by first computing the logarithm to the base 10 of the current density data, then minimizing the sum of the squared deviations of the data from the logarithm of the current density computed using equation (3). The minimization routine uses the Levenberg-Marquardt algorithm³², where a Jacobian matrix is derived from analytical expressions for the partial derivatives of with respect to each of the fitting variables; J₀, n, R_s and R_sh. This method provides an efficient and reliable fitting routine, provided the initial guess for the fitted variables is close to their fitted values. As seen in Fig. 3a, the solid lines are fitted curves, which are in good agreement with measured data. The performance of all devices in the dark are summarized in Table I.

Figure 3. Quantum confinement effect in dark current-voltage characteristics of PbS QD solar cells.

(a) Current density-voltage (J–V) characteristics in the dark for PbS nanocrystal QD Schottky-barrier solar cells with the structure of ITO/PbS QDs/LiF/Al and a varying QD size from 2.9 nm to 4.1 nm. The open symbols are the experimentally measured data, while the solid lines are fits according to a one diode model including series and shunt resistances (equation 3). The inset shows the equivalent circuit of the diode in the dark. (b–d) The quantum confinement effect on diode parameters, (b) series resistance (R_s), (c) shunt resistance (R_sh), and (d) saturation current density (J₀). A is the diode area (cm²). The inset of Fig. 3d shows the ideality factor (n) vs QD bandgap energy (E_g). (e) Calculated limit of the J₀ as a function of E_g and size in metal-PbS QD junction. The dash line indicates the radiative limit of J₀ calculated using equation (7). The literature values (square³⁹ and triangle⁴⁰) in J₀ for metal-PbS QD Schottky junction are shown for comparison.

A parasitic series and shunt resistance associated with the cells was shown to be mostly size dependent. As seen in Fig. 3b, the series resistance tends to increase significantly after decreasing the size by only 1 nm. A similar trend is also reported by Gao et al.¹⁶, as the PbS QD size changes from 2.4 nm to 6.4 nm. Overall the series resistance depends on a number of other parameters in the devices, such as resistance of the films, contact resistance and sometimes geometrical factors³¹. For these QD systems, it has been reported that size dependence of carrier mobility is responsible for the increased series resistance in PbS QD films as decreasing size¹⁶,³³.In addition, an increased series resistance is attributed to larger contact resistance to smaller QDs. This is because the contact resistance depends on the barrier height³¹, while the barrier height tends to increase for smaller QDs¹⁶. It is interesting to note that the shunt resistance increased by almost two orders of magnitude for smaller QDs (Fig. 3c). Although the quantum confinement effect on the shunt resistance is not well known, an increased shunt resistance may be attributed to dense and pin-hole free multilayered assemblies with smaller QDs³⁴, which potentially reduces the leakage across the junction. The quantum confinement effect on parasitic series and shunt resistances associated with QD solar cells is still under investigation.

It is important to note that several factors could contribute to the improving V_oc values seen in this study. First, the thickness of the LiF interfacial layer was carefully optimized³⁵ prior to the Al deposition onto the PbS QD layers. When 10 Å thick LiF was deposited between the PbS QDs and the Al, the J₀ decreased by one order of magnitude compared to a device with 6 Å thick LiF. Further increasing the LiF thickness up to 14 Å reduced the J₀ but at the expense of increasing the series resistances. These results suggest that the optimized LiF thickness is critical for reducing J₀ by passivating localized traps in the PbS QDs close to the junction¹²,²²,²⁵,²⁹,³⁶, thus suppressing non-radiative recombination processes in the cells. Further details are discussed in Supplementary information. Second, a sequential layer-by-layer spin-coating process in air was used to fabricate the devices, resulting in oxidation and a concomitant passivation effect on the PbS QD surface that eliminates trap centers²²,²⁹,³⁷. The X-ray photoelectron spectroscopy (XPS) confirmed the presence of multiple oxide compounds in the actual device samples fabricated in air (refer to Figure S3 in Supplementary information for detailed XPS data)²⁹,³⁷. In fact, Zhao et al.²⁹ report that a smaller recombination rate constant was observed for their air-annealed PbS QD devices, confirming that recombination processes are significantly suppressed due to passivation effects by some degree of oxidation, consequently leading to the highest V_oc of 0.47 V, compared with N₂-annealed, pristine, and ozone-treated devices²⁹.

From the measured and modeled J–V characteristics, J₀ and n were plotted as a function of QD bandgap energy. A strong quantum confinement effect in J₀ was observed in Figure 3d, showing that J₀ decreases by three orders of magnitude for a size decrease of only 1 nm. The ideality factors were varied between 1.7 and 2.4, showing no clear correlation with varying size (inset of Fig. 3d). The lower limit of J₀ is a function of bandgap (E_g)³⁸,

where J₀₀ is a prefactor (A/cm²) which depends on the current transport mechanism of the device³¹. From the slope and the intercept of the linear fit of experimental data using 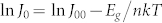, J₀₀ and n were estimated 51.6 ± 6.2 A/cm² and 1.92, respectively. Using equation (4) combined with the obtained values in J₀₀ and n, variations in J₀ across a wide range of bandgaps (from 0.7 eV to 1.5 eV) is predicted, as illustrated in Fig. 3e. Other experimental literature values of J₀ are also plotted for comparison (Fig. 3e)³⁹,⁴⁰, showing similar trends. For comparison we also show the radiative limit for J₀ (i. e., the ideal solar cell material).

Discussion

In the thermodynamic limit, the dark current density is limited only by radiative recombination and the EQE is unity for above bandgap photons and zero for all other photons. The dark current density is given by the generalized Planck formula

Here we have assumed the limiting optical arrangement, such that the device has a perfect mirror on one face and a vacuum on the other face⁴¹. In the Boltzmann approximation, the −1 in the denominator of this expression can be neglected and the integral then has a simple analytical form, allowing the radiative current density to be written as

where the radiative saturation current density (J_0,rad) is

J_0,rad was plotted as a function of bandgap using equation (7) in Fig. 3e. The difference between the measured J₀ for QD solar cells and the J_0,rad calculated when the radiative recombination process is dominant allows us to determine the theoretical upper limit of the V_oc available for device improvement. This assumes all non-radiative recombination processes in the metal-PbS QD Schottky junction solar cells are suppressed²⁵,²⁹,³⁶,³⁷. For example, the use of core/shell⁴² or core/shell/shell⁴³ nanocrystal QDs is expected to improve the V_oc by reducing a large number of traps associated with surface defects, greatly suppressing the non-radiative recombination contributions to the dark current.

Finally, we have analyzed the upper limit to the V_oc achievable with the experimentally measured J₀ values of the devices, using equation (2) with the ideality factor of 1.92 at 300 K. In this case, the limiting photocurrent was calculated under the ASTM AM1.5 G spectrum as a function of the QD bandgap, again assuming an external quantum efficiency (EQE) of unity for above bandgap photons. In this case, the short-circuit current density is given by

where I(λ) is the spectral irradiance in units of W m⁻²nm⁻¹ and the bandgap wavelength is given by 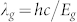. Thus, the upper limit of V_oc is:

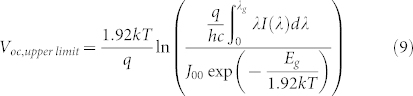where J₀₀ is 51.6 ± 6.2 A/cm² at 300 K. Similarly, we calculated the thermodynamic limit for the V_oc by substituting J_0,rad (Eq. 7) and the limiting J_sc obtained from equation 8 into equation (2):

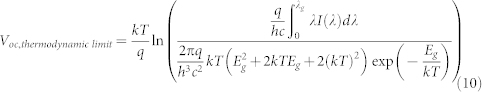In Figure 4, these two limits for V_oc values are plotted along with the experimentally measured V_oc values and the associated linear fit of 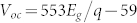in the range of 0.7 eV to 1.5 eV. As discussed earlier, the difference between the thermodynamic and upper limit for V_oc is due to the increased J₀ resulting from the non-radiative recombination processes in metal-QD junction solar cells. Comparing experimental V_oc values with the calculated upper limit of V_oc is a good indicator for assessing how much enhanced photocurrents could further improve the V_oc of PbS QD solar cells. These results clearly suggest that there is substantial opportunity for V_oc enhancement by increasing J_sc in this system. For example, the highest V_oc of 1129 mV can be achievable at a bandgap of 1.5 eV (i.e., ~ 2.6 nm PbS QDs), which is about 92% of the thermodynamic limit. One way to enhance the J_sc values could be to implement front semi-transparent metal contacts with anti-reflective coatings in metal-QD Schottky junctions, enabling thicker absorber layers to be used. In devices reported to date, the J_sc of the device is limited by the relatively thin active QD absorber layer thickness, a consequence of Schottky junction formation at the back metal contact (e.g. Al, LiF/Al, Mg/Al) rather than at the front contact (e.g. ITO).

Figure 4. Limit in the open-circuit voltage in metal-QD Schottky junction solar cells.

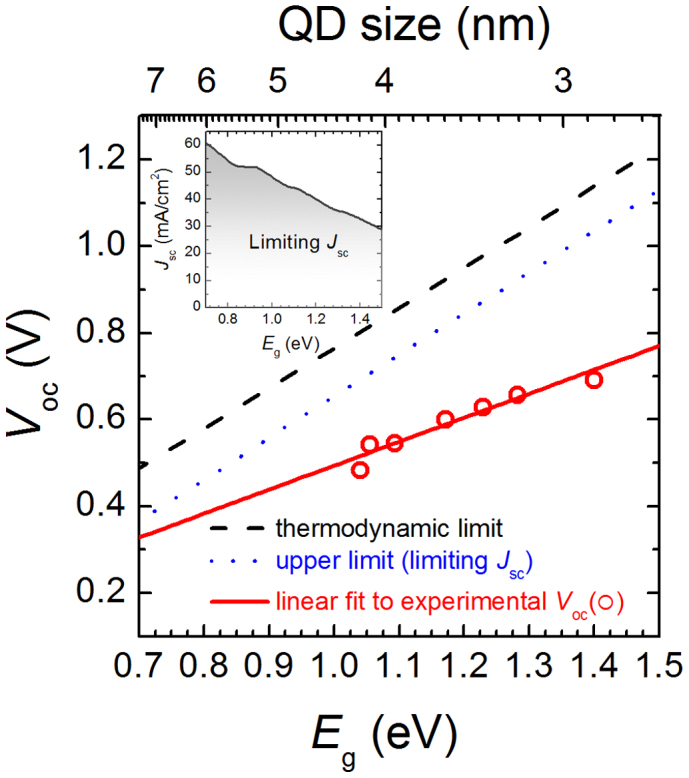
The limit of the V_oc as a function of the bandgap (E_g) of PbS QDs: the thermodynamic limit (dash) of V_oc calculated using limiting J_sc and J₀, respectively (Eq. 9); the upper limit (dot) of V_oc calculated using limiting J_sc and experimentally measured J₀ (Eq. 10); the experimentally measured V_oc (solid) as a function of PbS QD size. The inset shows the limiting J_sc in thermodynamic limit as a function of E_g under AM1.5 G.

To summarize, we report enhanced open-circuit voltages as a function of the QD bandgap for metal-PbS QD Schottky junction solar cells as a result of reduced non-radiative recombination processes. Under one sun illumination, we demonstrate the highest V_oc of 692 ± 7 mV (1.4 eV PbS QDs) ever reported for colloidal QD based solar cells. By analyzing the diode parameters extracted from the measured dark J–V characteristics, we find a strong quantum confinement effect on the saturation current density, which decreases by three orders of magnitude with only a 1 nm reduction in QD size. The parasitic series and shunt resistances associated with the devices are also shown to be strongly size dependent. Using the measurement of the size dependent saturation current and the short-circuit current calculated from a detailed balance model, the upper limit of the open-circuit voltage achievable for QD sizes varying in size from 2.6 nm to 7.4 nm is presented. By comparing experimental V_oc values with this upper limit, we suggest that it is possible to enhance the open-circuit voltage to greater than 1 V by using smaller QDs to minimize the short-circuit current losses in Schottky-barrier solar cells.

Methods

Material

Lead oxide (PbO, 99.9+%), oleic acid (OA, 90%), 1-octadecene (ODE, 90%), hexamethyldisilathiane (TMS, synthesis grade), hexanes (98.5%) and acetone (99.9%) were purchased from Sigma Aldrich. Ethanol (200 proof) was purchased from the Warner Graham Company. All chemicals were used as received.

PbS nanocrystal QD synthesis

The synthesis of PbS nanocrystal QDs followed the procedure developed by Hines and Scholes¹⁷, and was performed under inert conditions using standard Schlenk techniques. ODE (20 mL) was dried and degassed by heating to 110°C under vacuum for 1 hr, then TMS (658 μL) was added to create a stock solution of 151 mM TMS in ODE. In a typical synthesis, 376 mg PbO, 1.4 g OA and 11.8 g of ODA were mixed in a 50 mL three neck flask and heated to 110°C under vacuum for 30 minutes to create Pb(oleate)₂. The flask was purged with Ar and heated to an injection temperature between 130°C and 150°C. Next, 5 mL of TMS stock solution was injected into the Pb(oleate)₂ solution instantly turning the color black. After several minutes, the reaction was cooled by placing the flask in liquid nitrogen. To separate the QDs from unreacted reagents and byproducts, 2 mL of hexane and 10 mL of acetone and/or ethanol were added to the reaction mixture which was then centrifuged at 4000 rpm for 4 min. The precipitated QDs formed a black solid at the bottom of the centrifuge vial and the supernatant was removed by decanting. The QDs were washed one more time with hexane and acetone and/or ethanol, dried with Ar, and stored in a glove box. The reaction yield is nearly 100% relative to TMS. The mass of PbS in the final product was determined using a TA Instruments Q500 thermogravimetric analyzer (TGA). The QD diameter was varied by changing a combination of the injection temperature, growth time, and oleic acid to lead ratio (see Tables S1 and S2 in the Supplementary Information for full details of the synthesis).

PbS nanocrystal QD characterization

Attenuance spectra of the PbS QD films were obtained at room temperature using a Fourier Transform Infrared (FTIR) spectrometer (VERTEX 80 v, Bruker Optics) equipped with a CaF₂ beamsplitter and a DLaTGS detector. Samples were prepared by drop casting onto glass slides, and a portion of the substrate which was not coated with the PbS film was used as a reference. The samples were evacuated to 1.6 Torr in the sample chamber in order to minimize oxidation of the PbS surface and to suppress H₂O and CO₂ absorption features in the spectra.

The PL spectra of films of PbS QDs drop cast onto silicon wafers were obtained at room temperature with a triple spectrometer (Trivista 557, Princeton Instruments) utilizing a LN₂ cooled InGaAs linear array detector (OMA V, Princeton Instruments). The PL samples were mounted in an Oxford Instruments cryostat equipped with a ZnS window and pumped to ~ 10⁻⁵ mTorr. The samples were mounted in the cryostat in order to keep them under vacuum and minimize oxidation of the PbS surface and suppress absorption features in the spectra from H₂O and CO₂.

TEM samples were prepared by making dilute chloroform solutions and drop casting a small volume (<500 μL) onto lacey carbon TEM grids. TEM images were obtained on a JEOL 2200F3 transmission electron microscope operating at 200 kV. The CCD camera on which the images were recorded was calibrated with a gold lattice magnification standard.

X-ray photoelectron spectroscopy (XPS) (K-Alpha XPS system, Thermo Fisher Scientific Inc.) was performed in a commercial UHV system (typically 1 × 10⁻⁹ Torr base pressure) equipped with an Al Kα micro-focused monochromator.

X-ray power refraction (XRD) data was obtained on a Rigaku Smartlab instrument operating in parallel beam mode and indexed to bulk PbS by comparison to JCPDS card#1-880. Samples were prepared by drop casting concentrated CHCl₃ solutions of the PbS nanocrystals onto quartz substrates followed by solvent evaporation. For as-synthesized PbS QDs, the position of the PbS QD XRD diffraction peak is consistent with bulk PbS (refer to Figure S1 in Supplementary information).

Device fabrication

A sequential layer-by-layer spin-coating procedure was conducted as reported in the literature⁶to prepare the PbS QD active layers. Briefly, QD films were deposited onto pre-cleaned ITO-coated glass substrate by spin-coating ~ 5 mg/ml solution of PbS-OA in chloroform at 4000 rpm for 30 s. The PbS QD films were then immersed in 20 mM 1, 3-benzenedithiol (BDT, 99%, Aldrich) in acetonitrile for 30 s, followed by spin-coating at 4000 rpm for 30 s to remove residual solution (see Figure S4 in Supplementary information). This process was repeated until the desired film thickness had been achieved. All procedures were performed in air. Finally, the devices were completed by shadowmask evaporation of a LiF (1 nm)/Al (100 nm) top contact at 10⁻⁷ torr. Six devices were made on each substrate, each device with an active area of 0.11 cm².

Electrical characterization of devices

The current density–voltage (J−V) measurements were performed with a parameter analyzer (Agilent 4156C) in air without any encapsulation under the spectral output from a 150 W solar simulator (Newport Corporation) using an AM 1.5 G filter. The irradiance (100 mW/cm²) of the solar simulator was adjusted using a standard Si photodetector (818-SL-L, Newport Corporation) that had been cross-calibrated by a reference Si cell traceable to the National Renewable Energy Laboratory (NREL).

Author Contributions

W.Y. and J.G.T. conceived and designed the experiment. W.Y. carried out the experiments. J.E.B., D.P. and E.E.F. synthesized the materials. M.P.L conducted the theoretical study. W.Y. wrote the manuscript. All authors discussed the results and reviewed the manuscript.

Supplementary Material

Supplementary Information

Supplementary Information