USING DNASE DIGESTION DATA TO ACCURATELY IDENTIFY TRANSCRIPTION FACTOR BINDING SITES

Abstract

Identifying binding sites of transcription factors (TFs) is a key task in deciphering transcriptional regulation. ChIP-based methods are used to survey the genomic locations of a single TF in each experiment. But methods combining DNase digestion data with TF binding specificity information could potentially be used to survey the locations of many TFs in the same experiment, provided such methods permit reasonable levels of sensitivity and specificity. Here, we present a simple such method that outperforms a leading recent method, centipede, marginally in human but dramatically in yeast (average auROC across 20 TFs increases from 74% to 94%). Our method is based on logistic regression and thus benefits from supervision, but we show that partially and completely unsupervised variants perform nearly as well. Because the number of parameters in our method is at least an order of magnitude smaller than centipede, we dub it millipede.

1. Motivation

Identifying binding sites of transcription factors (TFs) is a key task in deciphering transcriptional regulation. Methods based on chromatin immunoprecipitation (ChIP) permit the identification of TF binding sites at varying degrees of precision (ChIP-chip < ChIP-seq < ChIP-exo),¹ but they can only survey the genomic locations of a single TF per experiment.

To increase throughput, a complementary strategy based on the genomic digestion products of deoxyribonuclease I (DNase I, which we will simply call DNase) might be considered. DNase cleaves DNA in a manner that depends, inter alia, on the chromatin state of the genome, with nucleotides bound by proteins being cleaved less frequently than unbound nucleotides. Thus, the frequency with which a particular nucleotide is cleaved provides (noisy) information about the degree to which that nucleotide is bound by a protein. The primary motivation for using DNase digestion is that it applies non-specifically to all proteins binding the genome, regardless of their identity. This non-specific property is both a strength—in that it overcomes the one-TF-at-a-time limitation of ChIP—and a weakness, since simply knowing that a nucleotide is bound does not reveal the identity of the protein that binds it.

However, the binding specificities of many DNA-binding proteins are known (in this work, we assume specificities are modeled using a position weight matrix (PWM), but our method is general and can use any binding specificity model). This raises the prospect that a computational method combining DNase digestion data with prior knowledge of TF binding specificities might be able to identify binding sites in a TF-specific manner, at least for TFs with sufficiently distinct binding specificities. This prospect has spurred the development of a number of promising methods over the past few years. Though these methods all use DNase data in conjunction with binding specificity information, they adopt one of two distinct strategies:

1. TF-generic DNase signature. Early methods started by scanning the mapped DNase data for signatures of TF binding (roughly: the cleavage frequency is elevated, then drops for a short interval, and is then elevated again). Once sites with these signatures are detected, the TF(s) putatively bound to each site may be assigned by searching for matches to known PWMs. This strategy was first adopted by Hesselberth et al. in yeast, where initial site-detection was performed using a greedy approach.² As a technical refinement applied to the same data, Chen et al. developed a dynamic Bayesian network (DBN) approach for initial site-detection.³ Boyle et al. developed a hidden Markov model (HMM) approach for initial site-detection, and applied it to DNase data from human cells.⁴ More recently, Cuellar-Partida et al. formulated an informative positional prior from the human DNase data, and then looked for strong posterior evidence of binding, using PWM matches for the likelihood;⁵ this method is essentially DNase-weighted motif scanning.

2. TF-specific DNase signature. One disadvantage of the previous strategy is that the DNase signature of TF binding is necessarily the same for all TFs. A more effective strategy might be to start by scanning the genome for sites that match TF binding specificities; these will be called ‘candidate binding sites’. The DNase data in the genomic region surrounding each candidate binding site can then be used (along with other relevant information, such as the strength of the PWM match) to estimate whether the TF is indeed bound there. The first (and to our knowledge only) such method, given the moniker centipede, was developed by Pique-Regi et al. and tested exclusively on human DNase data.⁶

Figure 1 shows two examples—Reb1 in yeast and REST (also known as NRSF) in human—of DNase data surrounding candidate binding sites that arise from PWM scanning of the genome. The figure illustrates that methods capable of using TF-specific DNase signatures are more likely to be effective at identifying TF binding sites. As such, in what follows, we focus exclusively on this second strategy.

Fig. 1.

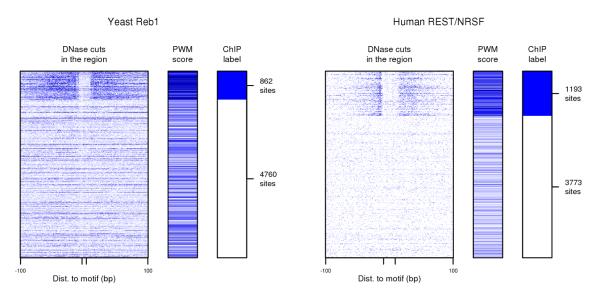
DNase digestion data used in conjunction with TF binding specificity information can be used to identify TF binding sites. Left panel shows data for Reb1 candidate binding sites in yeast, and right panel shows data for REST (also known as NRSF) candidate binding sites in human. In each case, rows represent candidate sites based on PWM matches; rows are grouped by ChIP labels into positive and negative sets and then randomly ordered within each set. For each candidate binding site, columns depict DNase cuts in the region 100bp up- and downstream, PWM score, and ChIP label. Darker blue in data columns indicates higher number of DNase cuts at each position or higher PWM score. The figure makes clear that (a) both DNase data and TF binding specificity information provide noisy evidence of TF binding, and (b) since DNase cuts near Reb1 binding sites have a distinct pattern from DNase cuts near REST binding sites, methods using TF-specific DNase signatures are more likely to be effective at identifying TF binding sites.

2. Background

centipede learns TF-specific DNase signatures in an unsupervised manner, using an EM algorithm to optimize a Bayesian mixture model.⁶ The model discriminates bound from unbound sites using DNase data, plus other prior information (e.g., strength of match to PWM, degree of conservation, proximity to TSS). The likelihood of the DNase data is modeled in terms of both the total number of DNase cleavage events (‘cuts’) in the region around the candidate binding site (using a negative binomial), and the specific ‘shape’ of the cuts as they are arranged in the region (using a multinomial). centipede’s discrimination power is largely driven by the PWM component of the prior and the multinomial component of the likelihood. However, the use of the highly flexible multinomial means that the model has the potential to over-fit irrelevant details in the shape of the DNase data—both in and around candidate binding sites—including random noise, systematic bias in DNase digestion, or artifacts arising from EM becoming trapped in a local mode. Indeed, the authors attempt to address the likely over-fitting by employing shrinkage estimators for their multinomial parameters, which improves certain evaluation metrics like area under the ROC curve (auROC), but at the expense of others, such as sensitivity at 1% false positive rate (FPR).

The authors of centipede also explored the use of activating and repressing histone marks in their likelihood, but reported limited benefit. Cuellar-Partida et al. later explored individual histone modifications, and proposed a TF-generic DNase signature method called H-p, intended to make better use of histone modification data (alongside DNase data and PWM scores).⁵ With the same six human TFs of Pique-Regi et al., they evaluated their proposed H-p method in comparison with (a) D-p, their method using DNase data and PWM scores, but omitting histone modifications, (b) D-s, a straw-man method using only the total number of nearby DNase cuts, but omitting both histone modifications and PWM scores, and (c) centipede. Surprisingly, in terms of auROC, the proposed H-p model was the worst performer across the board for all six human TFs, suggesting that histone modifications are not likely to be helpful for this task. Even more interestingly, the straw-man method D-s outperformed H-p and D-p, and was competitive with centipede, though it was not very sensitive at 1% FPR. This surprising set of results motivated us to ask the following questions:

1. Based on the observation that D-s was performing competitively even though it lacked a TF-specific DNase signature and ignored the strength of the PWM match, could we develop an effective model that would address these two shortcomings of D-s, yet be much simpler than centipede, to minimize the possibility of over-fitting?

2. Would such a model perform well across organisms, not only in the human data of Boyle et al.⁴ but also in the yeast data of Hesselberth et al.?² This is important for three reasons: (a) it would ensure that our conclusions about the relative merits of various approaches are not specific to human, (b) it would allow us to evaluate using a larger set of TFs because many TFs have been profiled by ChIP in yeast, and (c) we had observed that centipede performed quite poorly when applied to DNase data from yeast. In summary, could we develop a model that worked at least as well as centipede in human, but improved dramatically upon centipede in yeast?

In this paper, we describe a conceptually simple method for combining DNase data with information on TF binding specificity to identify TF binding sites. We show that our simple method outperforms centipede marginally in human and dramatically in yeast. Its superiority is robust to the choice of evaluation metric, as well as the definition of positive and negative binding sites. Our method is based on logistic regression and thus benefits from supervision, but we show that partially and completely unsupervised variants perform nearly as well. Because the number of parameters in our method is at least an order of magnitude smaller than centipede, we dub it millipede.

3. The millipede framework

millipede improves upon centipede in two primary ways. First, it reduces the number of parameters to be estimated by 1–2 orders of magnitude. This reduces the potential to over-fit irrelevant details in the DNase data, speeds up computation, and simplifies interpretation. The reduced number of parameters is a consequence of aggregating the DNase cut data within bins. One specific motivation for—and benefit of—such a strategy is that it reduces the prospect of fitting structure in the DNase signal that arises from digestion bias, which we show later may be important to address (though a more sophisticated approach would be to model the bias explicitly). Second, it is supervised, allowing the model to be trained to discriminate between bound and unbound sites rather than simply having to guess which sites are bound and unbound, as centipede does. When labeled data are not available (for instance, if one is interested in identifying binding sites for a TF that has no ChIP data), we show later that partially and completely unsupervised variants of millipede still perform admirably.

3.1. Bins for aggregating DNase cuts

Consider a candidate TF binding site, always oriented with respect to the strand on which the PWM is matched. As illustrated in Figure 2, within the binding site we construct two bins representing the left and right half of the site. Then, within the 100bp regions flanking the binding site both up- and downstream, we construct five equal-size bins (the choice of five is arbitrary: it allows the 100bp flanking regions to have some substructure, but not an excessive amount; we discuss this choice later). The result is 12 total bins across a genomic region of size 200 + w, where w is the width of the TF PWM.

Fig. 2.

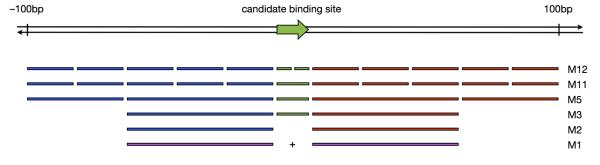
Understanding the relationships between bins in various millipede models. All bins are defined relative to the orientation of the candidate binding site: green bins are within the binding site, blue bins are upstream, and red bins are downstream. Models are arranged from most to least complex, so that each simpler model is derived from the one above it by merging or dropping bins. The simplest model M1 arises when the upstream and downstream bins of M2 are merged (thus shown in purple).

If we use all 12 bins in millipede, we call the model M12. However, not all of these bins may be important, so we can construct various model simplifications by merging or dropping bins. For example, we can merge the two bins of the left and right halves of the binding site into a single bin, resulting in 11 total bins, so we call this model M11. Next, we can merge bins in the up- and downstream flanking regions: by merging the more proximal three bins into a single bin, and merging the more distal two bins into a single bin, we are left with two bins upstream, two bins downstream, and one bin for the binding site, so we call this model M5. We can then drop the up- and downstream distal bins altogether, resulting in model M3. We can further drop the binding site bin, resulting in model M2. Finally, we can merge the two bins of M2, resulting in a model that has only one bin: M1. Specifically, M1 is a model that aggregates DNase cuts in the union of the two 60bp windows upstream and downstream of the binding site.

It is also possible to make the model more complex, for example by distinguishing between the forward and reverse strands when strand-specific DNase cleavage data is available. Strand-specific information was not available in the yeast DNase data from Hesselberth et al.,² but was available in the human DNase data from Boyle et al.⁴ For example, if we start with model M12 but elect to distinguish between forward- and reverse-strand cuts, we have a model with 24 bins, which we call M24.

3.2. Logistic regression

The millipede framework is based on standard logistic regression. Natural extensions with regularization (shrinkage or selection) are easily applied (though we do not explore them in this paper). Any relevant variables can be included, which makes the framework flexible and extensible. In what follows, the logistic regression covariates at each candidate binding site are simply (a) log₂-transformed counts of aggregate DNase cuts within each bin, (b) the PWM score, and (c) optionally, a score measuring the degree of conservation. Formally, the full millipede model for estimating the probability p_i that candidate binding site i is bound is:

$$\log \left(\frac{p_i}{1-p_i}\right)={\beta }_0+\sum _{b=1}^B{\beta }_b\times {\mathtt{D}}_{b,i}+{\beta }_{\mathtt{PWM}}\times {\mathtt{PWM}}_i+{\beta }_{\mathtt{CONS}}\times {\mathtt{CONS}}_i$$

where d_b,i is the log₂-transformed count of aggregate DNase cuts in bin b relative to site i, B is the total number of bins being considered in the model, and pwm_i and cons_i are the PWM and conservation scores of site i, respectively. Note that we could also choose to include other variables if they were deemed relevant. Specifically, we could add a term β_TSS × tss_i to include a score measuring proximity to the TSS for any TFs where that might be informative. We tested this but observed that TSS proximity scores were of negligible benefit; in what follows, we therefore omit them for simplicity.

When millipede is run in a supervised mode, we learn its various coefficients from training data (and we can interpret the resulting model by examining the learned coefficients). We describe later how millipede can also be run in completely or partially unsupervised modes.

4. Experimental methods

4.1. Human data

To facilitate comparison with the work of Pique-Regi et al.⁶ and Cuellar-Partida et al.⁵ in human, we used the exact same data wherever possible, kindly shared with us by Roger Pique-Regi. We used the same DNase digestion data in GM12878 cells, originally collected in the lab of Greg Crawford and reported in Boyle et al.⁴ We used the same candidate binding sites as reported by Pique-Regi et al.; to avoid mappability bias, Pique-Regi et al. filtered out candidate sites whose surrounding region contained more than 20% unmappable nucleotides. We used the same PWM, conservation, and TSS scores as reported by Pique-Regi et al. (eventually deciding to omit the TSS scores, as discussed above). For training and evaluation, we studied the same six TFs, constructing positive and negative sets using the same ENCODE ChIP-seq data in GM12878 cells, as processed by Pique-Regi et al.

4.2. Yeast data

We used DNase digestion data in α-factor arrested yeast cells, collected in the lab of John Stamatoyannopoulos and reported in Hesselberth et al.² When scanning for candidate binding sites, we used PWM models of TF binding specificities from MacIsaac et al.,⁷ and the sacCer2 (June 2008) version of the yeast genome. Following Pique-Regi et al., to avoid mappability bias, we filtered out candidate sites whose surrounding region contained more than 20% unmappable nucleotides. For training and evaluation, we studied 20 TFs, constructing positive and negative sets using ChIP-exo data from Rhee et al.,¹ where available (Reb1, Rap1, and Phd1), as well as the ChIP-chip data of Harbison et al.,⁸ as processed by MacIsaac et al.⁷ MacIsaac et al. used conservation information to define positive binding sites, so to avoid potential bias, we omit all conservation data when evaluating performance in yeast. In practice, the usefulness of conservation information when applying millipede in human suggests that it would likely also be useful in yeast.

4.3. Gold standard evaluation sets regarding TF binding

Cuellar-Partida et al.⁵ describe a ‘peak-centric’ approach for constructing gold standard evaluation sets, in contrast to what they term the ‘site-centric’ approach of Pique-Regi et al. As it happens, the two approaches construct positive sets quite similarly—requiring positive TF binding sites to have both sufficiently strong ChIP signal and sufficiently strong PWM score—but construct negative sets quite differently (more on this below).

4.3.1. Positive TF binding sites

Since site-centric and peak-centric approaches construct positive sets in roughly the same fashion, we defined our positive TF binding sites in a manner analogous to Pique-Regi et al.: among all candidate binding sites determined by PWM scanning along the genome, positives are those that fall within a ChIP peak. In human, we used the exact same positive set as Pique-Regi et al., while in yeast, we constructed our own positive set using ChIP-exo peaks (where available) and the TF binding sites of MacIsaac et al., derived from ChIP-chip signals (requiring a ChIP-chip p-value < 0.005, and a ‘moderate’ level of conservation). One small caveat is that although the peaks from ChIP-exo (for Reb1, Rap1, and Phd1 in yeast) and ChIP-seq (in human) are likely of high enough quality to serve as a fairly accurate gold standard, peaks from ChIP-chip in yeast are perhaps better described as a bronze standard.

4.3.2. Negative TF binding sites

Since we are trying to predict whether or not candidate binding sites are bound, a natural choice for a negative set would be all candidate binding sites that are not in the positive set (do not fall within a ChIP peak); these are the negative sets we use in this paper, and we refer to these as ‘millipede gold standards’. Under such a construction, every candidate binding site is either positive or negative. The two previous approaches for constructing negative sets are notably different. The negative sets of Pique-Regi et al. are roughly subsets of ours because they require both of the following: (a) the candidate binding site does not fall within a ChIP peak, and (b) the ChIP treatment signal is less than the ChIP control signal at the site. This reduces the size of the negative set by including only those sites with the strongest negative signal, which makes the discrimination task easier and may thus over-estimate performance. In contrast, the negative sets of Cuellar-Partida et al. are roughly supersets of ours because negatives are defined as all genomic sites that do not fall within a ChIP peak (whether they are candidate binding sites or not). However, since we are only making predictions on candidate binding sites, our definition of negatives is equivalent to that of Cuellar-Partida et al. for this task. To ensure our results do not depend importantly on our choice of negative sets, we also evaluate each method’s performance in human using the same negative sets that Pique-Regi et al. considered, referring to these as ‘centipede gold standards’.

4.4. Evaluation metrics

We evaluate the predictions of each model using four different metrics. To facilitate comparison with previous work, we report both area under the ROC curve (auROC) and sensitivity at 1% FPR. However, we also report area under the precision-recall curve (auPR) and precision at 1% FPR, which may be more realistic metrics of performance with imbalanced evaluation sets. When millipede is supervised, reported results are averages based on 5-fold cross-validation.

4.5. Availability

Software, data, complete numerical results, and other Supplemental Material are all available from http://www.cs.duke.edu/~amink.

5. Results

We compared the performance of our millipede model with centipede for 20 yeast TFs in G1-arrested cells and six human TFs in GM12878 cells. We used the millipede gold standard for both yeast and human TFs (in Supplementary Material, we also show results using the centipede gold standard for human TFs).

Since millipede can use various numbers of bins as covariates in its logistic regression model, we first explored the effect of merging and dropping bins to produce simplifications of the full millipede model. As illustrated in Figure 3, different simplifications of millipede have surprisingly similar performance; although we use yeast Reb1 and human REST as running examples in the manuscript, this is true across all TFs and all four of our evaluation metrics (full results in Supplementary Material). Looking more closely, we observe that model M5 generally shows the best performance with DNase data for both yeast and human TFs, with a mean auROC using the millipede gold standard of 94.2% across 20 yeast TFs, and 97.6% across six human TFs (the latter number becomes 98.6% when using the centipede gold standard). As an aside, we note that M12 usually outperforms M24 in human, suggesting the strand-specific information may not be too informative, at least for these six TFs.

Fig. 3.

millipede models with various numbers of bins perform similarly. As in Figure 1, rows represent candidate binding sites based on PWM matches to Reb1 in yeast (left) or REST in human (right). For each candidate binding site, columns depict DNase cuts in the region 100bp up- and downstream, probability of being bound under various millipede models, and ChIP label. Darker blue in data columns indicates higher number of DNase cuts or higher probability of being bound under the respective millipede model.

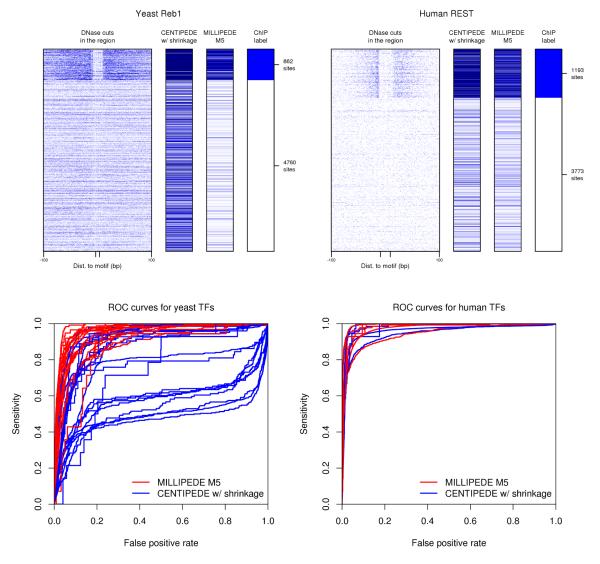
As demonstrated in the various panels of Figure 4 and the bar chart in Figure 5, our millipede M5 model achieves significantly better ROC performance for yeast TFs compared to centipede, and slight improvement for human TFs. In addition, M5 largely outperforms centipede (nearly 10% higher on average) when considering other metrics like auPR, and sensitivity or precision at 1% FPR, for both yeast and human TFs using the millipede gold standard (Supplementary Material). Finally, in terms of sensitivity at 1% FPR for human TFs using the centipede gold standard, millipede improves noticeably on the D-s straw-man method of Cuellar-Partida et al.,⁵ achieving 82.2% with M5 and 84.7% with M12, each at least 10% higher than D-s (Supplementary Material). Compared to D-s, millipede’s inclusion of PWM scores increases its ability to properly recognize the identity of the bound TF (versus other TFs that may be bound at those same candidate sites).

Fig. 4.

Comparing millipede model M5 to centipede across all yeast and human TFs. Top panels are akin to those of Figure 3, but compare millipede model M5 to centipede with shrinkage estimates of multinomial parameters for yeast Reb1 and human REST. To reduce clutter, we only show centipede results with shrinkage, since this performs noticeably better in an ROC setting than without (as shown in Figure 5). To confirm that results hold beyond the specific cases of Reb1 and REST, bottom panels show ROC curves for millipede (red) and centipede (blue) across all 20 yeast TFs (left) and all six human TFs (right). Two other yeast factors are shown later in Figure 6.

Fig. 5.

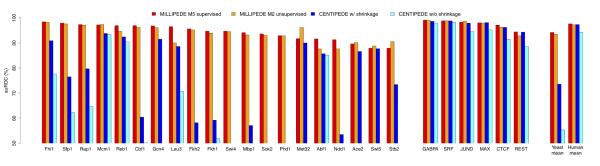
Area under the ROC curve for 20 yeast and six human TFs. Red bars are millipede model M5 run in a supervised mode, orange bars are millipede model M2 run in a completely unsupervised mode, blue bars are centipede with shrinkage, cyan bars are centipede without shrinkage. Bars start at 50% since that represents random performance for an ROC curve; values below 50% are just not shown (e.g., for centipede on Swi4, Sok2, and Phd1). The 20 yeast TFs are listed before the six human TFs; within each organism, the TFs are sorted such that the red bars decrease in height (the poor performance for Ace2 and Swi5 is perhaps unsurprising since the yeast DNase data are from cells arrested in G1). As summarized in the far right bars, mean performance is remarkably similar across the six human TFs, but millipede improves dramatically upon centipede in yeast, even when run completely unsupervised.

Normally, millipede is run in a supervised mode to achieve high accuracy with the help of ChIP training data. However, when no ChIP data are available, we can run millipede in a completely unsupervised mode: we choose a simple model and set the various coefficients to 1 (or −1 for bins that are either within a candidate binding site or distal). As shown in Figure 5, an unsupervised version of the millipede M2 model still exhibits quite satisfactory auROC performance across both yeast and human TFs. As an intermediate scenario, if we have some ChIP data available, but not for our TF of interest, we can run millipede in a ‘partially unsupervised’ mode. To do so, we simply use coefficients trained on other TFs and apply those same coefficients to the new DNase data and PWM scores. This crude form of transfer learning results in very high prediction accuracy. Using the coefficients of millipede M2 model trained on yeast Reb1 and applying it to the other 19 yeast TFs achieves a mean auROC of 93.9%, while using the coefficients of M2 trained on human REST and applying it to the other five human TFs leads to a mean auROC of 98.5% using the centipede gold standard. These results suggest that even a single ChIP experiment can go a long way toward learning effective millipede models.

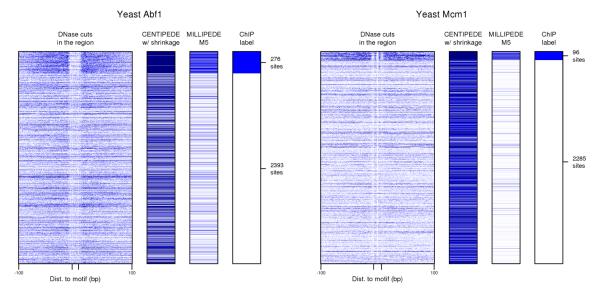
While examining the DNase cleavage patterns for yeast TFs, we sometimes found strikingly similar DNase cleavage patterns for both bound and unbound sites, as with Abf1 and Mcm1, shown in Figure 6. Hesselberth et al. showed a significant match between Mcm1’s DNase cleavage pattern within the binding site and the crystal structure of Mcm1-DNA contact,² but the similar patterns we see across all unbound sites (not just borderline cases) suggest the detailed cleavage patterns within the binding site are more likely a sequence-dependent artifact, perhaps arising from DNase digestion bias. To further test this claim, we also looked at the digestion patterns for Swi4, whose consensus binding sequence is CGCGAAA. Examining the more than 29,000 candidate binding sites that are unbound by Swi4, the number of cuts in the CG-rich left half of the candidate site is noticeably lower than the number in the AT-rich right half of the site (Supplementary Material).

Fig. 6.

DNase data can exhibit systematic artifacts such as sequence-dependent digestion bias. Left and right panels show yeast Abf1 and Mcm1 candidate binding sites, respectively. Notice that some fine details of the DNase cut data are preserved within and around candidate binding sites, whether the site is bound or unbound. centipede is prone to over-fit these details both because of the large number of parameters in the multinomial component of its likelihood, and because it is unsupervised and uses EM to assign labels to candidate sites.

Finally, we observed strong correspondence between DNase cleavage patterns in bound sites and the model coefficients learned in millipede models. For most TFs, including our running examples of Reb1 and REST, we see positive coefficients for the bins proximal to the binding site, and negative coefficients for bins within the binding region or distal to it. These models therefore recapitulate the TF-generic DNase signatures of early papers^2–4 in this area: cleavage frequency rises to elevated levels near the binding site, then drops for a short interval, and is then elevated before gradually falling again. However, for individual factors, we saw subtly distinct patterns, lending credence to the importance of TF-specific DNase signatures. We even observed striking exceptions for a few TFs. For instance, for yeast Fkh1, millipede models have significant positive coefficients for bins in the binding site and the bin immediately downstream, whereas for yeast Fkh2, millipede models have significant positive coefficients for bins in the binding site and the bin immediately upstream. Correspondingly, we also see elevated DNase digestion in those regions without clear depletion in the binding site. As Fkh1 and Fkh2 are known to bind with other TFs like Mcm1 and Ndd1, this result may reflect consistent positioning of each TF relative to other co-factors along the genome.

6. Discussion

millipede models achieve accurate and robust prediction performance under all four of our evaluation metrics across both yeast and human TFs. We have therefore demonstrated that a very simple model using only the most salient information from DNase data can perform as well as or better than more complex models like centipede, with the further attendant advantages of fast computation, easy interpretation, and low potential of over-fitting.

Because our millipede model is so simple, many variants can be imagined. For example, the number, widths, and locations of our bins have not been optimized in any way, though we briefly explored whether our results were sensitive to our admittedly arbitrary choices; we did not observe any notable change. Also, other covariates might be added to the model: millipede’s logistic regression framework permits great flexibility in including new covariates, should more information become available to further improve its performance. If the number of covariates becomes large, shrinkage or selection could be used to regularize the parameters.

Interestingly, we often observed detailed DNase cleavage patterns inside unbound candidate binding sites (especially in yeast), suggesting that some of the detail may be induced by sequence-dependent DNase digestion bias rather than actual protein-DNA protection at the single nucleotide level. This might also partially explain why centipede does not work nearly as well for identifying TF binding sites in yeast. By declining to fit the detailed signal at every nucleotide, millipede focuses its attention on the large-scale differences between bound and unbound sites, making it robust to biases that might arise at the single nucleotide level.

Since current technology for profiling TF occupancy requires a separate ChIP experiment for each TF being profiled, gaining a comprehensive understanding of the dynamic TF occupancy across the genome for all TFs across many tissues and conditions using only ChIP is utterly impractical. The prospect of using a complementary assay like DNase digestion has been tantalizing, but the sensitivity and specificity gap with ChIP has been too large to date. However, as more accurate methods like millipede are developed to close the gap, efficient means for profiling TF occupancy across the genome for many TFs at once may become a reality. Intriguingly, since it can operate in a supervised mode, millipede can leverage available ChIP data to train its models for identifying TF binding sites from DNase data alone.