Abstract
Prolonged standing has been associated with loss of balance, onset of low back pain symptoms and development of fatigue in lower extremity muscles in working populations. Although so far, it is unknown how individuals’ postural stability is affected by standing on rigid versus cushioned platform but many industries are opting for anti-fatigue mats at workstations to reduce fall and injury related socio-economic cost. The goal of this study is to test SATECH’s anti-fatigue mat for its effects on postural stability. A pilot test with seven healthy subjects (25–35 years old) has been conducted with a force plate to obtain kinetics of body when standing on two different platforms. The centers of pressure (COP) position of subjects were determined on rigid and anti-fatigue mats for quiet stance (each trial 60 seconds). In order to understand postural control along with dynamic or stochastic characteristics of the COP, stabilogram diffusion analysis (SDA) and Invariant density analysis methods are used. Subject specific patterns were seen in stabilogram diffusion plots and associated parameters in both conditions. We also found differences in some postural sway SDA parameters with anti-fatigue mats compared to rigid vinyl floor standing with open eyes condition. But no significant differences were found in sway IDA parameters. This work further provides insights whether anti fatigue mats can be helpful to workers involved with prolonged standing tasks.
Keywords: Center of Pressure, Stabilogram diffusion Analysis, Invariant Density Analysis
INTRODUCTION
Falls and injury are significant issues for the occupational population involved with prolonged standing tasks in food processing and packaging industries [1]. A variety of interventions have been practiced for reducing injuries due to falls in industrial environments such as the usage of no slip mats, railing around elevated working areas, modified ladders, training programs in fall prevention, and administrative intervention. Also, considering the prolonged standing task, anti-fatigue mats are used at the workstation. Furthermore, Anti-fatigue flooring are nowadays considered a safe option for reducing fatigue in postural muscles[2] but no effort has been done as of now to study human postural stability on anti-fatigue floors in comparison to that of rigid floors [3]. Anti-fatigue mats are commonly seen at workstations where prolonged standing work is performed such as machine operators, packing workers and others.
SATECH Inc. has developed a dual-stiffness floor to reduce fatigue in employees who spend significant amount of time standing during their work [4]. It has the potential of protecting against hip fractures, head injuries, and other fall-related injuries. Some researchers have tested the SATECH flooring with mobility tests like TUG (Timed up & Go), Berg Balance scores and they did not report any statistical difference between the rigid floors and the anti-fatigue floors for TUG time scores and Berg balance scores [5]. Timed “Up and Go” (TUG) test, designed and developed by Podsiadlo and Richardson [6] has been used to investigate functional mobility among elderly individuals. TUG test consists of day to day movement activities like standing up, walking, turning and sitting down. Previous research studies which used the TUG test indicate the total time was different between the two community-dwelling elderly groups - history of falls in the last six months and no fall history [7]. In our previous study, we have found significant differences in required coefficient of friction (RCOF) when walking on anti-fatigue floors [8]. It has been well known that different types of flooring can have an impact on the human perception of fatigue and outcome of falls and injuries [2, 9, 10]. There are floor specific adaptations in human stability and gait parameters when subjects encounter different floors [11–13] and these changes in stability parameters need to be examined before adoption of anti-fatigue floors in industrial environments.
Human postural control involves information from several different modalities; vestibular, visual and somatosensory systems. In previous research work, it has been proposed that open-loop (short term) and closed-loop (long term) postural control mechanisms are involved in the regulation of undisturbed, upright stance[14]. In this study, stabilogram-diffusion analysis (SDA) was used to examine how the anti-fatigue floor affects the postural control mechanisms. SDA provides with repeatable COP parameters that can be directly related to functional interaction of the neuromuscular mechanisms underlying the maintenance of erect standing posture[15]. SDA models COP data as random walk and is helpful in characterizing time dependent behavior of the COP trajectory. Invariant density analysis (IDA) uses a reduced order markov chain model of COP trajectory to describe the evolution of the state[16]. IDA provides new insights into long term behavior of COP data, and can successfully differentiate postural sway behaviors of faller and non-faller groups [17]. IDA assumes that COP data is stochastic and the movement of COP in its future state (location) depends on its present position. In this study, we have examined both SDA and IDA parameters for postural sway on rigid floors and anti-fatigue mats.
METHODS
Seven participants (5 males and 2 females) with (age 28±5 years, height 177±8 cm, and weight 89±22kg) volunteered from Blacksburg. The subjects did not have history of neurological, postural disorders or vision problems. Informed consent was given by all subjects before the experiment. An instrumented force platform (AMTI BP400600 SN 6780) was used to measure the time varying displacements of the COP under each subject’s feet during quiet standing. We tested the postural stability of the seven subjects with eyes open, eyes closed and eyes open with anti-fatigue mat condition. The total data collection was two minutes for each condition and appropriate rest was provided in order to ensure fatigue was not developed in lower extremity muscles.
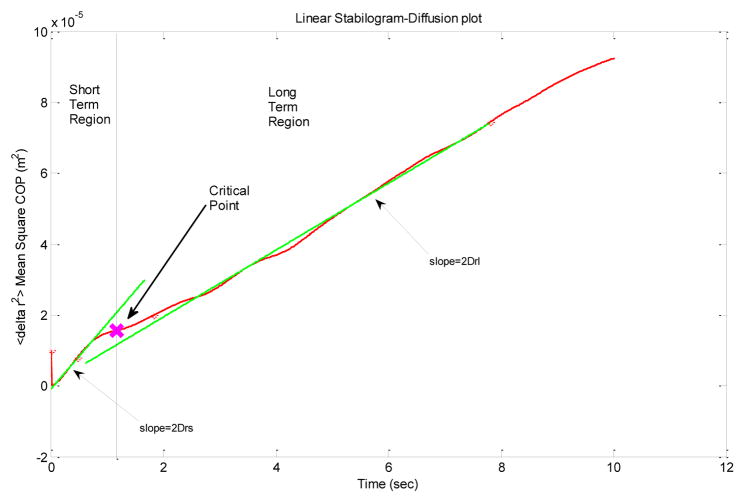
The COP trajectories were analyzed as one and two dimensional random walks, using SDA method [14]. Diffusion coefficients, scaling exponents and critical point coordinates were calculated from stabilogram diffusion plots. A short term region and long term region were identified in stabilogram diffusion plot. The stabilogram diffusion curves changed slope after a transition or critical point at some Δt. An estimate for each critical point, (Δtrc, <Δr2>c), was determined as the intersection point of the straight lines fitted to the two regions of each stabilogram diffusion plot. The effective diffusion coefficients Drs and Drl are computed from slopes of the lines fitted to the short-term and long term regions, respectively. The scaling exponents Hrs and Hrl are calculated from the slopes of the log-log plots of the short-term and long term regions, respectively[14].
The invariant density is probability distribution of finding the COP at any given distance away from centroid. The five IDA parameters include Ppeak, MeanDist, D95, EV2, and Entropy[17]. Ppeak, identifies the largest probability of invariant density, MeanDist is the weighted average state that contains the location of the COP, D95 is the state below which 95% of COP data is contained. EV2 is the second largest eigenvalue of the probability transition matrix, which corresponds to rate of change of the invariant density. Entropy describes the randomness of the system, where low entropy corresponds to a more deterministic system and high entropy refers to more stochastic system [17]. A “state” is defined as the distance from the centroid of the COP stabilogram to the COP current position (figure 2). Paired t-test was used to find intra individual differences in IDA parameters for the three conditions (eyes open on rigid floor, eyes closed on rigid floor, and eyes open on fatigue floor).
Figure 2.
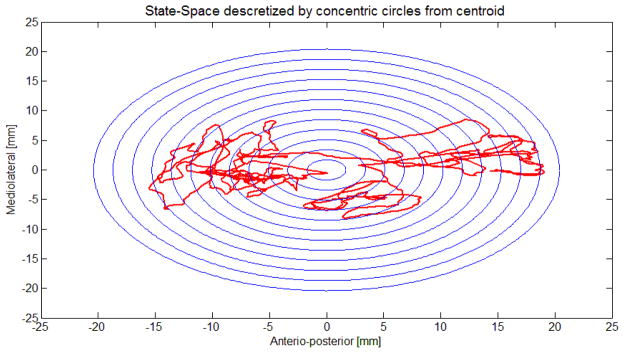
State space discretization of COP path into concentric circles of P5 participant with eyes open on rigid floor, with 12 states and width of each state ring is 1.2 mm
RESULTS
The means and standard deviations of the diffusion coefficients for the 7 participants are given in Table 1 below.
Table 1.
Diffusion coefficients (mm2s−1): means and standard deviations for the participants
| Subject ID→ | P1 | P2 | P3 | P4 | P5 | P6 | P7 | |
|---|---|---|---|---|---|---|---|---|
| Eyes closed on rigid floor | Dxs | 0.44±0.10 | 0.76±0.09 | 0.28±0.01 | 0.21±0.01 | 0.49±0.25 | 0.83±0.00 | 0.91±0.14 |
| Dxl | 1.49±0.35 | 2.85±0.41 | 0.66±0.17 | 0.67±0.04 | 1.44±0.31 | 4.07±0.00 | 2.19±0.46 | |
| Dys | 0.18±0.06 | 0.13±0.03 | 0.06±0.01 | 0.10±0.03 | 0.35±0.19 | 0.17±0.00 | 0.16±0.03 | |
| Dyl | 0.39±0.00 | 0.45±0.22 | 0.12±0.05 | 0.33±0.02 | 0.87±0.51 | 0.52±0.00 | 0.25±0.18 | |
| Drs | 0.61±0.06 | 0.87±0.13 | 0.34±0.00 | 0.31±0.04 | 0.82±0.42 | 1.00±0.00 | 1.06±0.18 | |
| Drl | 1.87±0.34 | 3.28±0.62 | 0.78±0.23 | 0.99±0.06 | 2.30±0.82 | 4.58±0.00 | 2.47±0.60 | |
| Eyes open on rigid floor | Dxs | 0.72±0.74 | 0.26±0.04 | 0.28±0.00 | 0.15±0.03 | 0.23±0.06 | 0.66±0.39 | 0.26±0.00 |
| Dxl | 1.26±0.88 | 0.73±0.04 | 0.43±0.00 | 0.46±0.04 | 0.82±0.08 | 2.16±0.50 | 0.80±0.00 | |
| Dys | 0.10±0.07 | 0.11±0.01 | 0.07±0.00 | 0.07±0.04 | 0.12±0.00 | 0.11±0.02 | 0.10±0.00 | |
| Dyl | 0.25±0.14 | 0.30±0.13 | 0.05±0.00 | 0.24±0.18 | 0.61±0.07 | 0.41±0.02 | 0.19±0.00 | |
| Drs | 0.82±0.81 | 0.38±0.05 | 0.36±0.00 | 0.22±0.06 | 0.34±0.07 | 0.76±0.41 | 0.35±0.00 | |
| Drl | 1.51±1.01 | 1.02±0.10 | 0.49±0.00 | 0.71±0.15 | 1.43±0.15 | 2.57±0.48 | 0.98±0.00 | |
| Eyes Open on Anti-fatigue mat | Dxs | 0.32±0.00 | 0.77±0.00 | 0.43±0.00 | 0.22±0.05 | 0.64±0.00 | 0.56±0.10 | 0.44±0.01 |
| Dxl | 1.39±0.00 | 2.68±0.00 | 0.75±0.00 | 0.68±0.17 | 1.96±0.00 | 2.59±0.60 | 1.19±0.08 | |
| Dys | 0.55±0.00 | 0.32±0.00 | 0.11±0.00 | 0.10±0.01 | 0.67±0.00 | 0.09±0.05 | 0.10±0.02 | |
| Dyl | 0.78±0.00 | 0.50±0.00 | 0.15±0.00 | 0.28±0.01 | 2.65±0.00 | 0.32±0.15 | 0.20±0.03 | |
| Drs | 0.81±0.00 | 1.07±0.00 | 0.54±0.00 | 0.33±0.06 | 1.26±0.00 | 0.65±0.15 | 0.54±0.02 | |
| Drl | 2.15±0.00 | 3.18±0.00 | 0.89±0.00 | 0.97±0.17 | 4.68±0.00 | 2.91±0.75 | 1.38±0.09 |
All short-term diffusion coefficients were much smaller than respective long term coefficients, i.e., Dxs<Dxl, Dys<Dyl, Drs<Drl. For majority of subjects, the anterioposterior diffusion coefficients were greater than their mediolateral counterpart, i.e., Dxs>Dys and Dxl>Dyl. This is due to the fact that anterioposterior sway is typically greater than that of mediolateral sway. It should be pointed out that means of diffusion coefficients in eyes closed condition are greater than eyes open condition on rigid floors (Table 2). This is well expected, as visual input increases postural stability. Also, means of diffusion coefficients in eyes open condition on anti-fatigue floor are found to be greater than that on rigid floor condition (Table 2).
Table 2.
Ranges, group means and standard deviations (SD) for the diffusion coefficients, scaling exponents, and critical point coordinates for eyes open on rigid floor, eyes closed on rigid floors and eyes open on anti-fatigue floor conditions. Dxs and Dxl are short term and long term diffusion coefficients respectively in anterio-posterior direction. Dys and Dyl are short term and long term diffusion coefficients respectively in medio-lateral direction. Drs and Drl are short term an long term planar diffusion coefficients respectively.
| Eyes closed on rigid floor | Eyes open on rigid floor | Eyes Open on Anti-fatigue Mat | |||||
|---|---|---|---|---|---|---|---|
| Parameter Diffusion coefficients (mm2 s−1) |
Mean ± SD | Range | Mean ± SD | Range | Mean ± SD | Range | |
| Dxs | 0.54±0.28 | 0.2018–1.01 | 0.38±0.34 | 0.1344–1.24 | 0.46±0.18 | 0.1901–0.77 | |
| Dxl | 1.74±1.07 | 0.5395–4.07 | 1.01±0.68 | 0.4302–2.52 | 1.57±0.85 | 0.5561–3.01 | |
| Dys | 0.16±0.11 | 0.0536–0.48 | 0.10±0.03 | 0.0359–0.15 | 0.22±0.22 | 0.0553–0.67 | |
| Dyl | 0.41±0.29 | 0.0808–1.23 | 0.32±0.18 | 0.0545–0.66 | 0.57±0.75 | 0.1510–2.65 | |
| Drs | 0.69±0.32 | 0.2770–1.20 | 0.48±0.36 | 0.1695–1.39 | 0.67±0.30 | 0.2846–1.26 | |
| Drl | 2.15±1.19 | 0.6203–4.58 | 1.33±0.75 | 0.4867–2.91 | 2.14±1.28 | 0.8510–4.68 | |
| Scaling exponents | Hxs | 0.76±0.10 | 0.5566–0.92 | 0.73±0.08 | 0.6254–0.86 | 0.77±0.06 | 0.6727–0.84 |
| Hxl | 0.68±0.06 | 0.5377–0.76 | 0.66±0.08 | 0.4813–0.77 | 0.68±0.07 | 0.5344–0.76 | |
| Hys | 0.71±0.12 | 0.5905–0.96 | 0.72±0.10 | 0.6269–0.90 | 0.79±0.12 | 0.6334–0.92 | |
| Hyl | 0.62±0.12 | 0.3072–0.74 | 0.66±0.13 | 0.3008–0.80 | 0.62±0.08 | 0.4396–0.72 | |
| Hrs | 0.74±0.10 | 0.5630–0.89 | 0.72±0.08 | 0.6260–0.86 | 0.77±0.07 | 0.6287–0.84 | |
| Hrl | 0.67±0.06 | 0.5249–0.75 | 0.67±0.09 | 0.4494–0.76 | 0.67±0.07 | 0.5136–0.75 | |
| Critical point coordinates (sec) | Δtxc | 0.19±0.66 | 0.0100–2.38 | 0.21±0.68 | 0.0100–2.37 | 0.26±0.79 | 0.0100–2.50 |
| Δtyc | 0.38±0.91 | 0.0003–2.10 | 0.21±0.68 | 0.0003–2.09 | 0.37±0.81 | 0.0004–3.30 | |
| Δtrc | 0.19±0.65 | 0.0100–2.50 | 0.21±0.68 | 0.0100–2.36 | 0.26±0.78 | 0.0100–2.40 | |
| Critical point coordinates (mm2) | <Δx2>c | 0.16±0.58 | 0.0002–1.32 | 0.18±0.60 | 0.0001–0.49 | 0.33±1.04 | 0.0001–0.84 |
| <Δy2>c | 0.13±0.37 | 0.0100–2.37 | 0.04±0.14 | 0.0100–2.36 | 0.16±0.34 | 0.0100–2.47 | |
| <Δr2>c | 0.19±0.68 | 0.0004–2.47 | 0.22±0.74 | 0.0005–2.57 | 0.41±1.30 | 0.0006–4.12 | |
The means and standard deviations of the computed stabilogram-diffusion scaling exponents for the seven subjects (table 2) are in general greater than 0.5. Thus, for both short term and long term region during quiet standing, COP trajectories exhibit persistent behavior. The transition points (Δt) occurred at relatively small time intervals, with minimum of about 0.0003 seconds (eyes closed on rigid floor) and maximum of 3.30 seconds (eyes open on anti-fatigue mat). On the other hand critical mean square displacements ranged from very small values, i.e., 0.0001 mm2 (<Δx2>c for eyes open condition for rigid and anti-fatigue mat) to rather large ones (<Δr2>c) as 4.12 mm2.
DISCUSSION
Postural stability has been limited by the lack of analytic techniques for extracting physiologically meaningful parameters from stabilogram. We have used eyes closed and eyes open conditions on rigid floor, as the role of vision in postural stability is not arguable. However, because of the complications associated with subject fatigue, we will have to accept some trade-off between reliability and experimental practicality. Our null hypothesis stated that the mean values of all IDA and SDA parameters remain same in all three testing conditions. Statistically significant differences were found in-between eyes open and eyes closed condition on rigid floor for three IDA parameters MeanDist, D95 and Entropy (Table 3). It is expected that mean distance of COP from centroid (MeanDist) will be more when the eyes are closed; this is because visual information is stopped when the eyes are closed. Also the 95% of COP data will lay in a larger sway area, with eyes closed condition. Slightly high entropy in eyes open condition predicts addition of determinism in this condition due to visual assistance. All mean diffusion coefficients (table 2) in eyes closed condition were found to be higher than that at eyes open condition on rigid floors. The magnitude of diffusion coefficients with anti-fatigue floors laid in-between those of eyes open and eyes closed conditions on rigid floor. Therefore, postural stability of participants is compromised to some extent on these anti-fatigue mats but the stability parameters do not show statistically significant difference in mean values. Thus, these results give insight to postural control on anti-fatigue floor as not being stable as that of eyes open condition on rigid floors and also not that much unstable as that of closed eyes condition on rigid floors.
Table 3.
IDA parameters with statistically significant differences between eyes closed and eyes open condition on rigid flooring.
| IDA Parameters | Eyes closed on rigid floor | Eyes open on rigid floor | p-value |
|---|---|---|---|
| Ppeak | 0.117±0.067 | 0.138±0.049 | 0.148 |
| MeanDist (mm) | 9.099±3.678 | 7.172±2.454 | 0.048* |
| D95 (mm) | 17.143±6.747 | 13.143±4.589 | 0.027* |
| EV2 | 0.9996±0.0003 | 0.9997±0.0002 | 0.6416 |
| Entropy | 3.931±0.690 | 3.598±0.496 | 0.049* |
Though there was no significant difference in the five IDA parameters, when tested for eyes open condition on rigid and anti-fatigue floor. But there was mean increase in sway SDA parameters to that on the rigid floor. There is a need for further investigation with higher statistical power and population size.
CONCLUSIONS
We did not find significant differences in IDA parameters for eyes open condition for rigid and anti-fatigue floor. But SDA parameter analysis provides insights into some stability aspects. Muscle fatigue develops in lower extremity and lower back due to prolonged standing. This development of fatigue may prevent us to understand the effects of anti-fatigue mat if tested for longer time. It is not yet known how much the stability deteriorates with time and prolonged standing, as these tests are practical only for short interval testing. There is a need for further research in this arena, if anti-fatigue mats are to be adopted for occupational environments.
Figure 1.

Anti-fatigue floor (SATECH Inc.)
Figure 3.
A schematic representation of a typical resultant planar stabilogram-diffusion plot (<Δr2> vs Δt) generated from COP time series. The effective diffusion coefficients Drs and Drl are computed from the slopes of the lines fitted to short-term and long-term regions, respectively. The critical point, (Δtrc, <Δr2>c), is defined by the intersection of the lines fitted to the two regions of the plot.
Table 4.
IDA parameters for eyes open condition for rigid floor and anti-fatigue mat
| IDA Parameters | Eyes open on rigid floor | Eyes open on anti-fatigue mat | p-value |
|---|---|---|---|
| Ppeak | 0.147±0.054 | 0.138±0.049 | 0.591 |
| MeanDist(mm) | 6.961±3.043 | 7.172±2.454 | 0.809 |
| D95 (mm) | 12.714±5.180 | 13.143±4.589 | 0.792 |
| EV2 | 0.9995±0.0004 | 0.9997±0.0002 | 0.3221 |
| Entropy | 3.527±0.576 | 3.598±0.496 | 0.686 |
Acknowledgments
We are very grateful to SATECH, Seamless Attenuating Technologies for providing Anti fatigue flooring for Laboratory testing.
References
[1] Use IEEE Transactions format. Do not include any references with the citation “to be published” or “submitted.” If the citation is a “personal communication,” include the source’s name, affiliation, and full postal address.
- 1.Spahn J. The Unique Hazards of Packing. 1976 Feb 24; Available: http://www.osha.gov/Publications/OSHA3108/osha3108.html.
- 2.Kim JY, Stuart-Buttle C, Marras WS. The effects of mats on back and leg fatigue. Appl Ergon. 1994 Feb;25:29–34. doi: 10.1016/0003-6870(94)90028-0. [DOI] [PubMed] [Google Scholar]
- 3.Tideiksaar R. How Flooring can reduce fall risk and injury. 2007 Feb 24; Available: http://www.cushionedfloors.com/images/SafeFlooring_ECPN%20Sept%202007.pdf.
- 4.SATECH Inc. Feb 24; Available: http://www.smartcellsmat.com/
- 5.Knoefel FD, Mousseau M, Berry M. Pilot Study to Assess Mobility Safety on a Dual-stifness Floor. Canadian Journal of Geriatrics. 2008;11:110–112. [Google Scholar]
- 6.Podsiadlo D, Richardson S. The timed “Up & Go”: a test of basic functional mobility for frail elderly persons. J Am Geriatr Soc. 1991 Feb;39:142–8. doi: 10.1111/j.1532-5415.1991.tb01616.x. [DOI] [PubMed] [Google Scholar]
- 7.Shumway-Cook A, Brauer S, Woollacott M. Predicting the probability for falls in community-dwelling older adults using the Timed Up & Go Test. Physical Therapy. 2000 Sep;80:896–903. [PubMed] [Google Scholar]
- 8.Soangra R, Jones B, Lockhart TE. Effects of Anti-Fatigue Flooring on Gait Parameters. Proceedings of the Human Factors and Ergonomics Society Annual Meeting. 2010 Sep;54:2019–2022. [Google Scholar]
- 9.Simpson AHRW, Lamb S, Roberts PJ, Gardner TN, Evans JG. Does the type of flooring affect the risk of hip fracture? Age and Ageing. 2004 May;33:242–246. doi: 10.1093/ageing/afh071. [DOI] [PubMed] [Google Scholar]
- 10.King PM. A comparison of the effects of floor mats and shoe in-soles on standing fatigue. Appl Ergon. 2002 Sep;33:477–84. doi: 10.1016/s0003-6870(02)00027-3. [DOI] [PubMed] [Google Scholar]
- 11.Cham R, Redfern MS. Changes in gait when anticipating slippery floors. Gait & Posture. 2002 Apr;15:159–171. doi: 10.1016/s0966-6362(01)00150-3. [DOI] [PubMed] [Google Scholar]
- 12.Chou YL, You JY, Su FC, Lin CJ, Chou PH. The modified gait patterns during stepping on slippery floor. Chinese Journal of Mechanics-Series A. 2000 Dec;16:227–233. [Google Scholar]
- 13.Yang BS, Hu HY. Effects of Floor Material Change on Gait Stability. 13th International Conference on Biomedical Engineering, vols 1–3. 2009;23:1797–1800. 2303. [Google Scholar]
- 14.Collins JJ, De Luca CJ. Open-loop and closed-loop control of posture: a random-walk analysis of center-of-pressure trajectories. Exp Brain Res. 1993;95:308–18. doi: 10.1007/BF00229788. [DOI] [PubMed] [Google Scholar]
- 15.Collins JJ, De Luca CJ, Burrows A, Lipsitz LA. Age-related changes in open-loop and closed-loop postural control mechanisms. Exp Brain Res. 1995;104:480–92. doi: 10.1007/BF00231982. [DOI] [PubMed] [Google Scholar]
- 16.Dellnitz M, Junge O. On the Approximation of Complicated Dynamical Behavior. SIAM Journal on Numerical Analysis. 1999;36:491. [Google Scholar]
- 17.Hur P, Kang HG, Lipsitz LA, Hsiao-Wecksler ET. Invariant Density Analysis of postural sway and prospective fall risk in community-dwelling elderly. 33rd Annual Meeting of the Amercan Society of Biomechanics; State College, PA. 2009. [Google Scholar]