The kinetic properties of the α3 rat glycine receptor make it suitable for mediating fast synaptic inhibition

Abstract

Glycine receptors mediate fast synaptic inhibition in spinal cord and brainstem. Two α subunits are present in adult neurones, α1, which forms most of the synaptic glycine receptors, and α3. The physiological role of α3 is not known, despite the fact that α3 expression is concentrated in areas involved in nociceptive processing, such as the superficial dorsal horn. In the present study, we characterized the kinetic properties of rat homomeric α3 glycine receptors heterologously expressed in HEK293 cells. We analysed steady state single channel activity at a range of different glycine concentrations by fitting kinetic schemes and found that α3 channels resemble α1 receptors in their high maximum open probability (99.1% cf. 98% for α1), but differ in that maximum open probability is reached when all five binding sites are occupied by glycine (cf. three out of five sites for α1). α3 activation was best described by kinetic schemes that allow the channel to open also when partially liganded and that contain more than the minimum number of shut states, either as desensitized distal states (Jones and Westbrook scheme) or as pre-open gating intermediates (flip scheme). We recorded also synaptic-like α3 currents elicited by the rapid application of 1 ms pulses of high concentration glycine to outside-out patches. These currents had fast deactivation, with a time constant of decay of 9 ms. Thus, if native synaptic currents can be mediated by α3 glycine receptors, they are likely to be very close in their kinetics to α1-mediated synaptic events.

Key points

• In the adult, most inhibitory transmission mediated by glycine uses channels containing α1 subunits, but both α1 and the related α3 subunit are present in spinal areas that process pain.

• We recorded the effect of a range of fixed glycine concentrations on the activity of individual glycine channels expressed in vitro to contain only α3 subunits.

• Glycine is very effective in opening α3 channels. At full activation, both α1 and α3 channels are open nearly 100% of the time, but α3 channels need all, or almost all, of the five glycine binding sites to be occupied, whereas α1 channels need only three.

• When channels were activated in synaptic-like conditions (fast, 1 ms, 10 mm glycine pulses), α3 responses decayed more slowly than α1 responses.

• This difference is likely to be too small to allow α1- and α3-mediated synaptic responses to be distinguishable on the basis of time course alone.

Introduction

It is well recognized that the kinetic properties of synaptic channels are the main factor that sets the time course of synaptic currents. Because of that, the same neurotransmitter can give rise to synaptic currents with different decay times at different synapses, depending on the nature of the receptors in the postsynaptic membrane. The composition of receptors for the same transmitter can vary considerably depending on developmental age, CNS area and presynaptic versus postsynaptic location, and receptors that contain different subunit isoforms can have profoundly different kinetics.

Glycinergic transmission is a good example of this phenomenon. Glycine receptors (GlyRs) are pentameric ligand-gated ion channels that are permeable to Cl⁻ and mediate much of the fast inhibitory synaptic transmission in the spinal cord and brainstem (Legendre, 2001; Lynch, 2004; Callister & Graham, 2010). GlyRs can be either homomeric (only α subunits), or heteromeric, e.g. contain both α and β subunits (Langosch et al. 1988). Four isoforms of the α subunit are known in mammals (α1, α2, α3 and α4) and their expression changes with development and differs across CNS regions.

At birth, rat GlyRs contain mostly α2 subunits (Legendre, 2001), but during development α2 expression decreases whereas α1 and α3 subunits become more abundant (Kuhse et al. 1990; Malosio et al. 1991; Harvey et al. 2004). α2 homomeric channels mediate currents with very slow deactivation kinetics, with a decay time constant of the order of 100 ms, and their properties make them unsuitable to mediate glycinergic IPSCs in the adult CNS (Mangin et al. 2003; Krashia et al. 2011). The time course of glycine synaptic currents is typically very fast, with decay time constants between 5 and 10 ms (Singer et al. 1998; Burzomato et al. 2004) and matches well the kinetic properties of α1β GlyR heteromers (Burzomato et al. 2004; Pitt et al. 2008).

It is not clear whether the α3 subunit has a synaptic role in adult CNS. We know that α3 expression increases with age (Kuhse et al. 1990) and that it is concentrated in discrete areas of the CNS (Harvey et al. 2004). For instance, in the spinal cord α1 is found throughout the grey matter, whereas α3 is confined to the superficial laminae of the dorsal horn (I and II), a distinctive pattern that strongly suggests that GlyR α3 is specifically involved in nociceptive circuits. This hypothesis was confirmed by the finding that mice genetically deficient in GlyR α3 display less central sensitization in some inflammatory pain models (Harvey et al. 2004; Harvey et al. 2009).

Recombinant GlyRs containing the α3 subunit have been characterized with respect to their conductance, agonist sensitivity and desensitization behaviour (Bormann et al. 1993; Breitinger et al. 2002; Heindl et al. 2007; Chen et al. 2009). However, nothing is known of their activation and deactivation kinetics, at either macroscopic or single channel level. It is particularly important to determine if the deactivation/burst kinetics of α3 GlyRs are distinguishable from those of α1-containing GlyRs. As deactivation sets the time course of synaptic currents, differences between the two receptors might allow us to identify synaptic currents mediated by each of the two subtypes, on the basis of their decay time courses.

Another important reason to characterize the kinetic properties of different channel isoforms is to understand how the molecular process of ion channel activation maps to the protein structure in homologous subunits. Mechanistic analysis of single channel records tells us how many agonist molecules are needed for maximum activation and whether the activation trajectory of the channel has to go through intermediate states. Fitting kinetic models to single-channel data from recombinant α1, α2 and α1β GlyRs led us to propose a detailed activation mechanism (‘flip’) that incorporates intermediate shut states between agonist binding and channel opening (Burzomato et al. 2004; Krashia et al. 2011). Mechanisms that include pre-open shut states, such as flip states or ‘primed’ states (Mukhtasimova et al. 2009), are now known to describe well the activation of a variety of wild-type and mutant Cys-loop channels, including glycine, muscle nicotinic, and GABA_A receptors (Burzomato et al. 2004; Plested et al. 2007; Mukhtasimova et al. 2009; Lape et al. 2009, 2012; Keramidas & Harrison, 2010). Microscopic affinity increases with flipping and this suggests that these intermediate shut states may be the kinetic reflection of conformational changes in the extracellular domain before channel opening.

Here we extend this approach to recombinant α3 GlyRs and their activation mechanism. We found that single-channel and macroscopic data from recombinant α3 homomers are well described by either a flip-type mechanism or a Jones and Westbrook mechanism (Jones & Westbrook, 1995). Notably, α3 channels differ from other GlyR isoforms in that their maximal activation requires the agonist glycine to occupy five binding sites. This suggests that all the five agonist binding sites in a homomeric Cys-loop channel can contribute to function.

Methods

Cell culture and transfection of cells

Cells from the human embryonic kidney cell line (HEK293; American Type Culture Collection) were maintained in a humidified incubator at 37°C (95% air–5% CO₂) in Dulbecco's modified Eagle's medium, supplemented with: sodium pyruvate (0.11 g l^-1), heat-inactivated fetal bovine serum (10% v/v) and penicillin G (100 U ml⁻¹)–streptomycin sulfate (100 μg ml⁻¹; all from Invitrogen, The Netherlands). Cells were plated onto polylysine-coated glass coverslips in 35 mm culture dishes containing 2 ml Dulbecco's modified Eagle's medium and immediately transfected using a calcium phosphate co-precipitation method (Groot-Kormelink et al. 2002) with a mixture of two pcDNA3 plasmids (Invitrogen), one coding for the long splice variant of the rat glycine receptor α3 subunit (GenBank accession number AJ310838) and the other for enhanced green fluorescent protein (eGFP; Clontech, UK). The mixture of DNA used for the cell transfection contained 82% glycine receptor α3 subunit DNA and 18% eGFP DNA. The total amount of the final cDNA mixture per plate was kept at 3 μg. Recordings were performed between 4 h and 2 days after washing off the transfection mixture.

We found α3-containing receptors more difficult to express than other isoforms of GlyR. For instance, when recording from α1 homomers, expression in HEK cells is so robust that we have to limit it by transfecting a mixture of cDNA in which some of the subunit-coding plasmid is replaced by an ‘empty’ plasmid, which lacks the subunit coding sequence. In a typical α1 transfection, the plasmid coding for the subunit represents only 2% of the total transfected cDNA. With α3, expression was relatively poor, even when the mixture contained the maximum amount of α3-coding plasmid, e.g. 82% of the transfected cDNA (the other 18% is eGFP-coding plasmid). Even so, only about 40% of recordings displayed channel activity. The level of expression was not improved by subcloning in a different vector (pCI). In addition to that, our attempts to obtain the heteromeric form of this channel, by expressing α3 with the β subunit from rat (GenBank accession number AJ310839), were unsuccessful. Channels likely to be heteromeric (because of their conductance) were observed in only two patches (out of approximately 90 patches obtained), and both of these patches also displayed many homomeric channel openings.

Single channel recording

All recordings were performed in the cell-attached configuration at 19–21°C with thick-walled borosilicate glass pipettes (with filament; Harvard Apparatus Ltd, Edenbridge, UK), coated near the tip with Sylgard (Dow Corning, Midland MI, USA) and fire-polished before use to a final resistance of 6–15 MΩ. The extracellular solution contained (mm): 20 sodium gluconate, 102.7 NaCl, 2 KCl, 2 CaCl₂, 1.2 MgCl₂, 10 Hepes, 20 TEA-Cl, 15 sucrose, and 14 glucose, pH 7.4 with NaOH; osmolarity 320 mosmol l^-1. The pipette solution was identical to the extracellular solution, except that it also contained glycine (50–10,000 μm). All solutions were prepared in HPLC-grade water (VWR International, Lutterworth, UK) to minimize contamination by glycine and filtered through a 0.2 μm Cyclopore track-etched membrane (GE Healthcare UK Ltd, Little Chalfont, UK) to remove impurities. The bath level was kept as low as possible to reduce noise. Currents were recorded with an Axopatch 200B amplifier (MDS Analytical Technologies, Sunnyvale CA, USA) at a pipette potential of +100 mV, with no correction for junction potential, as this was calculated to be at most +1 mV (Clampex 10.2; MDS Analytical Technologies). Recordings were prefiltered at 10 kHz (by the amplifier's 4-pole low-pass Bessel filter), digitized with Digidata 1322A (MDS Analytical Technologies), acquired with Clampex 10.2 software (sampling rate 100 kHz; MDS Analytical Technologies) and stored directly on the computer hard drive. For off-line analysis, data were filtered digitally (low-pass Gaussian filter) using the program Clampfit 10.2 (MDS Analytical Technologies) to achieve a final cut-off frequency of 4–6 kHz.

Analysis of single channel current recordings

Recordings were idealized (7000–10,000 transitions per patch) by time course fitting with the program SCAN. Segments showing seal breakdowns or multiple channel openings were excluded, and those intervals marked unusable. The aim of this stage of the analysis was to construct distributions of fitted amplitudes, shut times and open periods from the experimental data. The EKDIST program was used to characterize distributions of events by fitting Gaussian densities to the current amplitude histogram and a mixture of exponential densities to the dwell time histograms. Openings that had not reached their full amplitude (being shorter than twice the rise time of the filter) were excluded from the fitted amplitudes histogram. A single Gaussian was sufficient to produce a good fit of the amplitude histogram and the mean amplitude of the single channel currents was 5.8 ± 0.2 pA (SD of the mean; n= 21 patches). A time resolution of 30 μs was retrospectively imposed to both open and shut times using EKDIST (Colquhoun & Sigworth, 1995). The resolution is the duration of the shortest events that can be reliably detected. The initial characterization of the dwell time distributions was performed to determine a suitable value for the critical time, t_crit, to divide recordings into segments that are likely to arise from the activity of only one channel molecule (bursts or clusters; see below). The SCAN, EKDIST, HJCFIT and CVFIT programs can be downloaded from OneMol (http://www.onemol.org.uk).

Maximum-likelihood fitting

In order to evaluate kinetic schemes and estimate the rate constants associated with them, maximum likelihood fitting was performed with the HJCFIT program (Colquhoun et al. 1996, 2003). After idealization, data from single patches (n= 12) were grouped into three independent sets before fitting. Each set consisted of four patches at different glycine concentrations (Set 1, which is displayed in the figures; Set 2: 50, 200, 1000 and 10,000 μm; Set 3: 50, 300, 1000 and 10,000 μm). The four patches in each set were fitted simultaneously to obtain information on all parts of the mechanisms (Colquhoun et al. 2003). The imposed resolution of 30 μs was taken into account by HJCFIT in implementing the exact solution for missed events correction found by Hawkes, Jalali and Colquhoun (Hawkes et al. 1990, 1992).

In order to use HJC maximum likelihood fitting, all single channel records fed into HJCFIT had to be cut into segments using values of a critical time interval, t_crit, defined from shut time histograms. This was done to ensure that all openings in a segment should arise from the activity of only one channel molecule. The kinetic interpretation of t_crit is different at different glycine concentrations. At low agonist concentrations, channel activity consists of short groups of one or a few openings (‘bursts’). Each burst reflects the activity of a single channel molecule, but consecutive bursts may be produced by different channels. The shut intervals between bursts are concentration dependent in length, because they correspond to receptor sojourns in a fully unliganded resting state. At higher concentrations of glycine (greater than or equal to 200 μm), the pattern of activity was very different, with long groups of many openings, which we will refer to as ‘clusters’. Clusters were separated by very long shut intervals (seconds and above), which are likely to reflect visits of the receptor to long-lived desensitized states (Sakmann et al. 1980; Colquhoun & Ogden, 1988). Because of the high open probability within a cluster (more than 18% at 200 μm and up to 99% at 10 mm glycine), all openings within the cluster are likely to come from the same glycine channel. If a cluster were produced by the activity of two channels, the probability to see double openings would be high, if the cluster is long enough (Colquhoun & Hawkes, 1990; Horn, 1991).

In HJCFIT only shut times within these groups, e.g. shorter than t_crit, are directly used for fitting. At burst concentrations, shut times longer than the t_crit can be distorted by the number of channels in the patch (which is unknown). However, having more than one channel in a patch can only shorten the interburst shut times, and the real shut times (between the openings of the same channel) have to be at least as long as the observed ones. We use this information by employing CHS vectors in HJCFIT analysis of recordings at burst concentrations (Colquhoun et al. 1996). A t_crit value of 10 ms was chosen for bursts, by minimizing the total number of misclassified events in the shut time histogram (Jackson et al. 1983).

At cluster concentrations, shut times longer than the t_crit are long-lived desensitized states, which we did not attempt to characterize in our analysis. Gaps were classed as between clusters if longer than 1000 ms at 200 μm, 1000 ms at 300 μm, 10 ms at 1000 μm and 1 ms at 10,000 μm (see the example set in Fig. 1). The program HJCFIT calculates a likelihood value for each dataset of idealized sequences of events by using the postulated model together with the initial guesses for the rate constant values, and taking into account the imposed resolution. The rate constant values are then adjusted to maximize the likelihood. The fit to each dataset was repeated using several different initial guesses. Different starting points should result in the same rate constant values at convergence, if the likelihood surface has a single, well-defined maximum.

Figure 1. Activation of homomeric α3 glycine receptors by increasing concentrations of glycine.

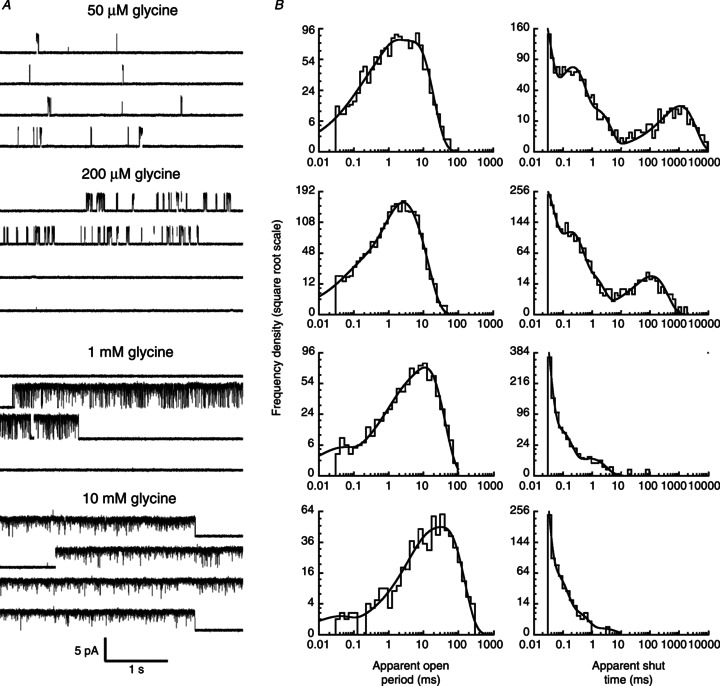
A, traces are continuous sweeps of cell-attached single channel recordings at 50, 200, 1000 and 10,000 μm glycine (3 kHz filter). Isolated bursts of openings are observed at 50 μm; at higher concentrations the bursts group together to form clusters. B, apparent open (left column) and shut time (right column) dwell time distributions, for the same patches shown in A. Distributions were fitted with a mixture of exponential probability density functions (Table 1).

To test the adequacy of fits, we used the mechanisms together with the rate constant estimates to calculate expected dwell time distributions, P_open curves and macroscopic current. These predictions were then compared with the experimental observations. We also used the results of fits to calculate the expected time course of macroscopic current relaxations to a glycine concentration jump and compared them to our experimental observations.

All data were expressed as mean ± SD of the mean. For the values of the estimated rate constants, we reported the mean of estimates obtained from different sets and the coefficient of variation (CV) of the mean.

Single channel open probability concentration curve

Clusters of openings are also useful for the measurement of the absolute open probability, P_open, and its dependence on agonist concentration. In each patch, the P_open value was estimated as the ratio between the total open time within clusters and the total cluster durations obtained from the idealized recordings (between two and four patches per concentration). This procedure weighs the contribution of each cluster to the P_open value according to its duration, because P_open estimates derived from longer clusters are more precise. These values were averaged and their relation with the agonist concentration was fitted empirically with the Hill equation (weighted least squares fit) using the CVFIT program. The parameters of this fit to the observed data points were compared with those calculated from the models and the rate constants obtained by fitting single channel data in HJCFIT. This predicted concentration dependence of P_open does not follow a Hill equation for any realistic channel model. Hence the expression for the model P_open does not have a linear Hill plot. In other words, its slope is not constant with agonist concentration (even though the deviation is small) and we have to specify at what agonist concentration we calculate the Hill slope for this predicted concentration dependence. The two curves (Hill equation and calculated P_open from the model) deviate from each other the most at low and high agonist concentrations, so we chose to calculate the model slope for our comparison at EC₅₀, where the two curves are very close.

The Hill slope was defined as the tangent to the dependence of P_open on concentration predicted by the fitted mechanism. This was calculated numerically at EC₅₀ by eqn (1) (where G is the glycine concentration):

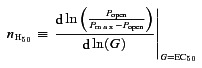(1)

Note that the P_open data points are affected by the finite bandwidth of our recordings (i.e. distorted by missed events). Once a model has been fitted to the data, we calculate and display the P_open curve that the model predicts, both for perfect resolution (dashed curves in Figs 4 and 5) and for our experimental resolution (continuous line). It is the latter that should be compared with the data points.

Figure 4. Fits of the Jones and Westbrook-type mechanisms to α3 GlyR single channel currents.

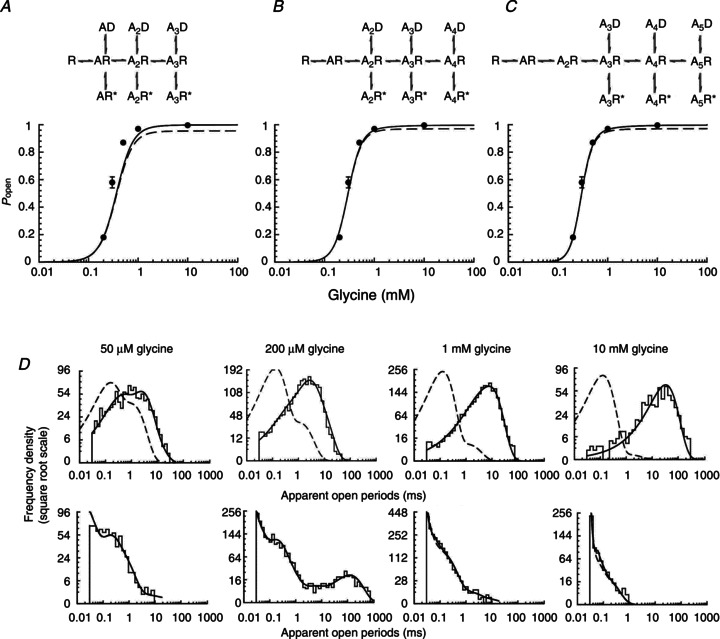
A–C, open probability curves predicted by rate constant estimates obtained by fits with Jones and Westbrook-type mechanisms (shown at top of the panels) with three, four or five agonist binding sites. Experimental P_open values are plotted as filled circles against the glycine concentration. The continuous line is the apparent P_open concentration curve predicted by the fitted scheme and rate constants, taking into account the effect of missed events. The dashed line is the ideal curve expected if no events are missed. D, probability density functions (continuous lines) predicted by the fit of Scheme 2 (five binding sites) for apparent open periods (top plots) and apparent shut times (bottom plots) are superimposed on the experimental histograms at four different glycine concentrations. The dashed lines are the distributions expected if there were no missed events.

Figure 5. Fits of the flip mechanisms to the homomeric α3 GlyR single channel currents.

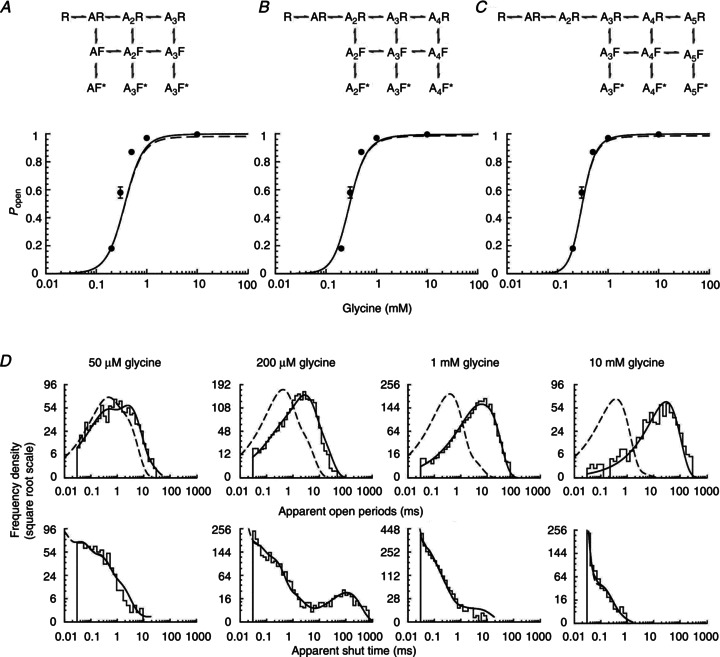
A–C, P_open curves predicted by rate constant estimates obtained by fits with flip mechanisms (shown at top of panels) with three, four or five agonist binding sites. Filled circles are experimental data, continuous lines are apparent P_open curves (corrected for missed events) and dashed lines are the ideal P_open curves expected if no events are missed. D, probability density functions (continuous lines) predicted by the fit of Scheme 4 (five binding sites) for apparent open periods (top plots) and apparent shut times (bottom plots) are superimposed on the experimental histograms at four different glycine concentrations. For more details see Fig. 3.

Macroscopic currents: recording and analysis

Macroscopic glycinergic currents were evoked by the application of agonist concentration pulses to outside-out patches. Patches were obtained with thick-walled borosilicate pipettes (with filament; Harvard Apparatus) and fire-polished to a final resistance of 6–15 MΩ when filled with ‘low Cl⁻ intracellular solution’ (mm): 121.1 potassium gluconate, 1 CaCl₂, 1 MgCl₂, 10 Hepes, 11 EGTA, 16 TEA-Cl and 2 MgATP, pH 7.2, adjusted with KOH; osmolarity 325 mosmol l^-1, adjusted with sucrose; 20 mm Cl⁻). The bath solution was the same as for single channel recordings. All outside-out recordings were performed at a nominal pipette holding potential of −100 mV, which corresponds to a transmembrane potential of −87 mV when corrected for the junction potential in low Cl⁻ solution (calculated with Clampex10.2). The internal chloride concentration has to be low in order to be comparable with that in the cytoplasm of HEK cells (in the single channel experiments). We chose 20 mm because this was the lowest intracellular chloride concentration that gave us reasonably large currents with our level of channel expression.

Glycine, dissolved in the bath solution, was applied to outside-out patches with an application pipette manufactured from theta glass tubing (Hilgenberg GmbH, Malsfeld, Germany) cut to a final diameter of ∼150 μm at the tip. The pipette was driven by a piezo stepper (Burleigh Instruments, Inc., Hitchin, UK). The exchange time was measured by the application of diluted bath solution (e.g. 30:70 bath solution:water) before the experiment (to optimize the electrode position) and after the rupture of the patch. Macroscopic currents were recorded with an Axopatch 200B (5 kHz filtering), digitized with a Digidata 1322A, and saved directly on a computer via Clampex software (20 kHz sampling rate).

In order to study the kinetics of macroscopic currents, 10–50 sweeps were recorded in response to pulses of 10 mm glycine, applied at intervals of at least 10 s. Responses for each patch were averaged, excluding failures or responses that contained patch breakdowns. Only experiments in which the rundown between the first and last three responses was <5% were included in the analysis. The rise time for average currents and open tip currents was measured as the time from 20 to 80% of the peak response using Clampfit software; experiments in which the open tip response (measured after the seal was lost and the patch recording had ended) had a 20–80% exchange time slower than 150 μs (for both rise and decay phases) were rejected. The time course of deactivation after short applications (1–1.5 ms) was fitted with one exponential from 80 to 20% of peak amplitude.

We calculated the time course predicted by each fitted model for the responses to glycine concentration jumps using realistic concentration profiles, where the time course of the rising and falling concentration was described by an error function (Sachs, 1999). Responses to a 1.5 ms glycine pulse with symmetrical 20–80% rise and fall times of 150 μs were calculated for rate constants obtained from fits to the three sets of single channel data (DC_PyPs; http://code.google.com/p/dc-pyps/).

Calculated responses were plotted and fitted in Clampfit. All schemes tested here predicted that the decay of macroscopic currents should be somewhat sigmoidal. This deviation from an exponential decay is small and not easily detectable by inspecting the calculated currents (see for example the traces in Fig. 7; note the small amplitude of the experimental current responses, on average 20 pA at peak). Bearing this in mind we have chosen to measure the decay at 80–20% of peak amplitude.

Figure 7. Comparison of experimental outside-out currents elicited by concentration pulses with the predictions obtained from the fit to single channel data.

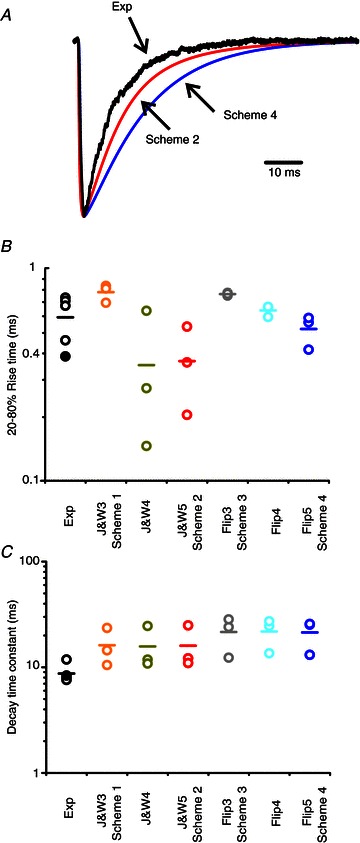
A, an experimental current trace recorded in response to a 1.5 ms pulse of 10 mm glycine (Exp) is superimposed on the responses calculated from the results of the fits of Scheme 2 and Scheme 4. The predicted traces are the averages of the responses calculated from each of the three sets of fitted rate constants. Calculated responses were normalized to the peak before averaging. B and C, dot plots summarizing the 20–80% rise times and the decay time constant for responses calculated from the fitted mechanisms and experimental jumps. The values for each fitted dataset are shown, and the mean is indicated as a bar. Black symbols indicate experimental jumps and the filled circle is the experiment plotted in A.

Note that the calculations of the model are based on single channel data, which are obtained in the cell-attached configuration, at a more hyperpolarized transmembrane potential than jumps (i.e. more negative than –100 mV for cell-attached experiments vs. −87 mV for jumps). In the single channel recordings we needed a more hyperpolarized potential in order to increase the amplitude of the single channel current, and therefore the signal-to-noise ratio of the data. In the cell-attached configuration, this is the only way to increase the signal, given that we cannot control intracellular chloride. However, it is difficult to obtain jumps at very negative holding potentials, because outside-out patches deteriorate too quickly if held negative to −100 mV. Deactivation is likely to be slower at more hyperpolarized potentials (Bormann et al. 1987; Legendre, 1999; Gill et al. 2006; Jin et al. 2009).

Results

Experimental dwell time distributions and P_open curve

The cell-attached recordings in Fig. 1A clearly show that the pattern of α3 GlyR single channel activity depends strongly on the glycine concentration. When this is low (e.g. 50 μm glycine, as in the top traces), channel openings occur in bursts, e.g. as single openings or as groups of few openings separated by long shut times. Each burst is likely to represent the activation of a single molecule (e.g. what happens between binding and unbinding of the agonist; Edmonds et al. 1995) and the shut times between bursts are terminated by agonist binding. Thus, at higher glycine concentrations, activations get closer and closer to each other and at 200 μm glycine and above, we observe clusters, long groups of openings that contain many events and are terminated by desensitized intervals (Sakmann et al. 1980; Colquhoun & Ogden, 1988).

After idealization of single channel current traces by time course fitting, the apparent open and shut time distributions were plotted and fitted with a mixture of exponential probability density functions (Fig. 1B). The term ‘apparent’ indicates that our estimate of the true duration of an opening or a shutting may be affected by our inability to detect short-lived events (e.g. shorter than 30 μs). The results of these empirical fits are used only to choose the appropriate t_crit for the second stage of analysis (Methods). Adequate fit of open and shut time distributions required three and four exponential components, respectively (see Table 1 for a summary).

Table 1.

Properties of dwell time distributions

Apparent open periods
Gly (μm)	τ1 (ms)	τ2 (ms)	τ3 (ms)
(n)	(area (%))	(area (%))	(area (%))	Mean open time (ms)
50	0.15 ± 0.05	0.9 ± 0.2	4.6 ± 0.6	2.2 ± 0.5
(4)	(20 ± 10)	(44 ± 4)	(40 ± 10)
200	0.09± 0.03	1.5 ± 0.1	5.3 ± 0.8	3.9 ± 0.6
(4)	(5 ± 1)	(33 ± 4)	(61 ± 5)
300	0.07± 0.04	1.7 ± 0.3	5.7 ± 0.3	5.1 ± 0.04
(3)	(3 ± 1)	(16 ± 3)	(81 ± 3)
1000	0.11± 0.09	3.8 ± 2	12 ± 2	8.6 ± 1.1
(4)	(8 ± 4)	(30 ± 10)	(60 ± 20)
10,000	0.07 ± 0.04	5.6 ± 3	30 ± 10	23.9 ± 8.9
(2)	(2.2 ± 0.4)	(17 ± 9)	(81 ± 9)

Apparent shut times
Gly (μm)	τ1 (ms)	τ2 (ms)	τ3 (ms)	τ4 (ms)
(n)	(area (%))	(area (%))	(area (%))	(area (%))
50	0.04 ± 0.02	0.33 ± 0.06	2.9 ± 0.8	1700 ± 600
(4)	(49 ± 7)	(28 ± 4)	(5 ± 1)	(17 ± 4)
200	0.03 ± 0.01	0.27± 0.07	30 ± 20	200 ± 60
(4)	(62 ± 1)	(26 ± 2)	(6 ± 1)	(5 ± 1)
300	0.009 ± 0.001	0.3 ± 0.2	0.50 ± 0.05	38 ± 6
(3)	(88 ± 2)	(8 ± 1)	(3 ± 1)	(0.9 ± 0.2)
1000	0.01 ± 0.004	0.05 ± 0.02	0.3 ± 0.1	1.9 ± 0.5
(4)	(61 ± 7)	(30 ± 6)	(9 ± 3)	(1 ± 0.3)
10,000	0.010 ± 0.001	0.03 ± 0.02	0.4 ± 0.2	1.2 ± 0.7
(2)	(70 ± 30)	(30 ± 30)	(2 ± 1)	(0.2 ± 0.1)

Distributions were fitted with mixtures of exponential probability density functions. n, the number of patches for each concentration (indicated in parentheses in the first column). The time constant of each component and its relative area (in parentheses) are given as mean ± SD of the mean.

Apparent open times (Fig. 1B, left column) shifted toward longer values at higher glycine concentrations, and the mean open time increased, from 2.2 ± 0.5 ms at 50 μm glycine, to 24 ± 9 ms at the highest glycine concentration, 10 mm (n= 4 and 2 patches, respectively, see Table 1).

In the shut time distributions, multiple components were clearly detectable. The longer components were concentration dependent and became shorter at the higher agonist concentrations. In particular, the mean duration of the longest shut times decreased from 1.7 ± 0.6 s at 50 μm glycine to 1.2 ± 0.7 ms at 10 mm glycine. On the other hand, the shortest shuttings remained relatively stable, with a mean duration of 40 ± 20 μs and 10 ± 1 μs at 50 μm and 10 mm glycine, respectively. It is this shortest component that dominates the shut time distribution at the higher agonist concentrations (Table 1). Because these shuttings are so short, with an average duration close to or below our experimental resolution, many of the shortest shuttings are likely to be missed in the idealization and will contribute to the apparent lengthening of the open times with increasing glycine concentrations.

The concentration dependence of single channel activity can be displayed and characterized as a P_open curve. This is done by identifying clusters, stretches of openings that arise from the activation of just one channel (see Methods). Examples of clusters at several concentrations of glycine are shown in Fig. 2A.

Figure 2. Concentration dependence of the open probability of homomeric α3 glycine receptor clusters.

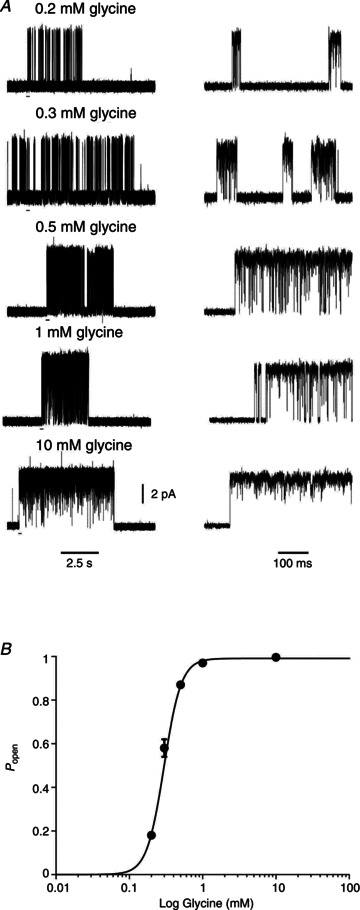
A, examples of clusters recorded at 200, 300, 500, 1000 and 10,000 μm glycine. The bars under the traces on the left show the regions expanded in time on the right. B, cluster open probability, P_open, plot versus glycine concentration. The symbols show the mean values (with error bars for the SD of the mean, where this is bigger than the symbol size) for the patches included in the analysis (2–4 at each concentration). P_open values were obtained for each patch from the ratio between the total open time and the total clusters duration, from recordings idealized by time course fitting. The continuous line is a fit of the Hill equation, which yielded an EC₅₀ of 297 ± 4 μm and a Hill slope of 3.7 ± 0.1.

The P_open values of such clusters were measured and plotted against glycine concentration in Fig. 2B (see Table 2 for a summary). Fitting these data points with the Hill equation gave a maximum open probability of 0.991 ± 0.003, an EC₅₀ of 297 ± 4 μm and a Hill slope of 3.7 ± 0.1. The Hill equation was fitted simply to obtain an empirical estimate of the steepness of the P_open curve that we could use for comparison with the predictions of postulated mechanisms (Burzomato et al. 2004), even though it describes no possible physical mechanism.

Table 2.

P_open values are obtained for each patch as ratios of total open time and total cluster duration (calculated from recordings idealized by time course fitting)

Glycine (μm)	Number of clusters	Number of patches	Number of openings	Cluster length (s)	Popen
200	19	4	500 ± 100	11 ± 3	0.18 ± 0.01
300	2	2	1600 ± 400	15 ± 3	0.58 ± 0.04
500	11	3	540 ± 90	2.2 ± 0.4	0.87 ± 0.01
1000	8	4	600 ± 200	5 ± 1	0.975 ± 0.004
10,000	4	2	230 ± 80	6 ± 3	0.996 ± 0.003

Values are means ± SD of the mean.

Fitting mechanisms

The HJCFIT method (Colquhoun et al. 2003) was used to fit several putative mechanisms to idealized single channel records. Sets of data from different recordings, each made at a different concentration, were fitted simultaneously. Each set contained four different glycine concentrations, spanning the whole of the P_open curve. At the end of fitting, the quality of the fits was assessed by visual inspection of the agreement between the model predictions and the experimental open/shut time distribution and P_open curve. We will describe only a subset (Fig. 3) of the approximately thirty models we tested. Two of the models discussed below (e.g. the five-binding site versions of the Jones and Westbrook model and of the ‘flip’ model, Fig. 3B and D, respectively) fitted the data well. For comparison, we describe also the results of fitting the same mechanisms in the three-binding site versions (Fig. 3A and C). These are known to describe adequately the behaviour of the related α1 and α1β glycine receptor isoforms (Burzomato et al. 2004), but we found that they failed to fit α3 data well. Other mechanisms tested and found inadequate (see Supplemental Fig. 1, available online only) include both simpler schemes (e.g. sequential schemes and subsets of the flip, and Jones and Westbrook, mechanisms) and variants of the ‘primed’ mechanisms such as those we applied to the startle disease mutant K276E (Lape et al. 2012).

Figure 3. Some of the kinetic schemes tested for α3 glycine receptor.

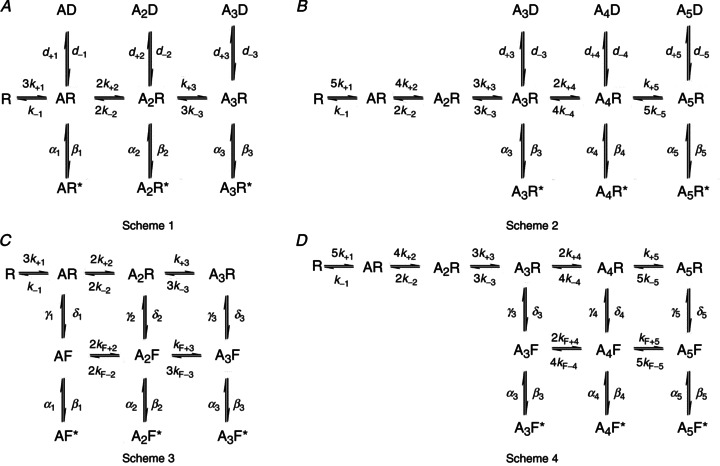
Scheme 1 and Scheme 2 are Jones and Westbrook-type mechanisms (Jones & Westbrook, 1995) modified to include three (A) or five (B) binding sites. The letter D indicates distal desensitized states. Scheme 3 (C) is the flip mechanism proposed for the heteromeric α1β glycine receptor (Burzomato et al. 2004). Scheme 4 (D) is a flip mechanism with five binding sites. In all schemes, the letter A denotes an agonist molecule and its subscript indicates the number of agonist molecules bound to the receptor. The letters R and R* denote resting shut states and open states of the receptor, respectively. The letter F indicates intermediate flipped shut states that connect resting and open states.

Jones and Westbrook-type mechanisms

The original form of this mechanism (with two binding steps) was proposed by Jones and Westbrook for the activation of GABA_A receptors (Jones & Westbrook, 1995). From each resting bound state, the channel can either open or enter a short-lived desensitized state. Scheme 1 in Fig. 3A shows how we adapted this mechanism for α1β heteromeric glycine receptors, to include three agonist binding sites, three short-lived ‘desensitized’ states and three open states (Burzomato et al. 2004). The main property of Scheme 1 is that the agonist binding sites are allowed to interact with each other, and change their affinity with the level of ligation. In fitting this type of scheme to α3 data, no constraints were imposed on the values of the binding rate constants across the mechanism, so the number of free parameters was 18.

The dwell time distributions calculated from this model and its fitted rate constants (not shown) were in good agreement with the experimental ones. However, the prediction of the P_open curve (Fig. 4A) was not satisfactory, particularly in terms of the Hill slope. The best fit of this model predicted a slope of 2.5 ± 0.2 and therefore could not match the steep slope of the experimental curve (3.7 ± 0.1). The other parameters of the observed curve, such as EC₅₀ and maximum P_open, were reasonably well described (EC₅₀= 310 ± 30 μm and maximum P_open 0.997 ± 0.001). The mean values for the rate constants estimated for Scheme 1 (and the other Jones and Westbrook-type schemes) are shown in Table 3. Data are the means of estimates obtained from fits to three independent single channel data sets. Equilibrium constant values were calculated for each set from the ratio of the appropriate rate constants and then averaged.

Table 3.

Mean rate constants, equilibrium constants and coefficients of variation from the fit of Jones and Westbrook-type schemes

	Units	J&W, 3 binding sites (Scheme 1)	J&W, 4 binding sites	J&W, 5 binding sites (Scheme 2)
α1	s−1	2980 ± 20%	—	—
β1	s−1	941 ± 65%	—	—
α2	s−1	825 ± 20%	2820 ± 16%	—
β2	s−1	20,700 ± 47%	934 ± 54%	—
α3	s−1	6150 ± 34%	832 ± 21%	2780 ± 14%
β3	s−1	180,000 ± 12%	21,200 ± 44%	922 ± 55%
α4	s−1	—	5830 ± 30%	849 ± 20%
β4	s−1	—	180,000 ± 12%	23,800 ± 43%
α5	s−1	—	—	5530 ± 24%
β5	s−1	—	—	180,500 ± 12%
d-1	s−1	262,000 ± 99%	—	—
d+1	s−1	96,900 ± 98%	—	—
d-2	s−1	6010 ± 10%	4060 ± 71%	—
d+2	s−1	8030 ± 6%	51,800 ± 97%	—
d-3	s−1	18,400 ± 22%	5840 ± 11%	124,500 ± 98%
d+3	s−1	1210 ± 38%	7800 ± 6%	6500 ± 72%
d-4	s−1	—	18,700 ± 25%	6370 ± 18%
d+4	s−1	—	1230 ± 35%	8290 ± 12%
d-5	s−1	—	—	21,100 ± 32%
d+5	s−1	—	—	1250 ± 28%
k-1	s−1	1260 ± 30%	342,000 ± 73%	2460 ± 90%
k+1	m−1 s−1	(3.50 × 104) ± 23%	(1.57 × 106) ± 51%	(7.93 × 105) ± 47%
k-2	s−1	2720 ± 31%	1636 ± 45%	34,125 ± 97%
k+2	m−1 s−1	(6.27 × 106) ± 45%	(1.77 × 107) ± 68%	(3.96 × 107) ± 98%
k-3	s−1	1328 ± 27%	1903 ± 32%	442 ± 38%
k+3	m−1 s−1	(7.78 × 106) ± 48%	(8.33 × 106) ± 4%	(3.38 × 105) ± 28%
k-4	s−1	—	1036 ± 26%	1548 ± 35%
k+4	m−1 s−1	—	(2.33 × 107) ± 48%	(6.18 × 106) ± 46%
k-5	s−1	—	—	875 ± 26%
k+5	m−1 s−1	—	—	(2.4 × 107) ± 47%
E1=β1/α1	—	0.37 ± 77%	—	—
E2=β2/α2	—	32 ± 58%	0.37 ± 64%	—
E3=β3/α3	—	33 ± 19%	33 ± 54%	0.36 ± 65%
E4=β4/α4	—	—	34 ± 16%	35 ± 51%
E5=β5/α5	—	—	—	34 ± 11%
D1=d+1/d−1	—	0.97 ± 40%	—	—
D2=d+2/d−2	—	1.35 ± 4%	6.02 ± 79%	—
D3=d+3/d−3	—	0.09 ± 53%	1 ± 5%	0.73 ± 69%
D4=d+4/d−4	—	—	0.09 ± 52%	1 ± 5%
D5=d+5/d−5	—	—	—	0.08 ± 49%
K1=k−1/k+1	μm	44,450 ± 40%	461,760 ± 61%	3240 ± 48%
K2=k−2/k+2	μm	820 ± 52%	284 ± 78%	1200 ± 15%
K3=k−3/k+3	μm	95 ± 46%	223 ± 30%	1200 ± 18%
K4=k−4/k+4	μm	—	71 ± 42%	502 ± 55%
K5=k−5/k+5	μm	—	—	58 ± 40%
EC50	μm	305 ± 10%	288 ± 6%	284 ± 5%
nH	—	2.5 ± 8%	3.4 ± 5%	3.7 ± 3%

All the rate constants were fitted freely in HJCFIT. The values for efficacy at each level of ligation, E, the dissociation equilibrium constants per site, K, the equilibrium constants for the entry into the extra shut states, D_n, the EC₅₀ and the Hill slope were calculated from the rate constants for each set and their means are listed at the bottom of the table. Values are means ± coefficient of variation (i.e. SD of the mean expressed as a percentage of the mean).

The failure of the mechanism with three binding sites to match the observed high slope of the P_open curve is a strong indication that α3 receptors may require the binding of more than three agonist molecules in order to achieve maximum open probability. We therefore proceeded to test Scheme 1 variants with four or five binding sites. For instance, Scheme 2 (Fig. 3B) has five glycine binding sites, three desensitized states and three open states. Here, the channel can access the desensitized and open states only from the three highest levels of ligation. Scheme 2 incorporates all the features of Scheme 1, but increasing the number of binding sites to five also increases the number of free parameters to 22.

Once again, the dwell time distributions predicted by the results of fitting Scheme 2 (Fig. 4D) were in good agreement with the data, and fits were good across the three sets. The fit of Scheme 2 predicted a Hill slope of 3.7 ± 0.1 for the P_open curve. This exactly matches the observed value (Fig. 4C) and is much better than the prediction of Scheme 1 (three binding sites, Fig. 4A).

We also tested a Jones and Westbrook variant with four glycine binding steps (Fig. 4B, top): fitting this scheme gave good descriptions of the dwell time distributions (data not shown), and predicted a somewhat shallower Hill slope for the P_open curve (3.4 ± 0.2; Fig. 4B, bottom).

The first feature that is apparent from the results of the fits of Scheme 2 shown in Table 3 is that, at the highest level of ligation, α3 channels open with a fast opening rate (180,000 ± 20,000 s⁻¹) and high efficacy (34 ± 4). These estimates are consistent across the sets, with CVs of about 10%. As the channel binds more glycine molecules, there is a clear increase in efficacy (nearly 100-fold). This is almost entirely due to an increase in the value of the opening rate constant, in a manner similar to that observed for other isoforms of the glycine channel (Burzomato et al. 2004). The poor reproducibility across data sets of the estimates of efficacy for the two lower-liganded states makes it hard to say whether each molecule of agonist bound contributes equally to the increase in efficacy with ligation. The values of the equilibrium constants for entry into desensitization also change with level of ligation, but in the opposite direction, favouring desensitization at the lower liganded states (note the high CV of D₃ and D₅). These features are very similar in the fits of the schemes with three and four bound molecules.

In the best-fitting Scheme 2, the affinity of agonist binding increases by more than 50-fold over the five binding steps. This is a consistent feature of this mechanism, despite the relatively high variability of the estimates of the dissociation constants (Table 3). In the mechanisms with fewer binding steps, the overall increase in affinity is greater, reaching more than 5000-fold in the mechanism with four binding steps.

Flip mechanisms

Scheme 3 depicted in Fig. 3C is the flip mechanism originally proposed by Burzomato et al. (2004). This scheme postulates the existence of an additional type of shut state, the flipped state, which represents a concerted conformational change that occurs before the channel opens. In flip-type models, the glycine binding sites are independent and the binding affinity depends only on the state of the receptor (i.e. resting or flipped), and not on the level of ligation. Hence the scheme specifies only two equilibrium constants for binding, one for the resting conformation (R) and one for the flipped conformation (F), regardless of how many sites are already occupied. This was done by applying the following constraints to the rate constants: k₊₁=k₊₂=k₊₃=k₊, k₋₁=k₋₂=k₋₃=k₋, k_F+2=k_F+3=k_F+ and k_F−3=k_F−2=k_F−. In addition to that, two rate constants (δ₁ and δ₃, mono- and triliganded unflipping, see Fig. 3C) were constrained in order to satisfy the requirement of microscopic reversibility for the two cycles in the flip scheme (Colquhoun et al. 2004). As a result this mechanism had only 14 free parameters.

As we did with the Jones and Westbrook-type mechanisms, we tested additional flip mechanisms, with four or five binding sites. For instance, Scheme 4 depicted in Fig. 3D has five binding sites. The main features of the original flip mechanism are conserved and the scheme maintains three open states and three flipped states, which are accessible from the most highly liganded resting states. Binding site independence was satisfied in Scheme 4 by applying the following constraints to the rate constants for binding: k₊₁=k₊₂=k₊₃=k₊₄=k₊₅, k₋₁=k₋₂=k₋₃=k₋₄=k₋₅, k_F+4=k_F+5 and k_F−5=k_F−4. Two unflipping rate constants, δ₃ and δ₅, were constrained to satisfy the requirement of microscopic reversibility (Colquhoun et al. 2004). As a result this mechanism had the same number of free parameters as Scheme 3.

After fitting flip mechanisms with three, four or five binding sites, we checked how well the P_open curve was described (Fig. 5A–C). The EC₅₀ predicted was similar for all three mechanism, at around 300 μm (cf. observed EC₅₀= 310 ± 30 μm). As expected, the predicted slope of the apparent P_open curve became steeper with increasing number of binding sites (2.2 ± 0.1 for Scheme 3 and 3.1 ± 0.1 for Scheme 4), but its maximum value was somewhat lower than the one reached by Scheme 2.

The predicted dwell time distributions were in good agreement with the data at all glycine concentrations and the quality of these predictions was similar for flip mechanisms with three, four or five binding sites. Figure 5D shows apparent open and shut time distributions predicted by the flip mechanism with five binding sites, superimposed onto experimental data histograms.

As we reported for other glycine receptor isoforms, α3 channel activity displays correlations between open and shut times, and the longer open times are found adjacent to the shortest shut times. The extent of these correlations and their concentration dependence was similar to that which we described for α1 receptors and were adequately described by all the variants of the Jones and Westbrook, and flip, mechanisms described here (data not shown).

Rate constants and equilibrium constants from the fits of the flip schemes are shown in Table 4 and Fig. 6. The values estimated for the flip mechanisms were much more consistent across the different sets than those estimated with Jones and Westbrook-type mechanisms, and the highest CV for rate constant values in Scheme 4 was 31% (cf. 98% for Scheme 2). The results in Table 4 have many features that resemble those we described earlier for α1-containing glycine channels. Fully-liganded α3 channels have a high opening rate (150,000 ± 20,000 s⁻¹). As more agonist molecules bind, both the pre-opening conformation change to the flipped state and the opening of the channel from the flipped state become more favourable. Thus the value of the flipping equilibrium constant, F, increased from 0.2 (flipping from A₃R) to 6 (flipping from A₅R) and that of the gating equilibrium constants, E, increased from 1 to 80. In the case of F, the presence of cycles in the mechanism constrains (by microscopic reversibility) the increase to be similar at each step. This constraint is not present for the estimation of E in the model we fitted and most of the increase in E was between the two lower liganded open states. Fits of a similar model with connected open states gave poorer results (data not shown), possibly because the interaction between the open channel and permeating chloride ions (Pitt et al. 2008; Houston et al. 2009; Moroni et al. 2011) is not specified in the model and results in the (apparent) breach of microscopic reversibility. As we reported for α1-containing channels, most of the increase in the value of E was due to the increase in the opening rate constant. The increase in glycine affinity with flipping was 6-fold (K_R= 890 μm and K_F= 160 μm), very close to that observed for α1 homomeric channels fitted with the flip model, but much smaller than the 65-fold increase seen in heteromeric α1β GlyR (Burzomato et al. 2004).

Table 4.

Mean rate constants, equilibrium constants and coefficients of variations from the fit of flip mechanisms with different numbers of binding sites

	Units	Flip, 3 binding sites (Scheme 3)	Flip, 4 binding sites	Flip, 5 binding sites (Scheme 4)
α1	s−1	2840 ± 30%	—	—
β1	s−1	1230 ± 4%	—	—
α2	s−1	498 ± 16%	2690 ± 27%	—
β2	s−1	18,800 ± 14%	1220 ± 7%	—
α3	s−1	2370 ± 28%	496 ± 14%	2520 ± 23%
β3	s−1	154,000 ± 15%	19,600 ± 13%	1260 ± 7%
α4	s−1	—	2030 ± 24%	497 ± 13%
β4	s−1	—	149,000 ± 16%	20,700 ± 10%
α5	s−1	—	—	1870 ± 22%
β5	s−1	—	—	147,000 ± 16%
γ1	s−1	1830 ± 23%	—	—
δ1	s−1	91 ± 20%	—	—
γ2	s−1	6180 ± 1%	1950 ± 13%	—
δ2	s−1	4280 ± 17%	223 ± 23%	—
γ3	s−1	2120 ± 27%	5900 ± 5%	2220 ± 13%
δ3	s−1	17,500 ± 10%	5060 ± 18%	419 ± 31%
γ4	s−1	—	2490 ± 26%	5800 ± 7%
δ4	s−1	—	14,500 ± 8%	5820 ± 22%
γ5	s−1	—	—	2550 ± 27%
δ5	s−1	—	—	12,700 ± 5%
k-	s−1	241 ± 1%	236 ± 15%	222 ± 23%
k+	m−1 s−1	(7.32 × 104) ± 9%	(1.60 × 105) ± 6%	(2.45 × 105) ± 14%
kf-	s−1	4480 ± 9%	5270 ± 13%	5920 ± 16%
kf+	m−1 s−1	(9.88 × 106) ± 29%	(9.73 × 106) ± 24%	(9.73 × 106) ± 21%
E1=β1/α1	—	0.52 ± 30%	—	—
E2=β2/α2	—	41 ± 24%	1 ± 28%	—
E3=β3/α3	—	70 ± 14%	42 ± 22%	1 ± 24%
E4=β4/α4	—	—	77 ± 11%	44 ± 19%
E5=β5/α5	—	—	—	80 ± 8%
F1=δ1/γ1	—	0.05 ± 31%	—	—
F2=δ2/γ2	—	0.69 ± 16%	0.11 ± 19%	—
F3=δ3/γ3	—	11 ± 45%	1 ± 24%	0.18 ± 20%
F4=δ4/γ4	—	—	7 ± 42%	1 ± 29%
F5=δ5/γ5	—	—	—	6 ± 42%
KR=k−/k+	μm	3350 ± 11%	1460 ± 10%	885 ± 9%
KF=kf−/kf+	μm	263 ± 25%	196 ± 19%	159 ± 15%
EC50	μm	320 ± 8%	300 ± 5%	275 ± 7%
nH	—	2.2 ± 5%	2.7 ± 4%	3.1 ± 3%

The fits constrain the binding and unbinding rates to be the same, regardless of the number of molecules bound, in any conformation. The equilibrium constants, E, F and K, and open probability curve EC₅₀ and the Hill slope, n_H, were calculated from the rate constants for each set and then averaged. Values are means ± coefficient of variation (i.e. SD of the mean expressed as a percentage of the mean).

Figure 6. Mean rate constants for Schemes 2 and 4.

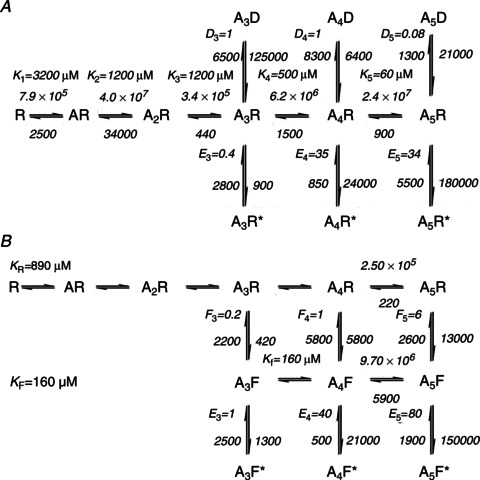
The best-fitting variants of Jones and Westbrook (A, Scheme 2), and flip (B, Scheme 4), mechanisms are shown with the averaged rate constants (units and constant names as in Tables 3 and 4) and equilibrium constants from three independent data sets.

In the flip model, overall agonist efficacy depends on the equilibrium constant for flipping (F) and the equilibrium constant (E) for the open–shut reaction. For the fully liganded receptor, we can define an ‘effective efficacy’, E_eff, as:

(2)

Both homomeric receptors have a very high maximum P_open and their overall efficacy is high (67 for α3 and 35 for α1 homomers).

Our adaptation of the flip mechanism has five binding sites, and the most general version of this mechanism should have five flipped and five open states (as in Burzomato et al. 2004). Mechanisms containing more than three open states gave much worse fits, which failed to describe the shut time distributions and had high coefficients of variation for the estimated rate constants (data not shown). It is worth noting that, in the mechanism with five binding sites and three open states (Scheme 4), the lowest liganded open state (triliganded) is visited relatively rarely, with a very low occupancy (<1%) even at the lowest glycine concentration (50 μm). This suggests that data at this agonist concentration may not contain sufficient information to fit explicitly additional open states with fewer than three agonists bound.

Macroscopic currents

In our final set of experiments, we recorded macroscopic currents elicited by the fast application of brief pulses of glycine to outside-out patches. The first aim of these recordings was to obtain an estimate of the time course of α3 channel deactivation and therefore an indication of the likely time course of an α3 native synaptic current. This information is not available at present for glycinergic currents mediated by α3 channels. In addition to that, channel behaviour in non-equilibrium conditions is another experimental observation that should be well described by any adequate model of channel activation. Experiments were carried out using a low (20 mm) intracellular chloride concentration, comparable to that likely to be present in the cytoplasm of the cells used in the single channel experiments. This choice was made to ensure that channels were exposed to similar intracellular chloride concentrations in the different patch configurations, and allow us to combine the information from different experimental protocols.

The black trace in Fig. 7A is an example of an outside-out current response of α3 homomeric GlyRs to the fast application of a 1.5 ms pulse of 10 mm glycine. These currents were fast, and the time course of their decay between 80 and 20% of the peak was well fitted with a single exponential with a time constant of 9 ± 0.8 ms (n= 5 patches). The rise time (also fitted between 20 and 80% of peak) was found to be 0.6 ± 0.1 ms (n= 5 patches). Note that the relatively poor expression of this subunit limited the size of the currents we recorded (mean peak amplitude 20 ± 10 pA) and consequently the precision with which we could characterize their time course.

Using the rate constant values from the fit of each set of single channel data with the different models, we calculated macroscopic currents expected in response to 1.5 ms 10 mm glycine pulses that had a time course similar to that achieved in our experiments (e.g. 150 μs 20–80% rise and fall). The time course of both rise time and decay of the calculated currents was measured in the same way as for the experimental currents. The predictions for the decay times are summarized in the graph in Fig. 7C, where each symbol represents the time constant predicted from the fit of one of the three independent sets of single channel data, and the bars are the mean of these three time constant values for each model.

The predicted deactivation time course was relatively similar across the schemes that successfully fitted the single channel data and was consistently slower than the decay that we observed experimentally (Fig. 7C). The two best schemes, e.g. the five-binding sites variant of the Jones and Westbrook, and the flip, mechanisms, predicted decay time constants of 16 ± 4 ms and 21 ± 4 ms, respectively. The picture was somewhat different for the rise time of the current response (Fig. 7B). The predictions of the five-binding sites variant of the flip scheme (0.5 ± 0.05 ms) were fairly consistent across the fitted sets and matched our experimental observations well (0.6 ms). On the other hand, the predictions of the Jones and Westbrook schemes varied considerably from one fitted set to the other, with a mean for the five-site variant of 0.4 ± 0.1 ms. Note that there are unavoidable experimental differences between the cell-attached single channel recordings and the outside-out macroscopic jumps (see Methods). In particular, the calculations from the fitted mechanism cannot include shifts in the chloride driving force that can take place as a result of the current itself. Such shifts ought to be relatively small, given that the responses we recorded here are small and short, but are expected to speed up the apparent deactivation (Moroni et al. 2011; Karlsson et al. 2011).

Discussion

The main aim of this paper was to characterize the activation mechanism of homomeric α3 GlyRs. We used the method of direct maximum likelihood fitting of kinetic mechanisms to idealized single channel data (Colquhoun et al. 2003). Establishing a reaction mechanism that describes to a good approximation the physical reality of channel activation is important in order to understand the relation between structure and function in a membrane protein. We attempted to fit 30 different reaction schemes to the steady-state single channel activity evoked by glycine concentrations from 50 μm to 10 mm and we described two schemes that gave good results. General features that were required for a mechanism to prove adequate included the presence of as many as five agonist binding sites, and the possibility of channel opening at the three highest levels of ligation, with opening efficacy increasing as more ligand molecules bind.

Both the Jones and Westbrook, and the flip, mechanisms with five binding steps provide an adequate description of the data

We have found that two schemes, Jones and Westbrook, and flip, describe the experimental data well, provided they incorporated five binding steps. Predictions of dwell time distributions were almost indistinguishable in quality for these mechanisms, independently of the number of binding sites. Schemes 1 and 2 are effectively variants of a sequential mechanism and all their parameters were allowed to vary freely, including the microscopic affinity of the successive binding steps.

Recent work from our lab has proposed a different mechanism to account for the activation of Cys-loop channels, namely the flip mechanism (Scheme 3; Burzomato et al. 2004). This scheme incorporates the idea of the Monod–Wyman–Changeux mechanism (Wyman & Allen, 1951; Monod et al. 1965), where ligand binding stabilizes the protein conformations that have higher ligand affinity. In the flip mechanism, these are the flipped shut states to which glycine binds with higher affinity (cf. resting state affinity, K_R, versus the ‘flipped’ state affinity, K_F). In mechanisms of this type, there is no interaction between binding sites, but there is an increase in the overall affinity after all subunits change their conformation in a concerted fashion. In our schemes, this behaviour is imposed by ligand-binding constraints, which mean that the flip mechanisms have only two equilibrium constants for binding, and therefore only 14 free parameters (for any number of binding sites).

If we consider exclusively the present data and analysis, both mechanisms describe well the α3 data, and it is not possible to judge which one is the best. The Jones and Westbrook mechanism with five binding sites gave a better prediction of the slope of the P_open curve (3.7 cf. 3.1 for flip), but it has many more free parameters than the flip mechanism with the same number of binding sites. Furthermore we found the parameter estimates for the Jones and Westbrook-type schemes to be highly variable across sets (Table 3).

Nevertheless, there are also other considerations that must be made. The most important is that the flipped closed states in the flip mechanism, but not in the Jones and Westbrook mechanism, have a plausible physical interpretation in that they may correspond to intermediate states in the receptor's trajectory to activation. Other lines of evidence, such as the results of Φ analysis (Auerbach, 2005), suggest that multiple such states may indeed exist. Finally, variants of the flip mechanism describe well the activity of many Cys-loop receptors (Burzomato et al. 2004; Plested et al. 2007; Keramidas & Harrison, 2010; Lape et al. 2012). We also tested variants of the ‘primed’ mechanism proposed by Sine and co-workers (Mukhtasimova et al. 2009). This mechanism hypothesizes that the activation intermediates arise from changes that are not concerted across the binding sites, but occur at each individual site in isolation. We could not obtain satisfactory fits of variants of this mechanism to α3 channel activity (data not shown). In the past we found that this mechanism performs poorly (essentially because it has many free parameters) when fitted to wild-type heteromeric glycine receptor data, but is necessary to describe well the data from a loss of function mutant that is slower in activating and can open from intermediate levels of priming (α1K276Eβ; Lape et al. 2012). This suggests that α3 channels also resemble α1β receptors in that the increase in affinity that occurs early after binding is so fast as to appear concerted (with the sensitivity of our method).

How many agonist molecules should bind to activate α3 GlyR?

Homomeric receptors in the Cys-loop family are made of five identical subunits and, thus, have five potential binding sites at which an agonist could possibly bind. Our early work on the activation of homomeric α1 and heteromeric α1β GlyRs strongly indicated that these channels open to three open states (Beato et al. 2002, 2004; Burzomato et al. 2004) in agreement with other data from native or recombinant receptors (Twyman & Macdonald, 1991; Lewis et al. 2003). In addition to that, the maximum P_open is reached when three (out of the possible five) binding sites in homomeric α1 channels are occupied by the agonist. This is in close agreement with the results of the elegant work by Sine, Bouzat and co-workers on chimeric nicotinic α7/5-HT_3A channels (Rayes et al. 2009).

The situation is quite different for α3 channels, where the much steeper Hill slope of the P_open curve cannot be accounted for if only three binding sites are included in the mechanism. Increasing the number of binding sites to five raises the values predicted by the mechanisms to 3.7 and 3.1 for the Jones and Westbrook, and flip, schemes, respectively, approaching the experimental value of 3.7. It is not clear why α3 homomers require all five binding sites to be occupied in order to open at maximum efficacy. Of course, even in homomeric α1 receptors, we could not exclude that all five binding sites can bind the agonist, even though maximum P_open is reached with three glycine bound. Structural data from ELIC and GluCl strongly suggest that all the binding sites can be occupied in channels in this super family, but cannot give us information on the efficacy of each state of ligation (Hilf & Dutzler, 2008; Hibbs & Gouaux, 2011).

The main indication for the number of bound glycine molecules needed for maximum efficacy is the steep slope of the P_open. This observation appears to be quite robustly reproducible, irrespective of choices made in the analysis, such as the value of t_crit chosen (at both high and low concentrations of agonist; data not shown). The slope of the P_open curve is so well determined that even removing either of the data points at the lowest concentrations of glycine (200 μm or 300 μm) leaves it effectively unchanged. An interesting parallel with our data is the observation that glycine is less potent and that partial agonists are less efficacious on α3 receptors than on α1 (Chen et al. 2009). The characterization of chimeric constructs in the same study suggested that the M4 transmembrane domain controlled much of the observed differences in agonist efficacy.

A specific synaptic role for α3 glycine receptors

Last but not least, our work shows that α3-containing GlyRs are fast channels that are suitable for synaptic activity. They resemble α1-containing GlyRs in their kinetics and may well mediate glycinergic synaptic currents in the adult. Comparison of our glycine concentration jump data across the two subunits indicates that synaptic currents mediated by α3 homomeric channels, if they exist, would have a decay time course (9 ms time constant; 20 mm intracellular chloride) slightly slower than that of α1-containing channels (4 and 6 ms time constants for α1 and α1β, respectively; 30 mm intracellular chloride, Pitt et al. 2008; Moroni et al. 2011). While this difference is consistent and easily detectable in our experimental protocols, it may well be too small to make identification of α3-mediated currents in neurons unambiguous.

Given that the decay of α3 currents is not particularly distinctive, could other properties of these receptors give them a synaptic role distinct from that of α1? We calculated the peak open probability predicted for α3 currents by the results of our best fitting mechanisms in response to a synaptic-like concentration pulse of glycine. Beato (2008) estimated that, at synapses onto rat lumbar motoneurons, glycine concentration peaks at 2.2–3.5 mm and decays with a time constant of 0.6–0.9 ms. If we take the concentration of glycine to peak at 3.5 mm and decay with a time constant of 0.9 μs, the peak P_open values predicted were strongly mechanism dependent, with values of 15 ± 1%, 40 ± 10%, 9 ± 1% and 15 ± 3% for Schemes 1, 2, 3 and 4, respectively (cf. 46% for the α1 glycine receptor, from the rate constants; Burzomato et al. 2004).

Our present data suffer from the limitation that we could not express α3 heteromers, which are the form of channel that one would expect to be present at synapses because of the interaction between the β subunit and gephyrin. It is interesting to note that recent work by Callister and Graham on A52S homozygous mice (Graham et al. 2011) suggests that pure α3 synapses are unlikely to be the majority, even in superficial dorsal horn neurons, where α3 expression is highest. Their hypothesis is that α3 often forms receptors together with α1 (and probably β), and it could be that α3β channels form efficiently only if they also incorporate α1. Thus the poor expression of the α3 subunit in our expression system (as a homomer and especially as an α/β heteromer) would not preclude its physiological function. The difficulty in expressing defined composition mixed receptors makes it impossible to test this hypothesis experimentally. It is hard to speculate what the properties of such a mixed α1/α3 receptor would be and why they would be appropriate to inhibition in nociceptive pathways. It is possible that such a receptor would have properties intermediate between α1 and α3 channels, and that the presence of α3 would reduce the open probability (especially at lower levels of ligation).

Our conclusion is that α3 GlyR activation can be well described by both ‘flip’ and ‘Jones and Westbrook’ mechanisms in a manner similar to that which we reported for α1β heteromeric GlyR. Inspection of the features revealed by the fits showed both intriguing differences and similarities between α3 and α1 homomers. The high sequence homology of these isoforms may allow us to investigate the structural basis of the differences by mutating the channels.

Glossary

CV

coefficient of variation

GlyR

glycine receptor

Additional information

Competing interests

None.

Author contributions

Conception and design of the experiments: A.M., R.L. and L.G.S.; collection, analysis and interpretation of data: A.M., R.L., M.M. and L.G.S.; writing the article: A.M., R.L. and L.G.S. All authors approved the final version of the manuscript for publication.

Funding

A.M. was supported by a UCL Impact studentship.

Author's present address

M. Moroni: Max Delbrück Center for Molecular Medicine, Berlin 12125, Germany.