Mechanics of a fiber network within a non-fibrillar matrix: model and comparison with collagen-agarose co-gels

Abstract

While collagen is recognized as the predominant mechanical component of soft connective tissues, the role of the non-fibrillar matrix (NFM) is less well understood. Even model systems, such as the collagen-agarose co-gel, can exhibit complex behavior, making it difficult to identify relative contributions of specific tissue constituents. In the present study, we developed a two-component microscale model of collagen-agarose tissue analogs and used it to elucidate the interaction between collagen and NFM in uniaxial tension. Collagen fibers were represented with Voronoi networks, and the NFM was modeled as a neo-Hookean solid. Model predictions of total normal stress and Poisson’s ratio matched experimental observations well (including high Poisson’s values of ~3), and the addition of NFM led to composition-dependent decreases in volume change and increases in fiber stretch. Because the NFM was more resistant to volume change than the fiber network, extension of the composite led to pressurization of the NFM. Within a specific range of parameter values (low shear modulus and moderate Poisson’s ratio), the magnitude of the reaction force decreased relative to this pressurization component resulting in a negative (compressive) NFM stress in the loading direction, even though the composite tissue was in tension.

INTRODUCTION

In order to understand fully the functional mechanics of soft tissues, it is necessary to characterize the mechanical properties of each tissue constituent and elucidate how they interact and function together. While the mechanical role of collagen (the primary structural component of connective tissues) is often evaluated, less is known about the role of non-fibrillar matrix (NFM, e.g., proteoglycans, glycosaminoglycans, cells, etc.), which varies compositionally across tissue types. Our recent work^35,37 evaluated collagen-agarose tissue analogs (with agarose as a representative NFM) in uniaxial tension and indentation to characterize the contribution of the NFM under different loading scenarios. In these studies, agarose was selected to represent non-fibrillar matrix because of several advantageous characteristics, namely its biocompatibility, uncharged nature, and ability to intersperse between fibers of a collagen gel without disrupting the collagen network.⁶² Results demonstrated that the NFM contributes significantly to the elastic and viscoelastic mechanical response and structural reorganization of soft tissues in a concentration-dependent manner, even in tensile testing in which collagen is normally assumed to be the predominant contributor. While these studies have provided useful information, the mechanism by which NFM interacts with the collagen network on the microscale to alter the macroscale composite tissue properties remains unknown. Thus, the objective for the current work was to use a two-component microstructural model of the collagen-agarose system under quasi-static loading to elucidate the interaction between the collagen and the agarose during uniaxial extension of the co-gel.

Various approaches have been used to incorporate structural information into mechanical models of soft tissues. Three broad categories of model can be identified: isolated fiber,^{4,11,14,21,25–27,32,39,42,44–46,49,50,63,64} regular-fiber-cell,^{3,9,30,33,48,54,60} and large-network.^{31,43,52,53,56–58} Isolated-fiber models, often expressed in terms of a continuum strain-energy function, are characterized by each fiber in the tissue behaving independently of the others and moving affinely with the macroscopic deformation. Regular-fiber-cell models involve a small unit cell (4–20 fibers) that is assumed to repeat within the tissue. These models capture some of the complex mechanical behavior of a tissue but can still be converted to a closed-form stress-strain (or strain energy) expression. Fibers within regular-fiber-cell models may be able to move non-affinely, but the cells themselves deform with the macroscopic boundary. Finally, large-network models involve a network of hundreds to thousands of fibers, often arranged randomly, that interact fully with each other. In this case, the network must be large enough that different networks with the same overall structural properties (alignment, crosslink density, etc.) produce the same stress-strain results even if the detailed structures are quite different. Highly non-affine kinematics exhibited by interacting fibers are consistent with reports that collagen fiber kinematics in native tissues do not follow the affine assumption.^{8,19,20,22,36}

Each of these three modeling approaches exhibit specific advantages, and models constructed at each domain size (isolated fiber, regular-fiber-cell, large-network) have provided insight into the mechanical behavior of a variety of materials, including native soft tissues,^{5,11,13–15,17,26,28,29,32,41,42,44,58} biological tissue analogs,^{16,43,45,48,52,56,57,60} and biomimetic synthetic materials.^2,30 In addition to representing the collagen component, several previous models have also considered the contribution of the NFM. Within models based on non-interacting fibers, NFM has been represented, often via a neo-Hookean or Mooney-Rivlin formulation, as a summed contribution to the collagen stress.^{11,14,21,25,42,44–46,49,61,63} Since each fiber in these models functions independently (of other fibers and the NFM) at the local level, interactions between tissue constituents cannot be evaluated. To capture such interactions, some models have included an additional term to incorporate the stress contribution due to interactions between the collagen network and NFM.^21,46,47,63 When the fiber architecture is precise and well known, the form of the interaction contribution can be suggested by the structure of the tissue (as in ²¹). Unfortunately, for an unstructured fiber network the appropriate definition for the interaction term is unknown. For regular-fiber-cell models, the general tendency is to evaluate the collagen network alone, but a few studies have incorporated a “bulk” term to describe the contribution from non-collagenous material.^9,33 To date, however, these models have focused on the fiber component and have not been used to specifically evaluate the role of NFM or how it interacts with fibrillar material to alter the composite tissue response. Similarly, large-network models have not generally included a representation of NFM. One exception is a previous study performed by our group,⁵⁸ in which a neo-Hookean NFM term was incorporated in parallel with collagen networks in a multiscale model to simulate the mechanical behavior of decellularized arteries. The current study employs a modified version of our previous approach, but constructed more closely with experimental data and with a more specific focus on microstructural properties and relationships. Therefore, the purpose of this study was to apply a large-network-based modeling approach to experimental co-gel data to evaluate the role of non-fibrillar matrix and the nature of microstructural collagen-matrix interactions in soft connective tissues.

METHODS

Material of interest

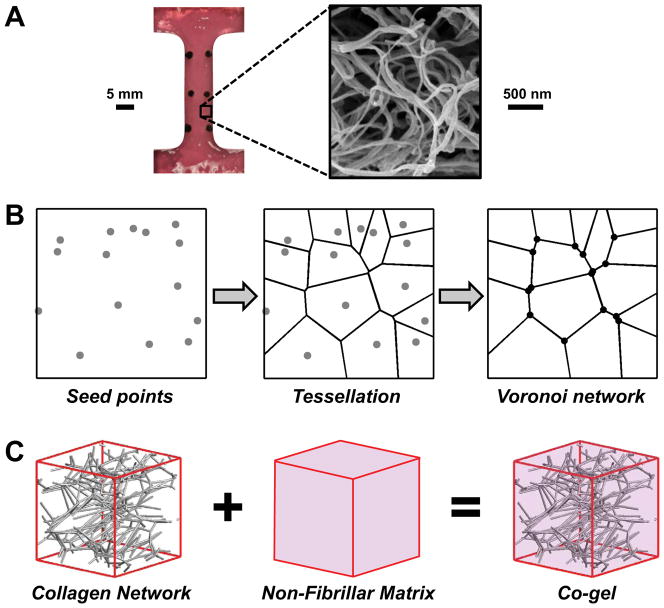
A microscale model was developed for collagen-agarose co-gels, of which experimental data was presented previously.³⁵ Although the fabrication and testing of the gels are described elsewhere, a brief description is provided here as part of the development of the model. Collagen-agarose co-gels composed of 1.0 mg/mL collagen and 0% (NoAg), 0.125% (LoAg) or 0.25% (HiAg) w/v agarose were cast in dog-bone shaped Teflon molds (Fig. 1A) and allowed to gel. Agarose, which constituted the NFM of this tissue analog system, formed an interspersed, web-like matrix within the collagen network.^35,62 Co-gels were subjected to a four-step incremental stress-relaxation tensile test, wherein the load, tissue strain, and cross-sectional area were recorded throughout testing, and quantitative polarized light imaging (QPLI) was used to quantify collagen fiber alignment and kinematics. The present study focused on the equilibrium (relaxed) data from the final step of these tests, corresponding to ~10% tensile strain.

Figure 1.

A microscale network model was used to simulate the response of collagen-agarose soft tissue analogs. (A) Representative dog-bone shaped collagen gel tested experimentally³⁵ and scanning electron micrograph showing the reconstituted collagen network. (B) Computational networks were generated by randomly placing seed points within a representative volume element (RVE), generating a Voronoi tessellation about those seed points, and placing pin joint nodes at each fiber-fiber connection (schematic shows 2D network for clarity; actual Voronoi networks were 3D). (C) Collagen-agarose co-gels were modeled by adding the contributions from the collagen network and the non-fibrillar matrix in parallel.

Model formulation

While several different types of computational networks have been used to represent collagen (e.g., random growth,^55,58 confocal microscopy reconstruction⁵⁶, scanning electron microscopy reconstruction¹²), Voronoi networks were used in this study. Such networks were recently shown to provide a close approximation to collagen gel behavior,⁴³ and the sparse arrangement and low nodal degree of Voronoi networks allowed for generation of networks that exhibited very large Poisson’s ratio values (~3) similar to those measured experimentally for our collagen-agarose co-gels.³⁵ Previous studies using other network types^54,59,60 have been unable to achieve Poisson’s ratio values as large as those measured experimentally for tissue analogs, which are likely caused by significant network reorientation, compaction and densification of the network, and exudation of interstitial fluid. In the present study, networks were created by randomly placing seed points within a representative volume element (RVE), generating a 3D Voronoi tessellation about these points, and placing nodes at the intersections of Voronoi edges (Fig. 1B). Networks were created in Matlab (Natick, MA) using the VORONOIN function, an implementation of the widely-used Qhull code. In order to ensure that results were not dependent on a specific placement of seed points, five different networks were created and evaluated in this study (i.e., n=5 for each simulation group) with ~700 fibers per network. Using an assumed fiber diameter of 70 nm, collagen density of 1.34 g/mL, and the experimental collagen concentration (1 mg/mL), the average edge length in undeformed RVEs was computed⁵⁸ to be ~20 μm; consequently, average RVE volume was ~8,000 μm³. Generated Voronoi networks were isotropic, so a pre-stretch was applied along the x-axis, and the RVEs were clipped to the original size, such that initial network alignment approximated the anisotropic alignment of co-gels measured via QPLI. The number of seed points (and hence, number of fibers) was adjusted until the Poisson’s ratio of stretched RVEs equaled values for NoAg gels. Nodes at fiber intersection points were modeled as freely rotating pin joints, and fibers were modeled as one-dimensional nonlinear springs, with the force on each fiber defined as:^{7,18,25,55,58}

$$F=\frac{E_{f}A}{B}(e^{B\epsilon }-1)$$ (1)

where E_f is the elastic modulus of the fibers at infinitesimal strain, A is the fiber cross-sectional area, B is a nonlinearity constant, and ε is the fiber Green strain given by $\epsilon =0.5({\lambda }_f^2-1)$. Parameter values for the fiber constitutive equation were used as previously⁵⁵ (fiber radius=35 nm; B=3.8), where the fiber modulus value E_f was set at 6.5 MPa in order to produce total stress values (calculated as defined below) approximately equal to experimentally-measured values for the NoAg group. With the fiber forces thus defined, the volume-averaged Cauchy stresses from the collagen network at each RVE surface were computed by:^10,59

$${\sigma }_{ij}^{\mathit{col}}=\frac{1}{V}{\sum }_{\mathit{bnd}\mathit{nodes}}{x}_i{F}_j$$ (2)

with V as the RVE volume and x_i corresponding to the position of each fiber (with force F_j) on a given RVE boundary.

As done in our previous study,⁵⁸ the non-fibrillar matrix (NFM) was represented using a compressible neo-Hookean solid formulation. Assuming no shear, Cauchy stress due to the NFM was defined as:²⁴

$${\sigma }^{\mathit{nfm}}=G\left(\frac{{\lambda }^2}{J}-J^{-2\beta -1}\right)$$ (3)

where G is the NFM shear modulus, λ is the RVE stretch, J is the Jacobian, β = ν_m/(1–2ν_m), and ν_m is the Poisson’s ratio of the matrix. Since the model represents the mechanical response at equilibrium (after relaxation and drainage of any pressurized interstitial water), ν_m was taken to be 0.1.⁴⁴ Values for G were specified by extrapolating experimental data for the shear modulus of pure agarose gels⁶ to concentration values used in our study such that G = 0, 110 and 720 Pa for NoAg, LoAg, and HiAg, respectively. In this way, the only difference between models representing the three experimental groups was in the specific value used for shear modulus. All other variables (e.g., organization of the Voronoi collagen network, parameter values for the fibers) were consistent across the three different co-gel models. The total stresses in the composite model were calculated by summing the contributions from the collagen network and the NFM (Fig. 1C) in a parallel manner:

$${\sigma }^{\mathit{tot}}=<{\sigma }^{\mathit{col}}>+{\sigma }^{\mathit{nfm}}$$ (4)

Model solution

A 10% strain was applied to each RVE in the 1-direction (λ₁=1.1), while the 2- and 3-directions had stress-free surfaces (Fig. 2). After the step displacement, the position of the internal nodes and the position of the unloaded boundaries (2- and 3-faces) were solved for using Newton’s method to ensure force balance at each internal node and minimal normal stresses on the free surfaces (i.e., σ₂₂ and σ₃₃; Fig. 2). For all three groups (NoAg, LoAg, HiAg), simulations were evaluated for each of the five networks. For each run of the microscale model, the total normal stress in the loaded direction (σ₁₁) and the Poisson’s ratio of the composite RVE were computed and compared to experimental co-gel data. In addition, the stresses due to each component (<σ₁₁^col>, σ₁₁^nfm) and the amount of stretch on each fiber (λ_f) were evaluated along with 3D maps showing network orientation and fiber stretch. All model simulations were performed in Matlab, with a run time of a few minutes.

Figure 2.

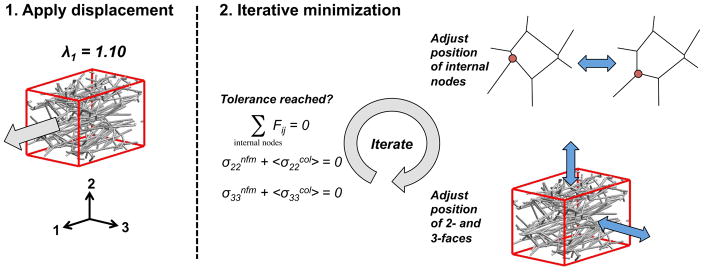
After applying a stretch of 1.1 in the 1-direction, an iterative minimization scheme adjusted the position of the internal nodes and of the 2- and 3-direction surfaces until a tolerance was reached for the nodal force balance and stress-free boundaries.

A second set of simulations was performed to explore the parameter space of the NFM neo-Hookean term. To characterize the parameter space, the shear modulus and Poisson’s ratio were varied across a range of values (G = 1, 10, 110, 330, 720, 1310 Pa; ν = 0, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.49), and RVEs were evaluated for each combination of parameter values.

Statistical analysis

A one-way ANOVA was utilized to compare mean fiber stretches across groups and post-hoc t-tests were used to identify statistically significant specific comparisons. Bonferroni corrections were applied when making multiple comparisons.

RESULTS

The model-predicted values of Poisson’s ratio and total stress (in the 1-direction) compared well with experimental values (Fig. 3A and Fig. 3B, respectively). Data trends showed qualitative agreement, indicating that the microscale model made good, if not exact, predictions of the experimental data. An examination of the relative proportion of the total stress contributed by each component (Fig. 3C) yielded a very small NFM contribution in the LoAg samples (average = 3.8% of total stress), and a larger NFM contribution for the HiAg samples (average = 18.6% of total stress).

Figure 3.

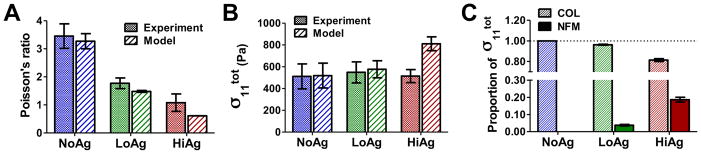
Model-predicted values of (A) Poisson’s ratio and (B) Cauchy stress in the 1-direction showed qualitative comparison with experimental values; (C) while stress in the NoAg samples was due (trivially) to collagen (COL) alone, the non-fibrillar matrix (NFM) contributed a small and moderate proportion of the total stress to the LoAg and HiAg groups, respectively (plots show mean ± 95%CI; n=5–7/group)

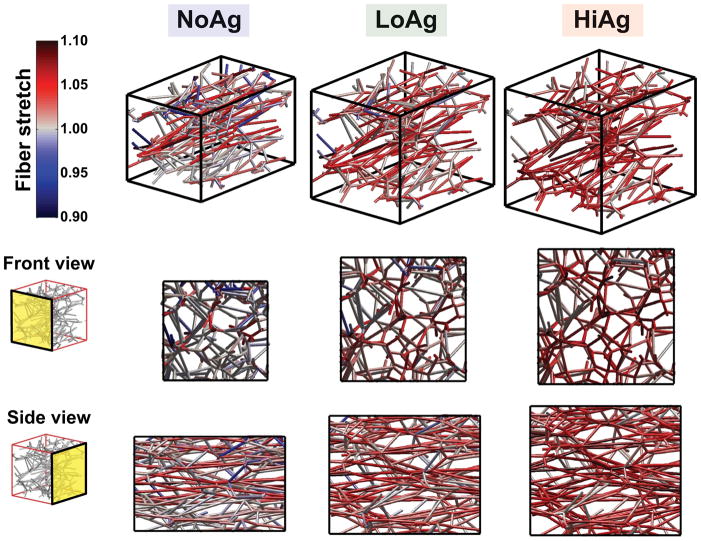
Representative network maps at 10% strain showed that fiber orientation and fiber stretch varied significantly across different groups (Fig. 4). In these plots, gray fibers are unstretched relative to the undeformed case (λ_f = 1), red fibers are in tension (λ_f > 1), and blue fibers are in compression (λ_f < 1). As the amount of NFM increased (from NoAg to LoAg to HiAg), the number of blue and gray fibers decreased and the intensity of red fibers increased, demonstrating an overall increase in fiber stretch due to the NFM. Fiber stretch was also evaluated quantitatively by comparing frequency distributions (Fig. 5A) and mean fiber stretch values (Fig. 5B), where significant differences were observed between the groups (p<0.001). Another observation from the network maps was the difference in volume change due to the presence/quantity of NFM; NoAg RVEs compacted significantly in the lateral directions, while the HiAg RVEs strongly resisted volume change (Fig. 4). Importantly, the NFM’s resistance to volume change (also demonstrated by decreasing Poisson’s ratio) likely resulted in the increased fiber stretches by not allowing the fibers to reorient in the direction of loading and compact the lateral boundaries.

Figure 4.

3D maps (and 2D projections) show how network organization and fiber stretch for a representative network changed as a function of NFM quantity: the amount of network compaction decreased and relative fiber stretch increased as NFM increased from NoAg to LoAg to HiAg (gray = unstretched relative to undeformed case, red = tensile stretch, blue = compressive stretch)

Figure 5.

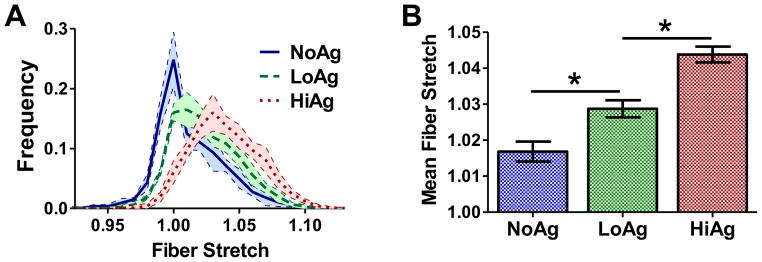
Fiber stretch increased with increasing NFM composition, as demonstrated by (A) frequency distribution curves and (B) mean fiber stretch values (mean± 95%CI; n=5/group; * = significant differences)

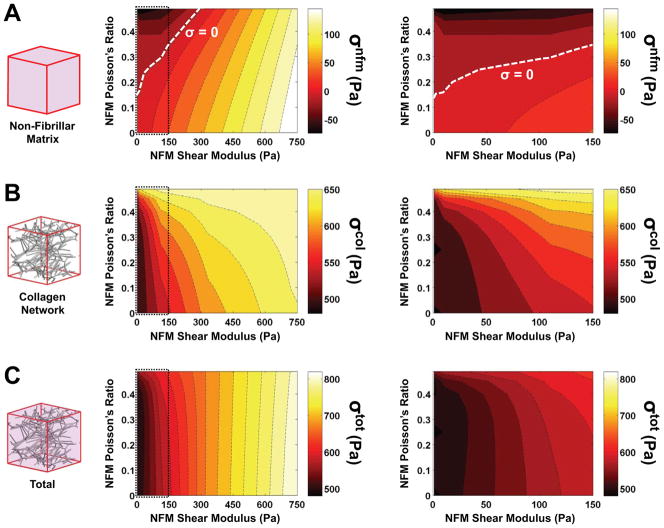
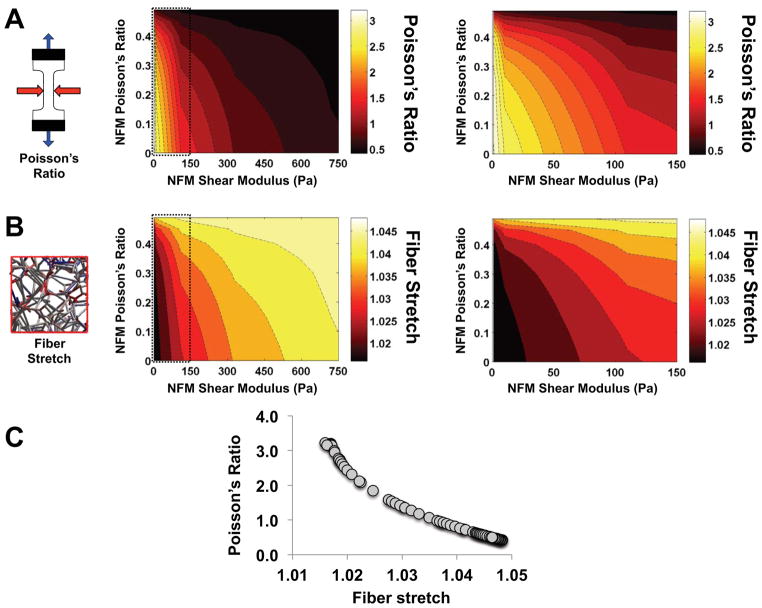
Parameter space plots (Fig. 6 and Fig. 7) demonstrate how output values changed as a function of the two parameters in the neo-Hookean NFM term (Poisson’s ratio ν_m and shear modulus G). Interestingly, at low G values and moderate ν_m values, the NFM stress (σ^nfm) was negative (Fig. 6A), indicating a compressive stress contribution from the NFM. With this transition from compressive to tensile stress, the parameter space for σ^nfm included a boundary along which the stress contribution from the NFM was zero (dashed line, Fig. 6A). The collagen network stress (σ^col) and the total stress (σ^tot) increased with increasing G (Fig. 6B and 6C, respectively). For all stress measures, increasing the value of ν_m had minimal impact at high G, but made a more significant impact at low values of G (Fig. 6, right column). In a similar manner, parameter maps for RVE Poisson’s ratio and fiber stretch (Fig. 7A and 7B, respectively) demonstrated relatively consistent values when G>300 Pa, but much greater variation in values at low G. As Poisson’s ratio of the NFM (ν_m) increased, the composite Poisson’s ratio decreased and λ_f increased. Furthermore, there was an inverse relationship between RVE Poisson’s ratio and mean fiber stretch (Fig. 7C).

Figure 6.

Parameter space plots demonstrate how the (A) NFM stress, (B) collagen stress and (C) total stress changed as a function of varying the two NFM input parameters of shear modulus and Poisson’s ratio (left = full parameter space; right = zoomed in low shear modulus region); of particular interest was the span of the NFM stress from negative to positive values, including the boundary (dashed line) where the contribution from the NFM was zero (mean values plotted; n=5/group)

Figure 7.

Parameter space plots demonstrate how the (A) RVE Poisson’s ratio and (B) fiber stretch changed as a function of varying the two NFM input parameters of shear modulus and Poisson’s ratio (left = full parameter space; right = zoomed in low shear modulus region; mean values plotted; n=5/group); (C) there was a strong correlation between Poisson’s ratio and fiber stretch values

DISCUSSION

In this study, a network-based microscale model was developed and fit to experimental data from collagen-based tissue analogs. After adding (in parallel) a term to describe the mechanical contribution from the non-fibrillar matrix (NFM), the model was able to predict qualitatively the composition-dependent mechanical response of collagen-agarose co-gels in tension (Fig. 3A and 3B). The microscale model utilized here allowed for the characterization of how the collagen fiber network (represented via Voronoi networks) was reoriented and stretched differentially as a function of increasing NFM.

Our experimental studies of collagen-agarose co-gels^35,37 suggested that agarose served a volume-preserving role in co-gel deformation. Similarly, the neo-Hookean term representing the NFM contribution in our microscale model increased resistance to volume change. Specifically, lateral compaction in the 2- and 3-directions that occurred during a stretch in the 1-direction decreased as a function of NFM concentration, as measured by average Poisson’s ratios from model simulations (Fig. 3A) and by comparing deformed dimensions of representative network maps (Fig. 4). As lateral compaction decreased, the reorientation of the fibers towards the direction of loading was limited, leading to increased stretching of the fibers (Fig. 4 and 5). In fact, further simulations yielded data that showed a distinct correlation between Poisson’s ratio of the RVE and mean fiber stretch (Fig. 7C). Parameter space plots show how these measures changed as parameter values for the NFM term (shear modulus G and NFM Poisson’s ratio ν_m) were varied across a full range of values (Fig. 7A and B). At high G (~400 Pa and above), RVE Poisson’s ratio and fiber stretch remained relatively consistent, even when ν_m was varied significantly; however, at low G these values were highly dependent on changes in G and ν_m.

The stress contribution due to the NFM was computed as predicted for the three sample groups: while trivially zero for the NoAg samples, the NFM stress was very small for the LoAg samples and moderate for the HiAg samples (Fig. 3C). Further exploration of the neo-Hookean NFM parameter space demonstrated a transition to negative (compressive) stress for the matrix at low shear modulus and moderate Poisson’s ratio (Fig. 6A). Although a compressive state in the unloaded (2- and 3-) directions is intuitive (in opposition to the collapsing collagen network due to the Poisson effect), a compressive NFM stress in the 1-direction is somewhat unexpected. Such a result indicates that, instead of providing a reaction-force-type response to the deformation (as the collagen network does), the NFM force acts in the direction of the grip and decreases the magnitude of the composite tensile stress. While this notion is initially counterintuitive, previous computational studies^26,27 have demonstrated a similar result for the hydrostatic pressure term in a fiber-based incompressible model, and our experimental co-gel data³⁵ suggested this possibility since peak stress values decreased with increasing amounts of NFM (i.e., agarose). In addition, our previous fiber-matrix multiscale model of artery mechanics⁵⁸ predicted that the non-collagenous matrix would be in compression in order to prevent the collapse (i.e., lateral compaction) of the collagen network. Thus, a compressive NFM stress in the loading direction due to pressurization of the composite material is plausible at certain parameter values of the NFM component.

A possible mechanism for compression of the NFM, and for how the NFM transitions to a tensile stress at different parameter values, is represented using a simple schematic (Fig. 8). For simplicity, a 2D representation of the 3D physical system is used. When collagen-only (NoAg) samples are stretched (Fig. 8A), the collagen provides a reaction force (F₁^col) in resistance to the deformation in the 1-direction, while the stress-free 2-boundary exhibits no net force (i.e., F₂^col =0). When added to the collagen network, NFM contributes to the composite mechanical response in two ways (Fig. 8B): through a reaction force (F^nfm) that resists deformation and through an isotropic pressure (P^nfm) that resists volume change. The presence of P^nfm balances the transverse tension in the collagen network F₂^col to help maintain volume and satisfy the zero total stress condition on the 2-boundary. In samples with small shear modulus (G) and moderate to high Poisson’s ratio (ν_m) values (Fig. 8B), F₁^nfm is relatively small because of low G, so P^nfm dominates, resulting in a negative (i.e., compressive) total stress from the NFM (σ₁^nfm). On the other hand, at large G and/or small ν_m (Fig. 8C), the high shear modulus increases the magnitude of F^nfm over that of the P^nfm, resulting in a positive (i.e., tensile) total σ₁^nfm.

Figure 8.

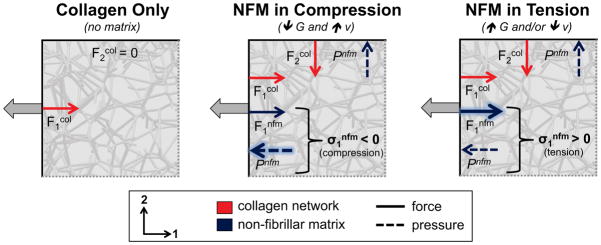
2D schematic demonstrating the proposed mechanism for the observed results. In the collagen-only (NoAg) case (left), collagen provided a reaction force (F₁^col) while the forces on the non-loaded boundary were zero. At low shear modulus and high Poisson’s ratio (middle), the pressure due to the NFM resisting volume change (P^nfm) was greater than the NFM reaction force (F₁^nfm), resulting in a negative (compressive) stress from the NFM. At high shear modulus and/or low Poisson’s ratio (right), the NFM reaction force (F₁^nfm) dominated over the pressure term (P^nfm), resulting in a positive (tensile) stress from the NFM.

Collagen-based tissue analogs and some collagenous native tissues (e.g., tendon and ligament) can exhibit very high Poisson’s ratio in uniaxial tension experiments.^23,34,35,40 Poisson’s values as high as 2–3 are due to a high degree of network reorientation towards the loading direction,^35,38 significant compaction and densification of the network due to fibers buckling under transverse strain,³⁰ and significant exudation of interstitial fluid.^1,65 Although one recent study presented a micromechanical finite element model that was able to predict high Poisson’s ratios using crimped fibers in a super-helical organization,⁵¹ previous regular-fiber-cell and large-network models have only been able to achieve maximum Poisson’s ratio values of ~1^54,59,60, thereby failing to replicate the high values measured experimentally.^56,60 Voronoi networks, which were previously reported to show quantitative agreement to collagen networks,⁴³ contain fewer fiber-fiber crosslinks than other network types used in previous models, thereby allowing for greater fiber reorganization and subsequent network compaction under load. In the present study, Voronoi networks representing the collagen-only gels exhibited Poisson’s ratios of ~3 in agreement with experimental data.

One difficultly in extending this modeling approach towards characterizing native tissues is identification of an appropriate mathematical formulation and corresponding material properties for the non-fibrillar matrix (NFM). As in several previous studies,^{14,25,42,44,45,49,58,61} the current work represented the NFM using a simple neo-Hookean solid with two input parameters: shear modulus and Poisson’s ratio. The model was compared to experimental data at the equilibrium phase of a stress-relaxation test, so a low Poisson’s value of 0.1 was used.⁴⁴ In addition, since the model was constructed to represent collagen-agarose co-gels, values for the shear modulus were based on properties of agarose-only gels tested experimentally,⁶ which are comparable to those used in other tissue modeling studies.^14,25,29,32 For native tissues, defining these parameters is more difficult because the NFM term, as presently defined, lumps all non-collagenous material together (i.e., there is no single definition of NFM), making tissue-specific definition of these parameters challenging, and the experimental measurement of NFM properties very difficult. Certainly this topic merits further investigation.

This study is not without limitations. Due to the parallel construction of the microscale model, our approach did not allow for examination of fiber-matrix interactions internal to each RVE, which likely result in a heterogeneous strain and stress fields throughout the sample. Ongoing work by our group is developing a coupled fiber-matrix microscale model that will allow for characterization of these internal interactions. Another difficulty lies in appropriately matching the initial fiber orientation of the Voronoi networks to experimental data. We used a method described previously⁵⁵ to match 3D network organization to the 2D experimental measures of sample alignment (using polarized light imaging), but the appropriate definition for the proportionality constant used in this analysis remains unclear. In spite of these concerns, the model developed and used in this study matched experimental observations well and demonstrated a mechanism by which pressurization of the NFM reduces lateral contraction of the collagen network and leads to a negative (compressive) stress in the NFM (σ₁₁^nfm) even though the composite tissue is in tension.