Primary motor cortex reports efferent control of vibrissa motion on multiple time scales

Abstract

Exploratory whisking in rat is an example of self-generated movement on multiple time scales, from slow variations in the envelope of whisking to the rapid sequence of muscle contractions during a single whisk cycle. We find that, as a population, spike trains of single units in primary vibrissa motor cortex report the absolute angle of vibrissa position. This representation persists after sensory nerve transection, indicating an efferent source. About two-thirds of the units are modulated by slow variations in the envelope of whisking while relatively few units report rapid changes in position within the whisk cycle. The combined results from this study and past measurements, which show that primary sensory cortex codes the whisking envelope as a motor copy signal, imply that signals present in both sensory and motor cortices are necessary to compute coordinates based on vibrissa touch.

INTRODUCTION

The purposeful movement of biological sensors, such as the motion of the eyes (Leigh et al., 1997) or hands (Shadmehr and Wise, 2005), is an essential part of perception. What algorithms incorporate movement as part of perception at the level of cortex? In particular, over what time-scales does motor cortex direct the motor plant associated with a sensory modality? Motor cortex may be hypothesized to maintain different pathways for fast and slow control of the motor plant. This is particularly relevant for the large repertoire of repetitive behaviors, such as those involved with scanning sensory systems involved with touch, vision, and even olfaction (Diamond et al., 2008; Nelson and MacIver, 2006), in which fast rhythmic motion is modulated by a slowly varying amplitude and/or change in orientation. To test this hypothesis, we address how trains of spikes from single units in primary motor (vM1) cortex represent the motion of the vibrissae during free whisking in rat.

The rodent vibrissa system is a scanning sensorimotor system in which the sensors, i.e., long hairs referred to as vibrissae, rapidly scan a region around the head of the animal (Carvell and Simons, 1990; Knutsen et al., 2006; Mehta et al., 2007) whose angular extent evolve only slowly in time. (Carvell and Simons, 1990; Guic-Robles et al., 1989). The primary sensory organ of the rat vibrissa system is the vibrissa-follicle complex. This is comprised of pressure-sensitive cells that respond to external stimulation as well as internal motor drive of a long hair that originates in the follicle (Szwed et al., 2006). The follicle is swept rhythmically back and forth by muscles in the mystacial pad to permit the hairs to touch and probe objects that are located close to the head of the animal (Kleinfeld et al., 2006). While the rat can exhibit a variety of whisking patterns (Berg and Kleinfeld, 2003a; Carvell and Simons, 1995; Mitchinson et al., 2007; Towal and Hartmann, 2006), we focus on exploratory rhythmic whisking in the absence of exafferent stimuli. Bouts of rhythmic whisking at a stable frequency in the 5 to 12 Hz band are readily elicited in free ranging as well as head-fixed rats (Hill et al., 2008). This behavior is characterized by temporal structure over a wide range of time scales, i.e., the extent of individual whisking bouts on the 1 to 10 s time-scale, changes in the envelope of vibrissae movement on the 1 s time scale, and the motion of the vibrissae on the 0.1 s period of rhythmic motion (Berg and Kleinfeld, 2003a; Carvell et al., 1991; Hill et al., 2008).

The presence of multiple time scales in whisking, together with the relatively small number of degrees of freedom in vibrissa control, suggest that vibrissa primary motor (vM1) cortex is an ideal cortical region to elucidate multiple time scales in motor control. Past electrophysiological measurements establish that neurons in vM1 cortex can exert fast control over vibrissa motion. Stimulation of vM1 cortex in anesthetized animals can elicit either rapid deflections of individual vibrissae (Berg and Kleinfeld, 2003b; Brecht et al., 2004) or extended whisking bouts that outlast the original stimulation (Cramer and Keller, 2006; Haiss and Schwarz, 2005). Measurement of the local field potential in vM1 cortex in awake animals indicate that units with rhythmic neural activity can lock to whisking (Ahrens and Kleinfeld, 2004; Castro-Alamancos, 2006). Complementary work established that the firing rate of neurons in vM1 cortex respond to sensory input (Chakrabarti et al., 2008; Ferezou et al., 2006; Kleinfeld et al., 2002). The response is band-limited in the sense that only the fundamental frequency of a periodic pulsatile input is represented, reminiscent of a control signal used to stabilize the output of servo-motors (Kleinfeld et al., 2002). Yet prior work did not address the critical issue of signaling of motor commands at different time scales, e.g., slow changes in amplitude over multiple whisk cycles, nor did it address the nature of single unit activity in directing motor output.

We separate whisking behavior into components that vary on distinct time scales and ask: (i) Do individual single units preferentially code different components of the motion? (ii) If so, is this representation driven by activity from a central source or by peripheral reafference? (iii) How many neurons are required to accurately represent vibrissa motion in real time? (iv) Given the high connectivity between vM1 and vibrissa primary sensory (vS1) cortices (Hoffer et al., 2003; Kim and Ebner, 1999), how does the representation of whisking behavior differ between these areas?

RESULTS

Rats were trained to whisk either while head-fixed or while freely exploring a raised platform (Hill et al., 2008). In the head-fixed paradigm, vibrissa position was monitored via a high-speed camera and processed to determine the azimuthal angle, defined as the angle in the horizontal plane and denoted θ(t), versus time. In both paradigms the electrical activity of the intrinsic muscle group, primarily responsible for protraction of the vibrissae, were recorded to form the differential rectified electromyogram (|∇EMG|) (Berg and Kleinfeld, 2003a). The animals were further implanted with a head stage to record extracellular potentials in the area identified as vM1 cortex based on mapping studies (Fig. S1). These signals were subsequently sorted into single units, as verified through the consistency of the extracellular spike waveform and the presence of relative and absolute refractory periods in the spike train (Fig. 1A–D). In addition, we required the recording of at least 100 whisks for each unit to be accepted for further analysis. Given these constraints, our results are based on 95 single units across 11 rats. In ancillary studies with a lesion to the infraorbital branch of the trigeminal nerve (IoN), an additional 74 single units across 7 animals were obtained.

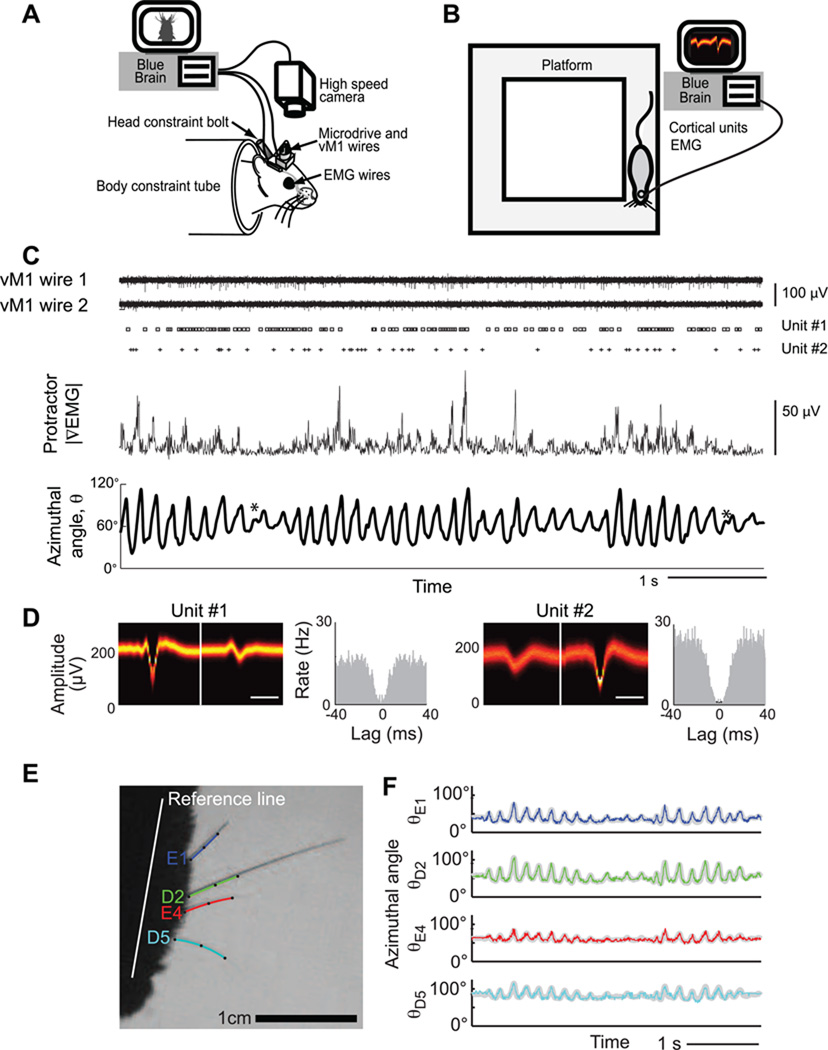
Figure 1. Experimental setups and uniformity of whisking behavior.

(A) Head-constraint apparatus. The animal’s head is held in place via a bolt embedded in its head mount. The array of vibrissae is trimmed down to a single row. Whisking is evoked by placing the home cage just out of reach. A high-speed camera is used to track vibrissa motion, and embedded microwires are used to record cortical units and EMG signals. (B) Apparatus for free ranging animals that explore a raised platform. All other experimental features are as in panel A, except no vibrissae are trimmed and their motion is not tracked. (C) Example of primary data taken in a behavioral session, including neuronal activity from both channels of stereotrode, spike trains from two sorted units, rectified ∇EMG of the protractor muscles, and position of the tracked vibrissa. An * indicates a possible double-pump whisk cycle. (D) Waveform and spike train autocorrelation for sorted units in panel C. (E) Videograph of a head-fixed rat with four tracked vibrissae, spanning rows D and E and arcs 1 to 4. (F) The motion of the four vibrissae versus time, superimposed on top of the motion calculated from only the first mode of the singular value decomposition (gray).

Rhythmic exploratory whisking behavior consists of extended bouts of contiguous whisk cycles (Carvell and Simons, 1995). Qualitatively, the range of motion and the average position of the vibrissae tend to be similar for adjacent whisk cycles, consistent with past reports (Berg and Kleinfeld, 2003a; Hill et al., 2008), and thus vary on a time scale that is much slower than that of the 0.1 s whisk cycle (Fig. 1C). In addition, the large vibrissae tend to move in unison during exploratory whisking (O'Connor et al., 2010a; Welker, 1964), implying that a single set of control signals is sufficient to uniformly drive the vibrissae. We examined the latter issue in detail by tracking the motion among sets of vibrissae that spanned rows and arcs (Fig. 1E). For the example of four vibrissae that span two rows and five arcs, we find a high degree of linear correlation between all vibrissae, as quantified by the first mode of the singular value decomposition which accounts for 0.95 of the variability in the motion across all vibrissae (cf colored and gray traces in Fig. 1F) (Eqs. 4 and 5). In general, we observe that correlations in the motion about the mean position exceeded 0.90 for vibrissae within or across rows (Fig. S2).

Linear analysis

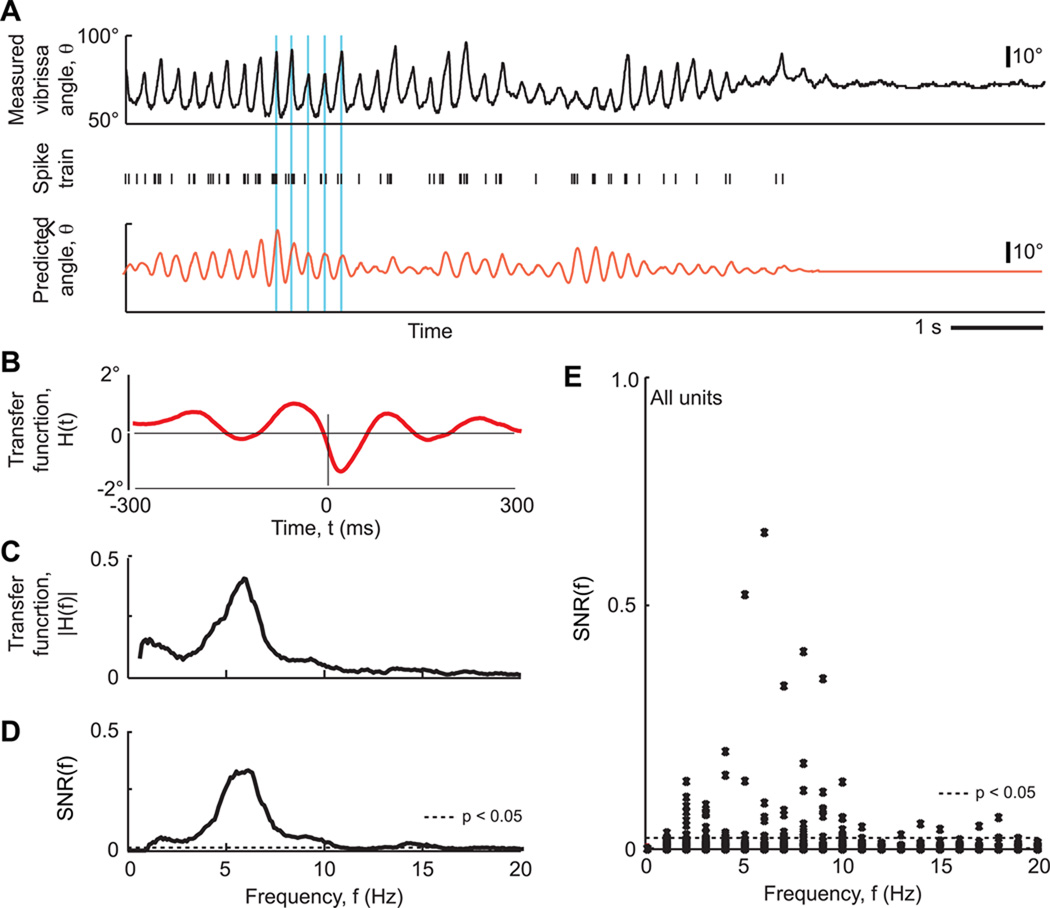
A minimal analysis is to test if both the slow and fast time scales of the vibrissa trajectory are coded linearly. We thus calculated the transfer function, H̃(f)(Eq. 6), as a function of frequency, f, between unit spike trains and vibrissa position using epochs that contained whisking and non-whisking behavior. The transfer function defines the linear relationship between the position of the vibrissae and a measured spike train. In practice, relatively few units tracked the angle of the vibrissae on a cycle-by-cycle basis. A particularly illustrative example of such data is shown in Figure 2A, together with the predicted whisking trajectory that was calculated by convolving the measured spike train with the transfer function (Fig. 2A,B). The predicted trajectory captures the phase of the motion rather well, but fails to capture the envelope of the motion. This result may be quantified by a signal-to-noise ratio, SNR(f) (Eq. 9), that measures how well the transfer function predicts vibrissa position from the measured spike trains. This function shows a peak near the whisking frequency but is low outside of this range (Fig. 2B,C). Across all units, the value of SNR(f) was especially small for f ~ 1 Hz (Fig. 2D). Thus individual units are not reliable coders of whisking behavior on slow time scales.

Figure 2. Absence of a strong linear relation between spike trains and whisking behavior.

(A) Example of measured vibrissa position and concurrent single-unit spike train, together with the vibrissa position predicted from the spike train. The time-domain representation of the transfer function is shown in the lower right. Blue vertical lines are a visual guide to the correspondence between predicted and measured phase. Note the strong tracking of phase, the weak tracking of amplitude, and the loss of the value of the offset. (B) The representation of the transfer function in the time domain. (C) The same transfer function versus frequency. (D) The SNR(f) of the transfer function of the same unit. Horizontal line is cutoff for significance. (E) The SNR(f) for all units. Horizontal line is cutoff for significance.

Decomposition of rhythmic whisks

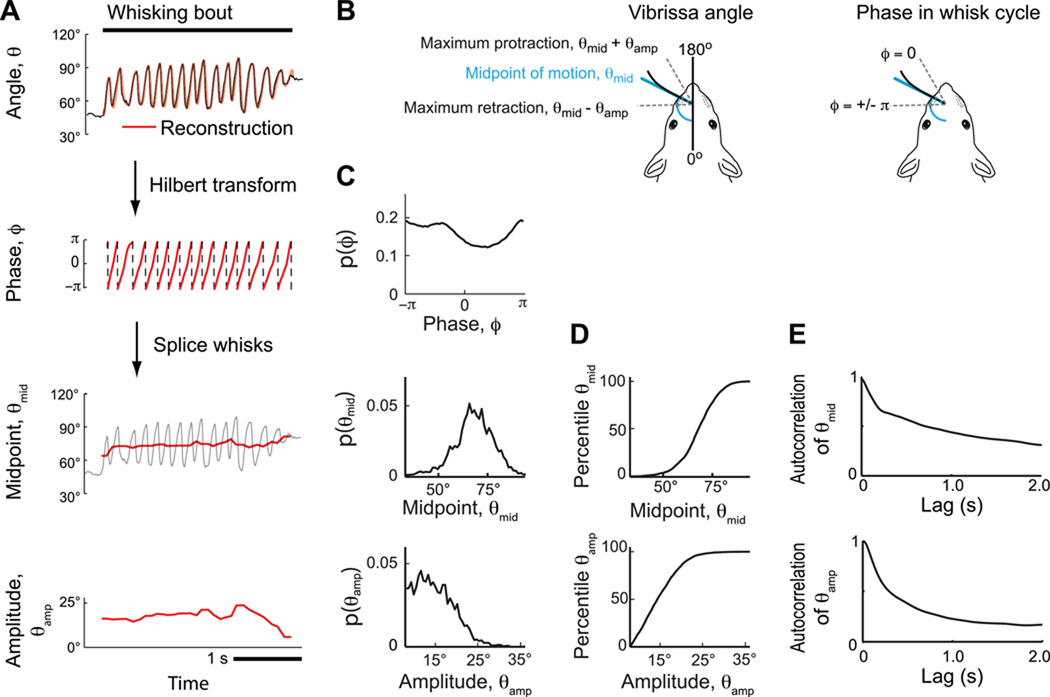
We conjecture that the coding of vibrissa motion involves both slow and fast control signals. To test this hypothesis, we first decompose the motion into slow and fast components. A Hilbert transform is used to extract a rapidly varying phase signal, ϕ(t), that increases from −π to π radians on each whisk cycle regardless of slow variations in amplitude and midpoint (Fig. 3A). Continuous estimates of the amplitude, θ_amp(t), and midpoint, θ_mid(t), were calculated on each whisk cycle at ϕ(t) = 0 and ϕ(t) = π and interpolated for other time points (Fig. 3B). As a consistency check on this parameterization, we reconstructed the position, θ̂(t), according to

$$\hat{\mathrm{\theta }}(\mathrm{t})={\mathrm{\theta }}_{\text{amp}}\text{cos}[\mathrm{\varphi }(\mathrm{t})]+{\mathrm{\theta }}_{\text{mid}}(\mathrm{t}).$$ (Eq. 1)

Figure 3. Decomposition of whisking into rapidly and slowly varying parameters.

(A) Top panel shows vibrissa position along with its reconstruction using a Hilbert transform. Lower panels show the phase, ϕ, as calculated from the Hilbert transform, along with the amplitude, θ_amp, and midpoint, θ_mid, of the envelope calculated from individual whisk cycles. Broken vertical lines indicate wrapping of phase from π to −π. (B) Schematic of the different angular parameters and their relation to phase in the whisk cycle for rhythmic motion. (C) Probability distribution functions for the phase, midpoint angle, and amplitude for all bouts in a session that included the data in panel A. (D) Mapping from angles to percentiles for the slow variables for the data in panel B. (E) Correlation coefficient of amplitude and midpoint as a function of time lag. Data is an average over rats (N = 5) and behavioral sessions (N ~ 12000 whisks).

The reconstruction of the vibrissa trajectory yields an absolute error of 2.7° between θ(t) and θ̂(t) as an average across time and behavioral sessions (Fig. 3A). The high quality of the fit shows that the motion may be well represented in terms of a slowly varying amplitude that modulates a rapidly changing phase.

This decomposition of the whisking motion allows us to construct the marginal probability density functions for the slow whisking parameters, denoted p(θ_amp), p(θ_mid), as well as for the fast parameter, p(ϕ). This is illustrated for all whisking bouts associated with the behavioral session from which the data in the example of Figure 3A was obtained (Fig. 3C), along with the associated cumulative distributions (Fig. 3D). The non-uniformity in phase is consistent with faster retraction than protraction in the whisk cycle (Gao et al., 2001). Note that the probability densities p(θ_amp) and p(θ_mid) can vary between behavioral sessions and depend largely on the row and arc of the monitored vibrissa (Curtis and Kleinfeld, 2009).

As a check on the stationarity of the slow variations across animals and trials, we computed the autocorrelations for both θ_amp and θ_mid across all animals and trials (Fig. 3E). Both correlations decay slowly. The midpoint is correlated for well beyond 2 s, while the amplitude decays with a time constant of approximately 1 s.

Relation of single-unit activity to whisking parameters

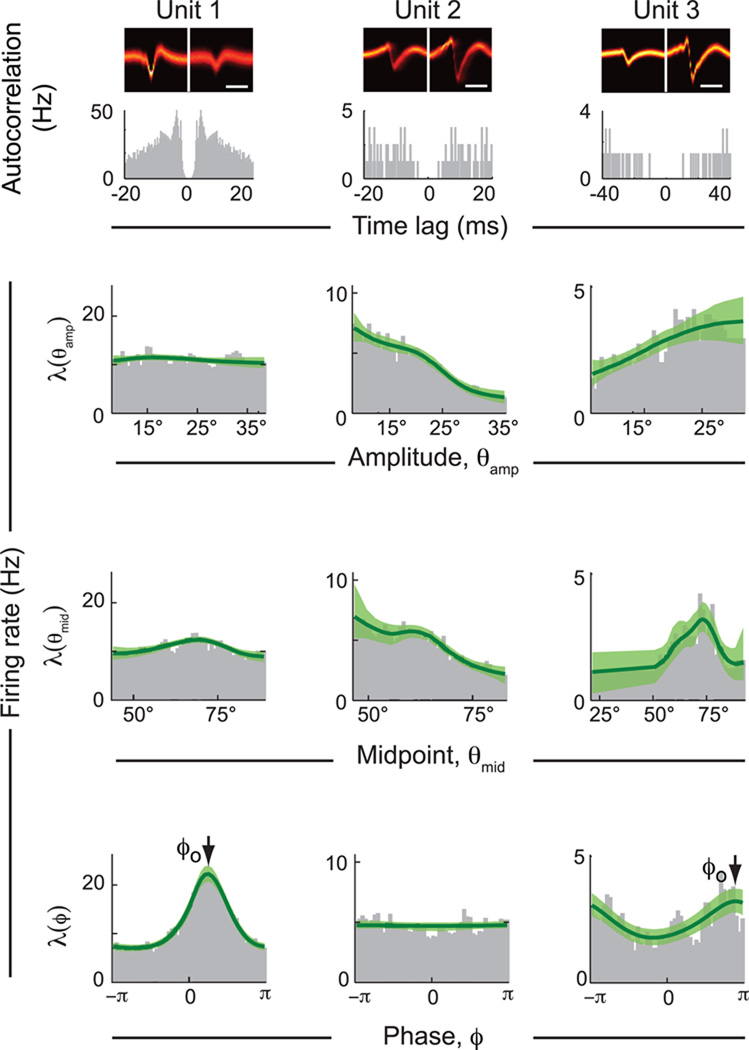
How well do the spike trains of single units report changes in the slow whisking parameters, θ_amp and θ_mid, as opposed to fast changes in phase, ϕ? As illustrated for three example units in Figure 4, we observe significant modulation of the spike rate for all three parameters. These firing rate tuning curves are denoted as λ(θ_amp), λ(θ_mid), and λ(ϕ) for modulation by changes in whisking amplitude, midpoint, and phase, respectively. Interestingly, strong modulation at one time scale is sometimes accompanied by weak modulation on the other (e.g., units 1 and 2 in Fig. 4).

Figure 4. Modulation profiles for three example units in vM1 cortex.

The three columns are profiles of units that show different relative modulation by fast and slow signals. The respective stereotrode waveforms and spike train autocorrelations are shown at top. Each plot is calculated by dividing the distribution of the respective signal at spike time by the distribution of that signal over the entire behavioral session. Green lines are fits from the BARS smoothing algorithm along with the 95% confidence band. The symbol ϕ_o labels the peak of the tuning curve, or the preferred phase for spiking within the whisk cycle.

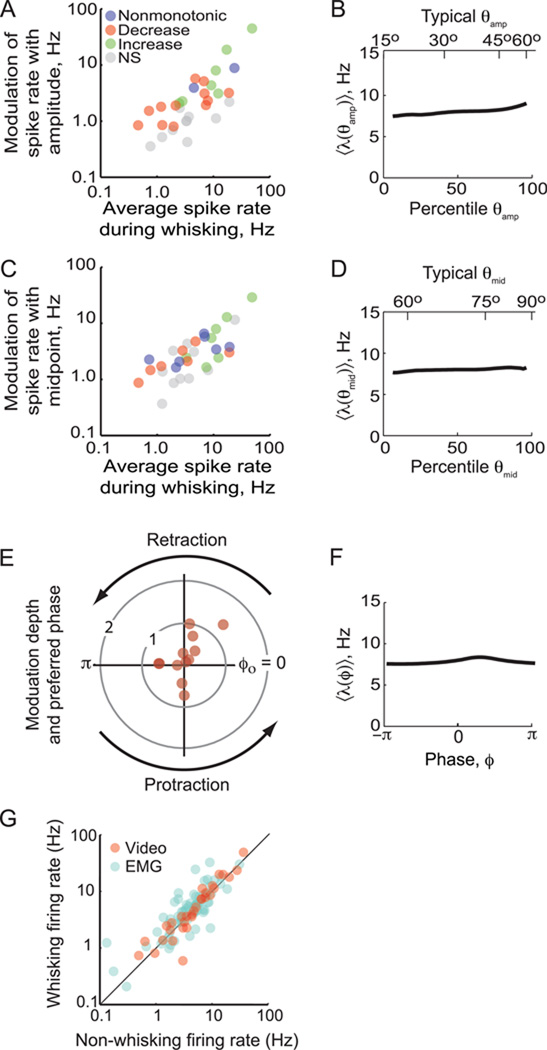
In general, the firing rates of most units in vM1 cortex are significantly modulated by at least one slow or fast parameter of whisking (Table 1). Approximately 65 % of all units were modulated by either amplitude or midpoint (Kolmogorov-Smirnov test, p < 0.05). The firing rates of significantly modulated units typically showed a monotonic dependence on amplitude or midpoint. A compilation of the change in rate, i.e., maximum minus minimum rate, is plotted against the average rate for all units (Fig. 5A,C). The firing rate could increase or decrease with either signal such that the average tuning curve across all units was nearly flat (Fig. 5B,D). The mean rate of neurons that encoded amplitude was significantly related to the slope of the rate versus amplitude curve, with an average mean firing rate of 15 Hz for cells that increased their firing rate with amplitude and 4.6 Hz for cells that decreased their firing rate with amplitude (Fig. 5A) (Kolmogorov-Smirnov test, p < 0.05). Nonetheless, the fidelity of reporting amplitude and midpoint cannot be increased by a simple summation of spikes across the population of neurons. Lastly, we found no obvious correlation between the modulation by amplitude and by midpoint in single units.

Table 1.

Modulation of firing rates

		Percentage of population significanty modulated
Condition	Number of units	Fast vatiable (phase) only	Slow variable (amplitude, midpoint, or EMG) only	Both fast and slow
vM1, Intact	95	6	51	16
vM1, nerve transected	74	7	61	9
vS1, Intact	71	34	15	13

Figure 5. Summary of the coding of fast and slow time scales by single units.

(A) Scatter plot of the modulation depth, defined as the maximum rate minus the minimum rate, for amplitude versus mean spike rate for each unit (N = 31). DIfferent colors distinguish increasing versus decreasing spike rate with an increase with angle, as noted. (B) The mean tuning curve for amplitude across the population. Data for slow variables were transformed into percentiles before averaging, as different vibrissae show distinct ranges of amplitude. The upper scale is the average angle for a given percentile (Fig. 3D). (C) Scatter plot of the modulation depth for midpoint versus mean spike rate for each unit (N = 31). (D) The mean tuning curve for midpoint across the population. The upper scale is the average angle for a given percentile (Fig. 3D). (E) Polar plot of the normalized modulation depth, defined as the maximum rate minus the minimum rate divided by the mean rate, as a function of the preferred phase for the unit, ϕ_o. Only points for significantly modulated units are plotted (N = 12). (F) The mean tuning curve as a function of phase across the population. (G) Firing rate of all units during whisking behavior recorded by videography (N = 32) or through the |∇EMG| (N = 69).

In contrast to the high yield of units modulated by slow parameters, only 22 % of all units showed a firing rate that was significantly modulated by phase in the whisk cycle (Kuiper test, p < 0.05). The tuning curve for λ(ϕ) is parameterized in terms of its peak at the preferred phase in the whisk cycle, denoted ϕ_o. The maximum firing rate tended to occur during retraction of the vibrissae (Fig. 5E,F), similar to reports of phase modulation of activity in vS1 cortex (Crochet and Petersen, 2006; Curtis and Kleinfeld, 2009; Fee et al., 1997). The relative modulation appears large in many cases because the baseline rate was quite small for many of these cells. Most of these phase-sensitive units were also modulated on the slow time scale (Table 1). Lastly, while fast spiking units make up about 20 % of recorded cells (Fig. S3), they are 50 % more likely to show significant modulation with phase or one of the slow variables.

We tested for the possibility that the coding properties of units in vM1 cortex were affected by head fixation. The above analysis was repeated using data from free-ranging animals, for which the |∇EMG| of the intrinsic muscles served as a surrogate of vibrissa position. We found that the modulation of the envelope of the |∇EMG| with the whisk amplitude was similar to that using videographic data with head-fixed animals (Fig.S3). Further, the reliability of the phase variable was unchanged using data from the |∇EMG| versus videographic data (Fig. S4).

Our past studies focused on coding of motion in vS1 cortex, in which past work emphasized the role of phase coding. To compare the representation of self-motion in sensory versus motor cortices, we reanalyzed data from vS1 cortex that involved epochs of whisking in air (Curtis and Kleinfeld, 2009) in free-ranging animals (71 single units from 7 rats). In contrast to our results for vM1 cortex, relatively few units in vS1 cortex coded only slow changes in the amplitude of the |∇EMG| compared with units coding only phase, i.e., 15 % versus 34 %, respectively. This reanalysis supports the essential role of vM1 cortex in representing the envelope of whisking (Fig. S5).

While we found that units could increase or decrease their relative rate of spiking as a function of increases in amplitude or midpoint (Figs. 4 and 5A,C), it is possible that the baseline rate of firing could be gated during whisking versus non-whisking epochs. To test for this, we compared the rates between whisking and non-whisking periods. We find that the spike rates in vM1 cortical units are unchanged on average (Fig. 5G). This finding is similar to that reported for units in vS1 cortex during periods of whisking compared with periods of quiet (Curtis and Kleinfeld, 2009) (Fig. S5). Thus whisking alters the timing of spikes relative to the whisking behavior but does not change the overall rate of spiking.

Population averaging for reliable decoding of the vibrissa trajectory

No individual single unit reports all aspects of the whisking trajectory in a reliable manner. We thus estimate the size of the population required to report the absolute angle of vibrissa position in real time. The accuracy of the vibrissa trajectory reconstructed from the spike trains of increasing numbers of neurons may be estimated from an ideal observer model. The observer serves as a hypothetical neuron, or network of neurons, that decodes the spiking output of neurons that encode vibrissa motion. For the cases of amplitude and midpoint, we assume that the information is encoded by Poisson spike count, where the mean firing rate of each cell is based on our measured tuning curves (Figs. 4 and 5). We assume an integration time of 0.25 s, a behaviorally relevant time period (Knutsen et al., 2006; Mehta et al., 2007; O'Connor et al., 2010a), over which the amplitude and midpoint are relatively constant (Fig. 3E). In the case of phase, we assume that the information may be decoded using a linear filter (Fig. 2) that defines the accuracy of a simulated neuron.

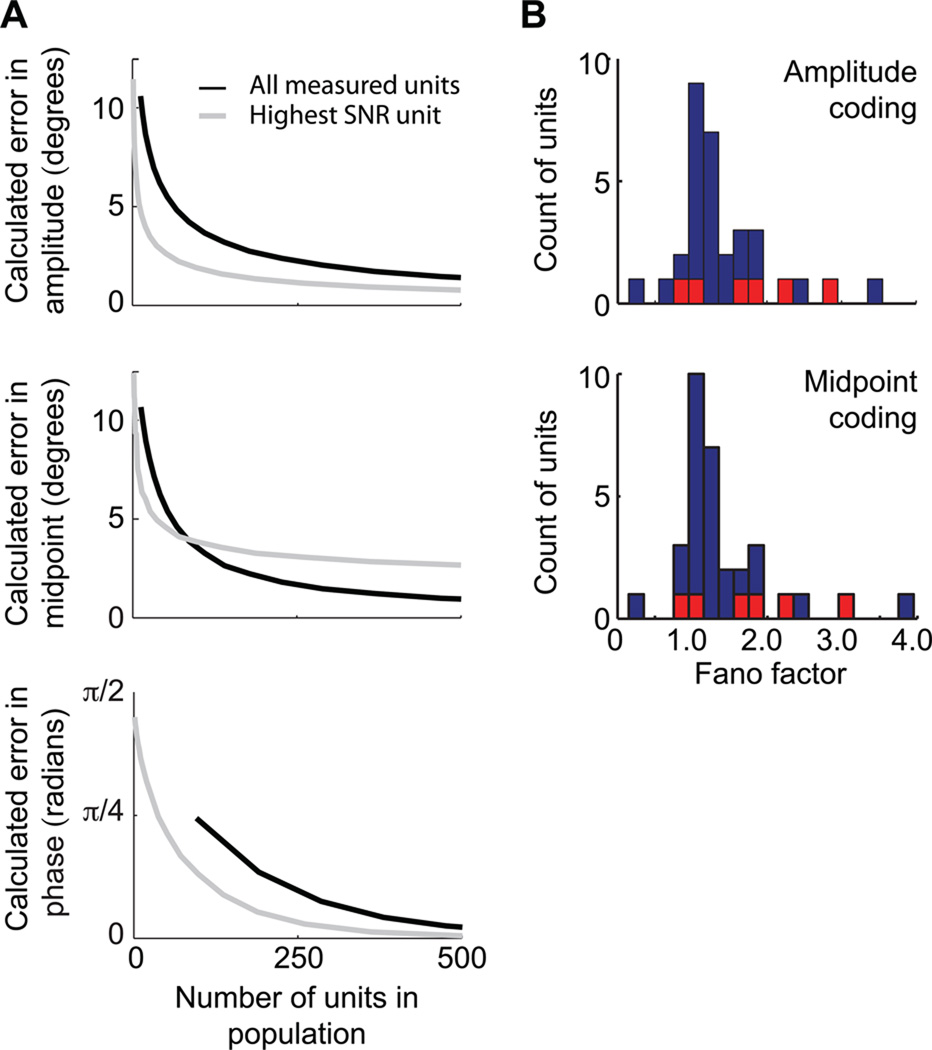
The results of our simulations indicate that the amplitude, midpoint, and phase of whisking can be accurately decoded from a modestly sized population of units (Fig. 6A). Either amplitude or midpoint can be decoded to within a mean error of δθ_amp ≈ 2° and δθ_mid ≈ 2° from simulated population activity of nearly 300 neurons, corresponding to relative errors of about 5 %. A simulated population based on the most highly modulated unit was not necessarily a better encoder than a population representing all recorded units (Fig. 6A). This occurs since a highly modulated unit may still poorly encode a signal over a particular range of values.

Figure 6. Estimated accuracy of coding as a function of population size.

(A) Simulations of neuronal populations were either based on the entire measured data set (black line) or only on the unit with the highest recorded modulation (gray line). Errors were drawn from 1000 simulations of each value and weighted by their prior distributions. Top row. Mean error for amplitude estimation assuming a firing rate code and an integration time of T = 0.25 s. Middle row. Mean error for midpoint estimation assuming a firing rate code and an integration time of T = 0.25 s. Bottom row. Mean error for phase estimation assuming a linear code. (B) Histograms of the Fano factors computed in a 0.25 s window for all units; F = 1.0 is the limit of a Poisson counting process. The colored points correspond to fast spiking units (Fig. S3).

For the case of phase decoding, we observed that a small fraction of units showed substantially greater phase modulation than other cells in the population. A decoder that utilizes six copies of the most phase-modulated cell could estimate phase to within a mean error of π/5 radians, or 5 % of the whisk cycle (Fig. 6A). These results suggest that coding of the rapidly changing phase in vM1 cortex may involve a small number of highly modulated units. In toto, a population on the order of a few hundred cells is required to accurately report the amplitude, midpoint, and phase of whisking on the time scale of 0.25 s.

How good is the assumption of a Poisson spike process? We estimate the Fano factor, which measures deviations in the variance from a Poisson process. The Fano factor is the ratio of the variance in the spike rate to the mean rate, i.e.,

$$\mathrm{F}\equiv \langle \frac{\langle {(\text{expected spike count}-\text{actual spike count})}^2\rangle }{\text{expected spike count}}\rangle$$ (Eq. 2)

where 〈⋯〉 denotes an average across all intervals and F = 1.0 for a Poisson process. We estimated these quantities over the assumed integration interval of 0.25 s. For each interval, either the mean amplitude or midpoint was used to determine the expected spike count for a particular unit. We found that the variance is linearly proportional to the mean, λ, but with an average value of F = 1.47 (Fig. 6B). The deviation from a Poisson process was not the result of too small of a sample (Eden and Kramer, 2010) and applied to both regular and fast-spiking units (cf red versus black bars in Fig. 6B; Fig. S3). To the extent that the read-out of vM1 cortex is based on a spike count, as opposed to the temporal signature of spiking, these results imply that a population average based on a Poisson spike model will underestimate the number of required neurons. This error is small, nominally a factor of F.

Origin of the representation of self-motion

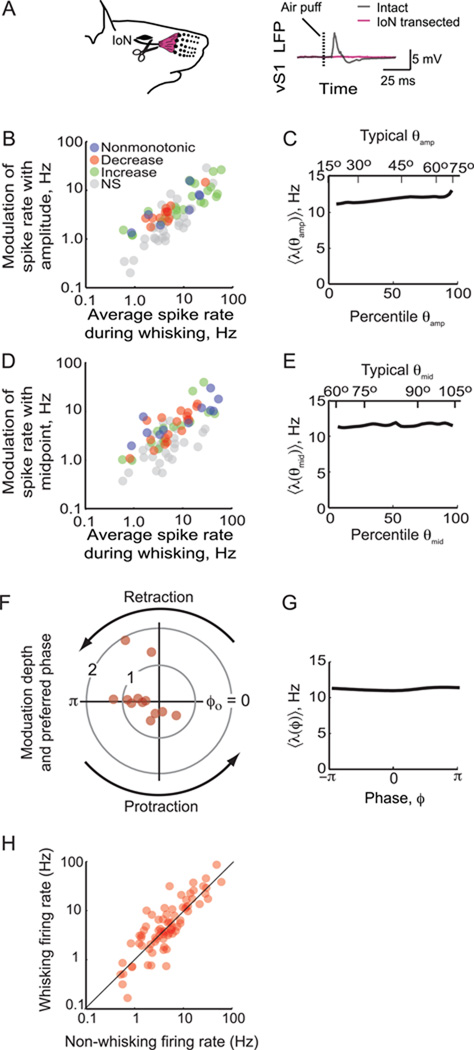
All aspects of vibrissa motion are represented in vM1 cortex of rats (Figs. 4 and 5), albeit in a weak and distributed manner. Do these signals arise from proprioception, motor commands, or efferent copy? To address this, we disrupted sensory feedback to vM1 cortex in a set of animals through bilateral transection of the infraorbital branch of the trigeminal nerve (IoN). This nerve branch is thought to be the only source of proprioceptive feedback from the vibrissae as the associated facial muscles do not contain muscle spindles (Arvidsson and Rice, 1991). Each transection was verified by a loss of the local field potential (LFP) response in vS1 cortex to air puffs against the face (Fig. 7A). In two animals, we confirmed that this response did not recover within the first two weeks after transection.

Figure 7. Summary of the coding of fast and slow time scales for units in vM1 cortex after transection of the IoN.

(A) Diagram of the IoN branch of the trigeminal nerve, along with the mean LFP response in vS1 cortex to 50 puffs to the vibrissa shown before and after bilateral nerve transection. (B) Scatter plot of the modulation depth of amplitude versus mean spike rate for all units after nerve transection (N = 78). (C) The mean tuning curve for amplitude across the population. Data for slow variables were transformed into percentiles before averaging, as different vibrissae show distinct ranges of amplitude. The upper scale is the average angle for a given percentile (Fig. 3D). (D) Scatter plot of the modulation depth of midpoint versus mean spike rate for all units after nerve transaction (N = 74). (E) The mean tuning curve for midpoint across the population. The upper scale is the average angle for a given percentile (Fig. 3D). (F) Polar plot of the normalized modulation depth as a function of the preferred phase for the unit, ϕ_o; only points for significantly modulated units are plotted (N = 12). (G) The mean tuning curve as a function of phase across the population. (H) Firing rate of all units during whisking behavior (N = 78).

The encoding of vibrissa motion was similar before and after nerve transection. Both fast and slow time scales were represented (cf Figs. S6 and 4), and the percentage of cells that encoded the slow versus fast times scales was not significantly different in transected versus normal animals (Table 1). A compilation of the modulation in spike rate is qualitatively similar for the animals with transected IoNs versus normal animals (cf Fig. 7B,D,F with Fig. 5A,C,E). As for normal animals, the firing rate could increase or decrease with either signal such that the average tuning curve across all units was nearly flat (cf Fig. 7C,E,G with Fig. 5B,D,F). Also, as in normal animals, the mean rate of neurons that encoded amplitude was significantly related to the slope of the rate versus amplitude curve, with a mean firing rate of 22 Hz for cells that increased their firing rate with amplitude and 7.0 Hz for cells that decreased their firing rate with amplitude (Fig. 7B). These data show that the signatures of vibrissa motion in vM1 cortex do not require sensory feedback through the trigeminal nerve. Lastly, the mean firing rate during whisking was greater in transected versus normal animals (cf Fig. 7H with Fig. 5G), and this was matched by a similar increase in the average slopes of the tuning curves λ(θ_amp) and λ(θ_mid). As a consequence of this balance the population analysis was essentially the same in the case of transection (Fig. S7).

DISCUSSION

We have addressed the issue of coding vibrissa position in head centered coordinates. Two time scales are involved, a slow, ~ 1 s scale associated with changes in the amplitude and midpoint of the envelope of whisking motion and a fast scale associated with rhythmic variation in position (Figs. 2 and 3). We find that a majority of single units in vM1 cortex code for variation in amplitude and midpoint, while a minority of units coded the phase of whisking (Fig. 4). None of these signals are abolished or modified by a total block of the trigeminal sensory input, implying that they are generated by a central source (Fig. 7).

The modulation of the firing rate of different units in vM1 cortex by the slowly evolving parameters of whisking is strong (Fig. 4). Yet the firing rates of these cells are low so that the contribution of individual units to decoding is low (Figs. 5 and 6). This situation is similar to the case of units that code the direction of arm movement in motor cortex in monkey (Schwartz et al., 1988). Nonetheless, our ideal observer analysis shows that populations of a few hundred such cells can report the amplitude and midpoint of the vibrissae with a less than 5 % error (Fig. 6).

We chose to extract the amplitude, midpoint, and phase of whisking with a modified Hilbert transform (Fig. 3A). This method is sensitive to changes in the phase, as opposed to the assumption of linear phase when fitting a sinusoid and offset to each whisk (Curtis and Kleinfeld, 2009; Gao et al., 2001; Leiser and Moxon, 2007). The decomposition of the whisking trajectory into these parameters appears to be behaviorally relevant (Fig. 3). Further, except for rare occurrences such as double pumps, i.e., a slight retraction during protraction followed by further protraction to complete the whisk cycle (Moxon, 2008; Towal and Hartmann, 2008; Welker, 1964) (* in Fig. 1C), the phase was a monotonic function of time in the vast majority of our data. However, it is important to note that ours is not the only possible decomposition of whisking behavior. Units are also highly modulated by other slowly varying parameters, such as frequency of the whisk cycles and the mean speed of vibrissa motion. Further, the control of midpoint and amplitude are coupled through the mechanics of the mystacial pad (Hill et al., 2008; Simony et al., 2010). Lastly, while the parameterization of vibrissa motion into fast and slow components may still be appropriate under conditions of arrhythmic whisking (Mehta et al., 2007; O'Connor et al., 2010a; Towal and Hartmann, 2006), the notion of phase breaks down under such motion.

Past studies have addressed signaling in vM1 cortex during self-generated whisking. Measurement of multiunit spike trains showed that groups of neurons increase their rate of spiking during periods of whisking versus non-whisking (Carvell et al., 1996) which is consistent with an increase in local field potential activity found at the onset of whisking bouts (Friedman et al., 2006). The present results show that, in fact, both increases and decreases in rate occur so that the average rate across the population is little changed (Fig. 5B,D,F). Measurements of the local field potential also yield a weak but significant correlation of the LFP with rhythmic motion of the vibrissae (Ahrens and Kleinfeld, 2004). This implies that the current flow from different units sums to a non-zero value. Here we found single units in vM1 cortex whose spiking is locked to the cycle-by-cycle change in vibrissa position (Figs. 4 and 5E). The spike rates for different units is peaks at different preferred phases, yet there is no significant bias across the population of units for the cases of both an intact and a bilaterally transected IoN (Figs. 5F and 7G).

Composite view of sensorimotor processing

How does the response of single units in vM1 cortex compare with those in vS1 cortex during rhythmic whisking? The motor area predominantly codes the slowly varying amplitude and midpoint of whisking (Fig. 5). In contrast, the majority of single units in vS1 cortex report a rapidly varying signal (Crochet and Petersen, 2006; Curtis and Kleinfeld, 2009; de Kock and Sakmann, 2009; Fee et al., 1997; Lundstrom et al., 2010; O'Connor et al., 2010b) that corresponds to the phase of the motion during rhythmic whisking (Curtis and Kleinfeld, 2009). As in the visual system (Fairhall et al., 2001), phase coding offers efficiency, in that all neurons sensitive to self-motion adapt to the envelope of whisking and thus code the position of the vibrissae in normalized coordinates. This is in contrast to a system based on tuning to absolute angle in which only neurons sensitive to the particular range of motion would be active. However, phase coding is ambiguous in that the absolute position is not coded by the firing rate. We conjecture that phase information in vS1 cortex is combined with envelope information in vM1 cortex to compute the absolute position of objects upon touch (Eq. 1). The locus of this interaction remains to be found.

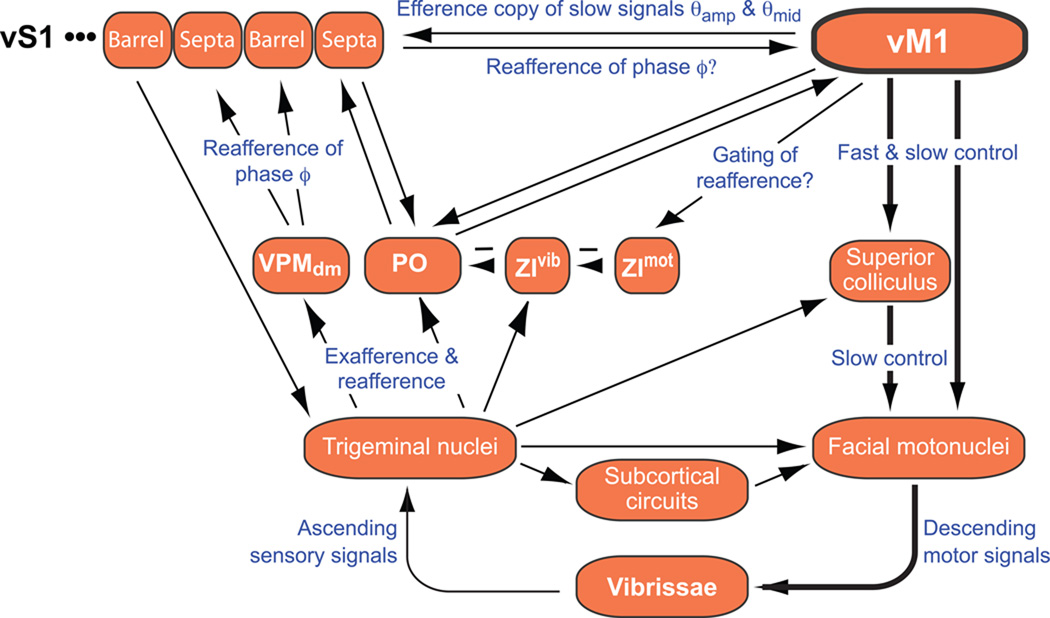
The slow components of the envelope of whisking are efferent in origin in both vM1 and vS1 cortices (Fee et al., 1997) (Fig. 7). In contrast, the phase signal appears to originate centrally in vM1 cortex but is derived from peripheral reafference in vS1 cortex (Fee et al., 1997), save for a subthreshold component that has a central origin (Ahrens and Kleinfeld, 2004). It is an open issue as to where any differences between the internally generated phase and the sensed phase are computed. Anatomically, this could occur in either vM1 or vS1 cortices, as well as in posteriomedial (PO) thalamus (Fig. 8). A defined role for vM1 cortex involves gating of the sensory stream along the pathway through PO thalamus, via the disinhibition of units in zona incerta (Urbain and Deschênes, 2007) (Fig. 8). Units that respond to the envelope of whisking are well suited to readily control the flow and transformation (Ahissar et al., 2000) of signals through PO thalamus.

Figure 8. Diagram of signal flow within loops that encompass vM1 cortex in the vibrissa sensorimotor system.

We shown only the subset of sensorimotor pathways that encompass the known flow of spike-based signaling in the rodent (Chakrabarti and Alloway, 2006; Kleinfeld et al., 2006; Urbain and Deschênes, 2007); the diagram is thus incomplete, especially with regard to basal ganglia (Hoffer et al., 2005) and cerebellar circuits (Lang et al., 2006; O'Connor et al., 2002). Minus signs mark inhibitory pathways. The brainstem nuclei include a hypothetical central pattern generator. Symbols: VPM, ventral posterior medial thalamus; PO, posterior medial thalamus, ZI_v^mot and ZL_v^vib, motor and vibrissa subdivision, of ventral zona incerta, respectively. Functional projections are labeled in blue.

Rhythmic motion appears to be a dominant mode of whisking (Berg and Kleinfeld, 2003a; Carvell and Simons, 1995), yet recent behavioral studies document how rodents use non-rhythmic motion to determine the relative position of a pin presented to one side of the face (Mehta et al., 2007; O'Connor et al., 2010a). While the angular position of the vibrissae changed rapidly, their maximum excursion evolved only slowly. The slowly varying amplitude and midpoint, θ_amp and θ_mid, are valid descriptions of vibrissa motion under conditions of rhythmic and non-rhythmic whisking. The phase, ϕ(t), is an inherently rhythmic quantity that also describes the relative range of vibrissa motion. In this sense phase describes both rhythmic and spatial aspects of whisking behavior. In the case of non-rhythmic whisking phase loses meaning in terms of dynamics, but the spatial component remains, i.e., rats tend to limit the spatial extent of whisking in a task dependent manner (Knutsen et al., 2006; Mehta et al., 2007). Additionally, phase can be considered as a rapidly varying non-rhythmic variable, which suggests why different sensory (Curtis and Kleinfeld, 2009; Fee et al., 1997) as well as motor neurons (Fig. 5E) have a multiplicity of preferred phases, when, for a purely rhythmic system, only a single phase is needed.

The present experiments indicate a central origin for the report of both slow and fast components of whisking by single units in vM1 cortex (Fig. 7), in contrast to the case for vS1 cortex (Fee et al., 1997). Yet our results do not distinguish if these signals originate within vM1 cortex per se or if they are generated in a downstream motor area that projects to vM1 cortex through an as yet unknown ascending pathway. A central origin for the generation of rhythmic whisking, as one of many potential rhythmic sources, is supported by evidence that ablation of vM1 cortex disrupts the regular pattern of whisking (Gao et al., 2003). Complementary studies show that rhythmic microstimulation of vM1 cortex in awake and aroused animals leads to the two-phase alternation of protraction with retraction seen during exploratory whisking (Berg and Kleinfeld, 2003b; Castro-Alamancos, 2006). Protraction occurs via efferent pathways from vM1 cortex to the facial motoneurons, while retraction may involve a corticocortical pathway through vS1 cortex (Matyas et al., 2010) that descends to the trigeminal nuclei and then projects to the motoneurons (Nguyen and Kleinfeld, 2005). Further, the possibility that neurons in vM1 cortex can directly drive rhythmic motion of the vibrissae (Cramer and Keller, 2006; Haiss and Schwarz, 2005), and not merely modulate the output of a hypothesized central pattern generator for whisking (Gao et al., 2001), is consistent with direct, albeit limited, projections from vM1 cortex to the facial motoneurons (Grinevich et al., 2005). Drive to the vibrissae can thus be created at multiple levels, from brainstem nuclei that include a hypothetical central pattern generator through cortex, and integrated by vibrissa motoneurons of the facial motor nucleus (Fig. 8).

What advantage is associated with coding motion in terms of a slowly varying envelope and a rapidly varying carrier, even a non-rhythmic one? One possibility is that vibrissa control is split into channels that support different computational roles. The midpoint of motion corresponds to the direction of greatest attention by the rat, not unlike foveation in vision. Biophysically, it represents a differential level of activation among populations of vibrissa motoneurons that control protraction versus retraction (Hill et al., 2008). The amplitude defines the range of the search and may gate the sensory stream along the pathway through PO thalamus, presumably via the disinhibition of units in zona incerta (Urbain and Deschênes, 2007) (Fig. 8), to control the flow and transformation (Ahissar et al., 2000) of signals through PO thalamus. Our analysis suggests that the slow and fast drive are separate channels in the brainstem (Fig. 8). This is consistent with recent studies of the differential control of the amplitude and phase of motoneurons in the facial motor nucleus (Pietr et al., 2010) and with the observation that direct stimulation of the superior colliculus leads to a sustained protraction of the vibrissa, while stimulation of M1 can lead to rhythmic motion (Hemelt and Keller, 2008). A further advantage of maintaining a rhythmic channel with independently controlled amplitude is that whisking can more effectively phase lock (Grannan et al., 1993) with other rhythmic orofacial behaviors. Such locking is known to exist in sniffing (Welker, 1964). In fact, coordination among orofacial nuclei is an essential aspect of breathing and feeding (Travers, 1995).

EXPERIMENTAL PROCEDURES

Subjects

We report data from 18 adult female Long-Evans rats (Charles River) with masses of 200 to 300 g. Thirteen of these rats were acclimated to head-restraint (Fig. 1A) and five were trained to whisk on a raised platform (Fig. 1B) (Fee et al., 1997; Ganguly and Kleinfeld, 2004; Hill et al., 2008). Successful training was followed by the chronic implantation of a microdrive (Curtis and Kleinfeld, 2009; Ventakachalam et al., 1999) above the area of frontal cortex stereotaxically identified as vM1 cortex (2.5 mm A–P and 1.5 mm M-L relative to bregma) (Kleinfeld et al., 2002). In select animals, the intrinsic papillary muscles of the mystacial pad, were implanted with pairs of microwires to measure the electromyogram (EMG) (Hill et al., 2008). In animals conditioned to head restraint, a restraining bolt was also implanted posterior to the microdrive.

In seven of the subjects trained for head restraint, the infraorbital branch of the trigeminal nerve (IoN) was bilaterally transected at its entrance to the orbit (Berg and Kleinfeld, 2003a). Complete transection of the nerve was verified by the extinction of the LFP in vS1 cortex in response to puffs of air against the vibrissae (Fig. 4A). After the surgical procedure, no recovery of sensation was observed as verified by the inability of the animal to cease whisking on contact with an object. All procedures were performed under isoflurane anesthesia.

The care and experimental manipulation of our animals were in strict accord with guidelines from the US National Institutes of Health and have been reviewed and approved by the Institutional Animal Care and Use Committee of the University of California, San Diego.

Data acquisition

Behavioral sessions consisted of trials of 10 to 30 s in duration. Whisking behavior was induced during these trials by presentation of the home cage just out of reach of the vibrissae (Ganguly and Kleinfeld, 2004; Premack and Shanab, 1968). To facilitate vibrissa tracking in head-restrained animals, the vibrissae were trimmed to the base except for three vibrissae in row C. A high-speed camera (Basler A602f) was used to monitor vibrissa position with a 300 Hz frame rate at 150 µm spatial resolution. Vibrissa position was obtained from each frame with one of two semi-automated algorithms written in MATLAB™ (Hill et al., 2008; Knutsen et al., 2005). The angle is formed between the anterior-posterior axis of the rat and a line drawn through the image of the vibrissa that extends from the skin to a point 5 mm further up the shaft. The time series of the angle was low-pass filtered at 25 Hz (4 pole Butterworth filter run in forward and reverse directions) and up-sampled to 1 kHz. We included only whisking events in which (i) the whisk was part of a 0.5 s or longer bout; (ii) the amplitude of each whisk exceeded 7.5°, thus ensuring that chattering and twitching were not included (Harvey et al., 2001), (iii) the frequency of whisk cycles was between 4 and 20 Hz; and (iv) in records based on EMG, the protractor and retractor muscles did not co-activate in phase, as occurs during twitching and chattering (Berg and Kleinfeld, 2003a).

Voltage signals from the cortical and EMG microwire electrodes were impedance buffered, amplified, band-pass filtered from 1 Hz to 10 kHz and sampled at 36 kHz (Ganguly and Kleinfeld, 2004). The cortical recordings were band-pass filtered between 600 Hz and 6 kHz (6 pole Butterworth filter run in forward and reverse directions) to isolate the spectral power of extracellular spike waveforms (Fee et al., 1996b). The voltage difference between the two EMG signals from each implanted muscle was calculated numerically, band-pass filtered between 400 Hz and 3 kHz (4 pole Butterworth filter run in forward and reverse directions), rectified, low-pass filtered at 250 Hz, and down-sampled to 1 kHz to form the differential rectified EMG signal (|∇EMG|).

Cortical recordings were analyzed with an offline non-Gaussian cluster analysis algorithm to obtain single unit spike trains (Fee et al., 1996a). Putative single units were accepted for analysis if the number of spikes that violated an imposed absolute refractory period of 2.5 ms was consistent with less than 10 % level of contamination by unresolved units with Poisson spike rates. Further, the waveforms of the putative single units were visually inspected for separation from background noise and other waveform clusters obtained in the same recordings. We estimated false negative and false positive errors (Hill et al., 2011) and found that 75 % of our putative single unit clusters had a false negative contamination of less than 10 %, while 90 % contained less than 20 % contamination. In addition, that 88 % of our putative single unit clusters had a false positive contamination of less than 10 %, while 95 % contained less than 20 % contamination. The relatively small false positive rate supports the claim that the same single units can code multiple stimulus dimensions (Figs. 4, 5 and 7). These particular quality metrics could not be applied to the reevaluation of the data set from vS1 cortex (Fig. S5).

Basic analysis

Correlation analysis based on singular value decomposition

The correlation between a set of signals may be defined through the singular value decomposition (Golub and Kahan, 1965), a standard matrix factorization procedure that has previously been applied to determine correlations within space-time data (Prechtl et al., 1997). For the case of whisking motion across multiple vibrissae, we define the matrix Θ(x,t), where x labels the individual vibrissa and t is discrete time. This matrix can be factored as

$$\mathrm{\Theta }(\mathrm{x},\mathrm{t})={\displaystyle \sum _{\mathrm{n}=1}^{\mathrm{N}}}{\lambda }_{\mathrm{n}}{\mathrm{X}}_{\mathrm{n}}^{\mathrm{T}}(\mathrm{x}){\mathrm{T}}_{\mathrm{n}}(\mathrm{t})$$ (Eq. 3)

where X_n(x) is the n-th spatial mode, a vector whose length equals the number of vibrissae in the data set, and T_n(t) is the n-th temporal mode, a vector whose length is the number of time points. The rank N is the smaller of the two lengths, typically the number of vibrissae in the image. Finally, the expansion coefficients λ_n determine the energy in each mode. When the individual waveforms that constitute the rows of Θ(x,t) are correlated, one or a few terms in the expansion may account for the majority of the variance across all waveforms. A measure of correlation across all waveforms is found by solving for the λ_n and computing the correlation coefficient

$$\mathrm{C}\equiv \frac{{\lambda }_1^2}{{\displaystyle \sum _{\mathrm{n}=1}^{\mathrm{N}}}{\lambda }_{\mathrm{n}}^2}.$$ (Eq. 4)

The expansion of the original data in terms of just a single mode is given by

$$\hat{\mathrm{\Theta }}(\mathrm{x},\mathrm{t})={\displaystyle \underset{\text{All time}}{\int }}\text{dt }{\mathrm{T}}_1(\mathrm{t})\mathrm{\Theta }(\mathrm{x},\mathrm{t}).$$ (Eq. 5)

Linear decoding by single units

The linear transfer function (Wiener, 1949) is used to predict vibrissa motion from the spike trains of single neurons (Fee et al., 1997). Let ${\tilde{\mathrm{S}}}_{\mathrm{k}}^{\mathrm{j}}(\mathrm{f})$ denote the Fourier transform of the k^th measured unit’s spike train on the j^th trial at frequency f and let ${\tilde{\mathrm{\theta }}}_{\mathrm{k}}^{\mathrm{j}}(\mathrm{f})$ denote the Fourier transform of the corresponding vibrissa position data. The transfer function, H̃_k (f), is

$${\tilde{\mathrm{H}}}_{\mathrm{k}}(\mathrm{f})=\frac{\langle {\tilde{\mathrm{S}}}_{\mathrm{k}}^{\mathrm{j}}(\mathrm{f}){\tilde{\mathrm{\theta }}}_{\mathrm{k}}^{\mathrm{j}}{(\mathrm{f})}^{*}\rangle }{\langle {\left|{\tilde{\mathrm{S}}}_{\mathrm{k}}^{\mathrm{j}}(\mathrm{f})\right|}^2\rangle }.$$ (Eq. 6)

where an asterisk indicates the complex conjugate and the angular brackets denote an average over trials and tapers. Multi-taper estimates of H̃_k(f) were calculated using the Chronux toolbox (http://www.chronux.org) (Percival and Walden, 1993).

The trials used to calculate the transfer function were 10 s epochs that included both whisking and non-whisking periods and comprised all behavioral data for that unit except for one trial. The transfer function was applied to the data from this excluded trial to calculate the predicted Fourier transform of the motion, θ̃_k (f), as

$${\tilde{\theta }}_{\mathrm{k}}^{\mathrm{i}}(\mathrm{f})={\tilde{\mathrm{H}}}_{\mathrm{k}}(\mathrm{f}){\tilde{\mathrm{S}}}_{\mathrm{k}}^{\mathrm{i}}(\mathrm{f})$$ (Eq. 7)

where i is the index of the trial that was left out. This function was then inverse Fourier transformed to form the predicted vibrissa trajectory, ${\hat{\mathrm{\theta }}}_{\mathrm{k}}^{\mathrm{i}}(\mathrm{t})$.

Fidelity of the relation between spiking and whisking

To quantify the covariation of the output of a single neuron with the motion of the vibrissae, we calculated the coherence between its spike train and the concurrent angular motion of the vibrissae. The coherence, denoted C(f), between vibrissa motion and the spike train is given by

$$C(\mathrm{f})=\frac{\langle {\tilde{\mathrm{S}}}_{\mathrm{k}}^{\mathrm{j}}(\mathrm{f}){\tilde{\theta }}_{\mathrm{k}}^{\mathrm{j}}{(\mathrm{f})}^{*}\rangle }{\sqrt{\langle {\left|{\tilde{\mathrm{S}}}_{\mathrm{k}}^{\mathrm{j}}(\mathrm{f})\right|}^2\rangle \langle {\left|{\tilde{\theta }}_{\mathrm{k}}^{\mathrm{j}}(\mathrm{f})\right|}^2\rangle }}.$$ (Eq. 8)

where multi-taper estimates of C(f) were calculated using the Chronux toolbox. The corresponding signal-to-noise ratio, SNR(f), is given by

$$\text{SNR}(\mathrm{f})=\frac{{|\mathrm{C}(\mathrm{f})|}^2}{1-{|\mathrm{C}(\mathrm{f})|}^2}.$$ (Eq. 9)

Decomposition of vibrissae motion

Vibrissa motion was parameterized into separate amplitude, θ_amp(t), midpoint, θ_mid(t), and phase, ϕ(t), signals through use of the Hilbert transform (Fig. 3A). Whisking epochs of at least 500 ms were isolated and the motion signal was band-pass filtered between 4 and 25 Hz (4 pole Butterworth filter run in forward and reverse directions). The Fourier transform was computed, the power at negative frequencies was set to zero, and a complex-valued time series was generated via the inverse Fourier transform (Black, 1953). The angle of this signal in polar coordinates was taken as the phase of the whisking cycle, where ϕ(t) = 0 corresponds to the end of protraction and ϕ(t) = ±π corresponds to the end of retraction. The time points of maximum retraction and protraction were used to calculate θ_amp(t), defined as the range of angular motion over a single cycle, and θ_mid(t), defined as the center angle that is swept out during a single whisk. Amplitude and midpoint were linearly interpolated for phase values between 0 and ±π.

In behavioral sessions where the |∇EMG| was measured from the papillary muscles, the Hilbert transform was applied to the |∇EMG| to calculate the phase of whisking. The estimate of phase from the |∇EMG| was found to have an advance of 1.0 ± 0.7 radians (mean ± SD) compared to the phase measured from videography; that corresponds to the delay between muscle activation and movement. Thus estimates of phase based solely on EMG data, used for comparisons for literature reports of vibrissa movement, were corrected with an imposed phase lag of 1.0 radians.

Normalization and significance of whisking parameters

The modulation of the firing rate of a unit as a function of θ_amp, θ_mid, and ϕ was determined from all whisking epochs over the entire behavioral session. The distribution of spike events for each whisking parameter was binned into percentiles that represented 2 % of the data, so that the total number of bins was M = 50, and a histogram was calculated of the number of spikes in each bin. This histogram was normalized by the total amount of time spent in each bin to yield values in terms of firing rate. These response histograms were smoothed and the 95 % confidence interval was calculated using the Poisson-distributed Bayesian adaptive regression splines algorithm (DiMatteo et al., 2001). The significance of firing rate modulation was determined by comparing the distribution of the parameter at all times to its distribution at spike times. In the case of phase, which is a circular random variable, we applied a 2-sample Kuiper test. For all other parameters, we used a 2-sample Kolmogorov-Smirnov test.

Neural encoding by populations of units

Slow variables

We focus first on the case of population coding of the amplitude, θ_amp, and the reliability of its estimation (Fig. S8). In our model, an ideal observer counts spikes for a fixed period T. The mean count for the k-th neuron is thus λ_k(θ_amp)T, where the modulation of the spike rate is found experimentally (Fig. 4A). We make the assumption, the first of three, that the probability of observing N_k spikes for a specific value of the amplitude, denoted θ_0;m, is a Poisson process, i.e.,

$$\mathrm{p}({\mathrm{N}}_{\mathrm{k}}|{\mathrm{\theta }}_{\text{amp};\mathrm{m}})=\frac{{\left[{\mathrm{\lambda }}_{\mathrm{k}}({\mathrm{\theta }}_{\text{amp};\mathrm{m}})\mathrm{T}\right]}^{{\mathrm{N}}_{\mathrm{k}}}{\mathrm{e}}^{-\left[{\mathrm{\lambda }}_{\mathrm{k}}({\mathrm{\theta }}_{\text{amp};\mathrm{m}})\mathrm{T}\right]}}{{\mathrm{N}}_{\mathrm{k}}!}.$$ (Eq. 10)

As we have largely recorded neurons in separate sessions, we treat them as independent encoders. Bayes’ rule then allows us to invert the relation between spike count and whisking parameter to estimate the probability of obtaining a specific value of the parameter as a function of the observed spike count. Thus

$$\mathrm{p}({\mathrm{\theta }}_{\text{amp};\mathrm{m}}|{\mathrm{N}}_{\mathrm{k}})=\frac{\mathrm{p}\left({\mathrm{N}}_{\mathrm{k}}|{\mathrm{\theta }}_{\text{amp};\mathrm{m}}\right)\mathrm{p}\left({\mathrm{\theta }}_{\text{amp};\mathrm{m}}\right)}{\mathrm{p}\left({\mathrm{N}}_{\mathrm{k}}\right)}$$ (Eq. 11)

where p(θ_amp;m) is the distribution of occurrences of each amplitude θ_amp;m (Fig. 3C) and

$$\mathrm{p}\left({\mathrm{N}}_{\mathrm{k}}\right)={\displaystyle \sum _{\mathrm{m}=1}^{\mathrm{M}}}\mathrm{p}\left({\mathrm{N}}_{\mathrm{k}}|{\mathrm{\theta }}_{\text{amp};\mathrm{m}}\right)\mathrm{p}\left({\mathrm{\theta }}_{\text{amp};\mathrm{m}}\right)$$ (Eq. 12)

where M is the number of bins. The joint probability for the estimate of the amplitude across a population of K units, given the assumption of independent neurons, is

$$\mathrm{p}({\mathrm{\theta }}_{\text{amp};\mathrm{m}}|{\mathrm{N}}_1,\dots ,{\mathrm{N}}_{\mathrm{K}})={\displaystyle \prod _{\mathrm{k}=1}^{\mathrm{K}}}\mathrm{p}({\mathrm{\theta }}_{\text{amp};\mathrm{m}}|{\mathrm{N}}_{\mathrm{k}})$$ (Eq. 13)

From this distribution, we finally assume that the value of the parameter is estimated using maximum a posteriori decoding (Dayan and Abbott, 2001):

$${\hat{\mathrm{\theta }}}_{\text{amp};\mathrm{m}}(\mathrm{K})=\underset{{\mathrm{\theta }}_{\text{amp};\mathrm{m}}}{\text{argmax}}\left\{\mathrm{p}({\mathrm{\theta }}_{\text{amp};\mathrm{m}}|{\mathrm{N}}_1={\mathrm{n}}_1,\dots ,{\mathrm{N}}_{\mathrm{K}}={\mathrm{n}}_{\mathrm{K}})\right\}.$$ (Eq. 14)

Given this decoding model for the amplitude (Eqs. 6 to 9), we now wish to evaluate its predictive accuracy. As we are interested in the effects of sampling from a limited number of neurons, we use a Monte Carlo resampling process to compare the results from the model to the original amplitude. We draw a random number of spikes for each of the K neurons based on Poisson statistics and a fixed value of θ_amp;m (Eq. 6); this defines a set of K spike counts, (n₁, …, n_K) that are used to estimate the joint probability (Eq. 9). We then use Equation 14 to estimate θ̂_amp;m (K). We repeat the process of draws and estimation 1000 times to form a distribution of errors δθ_amp;m (K), where

$$\mathrm{\delta }{\mathrm{\theta }}_{\text{amp};\mathrm{m}}(\mathrm{K})={\hat{\mathrm{\theta }}}_{\text{amp};\mathrm{m}}(\mathrm{K})-{\mathrm{\theta }}_{\text{amp};\mathrm{m}}.$$ (Eq. 15)

The mean of this distribution approaches zero and the root-mean-square width defines the accuracy with which the amplitude can be reconstructed. The entire procedure is repeated as a function of K for each value of θ_amp;m. Finally, we report the expected value of the accuracy as a weighted average over all amplitudes, denoted δθ_amp(K), where

$$\mathrm{\delta }{\mathrm{\theta }}_{\text{amp}}(\mathrm{K})={\displaystyle \sum _{\mathrm{m}=1}^{\mathrm{M}}}\mathrm{p}({\mathrm{\theta }}_{\text{amp};\mathrm{m}})\mathrm{\delta }{\mathrm{\theta }}_{\text{amp};\mathrm{m}}(\mathrm{K}).$$ (Eq. 16)

An analogous set of procedures holds for the accuracy of predicting the midpoint, denoted δθ_mid(K). All units were represented in each simulation unless otherwise specified. For simulations of populations that were larger than the number of experimentally recorded cells, every unit was duplicated into an equal number of copies so that each unit was equally represented.

A final issue concerns implementation. The range of amplitudes as well as the range of midpoints are not equal for different animals. Thus, for purposes of calculation, we normalized our responses in terms of percentiles of the range of motion (Fig. 3C) so that units from different animals could be averaged together. Thus we first transform from θ_amp (or θ_mid) to percentile, noting that the percentile steps are uniform so the transformed prior probabilities p(θ_amp) and p(θ_mid) have value 1/M = 0.02, then we complete the resampling procedure in terms of percentiles, and finally transform back to absolute angles to determine δθ_amp(K) and δθ_mid(K).

Prediction of the rapidly varying phase

Here we calculated the transfer function to characterize the ability of a single unit to predict only the phase of the whisk cycle (Eq. 1) (Fig. S9). We compared the corresponding measured phase, ϕ^j (t), to the phase predicted by the unit, ${\mathrm{\xi }}_{\mathrm{k}}^{\mathrm{j}}(\mathrm{t})$, to form the probability distribution of error p(ξ_k | ϕ). In all calculations, values of phase were discretized onto 20 equally spaced intervals between 0 and 2π.

In each simulation, a target value for the phase, ϕ = ϕ_m, was chosen and an estimate of the phase, ξ_k = ϕ_m., was drawn at random for each simulated unit from its probability distribution p(ξ_k | ϕ = Φ), where k = 1, …, K. These single unit estimates were pooled into a posterior distribution under the assumption of statistical independence,

$$\mathrm{p}(\mathrm{\varphi }|{\mathrm{\xi }}_1,\dots ,{\mathrm{\xi }}_{\mathrm{K}})={\displaystyle \prod _{\mathrm{k}=1}^{\mathrm{K}}}\mathrm{p}(\mathrm{\varphi }|{\mathrm{\xi }}_{\mathrm{k}})={\displaystyle \prod _{\mathrm{k}=1}^{\mathrm{K}}}\frac{\mathrm{p}({\xi }_{\mathrm{k}}|\mathrm{\varphi })\mathrm{p}(\mathrm{\varphi })}{{\displaystyle \sum _{\mathrm{\varphi }}}\mathrm{p}({\mathrm{\xi }}_{\mathrm{k}}|\mathrm{\varphi })\mathrm{p}(\mathrm{\varphi })}$$ (Eq. 17)

where we applied Bayes’ rule for the second step. At this point the calculation proceeds with steps analogous to those for the slow variables to determine the accuracy of predicting phase, denoted δϕ(K).

Abbreviations

BARS

Bayesian adaptive regression splines

C

Correlation

EMG

Electromyogram

|∇EMG|

Rectified differential electromyogram

INT

intrinsic facial muscles

IoN

Infraorbital branch of the trigeminal nerve

LFP

Local field potential

MAP

Maximum a posteriori

NL

m. nasolabialis

RMS

Root mean square

SD

Standard deviation

SE

Standard error (standard deviation of the mean)

SNR

Signal-to-noise ratio

vM1

Vibrissa area of primary motor cortex

vS1

Vibrissa area of primary sensory cortex