Inhibition in Multiclass Classification

Abstract

The role of inhibition is investigated in a multiclass support vector machine formalism inspired by the brain structure of insects. The so-called mushroom bodies have a set of output neurons, or classification functions, that compete with each other to encode a particular input. Strongly active output neurons depress or inhibit the remaining outputs without knowing which is correct or incorrect. Accordingly, we propose to use a classification function that embodies unselective inhibition and train it in the large margin classifier framework. Inhibition leads to more robust classifiers in the sense that they perform better on larger areas of appropriate hyperparameters when assessed with leave-one-out strategies. We also show that the classifier with inhibition is a tight bound to probabilistic exponential models and is Bayes consistent for 3-class problems. These properties make this approach useful for data sets with a limited number of labeled examples. For larger data sets, there is no significant comparative advantage to other multiclass SVM approaches.

1 Introduction

The question of what algorithms neural media use to solve challenging pattern recognition problems remains one of the most fascinating and elusive problems in the neurosciences, as well as in artificial intelligence. Perceptrons and artificial neural networks were originally inspired by neural computation, but thereafter, a new generation of powerful algorithms for pattern recognition returned to Fisher discriminant ideas and addressed the fundamental question of minimizing the generalization error by using statistical principles. Kernel-based methods, in particular support vector machines (SVMs), became prevalent due to the convenience and simplicity of their algorithms. These methods became standard, and the original inspiration from neural computation faded away. The heuristics of neural integration, neural networks, plasticity in the form of Hebbian learning, and the regulatory effect of inhibitory neurons were less needed, and the bioinspiration from neuroscience and AI fields grew increasingly distant from each other.

We seek to bridge this gap and identify the similarities and, in some cases, equivalence between neural information processing and large margin classifiers. We use the large margin classifier formalism and attempt to identify a correspondence to neural mechanisms for pattern recognition, putting emphasis on the role of inhibition (Huerta, Nowotny, Garcia-Sanchez, Abarbanel, & Rabinovich, 2004; Huerta & Nowotny, 2009; O’Reilly, 2001). We use insect olfaction as our biological model system for two main reasons: (1) the simplicity and consistency of the structural organization of the olfactory pathway in many species and its similarity to the structure of a SVM and (2) the large body of knowledge concerning the location of learning in insects during odor conditioning, which matches the location of plasticity in SVMs.

The mushroom bodies in the brains of insects contain many classifiers that compete with each other. The mechanism to organize this competition such that a single winner (class) emerges is inhibition (Cassenaer & Laurent, 2012; Huerta et al., 2004; Nowotny, Huerta, Abarbanel, & Rabinovich, 2005; Huerta et al., 2009; O’Reilly, 2001). Each individual classifier exerts downward pressure on the rest, with a strength that has to be regulated. The SVM formalism provides a framework in which to understand the consequences of inhibition in multiclass classification problems.

The solution of the value of the inhibition using the SVM formalism leads to a unique solution, it is robust to parameter variations, and it is a tight bound of probabilistic exponential models. We also show simple sequential algorithms to solve the problem using the sequential minimization algorithm (Platt, 1999a, 1999b; Keerthi, Shevade, Bhattacharyya, & Murthy, 2001) and a stochastic gradient descent (Chapelle, 2007; Kivinen, Smola, & Williamson, 2010). We provide efficient software for both algorithms written in C/C++ for others to experiment with (http://inls.ucsd.edu/~huerta/ISVM.tar.gz).

We present extensive experimental results using a collection of easy and difficult data sets, some with heavily unbalanced classes. The data sets are from the UCI repository except for the MNIST digits data set. Results show that the inhibitory SVM framework generalizes better than the leading alternative methods with a small number of training examples. The mechanism of inhibition provides robustness. The inhibitory models, for a large sample of meta parameters, outperform 1-versus-all SVMs and Weston-Watkins multiclass SVMs (Weston & Watkins, 1999). For large data sets when there is sufficient data to estimate the metaparameters by leave-one-out strategies, the ISVM does not provide a significant advantage. Moreover, in terms of Bayes consistency (Tewari & Bartlett, 2007), the inhibitory SVM is better than other methods with the exception of Lee, Lin, and Wahba (2004).

This letter starts by explaining the notation and the insect-inspired formalism of the inhibitory classifier, followed by a comparison to previous methods using the same notation. Then we solve the formulation to write efficient and simple algorithms. We conclude with experimental results.

2 Insect Brain Anatomy

The three areas of the insect brain involved in olfaction are the olfactory receptor cells or sensors, the antennal lobe (AL) or feature extraction device, and the mushroom body (MB) or classifier (see Figure 1). When a gas is present, olfactory receptor cells feed this information into the AL, which extracts the features that will be classified by the MB.

Figure 1.

Illustration of the correspondence between the insect brain and kernel classification. (Left) Anatomical picture of the honeybee brain (courtesy of Robert Brandt, Paul Szyszka, and Giovanni Galizia). The antennal lobe is circled in dashed yellow, and the MB is circled in red. The projection neurons (in green) send direct synapses to the Kenyon cells in the calyx. The Kenyon cells carry the connections w that are the equivalent to the SVM hyperplane. (Right) Equivalent circuit representation in SVM language.

The input, and hence the evoked feature pattern x in the AL, can be associated with either a reward +1 or with punishment −1 at the level of the output of the MB that we denote by y. Given N inputs, the problem consists of training the MB to correctly match y_i = f (x_i) for i = 1, …, N.

The MB function consists of two phases (Heisemberg, 2003; Laurent, 2002): (1) a projection into an explicit high-dimensional space Φ(x) named calyx and consisting of hundreds of thousands of Kenyon cell neurons (KC) and (2) a perceptron-like layer in the MB lobes (Huerta & Nowotny, 2009) where the classification function of each output neuron is implemented, f_k (x) = 〈w_kj, Φ(x)〉 = Σ_jw_kj Φ_j (x).¹ The inner product reflects the synaptic integration of KC outputs in MB lobe neurons. Huerta and Nowotny (2009) and Huerta et al. (2004) showed that simple Hebbian rules can solve discrimination and classification problems because they closely resemble the learning obtained by calculating the subgradient in an SVM framework. In particular, it can be shown that the change in the synaptic connections, Δw, is proportional to Φ_j (x). These rules are also equivalent to the perceptron algorithm, as Freund and Schapire (1999) showed.

In addition, the MB lobes contain hundreds of neurons that operate in parallel and compete via synaptic inhibition that they receive from each other, in addition to the input Φ(x) from the calyx. The output neurons can, in principle, code for different stimulus classes. They can be situated in different MB lobes specializing in different functions, and they are modulated by neuromodulators like dopamine, octopamine, and others that are the focus of intense research in neuroscience.

The concept of inhibition does not directly appear in the SVM literature, although a fairly large body of research on multiclass SVMs uses similar concepts. Our goal here is to directly integrate the concept of inhibition into the SVM formalism in order to provide a simple algorithm for multiclass classification.

3 The Inhibitory Classifier

Consider a training set of data points x_i for i = 1,…, N where N is the number of data points. Each point i belongs to a known class ŷ_i whose value is an integer in the range [1, L]. We first make a change of variables from the vector ŷ to the N × L matrix y (called a coding matrix by Diettrich & Bakiri, 1995) defined by

$$y_{ij}=\{\begin{array}{ll}1\hfill & \text{if}{\widehat{y}}_i=j\hfill \\ -1\hfill & \text{otherwise}\hfill \end{array},$$ (3.1)

that is, y_ij is 1 if the data point x_i belongs to the class j; otherwise the entry is −1.²

Next, we create a vector χⁱ as L concatenations of x_i, that is,

$${\mathbf{\chi }}^i=\underset{L\text{times}}{\underbrace{({\mathbf{x}}_i,{\mathbf{x}}_i,\dots ,{\mathbf{x}}_i)}}.$$ (3.2)

If x_i ∈ ℜ^M, then the number of components of χⁱ is L · M. More generally, given an arbitrary data point x ∈ ℜ^M, define 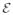(ℜ^M) ⊂ ℜ^LM to be the subspace of intrinsic dimension M built by vectors of the form χ = (x, x, …, x) (x repeated L times). We say sometimes that χ = (χ₁, …, χ_LM) is the embedding of x into 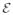(ℜ^M). The inverse relation is given by x = (χ_kL+1, χ_kL+2, …, χ_(k+1)L) for any k = 0, 1, …, M − 1.

When discussing SVMs, it is common to assume a nonlinear transformation Φ : ℜ^M → 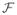from the original data space ℜ^M to a feature vector space 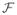in order to facilitate the separability of data points. Moreover, we assume that 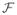is endowed with a dot product 〈·, ·〉 : 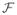× 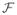→ ℜ. The inhibitory SVM proposed here uses a feature space that is the Cartesian product = 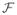×···× 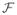(L times). Correspondingly, we extend Φ to a nonlinear transformation Ψ : 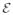(ℜ^M) → 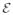( 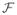), where 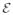( 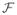) ⊂ is the subspace of dimension dim 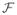built analogously as before, by repeated concatenation of the first dim 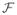components, and

$$\mathrm{\Psi }(\mathbf{\chi })=(\mathrm{\Phi }(\mathbf{x}),\mathrm{\Phi }(\mathbf{x}),\dots ,\mathrm{\Phi }(\mathbf{x})),$$ (3.3)

where χ is the embedding of x into 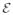(ℜ^M). Furthermore, let Ψ_j : 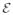(ℜ^M) → be the composition of Ψ with the projection operator onto the jth coordinate subspace of corresponding to the class j, that is,

$${\mathrm{\Psi }}_j(\mathbf{\chi })=(\mathbf{0},\dots ,\mathbf{0},\mathrm{\Phi }(\mathbf{x}),\mathbf{0},\dots ,\mathbf{0}).$$ (3.4)

To ease the notation, the indices i, i′ will refer henceforth to data points in ℜ^M, while the indices j, j′ will refer to the classification classes. Their ranges are thus i, i′ ∈ {1, …, N} and j, j′ ∈ {1, …, L}.

The new inhibitory classifier for a data point x_i and class j, f_j : 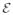(ℜ^M) → ℜ, has the form

$$f_j({\mathbf{\chi }}^i)=\langle \mathbf{w},{\mathrm{\Psi }}_j({\mathbf{\chi }}^i)\rangle -\mu \langle \mathbf{w},\mathrm{\Psi }({\mathbf{\chi }}^i)\rangle =\langle \mathbf{w},{\mathrm{\Psi }}_j({\mathbf{\chi }}^i)-\mu \mathrm{\Psi }({\mathbf{\chi }}^i)\rangle ,$$ (3.5)

where w ∈ , w ≠ 0, is a hyperplane. Here 〈·, ·〉 is the dot product in , defined as the sum of the dot products of corresponding projections onto each factor space 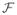. The scalar μ is the inhibitory factor and is the key novelty compared to other multiclass SVM methods because it is directly used in the evaluation of the classification function. As we will show, the value of the inhibitory factor μ can be derived directly from the minimization of the Lagrangian form and is data set independent. Note that

$$\begin{array}{l}\sum _j{f}_j({\mathbf{\chi }}^i)=\sum _j\langle \mathbf{w},{\mathrm{\Psi }}_j({\mathbf{\chi }}^i)\rangle -\mu L\langle \mathbf{w},\mathrm{\Psi }({\mathbf{\chi }}^i)\rangle \\ =\langle \mathbf{w},\mathrm{\Psi }({\mathbf{\chi }}^i)\rangle -\mu L\langle \mathbf{w},\mathrm{\Psi }({\mathbf{\chi }}^i)\rangle \\ =(1-\mu L)\langle \mathbf{w},\psi ({\mathbf{\chi }}^i)\rangle \end{array}$$ (3.6)

for all i = 1, …, N.

The transformations Ψ and Ψ_j inherit many properties from the transformation function of standard SVMs, Φ : ℜ^M → 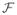. In particular (see equations 3.3 and 3.4),

$$\langle \mathrm{\Psi }({\mathbf{\chi }}^i),\mathrm{\Psi }({\mathbf{\chi }}^{i^{\prime }})\rangle =L·\langle \mathrm{\Phi }({\mathbf{x}}_i),\mathrm{\Phi }({\mathbf{x}}_{i^{\prime }})\rangle ,$$ (3.7)

$$\langle {\mathrm{\Psi }}_j({\mathbf{\chi }}^i),\mathrm{\Psi }({\mathbf{\chi }}^{i^{\prime }})\rangle =\langle \mathrm{\Phi }({\mathbf{x}}_i),\mathrm{\Phi }({\mathbf{x}}_{i^{\prime }})\rangle ,$$ (3.8)

$$\langle {\mathrm{\Psi }}_j({\mathbf{\chi }}^i),{\mathrm{\Psi }}_{j^{\prime }}({\mathbf{\chi }}^{i^{\prime }})\rangle =I(j=j^{\prime })\langle \mathrm{\Phi }({\mathbf{x}}_i),\mathrm{\Phi }({\mathbf{x}}_{i^{\prime }})\rangle ,$$ (3.9)

where the dot product 〈·, ·〉 on the left-hand side of equations 3.7 to 3.9 is taken in the product space , while the dot product on the right-hand side is taken in 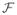, and the indicator function I(j = j′) is 1 if j = j′ and 0 otherwise. The dot product 〈Φ(x_i), Φ(x_i′)〉 can be computed effectively by a standard SVM kernel evaluation K_ii′ = K(x_i, x_i′) = 〈Φ(x_i), Φ(x_i′)〉. Thus, we can develop the inhibitory multiclass SVM formulation using the standard kernel trick.

The basic idea behind equation 3.5 is to train f_j classifiers that inhibit each other by a factor μ, which is data set independent. In the current form, we seek a single winner by virtue of the matrix y_ij. However, the approach can be used with data points assigned to multiple classes. All the subclassifiers f_j must adjust, using the inhibitory factor, to classify the whole training set as well as possible. The conditions to have all the training points properly classified are

$$y_{ij}{f}_j({\mathbf{\chi }}^i)\ge 1-{\eta }_{ij},$$

where η_{i j} = 0 are N · L slack variables.

Inhibition is not a new concept in machine learning. In particular, it has already been proposed in the context of energy-based learning via the so-called generalized margin loss (GML) function (LeCun, Chopra, Hadshell, Ranzato, & Jie, 2006). The word inhibition is not used explicitly in LeCun et al., but there are manifest similarities. The GML function represents the distance between the correct answer and the most offending incorrect answer. GML learning algorithms must change parameter values in order to make this distance be above a margin m. One can express the GML using our notation as

$$f_j^{\mathit{GML}}({\mathbf{\chi }}^i)=\langle \mathbf{w},{\mathrm{\Psi }}_j({\mathbf{\chi }}^i)\rangle -\underset{\forall j^{\prime }\ne j}{max}\left\{\langle \mathbf{w},{\mathrm{\Psi }}_{j^{\prime }}({\mathbf{\chi }}^i)\rangle \right\}.$$

The goal of training is to achieve $y_{ij}{f}_j^{\mathit{GML}}({\mathbf{\chi }}^i)\ge m-{\eta }_{ij}$ for all y_{i j} = 1, where m is an arbitrary margin value. The inhibitory formulation that we propose replaces the max operation by a summation and a multiplicative factor μ. Thus, we retain differentiability, which is advantageous for subsequent developments. A second difference is that the SVM formulation requires margin constraints to be satisfied for y_{i j} = −1. As we will see in the next few sections, these modifications allow us to create an effective, straightforward version of inhibition for SVMs.

Regular SVMs have been related to probabilistic exponential models (Canu & Smola, 2005; Pletscher, Soon Ong, & Buhmann, 2010). The inhibitory SVM can remarkably also be connected to log-linear models. Using our notation in a log-linear model, the probability of the label j given the data point χ and parameters w is

$$p(j\mid \chi ;\mathbf{w})=\frac{e^{\langle \mathbf{w},{\mathrm{\Psi }}_j(\mathbf{\chi })\rangle }}{{\sum }_k{e}^{(\mathbf{w},{\mathrm{\Psi }}_k(\mathbf{\chi }))}},$$

where the indices j and k run over the classes 1 to L. Taking the logarithm of the previous expression gives

$$logp(j\mid \chi ;\mathbf{w})=\langle \mathbf{w},{\mathrm{\Psi }}_j(\mathbf{\chi })\rangle -log\sum _k{e}^{\langle \mathbf{w},{\mathrm{\Psi }}_k(\mathbf{\chi })\rangle }.$$

Lemma 1

Given f = (f₁, …, f_L) ∈ ℜ^L, then

$$\begin{array}{l}a:\mathit{log}\sum _{k=1}^L\mathit{exp}{f}_k-\frac{1}{L}\sum _{k=1}^L{f}_k-\mathit{log}L\ge 0\\ b:\mathit{log}\sum _{k=1}^L\mathit{exp}{f}_k-\frac{1}{L}\sum _{k=1}^L{f}_k-\mathit{log}L=0\end{array}$$ (3.10)

for f₁, = ··· = f_L only

The proof can be found in appendix A. By applying lemma 1, one can write

$$logp(j\mid \chi ;\mathbf{w})\le \langle \mathbf{w},{\psi }_j(\mathbf{\chi })\rangle -\frac{1}{L}\langle \mathbf{w},\mathrm{\Psi }(\mathbf{\chi })\rangle -logL,$$ (3.11)

which is an equality if and only if f_j := 〈w, Ψ_j (χ)〉 = 〈w, Ψ_k(χ)〉=: f_k, for all 1 ≤ j, k ≤ L.

Note that most of the values of 〈w, Ψ_j(χ)〉 will be in the range [−1, 1] due to the large margin optimization of y_{i j} f_j (χⁱ) ≥ 1 − η_{i j}. That means that the equality is a close bound to p(j|χ; w) for most of the χⁱ. This approximation to log p(j|χ; w) is similar to equation 3.5, where μ is in this case 1/L, as shown below in the derivation. The universality of the inhibitory factor is prevalent. The idea of inhibition can thus be expressed by a normalization factor that depends on the outcome of all classifiers.

4 The Primal Problem

The primal objective function is the sum of the loss on each training example and a regularization term that reduces the complexity of the solution (Vapnik, 1995; Muller, Mika, Ratsch, Tsuda, & Schölkopf, 2001). The relative weight of the regularization term is controlled by a constant C > 0. The primal optimization problem can be expressed as

$$\begin{array}{ll}\text{minimize}\hfill & E(\mathbf{w},\mu )=\frac{1}{2}{\left|\right|\mathbf{w}\left|\right|}^2+C{\sum }_{ij}{\eta }_{ij}(\mathbf{w},\mu )\hfill \\ \text{subject}\text{to}\hfill & (\text{i}){\eta }_{ij}(\mathbf{w},\mu )\ge 0\hfill \\ \hfill & (\text{ii})y_{ij}{f}_j({\mathbf{\chi }}^i)-1+{\eta }_{ij}(\mathbf{w},\mu )\ge 0.\hfill \end{array}$$ (4.1)

Thus, we have L · dim 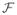+ 1 variables (w ∈ \{0} and μ ∈ ℜ) and 2NL constraints. This problem is not convex in general due to the dependence of η_{i j} on w and μ. Observe that f_j (χⁱ) also depends on w and μ (see equation 3.5). If dom η = ∩_{i j} dom η_{i j} denotes the common domain of the maps η_{i j,} then the domain of the problem, equation 4.1, is 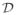= ( \{0} × ℜ)∩ dom η. Moreover, we assume that all η_{i j} are continuously differentiable. For practical purposes, the latter codition can be relaxed to hold except on a zero-measure set.

Consider the Lagrangian associated with equation 4.1:

$$\mathcal{L}(\mathbf{w},\mu ,\mathit{\alpha },\mathit{\beta })=\frac{1}{2}{\left|\right|\mathbf{w}\left|\right|}^2+C\sum _{ij}{\eta }_{ij}-\sum _{ij}{\beta }_i{\eta }_{ij}$$ (4.2)

$$-\sum _{ij}{\alpha }_{ij}(y_{ij}[\langle \mathbf{w},{\mathrm{\Psi }}_j({\mathbf{\chi }}^i)\rangle -\mu \langle \mathbf{w},\mathrm{\Psi }({\mathbf{\chi }}^i)\rangle ]-1+{\eta }_{ij}),$$ (4.3)

where α = (α_{i j}) ∈ ℜ^NL, β = (β_{i j}) ∈ ℜ^NL are the Lagrange multipliers. The Lagrange dual function (Boyd & Vandenberghe, 2004),

$$\mathcal{G}(\mathit{\alpha },\mathit{\beta })=\underset{(\mathbf{w},\mu )\in \mathcal{D}}{inf}\mathcal{L}(\mathbf{w},\mu ,\mathit{\alpha },\mathit{\beta }),$$ (4.4)

then yields a lower bound on the optimal value p^* of the primal problem, equation 4.1, for all α_{i j} ≥ 0 and β_{i j} ≥ 0.

Thus, 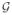(α, β) is determined by the critical points of (w, μ, α, β) for each value of α and β. Since is a C¹ function of all its variables, we take the partial derivatives of with respect to w and μ and equate to zero in order to get its critical points:

$$\mathbf{w}-\sum _{ij}({\beta }_{ij}-C+{\alpha }_{ij}){\partial }_{\mathbf{w}}{\eta }_{ij}-\sum _{ij}{\alpha }_{ij}{y}_{ij}\left[{\mathrm{\Psi }}_j({\mathbf{\chi }}^i)-\mu \mathrm{\Psi }({\mathbf{\chi }}^i)\right]=0$$ (4.5)

$$-\sum _{ij}({\beta }_{ij}-C+{\alpha }_{ij}){\partial }_{\mu }{\eta }_{ij}+\sum _{ij}{\alpha }_{ij}{y}_{ij}\langle \mathbf{w},\mathrm{\Psi }({\mathbf{\chi }}^i)\rangle =0.$$ (4.6)

According to the implicit function theorem, the solutions of equations 4.5 and 4.6 provide local functions w = w_crit (α, β) and μ = μ_crit (α, β), except possibly for a zero measure set (actually a manifold) comprising those α_{i j,} β_{i j} values that make the Jacobian determinant vanish:

$$detJ(\mathbf{w},\mu ,\mathit{\alpha },\mathit{\beta })=0.$$ (4.7)

Moreover, these functions are continuously differentiable on account of all functional dependencies in equations 4.5 and 4.6 being continuously differentiable. Note that the infimum in equation 4.4 is taken over points (w, μ) ∈ 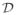, but (w_crit (α, β), μ_crit (α, β)) need not be in 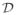for all values of α and β that parameterize the implicit solutions. This being the case, we have that

$$\mathcal{G}(\mathit{\alpha },\mathit{\beta })=\mathcal{L}({\mathbf{w}}_{\mathit{crit}}(\mathit{\alpha },\mathit{\beta }),{\mu }_{\mathit{crit}}(\mathit{\alpha },\mathit{\beta }),\mathit{\alpha },\mathit{\beta })$$ (4.8)

for all α, β such that det J(w, μ, α, β) ≠ 0 and (w_crit (α, β), μ_crit (α, β)) ∈ .

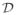For our purposes, it will suffice to study the critical points on the NL-dimensional plane α + β − C = 0 (intersection of the NL hyperplanes α_{i j} + β_{i j} = C), where C = (C_{i j}) ∈ ℜ^NL with C_{i j} = C > 0 for all i, j.

Lemma 2

From equations 4.5 and 4.6, it follows that

$${\mu }_{\mathit{crit}}(\mathit{\alpha },\mathit{C}-\mathit{\alpha })=\frac{1}{L}$$ (4.9)

and

$${\mathbf{w}}_{\mathit{crit}}(\mathit{\alpha },\mathit{C}-\mathit{\alpha })=\sum _{ij}{\alpha }_{ij}{y}_{ij}\left[{\psi }_j({\mathbf{\chi }}^i)-\frac{1}{L}\mathrm{\Psi }({\mathbf{\chi }}^i)\right]$$ (4.10)

for all α=(α_{i j}) ∈ ℜ^NL such that Σ_{i j} α_{i j} y_{i j} Ψ (χⁱ) ≠ 0.

The proof can be found in appendix B. Note that C in equation 4.9 is fixed but arbitrary. If follows that μ_crit (α, β) does not depend on either α or β; hence,

$${\mu }_{\mathit{crit}}(\mathit{\alpha },\mathit{\beta })=\frac{1}{L}.$$ (4.11)

Theorem 1

Let E(w^*, μ ^*) be the optimal value of the primal problem, equation 4.1. Then

$${\mu }^{\ast }=\frac{1}{L}.$$

The proof can be found in appendix C. The optimal solution $\mu =\frac{1}{L}$ renders the average output of all subclassifiers to be $\frac{1}{L}\langle \mathbf{w},\mathrm{\Psi }({\mathbf{\chi }}^i)\rangle =\frac{1}{L}{\sum }_j\langle \mathbf{w},{\mathrm{\Psi }}_j({\mathbf{\chi }}^i)\rangle$. The inhibitory factor turns out to be data set independent. Furthermore, from equation 3.6, it follows that Σ_j f_j (χⁱ) = 0.

The next step consists of putting all the constraints back into the classifier given by equation 3.5 to obtain

$$f_j(\mathbf{\chi })=\sum _{i^{\prime }=1}^N\sum _{j^{\prime }=1}^L{\alpha }_{i^{\prime }{j}^{\prime }}{y}_{i^{\prime }{j}^{\prime }}K({\mathbf{x}}_{i^{\prime }},\mathbf{x})(I(j=j^{\prime })-1/L)\equiv f_j(\mathbf{x}),$$ (4.12)

where χ = (x, x, …, x) ∈ 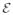(ℜ^M). To decide which class to choose for a given data point x, one uses the same decision function as in Weston and Watkins (1999) and Crammer and Singer (2001):

$$arg\underset{j}{max}{f}_j(\mathbf{x}).$$ (4.13)

It is important to note that during classification, all of the f_j (x) can be simplified because they are shifted by the same amount, that is,

$$f_j(\mathbf{\chi })=\sum _{i^{\prime }=1}^N\sum _{j^{\prime }=1}^L{\alpha }_{i^{\prime }{j}^{\prime }}{y}_{i^{\prime }{j}^{\prime }}K({\mathbf{x}}_{i^{\prime }},\mathbf{x})I(j=j^{\prime })-\frac{1}{L}\sum _{i^{\prime }=1}^N\sum _{j^{\prime }=1}^L{\alpha }_{i^{\prime }{j}^{\prime }}{y}_{i^{\prime }{j}^{\prime }}K({\mathbf{x}}_{i^{\prime }},\mathbf{x})={\stackrel{\sim }{f}}_j(\mathbf{x})+G(\mathbf{x}).$$ (4.14)

We can simplify the evaluation on the test set by just calculating

$${\stackrel{\sim }{f}}_j(\mathbf{x})=\sum _{i^{\prime }=1}^N{\alpha }_{i^{\prime }j}{y}_{i^{\prime }j}K({\mathbf{x}}_{i^{\prime }},\mathbf{x})$$ (4.15)

and selecting the class as

$$arg\underset{j}{max}{f}_j(\mathbf{x})=arg\underset{j}{max}{\stackrel{\sim }{f}}_j(\mathbf{x}).$$ (4.16)

5 Previous Integrated Multiclass Formulations

This section places the new inhibitory SVM in the context of previous work. As described in section 1, the most common approach to multiclass classification is to combine models trained for a set of separate binary problems. A few previous approaches have integrated all classes into a single formulation. Generally, for class j, the output of the integrated approaches uses the classification function

$$f_j(\mathbf{\chi })=\langle \mathbf{w},{\mathrm{\Psi }}_j(\mathbf{\chi })\rangle +b_j$$

where b_j is a bias term, with decision function 4.13. Weston and Watkins (1999) were the first to put multiclass SVM classification into a single formulation. Using our notation, they solved the problem

$$\underset{\mathbf{w},\eta }{min}E=\frac{1}{2}{\left|\right|\mathbf{w}\left|\right|}^2+C\sum _{ij\mathbf{s}.\mathbf{t}.y_{ij}\ne 1}{\eta }_{ij},$$ (5.1)

but with different constraints,

$$\langle \mathbf{w},{\mathrm{\Psi }}_j({\mathbf{\chi }}^i)-{\mathrm{\Psi }}_{j^{\prime }}({\mathbf{\chi }}^i)\rangle +(b_j-b_{j^{\prime }})\ge 2-{\eta }_{ij}$$

for all j such that y_{i j} = 1 and for all j′ such that y_{i j} = −1, where b_j, b_j′ are bias terms and η_{i j} ≥ 0. The constraints imply that the SVM scores of all data points belonging to a given class need to be greater than the margin (see appendix E for details).

The large number of constraints hinders solving the quadratic programming problem. Crammer and Singer (2001) proposed to reduce the number of slack variables by solving

$$\underset{\mathbf{w},\eta }{min}E=\frac{1}{2}{\left|\right|\mathbf{w}\left|\right|}^2+C\sum _i{\eta }_i$$ (5.2)

with constraints

$$\langle \mathbf{w},{\mathrm{\Psi }}_j({\mathbf{\chi }}^i)-{\mathrm{\Psi }}_{j^{\prime }}({\mathbf{\chi }}^i)\rangle +I(y_{ij}=y_{{ij}^{\prime }})\ge 1-{\eta }_i$$

for all j such that y_{i j} = 1, j′ ≠ j and for all data points i. The main differences with respect to Weston and Watkins (1999) are the reduced number of slack variables (see appendix F for details).

Tsochantaridis, Joachims, Hofmann, and Altun (2005) propose solving a similar problem as in equation 5.2 by rescaling the slack as

$$\langle \mathbf{w},{\mathrm{\Psi }}_j({\mathbf{\chi }}^i)-{\mathrm{\Psi }}_{j^{\prime }}({\mathbf{\chi }}^i)\rangle \ge 1-\frac{{\eta }_i}{\mathrm{\Delta }(y_{ij},y_{{ij}^{\prime }})}$$

for all j such that y_{i j} = 1. The function Δ(y_{i j,} y_{i j′}) allows the loss to be penalized in a flexible manner, with Δ(1, 1) = 0. A second version proposes rescaling the margin as

$$\langle \mathbf{w},{\mathrm{\Psi }}_j({\mathbf{\chi }}^i)-{\mathrm{\Psi }}_{j^{\prime }}({\mathbf{\chi }}^i)\rangle \ge \mathrm{\Delta }(y_{ij},y_{{ij}^{\prime }})-{\eta }_i.$$

Both approaches lead to similar accuracies on test sets, as shown in Tsochantaridis et al. (2005).

A remarkable approach is the formalism proposed by Lee et al. (2004) where the authors rewrite the constraints to match the Bayes decision rule (see section 10 for details) such that the most probable class of a particular example χ is the same as the one obtained by minimizing the primal problem. Lee and coauthors solve constraints as

$$-\langle \mathbf{w},{\mathrm{\Psi }}_j({\mathbf{\chi }}^i)\rangle \ge \frac{1}{L-1}-{\eta }_{ij}$$

such that j is chosen from the set {j ∈ {1, L}, s.t.y_{i j} ≠ 1} with the additional constraint 〈w, Ψ(χⁱ)〉 = 0. These constraints pose a cumbersome optimization problem but yield Bayes consistency (Tewari & Bartlett, 2007).

Table 1 presents a summary of the constraints used in each of the described methods. The main difference between our inhibitory multiclass method and the methods just described is in the way the classifier for class j is compared to the other classifiers. The inhibitory method essentially compares to the average of the outputs of all classifiers, while the previous methods perform pairwise comparisons. The second important difference of the inhibitory method is that inhibition is incorporated directly into the classification function itself.

Table 1.

Summary of the Constraints for Several Integrated SVM Multiclass Formulations.

Method	Constraints	Number of Constraints	Bayes Consistency
Weston and Watkins, 1999	〈w, Ψj(χi)− Ψj′(χi)〉+(bj−bj′)≥2− ηij	N· (L − 1)	L < 3
Crammer and Singer, 2001	〈w, Ψj(χi)−Ψj′(χi)〉+I(yij=yij′)≥1−ηi	N·L	L < 3
Tsochantaridis et al., 2005, slack rescaling	〈w, Ψj (χi)−Ψj′(χi)〉≥1−ηi/Δ(yij, yij′)	N·L	L < 3
Tsochantaridis et al., 2005, margin rescaling	〈w, Ψj(χi)−Ψj′(χi)〉≥Δ(yij, yij′)−ηi	N·L	L < 3
Lee et al., 2004	$-\langle \mathbf{w},{\mathrm{\Psi }}_j({\mathbf{\chi }}_i)\rangle \ge \frac{1}{L-1}-{\eta }_{ij}$ and 〈w, Ψj(χi)〉 = 0	N ·L	L ≥ 2
Inhibitory multiclass (ISVM)	yij 〈w, Ψj (χi)−μΨ(χi)〉≥1−ηij	N·L	L < 4

6 The Dual Problem of the Inhibitory Multiclass Problem

The dual problem is obtained by replacing all the constraints given by equations 4.9 and 4.10 with the solution μ = 1/L in the Lagrangian, equations 4.2 and 4.3, which yields the dual cost function, W. This cost function has to be maximized with respect to the Lagrange multipliers, α_{i j,} as follows:

$$\begin{array}{l}\underset{\alpha }{max}W=\sum _{ij}{\alpha }_{ij}-\frac{1}{2}\sum _{ij}\sum _{i^{\prime }{j}^{\prime }}{\alpha }_{ij}{y}_{ij}{\alpha }_{i^{\prime }{y}^{\prime }}{y}_{i^{\prime }{j}^{\prime }}{K}_{i^{\prime }i}\left[I(j=j^{\prime })-\frac{1}{L}\right]\\ \text{and}0\le {\alpha }_{ij}\le C.\end{array}$$

The double index notation in α_{i j} and elsewhere is inconvenient to compare with previous published work and with the primal formulation explained in the following sections. Thus, we change the notation from i, j to a new index k running from 1 to N · L. Thus, we order the α_{i j} ’s lexicographically: α_1,1, …, α_1,L, α_2,1, …, α_(N−1),L, α_N,1, …, α_N,L. With the new notation, we can write the dual problem as

$$\underset{\alpha }{max}W=\sum _k{\alpha }_k-\frac{1}{2}\sum _k\sum _{k^{\prime }}{\alpha }_k{y}_k{\alpha }_{k^{\prime }}{y}_{k^{\prime }}{G}_{{kk}^{\prime }}$$ (6.1)

$$\text{and}0\le {\alpha }_k\le C,$$ (6.2)

where k, k′ = 1, …, N · L and

$$G_{{kk}^{\prime }}=K_{\lfloor \frac{k-1}{L}\rfloor +1,\lfloor \frac{k^{\prime }-1}{L}\rfloor +1}\left[I([\mathit{k}modL]=[k^{\prime }modL])-\frac{1}{L}\right].$$ (6.3)

If one uses C-language type indexing with i = 0, …, N − 1, j = 0, …, N − 1, and k = 0, …, N L − 1, then the following kernel call is suggested:

$$G_{{kk}^{\prime }}=K_{\lfloor \frac{k}{L}\rfloor ,\lfloor \frac{k^{\prime }}{L}\rfloor }\left[I([\mathit{k}modL]=[k^{\prime }modL])-\frac{1}{L}\right].$$ (6.4)

The Karush-Kuhn-Tucker (KKT) conditions for this problem can be calculated by constructing the Lagrangian from the dual as in Keerthi et al. (2001):

$$\begin{array}{l}L=-\sum _k{\alpha }_k+\frac{1}{2}\sum _k\sum _{k^{\prime }}{\alpha }_k{y}_k{\alpha }_{k^{\prime }}{y}_{k^{\prime }}{G}_{{kk}^{\prime }}-\sum _k{u}_k{\alpha }_k-\sum _k{l}_k(C-{\alpha }_k)\\ 0\le {\alpha }_k\le C,\\ u_k,l_k\ge 0,\end{array}$$

which leads to

$$\begin{array}{r}{y}_i{E}_i-u_i+l_i=0,\\ u_i,l_i\ge 0,\\ {\alpha }_k{u}_k=0,\\ l_k(C-{\alpha }_k)=0,\end{array}$$

where E_i = f_i − y_i and f_i = Σ_k α_ky_kG_ki. We obtain the standard KKT conditions for the SVM training problem:

$$y_i{E}_i\ge 0\text{for}{\alpha }_i=0,$$ (6.5)

$$y_i{E}_i=0\text{for}0<{\alpha }_i<C,$$ (6.6)

$$y_i{E}_i\le 0\text{for}{\alpha }_i=C.$$ (6.7)

It is useful to define a new variable V_i = y_iE_i that indicates the proximity to the margin and saves computation time.

7 Stochastic Sequential Minimal Optimization

Prior to the first sequential minimal optimization (SMO) methods (Platt, 1999a, 1999b), the quadratic programming algorithms available at the time made SVMs unfeasible for large-scale problems. The straightforward implementation of SMO enabled a significant thrust of developments and improvements (Keerthi et al., 2001). The multiclass problem investigated in equations 6.1 and 6.2 has an advantage due to the absence of the constraint Σ_k α_ky_k = 0, which is typical in the dual SVM formulation. This constraint appears after solving the primal problem for the bias b of the classifier. It is avoidable in the multiclass problem due to the mutual competition among the classifiers by means of the inhibitory factor μ.

The idea of optimizing the quadratic function for a pair of multipliers is needed because one cannot modify the values of a single multiplier without violating the constraint Σ_k α_ky_k = 0 (Platt, 1999a, 1999b). In the inhibitory SVM, a single multiplier can be modified at a time. The analytical solution for a single multiplier i is derived from

$$W=\text{constant}+{\alpha }_i-\frac{1}{2}{G}_{ii}{\alpha }_i^2-{\alpha }_i{y}_i\left[f_i-{\alpha }_i^{\mathit{old}}{y}_i{G}_{ii}\right],$$

whose solution is obtained from $\frac{\partial W}{\partial {\alpha }_i}=0$ to yield

$$1-G_{ii}{\alpha }_i-y_i\left[f_i-{\alpha }_i^{\mathit{old}}{y}_i{G}_{ii}\right]=0.$$

This can be rewritten as

$${\alpha }_i=\left[{\alpha }_i^{\mathit{old}}+\frac{1}{G_{ii}}(1-y_i{E}_i)\right],$$ (7.1)

where ${\alpha }_i^{\mathit{old}}$ is the value of the multiplier in the previous iteration. Every time an α_i is updated, each error updates according to $E_j(t+1)=E_j(t)+({\alpha }_i-{\alpha }_i^{\mathit{old}})y_i{G}_{ij}$. In terms of the margin variable V_i, one can write

$$V_j(t+1)=V_j(t)+({\alpha }_i-{\alpha }_i^{\mathit{old}})y_i{y}_j{G}_{ij}\text{for}j=1,\dots ,NL.$$ (7.2)

The randomized SMO algorithm is given in algorithm 1. One can improve the performance of the algorithm by remembering the indices of the multipliers that violate the KKT conditions. Then, instead of choosing among all possible multipliers, one chooses among those that need to be changed. The KKT distance function in algorithm 1 is

Algorithm 1.

Stochastic SMO Algorithm.

t := 1

αi:= 0 and Vi := −1 for i = 1, …, N L

do {

Choose one index from k ∈ [1, …, N L].

${\alpha }^{\mathit{new}}={\alpha }_k-\frac{V_k}{G_{kk}}$,

αnew = max{0, αnew} and αnew = min{C, αnew}

Initialize the KKT distance: KKT := 0

loop over all i = 1, …, N L

Vi := Vi + (αnew − αk) yiykGik

KKT := KKT + KKT distance(Vi, αi)

end loop

αk = αnew

KKT := KKT/(N L)

t := t + 1

} while (KKT >θ)

Note: N is the number of data points, L is the number of classes, and θ is the termination threshold, which we generally set to the same value as the tolerance T (10⁻³).

$$\mathit{KKT}\mathit{distance}(V_i,{\alpha }_i)=\{\begin{array}{llll}\hfill -V_i& \text{if}{V}_i<-T\hfill & \text{and}\hfill & {\alpha }_i<\epsilon ,\hfill \\ \hfill V_i& \text{if}{V}_i>T\hfill & \text{and}\hfill & {\alpha }_i>C-\epsilon ,\hfill \\ \hfill \mid V_i\mid & \text{if}\mid V_i\mid >T\hfill & \text{and}\hfill & \epsilon <{\alpha }_i<C-\epsilon ,\hfill \\ \hfill 0& \text{rest}\text{of}\text{cases}.\hfill & \hfill & \hfill \end{array}$$

Above, T is the resolution of the proximity to the KKT condition, which we typically fix to 10⁻³ as originally proposed by Platt, and ε is the numerical resolution that depends on the machine precision that we typically set to 10⁻⁶. Generally, for all data sets tested, one can stop the algorithm early without impairing accuracy significantly.

8 Stochastic Gradient Descent in Hilbert Space

Synaptic changes do not occur in a deterministic manner (Harvey & Svoboda, 2007; Abbott & Regehr, 2004). Axons are believed to make additional connections to dendrites of other neurons in a stochastic manner, suggesting that the formation or removal of synapses to strengthen or weaken a connection between two neurons is best described as a stochastic process (Seung, 2003; Abbott & Regehr, 2004). On the other hand, in recent times, variants of stochastic gradient descent (SGD) have been used to solve the SVM problem in the primal formulation (Bottou & Bousquet, 2008; Zhang, 2004; Shalev-Shwartz, Singer, & Srebro, 2007). The algorithms obtained for the modification of the synaptic weights w resemble closely Hebbian learning or perceptron rules. We are primarily dealing with nonlinear kernels, so let us bridge the dual formulation with stochastic gradient descent using a Hilbert space.

Let us rewrite the primal formulation in equation 4.1 using a reproducing kernel Hilbert space (RKHS) as proposed in Chapelle (2007) and Kivinen et al. (2010). Let S be the training data set. For our specific problem, the RKHS = {f : S→ ℜ} has a kernel G : S × S → ℜ with a dot product 〈·, ·〉 such that 〈G(·, χ), f〉 = f (χ), with χ ∈ S and f ∈ . The primal formulation then can be expressed as

$$\begin{array}{l}\underset{f\in \mathcal{H}}{min}E=\underset{f\in \mathcal{H}}{min}\left[\frac{1}{2}{\left|\right|f\left|\right|}_{\mathcal{H}}^2+C\sum _{i=1}^{NL}max\{0,1-y_{i}f({\mathbf{\chi }}^i)\}\right]\\ =\underset{f\in \mathcal{H}}{min}\left[\frac{1}{2}{\langle f,f\rangle }_{\mathcal{H}}+C\sum _{i=1}^{NL}max\{0,1-y_i{\langle f,G({\mathbf{\chi }}^i,·)\rangle }_{\mathcal{H}}\}\right].\end{array}$$ (8.1)

The formal expression of f is a linear combination of the kernel functions such that $f(\mathbf{\chi })={\sum }_{i=1}^{NL}{\widehat{\alpha }}_{i}G({\mathbf{\chi }}^i,\mathbf{\chi })$. In appendix D we show how the updating rule is derived as

$${\widehat{\alpha }}_i(t+1)=(1-\eta ){\widehat{\alpha }}_i(t)+\eta {Cy}_i\overline{\mathbf{1}}(y_i{f}_t({\mathbf{\chi }}^i)-1),$$ (8.2)

with

$$\overline{\mathbf{1}}(u)=\{\begin{array}{ll}1\hfill & \text{if}u<0\hfill \\ 0\hfill & \text{if}u>0\hfill \\ [0,1]\hfill & \text{if}u=0\hfill \end{array},$$ (8.3)

and η is the learning rate. For the evaluation of f_t (χ) we use the kernel derived from the Lagrange multipliers function given by equation 6.3 because we know from the minimization of the Lagrangian that μ = 1/L. The corresponding i index of χ is the one that verifies χ= χⁱ in the training set. For stochastic updating, it is convenient to track the evolution of the margin proximity variable V_i = y_i f_t (χⁱ) − 1 every time a coefficient α̂_i is changed:

$$V_j(t+1)=V_j(t)+y_i({\widehat{\alpha }}_i(t+1)-{\widehat{\alpha }}_i(t))G({\mathbf{\chi }}^i,{\mathbf{\chi }}^j)\text{for}j=1,\dots ,NL,$$

which is very similar to equation 7.2 obtained in the dual form.

Many approaches using stochastic gradient descent use a scaling factor in the learning rate proportional to (1/iteration number) in order to guarantee convergence (Zhang, 2004; Shalev-Shwartz et al., 2007). We propose here a different approach that leads to an algorithm that is almost equivalent to the stochastic SMO method. As in that method, we make use of the KKT conditions, which requires computing the current state of training at each iteration. Note that the variable V_i provides guidance concerning distance to the margin.

If the algorithm chooses the index k, then the change α̂_k (t + 1) − α̂_k (t) = Δ_k is derived from

$$0=V_k(t)+y_k{\mathrm{\Delta }}_{k}G({\mathbf{\chi }}^k,{\mathbf{\chi }}^k),$$

so

$${\mathrm{\Delta }}_k=-\frac{V_k(t)}{y_{k}G({\mathbf{\chi }}^k,{\mathbf{\chi }}^k)},$$ (8.4)

assuming that G(χ^k, χ^k) ≠ 0. We combine equations 8.4 and 8.2 to obtain the learning rate η that would take the data point k exactly to the margin as

$$\eta (t)=\frac{V_k}{y_{k}G({\mathbf{\chi }}^k,{\mathbf{\chi }}^k)\left(\lambda {\widehat{\alpha }}_k(t)-y_k\overline{\mathbf{1}}(V_k)\right)}.$$

To avoid the computation inherent in the previous formula one can change Δ_k to

$${\mathrm{\Delta }}_k=-{\eta }_{\mathit{eff}}\frac{V_k(t)}{y_{k}G({\mathbf{\chi }}^k,{\mathbf{\chi }}^k)}.$$ (8.5)

When η_eff = 1, the update takes data point x to the margin.

When we use η_eff = 1, we recover the SMO solution given in equation 7.1. The corresponding SGD algorithm is presented in algorithm 2. Algorithms 1 and 2 are almost identical. C++ implementations of both algorithms can be found in the software package ISVM.

Algorithm 2.

Stochastic Gradient Descent (SGD) with Endogenous Learning Rate.

t := 1

αi:= 0 and Vi:= −1 for i = 1, …, N L

do {

Choose one index from k ∈ [1, …, N L].

${\alpha }^{\mathit{new}}={\widehat{\alpha }}_k-{\eta }_{\mathit{eff}}\frac{V_k(t)}{y_k{G}_{kk}}$

αnew = max{C, αnew} and αnew = min{−C, αnew}

Initialize the KKT distance: KKT := 0

loop over all i = 1, …, N L

Vi := Vi + yi(αnew − α̂k)Gik

KKT := KKT + KKT distance(Vi, yiα̂i)

end loop

KKT := KKT/(N L)

α̂k = αnew

t:= t + 1

} while (KKT > θ)

Note: N is the number of data points, L is the number of classes, η_eff is the learning rate, and θ is the stopping criterion. Note that this algorithm needs to compute the V_i values.

When making a prediction for a test example using $f_j(\mathbf{\chi })={\sum }_{i=1}^{NL}{\widehat{\alpha }}_i^{\ast }G({\mathbf{\chi }}^i,\mathbf{\chi })$, we replace G(χⁱ, χ) by K(x_i′, x)(I(j = j′) −1/L) ≡ f_j(x), which means that we need to make L evaluations for each data point from j = 1, …, L and select the one with the largest margin. This procedure is equivalent to equations 4.12 and 4.13.

The primal and the dual formalism lead to an almost identical algorithm for the inhibitory multiclass problem. A major appealing feature of the algorithms is the simplicity of their implementation.

9 Experimental Robustness

In this section we show experimentally that the inhibitory SVM (ISVM) method generally achieves better generalization than other multiclass SVM methods for small training set sizes. With large training sets, all methods converge to similar levels of accuracy, and it is not possible to obtain a clear distinction between methods. Rifkin and Klautau (2004) and Hsu and Lin (2002) showed that the performance of one-versus-all and one-versus-one approaches is good on many occasions with faster training times than the rest.

For this investigation, we use a gaussian kernel as exp (− γ||x − x′||²/M). Then we have a pair of metaparameters C > 0 and γ> 0 to investigate. The key issue, in terms of robustness, is to determine whether the inhibitory SVM leads to better average performance than 1-versus-all and Weston-Watkins multiclass approaches for any pair (C, γ). It is obviously not possible to cover the whole space of metaparameters, but one can sample it and get estimates. Our sampling methodology picks the best models at different percentile cuts—10%, 25%, and 50%—because one expects to explore parameter areas with a higher likelihood of achieving better performance. Thus, we ran an empirical leave-one-out verification strategy scanning the three hyperparameter values γ= 5, 10 and varying C from 0.1 to 100 at steps of 0.5. The lower bound C = 0.1 is set because for small data sets, the SVM evaluation functions hardly reach the margin, and the performance drops considerably for all the methods. Note also that since we discard all solutions below the 50% performance, we do not explore these solutions. We used the same stochastic SMO algorithms and the same C++ implementation for 1-versus-all, Weston-Watkins, and ISVM. Note that the only difference in the methods is the factors multiplying the kernel: K(x_i, x_i′)(I(j = j′) − 1/L) for ISVM, K(x_i, x_i′)I(j = j′) for SVM, and $K({\mathbf{x}}_i,{\mathbf{x}}_{i^{\prime }})({\sum }_{k=1}^L(I(j=j^{\prime })+\frac{y_{ik}+1}{2}\frac{y_{i^{\prime }k}+1}{2}))$ for Weston-Watkins.

In order to demonstrate the higher robustness of inhibition in a systematic manner we ran comparisons in 14 datasets for several different sizes of the training set N_s = 50, 100, 150, 200, 500 (see Table 2). Then we took an average of 100 random samples of each data set of size N_s. In Table 3, we report the results of pooling the leave-one-out performances for a grid of metaparameters using the gaussian kernel, exp(−γ ||x − x′||²/M)). The 10% best models were pooled and the average calculated. The same procedure is carried out for the 25% and 50% best to illustrate the drop of performance as we increased the area of the parameter set.

Table 2.

Summary of the Data Sets Used for Robustness Calculation.

Data Set	Number of Examples	Number of Classes	Base Performance
Abalone	4,177	6 (age/5)a	36%
DNA	3,186	3	52
E. coli	332	6b	43
Glass Identification	214	7	35
Iris	150	3	33.33
Image Segmentation	330	7	14
Landsat Satellite	6,435	6	23.8
Letter	20,000	26	4
MNIST	60,000	10	10
Shuttle	58,000	7	78
Vehicle	946	4	25.7
Vowel Recognition	528	11	9
Wine recognition	178	3	40
Yeast	1,462	10	30

Notes: We indicate the number of examples, the number of classes, and the worst possible performance by choosing as the default answer the most probable class in the data sets.

^aThis data set predicts age from 1 to 29. It is more of a regression problem. Thus, we predict age bands dividing age by 5.

^bimL and imS classes removed because they have two examples each.

Table 3.

Average Performance Comparison for ISVM, 1-Versus-All and Weston-Watkins Using 14 Data Sets and Running LOO on 100 Random Samples for Each Data Set.

Data Set	NS	Inhibitory SVM			1-Versus-All			Weston-Watkins
		10%	25%	50%	10%	25%	50%	10%	25%	50%
Abalone	50	61.43%	60.69%	60.09%	60.83%	59.69%	58.85%	60.07%	59.47%	59.10%
Abalone	100	66.55	65.91	65.16	65.47	64.13	63.12	64.18	64.12	64.06
Abalone	200	67.00	66.61	66.08	65.97	65.07	64.08	63.63	63.61	63.58
Abalone	500	67.77	67.48	67.09	67.63	66.87	65.79	64.24	64.23	64.22
DNA	50	49.59	49.25	49.14	49.28	49.13	49.08	49.77	49.18	47.99
DNA	100	54.08	54.04	54.02	54.04	54.04	54.01	52.78	52.29	52.02
DNA	200	56.24	56.19	56.16	56.20	56.18	56.13	53.33	53.18	52.66
DNA	500	60.90	60.87	60.82	60.92	60.90	60.84	53.57	53.57	53.56
E. coli	50	82.05	81.24	80.25	80.60	79.04	78.44	81.02	80.83	80.58
E. coli	100	84.06	83.60	82.78	83.23	81.56	80.55	82.97	82.90	82.78
E. coli	200	87.02	86.52	85.78	86.32	84.85	83.41	85.34	85.32	85.30
Glass	50	64.52	64.36	64.13	63.82	63.29	62.83	61.00	60.97	60.92
Glass	100	71.92	71.80	71.35	71.08	70.79	70.41	63.99	63.97	63.94
Glass	200	75.23	74.78	74.37	75.27	74.79	74.12	65.79	65.79	65.76
Iris	50	89.45	89.37	89.26	89.31	89.14	88.91	87.19	86.54	85.81
Iris	100	91.94	91.86	91.65	91.88	91.55	91.38	90.88	90.20	89.13
Iris	140	93.16	93.03	92.81	92.95	92.71	92.54	92.39	92.27	91.95
L. Sat	50	82.43	82.24	81.99	81.91	81.56	81.44	82.37	82.30	82.24
L. Sat	100	83.00	82.88	82.64	82.61	82.33	82.24	83.00	82.97	82.93
L. Sat	200	85.49	85.38	85.16	85.17	84.86	84.75	84.81	84.80	84.79
L. Sat	500	89.08	88.74	88.47	88.58	88.34	88.26	85.94	85.93	85.93
Letter	50	30.68	30.65	30.61	30.64	30.64	30.63	30.00	30.00	30.00
Letter	100	40.69	40.57	40.27	39.95	39.93	39.91	39.98	39.98	39.98
Letter	200	51.53	51.46	51.35	50.96	50.95	50.94	52.41	52.41	52.40
Letter	500	66.54	66.45	66.27	64.57	64.44	64.39	68.09	68.08	68.08
MNIST	50	53.76	53.76	53.38	53.80	53.80	53.72	51.88	51.86	51.85
MNIST	100	67.22	67.22	66.50	67.18	67.18	67.03	64.58	64.58	64.58
MNIST	200	77.53	77.53	76.76	77.51	77.51	77.34	75.40	75.40	75.40
MNIST	500	85.82	85.80	85.08	85.62	85.61	85.44	83.65	83.65	83.65
Segment	50	77.72	77.63	77.53	77.71	77.58	77.46	75.35	75.02	74.65
Segment	100	83.74	83.71	83.61	83.90	83.82	83.67	81.86	81.82	81.77
Segment	200	87.86	87.79	87.63	87.85	87.82	87.74	85.48	85.46	85.44
Shuttle	50	90.85	90.84	90.83	90.76	90.76	90.72	90.22	90.15	90.08
Shuttle	100	94.31	94.29	94.18	93.95	93.94	93.92	93.91	93.89	93.84
Shuttle	200	97.02	97.01	96.95	96.88	96.85	96.81	96.29	96.28	96.28
Shuttle	500	98.60	98.53	98.41	98.40	98.30	98.25	97.68	97.68	97.67
Vehicle	50	61.06	61.02	60.70	60.91	60.89	60.69	58.13	57.86	57.56
Vehicle	100	66.28	66.28	65.99	66.14	66.14	66.03	63.36	63.14	62.86
Vehicle	200	70.13	70.07	69.85	70.01	69.97	69.88	67.63	67.58	67.51
Vehicle	500	75.26	74.36	73.89	74.66	74.13	73.95	71.23	71.16	71.03
Vowel	50	46.61	46.61	46.48	46.60	46.60	46.57	46.76	46.76	46.76
Vowel	100	61.61	61.58	61.37	61.48	61.48	61.45	62.08	62.07	62.06
Vowel	200	77.73	77.65	77.54	77.78	77.77	77.74	77.76	77.75	77.75
Vowel	500	95.00	94.87	94.83	95.20	95.20	95.16	94.52	94.52	94.52
Wine	50	93.17	93.17	93.12	93.16	93.16	93.12	93.32	93.30	93.25
Wine	100	94.26	94.23	94.21	94.21	94.20	94.20	94.24	94.22	94.20
Wine	150	95.29	95.29	95.27	95.29	95.29	95.28	94.85	94.82	94.81
Yeast	50	48.36	47.60	46.98	47.21	46.39	46.09	47.99	47.71	47.44
Yeast	100	52.57	51.63	50.74	50.66	49.11	48.56	51.58	51.57	51.55
Yeast	200	55.00	54.28	53.16	53.01	50.55	49.60	53.06	53.05	53.02
Yeast	500	60.26	59.27	57.75	55.92	51.95	49.88	54.89	54.89	54.89

Notes: The kernel used is exp(− γ||x − x′||²/M)), such that the radial basis functions are normalized to the number of features. The performance shown is based on the leave-of-out calculation of N_s samples run over 100 different realizations. The performances of all explored metaparameters for C = 0.1 to 50 and γ = 5, 10 are pooled and sorted. The table shows the average performance of the 10%, 25%, and 50% best models. In most of the cases, the inhibitory SVM outperforms the rest, with Weston-Watkins being competitive for smaller sizes and 1-versus-all becoming competitive for N_s ≥ 200.

The main conclusion from this assessment is that the average performance for areas of parameter values that provide a near-optimal performance is higher for the ISVM than for the 1-versus-all and Weston-Watkins. In general, one can see that for small data sets, the performance of the ISVM is better, although it curves down for a higher number of examples. The Weston-Watkins method is competitive for small data sets but then loses performance for a higher number of samples. In general, the ISVM demonstrates better overall robustness and performance for small data sets. To summarize the results and add interpretation to the table, we tested the null hypotheses that either the SVM or WW method has average performance better than or equal to the ISVM method. We performed a maximum likelihood ratio test (Dempster, 1997; Rodriguez & Huerta, 2009) as it has, according to the Neyman-Pearson lemma, optimal power for a given significance niveau (Neyman & Pearson, 1933). For the 14-trial (data set) test, can be rejected at significance niveau 5% if the likelihood ratio L is larger than c = 3.77. Table 4 summarizes the results by showing that most of the time we can reject the hypothesis. If, on the other hand, one runs the test against the alternative hypothesis “ISVM is better than or equal to SVM or WW,” it cannot be rejected in any of the cases.

Table 4.

Likelihood Ratio Values Using the 14 Data Sets.

: SVM Better Than ISVM				: WW Better Than ISVM
NS	10%	25%	50%	10%	25%	50%
50	446**	446**	3.77*	11.35*	3.77*	1.78
100	446**	446**	3.77*	446**	11.35**	3.77*
200	52**	3.77*	1.78	52**	52**	52**
500	4.35*	4.35*	1.05	22.17**	22.17**	22.17**

Notes: c-values ≥ 3.77 reflect a significance niveau of Pr(L ≥ c| ) ≤ 0.05 (*) and c values ≥ 11.35 reflect a significance of Pr(L ≥ c| ) ≤ 0.01 (**). For the 9 data sets with size 500, the rejection thresholds are 4.35 and 22.17. Thus, the null hypothesis can be rejected in most cases. If the null hypothesis is reversed (ISVM better than SVM and ISVM better than WW), then we cannot reject it in any of the cases.

In terms of training time, the Weston-Watkins algorithm is the fastest of all the methods and runs eight times faster than the ISVM on the leave-one-out error task from C = 0.1 to 50 for all the data sets and two times faster than the 1-versus-all. The three methods were implemented using the same code and the same stochastic SMO, so the better performance and robustness come with a cost in training, although there is not significant time difference in execution.

10 Bayes Consistency

Our overall goal is to find a classification function f with a minimal probability of misclassification R(f) (Lugosi & Vayatis, 2004). In a multiclass setting (Tewari & Bartlett, 2007), given the posterior probabilities p_j ≡ p(o = y_j |x) with j labeling all L output classes and given the outputs $f_j^{\ast }(x)$ after training, $arg{max}_j{f}_j^{\ast }$ must match arg max_j p_j. In other words, the classifier function, f = {f₁, …, f_L} must select the most probable class (or the most probable classes if several classes have equal probability). This condition is called classification calibration, and theorem 2 in Tewari and Bartlett (2007) asserts that classification calibration is necessary and sufficient for convergence to the optimal Bayes risk. Tewari and Bartlett use

$$\underset{\mathbf{f}}{inf}R(f)=\underset{\mathbf{f}}{inf}\sum _j{p}_{j}h(f_j),$$ (10.1)

where h(f_j) is the cost function without the regularization term. The inhibitory SVM has

$$h(f_j)={[1-(f_j-\widehat{f})]}_{+}+\sum _{i\ne j}{[1+(f_i-\widehat{f})]}_{+}$$

where $\widehat{f}=\frac{1}{L}{\sum }_i{f}_i$ and f_j ∈ ℜ. The problem, equation 10.1 is thus equivalent to solving a linear problem with inf_z Σ_j p_j z_j, where z takes all the admissible values induced by f ∈ ℜ^L. The consistency condition is

$$arg\underset{i}{min}{z}_i=arg\underset{i}{max}{p}_i.$$

Tewari and Bartlett (2007) analyze the consistency of several multiclass classifiers, which requires characterizing the induced sets of z by f. Because the proofs can be cumbersome due to the topological complexity of the intersecting hyperplanes induced by f, Monte Carlo simulations are a viable alternative to quickly evaluate the consistency of a classifier. Algorithm 3 is a straightforward algorithm.

Algorithm 3.

Monte Carlo Algorithm to Check Bayes Consistency.

c := 1, N := 1, L := L*

do {

Choose p ∈ (ℜ+)L and normalize pi := pi/Σj pj

Find the infimum of Σi pih(fi)

if arg mini h(fi) = arg maxi pi then c := c + 1

N := N + 1

} while (N ≤ Nmax)

$\text{risk}=1-\frac{c}{N_{max}}$

Table 5 lists the consistency risks observed. An advantage of the ISVM is its consistency for 3-class problems and a lower probability of reaching inconsistencies for L > 3.

Table 5.

Monte Carlo Simulation of Consistency Using 100,000 Runs.

L	Regular SVM	ISVM	Weston-Watkins
2	0%	0%	0%
3	5	0	15
4	25	10	39
5	37	17	48

Notes: We found 0% consistency errors, not surprisingly, for binary problems. The ISVM is also consistent for L = 3, and then it becomes inconsistent. Note that the probability of having a harder problem increases with the number of classes.

11 Conclusion

In this letter, we have developed a new variation on the support vector machine theme using the concept of inhibition that is widespread in animal neural systems (Cassenaer, & Laurent, 2012). The main engineering advantage of inhibition is the ability to achieve better average accuracy for a broad metaparameter space with a small number of training examples, shown across multiple learning tasks. This success of the inhibitory SVM method is reminiscent of the low number of examples that insects need to learn odor recognition (Smith, Abramson, & Tobin, 1991; Smith, Wright, & Daly, 2005).

The underlying reason that ISVMs perform better in the cases reported here appears to be that the inhibition provides a wider area of the hyperparameters C and γ that are close to the optimum, making finding good hyperparameters easier. Consistency analysis shows that ISVM are still consistent for 3-class problems and show a smaller percentage of inconsistencies overall. The ISVM can be made consistent by eliminating the positive examples y_{i j} = 1 from the primal function, but this point is left for further analysis. Finally, it is important to emphasize that by using lemma 1, we show that log-linear models are almost equivalent to the inhibitory SVM framework, reflecting the universality of inhibition in different classification formalisms.

Appendix A: Proof of Lemma 1

1. Jensen’s inequality for convex functions applied to the exponential map reads (see section 3.1.8 of Boyd & Vandenberghe, 2004)

   $$\frac{1}{L}\left(\sum _{k=1}^{L}exp{f}_k\right)\ge exp\left(\frac{1}{L}\sum _{k=1}^L{f}_k\right)$$ (A.1)
   for all f₁, …, f_L ∈ ℜ. Use the increasing monotonicity of the logarithm function to derive

   $$log\frac{1}{L}+log\left(\sum _{k=1}^{L}exp{f}_k\right)\ge \frac{1}{L}\sum _{k=1}^L{f}_k,$$

   which is equation 3.10.

2. From the graphical interpretation of Jensen’s inequality, it is plain that the equality in equation A.1 holds if and only if f₁ = ···= f_L, that is, if all the components of f are equal.

Appendix B: Proof of Lemma 2

Since α_{i j} and β_{i j} are arbitrary in equations 4.5 and 4.6, set β_{i j} = C − α_{i j} to get the simplified expressions

$$\mathbf{w}-\sum _{ij}{\alpha }_{ij}{y}_{ij}\left[{\mathrm{\Psi }}_j({\mathbf{\chi }}^i)-\mu \mathrm{\Psi }({\mathbf{\chi }}^i)\right]=0,$$ (B.1)

$$\sum _{ij}{\alpha }_{ij}{y}_{ij}\langle \mathbf{w},\mathrm{\Psi }({\mathbf{\chi }}^i)\rangle =0.$$ (B.2)

Next solve for w in equation B.1 and replace in equation B.2 to obtain

$$\begin{array}{l}0=\sum _{ij}\sum _{i^{\prime }{j}^{\prime }}{\alpha }_{ij}{y}_{ij}{\alpha }_{i^{\prime }{j}^{\prime }}{y}_{i^{\prime }{j}^{\prime }}\langle {\mathrm{\Psi }}_{j^{\prime }}({\mathbf{\chi }}^{i^{\prime }})-\mu \mathrm{\Psi }({\mathbf{\chi }}^{i^{\prime }}),\mathrm{\Psi }({\mathbf{\chi }}^i)\rangle \\ =\sum _{ij}\sum _{i^{\prime }{j}^{\prime }}{\alpha }_{ij}{y}_{ij}{\alpha }_{i^{\prime }{j}^{\prime }}{y}_{i^{\prime }{j}^{\prime }}\left[\langle {\mathrm{\Psi }}_{j^{\prime }}({\mathbf{\chi }}^{i^{\prime }}),\mathrm{\Psi }({\mathbf{\chi }}^i)\rangle -\mu \langle \mathrm{\Psi }({\mathbf{\chi }}^{i^{\prime }}),\mathrm{\Psi }({\mathbf{\chi }}^i)\rangle \right]\\ =\sum _{ij}\sum _{i^{\prime }{j}^{\prime }}{\alpha }_{ij}{y}_{ij}{\alpha }_{i^{\prime }{j}^{\prime }}{y}_{i^{\prime }{j}^{\prime }}\left[\langle \mathrm{\Phi }({\mathbf{x}}_{i^{\prime }}),\mathrm{\Phi }({\mathbf{x}}_i)\rangle -\mu L\langle \mathrm{\Phi }({\mathbf{x}}_{i^{\prime }}),\mathrm{\Phi }({\mathbf{x}}_i)\rangle \right]\\ =(1-\mu L)\langle \sum _{i^{\prime }{j}^{\prime }}{\alpha }_{i^{\prime }{j}^{\prime }}{y}_{i^{\prime }{j}^{\prime }}\mathrm{\Phi }({\mathbf{x}}_{i^{\prime }}),\sum _{ij}{\alpha }_{ij}{y}_{ij}\mathrm{\Phi }({\mathbf{x}}_i)\rangle \\ =(1-\mu L){\Vert \sum _{ij}{\alpha }_{ij}{y}_{ij}\mathrm{\Phi }({\mathbf{x}}_i)\Vert }^2,\end{array}$$ (B.3)

where we employed equations 3.7 to 3.9. Hence $\mu =\frac{1}{L}$ if Σ_{i j} α_{i j} y_{i j} Φ(χⁱ) ≠ 0. Finally, note that the latter inequality holds true if and only if Σ_{i j} α_{i j} y_{i j} Ψ(χⁱ) ≠ 0 in virtue of equation 3.3.

Appendix C: Proof of Theorem 1

Let E(w^*, μ ^*) be the optimal value of the primal problem, equation 4.1.

1. In the generic case, det J(w^*, μ^*, α^*, β^*) ≠ 0. Then w^* = w_crit (α^*, β^*) and

   $${\mu }^{\ast }={\mu }_{\mathit{crit}}({\mathit{\alpha }}^{\ast },{\mathit{\beta }}^{\ast })=\frac{1}{L}$$

   because μ_crit (α, β) is the constant $\frac{1}{L}$, equation 4.11.

2. If, otherwise, det J(w^*, μ^*, α^*, β^*) = 0, then an argument based on the continuity of the Jacobian determinant with respect to all of its variables leads to the same conclusion. Indeed, let ${({\mathit{\alpha }}_n^{\ast })}_{n\ge 1}$ and ${({\mathit{\beta }}_n^{\ast })}_{n\ge 1}$ be sequences such that det $detJ({\mathbf{w}}^{\ast },{\mu }^{\ast },{\mathit{\alpha }}_n^{\ast },{\mathit{\beta }}^{\ast })\ne 0,{\mathit{\alpha }}_n^{\ast }\to {\mathit{\alpha }}^{\ast }$, and ${\mathit{\beta }}_n^{\ast }\to {\mathit{\beta }}^{\ast }$. (This is always possible because the solutions of det J(w, μ, α, β) = 0 build an (L dim F + 2NL)-dimensional manifold in an (L dim F + 2NL + 1) -dimensional domain.) Then ${\mathbf{w}}_{\mathit{crit}}({\mathit{\alpha }}_n^{\ast },{\mathit{\beta }}_n^{\ast })\to {\mathbf{w}}^{\ast }$ and ${\mu }_{\mathit{crit}}({\mathit{\alpha }}_n^{\ast },{\mathit{\beta }}_n^{\ast })\to {\mu }^{\ast }$. Since ${\mu }_{\mathit{crit}}({\mathit{\alpha }}_n^{\ast },{\mathit{\beta }}_n^{\ast })=\frac{1}{L}$ for all n ≥ 1, it follows that ${\mu }^{\ast }=\frac{1}{L}$.

Appendix D: Stochastic Gradient Descent on the RKHS

Let us calculate the minimum by taking the gradient of E in equation 8.1 with respect to f. To this end, note that the partial derivative of max{0, 1 − y_i f (χⁱ)} for y_i f (χⁱ) = 1 does not exist uniquely but is bounded between 0 and 1. If 1̄(·) is the function defined as

$$\overline{\mathbf{1}}(u)=\{\begin{array}{ll}1\hfill & \text{if}u<0\hfill \\ 0\hfill & \text{if}u>0,\hfill \\ [0,1]\hfill & \text{if}u=0,\hfill \end{array}$$ (D.1)

then

$${\partial }_{f}E=f-C\sum _{i=1}^{NL}{y}_i\overline{\mathbf{1}}(y_{i}f({\mathbf{\chi }}^i)-1)G({\mathbf{\chi }}^i,·).$$ (D.2)

We are looking for a solution of the form $f(\chi )={\sum }_{i=i}^{NL}{\widehat{\alpha }}_i^{\ast }G({\mathbf{\chi }}^i,\mathbf{\chi })$ such that ∂_f E = 0. Therefore, we insert f (χ) into equation D.2 to obtain

$$\begin{array}{l}0=\sum _{i=1}^{NL}{\widehat{\alpha }}_i^{\ast }G({\mathbf{\chi }}^i,\mathbf{\chi })-C\sum _{i=1}^{NL}{y}_i\overline{\mathbf{1}}(y_{i}f({\mathbf{\chi }}^i)-1)G({\mathbf{\chi }}^i,\mathbf{\chi }),\\ 0=\sum _{i=1}^{NL}\{{\widehat{\alpha }}_i^{\ast }-{Cy}_i\overline{\mathbf{1}}(y_{i}f({\mathbf{\chi }}^i)-1)\}G({\mathbf{\chi }}^i,\mathbf{\chi }),\end{array}$$

which leads to

$${\widehat{\alpha }}_i^{\ast }{y}_i=C\overline{\mathbf{1}}(y_{k}f({\mathbf{\chi }}^i)-1)$$

for 1 ≤ i ≤ NL. From the previous equation, we distinguish three types of solution:

$$\begin{array}{ll}{y}_i(f({\mathbf{\chi }}^i)-y_i)\ge 0\hfill & \text{for}{y}_i{\widehat{\alpha }}_i^{\ast }=0,\hfill \\ y_i(f({\mathbf{\chi }}^i)-y_i)=0\hfill & \text{for}0<y_i{\widehat{\alpha }}_i^{\ast }<C,\hfill \\ y_i(f({\mathbf{\chi }}^i)-y_i)\le 0\hfill & \text{for}{y}_i{\widehat{\alpha }}_i^{\ast }=C,\hfill \end{array}$$

which are identical to the KKT conditions obtained in the dual problem and shown in equations 6.5 to 6.7. The gradient rule for the whole system f_t+1 = f_t − η∂_f E is then

$$\begin{array}{l}{f}_{t+1}=(1-\eta \lambda )f_t+\eta C\sum _{i=1}^{NL}{y}_i\overline{\mathbf{1}}(y_i{f}_t({\mathbf{\chi }}^i)-1)G({\mathbf{\chi }}^i,·)\\ =\sum _{i=1}^{NL}\{(1-\eta \lambda ){\widehat{\alpha }}_i(t)+\eta {Cy}_i\overline{\mathbf{1}}(y_i{f}_t({\mathbf{\chi }}^i)-1)\}G({\mathbf{\chi }}^i,·),\end{array}$$

which leads to the updating rule,

$${\widehat{\alpha }}_i(t+1)=(1-\eta ){\widehat{\alpha }}_i(t)+\eta {Cy}_i\overline{\mathbf{1}}(y_i{f}_t({\mathbf{\chi }}^i)-1).$$ (D.3)

Appendix E: Weston-Watkins Method

The Weston-Watkins can be written using our notation as

$$\begin{array}{ll}\text{minimize}\hfill & E(\mathbf{w},{\eta }_{ij})=\frac{1}{2}{\left|\right|\mathbf{w}\left|\right|}^2+C\sum _{i,j\in j^{\ast }(\text{i})}{\eta }_{ij}\hfill \\ \text{subject}\text{to}\hfill & (i){\eta }_{ij}\ge 0,\hfill \\ \hfill & (\text{ii})\langle \mathbf{w},\left[\sum _{k=1}^L{\phi }_k({\mathbf{\chi }}^i)\frac{y_{ik}+1}{2}\right]-{\mathrm{\Phi }}_j({\mathbf{\chi }}^i)\rangle \ge 1-{\eta }_{ij},\hfill \\ \hfill & (\text{iii})j^{\ast }(i)=\{j=1,\dots Ls.t.y_{ij}=-1\}.\hfill \end{array}$$ (E.1)

Note that in Weston-Watkins, the margin value is 2 but we replaced it by 1 for consistency with other methods. After building the Lagrangian and taking all the necessary steps, one can express the solution as

$$\begin{array}{l}\mathbf{w}=\sum _{i,j\in j^{\ast }(i)}{\alpha }_{ij}\left(\left[\sum _{k=1}^L{\mathrm{\Phi }}_k({\mathbf{\chi }}^i)\frac{y_{ik}+1}{2}\right]-{\mathrm{\Phi }}_j({\mathbf{\chi }}^i)\right),\\ {\alpha }_{ij}\in [0,C].\end{array}$$ (E.2)

Using property 3.9, one obtains the dual problem for Weston-Watkins as

$$\begin{array}{ll}\text{maximize}\hfill & W=\sum _{i=1}^N\sum _{j\in j^{\ast }(i)}{\alpha }_{ij}-\frac{1}{2}\sum _{i,i^{\prime }=1}^N\sum _{j\in j^{\ast }(i),j^{\prime }\in j^{\ast }(i^{\prime })}{\alpha }_{ij}{\alpha }_{i^{\prime }{j}^{\prime }}{G}_{{\mathit{iji}}^{\prime }{j}^{\prime }}\hfill \\ \text{subject}\text{to}\hfill & {\alpha }_{ij}\in [0,C],\hfill \end{array}$$ (E.3)

where the kernel is expressed as

$$\begin{array}{l}{G}_{{\mathit{iji}}^{\prime }{j}^{\prime }}=K({\mathbf{x}}_i,{\mathbf{x}}_{i^{\prime }})\left(\sum _{k=1}^L\left(\frac{y_{ik}+1}{2}\frac{y_{i^{\prime }k}+1}{2}\right)-\frac{y_{{ij}^{\prime }}+1}{2}-\frac{y_{i^{\prime }j}+1}{2}+I(j=j^{\prime })\right)\\ =K({\mathbf{x}}_i,{\mathbf{x}}_{i^{\prime }})\left(\sum _{k=1}^L\left(\frac{y_{ik}+1}{2}\frac{y_{i^{\prime }k}+1}{2}\right)+I(j=j^{\prime })\right)\\ =G_{i^{\prime }{j}^{\prime }ij},\end{array}$$

with j ∈ j^*(i), j′ ∈ j′^* (i′), and the KKT conditions are

$$\begin{array}{ll}-1+\sum _{i^{\prime },{j^{\prime }}^{\ast }(i^{\prime })}{G}_{{\mathit{iji}}^{\prime }{j}^{\prime }}{\alpha }_{i^{\prime }{j}^{\prime }}\ge 0\hfill & \text{for}{\alpha }_{ij}=0,\hfill \\ -1+\sum _{i^{\prime },{j^{\prime }}^{\ast }(i^{\prime })}{G}_{{\mathit{iji}}^{\prime }j}{\alpha }_{i^{\prime }{j}^{\prime }}=0\hfill & \text{for}0<{\alpha }_{ij}<C,\hfill \\ -1+\sum _{i^{\prime },{j^{\prime }}^{\ast }(i^{\prime })}{G}_{{\mathit{iji}}^{\prime }{j}^{\prime }}{\alpha }_{i^{\prime }{j}^{\prime }}\le 0\hfill & \text{for}{\alpha }_{ij}=C.\hfill \end{array}$$

On defining the margin variables as: V_{i j} = −1 + ·_{i′, j′* (i′}) G_{i ji′ j′} α_{i′ j′}, we can directly apply the stochastic SMO algorithm described in the main text.

Appendix F: Crammer-Singer Method

The Crammer-Singer multiclass problem can be written as

$$\begin{array}{ll}\text{minimize}\hfill & E(\mathbf{w},{\eta }_i)=\frac{1}{2}{\left|\right|\mathbf{w}\left|\right|}^2+C\sum _i{\eta }_i\hfill \\ \text{subject}\text{to}\hfill & (\text{i}){\eta }_i\ge 0,\hfill \\ \hfill & (\text{ii})\langle \mathbf{w},\left[\sum _{k=1}^L{\mathrm{\Phi }}_k({\mathbf{\chi }}^i)\frac{y_{ik}+1}{2}\right]-{\mathrm{\Phi }}_j({\mathbf{\chi }}^i)\rangle +\frac{y_{ij}+1}{2}\ge 1-{\eta }_i.\hfill \end{array}$$ (F.1)

Note the similarity with the Weston-Watkins method except for the number of constraints and slack variables. Since the constraints in (ii) are always verified for y_{i j} = 1, we can loop the j index for the set j^*(i) as defined in equation E.1. The problem can be expressed as the Lagrangian,

$$\begin{array}{l}L=\frac{1}{2}{\left|\right|\mathbf{w}\left|\right|}^2+C\sum _{i=1}^N{\eta }_i-\sum _{i=1}^N{\kappa }_i{\eta }_i-\sum _{i=1}^N\sum _{j\in j^{\ast }(i)}{\alpha }_{ij}\left(\langle \mathbf{w},\left[\sum _{k=1}^L{\mathrm{\Phi }}_k({\mathbf{\chi }}^i)\frac{y_{ik}+1}{2}\right]-{\mathrm{\Phi }}_j({\mathbf{\chi }}^i)\rangle +\frac{y_{ij}+1}{2}-1+{\eta }_i\right)\\ \begin{array}{ll}\text{subject}\text{to}\hfill & (\text{i}){\kappa }_i\ge 0,\hfill \\ \hfill & (\text{ii}){\alpha }_{ij}\ge 0.\hfill \end{array}\end{array}$$ (F.2)

By calculating the gradient respect to w and η_m,

$$\begin{array}{l}\mathbf{w}=\sum _{i,j\in j^{\ast }(i)}{\alpha }_{ij}\left(\left[\sum _{k=1}^L{\mathrm{\Phi }}_k({\mathbf{\chi }}^i)\frac{y_{ik}+1}{2}\right]-{\mathrm{\Phi }}_j({\mathbf{\chi }}^i)\right),\\ \sum _{j\in j^{\ast }(m)}{\alpha }_{mj}=C-{\kappa }_m,\end{array}$$ (F.3)

replacing the two previous equations back into the Lagrangian and using the property 3.9, one obtains the dual problem

$$\begin{array}{ll}\text{maximize}\hfill & W=\sum _{i=1}^N\sum _{j\in j^{\ast }(i)}{\alpha }_{ij}-\frac{1}{2}\sum _{i,i^{\prime }=1}^N\sum _{j\in j^{\ast }(i),j^{\prime }\in {j^{\prime }}^{\ast }(i^{\prime })}{\alpha }_{ij}{\alpha }_{i^{\prime }{j}^{\prime }}{G}_{{\mathit{iji}}^{\prime }{j}^{\prime }}\hfill \\ \text{subject}\text{to}\hfill & \sum _{j\in j^{\ast }(i)}{\alpha }_{mj}\in [0,C],\hfill \end{array}$$ (F.4)

where the multiclass kernel is exactly the same as Watson-Watkins:

$$\begin{array}{l}{G}_{{\mathit{iji}}^{\prime }{j}^{\prime }}=K({\mathbf{x}}_i,{\mathbf{x}}_{i^{\prime }})\left(\sum _{k=1}^L\left(\frac{y_{ik}+1}{2}\frac{y_{i^{\prime }k}+1}{2}\right)-\frac{y_{{ij}^{\prime }}+1}{2}-\frac{y_{i^{\prime }j}+1}{2}+I(j=j^{\prime })\right)\\ =K({\mathbf{x}}_i,{\mathbf{x}}_{i^{\prime }})\left(\sum _{k=1}^L\left(\frac{y_{ik}+1}{2}\frac{y_{i^{\prime }k}+1}{2}\right)+I(j=j^{\prime })\right)\\ =G_{i^{\prime }{j}^{\prime }ij}.\end{array}$$

This problem is nearly identical to the Weston-Watkins approach but with minor differences in the constraints of the Lagrange multipliers due to the use of a lower number of slack variables. Note also that constraint F.4 is different from the one used in Crammer and Singer (2001), where η_i ≥ 0 was not enforced in the Lagrangian (see Tsochantaridis et al., 2005, for an appropriate derivation).