A national-level analysis of neighborhood form metrics

Abstract

Interest in urban neighborhood form is strong among scholars trained in multiple disciplines. The increasing popularity of this field calls for a set of metrics that can be used to describe meaningful patterns of built features in neighborhood environments. This study employs national-level datasets from Add Health, the National Land Cover Dataset (NLCD) 2001, the U.S. Census TIGER, and the U.S. Geological Survey to construct neighborhood form metrics for 20,467 residents, whose residential environments cover a wide array of geographic areas representative of comprehensive neighborhood types across the United States. Buffers of different sizes (1 km, 3 km, 5 km, and 8 km, respectively) are drawn around each resident’s location as the unit of analysis. For the four sets of 20,467 neighborhood environments, 27 neighborhood form metrics are selected, computed, and further reduced through factor analysis. The results suggest that the derived subsets of univariate metrics can be applied across neighborhood types to characterize diverse neighborhood environments.

1. Introduction

In recent decades, increasing public concern over the set of negative impacts of urban sprawl – the loss of open land resources, longer commutes, increased greenhouse gas emissions, and lower levels of physical activity – has led to policy efforts that seek to change the course of urban growth patterns (Calthorpe and Fulton 2001). Notably, a range of urban and city planning efforts, such as the smart growth movement that emerged in the 1980s, openly sought to avoid urban sprawl and improve public health through reshaped physical form of neighborhoods (Duany and Plater-Zyberk 1992; Centers for Disease Control and Prevention 2005), and to create “place types” to help policy makers and the public choose desirable patterns of urban development (Wheeler and Beebe 2011). These movements still popularly appear in the dialogue between research scholars, land use planners, policymakers and the general public.

The continuing efforts in creating alternative types of neighborhoods have brought increasing attention to the need for understanding neighborhood form attributes in order to describe patterns of development at the neighborhood scale. Researchers and practitioners have developed numerous metrics to quantify the physical form of neighborhoods. However, despite ongoing efforts on developing measures of neighborhood form, there are several issues with current practice in computing measures. First, the set of measures included in one study sometimes do not sufficiently capture the complexity of urban form. Description of urban form relying on one-dimensional measures, like development density or land use, has failed to adequately describe neighborhoods in a comprehensive manner (Gill et al. 2008). Thus there is a need for a set of metrics covering different dimensions of neighborhood form. Second, some commonly used indicators are possibly ill-defined. As Talen (2003) writes, “too much discussion about cities is devoid of measurement … Examples are words such as suburb, public realm, mixed use, diversity and access. These concepts are vital to the discussion, but have been difficult to pin down.” It is necessary to have better-defined and measurable metrics, which can be either quantitative or qualitative. Third, more recently, the proliferation of spatial data sources and Geographic Information System (GIS) tools for spatial data analysis has made a variety of new spatial metrics available. However, many of these computed spatial metrics are correlated and redundant measures. For example, when quantifying street network connectivity, shall we calculate the Alph or the Beta Connectivity Index, or both? Calculating highly correlated metrics creates computational burden and thus necessitates the identification of the most relevant set of metrics (Schwarz 2010).

There is also a lack of consistent metrics across different studies, limiting our ability to study and compare urban environments across cities, regions, or countries (Schwarz 2010). Few studies use nationally representative data sets to establish metrics and describe the full gamut of neighborhood characteristics, due to the difficulty of compiling and standardizing nation-wide neighborhood data. Rather, the majority of the literature on neighborhood form metrics draws conclusions from only a small subset of neighborhoods in one or several metropolitan areas. For examples, Southworth and Owens (1993) observe eight suburban neighborhoods in metropolitan San Francisco by qualitatively illustrating a set of metrics related to streetscapes, growth patterns, land use organizations, and size and shape of lots and houses. Similarly, Wheeler (2003) includes two cities (Portland, Oregon, and Toronto, Ontario) in his studies on categorizing development patterns. He employs attributes including street patterns, size and shape of lots, designing features of buildings and sites, and land use mix to define a range of neighborhoods developed at different historical periods. More recently, Song and Knaap (2007) have developed a range of metrics to quantify neighborhood form for Portland metropolitan area and these metrics capture dimensions such as street design, density, land use mix, and access to commercial activities and different transportation modes. They employ the parcel-level GIS data to compute the metrics and these data might not be available in other localities.

To address some of the aforementioned issues, the purpose of this study is to help choose a set of neighborhood form metrics that one study can employ to capture a range of important aspects of neighborhood form, such as connectivity, access, density, and land use variety. Through applying the method of factor analysis, we can identify a reduced set of metrics minimizing the computation of correlated and single out redundant measures. To do so, we first calculated a large number of candidate metrics for a sample of 20,467 representative neighborhoods across the U.S., a factors analysis is then used to single out a smaller number of independent axes. Such an analysis suggests a minimum set of metrics that can used to quantify physical form of neighborhoods. We also perform a cluster analysis to validate that the reduced set of metrics sufficiently produces consistent results. Previous studies have employed factor analysis to identify a small set of urban form metrics (Riitters et al. 1995; Schwarz 2010). For example, Riitters et al. calculated fifty-five metrics of landscape pattern for 85 maps of land use and land cover and used a factor analysis to identify a reduced set of 26 metrics. Our study expands Riitters et al.’s study but differs in that we are interested in identifying neighborhood form metrics for smaller scale neighborhoods, while Riitters et al. aimed to identify metrics for 120km by 180km landscape maps.

It is necessary to note that in addition to the apparent benefit of reducing computation work by having a smaller but sufficient set of quantitative neighborhood form metrics, having such a set of metrics is also useful for conducting many sorts of statistical analysis (Wheeler 2008). In studies of neighborhood form and its associated outcomes, a small set of uncorrelated metrics can be included as independent variables in regression equations to test their implications on outcomes such as residents’ transportation and exercising behaviors and health outcomes. Researchers have been interested in examining quantitatively the relationship between neighborhood form and transportation outcomes, including trip generation, mode choices, distance traveled and auto ownership (for examples, Ewing and Cervero 2010, Greenwarld and Boarnet 2001, Handy 1996, Krizek 2003). For health-related disciplines, the emergence of ecologic models (Stokols 1992) has underscored the levels at which multiple factors (personal, interpersonal, neighborhood, environment and policy) can influence individual behavior and health outcomes. As a result, neighborhood forms metrics on accessibility, intensity, and diversity of nonresidential land uses are used to examine physical activity outcomes such as walking behavior and obesity (for examples, Forsyth et al. 2008, Nelson et al. 2006, and McConville et al. 2010). Neighborhood forms have also been related to housing markets and individuals’ preferences for neighborhood types. Metrics such as connectivity, land use mixture and accessibility generally correlate with higher residential land prices (Song and Knaap 2004). In summary, there is a demand for neighborhood form metrics in quantitative analyses to associate neighborhood forms with community and ecological outcomes. A reduced set of uncorrelated neighborhood form metrics may be desirable to yield more generalizable results. The next section describes the methodology and computes twenty-seven candidate metrics for 20,467 neighborhoods defined at different scales using GIS data. We then use a multivariate factor analysis to obtain a smaller set of reduced metrics, which are then validated to show that they produce consistent results in quantifying different types of neighborhood form.

2. Methods

The methodology for this study consists of the following steps: (1) Acquire national level datasets. (2) Identify the unit of analysis, i.e., the neighborhood boundaries. (3) Select and compute a range of neighborhood form metrics. (4) Identify a minimal set of metrics using factor analysis and validate this set of metrics using cluster analysis.

2.1 National Data sources

Four main national-level data sources are employed for this study. To extract a national sample of neighborhoods, data is employed from Add Health, which is a school-based longitudinal survey of youths. In the dataset, a random sample of 80 high schools and 52 junior high feeder schools was selected in 2001. Home street addresses of the participants were identified and geocoded, with street address matches using commercial GIS databases or global positioning system (GPS) units. The Add Health study design incorporated systematic sampling methods and implicit stratification to ensure this sample is representative of US schools with respect to region of country, urbanicity, school size, school type, and ethnicity (Harris et al. 2009). Therefore, although Add Health dataset is constructed to have a representative sample of youth, the dataset includes a wide-ranging set of geographic areas also representative of comprehensive neighborhood types across the United States (Nelson et al. 2006). The dataset contains 20,467 observations, thus generating a sample of 20,467 neighborhoods. It is necessary to note that in addition to the Add Health dataset which can be used to extract a sample of representative residential neighborhoods in the U.S., random samples of other geographic units such as zip codes, census tracts or blockgroups can also be employed to generate a sample of neighborhoods.

The second data source is the 2001 National Land Cover Dataset (NLCD). This dataset is employed to originate land cover information for neighborhood environment. NLCD land cover classifications are collapsed into six generalized classes for analysis (Table 1). Using the NLCD is favorable because it can provide consistent nation-wide data sets with high level of details. While other datasets such as parcel-based land use data can provide more fine-grained details such as lot shape, these datasets are typically localized and not available at the national level.

Table 1.

Definition of land cover classifications

Land Cover Analysis Class in This Study	NLCD 2001 Level II Code
1 Water or Perennial Ice	11 Open Water; 12 Perennial Ice/Snow
2 Developed, Low and Medium Density	22 Developed, Low Intensity; 23 Developed, Medium Intensity
3 Developed, High Density	24 Developed, High Intensity
4 Developed, Recreational	21 Developed, Open Space
5 Undeveloped/Natural	31 Barren Land (Rock/Sand/Clay); 32 Unconsolidated Shore; 41 Deciduous Forest; 42 Evergreen Forest; 43 Mixed Forest; 51 Dwarf Scrub; 52 Shrub/Scrub; 71 Grassland/Herbaceous; 72 Sedge/Herbaceous; 73 Lichens; 74 Moss; 90 Woody Wetlands; 91 Palustrine Forested Wetland; 92 Palustrine Scrub/Shrub Wetland; 93 Estuarine Forested Wetland; 94 Estuarine Scrub/Shrub Wetland; 95 Emergent Herbaceous Wetlands; 96 Palustrine Emergent Wetland (Persistent); 97 Estuarine Emergent Wetland; 98 Palustrine Aquatic Bed; 99 Estuarine Aquatic Bed
6 Agricultural	81 Pasture/Hay; 82 Cultivated Crops

The third dataset is the 2000 U.S. Census TIGER (topologically integrated geographic encoding and referencing) line files, which are employed to assess road types.

Finally, aerial photographs from the U.S. Geological Survey are used to retrieve information on the availability of parks.

2.2 Unit of analysis

The unit of analysis in this study is the individual neighborhood defined by various sizes of buffers. In the study of neighborhoods, there is no consensus on what constitutes a neighborhood (Cervero and Gorham 1995). Previous studies on neighborhoods use measures such as buffers of different sizes (Boone-Heinonen et al. 2010; Nelson et al. 2006), U.S. Census-defined boundaries such as zip codes (Gordon-Larsen et al. 2005), census tracts and census blockgroups (Song and Knaap 2004), and self-defined boundaries. In this study, to assess neighborhood characteristics, buffers of four different sizes (1 km, 3 km, 5 km, and 8 km, respectively) used in previous studies (Boone-Heinonen et al. 2010) are drawn around each respondent’s residential location to create a sample of neighborhoods. By including different sizes of buffers, we intend to identify four reduced sets of metrics. Researchers have adopted buffers of different sizes to associate neighborhood forms with different outcomes (Boone-Heinonen et al. 2010). For examples, smaller-scale buffers such as 1-km and 3-km buffers are used to explore associations between neighborhood forms and adolescent physical activity (Nelson et al. 2006) while 5-km and 8-km buffers are used to test how the area affects adults’ travel and physical activity behaviors (Sallis et al. 1990).

It is necessary to note that although the neighborhoods are defined by buffers surrounding respondents’ point address locations, neighborhood form metrics (identified in the next section) can be calculated for different neighborhood definitions such as zip codes, tracts, block groups, or other user-defined boundaries.

2.3 Neighborhood form metrics

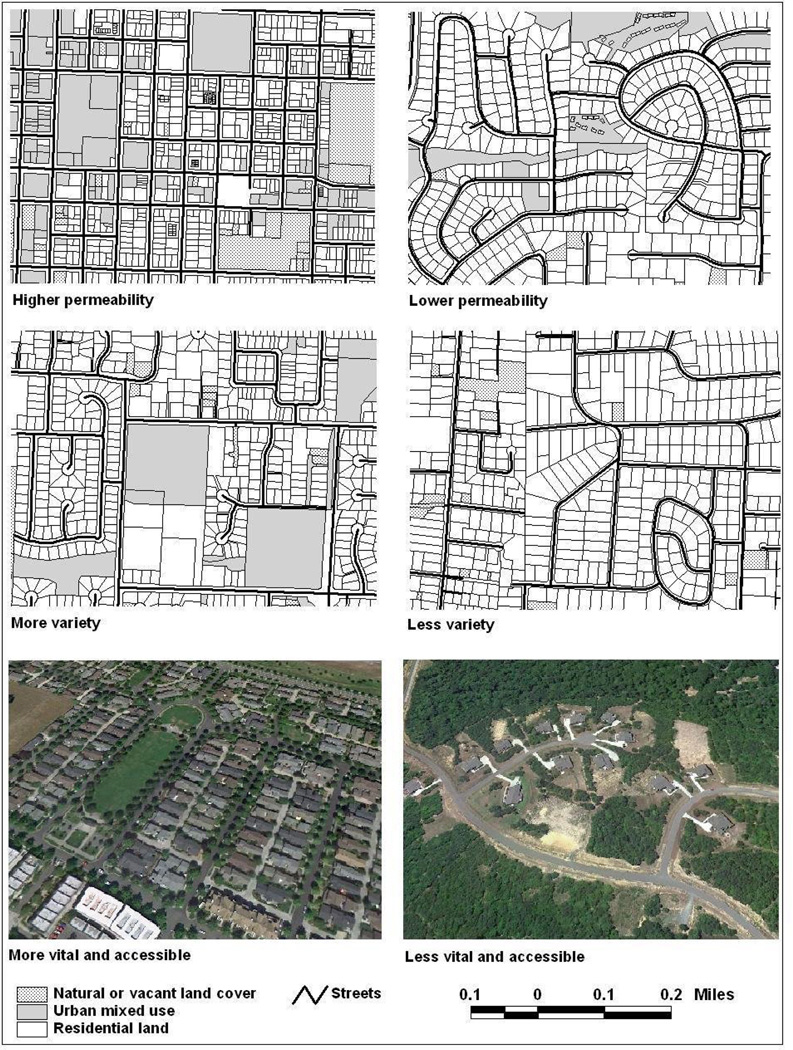
In order to identify neighborhood form metrics, we take two steps – identifying dimensions of neighborhood forms that are theoretically sound and choosing metrics that were developed, modified and tested by previous studies. First, we rely on theory of good urban form to identify dimensions of neighborhood forms: permeability, the connectiveness of places, which prescribes a street network system through which travelers can move with ease; vitality and accessibility, the vibrancy and convenience of places, which are ensured by having an agglomeration of accessible and high density places; and variety, the mix of an appropriate set of land uses, which generates greater opportunities for social interaction (Lynch 1960; Lynch 1981; Jacobs 1984; Kostof et al. 1992; Calthorpe 1993).

Second, based on previous studies, we adopt a set of 27 metrics to characterize the above identified dimensions of neighborhood form for each neighborhood: street network design, development density, and distribution of mixed land uses including residential, and nature and recreational uses (Cervero and Radisch 1996; Galster et al. 2001; Song and Knaap 2004; Song and Knaap 2007; Miles and Song 2009; Galster et al, 2000). After computing these variables for neighborhoods with different sizes, we interpret and evaluate these metrics to examine their ability of illustrating neighborhood form. Figure 1 presents examples of neighborhoods that present these concepts. It is necessary to note there are limitations associated with the set of selected metrics. We choose the metrics that can be relatively easily quantified, such as street connectivity to quantify permeability. However, there are other qualitative measures, such as layout of alleys, availability of bike connections and sidewalks, presence of fences or other means of preventing access, which can better describe the attributes of a street network system enabling travelers of moving with ease. For another example, we simplify the measurement of neighborhood form dimensions such as “vitality” by a metric of development density. However, Lynch used the term of vitality to include human use of places, which cannot be easily determined with quantitative measures. Future qualitative studies need to be carried out to identify ways to describe different neighborhoods from fine-grained and first-hand observation of human use of place.

Figure 1.

Conceptualization of neighborhood metrics

2.3.1. Permeability Measures

The concept of permeability is captured partly by the level of connectivity of street networks. Better permeability, indicated by more connective streets, more intersections but less street cul-de-sacs (illustrated in top left, Figure 1), could enhance the easiness of traveling, thus increasing probability of using alternative travel modes such as biking, walking, or taking the transit (Benfield et al. 1999). The TIGER dataset is used to calculate measures for four sets of neighborhood buffers. To begin with the analysis, we include a large set of measures on street length, street density by type, intersection types, and connectivity indices. In our next step, the purpose is to select the most relevant metrics from this list.

• Road Length ( totkm) - Absolute total length of roads within each buffer;

• Road Density by Road Types (a10pct, a20pct, a30pct, and a40pct) – The proportion of primary roads with limited access (a10pct), primary roads without limited access (a20pct), secondary roads (a30pct), and local roads with lower speed limits and possibly sidewalks (a40pct), respectively, in each buffer. (For more on road types, please see http://www.census.gov/geo/www/tiger/appendxe.asc.);

• Intersection Density (intd) – 3-way & 4-way intersection density per buffer;

• Intersection Proportion (intp) – Proportion of 3-way & 4-way intersections per buffer;

• Cul-de-sac Density (culd) – Number of cul-de-sacs per buffer;

• Connectivity Beta Index (beta) – Number of links (connections between nodes) divided by number of nodes in each neighborhood buffer;

• Connectivity Gamma Index (gamm) – Number of observed links divided by maximum possible number of links in each buffer (where maximum possible number of links in a network equals to 3*(Number of nodes-2);

• Connectivity Alpha Index (alph) – Ratio measure of observed to maximum possible route alternatives (circuitry) between nodes in each buffer. The maximum possible number of circuits is the greatest possible number of links, 3*(Number of nodes-2), minus the number of links in a minimally connected network, (Number of nodes − 1);

• Connectivity Cyclomatic Index (cycl) - Number of route alternatives (circuits) between nodes in each buffer, which is calculated by (Number of links - Number of nodes + 1).

2.3.2. Vitality and Accessibility Measures

Vitality and accessibility, richness and convenience of places, are symbolized by development density. Higher density developments that have good access to other activities (illustrated in bottom left, Figure 1) facilitate social interactions, reduce commuting costs, and protect farmland resources (American Planning Association 1998). This study includes the following two sets of measures: the first set measures urban development density and includes area of development with different densities; and the second set measures land patch size and density.

• Development Area (ca_c2 and ca_c3) – Area of two land classes in each buffer, respectively: Class 2, the low and medium density development and Class 3, the high density development;

• Land Patch Size and Density – Attributes of land uses can be represented using spatially explicit patch-based indices such as size and patch density. Patches are defined as homogenous regions for a specific landscape property of interest, such as “industrial land” or “high-density residential zone.” We include the following three measures of land patch size and density: the mean land patch size (armn), the root mean squared error (deviation from the mean) in patch size (arsd), and land patch density (pd) which equals the number of patches in the landscape or class divided by total buffer area - are employed (McGarigal et al. 2002).

2.3.3. Variety Measures

Variety of neighborhood form is quantified by extent of land use mixture. Greater variety with appropriately mixed land uses (illustrated in middle left, Figure 1) puts different urban activities closer to each other, thereby facilitating walking and biking, lowering vehicle miles traveled (VMT), and improving air quality (American Planning Association 1998). In addition, preserving an appropriate amount of nature and recreational facilities in neighborhoods can help increase physical activity and thus has good implications for public health. This analysis includes three set of measures of variety: number of land use types, amount of natural and recreational land uses, and land use configuration (McGarigal et al. 2002).

• Land Type Richness (pr) – Number of different types of land classes present within each neighborhood buffer;

• Recreation (ca_c4) – Area of developed recreational land use in each buffer;

• Nature (ca_c5) – Area of undeveloped natural land in each buffer;

• Rural Area (ca_c6) – Area of agricultural land in each buffer;

• Parks (parks) – Number of parks in each buffer;

• Simpson's Diversity Index (sidi) – Diversity measure of distribution of different type of land classes.

• Contagion Index (contag) – Interspersion measure of type of land patches.

• Perimeter-area fractal dimension (pafr) – Measures perimeter and shape complexity.

• Mean Shape Index (shmn) – The simplest and perhaps most straightforward measure of overall shape complexity.

• Mean Fractal Dimension Index (frmn) –A measure of perimeter and shape complexity.

To compute the above measures of spatial patterns using nation-wide data, this analysis uses a combination of national-level datasets including the NLCD, TIGER, and aerial photos. For each neighborhood at four different buffer scales, these 27 metrics of neighborhood form are computed. Many of these metrics are landscape metrics since we are using land cover dataset. Derived in the late 1980s, landscape metrics can be computed from the digital analysis of thematic-categorical land cover maps with spatial heterogeneity (Wu et al. 2000; Clark et al. 2009; Schwarz 2010). Ground in the work of O’Neill et al. (1988), abundant set of landscape metrics for a given spatial scale and resolution have been created and tested for their validity (Riitters et al. 1995; McGarigal et al. 2002). FRAGSTATS, the public domain statistical package, is used to compute the set of quantitative landscape metrics (McGarigal et al. 2002). While landscape metrics are useful summarizing information based on land cover data, we also supplement the analysis with ancillary TIGER data on linear street networks to improve the measurement of spatial patterns.

In summary, guided by urban form theory, 27 metrics are identified and computed to measure neighborhood form. Table 2 provides further information on the definitions and measurements of these 27 metrics. It is important to note that since we are relying on publicly available datasets at the national level to establish neighborhood form metrics, the trade-off is to leave out measures of on-the-ground urban planning considerations which require localized and qualitative datasets on, for examples, availability of sidewalks, setback of buildings and so on.

Table 2.

A list of 27 neighborhood environment metrics and the definitions

Variable	Definitions and measurements
ca_c2	Area of the low and medium density development in each buffer
ca_c3	Area of the high density development in each buffer
ca_c4	Area of developed recreational land use in each buffer
ca_c5	Area of undeveloped natural land in each buffer
ca_c6	Area of agricultural land in each buffer
totkm	Total length of roads in km
a10pct	The proportion of primary roads with limited access in the neighborhood
a20pct	The proportion of primary roads without limited access in the neighborhood
a30pct	The proportion of secondary roads in the neighborhood
a40pct	The proportion of and local roads with lower speed limits and possibly sidewalks in the neighborhood
parks	Number of parks in each buffer
alph	Ratio measure of observed to maximum possible route alternatives (circuitry) between nodes; alph $=\frac{L-V+1}{2V-5}$, where V is the number of nodes and L is the number of links (connections between nodes)
beta	Ratio measure of links and nodes; beta = $\frac{L}{V}$, where V is the number of nodes and L is the number of links
gamm	Ratio measure of observed links and maximum possible number of links; gamm $=\frac{L_{\mathit{\text{obs}}}}{3(V-2)}$, where Lobs is the number of ob links and the maximum possible number of links in a network = 3(V-2)
cycl	Number of route alternatives (circuits) between nodes; cycl = L−V+ 1, where V is the number of nodes and L is the number of links
culd	Number of cul-de-sacs per neighborhood
intd	3-way & 4-way intersection density per neighborhood
intp	Proportion of 3-way & 4-way intersections
armn	The mean land patch size
arsd	The root mean squared error (deviation from the mean) in patch size, calculated by the square root of the sum of the squared deviations of patch size from the mean value of patch size computed for all patches in the landscape, divided by the total number of patches
cntg	A measure of the level of interspersion of land patch types with a range value between 0 and 100; cntg approaches 0 when the patch types are maximally disaggregated (i.e., every cell is a different patch type) and interspersed (equal proportions of all pairwise adjacencies), it equals to 100 when all patch types are maximally aggregated; i.e., when the landscape consists of single patch
frmn	Mean Fractal Dimension Index, a measure of perimeter and shape complexity
pafr	Perimeter-area Fractal Dimension, also a measure of perimeter and shape complexity
pd	Land patch density, calculated by the number of patches in the landscape or class divided by total buffer area
pr	Number of different types of land classes present within each neighborhood buffer
shmn	Mean Shape Index, a measure of overall shape complexity; calculated by patch perimeter (given in number of cell surfaces) divided by the minimum perimeter (given in number of cell surfaces) possible for a maximally compact patch (in a square raster format) of the corresponding patch area.
sidi	Simpson’s Diversity Index, a measure of distribution of different type of land classes; Sidi equals 0 when the neighborhood contains only one land class (i.e., no diversity), and approaches 1 as the number of different land classes (i.e., land type richness, pr) increases and the proportional distribution of area among land classes is more equitable.

2.4 Factor analysis

The main purpose of this analysis is to select a smaller set of metrics that span the above mentioned dimensions but are not redundant. Our first step is to conduct factor analysis on the 27 variables to derive a range of factors so that the 27 metrics are grouped by factors. Within each factor, correlations among metrics are large while across factors, correlations are small. The number of factors is chosen based on three considerations: the eigenvalues associated with each factor, the plot of eigenvalues versus component number, and the cumulative proportion of variance explained by an additional factor. The purpose of this first step is to derive and interpret factors so that we can understand which dimensions the selected metrics belong to in the next step.

Our second step is to choose a reduced set of metrics. Riitters et al. (1995) and Schwarz (2010) suggested and applied an approach to use factor analysis to select a reduced set of metrics. The general purpose of factor analysis is to describe the covariance structure among many variables in terms of a few underlying quantities which are called ‘factors’. From each factor, one single metric with the highest loading on each factor is retained as the most representative metric. Although selecting one single metric from each factor is a simplification, the approach provides a method avoiding the need to calculate all 27 metrics for all neighborhoods. It is necessary to note that other criteria such as normality, relative coefficients of variation, and ease of computation can also be used for choosing the reduced set of metrics.

Finally, we employ cluster analysis to group 20,467 neighborhoods into types of neighborhoods, using the original set of 27 metrics and the reduced set of metrics respectively. By doing so, we are able to evaluate whether the reduced set of metrics produces consistent results. Cluster analysis can be used to identify a set of homogeneous and non-overlapping neighborhood types (Song and Knapp 2007; Nelson et al. 2006; Schwarz 2010). By comparing results from cluster analysis between using the large and the reduced set of metrics, we are able to investigate whether the reduced set of metrics suffices in describing different neighborhood types. Using SAS FASTCLUS, we use the hierarchical clustering (i.e., the Ward procedure) and rely on the “elbow-criterion” which focuses on the percentage of variance explained as a function of the number of clusters. Thus the optimal number of clusters is the number after which the marginal gain of adding one more cluster drops sharply (Schwardz 2010). This method results in homogeneity within clusters and heterogeneity between clusters (Nelson et al. 2006). Z-core transformations of the raw values of metrics are used to generate clusters, thus, variables with different scales are adjusted with appropriate weighting (Aldenderfer and Blashfield 1984). For the 1-km buffers, for example, the best solution is the seven-cluster solution when using both the large and the reduced set of metrics. In next section, we will compare the level of consistency with regard to the number of neighborhoods assigned to each neighborhood type when two different sets of metrics are used to conduct cluster analyses.

3. Results

Summary statistics for the above 27 metrics computed at four different neighborhood scales are provided in Table 3. For almost two thirds of the metrics, standard deviation decreases when buffer size increases. This indicates that the 1 km buffer captures more variation across neighborhoods, while much of the variation flats out at larger buffer scales.

Table 3.

Summary statistics for 27 neighborhood environment metrics from 20,467 neighborhoods

	1 km buffer				3 km buffer				5 km buffer				8 km buffer
Variable	Mean	Std. Dev	Min	Max	Mean	Std. Dev	Min	Max	Mean	Std. Dev	Min	Max	Mean	Std. Dev	Min	Max
ca_c2	90.83	69.46	0.00	291.60	639.44	515.94	0.00	2455.29	1542.42	1299.92	0.00	6095.70	3487.90	3045.41	0.00	13815.99
ca_c3	78.30	76.50	0.00	312.12	624.54	619.77	0.00	2692.53	1579.14	1626.52	0.00	7253.91	3663.51	3897.97	0.00	18335.43
ca_c4	9.62	14.72	0.00	128.25	78.93	93.10	0.00	793.08	201.70	225.47	0.00	1458.00	481.71	502.91	0.00	2980.80
ca_c5	87.58	80.71	0.00	315.35	922.17	709.90	0.72	2828.07	2765.47	1981.94	49.32	7853.49	7628.38	5123.35	223.56	20312.28
ca_c6	41.47	64.07	0.00	314.28	447.40	586.81	0.00	2818.08	1322.88	1614.92	0.00	7758.81	3563.71	4096.06	0.00	19825.56
totkm	30.70	15.41	0.00	82.31	204.08	118.26	9.02	611.48	490.16	299.18	20.33	1314.79	1112.89	711.36	55.64	3234.70
a10pct	0.03	0.08	0.00	0.91	0.05	0.06	0.00	0.55	0.05	0.04	0.00	0.44	0.05	0.03	0.00	0.36
a20pct	0.03	0.07	0.00	1.00	0.03	0.04	0.00	0.56	0.03	0.03	0.00	0.39	0.03	0.03	0.00	0.19
a30pct	0.15	0.11	0.00	1.00	0.15	0.07	0.00	1.00	0.15	0.05	0.00	0.72	0.15	0.04	0.00	0.61
a40pct	0.77	0.15	0.00	1.00	0.75	0.10	0.00	1.00	0.75	0.08	0.08	1.00	0.76	0.06	0.14	1.00
parks	0.00	0.08	0.00	7.00	0.05	0.29	0.00	8.00	0.16	0.56	0.00	11.00	0.35	0.93	0.00	13.00
alph	0.31	0.75	−8.00	8.00	0.24	0.10	−2.00	4.00	0.22	0.07	0.06	1.20	0.22	0.06	0.05	0.54
beta	1.61	0.32	1.00	5.00	1.46	0.16	1.05	2.70	1.44	0.14	1.08	2.31	1.43	0.13	1.10	2.03
gamm	0.56	0.30	−1.67	3.33	0.49	0.06	−0.17	2.00	0.48	0.05	0.37	1.11	0.48	0.04	0.37	0.69
cycl	73.67	62.73	1.00	446.00	422.96	391.88	2.00	2947.00	972.03	916.54	3.00	5315.00	2130.24	2043.04	4.00	11306.00
culd	5.88	5.14	0.00	36.92	4.66	3.66	0.00	24.79	4.00	3.13	0.00	20.96	3.45	2.81	0.00	15.27
intd	31.37	23.34	0.00	168.07	23.49	18.46	0.00	121.45	20.08	16.25	0.05	77.31	17.32	14.49	0.05	67.64
intp	0.81	0.13	0.00	1.00	0.80	0.09	0.33	1.00	0.80	0.08	0.47	1.00	0.80	0.07	0.48	0.99
armn	4.26	17.89	0.74	315.27	5.91	62.51	0.94	2828.07	4.95	22.96	1.10	1570.79	5.13	15.07	1.18	1070.58
arsd	17.27	15.67	0.00	157.64	53.99	65.38	0.00	1412.01	92.63	109.52	13.90	3141.13	153.10	168.07	21.24	4528.09
cntg	48.14	16.35	9.05	100.00	50.13	14.70	21.57	100.00	50.96	14.51	24.47	99.88	51.54	14.64	27.18	99.31
frmn	1.04	0.01	1.00	1.10	1.04	0.01	1.01	1.13	1.04	0.00	1.01	1.10	1.04	0.00	1.02	1.08
pafr	1.49	0.08	1.06	1.67	1.51	0.06	1.04	1.65	1.51	0.05	1.02	1.62	1.51	0.05	1.10	1.61
pd	53.20	25.79	0.32	134.94	43.86	21.37	0.04	105.88	39.65	20.15	0.06	90.53	36.04	19.55	0.09	84.64
pr	5.09	0.95	1.00	6.00	5.77	0.55	1.00	6.00	5.91	0.35	2.00	6.00	5.96	0.21	3.00	6.00
shmn	1.28	0.08	1.03	1.75	1.26	0.05	1.02	2.30	1.25	0.04	1.04	1.84	1.25	0.03	1.06	1.74
sidi	0.54	0.18	0.00	0.83	0.57	0.17	0.00	0.81	0.58	0.16	0.00	0.82	0.58	0.16	0.00	0.80

All pair-wise correlation coefficients among the 27 metrics are computed and the results for the 1 km buffer are shown in Table 4. Almost half of the coefficients are statistically significant (> ± 0.27, p = 0.01). For brevity, the results for the other buffer sizes are not shown here but are available upon request from the authors.

Table 4.

Pearson correlation coefficients (n=20,467) among the metrics – 1km buffer

	ca_c2	ca_c3	ca_c4	ca_c5	ca_c6	totkm	a10pct	a20pct	a30pct	a40pct	parks	alph	beta	gamm	cycl	culd	intd	intp	armn	arsd	cntg	frmn	pafr	pd	pr	shmn	sidi
ca_c2	1.00
ca_c3	0.03	1.00
ca_c4	0.09	0.01	1.00
ca_c5	−0.52***	−0.60***	−0.17	1.00
ca_c6	−0.48***	−0.48***	−0.12	0.13	1.00
totkm	0.52***	0.75***	0.03	−0.71***	−0.59***	1.00
a10pct	−0.04	0.10	0.01	0.00	−0.07	0.15	1.00
a20pct	−0.16	−0.11	−0.04	0.17	0.11	−0.16	−0.09	1.00
a30pct	−0.06	0.01	0.01	0.04	0.02	−0.06	−0.07	−0.15	1.00
a40pct	0.15	−0.02	0.01	−0.08	−0.06	0.02	−0.52***	−0.26*	−0.63***	1.00
parks	−0.04	0.09	−0.01	−0.04	−0.04	0.04	−0.01	−0.01	0.01	0.01	1.00
alph	−0.19	−0.07	−0.08	0.12	0.17	−0.13	−0.02	0.04	−0.02	0.00	0.00	1.00
beta	−0.15	0.15	−0.08	−0.10	0.13	0.09	−0.08	0.03	0.03	−0.01	0.02	0.24*	1.00
gamm	−0.14	−0.01	−0.05	0.06	0.10	−0.05	−0.02	0.04	−0.01	−0.01	0.00	0.91***	0.01	1.00
cycl	0.40***	0.70***	−0.01	−0.64***	−0.49***	0.91***	−0.04	−0.11	−0.03	0.10	0.05	−0.05	0.26**	0.01	1.00
culd	0.42***	0.18	0.04	−0.26*	−0.34***	0.36***	0.10	−0.16	−0.06	0.06	0.01	−0.25*	−0.48***	−0.24*	0.10	1.00
intd	0.50***	0.67***	−0.01	−0.66***	−0.54***	0.94***	−0.03	−0.14	−0.05	0.12	0.05	−0.12	0.11	−0.05	0.96***	0.33**	1.00
intp	0.15	0.38**	0.02	−0.41***	−0.13	0.45***	−0.14	−0.01	0.02	0.06	0.03	0.16	0.62***	0.15	0.57***	−0.37***	0.47***	1.00
armn	−0.40***	−0.19	−0.23	0.44***	0.19	−0.33**	−0.05	0.11	−0.05	0.03	0.00	0.27**	0.30**	0.17	−0.21*	−0.34**	−0.30**	−0.07	1.00
arsd	−0.37**	−0.09	−0.26*	0.37**	0.14	−0.23*	−0.06	0.09	−0.04	0.03	0.02	0.27**	0.35***	0.18	−0.10	−0.36**	−0.21*	0.00	0.90***	1.00
cntg	−0.27**	0.08	−0.31**	0.19	0.06	−0.03	−0.02	0.09	−0.04	0.01	0.05	0.20*	0.35***	0.17	0.10	−0.37***	−0.03	0.12	0.63***	0.83***	1.00
frmn	−0.20	−0.24*	−0.02	0.21*	0.23*	−0.28**	0.01	0.08	0.00	−0.03	−0.05	0.04	−0.06	0.03	−0.25*	−0.09	−0.25*	−0.14	−0.01	−0.15	−0.26*	1.00
pafr	0.36**	0.19	0.10	−0.32**	−0.22*	0.31**	0.07	−0.12	0.01	−0.02	−0.03	−0.22*	−0.28**	−0.15	0.18	0.40***	0.28**	−0.02	−0.76***	−0.79***	−0.66***	0.28**	1.00
pd	0.36**	0.16	0.30**	−0.31**	−0.26*	0.26*	0.06	−0.11	0.03	−0.04	−0.02	−0.24*	−0.32**	−0.19	0.10	0.43***	0.22*	−0.04	−0.68***	−0.77***	−0.76***	−0.06	0.71***	1.00
pr	0.04	0.13	0.19	−0.17	−0.09	0.12	0.06	0.06	−0.01	−0.06	0.04	−0.17	−0.16	−0.08	0.12	−0.02	0.12	0.11	−0.45***	−0.45***	−0.12	0.02	0.30**	0.36**	1.00
shmn	−0.18	−0.18	−0.10	0.18	0.21*	−0.21*	0.01	0.05	−0.02	0.00	−0.06	0.06	−0.03	0.04	−0.18	−0.06	−0.18	−0.12	0.02	−0.15	−0.26*	0.91***	0.34***	−0.13	−0.03	1.00
sidi	0.20*	−0.10	0.30**	−0.18	−0.01	−0.01	0.01	−0.06	0.04	0.00	−0.03	−0.20*	−0.34***	−0.15	−0.11	0.27**	0.01	−0.08	−0.64***	−0.87***	−0.91***	0.30***	0.61***	0.67***	0.39***	0.31**	1.00

^*P<0.5

^**P<.01

^***P<.001

The extent of having significant correlation coefficients suggests that it is necessary and desirable to have a reduced set of metrics to minimize computation efforts. In what follows, we first present and interpret the results from the factor analysis for all four different neighborhood scales. To interpret each factor, we investigate the common characteristics of metrics. Inevitably, the process of interpreting features of all factors descriptively involves subjective judgment. Following previous studies (for example, Schwartz 2010), in addition to identifying the main highest loadings for each factor, metrics with high factor loadings are also identified in order to interpret the factors since these metrics with larger values are more important ones contributing to the factor. Metrics with negative loadings are negatively correlated with other metrics in the same factor. It is necessary to note that these identified metrics are used for the purpose of interpreting factors only. In the second step, we retain the set of metrics with the highest loading on each factor following suggestions by Riitters et al. (1995) and Schwarz (2010).

When neighborhoods are defined by 1 km buffers, the first nine factors explain 81% of the variation in the 27 metrics (Table 5). Only nine factors are retained because their associated eigenvalues are greater than one. The communality value for each measure (shown by the last column of Table 5) is the squared multiple correlation for predicting that measure from the nine factors; lower communality values indicate a higher level of the unexplained variance in the correlation matrix (Riitters et al. 1995). The loadings of each metric on each of the nine factors after orthogonal Varimax rotation are also shown in Table 5. By examining the factor pattern presented in Table 5, we interpret the nine factors as follows. The first factor is termed as land diversity, because it is highly correlated with measures of land patch size diversity (arsd and pd) and land patch type diversity (sidi and cntg). The second factor is street density, which is the most highly correlated with street length (totkm) and intersection density (intd). The third factor, factual connectivity, measures street link-to-node ratio (beta) and proportions of cul-de-sacs (culd) to intersections (intp). The fourth factor is correlated only with the prevalence of secondary roads (a30pct). The fifth factor measures land patch shape complexity (shmn and frmn). The sixth factor is highly correlated with observed-to-maximum possible (links or routes) connectivity measures (alph and gamm) thus leading to its name probable connectivity. The seventh factor is conveniently labeled as accessible primary roads (a20pct). The eighth factor can be labeled as number of parks (parks). Finally, the ninth factor is termed as inaccessible primary roads (a10pct). From the above interpreted factors, we retain nine metrics with the highest loading on each factor to encompass neighborhood form dimensions: permeability is represented by connectivity and densities of different type of streets (beta, gamm, a10pct, a20pct, a30pct, and totkm), vitality and accessibility of places is represented by differentiation in land patch size (arsd), and variety is represented by land patch shape and specific land use type (shmn and parks).

Table 5.

Results of factor analysis and Varimax rotation of the first 9 factors – 1km buffer

Factors	1	2	3	4	5	6	7	8	9
Eigenvalue	7.2950	4.7718	2.2299	1.8699	1.6880	1.5732	1.2033	1.0319	1.0014
Cum. variance	0.2605	0.4309	0.5106	0.5774	0.6377	0.6938	0.7368	0.7737	0.8094
Factor pattern after Varimax rotation										Communality
ca_c2k1	0.3339	0.4801	−0.2793	−0.0600	−0.1800	−0.0787	−0.1303	−0.3078	0.2499	0.6364
ca_c3k1	0.0110	0.7827	0.0801	0.0190	−0.0786	−0.0212	−0.0116	0.2194	−0.2144	0.7204
ca_c4k1	0.4114	−0.1006	0.2510	−0.1466	−0.2524	−0.0312	−0.1463	−0.0339	−0.1712	0.3804
ca_c5k1	−0.3192	−0.6898	−0.1849	0.0551	0.1219	0.0382	0.1656	0.0216	−0.0130	0.6593
ca_c6k1	−0.0993	−0.5877	0.3531	0.0279	0.1930	0.0789	−0.0305	0.0126	0.0290	0.5260
totkmk1	0.1272	0.9565	−0.0525	−0.0220	−0.1062	−0.0321	−0.0558	−0.0254	−0.1102	0.9626
a10pctk1	0.0144	0.0492	−0.1110	0.0883	0.0315	−0.0013	−0.0687	−0.0595	−0.9277	0.8926
a20pctk1	−0.0819	−0.1072	0.0280	0.0117	0.0351	0.0217	0.9106	−0.0682	0.0524	0.8574
a30pctk1	0.0546	−0.0471	0.0592	0.9370	−0.0328	−0.0155	−0.1454	0.0468	0.1113	0.9236
a40pctk1	−0.0247	0.0531	−0.0107	−0.8014	0.0036	−0.0088	−0.2629	0.0357	0.4896	0.9560
parksk1	−0.0352	0.0601	−0.0544	0.0298	−0.0291	0.0099	−0.0754	0.8807	0.0859	0.7983
alphk1	−0.1748	−0.0628	0.1121	−0.0014	0.0320	0.9317	−0.0236	−0.0221	0.0098	0.9533
betak1	−0.3632	0.2080	0.7208	0.0774	0.0337	0.0326	−0.0796	−0.0923	0.0769	0.7237
gammk1	−0.0988	−0.0035	0.0229	−0.0073	0.0156	0.9765	0.0374	0.0270	−0.0081	0.9663
cyclk1	−0.0038	0.9213	0.1446	−0.0254	−0.0680	0.0024	0.0083	0.0175	0.0635	0.9174
culdk1	0.3243	0.2596	−0.7162	−0.0498	−0.0521	−0.1580	−0.1590	−0.0482	−0.0274	0.7440
intdk1	0.1060	0.9311	−0.0315	−0.0377	−0.0681	−0.0384	−0.0233	−0.0040	0.0794	0.9183
intpk1	−0.0182	0.5380	0.6903	0.0288	−0.0471	0.1452	0.0212	−0.0381	0.1670	0.8202
armn_lk1	−0.8297	−0.2467	0.0253	−0.0312	0.0100	0.1047	−0.0281	−0.0474	0.0122	0.7651
arsd_lk1	−0.9405	−0.1251	0.0399	−0.0141	−0.1160	0.0962	−0.0116	−0.0153	0.0090	0.9252
cntg_lk1	−0.8719	0.0822	0.1150	−0.0306	−0.1944	0.0555	0.1280	0.1137	−0.0573	0.8545
frmn_lk1	0.1252	−0.2081	0.0328	−0.0174	0.9044	0.0203	0.0328	−0.0018	−0.0266	0.8805
pafr_lk1	0.7629	0.2690	−0.1708	0.0304	0.3304	−0.0692	−0.0147	−0.0102	−0.0100	0.7988
pd_lk1	0.8816	0.1198	−0.1357	0.0247	−0.1840	−0.0729	−0.0173	−0.0081	−0.0399	0.8518
pr_lk1	0.4788	0.0779	0.2324	−0.1055	−0.0876	−0.0966	0.3590	0.3113	−0.2012	0.5837
shmn_lk1	0.0839	−0.1233	0.0036	−0.0206	0.9632	0.0330	0.0019	−0.0226	−0.0088	0.9522
sidi_lk1	0.8794	−0.1111	0.0033	−0.0202	0.2295	−0.0693	−0.0188	−0.0017	0.0251	0.8446

When neighborhoods are defined by 3 km buffers, the first seven factors explain 79% of variation in the 27 metrics (Table 6). These seven factors are retained because their associated eigenvalues are greater than one. The first factor is termed as land diversity because it is highly correlated with measures of land patch size diversity (arsd and pd) and land patch type diversity (sidi and cntg). The second factor is termed as connectivity since it is associated with measures on street network connectivity (beta, gamm, alph, and intp). The third factor measures land patch shape complexity (shmn and frmn). The fourth is named inaccessible primary roads (a10pct). The fifth factor, street density, is most highly correlated with street length (totkm) and intersection density (intd). The sixth factor is labeled as number of parks (parks). Finally, the seventh factor is correlated only with the amount of secondary roads (a30pct). From the above interpreted factors, we retain seven metrics with the highest loading on each factor: permeability is represented by connectivity and densities of different type of streets (beta, a10pct, a30pct, and totkm), vitality and accessibility of places is represented by differentiation in land patch size (arsd), and variety is represented by land patch shape and specific land use type (shmn and parks).

Table 6.

Results of factor analysis and Varimax rotation of the first 7 factors – 3km buffer

Factors	1	2	3	4	5	6	7
Eigenvalue	8.5063	5.4600	2.8061	1.8203	1.3510	1.0982	1.0423
Cum. variance	0.3038	0.4988	0.5990	0.6640	0.7123	0.7515	0.7887
Factor pattern after Varimax rotation								Communality
ca_c2k3	0.4620	−0.0817	−0.1469	−0.1171	0.5868	−0.2539	0.1003	0.6742
ca_c3k3	0.1481	0.3470	−0.1202	0.1447	0.7627	0.1175	−0.0565	0.7764
ca_c4k3	0.4962	0.1146	−0.3833	0.1181	0.0213	−0.0347	0.2766	0.4984
ca_c5k3	−0.5014	−0.4459	0.0706	0.0417	−0.4789	0.0236	0.0100	0.6870
ca_c6k3	−0.0427	0.1700	0.2117	−0.0712	−0.7148	0.0077	−0.0630	0.5955
totkmk3	0.2898	0.2848	−0.1105	0.0396	0.8877	−0.0162	0.0140	0.9674
a10pctk3	0.0975	−0.0865	0.0574	0.8994	0.0889	−0.0784	0.0850	0.8504
a20pctk3	−0.1656	−0.0317	−0.0090	0.0518	−0.2765	0.5575	0.3010	0.5091
a30pctk3	0.1141	−0.0041	−0.0643	0.1136	−0.0268	−0.0383	−0.9221	0.8825
a40pctk3	−0.0808	0.0445	0.0268	−0.7854	0.0819	−0.1637	0.4739	0.8842
parksk3	−0.1231	0.1336	−0.0383	0.0535	0.2918	0.5667	−0.0816	0.4503
alphk3	−0.1561	0.9169	−0.0399	−0.0099	0.0910	−0.0508	0.0012	0.8776
betak3	−0.0635	0.9525	−0.0531	−0.0397	0.2144	0.0516	0.0016	0.9637
gammk3	−0.1862	0.9365	−0.0424	−0.0149	0.0855	−0.0404	0.0088	0.9228
cyclk3	0.1264	0.4791	−0.0911	−0.0450	0.8113	0.0766	−0.0064	0.9199
culdk3	0.4074	−0.4165	−0.0262	−0.0046	0.6514	−0.2022	0.0045	0.8053
intdk3	0.2308	0.3241	−0.0803	−0.0528	0.8777	0.0118	0.0045	0.9380
intpk3	0.1622	0.8509	−0.0320	−0.0916	0.2683	0.1040	0.0020	0.8425
armn_lk3	−0.6641	−0.0984	−0.1904	0.0557	−0.0866	−0.2984	0.2002	0.6267
arsd_lk3	−0.8967	−0.0394	−0.2332	0.0083	−0.1524	−0.1593	0.1331	0.9086
cntg_lk3	−0.8535	0.0813	−0.1639	−0.0580	−0.1656	0.1207	−0.0258	0.8804
frmn_lk3	0.2196	−0.0803	0.8802	0.0244	−0.2145	0.0035	0.0471	0.8783
pafr_lk3	0.6957	−0.0807	0.3409	0.0915	0.3498	0.0868	−0.1611	0.7709
pd_lk3	0.7893	−0.1902	−0.1159	0.1473	0.3802	−0.1358	−0.0120	0.8574
pr_lk3	0.5476	−0.0406	−0.0911	−0.0002	0.0111	0.4597	−0.0337	0.5224
shmn_lk3	0.1744	−0.0714	0.9286	0.0187	−0.1634	−0.0220	0.0398	0.9268
sidi_lk3	0.8687	−0.0392	0.2190	−0.0098	0.0575	−0.0515	0.0017	0.8103

When neighborhoods are defined by 5 km buffers, the first six factors explain 78% of the variation in the 27 metrics (Table 7). These six factors are retained because their associated eigenvalues are greater than one. The first factor is labeled as street density since it is most correlated with street nodes density (culd and intd) and street length (totkm). The second factor is termed as connectivity since it is associated with measures on street network connectivity (beta, gamm, alph, and intp). The third factor measures land patch shape complexity (shmn and frmn). The fourth is termed as local roads (a40pct). The fifth factor, land patch size diversity, is highly correlated with the measures of patch sizes (arsd and armn). The last factor correlates to secondary roads (a30pct). From the above interpreted factors, we retain six metrics: permeability is represented by connectivity and densities of different type of streets (beta, culd, a30pct and a40pct), vitality and accessibility of places is represented by differentiation in land patch size (arsd), and variety is represented by land patch shape (shmn).

Table 7.

Results of factor analysis and Varimax rotation of the first 6 factors – 5km buffer

Factors	1	2	3	4	5	6
Eigenvalue	9.5787	5.0714	2.7708	1.8599	1.3575	1.1155
Cum. variance	0.3421	0.5232	0.6222	0.6886	0.7371	0.7769
Factor pattern after Varimax rotation							Communality
ca_c2k5	0.8118	0.0474	−0.0030	0.0704	−0.2032	0.1141	0.7205
ca_c3k5	0.6046	0.6067	−0.1872	−0.0966	−0.0365	−0.1206	0.7939
ca_c4k5	0.3992	0.1223	−0.1031	−0.2121	−0.2200	0.4396	0.4716
ca_c5k5	−0.4567	−0.6076	−0.0322	0.0549	0.3680	−0.0991	0.7270
ca_c6k5	−0.6941	−0.0431	0.2595	−0.0311	−0.1814	0.0815	0.5915
totkmk5	0.8017	0.5359	−0.1324	−0.0120	−0.0997	−0.0361	0.9588
a10pctk5	0.1423	−0.0392	−0.0123	−0.8081	−0.0430	0.1458	0.6980
a20pctk5	−0.4222	−0.0921	−0.1125	−0.0643	0.0692	0.3294	0.3168
a30pctk5	0.0714	0.0139	0.0178	−0.2947	−0.1589	−0.8009	0.7592
a40pctk5	0.0327	0.0270	0.0527	0.8582	0.0930	0.3652	0.8832
parksk5	0.0945	0.4547	−0.2024	−0.1508	0.0607	−0.0053	0.2831
alphk5	−0.0178	0.9653	−0.0481	0.0161	−0.0083	0.0015	0.9631
betak5	0.0141	0.9833	−0.0479	0.0136	−0.0329	0.0022	0.9704
gammk5	−0.0291	0.9521	−0.0505	0.0167	0.0019	0.0007	0.9605
cyclk5	0.6150	0.7143	−0.1652	0.0333	−0.0180	−0.0589	0.9206
culdk5	0.8825	−0.1583	−0.0023	0.0540	−0.1779	−0.0410	0.8400
intdk5	0.7557	0.5780	−0.1279	0.0468	−0.0671	−0.0489	0.9305
intpk5	0.0625	0.9348	0.0348	0.0185	−0.1486	0.0331	0.9024
armn_lk5	−0.0149	−0.0922	0.0833	−0.0645	0.8254	0.1552	0.7252
arsd_lk5	−0.2998	−0.1254	−0.2044	0.0582	0.8759	0.0546	0.9210
cntg_lk5	−0.5902	−0.0339	−0.3604	0.1791	0.5984	−0.1419	0.8897
frmn_lk5	−0.0695	−0.1211	0.9351	0.0180	−0.0854	−0.0005	0.9016
pafr_lk5	0.4947	0.0492	0.2332	−0.1166	−0.5737	−0.2498	0.7066
pd_lk5	0.7714	−0.0523	0.0641	−0.2201	−0.4496	0.0172	0.8528
pr_lk5	0.1117	0.0746	−0.0863	−0.0445	−0.6842	0.0248	0.4962
shmn_lk5	−0.0744	−0.0909	0.9453	0.0462	−0.1108	−0.0407	0.9234
sidi_1k5	0.4460	0.0812	0.4118	−0.1176	−0.6204	0.1398	0.7933

Finally, when neighborhoods are defined by 8 km buffers, the first six retained factors explain 80% of variation in the 27 metrics (Table 8). The first five dimensions are identical to the ones identified by the factor analysis at the 5 km buffer level. The last dimension is termed as inaccessible primary roads (a10pct). From the above interpreted factors, we retain six metrics: permeability is represented by connectivity and densities of different type of streets (beta, culd, a10pct and a40pct), vitality and accessibility of places is represented by differentiation in land patch size (arsd), and variety is represented by land patch shape (shmn).

Table 8.

Results of factor analysis and Varimax rotation of the first 6 factors – 8km buffer

Factors	1	2	3	4	5	6
Eigenvalue	10.7195	4.4039	2.7920	1.9493	1.3889	1.0718
Cum. variance	0.3828	0.5401	0.6398	0.7094	0.7590	0.7973
Factor pattern after Varimax rotation							Communality
ca_2k8	0.8676	0.0821	0.0336	0.0661	−0.1071	0.0693	0.7813
ca_c3k8	0.6023	0.6519	−0.2035	−0.0862	0.0014	−0.1049	0.8475
ca_c4k8	0.5259	0.1533	−0.1342	0.0382	−0.1230	0.4324	0.5217
ca_c5k8	−0.4592	−0.6480	−0.0595	0.0188	0.3027	−0.2294	0.7789
ca_c6k8	−0.6432	−0.0666	0.2701	0.0179	−0.2368	0.3035	0.6396
totkmk8	0.7988	0.5511	−0.1322	−0.0165	−0.0441	−0.0687	0.9662
a10pctk8	0.1644	0.0038	−0.0997	−0.6131	−0.0203	0.5242	0.6879
a20pctk8	−0.4056	−0.1631	−0.1264	0.0503	0.1698	0.2031	0.2797
a30pctk8	0.0948	0.0285	0.0744	−0.7191	−0.1864	−0.4340	0.7556
a40pctk8	−0.0209	0.0168	0.0755	0.9465	0.0326	−0.0817	0.9096
parksk8	0.1316	0.5436	−0.2844	−0.0404	0.0387	0.0063	0.3969
alphk8	0.0365	0.9430	−0.0261	0.0014	−0.0632	0.0136	0.9737
betak8	0.0494	0.9837	−0.0249	0.0000	−0.0693	0.0128	0.9750
gammk8	0.0315	0.9310	−0.0276	0.0015	−0.0601	0.0137	0.9732
cyclk8	0.6108	0.7236	−0.1753	−0.0215	0.0104	−0.1181	0.9419
culdk8	0.9160	−0.0804	−0.0186	0.0587	−0.1063	−0.0717	0.8656
intdk8	0.7523	0.5921	−0.1380	0.0020	−0.0202	−0.1078	0.9476
intpk8	0.0627	0.9474	0.0634	0.0158	−0.1345	0.0439	0.9258
armn_lk8	−0.1056	−0.0949	0.0559	0.0817	0.8090	0.1216	0.7656
arsd_lk8	−0.4043	−0.1828	−0.2205	0.1335	0.8462	−0.0645	0.9174
cntg_lk8	−0.7060	−0.1375	−0.3150	0.1159	0.4521	−0.2830	0.9145
frmn_lk8	−0.0128	−0.0998	0.9488	0.0263	−0.0388	0.0031	0.9125
pafr_lk8	0.5896	0.1030	0.2052	−0.2594	−0.3827	−0.1961	0.6525
pd_lk8	0.8602	0.0537	0.0508	−0.1522	−0.2727	0.1464	0.8643
pr_lk8	0.1464	0.1267	−0.0198	0.1228	−0.6790	0.0761	0.5197
shmn_lk8	−0.0227	−0.0609	0.9579	0.0478	−0.0798	−0.0396	0.9321
sidi_lk8	0.5496	0.1931	0.3845	−0.0812	−0.5013	0.2636	0.8145

Table 9 summarizes the set of metrics with highest loadings at different neighborhood buffer sizes. This set of results is also compared to the results from the oblique rotation and the maximum likelihood method of factoring. The interpretation of all sets of results employing different factoring methods remains to be consistent.

Table 9.

Summary table of loadings of retained metrics at different neighborhood scales

Metrics	Symbol	1 km buffer	3 km buffer	5 km buffer	8 km buffer
Road Density of Primary Roads With Limited Access	a10pct	−0.9277	0.8994	-	0.5240
Road Density of Primary Roads Without Limited Access	a20pct	0.9106	-	-	-
Road Density of Secondary Roads	a30pct	0.9370	−0.9221	−0.8009	-
Road Density of Local roads	a40pct	-	-	0.8582	0.9463
Land Patch Size (Root Mean Squared Error)	arsd	−0.9405	−0.8967	0.8759	0.8462
Connectivity Beta Index	beta	0.7200	0.9522	0.9832	0.9834
Cul-de-sac Density	culd	-	-	0.8825	0.9160
Connectivity Gamma Index	gamm	0.9765	-	-	-
Parks	parks	0.8807	0.5667	-	-
Mean Shape Index	shmn	0.9632	0.9286	0.9453	0.9579
Road Length	totkm	0.9565	0.8877	-	-

Validation results from cluster analyses further indicate that the reduced set of metrics is sufficient in interpreting different types of neighborhood forms. As shown in Table 10, when neighborhoods are defined by 1 km buffers, the cluster analysis on both sets of metrics – the original set of 27 metrics and the reduced set of 9 metrics – delineates 20,467 neighborhoods into seven types of neighborhoods: rural, rural cluster, exurban, greenfield suburban, outer suburban, inner suburban, and urban core. Furthermore, 94 percent of neighborhoods are defined to be in the same neighborhood type by two sets of results. This indicates that when the reduced set of metrics is used to define different neighborhood types, the results are to a great extent identical to those when a large set of redundant metrics are used. For brevity, results from cluster analyses for the other buffer sizes are not shown here but are available upon request from the authors.

Table 10.

Validation Results for 1-km buffers

Cluster Type	Descriptions of types (clusters) of neighborhood form	# of neighborhoods in each cluster (with 27 metrics)	# of neighborhoods in each cluster (with 9 metrics)	# of neighborhoods in the intersection of two sets of results
1	Rural: Extremely low road density and street connectivity, large land patches with almost no variety of land uses	4531	4548	4419
2	Rural cluster: very low road density and street connectivity, large land patches with limited variety of land uses	1839	1889	1721
3	Exurban: Very low road density and street connectivity, large land patches with limited variety of land uses	2744	2789	2529
4	Greenfield suburban: Low road density and connectivity, highway access, moderate size of land patches, limited variety of land uses	2554	2369	2260
5	Outer suburban: Moderate road density, low street connectivity, mid-size land patches, a bit variety of land uses	3732	3840	3630
6	Inner suburban: Moderate road density and connectivity, small-size land patches, moderate variety of land uses	2769	2648	2529
7	Urban core: High road density and connectivity, very small land patches, a high level of variety of land uses	2298	2214	2101
	Total:	20467	20467	19189 (94% of 20467)

4. Discussion and Conclusion

The exploration on neighborhood form and its associated outcomes has attracted a lot of attention by researchers and practitioners in recent decade. These studies on neighborhood form have relied either on limited and ill-defined metrics or on multiple but often highly intercorrelated measures of neighborhood form. There is a need for identifying a smaller set of metrics encompassing different dimensions of neighborhood form. This set of metrics has its benefits, including reducing computation work and being useful in statistical analysis on urban form and its associated outcomes. For example, in studies of physical activity, travel, and air quality outcomes of neighborhood form, a small set of uncorrelated metrics can be included as independent variables in regression equations to test their implications.

In this study, we first identify twenty-seven metrics of neighborhood form, grounded in the theoretical literature, that describe 20,467 neighborhoods using public, nationally available Geographic Information System (GIS) data. We then use factor analysis to reduce these metrics to six to nine measures depending on neighborhood sizes. Validation results further indicate that these factors sufficiently characterize neighborhood environments and they are: land diversity, street density, connectivity (both factual and probable), land shape complexity, number of parks, and road types (including accessible primary roads, limited primary roads, secondary roads, and local roads). These results suggest that a subset of neighborhood environment factors can be statistically isolated from a larger set of characteristics, and that the composition of the subset is only partially dependent on neighborhood size. Overall, the number of significant factors decreases as neighborhood size increases. Five of the nine factors are significant across three or more different neighborhood sizes, showing that this method produces relatively stable results as neighborhood size varies (Table 9). The most consistently significant factors include the density of limited primary roads and secondary roads, street network connectivity, neighborhood shape and variation in land patch size. Cul-de-sac density and the density of local roads are only significant for the larger (5 km and 8 km) neighborhood sizes. Road length and the number of parks are only significant for small (1 and 3 km) neighborhood sizes. Other findings of the study suggest that raw metrics have greater variation and thus result in a larger set of dimensions when the neighborhoods are defined by smaller buffers.

The metrics of neighborhood form identified in this study contributes to research in several ways. First, the metrics are quantifiable with clarity in illustrating concepts such as access and diversity. Second, the reduced metrics encompass different dimensions of urban form. Third, by minimizing intercorrelation between variables, these metrics are efficient to describe neighborhood form. Finally, since this sample of 20,467 neighborhoods covers a variety of representative neighborhood types across the United States (Nelson et al. 2006), the reduced set of metrics generated in this exercise may persist to other studies using different neighborhood definitions, such as zip codes, tracts, block groups, or user-defined boundaries.

Despite the above mentioned advantages, it is necessary to point out that our identification of metrics is limited by data availability, thus missing a range of both quantitative and qualitative indicators of neighborhood form such as the availability of public transit, bike lanes, sidewalks, scale of buildings, placement of buildings on lots, and so on. In addition, this quantitative approach of examining a national sample of neighborhoods is not feasible for carrying out visual analysis of neighborhood maps and aerial photos and in-the-field mapping of qualitative neighborhood characteristics. In comparison to qualitative metrics, the developed quantitative metrics are relatively abstract and are thus difficult for many members of the public to understand (Wheeler 2008). Nevertheless, this study generates a set of quantitative metrics which would be more convenient to researchers to facilitate studies of neighborhood form and associated outcomes at regional or national level. Future studies need to be carried out to include qualitative metrics developed in the field of urban design to achieve multiple research purposes, such as proposing sustainable urban design principles, based on fine-grained and policy-relevant assessment of neighborhood characteristics.

Research Highlights.

• We identify a reduced set of metrics to quantify neighborhood form for neighborhoods with varying sizes.

• Land diversity, street density, connectivity, shape complexity, and proportion of different road types can be used to quantify neighborhood forms sufficiently.

• A reduced set of neighborhood metrics reduces computation efforts.

• These neighborhood metrics can facilitate statistical analyses testing neighborhood form and community outcomes.