Linking In-Vehicle Ultrafine Particle Exposures to On-Road Concentrations

Abstract

For traffic-related pollutants like ultrafine particles (UFP, D_p < 100 nm), a significant fraction of overall exposure occurs within or close to the transit microenvironment. Therefore, understanding exposure to these pollutants in such microenvironments is crucial to accurately assessing overall UFP exposure. The aim of this study was to develop models for predicting in-cabin UFP concentrations if roadway concentrations are known, taking into account vehicle characteristics, ventilation settings, driving conditions and air exchange rates (AER). Particle concentrations and AER were measured in 43 and 73 vehicles, respectively, under various ventilation settings and driving speeds. Multiple linear regression (MLR) and generalized estimating equation (GEE) regression models were used to identify and quantify the factors that determine inside-to-outside (I/O) UFP ratios and AERs across a full range of vehicle types and ages. AER was the most significant determinant of UFP I/O ratios, and was strongly influenced by ventilation setting (recirculation or outside air intake). Inclusion of ventilation fan speed, vehicle age or mileage, and driving speed explained greater than 79% of the variability in measured UFP I/O ratios.

1. Introduction

Exposure to traffic related pollutants has been associated with detrimental health outcomes like asthma, exacerbation of adverse respiratory (Brauer et al., 2002; Gauderman et al., 2005; McConnell et al., 2006, Gan et al., 2011) and cardiovascular outcomes (Delfino et al., 2005), coronary artery atherosclerosis (Araujo et al., 2008; Kunzli et al. 2010), and an increase in mortality (Hoek et al., 2002; Stölzel et al., 2007; Wichmann et al., 2000). The particular components of traffic emissions responsible for causing adverse health effects are not known (Sioutas et al., 2005; Delfino et al., 2005), but ultrafine particles (UFP), defined as particles having aerodynamic diameter less than 100 nm, are of particular interest due to their large cumulative surface area, ability to trans-locate through the epithelium, as well as their elevated proportion of organic material and metals that results in high oxidative potential (Li et al., 2009; Delfino et al., 2005; Morgan et al., 2011).

Numerous studies (e.g., Leung and Harrison 1999; Westerdahl et al., 2005) have shown that UFP concentrations on or in the vicinity of roadways are frequently almost one order of magnitude higher than ambient levels. This has important implications for exposure assessment. For example, less than 10% of daily time spent in vehicular transit microenvironments (Klepeis et al., 2001) has been estimated to contribute 35-50% of total UFP exposure by Fruin et al. (2008) for Los Angeles residents under open window conditions, and 17% by Wallace and Ott (2011) for more suburban locations. However, large variations in exposure inside vehicles are expected to occur not only due to differences in roadway environments, but also because inside-to-outside (I/O) ratios (i.e., in-vehicle to roadway concentration ratios) vary vehicle to vehicle from nearly zero to one (Knibbs et al., 2010; Hudda et al., 2011).

Recent studies have shown that I/O ratio is strongly dependent on air exchange rate (AER), which is defined as the number of times per hour vehicle cabin air is replaced by roadway or outside air. Knibbs et al. (2010) reported an r² of 0.81 (Pearson correlation coefficient) between AER and I/O ratios and Hudda et al. (2011) reported an r² of 0.75 or 0.80, depending on ventilation choice. Both of these studies performed measurements under real driving conditions (multiple speed and ventilation conditions) and found that ventilation preference (windows open, outside air intake or in-cabin air recirculation) and ventilation fan setting strongly influence AER and the resulting I/O ratio. With closed windows and ventilation set to re-circulate cabin air, I/O ratios were lowest, but widely ranging, with vehicle speed and vehicle age strongly affecting AER and I/O ratios (Fruin et al., 2011; Hudda et al., 2011). For closed window conditions with ventilation set to outside air intake, I/O ratios were higher, and ventilation fan strength was the primary determinant of AER (Fruin et al., 2011) as well as I/O ratio (Hudda et al., 2011). Open windows typically led to such high AER that I/O ratios were nearly 1.0 (Hudda et al., 2011).

Other studies that have measured UFP I/O ratios include Pui et al. (2008) and Qi et al. (2008), who investigated in-cabin air filter efficiency, and found large UFP reductions inside two new vehicles under recirculating conditions, although AER or speed was not reported. Zhu et al. (2007) also reported large reductions in in-vehicle UFP concentrations in three vehicles. As their measurements were performed under conditions of variable speeds, AER fluctuated and only estimated indirectly from concentration change time lags. Therefore, prior to Knibbs et al. (2010), no in-vehicle UFP I/O ratio results have been reported in a form that can be generalized. Other recent studies (Gong et al., 2009; Xu et al., 2009) that have produced mechanistic models of particle losses inside vehicles relied on parameters like particle penetration through cracks and surface deposition rates, which while useful, are not obtainable outside of a laboratory setting.

As it is impractical to measure either the I/O ratio or AER for large numbers of subjects’ vehicles as required in an epidemiological study addressing drive-time exposure, predictive models are needed for estimating AER and I/O ratios. If these models could be based on information that can be collected via questionnaire, for example, they would be useful tools for more accurately estimating personal UFP exposures. The purpose of this study was to measure UFP I/O ratios (and AER) in a sufficiently large number of vehicles to develop accurate predictive models for assessing drive-time UFP exposure based on easy-to-obtain information.

2. Methods

2.1 Vehicle selection and ventilation conditions tested

Vehicles were selected to provide a wide distribution of age and mileage, which are both important factors affecting AER, albeit highly correlated. See Fruin et al. (2011) for more details. Although the measurements presented in Hudda et al. (2011) are included in the models presented here, we more than doubled the previous I/O and AER measurement dataset to adequately cover the full range of speed, vehicle, and ventilation settings necessary for optimum model performance. Finally, to incorporate both all ventilation conditions and particle measurements under non-steady speeds in this modelling, we included data from Sydney (Australia) with ours collected in Los Angeles (Knibbs et al., 2009; 2010).

All together, measurements were performed in 73 vehicles that were selected from different size categories (sub-compact, compact, mid-size, etc.) in proportions similar to their presence in U.S. fleet. Table S1 in Supporting Information summarizes the vehicle make, model, age and mileage at the time of testing and Section S.3.1 gives the study fleet age distribution comparison to the U.S. fleet from the U.S. EPA's Office of Transportation and Air Quality's Motor Vehicle Emission Simulator (MOVES) data.

Measurements were made with the air conditioning system operating at both ventilation setting options: recirculation (RC), where the in-cabin air is re-circulated, and outside air intake (OA), where outside air is drawn into the vehicle cabin and passed through a filter (if present). Almost all vehicles tested in Los Angeles had cabin air filters in the ventilation loop (i.e. capable of filtering air under both RC and OA). Only two of the vehicles tested in Sydney had filters, and these were of the basic ‘pollen filter’ type, and filtered OA but not RC air. This resulted in slightly higher I/O ratios in the vehicles tested in Sydney as cabin filters typically reduce I/O ratios by 0.1 or less (Hudda et al., 2011). Overall, AER was measured for 453 specific combinations of vehicle, speed, and ventilation fan setting in 73 vehicles (308 at RC and 145 at OA setting) and I/O ratio was measured for 241 combinations in 43 vehicles (110 at RC and 131 at OA setting).

2.2 Speed and routes driven

In the Los Angeles measurements, in order to maintain a steady AER measurements were made while driving at near constant speeds that ranged from 20- 65 miles h^-1. Experiments at speeds up to 35 miles h^-1 were conducted around the Rose Bowl, Pasadena, a 3.3 mile continuous loop where vehicular traffic was light. Measurements at speeds ranging from 55-70 miles h^-1 were made on Freeways I-10, CA-60 and I-605 during free flowing traffic conditions. An on-board Global Positioning System (GPS) device (Garmin GPSMAP 76CSC) recorded the location and speed of the car at one second interval.

In Sydney, UFP measurements were performed during trips through a 2.5 mile long road tunnel and on above-ground roads in its vicinity. AER measurements were performed separately with test vehicles stationary and when driving on open roads at 37 and 68 miles h^-1. The UFP and ventilation measurements are described in detail by Knibbs et al. (2009) and (2010), respectively. Each I/O ratio sampling session in a given vehicle involved multiple trips through the tunnel (reported in Knibbs et al. (2010)) interspersed with above-ground travel; data from both of these locations were used to develop the models described in this paper. Average vehicle speeds on each segment of the sampling route were calculated based on known distance and time taken, because poor satellite reception impeded GPS based measurements of speed.

2.3 AER, particle concentration, and I/O ratio measurement

Air exchange rates were determined using Carbon Dioxide (CO₂) as a tracer gas and measurements were made using either TSI Q-Trak model 7565 (TSI Inc., MN, USA) or LICOR Li-820 units (LI-COR Biosciences, NE, USA) for the vehicles that were tested in Los Angeles. The AER determination procedure is detailed in Fruin et al. (2011) and Hudda et al. (2011). Sulfur hexafluoride was used as a tracer gas for the vehicles tested in Sydney using an Innova 1412 (Lumasense Technologies, Ballerup, Denmark) photo-acoustic field gas monitor and Innova 1303 multipoint sampler and doser. Further details for these measurements can be found in Knibbs et al. (2009). Fruin et al. (2011) have previously demonstrated very good agreement between their predictions of results reported by Knibbs et al. (2009) (Pearson r² = 0.83), despite the use of different tracer gases.

Particle number concentrations measurements at both locations were performed with a TSI Model 3007 Condensation Particle Counter (CPC) with a 50% lower size detection limit of 10 nm. Two CPCs were used to measure inside and outside concentrations simultaneously in Los Angeles, except for a small number of measurements where inside and outside measurements were conducted in an alternating manner. For those tests, on road concentrations were shown to be stable during the measurement periods. The CPC recording outside concentrations pulled through a meter long conductive silicon tube during mobile tests and particle losses were insignificant. Inside concentration measurements required no tubing. Measurements in Australia were conducted using a single CPC that alternated between inside and outside measurements every 20-25 seconds. Only the last 10 seconds of data in each 20-25 second block was used in further analyses in order to allow for sample clearance time and instrument response.

In Los Angeles, in-vehicle to roadway concentration ratios were determined as the average value observed for at least 10 minutes of measurement after a stable value had been attained (i.e., a standard deviation less than 5%). To harmonize the I/O ratio measurements across the two study locations, those performed in Sydney (Knibbs et al., 2010) were weighted by their respective durations. Data quality assurance at both locations comprised regular flow and zero reading checks. In Los Angeles, all instruments used were run simultaneously before and after test runs to check for consistency of response and ambient concentrations. All instruments were synced to within one second of the time recorded by GPS. Table S2 in the Supporting Information provides further information on instruments.

2.4 Predictive models

Models were developed to predict AER and I/O ratios for UFPs under both RC and OA conditions, using the following as candidate independent variables: ventilation fan (fraction of maximum setting), vehicle age (years), mileage (thousands of miles), speed (miles h^-1), manufacturer (United States, Japan or Germany/Other), interior volume (ft³), and the product of coefficient of drag (C_d) and frontal area (A, m²) along with pair-wise interactions between vehicle speed, age, and fan setting, and between C_d and frontal area of the vehicle. Ventilation fan fraction was defined as the ratio of the selected fan setting to the total number of options for fan setting. For example, if a vehicle had seven fan setting options and was operated at the third strongest option, the fan setting was set to 3/7 (or, = 0.43) in the models.

Since AER was positively skewed, natural log transformed AER (lnAER) was used as the outcome in AER prediction models. For I/O ratios, which varied between 0 and 1, a logit transformation (the natural log of [I/O]/ [1-(I/O)]) was used, often more appropriate for fractions. Predicted values on the original scales can be recovered using the equations AER = exp(lnAER) and I/O = exp(logit I/O)/(1+exp(logit I/O)).

Because multiple measurements of I/O ratio and AER were performed in each vehicle at different speeds and/or ventilation settings, these repeated measurements were sometimes correlated. This correlation violates the assumption of completely independent observations in multiple linear regression (MLR) models, and MLR models fit to correlated data have unbiased regression coefficients but incorrect standard errors (Diggle et al., 2002). To account for correlated observations, we present results from Generalized Estimating Equation (GEE) models (Liang et al., 1986) for continuous outcomes, with an exchangeable correlation structure (assumes that there is a single, uniform correlation between all repeated measurements from the same vehicle, after controlling for the included predictor variables) and robust sandwich estimates of regression coefficient standard errors (produces valid standard errors even if the covariance structure is misspecified). MLR estimated regression coefficients were similar to those from GEE and are provided for comparison. Model fit was assessed by adjusted R² and by leave-one-vehicle-out cross-validated adjusted R², which provides a more reliable estimate of the predictive ability of the same model fit to a new dataset containing information on different vehicles.

All-subset MLR was used to identify the most important set of predictor variables. From this set, a parsimonious GEE model was developed that included all lower-ordered terms of any interactions or squared variables, had high cross-validated adjusted R², statistically significant predictor effects (α = 0.10), and satisfied linear model assumptions. For each model, significance of an indicator variable for Sydney data was also evaluated. Residuals were inspected to assess model assumptions of linearity, normality, and homoskedasticity.

3. Results and discussion

3.1 In-vehicle-to-roadway concentration ratios

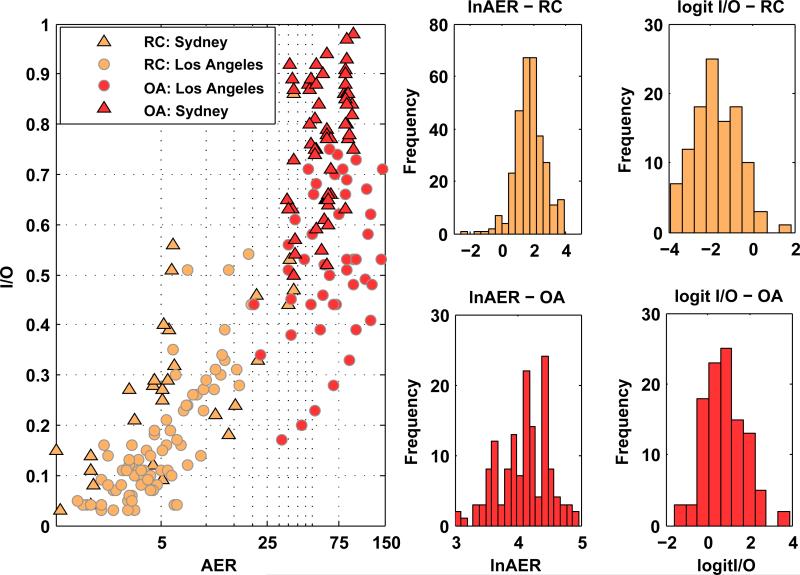
The I/O ratios measured under RC conditions were far lower than those under OA conditions due to lower AERs under RC (Hudda et al., 2011). The median I/O ratio value at RC was 0.11 (inter-quartile range: 0.07-0.22) compared to 0.66 at OA (inter-quartile range: 0.53-0.80). The median AER value at RC was 6.0 h^-1 (inter quartile range: 3.6-10 h^-1) compared to 63 h^-1 for OA (inter quartile range: 47-83 h^-1). The maximum uncertainty associated with AERs was 7.5%, using root mean square error propagation accounting for both instrument accuracy and stability of continuous measurements for AER measurements. The uncertainties of the I/O ratios were slightly less, 7%, since it is only determined by the stability of continuous measurements for I/O ratio. Figure 1 shows the distributions of AER and I/O ratio results and their transformed values, under both RC and OA ventilation mode. The measurements in Los Angeles and Sydney have been differentiated in the sub-figures.

Figure 1.

Distributions and relationship between measured AER and measured I/O ratios used in models.

3.2 Predictive model for ln(AER) at RC and OA setting

The GEE model gave the following Equations 1 and 2 for predicting lnAER under RC and OA condition, respectively.

$$ln\left(AER\right)=2.79+(0.019\times speed)+[0.015\times age+3.3\times {10}^{-3}ag{e}^2]+[-0.023\times vol+6.6\times {10}^{-5}vo{l}^2]+ManufAdjustment$$ Equation 1

where the manufacturer adjustment is -0.71 for German vehicles and -0.39 for Japanese vehicles. If the speed is zero, a -0.51 factor should be added.

$$ln\left(AER\right)=4.20+[(1.88\times fanstrength)+(-0.92\times fanstrengt{h}^2)]+(0.0048\times speed)+(-0.0073\times vol)$$ Equation 2

where the coefficients for fan strength and fan strength² should be 0.40 and 0.13, respectively, at zero speed, and the speed term should be -0.32 at zero speed.

These models had good fit and are likely to have a similar ability to predict AER in different datasets (GEE adjusted R²: 0.68 for RC and 0.79 for OA; GEE cross-validated adjusted R²: 0.60 for RC and 0.73 for OA). MLR and GEE regression coefficients were similar, but the GEE confidence intervals (which appropriately account for the correlation of repeat measurements on the same vehicles) were roughly a third larger than MLR intervals (Tables 1 and 2). In all AER model runs, an indicator variable for Sydney data was not significant.

Table 1.

AER under RC Model Coefficients, Confidence Intervals, and P Values

GEE	Estimate	Std.err	Wald	Pr(>|W|)	Confidence Intervals
					2.5%	97.5%
Intercept	2.79	0.36	62	4.10E-15	2.1	1.1
speed > 0 (miles h-1)	0.019	0.0013	223	< 2e-16	0.017	0.0038
speed = 0	-0.51	0.12	19	1.60E-05	-0.75	0.36
age (yr)	0.015	0.031	0.24	0.62	-0.046	0.092
age2 (yr2)	0.0033	0.0017	4.0	0.045	-0.000032	0.0050
vol (ft3)	-0.023	0.0049	21	4.00E-06	-0.033	0.015
vol2 (ft6)	0.000066	0.000015	18	1.90E-05	0.000037	0.000044
Manuf: Japan	-0.39	0.12	11	0.00091	-0.63	0.36
Manuf: Germany	-0.71	0.25	8.1	0.0045	-1.2	0.74

MLR	Estimate	Std. Error	t value	Pr(>|t|)	Confidence Intervals
					2.5%	97.5%
Intercept	2.97	0.28	10.75	< 2e-16	2.43	3.52
speed > 0 (miles h-1)	0.018	0.0020	8.93	< 2e-16	0.014	0.022
speed = 0	-0.49	0.11	-4.34	2.00E-05	-0.71	-0.27
age (yr)	0.010	0.019	0.53	0.59313	-0.027	0.047
age2 (yr2)	0.0039	0.0011	3.67	0.00029	0.0018	0.0060
vol (ft3)	-0.025	0.0037	-6.77	6.80E-11	-0.032	-0.018
vol2 (ft6)	0.000074	0.000013	5.69	3.00E-08	0.000048	0.000099
Manuf: Japan	-0.34	0.070	-4.86	1.90E-06	-0.48	-0.20
Manuf: Germany	-0.88	0.12	-7.26	3.30E-12	-1.11	-0.64

Table 2.

AER under OA Model Coefficients, Confidence Intervals, and P Values

GEE	Estimate	Std.err	Wald	Pr(>|W|)	Confidence Intervals
					2.5%	97.5%
Intercept	4.2	0.24	295	< 2e-16	3.7	0.7
fan strength	1.88	0.14	170	< 2e-16	1.6	0.43
fan strength2	-0.92	0.11	70	< 2e-16	-1.1	0.33
speed = 0	-0.32	0.09	11	0.0007	-0.50	0.28
speed > 0 (miles h-1)	0.0048	0.0013	14	0.0002	0.0023	0.0038
vol (ft3)	-0.0073	0.0019	15	0.0001	-0.011	0.0056
fan strength at speed = 0	0.40	0.26	2.5	0.12	-0.10	0.76
fan strength2 at speed = 0	0.13	0.20	0.45	0.50	-0.26	0.59

MLR	Estimate	Std. Error	t value	Pr(>|t|)	Confidence Intervals
					2.5%	97.5%
Intercept	4.2	0.14	29	< 2e-16	3.9	4.5
fan strength	2.3	0.40	5.7	0	1.5	3.1
fan strength2	-1.3	0.36	-3.7	0.00040	-2.1	-0.61
speed = 0	-0.34	0.15	-2.3	0.023	-0.63	-0.047
speed > 0 (miles h-1)	0.0043	0.0014	3.0	0.0028	0.0015	0.0071
vol (ft3)	-0.0074	0.00080	-8.8	0	-0.0090	-0.0057
fan strength at speed = 0	0.077	0.56	0.14	0.89	-1.0	1.2
fan strength2 at speed = 0	0.45	0.49	0.91	0.36	-0.5	1.4

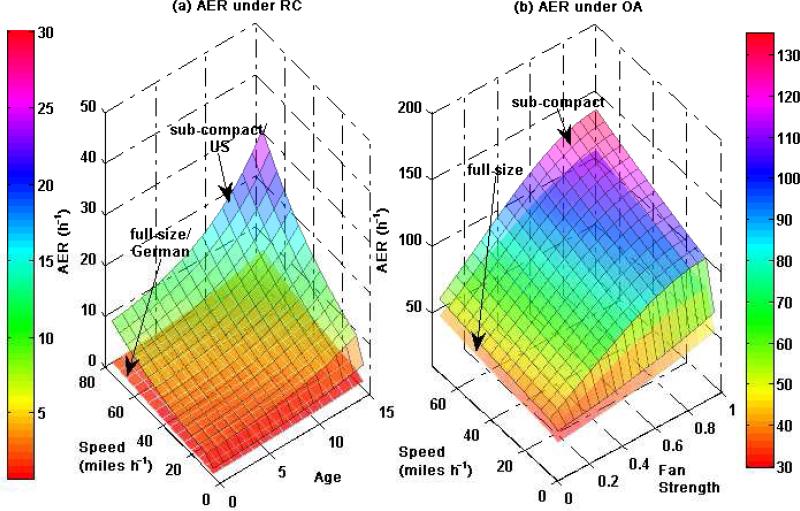
The predicted AER under RC conditions is plotted against the two most significant determinants of AER, speed and age, in Figure 2 (a). Model results suggest that an 11 year old vehicle (~ 75^th age percentile) has an AER that is about 1.5 times higher than that of a 4 year old vehicle (~25^th age percentile). Furthermore, AER during typical freeway driving speed (65 miles h^-1) is expected to be 1.8 times higher than under typical arterial driving conditions (35 miles h^-1). See Figures S-1 and S-2 in Supporting Information for predicted lnAER vs. measured lnAER plots.

Figure 2.

Predicted values for AER plotted against two most significant variables under RC and OA ventilation modes.

The two surfaces plotted in 2 (a) represent the extremes of other model inputs under RC conditions: a U.S. manufactured sub-compact vehicle (85 ft³ cabin) and a German manufactured large vehicle (120 ft³ cabin), the range of AER variation that can be expected due to manufacturer and volume. A U.S. manufacturer's vehicle is expected to have an AER nearly 50% higher than a Japanese vehicle and about twice as high as a German manufactured vehicle, for given cabin volume, age and speed. It is interesting that cabin volume was negatively correlated with AER when expressed in units of air changes per hour under RC conditions (Similar relationship was found with I/O ratio, discussed in following section). For example, an 85 ft³ vehicle is expected to have an AER, which is 2.2 times that in a 120 ft³ vehicle (or 1.6 times higher if AER units are ft³ h^-1). To provide a typical AER value under RC conditions for reference, a seven-year-old vehicle (50^th age percentile, U.S. manufactured, and 110 ft³, the average U.S. fleet cabin volume) would have an AER of 3.7 h^-1 at 35 miles h^-1 and 6.7 h^-1 at 65 miles h^-1.

Under OA conditions, fan strength explained the most variability in lnAER, followed by speed. For example, increasing a four-setting fan from low (0.25) to medium (0.5) to highest (1.0) increased the AER by a factor of 1.3 and 1.7, respectively. In comparison, increasing the driving speed, the second most significant variable, from arterial to freeway speeds only increased the AER by 1.2. Vehicle cabin volume was also found to be significant, with higher volume vehicles having lower predicted AER (h^-1). An 85 ft³ sub-compact vehicle had 1.3 times higher AER than a 120 ft³ large sedan. Fan strength and zero speed interaction terms, while not significant individually, were significant as a pair, so included in the OA model.

Figure 2 (b) shows the model predictions plotted against the two most significant determinants of AER under OA conditions; ventilation fan strength and vehicle speed, for a sub-compact (85 ft³) and large sedan vehicle (120 ft³), thus capturing the full range of AERs that can be expected under OA condition. For the previously mentioned reference vehicle travelling at 35 and 65 miles h^-1, AER would be 72 h^-1 and 83 h^-1, respectively, at the middle fan setting, roughly an order of magnitude higher than under RC conditions.

3.3 Predictive model for logit(I/O) under RC and OA setting

I/O ratios under both ventilation conditions were modeled together, using a binary indicator variable for RC setting, (i.e., variable RC = 1 under RC setting and zero otherwise). The resultant Equations 3 and 4 from the GEE model for predicting I/O ratios under RC and OA conditions are as follows:

$$\text{logit}(I∕O)=-(0.29+2.93)+0.54\times fanstrengthh+0.025\times speed+(0.017+0.086)\times age$$ Equation 3

$$\text{logit}(I∕O)=-0.29+0.54\times fanstrength+0.025\times speed+0.017\times age$$ Equation 4

This estimated model (Table 3) also had good fit and predictive ability (GEE adjusted R²: 0.79; GEE cross-validated adjusted R²: 0.76) using only vehicle age, speed, ventilation fan strength, and ventilation setting. For the I/O ratio modelling, the indicator variable for Sydney was significant (p-value: 0.02), but including this variable did not substantially improve the predictive ability of the model (GEE cross-validated adjusted R²: 0.78). This variable was omitted in the final model since it would not be useful to other users of the model. The final models do not include AER as a predictor variable because preliminary models that included measured or predicted AER had similar R² to the final models. Therefore, after stratifying on ventilation setting, and including fan strength, age and speed as predictor variables (most of which are strong predictors of AER) in the models for logit(I/O), additional inclusion of AER itself did not explain an important amount of additional variability in logit(I/O). See Figure S-3 in the Supporting Information for predicted logit(I/O) vs. measured logit(I/O) plot.

Table 3.

I/O ratio GEE Model Coefficients, confidence intervals and p-values

GEE Model
	Estimate	Std.err	Wald	Pr(>|W|)	Confidence Intervals
					2.5%	2.5%
Intercept	-0.29	0.19	2.4	0.12	-0.65	0.078
fan strength	0.54	0.21	6.8	0.0091	0.14	0.95
speed (miles h-1)	0.025	0.0028	81	< 2e-16	0.019	0.030
age (yr)	0.017	0.02	0.84	0.36	-0.020	0.055
RC	-2.95	0.14	468	< 2e-16	-3.2	-2.7
RC ×age (yr)	0.086	0.019	20	7.0e-6	0.048	0.12

MLR Model
	Estimate	Std.err	Wald	Pr(>|W|)	Confidence Intervals
					2.5%	2.5%
Intercept	-0.31	0.14	-2.2	0.033	-0.59	-0.026
fan strength	0.30	0.17	1.8	0.074	-0.029	0.62
speed (miles h-1)	0.033	0.0027	12	< 2e-16	0.028	0.039
age (yr)	0.042	0.011	3.9	0.00013	0.021	0.063
RC	-2.93	0.13	-22	< 2e-16	-3.19	-2.67
RC ×age (yr)	0.06	0.02	3.9	0.00013	0.031	0.093

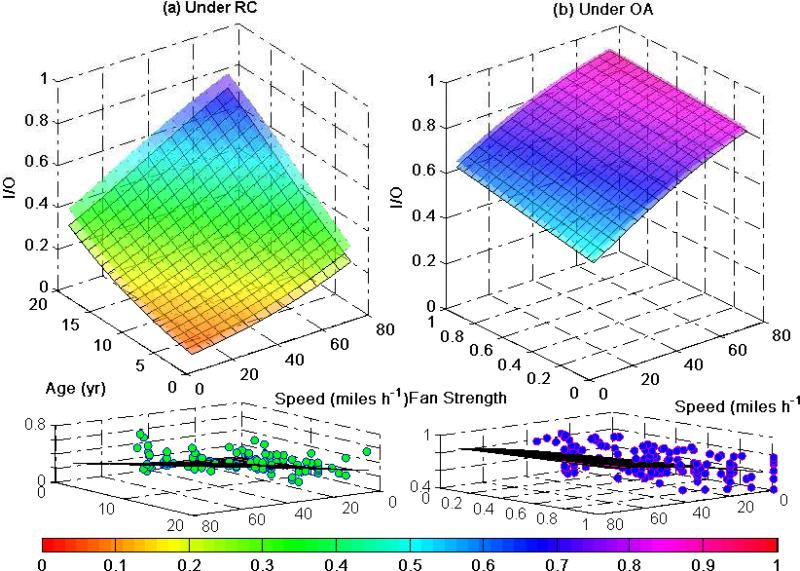
Figure 3 (a) shows the full range of I/O ratios that can be expected in vehicles up to 20 years old and travelling at speeds up to 75 miles h^-1, with age and speed being the most important predictors. Under RC ventilation conditions, I/O ratios can be expected to vary from less than 0.1 to nearly 0.8 in the most leaky vehicles (old and travelling at high speeds). The two surfaces mark the upper (full fan) and lower limits (low fan setting, equal to 0.33) of variation that can be expected due to the third most significant variable, fan strength. Under RC conditions, fan setting was relatively unimportant. For the entire range of age/speed plotted in Figure 3 (a), fan strength made an average difference of only 0.07 ± 0.02 in I/O ratio.

Figure 3.

Predicted values for I/O ratios under RC and OA ventilation mode versus two most important model variables for each mode. Bottom subsets show actual measurements versus surface of median model predictions.

In contrast, under OA conditions, I/O ratios were most strongly dependent on vehicle speed and fan speed. I/O ratios were higher but had a smaller range compared to RC conditions, varying from 0.5 – 0.9 (Figure 3 (b)). The plotted surfaces in Figure 3 (b) mark the lower (25^th age percentile) and upper bounds (75^th age percentile) of predicted I/O ratios due to variation in the third variable, vehicle age, though the distinction is barely discernible. Age (by itself) under OA was not significant and made a maximum difference of 0.03 in I/O ratios predicted using Equation 4. The lower subset figures show measured I/O ratios plotted along with median predicted surface to show modeled data fit.

We performed a sensitivity analysis based on maximum expected variable measurement uncertainty: 5 miles h^-1 uncertainty in speed, 1 year in vehicle age, and a 10% uncertainty in fan speed based on fraction of maximum. These uncertainties led to 8.0, 5.6, and 3.4% difference in I/O ratio, respectively. These relatively modest changes reflect maximum uncertainties. Typical uncertainties would tend to be smaller, and since independent, would tend to cancel each other out (i.e., they are just as likely to be positive as negative). However, the model predictions may be less accurate for vehicles older than 15 years and at speeds exceeding 60 miles h^-1 due to limited coverage of measured data for such conditions.

3.4 Fleet-wide distributions of AER and I/O ratio

To calculate individual in-vehicle UFP exposures, the models presented in previous sections for prediction of AER and I/O ratios require six inputs: (a) ventilation setting; (b) fan setting; (c) manufacturer; (d) vehicle age; (e) speed; and (f) vehicle volume. For conducting a large epidemiological study, these variables can be gathered directly through a questionnaire or generated from vehicle-related information like age, vehicle identification number (which holds information on model, make and manufacturer), and driving/trip related information like ventilation setting choice, fan setting, and trip time and destination.

To calculate population-size distributions of in-vehicle UFP exposure, the distribution of predicted AER and I/O ratios in a fleet of vehicles can be computed if required input variable distributions for the fleet are known. As an example, probability distributions for AER and I/O ratio (predicted using Equations 1, 2, 3 and 4) were computed for a fleet of sedan type vehicles using input distributions based on the U.S. fleet.

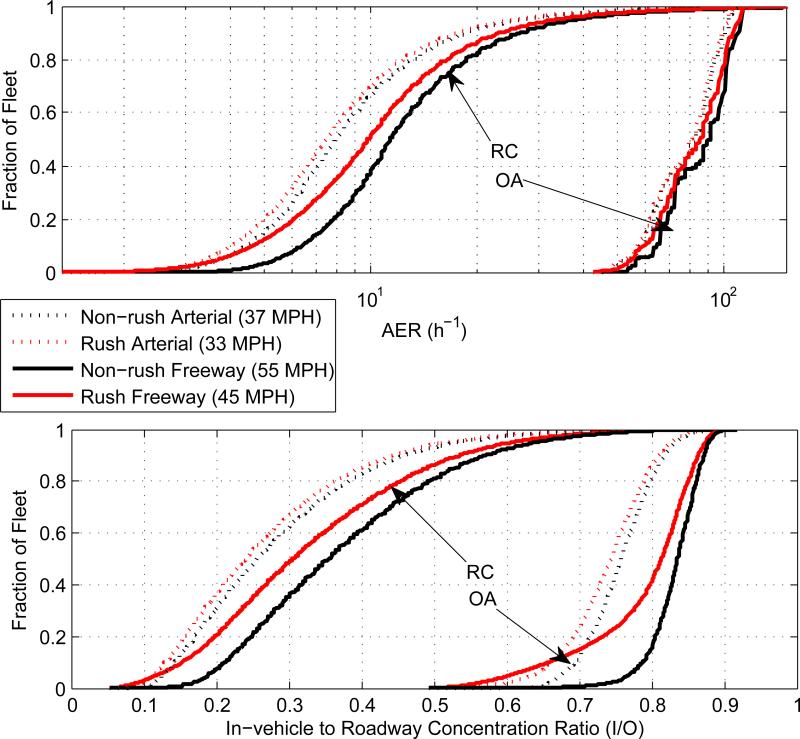
Vehicles were divided into three categories based on average cabin volume for three size categories: compact (99 ft³), mid-size (112 ft³) or full-size (135 ft³). The frequency of each size was determined from the fraction of passenger cars in each volume category for the years 1990-2010, EPA (2010). For fan setting, it was arbitrarily assumed that an equal fraction of vehicles were being driven at three fan settings, low (fan setting = 0.33), medium (0.67) and highest (1.0). The current fractions of manufacturer share were used: (44.5% U.S., 42% Japanese and 13.5% German/other). For age and speed, EPA Motor Vehicle Emission Simulator (MOVES) default age and speed inputs for gasoline passenger cars were used. Different speed distributions were used for arterial roads and freeways, which also varied with respect to time of day (i.e., rush hour or non-rush hour). The weighted average speeds were 33 and 37 miles h^-1, respectively, for arterial roads during rush hours and non-rush hours, and 45 and 55 miles h^-1, respectively, for freeways. Further details on all these input distributions have been presented in the Supporting Information.

The fractions of vehicles having a specific AER or I/O ratio are plotted in Figure 4 for both ventilation choices (RC and OA). Several important observations can be made from Figure 4. First and foremost, though roadway type and associated speed differences affect AER and I/O ratios, the most significant difference occurs due to ventilation setting choice. Under RC conditions, 80% of the fleet is expected to have I/O ratio between 0.15 and 0.5—significant protection—under all road types and speeds, but for OA conditions, 80% all vehicles are expected to have I/O ratios from 0.65 to 0.85, only moderately reduced concentrations. Looked at another way, under RC conditions, the fraction of vehicle fleet that will experience cabin concentrations lower than half of on-road concentrations exceeds 80%, but virtually none of the fleet is expected to have I/O ratios less than 0.5 under OA conditions. Furthermore, the difference between rush hour and non-rush hour speed distributions leads to a far more significant difference in AER and I/O ratio distribution for freeway driving than arterial driving.

Figure 4.

Distribution for AER and I/O ratio for a fleet similar to U.S. passenger car fleet in terms of manufacturer's market share, vehicle volume and age.

3.5 Expected in-cabin concentrations for given roadway concentrations

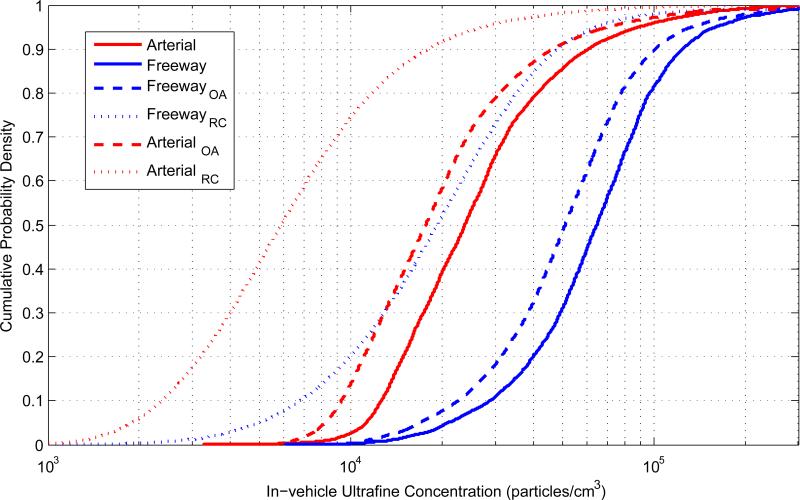
The ultimate goal of generating predictive models for I/O ratios is to be able to predict in-cabin concentrations from roadway concentrations (calculated as Concentration_in-cabin = I/O x Concentration_roadway). To illustrate, representative probability distributions of UFP concentrations were generated from sampling on arterial roads and freeway I-710 in Los Angeles and are shown in Figure 5. (Actual concentrations at various percentiles are presented in the Supporting Information.) In turn, these distributions were joined in a Monte Carlo-type sampling method with the I/O ratio distributions in Figure 4 to generate distributions of UFP concentrations inside the U.S. vehicle fleet if driven on those Los Angeles roads.

Figure 5.

Expected in-cabin concentration for U.S. vehicle fleet travelling on Los Angeles arterial roads and freeway I-710.

Comparison of the measured roadway concentrations and the predicted in-cabin concentrations under RC and OA conditions shown in Figure 5 suggests that for the range of fleet vehicle characteristics such as age and mileage (e.g., 25^th to 75^th percentile differences for a ventilation setting and road type), we would expect a two to three-fold range in in-vehicle UFP exposures (more under RC than OA), while the differences due to ventilation mode selection alone for a given vehicle on either road type were larger, with factors ranging from two to four. The increase in speed going from arterial to freeway speeds, along with increase in on-road concentrations on freeways, increased in-vehicle UFP exposure for a given vehicle at either ventilation mode by nearly three-fold.

4. Conclusions

Models have been presented for predicting UFP in-vehicle to roadway concentration ratios (I/O) based on simple driving preferences and vehicle characteristics. Scalability of these models was demonstrated at a fleet-wide level and in dynamic roadway environments. In general, factors that increase air exchange rates (AER) increase UFP I/O ratio. Age was significant and positively correlated with both AER and I/O ratios under recirculation ventilation setting (RC), but age was not significant under fresh air intake setting (OA). Under OA conditions, fan strength was a strong determinant and positively correlated with I/O ratio. Under both ventilation settings, an increase in vehicle volume decreased I/O ratios. Overall, combining these results with on road UFP concentration distributions measured on Los Angeles roadways, in-cabin UFP exposure concentrations during freeway driving were up to three times that of arterial driving, but the switch from OA ventilation condition to RC dropped the in-vehicle concentration on either road type two- to four-fold.

Highlights.

• Significant overall ultrafine particle (UFP) exposure occurs in vehicles

• In-vehicle exposures depend on inside-to-outside UFP ratios (I/O)

• At outside air setting (OA), I/O is determined mostly by fan strength

• Under recirculation (RC), I/O is determined by vehicle age and speed

• Fleet-wide UFP exposure varies 10-fold