Abstract
Gleason patterns of prostate cancer histopathology, characterized primarily by morphological and architectural attributes of histological structures (glands and nuclei), have been found to be highly correlated with disease aggressiveness and patient outcome. Gleason patterns 4 and 5 are highly correlated with more aggressive disease and poorer patient outcome, while Gleason patterns 1–3 tend to reflect more favorable patient outcome. Because Gleason grading is done manually by a pathologist visually examining glass (or digital) slides subtle morphologic and architectural differences of histological attributes, in addition to other factors, may result in grading errors and hence cause high inter-observer variability. Recently some researchers have proposed computerized decision support systems to automatically grade Gleason patterns by using features pertaining to nuclear architecture, gland morphology, as well as tissue texture. Automated characterization of gland morphology has been shown to distinguish between intermediate Gleason patterns 3 and 4 with high accuracy. Manifold learning (ML) schemes attempt to generate a low dimensional manifold representation of a higher dimensional feature space while simultaneously preserving nonlinear relationships between object instances. Classification can then be performed in the low dimensional space with high accuracy. However ML is sensitive to the samples contained in the dataset; changes in the dataset may alter the manifold structure. In this paper we present a manifold regularization technique to constrain the low dimensional manifold to a specific range of possible manifold shapes, the range being determined via a statistical shape model of manifolds (SSMM). In this work we demonstrate applications of the SSMM in (1) identifying samples on the manifold which contain noise, defined as those samples which deviate from the SSMM, and (2) accurate out-of-sample extrapolation (OSE) of newly acquired samples onto a manifold constrained by the SSMM. We demonstrate these applications of the SSMM in the context of distinguish between Gleason patterns 3 and 4 using glandular morphologic features in a prostate histopathology dataset of 58 patient studies. Identifying and eliminating noisy samples from the manifold via the SSMM results in a statistically significant improvement in area under the receiver operator characteristic curve (AUC), 0.832 ± 0.048 with removal of noisy samples compared to a AUC of 0.779 ± 0.075 without removal of samples. The use of the SSMM for OSE of newly acquired glands also shows statistically significant improvement in AUC, 0.834 ± 0.051 with the SSMM compared to 0.779 ± 0.054 without the SSMM. Similar results were observed for the synthetic Swiss Roll and Helix datasets.
Keywords: Manifold Learning, Statistical Shape Models, Regularization, Prostate Histology, Gleason Grading
1. Introduction
Blinded needle sextant biopsy is the current gold standard for prostate cancer (CaP) diagnosis; each biopsy yields 12–18 needle cores which are then analyzed under a microscope by a pathologist [1, 2]. If CaP is identified, a pathologist will then assign a Gleason score to the biopsy samples, determined as a summation of the two most prevalent Gleason patterns which range from 1 to 5, hence, Gleason score has a range of 2–10 [3]. Low Gleason patterns (1–3) are characterized by a coherent spatial architecture with distinct gland lumen surrounded by cell nuclei [3, 4]. For higher Gleason patterns (4 and 5), the arrangement and morphology of histological structures begins to breakdown with gland lumen becoming indistinct and crowded with an increase in the concentration of cell nuclei. The most dominant Gleason patterns seen on needle biopsies are patterns 3 and 4 [5]. Accurately distinguishing intermediate Gleason patterns 3 and 4 manually is a difficult problem; previous studies having reported an inter-observer agreement between pathologists of 0.47–0.64 (reflecting low to moderate agreement) [6, 7]. Gleason score aids in determining the course of treatment, patients with less aggressive CaP (Gleason score 6 and under) may be enrolled in active surveillance programs while patients with more aggressive CaP (Gleason score 7 and above) will undergo radiation therapy or surgery [8].
Availability of digital prostate histology samples [9] has led to the development of computer assisted decision support tools which allow for quantification of subtle morphologic changes in prostate tissue and may potentially allow for better and more reproducible discrimination between Gleason patterns [10–19]. Previous attempts at building computer aided decision support tools for Gleason scoring have employed the use of image texture [10, 14, 18], arrangement and morphology of nuclei [12, 13, 15, 19], or morphology of glands [16, 17]. However, a large number of features are typically necessary to accurately perform Gleason grading of histology images, resulting in a high dimensional feature space [12, 15]. The high dimensional feature space may have more dimensions than samples in the dataset, referred to as the curse of dimensionality, which makes classification infeasible [20].
Dimensionality reduction offers a way to overcome the curse of dimensionality by constructing a low dimensional space in which to perform classification while not compromising object-class relationships. Manifold learning (ML) refers to a class of nonlinear dimensionality reduction methods that aim to learn a low dimensional embedding space that can preserve subtle relationships between samples in the high dimensional space [21–23]. Previous applications of ML to histopathology datasets have demonstrated that the low dimensional embedding space is better suited to classification compared to the original high dimensional space [11, 17, 24].
ML finds a low dimensional manifold representation
 from a dataset O which preserves relationships between samples in O. Most ML methods assume that O is contained in a high dimensional space ℝD [21–23, 25]. Additionally, ML assumes that O is densely clustered and concentrated within a small region of ℝD. An example of dense clustering can be seen in Figure 1(a) which shows an example of the synthetic Swiss Roll dataset. In ℝ3 the samples cluster along a 2D planar structure.
from a dataset O which preserves relationships between samples in O. Most ML methods assume that O is contained in a high dimensional space ℝD [21–23, 25]. Additionally, ML assumes that O is densely clustered and concentrated within a small region of ℝD. An example of dense clustering can be seen in Figure 1(a) which shows an example of the synthetic Swiss Roll dataset. In ℝ3 the samples cluster along a 2D planar structure.
Figure 1.

(a) Original 3D Swiss Roll dataset with Gaussian noise added to 2% of samples in the datasest. (b) 2D manifold
 in the absence of noise. This manifold structure best preserves the relationships between samples in the original high dimensional space. (c) Manifold
in the absence of noise. This manifold structure best preserves the relationships between samples in the original high dimensional space. (c) Manifold
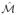 found by applying ML to a dataset containing noise and (d) the manifold
found by applying ML to a dataset containing noise and (d) the manifold
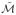 found by regularization of
found by regularization of
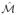 using the SSMM.
using the SSMM.
To calculate
 , ML techniques typically construct a dissimilarity matrix A which quantifies dissimilarity between samples in ℝD [21–23]. For a dataset O containing N samples, A is a N × N dissimilarity matrix defined such that A(oi, oj) quantifies the differences between the samples oi, oj ∈ O. Typically A(oi, oj) = ψ(oi, oj) where ψ(·, ·) is a dissimilarity measure (e.g. heat kernel [11, 26], geodesic distance [22], Diffeomorphic Based Similarity [17]) which is dataset and feature set dependent. ML then calculates
, ML techniques typically construct a dissimilarity matrix A which quantifies dissimilarity between samples in ℝD [21–23]. For a dataset O containing N samples, A is a N × N dissimilarity matrix defined such that A(oi, oj) quantifies the differences between the samples oi, oj ∈ O. Typically A(oi, oj) = ψ(oi, oj) where ψ(·, ·) is a dissimilarity measure (e.g. heat kernel [11, 26], geodesic distance [22], Diffeomorphic Based Similarity [17]) which is dataset and feature set dependent. ML then calculates
 to best preserve the relationships in A. ML techniques preserve relationships in A differently, some methods such as Local Linear Embedding (LLE) [21] try to preserve the local neighborhood relationships between samples. Isomaps [22] and Graph Embedding (GE) [23] find the best embedding space to preserve the global structure of A, albeit with different underlying algorithms.
to best preserve the relationships in A. ML techniques preserve relationships in A differently, some methods such as Local Linear Embedding (LLE) [21] try to preserve the local neighborhood relationships between samples. Isomaps [22] and Graph Embedding (GE) [23] find the best embedding space to preserve the global structure of A, albeit with different underlying algorithms.
ML schemes tend to be sensitive to the dataset considered, and changes in the dataset may cause changes to the learned manifold [27]. Consider a sample oi ∈ O perturbed by some error ε; the new location for oi would be ôi = oi + ε. A would have to be altered such that Â(ôi, oj) = ψ(ôi, oj) for all oj contained in O, resulting in changes to 2N − 2 elements in A. The manifold
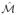 learned from  will reflect those changes. Hence even a small change in O may cause large changes to
learned from  will reflect those changes. Hence even a small change in O may cause large changes to
 . Figure 2 demonstrates this phenomenon for a prostate histology dataset comprising 888 glands. Two manifolds were generated by applying ML to 90% of samples in the dataset (800 glands) such that for each manifold a different set of 88 samples were excluded. Each manifold has a distinct structure evident by (a) changes in the planar structure of the manifold and (b) changes in object-class relationships on the manifold, displayed as color differences between manifolds.
. Figure 2 demonstrates this phenomenon for a prostate histology dataset comprising 888 glands. Two manifolds were generated by applying ML to 90% of samples in the dataset (800 glands) such that for each manifold a different set of 88 samples were excluded. Each manifold has a distinct structure evident by (a) changes in the planar structure of the manifold and (b) changes in object-class relationships on the manifold, displayed as color differences between manifolds.
Figure 2.
(a), (c) Two manifolds
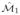 and
and
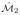 generated by performing ML on quantitative morphologic features extracted from 800 prostate histopathology glands. The manifolds
generated by performing ML on quantitative morphologic features extracted from 800 prostate histopathology glands. The manifolds
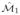 and
and
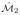 were generated from two distinct datasets O1 and O2 such that 88 glands excluded from either O1 or O2. (b), (d) Manifold region enclosed by the black box in (a) and (c) respectively. Representative glands for (f) benign (BE), (e), (g) Gleason pattern 3 (G3), and (h) pattern 4 (G4) classes. A classifier trained in the reduced dimensional space allows for assignment of a single class to each region on the manifold, such that blue regions correspond to BE, green regions correspond to G3, and red regions correspond to G4. Differences between the manifolds can be seen in changes in global structure as well as class-object relationships on the manifold, which are evident by changes in region color. In the case of (h) a representative G4 gland, in one manifold ( (c)) the gland was incorrectly projected on to the G3 class region.
were generated from two distinct datasets O1 and O2 such that 88 glands excluded from either O1 or O2. (b), (d) Manifold region enclosed by the black box in (a) and (c) respectively. Representative glands for (f) benign (BE), (e), (g) Gleason pattern 3 (G3), and (h) pattern 4 (G4) classes. A classifier trained in the reduced dimensional space allows for assignment of a single class to each region on the manifold, such that blue regions correspond to BE, green regions correspond to G3, and red regions correspond to G4. Differences between the manifolds can be seen in changes in global structure as well as class-object relationships on the manifold, which are evident by changes in region color. In the case of (h) a representative G4 gland, in one manifold ( (c)) the gland was incorrectly projected on to the G3 class region.
Consider a large dataset O from which the manifold
 is generated. In the absence of knowing the true manifold,
is generated. In the absence of knowing the true manifold,
 is the best manifold representation to capture the relationships between samples in the dataset. If we consider a subset Ô ⊂ O then Ô can be used to create an alternative manifold
is the best manifold representation to capture the relationships between samples in the dataset. If we consider a subset Ô ⊂ O then Ô can be used to create an alternative manifold
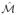 which approximates
which approximates
 . Manifold regularization constrains the structure of
. Manifold regularization constrains the structure of
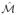 giving a better approximation of
giving a better approximation of
 and hence resulting in a better representation of the relationships between samples in Ô.
and hence resulting in a better representation of the relationships between samples in Ô.
In this work we present a statistical shape model of manifolds (SSMMs) to perform manifold regularization. SSMM merges the theory of ensemble learning [28] with statistical shape models (SSMs) [29]. The theory behind ensemble learning is that an ensemble of weak classifiers has higher accuracy compared to any single weak classifier [30]. Similarly, consensus clustering takes a ensemble of weak clusterings of a dataset, obtained by applying an unstable clustering method such as k-mean clustering to a dataset multiple times, and combines the ensemble to generate a strong clustering of the dataset [31]. Viswanath et. al. [32] demonstrated that consensus embedding, obtained by generating an ensemble of manifolds from a single dataset, produced a more stable low dimensional manifold compared to any single manifold in the ensemble. In this work we hypothesize an ensemble of manifolds will have a more accurate representation of the manifold shape that any single manifold. The concept of SSMMs is that an ensemble of manifolds can be modeled with a SSM. SSMs have been proposed to model shape variation in anatomical structures [29]. In much the same way, we utilize a SSM to model which manifold shapes are statistically most likely to occur. The SSMM describes the maximum likelihood estimate (MLE) of the manifold shape and primary modes of variation for a series of different manifolds constructed by randomly selecting a subset of samples from a dataset. For a new, related dataset, the resulting manifold can be constrained to only the range of shapes dictated by the SSMM. Hence every sample on the new manifold is spatially and locally constrained to within 2 standard deviations of its location on the average manifold shape.
The SSMM can be utilized in several ways. (1) Regions on a new, related manifold which deviate from the SSMM can be identified. By identifying these regions, meaningful differences between the dataset and the SSMM may be determined. (2) Noisy samples on a manifold can be identified based on their deviation from the SSMM. Removing these samples from the dataset may result in a more accurate low dimensional manifold, and hence improve classification accuracy. (3) A classifier can be trained on the SSMM which would allow for (a) classifier decision boundaries to be applied to a new, related manifold without retraining the classifier or (b) new, related samples could be projection onto the SSMM. The projection of newly acquired samples onto a previously calculated manifold can be performed by out-of-sample extrapolation (OSE) [33].
The remainder of the paper is organized as follows. Section 2 describes previous work in Gleason grading of prostate histology and manifold regularization. An overview of SSMM construction and its novel contributions are discussed in Section 3. In Section 4 an ensemble based theoretical framework for the SSMM is presented. Section 5 describes the methodology to construct a SSMM and its application to (a) outlier identification and (b) OSE of newly acquired samples onto the SSMM. Section 6 describes the experimental design and results for two synthetic datasets as well as a prostate histology dataset. Concluding remarks are presented in Section 7.
2. Previous Work
2.1. Automated Gleason Grading
Pathologists perform Gleason grading of prostate cancer tissue specimens via qualitative, visual evaluation of a tissue section previously stained with Hemotoxilyin and Eosin (H& E) [3]. The primary discriminating traits of Gleason patterns on histopathology are the difference in the arrangement and morphology of the nuclei and glands within a tissue sample [3, 4]. In devising automated pattern recognition methods for distinguishing different Gleason patterns on histopathology, the key questions to consider are (1) what is the best feature set to distinguish between Gleason patterns? and (2) what is the best method to reduce the dimensionality of the feature set prior to classification?
Jafari et. al. [10] characterized tissue patch texture via wavelet features and classified Gleason patterns with an accuracy of 97% for the best performing feature. Huang et. al. [14] characterized tissue patch texture via Fractal Dimension and achieved an accuracy of 95%. However, a limitation of these approaches were that the image patches were manually selected to obtain regions which contained only one tissue class on the digitized slide. DiFranco et. al. [18] characterized tissue patch texture for each color channel independently showing 90% accuracy classifying images on a per tile. Although tiles were automatically determined, tiles which contained more than one tissue class were removed from the dataset.
Structural features (as opposed to texture features) have also been explored by some researchers for automated categorization of Gleason patterns. Veltri et. al. [13] and Ali et. al. [19] showed that the quantitative characterization of the shape of individual nuclei on tissue microarrays can distinguish between Gleason patterns with high accuracy. In a preliminary study by Veltri et. al. [13] characterization of manually segmented nuclei were able to distinguish between Gleason pattern 3, 4, and 5 with 73–80% accuracy. Ali et. al. [19] automated the nuclear segmentation and classification steps in [13], yeilded an 84% accuracy on 80 tissue microarrays. Doyle et. al. [15] characterized manually selected image patches according to nuclear arrangement, reporting a predictive positive value of 76.0% in distinguishing between Gleason patterns 3, 4, and 5 within a multi-classification scheme.
In previous work we have shown that gland morphology, quantified by Diffeomorphic Based Similarity (DBS), is able to distinguish between Gleason 3 and 4 patterns with 88% accuracy in 58 patient studies [17]. DBS is calculated by constructing shape models for each gland contained in a set of histology images and then quantifying the differences between shape models.
Tabesh et. al. [12] combined gland morphology, texture features, color channel variance, and nuclear arrangement to classify different Gleason patterns with 81.0% accuracy. Golugula et. al. [24] used proteomic data in conjunction with histology derived image features to distinguish between prostate cancer patients who following radical prostatectomy had biochemical recurrence within 5 years from patients who did not.
Most automated Gleason grading systems are described by a high dimensional feature space [12, 15, 17, 18, 24]. To perform accurate classification, the high dimensional feature space must be reduced to a lower dimensional space [20]. One approach to reduce the high dimensional feature space is to perform feature selection, thereby determining a small subset of the original feature space in which accurate classification can be performed [12, 15, 18]. Difranco et. al. [18] utilized a random forest feature selection algorithm. Doyle et. al. [15] utilized a cascaded classification approach to perform feature selection for a series of pairwise classification tasks. Feature selection schemes have the advantage of selecting those features that give the most accurate classification while discarding features, which may contain noise, that have relatively poorer classification accuracy [12, 15]. However, a limitation of these approaches is that the excluded features may contain important classification information, and their removal may diminish classification accuracy in some tasks [34].
Dimensionality reduction methods learn a low dimensional embedding space which best preserves the original high dimensional feature space [11, 17, 24]. For instance Golugula et. al. [24] performed dimensionality reduction via supervised canonical correlation analysis to learn a low dimensional space in which patient classification was performed. Naik et. al. [11] demonstrated that GE is well suited for the preservation of a high dimensional feature space which characterized histological differences in texture, nuclear architecture, and gland morphology. Similarly, DBS features in conjunction with GE resulted in 88% classification accuracy for Gleason pattern 3 and 4 glands [17]. However, all of these schemes have utilized the full dataset to perform ML and then trained a classifier within the low dimensional embedding space. These methods are sensitive to noise in the high dimensional feature space as well as the samples considered when learning the low dimensional space. If newly acquired samples or samples which contain noise are included in these systems they will alter the low dimensional embedding space and may detrimentally affect classification performance. Manifold regularization can alleviate this problem by constraining the manifold shape to only shapes which are most likely to occur.
2.2. Manifold Regularization
ML is well known to be sensitive to the dataset considered, as well as noise and outliers contained within a dataset [26, 27]. Perturbations in the manifold structure may reduce classification performance in the low dimensional embedding space as object-class relationships may be obscured. Manifold regularization techniques have been proposed which impose additional constraints on ML to better preserve object-class relationships in the low dimensional space. For instance, Chang et. al. [27] proposed a weighted ML scheme, where outlier samples were assigned low weights, to reduce the effect outliers have on learning the manifold. Other manifold regularizers perform local smoothing on the learned manifold [35]. Manifold regularization techniques may add a smoothness constraint into the ML algorithm [26, 36]. All of these methods over smooth the manifold, as they reduce the effects of outliers which including meaningful information as well as noise.
Another type of regularization learns a consensus embedding (CE) from a set of manifolds. Hou et. al. [37] learned a set of manifolds by obtaining multiple views for each sample in the dataset and then generated a consensus manifold across the views. Other CE schemes have varied the parameters or samples considered to find a manifold set, and then generated a CE from the set [38, 39]. These methods rely on the manifolds in the set being independent, which may not be a valid assumption when generating manifold sets across ML parameters. Additionally, relationships between samples across the individual manifolds are not taken into account when determining a CE.
3. Brief Overview and Novel Contributions
A flowchart of the proposed SSMM methodology is displayed in Figure 3. Table 1 list the notation used throughout the paper. To construct the SSMM we (1) generate a set of manifolds
 for a dataset O. For this task we divide the dataset O into K folds, and then generate
for a dataset O. For this task we divide the dataset O into K folds, and then generate
 using a leave-one-fold-out scheme. (2) As manifolds in
using a leave-one-fold-out scheme. (2) As manifolds in
 will be misaligned, primarily due to rotational and translational differences, a Procrustes based registration scheme aligns all the manifolds in
will be misaligned, primarily due to rotational and translational differences, a Procrustes based registration scheme aligns all the manifolds in
 . (3) Calculate the MLE and primary modes of variation for
. (3) Calculate the MLE and primary modes of variation for
 . Once constructed the SSMM constrains a new manifold instance
. Once constructed the SSMM constrains a new manifold instance
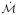 of related datasets to only those shapes statistically most likely to occur resulting in the regularized manifold
of related datasets to only those shapes statistically most likely to occur resulting in the regularized manifold
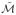 . In this work we demonstrate that the SSMM can (a) determine noisy samples by identifying samples which deviate from the SSMM, and (b) accurately perform OSE of newly acquired samples onto a manifold constrained by the SSMM.
. In this work we demonstrate that the SSMM can (a) determine noisy samples by identifying samples which deviate from the SSMM, and (b) accurately perform OSE of newly acquired samples onto a manifold constrained by the SSMM.
Figure 3.
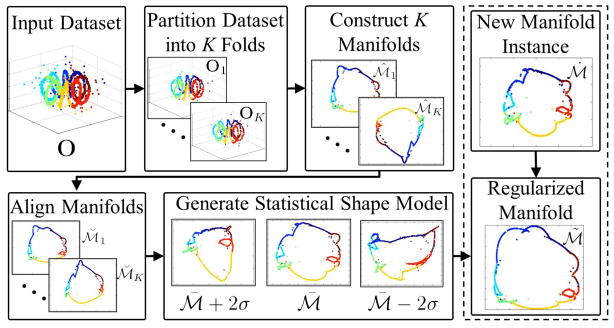
Flowchart which describes the construction of the SSMM and its application to manifold regularization for the synthetic Helix dataset. SSMM construction consists of dividing the dataset O into K folds, denoted as {O1, …, OK}. The K folds of O are utilized to find the manifold set
 = {
= {
 , …,
, …,
 }. The manifolds in
}. The manifolds in
 are then aligned via Procrustes based registration scheme resulting in the aligned manifold set
are then aligned via Procrustes based registration scheme resulting in the aligned manifold set
 = {
= {
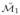 , …,
, …,
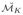 }. The SSMM finds the MLE (
}. The SSMM finds the MLE (
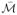 ) and primary modes of variation for
) and primary modes of variation for
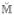 . Shown are the modes of variation corresponding to the statistical extremes of the model
. Shown are the modes of variation corresponding to the statistical extremes of the model
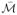 − 2σ and
− 2σ and
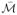 + 2σ. Given a new manifold instance
+ 2σ. Given a new manifold instance
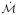 the SSMM constrains the structure to only those statistically likely to occur (
the SSMM constrains the structure to only those statistically likely to occur (
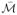 ± 2σ). This results in the regularized manifold
± 2σ). This results in the regularized manifold
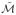 which is a better approximation of the underlying relationships in O than any constituent manifold in
which is a better approximation of the underlying relationships in O than any constituent manifold in
 . For the synthetic Helix dataset shown in this flowchart the ideal manifold is a 2D circular structure.
. For the synthetic Helix dataset shown in this flowchart the ideal manifold is a 2D circular structure.
Table 1.
Notation used in the paper.
| Symbol | Description |
|---|---|
| O | Dataset |
| oi, oj | Samples contained in O |
| Ok | kth fold of O for k ∈ {1, …, K} |
| ℝD | High dimensional feature space |
| ψ(·, ·) | Dissimilarity measure |
| A | Dissimilarity matrix defined as ψ(oi, oj) evaluated for all oi, oj ∈ O |
| γ | GE scaling term |
| ℝn | Low dimensional embedding space |
|
|
Ensemble manifold set |
|
|
kth manifold in

|
| ŷk | Embedding locations on
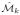
|
| yi,k | Embedding location for oi on
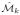
|
| Ta,b | Transformation to align
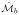 to to
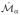
|
| ||·|| | L2 norm |
|
|
Aligned manifold set |
|
|
MLE for
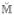
|
| P | Primary modes of variation for
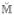
|
|
|
New manifold instance |
|
|
Manifold constrained via the SSMM |
| Q | New dataset instance |
| Qn | Samples which contain noise in Q |
| Qc | Samples which do not contain noise in Q |
| τ | Threshold to determine sample deviation from the SSMM |
|
|
Manifold generated from Qc |
| Qte | Testing samples not contained in Q |
|
|
Manifold with samples in Qte projected onto
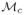 . . |
The novel contributions of the SSMM are:
A computerized decision support system which utilizes a SSMM based on the morphologic features of glands on prostate histopathology to automatically distinguish between Gleason patterns 3 and 4.
A novel combination of SSMs and ensemble learning theory to generate a more accurate manifold representation of O.
A novel method to generate
 , an set of K manifolds, containing all samples in O.
, an set of K manifolds, containing all samples in O.A novel manifold registration to align all manifolds in
 . As each sample oi ∈ O has a corresponding embedding location yi,k on the manifold
. As each sample oi ∈ O has a corresponding embedding location yi,k on the manifold
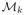 , the registration algorithm minimizes the differences between yi,k for all k ∈ {1, …, K} and all oi ∈ O via Procrustes registration [40].
, the registration algorithm minimizes the differences between yi,k for all k ∈ {1, …, K} and all oi ∈ O via Procrustes registration [40].
4. Statistical Shape Model of Manifolds Theory
We prove theoretically that SSMMs are appropriate to determine the MLE of a manifold shape. Specifically, we prove that constructing a SSMM from a set of manifolds is guaranteed to represent the underlying manifold structure at least as well as any manifold contained in the set. To perform the theoretical analysis we utilize the theory of ensemble learning [28].
A dataset of N samples is defined as O = {o1, …, oN }. A sample oi ∈ O is defined as a point in a D-dimensional space ℝD.
Definition 1
A true manifold
 ∈ ℝd is defined by a set of N true embedding locations
∈ ℝd is defined by a set of N true embedding locations
 = {x1, …, xN }. Each true embedding location xi ∈ ℝd corresponds to a sample oi ∈ ℝD where d ≪ D.
= {x1, …, xN }. Each true embedding location xi ∈ ℝd corresponds to a sample oi ∈ ℝD where d ≪ D.
Definition 2
A manifold
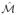 estimates
estimates
 by a set of N embedding locations
by a set of N embedding locations
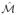 = {x̂1, …, x̂N }. Each embedding location x̂i ∈ ℝd corresponds to a sample oi ∈ ℝD where d ≪ D.
= {x̂1, …, x̂N }. Each embedding location x̂i ∈ ℝd corresponds to a sample oi ∈ ℝD where d ≪ D.
Definition 3
The manifold
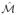 approximates
approximates
 with an error ε
with an error ε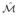 given as,
given as,
| (1) |
where Ei is the mean over i = {1, …, N}.
Proposition 1
Given a set of K independent, identically distributed manifolds
 = {
= {
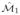 , …,
, …,
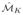 }, a manifold
}, a manifold
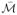 exists such that
exists such that
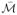 →
→
 as K → ∞.
as K → ∞.
Proof
Each estimated manifold
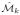 is defined by the embedding locations x̂i,k ∈
is defined by the embedding locations x̂i,k ∈
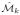 : i ∈ {1, …, N }, k ∈ {1, …, K}. Assuming that each embedding location x̂i,k ∈
: i ∈ {1, …, N }, k ∈ {1, …, K}. Assuming that each embedding location x̂i,k ∈
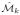 : i ∈ {1, …, N }, k ∈ {1, …, K} is normally distributed about xi, the Central Limit Theorem states,
: i ∈ {1, …, N }, k ∈ {1, …, K} is normally distributed about xi, the Central Limit Theorem states,
| (2) |
where Ek is the mean over k = {1, …, K}. Therefore
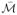 exists and is defined
exists and is defined
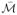 = Ek(x̂i,k): i ∈ {1, …, N}.
= Ek(x̂i,k): i ∈ {1, …, N}.
The error between
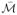 and
and
 is defined as (similar to Equation 1),
is defined as (similar to Equation 1),
| (3) |
where x̄i = Ek(x̂i,k). From Equation 1 the error over K embeddings is given as,
| (4) |
Proposition 2
Given K independent, identically distributed manifolds,
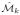 ∈
∈
 , εK,
, εK,
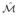 ≥ ε
≥ ε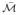 .
.
Proof
Comparing Equation 4 and Equation 3 in a manner analogous to Bagging [28] gives the proof. In Bagging, an ensemble classifier is constructed from a set of weak classifiers. Similarly, the
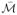 obtained from the SSMM can be viewed as an ensemble embedding constructed from a set of weak embeddings
obtained from the SSMM can be viewed as an ensemble embedding constructed from a set of weak embeddings
 . Hence the result follows.
. Hence the result follows.
5. Construction of Statistical Shape Manifold Model (SSMM)
In this section we present our methodology for constructing a SSMM. In Section 5.1 we provide an overview of ML. We then describe our novel K fold algorithm to calculate
 in Section 5.2. Section 5.3 presents the Procrustes based registration of manifolds in
in Section 5.2. Section 5.3 presents the Procrustes based registration of manifolds in
 . In Section 5.4 we discuss SSMM construction and Section 5.5 describes the fitting of
. In Section 5.4 we discuss SSMM construction and Section 5.5 describes the fitting of
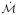 to the SSMM. Finally we present two novel algorithms for (a) noise identification and removal in Section 5.6 and (b) OSE of newly acquired samples onto the SSMM in Section 5.7.
to the SSMM. Finally we present two novel algorithms for (a) noise identification and removal in Section 5.6 and (b) OSE of newly acquired samples onto the SSMM in Section 5.7.
5.1. Review of Manifold Learning
5.1.1. Graph Embedding (GE)
In this work, we implemented the ML scheme GE [23] to perform nonlinear dimensionality reduction as it has few parameters to optimize over (only γ an empirically determined scaling term) and is relatively computationally efficient. GE learns a manifold estimate
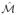 for a dataset OT ∈ ℝD.
for a dataset OT ∈ ℝD.
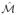 is described by a set of embedding locations ŷ ∈ ℝn where n ≪ D. ŷ is obtained by performing the eigenvalue decomposition (EVD),
is described by a set of embedding locations ŷ ∈ ℝn where n ≪ D. ŷ is obtained by performing the eigenvalue decomposition (EVD),
| (5) |
where W(a, b) = e−A(a,b)/γ, γ is an empirically determined scaling term, and L is the diagonal matrix L(a, a) = Σb W (a, b). ŷ is defined as the n eigenvectors which correspond to the top n eigenvalues in λ̂.
5.1.2. Out-of-Sample Extrapolation (OSE)
A sample not in the original dataset, i.e. ok ∉ OT, will not have a corresponding embedding location in ŷ. To calculate the embedding location ŷk the dissimilarity matrix A and the EVD would have to be recomputed to include ok in OT. Repeating ML for every new sample acquired is computationally infeasible [33]. The aim of OSE is to determine embedding locations ỹ for samples in a newly acquired dataset defined as OR.
The Nsytröm Method (NM) is a OSE algorithm which estimates ỹ as a weighted sum of the known embeddings ŷ [33]. Given ŷ for OT generated in Section 5.1.1, ỹ for OR are calculated as,
| (6) |
where d ∈ {1, …, n} is the dth embedding dimension corresponding to the dth largest eigenvalue λ̂d. OSE does not alter the underlying relationships contained in ŷ. Furthermore the samples contained in OR in no way alter or affect the relationships contained in ŷ.
5.2. Construction of the Manifold Set
A set of K manifolds
 = {
= {
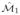 , …,
, …,
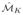 } are obtained from a dataset of N samples defined as O = {o1, …, oN}.
} are obtained from a dataset of N samples defined as O = {o1, …, oN}.
 is generated utilizing a K fold scheme via the following steps:
is generated utilizing a K fold scheme via the following steps:
Samples in O are randomly divided into K equal partitions such that O = {O1 ∪ … ∪ OK}.
Testing and training sets are obtained via a leave one fold out scheme. A testing set is defined as OR,k = Ok: k ∈ {1, …, K} and the corresponding training set is defined as OT,k ∈ OR,k = O.
Each training set OT,k is utilized to find ŷk which defines
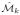 via GE as described in Section 5.1.1. The samples in OT,k are then used to determine the structure of the manifold
via GE as described in Section 5.1.1. The samples in OT,k are then used to determine the structure of the manifold
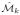 .
.Each test set OR,k is extrapolated into the manifold
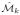 to determine ỹk via NM as described in Section 5.1.2.
to determine ỹk via NM as described in Section 5.1.2.Training and testing sets are combined to determine yk = {ŷk, ỹk}. This combination allows for point correspondence between manifolds in
 to be estimated.
to be estimated.
In this work K = 10 was chosen to construct
 , and the steps described above were performed 5 times for a total of 50 constituent manifolds in
, and the steps described above were performed 5 times for a total of 50 constituent manifolds in
 . GE and NM were chosen for experiments showcased in this work, but it is worth noting any ML [21–23, 25] and OSE [33, 41] scheme can be used to construct
. GE and NM were chosen for experiments showcased in this work, but it is worth noting any ML [21–23, 25] and OSE [33, 41] scheme can be used to construct
 .
.
5.3. Manifold Alignment via Procrustes Based Registration
Manifolds contained in
 may not align, the algorithm for ML preserves pairwise relationships between samples but may not preserve the global relationship of samples in the low dimensional embedding space. Procrustes registration is applied to align all manifolds in
may not align, the algorithm for ML preserves pairwise relationships between samples but may not preserve the global relationship of samples in the low dimensional embedding space. Procrustes registration is applied to align all manifolds in
 [40]. Procrustes registration can be performed since there are point correspondences between all manifolds in
[40]. Procrustes registration can be performed since there are point correspondences between all manifolds in
 as each sample in O has a location on every manifold in
as each sample in O has a location on every manifold in
 .
.
A reference manifold
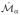 : a ∈ {1, …, K} is randomly selected. All other manifolds,
: a ∈ {1, …, K} is randomly selected. All other manifolds,
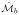 : b ≠ a are registered to
: b ≠ a are registered to
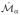 by minimizing,
by minimizing,
| (7) |
where yi,a is a embedding location in
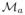 for a sample oi and yi,b is a embedding location in
for a sample oi and yi,b is a embedding location in
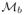 for a sample oi. The transform Ta,b selected was a rigid transform, to take into account scale and rotational differences between
for a sample oi. The transform Ta,b selected was a rigid transform, to take into account scale and rotational differences between
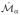 and
and
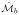 . ||·|| denotes the L2-norm. Registration is performed for all
. ||·|| denotes the L2-norm. Registration is performed for all
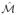 ∈
∈
 to obtain the aligned set of manifolds
to obtain the aligned set of manifolds
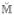 .
.
5.4. Statistical Shape Manifold Model (SSMM)
Once all manifolds are aligned the statistical properties of the manifold set can be determined. The SSMM is defined via the mean and principal modes of variation for
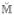 . The mean of
. The mean of
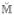 is calculated by,
is calculated by,
| (8) |
The principal modes of variation for the manifold defined as P are obtained by performing PCA on
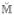 [29]. Only the P corresponding to the top 95% of variance in the sample locations yi,k for all k ∈ {1, …, K} are retrained to constrain the SSMM to those shapes within 2 standard deviations of the mean shape.
[29]. Only the P corresponding to the top 95% of variance in the sample locations yi,k for all k ∈ {1, …, K} are retrained to constrain the SSMM to those shapes within 2 standard deviations of the mean shape.
5.5. Constraining a New Manifold Instance to the SSMM
A new manifold
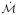 is obtained by applying GE to O.
is obtained by applying GE to O.
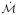 is constrained to only likely shapes as defined by the SSMM obtained in Section 5.4.
is constrained to only likely shapes as defined by the SSMM obtained in Section 5.4.
| (9) |
where b controls the shape of
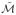 and Ta,K+1 is a rigid transformation between the SSMM and
and Ta,K+1 is a rigid transformation between the SSMM and
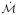 . b is found via a linear least squares fit between the SSMM and
. b is found via a linear least squares fit between the SSMM and
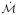 and is constrained to
and is constrained to
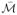 ± 2σ to limit the SSMM to only those shapes statistically most likely to occur [29].
± 2σ to limit the SSMM to only those shapes statistically most likely to occur [29].
5.6. Application of SSMM to Identify Noisy Samples
The SSMM can aid in the identification of samples which contain noise. The algorithm FilterManifold assumes samples which contain noise are those samples which deviate most from the SSMM.
A dataset contains N samples defined as Q = {q1, …, qN }. The following algorithm can be used to identify the samples which contain noise Qn and the samples which do not contain noise Qc within Q given a user defined threshold τ. The value assigned to τ is dataset specific as sample variation across datasets may vary. In this work τ was chosen such that 5% of the samples in the dataset were excluded.
Algorithm.
FilterManifold
| Input: Q, τ |
Output:
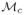
|
| begin |
1. Obtain
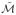 from Q via application of the SSMM. from Q via application of the SSMM. |
2. Obtain
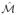 from Q by GE (Eq. 5). from Q by GE (Eq. 5). |
| 3. Calculate e(qi) = ||ŷi − ỹi||. |
| 4. Obtain Qn = qi: qi ∈ Q, e(qi) ≥ τ. |
| 5. Obtain Qc: Qc ∩ Qn = ∅. |
6. Obtain
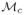 for Qc via GE (Eq. 5) for Qc via GE (Eq. 5) |
| end |
5.7. Application of SSMM to OSE
The SSMM can be utilized for robust OSE, by generating a more accurate manifold representation of a dataset. The algorithm OSE-SSMM demonstrates how the SSMM can be used for this purpose.
A dataset Q is divided into training samples Qtr and testing samples Qte such that Qtr ∩ Qte = ∅. To find a set of testing embeddings
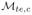 for a filtered manifold we apply the following algorithm,
for a filtered manifold we apply the following algorithm,
Algorithm.
OSE-SSMM
| Input: Qtr, Qte, τ |
Output:
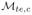
|
| begin |
1. Obtain
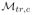 for Qtr via FilterManifold. for Qtr via FilterManifold. |
2. Obtain
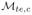 for Qte via NM (Eq. 6) with for Qte via NM (Eq. 6) with
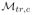 as the training manifold. as the training manifold. |
| end |
6. Experimental Design and Results
6.1. Dataset Description
6.1.1. Synthetic Datasets
Two synthetic datasets, Swiss Roll and Helix, described in Table 2 were utilized to demonstrate the application of SSMM to manifold regularization. The Swiss Roll is a 2D planar manifold divided into two classes which exists in a 3D space. The Helix is a 1D circular manifold divided into six classes which exists in a 3D space. The benefit of both datasets is that the high dimensional 3D space and the low dimensional 2D embedding space may be visualized. Gaussian noise was added to 5% of samples within each dataset where the standard deviation of the noise was set equal to 15% of the standard deviation of samples in the dataset. The dissimilarity measures for both datasets are reported in Table 2.
Table 2.
Description of datasets and their dissimilarity measures.
6.1.2. Prostate Histopathology
Prostate needle core tissue biopsies were obtained from 58 patients. Biopsies were stained with H & E and digitized at 40× optical magnification using an Aeperio scanner. An expert pathologist selected regions of interest (ROIs) on each biopsy. In total 120 ROIs were selected across. Each ROI was assigned a Gleason pattern of either BE, G3, or G4. All glands contained within each ROI were manually segmented to obtain a total of 888 glands from BE (N = 93), G3 (N = 748), and G4 (N = 47) ROIs. For this set of experiments only G3 and G4 glands were considered during classification. DBS was the dissimilarity measure utilized to quantify morphologic differences between glands [17].
6.2. Evaluation Measures
6.2.1. Silhouette Index (SI)
SI is a measure of how well samples cluster by class label [42] with 1 corresponding to perfect clustering by class and −1 corresponding to no clustering by class. SI is calculated as, where C(i) = Σj,lj=li||ỹi − ỹj|| and G(i) = Σj,lj≠li||ỹi − ỹj||.
6.2.2. Area Under the Receiver Operator Characteristic (ROC) Curve (AUC)
A probabilistic boosting tree (PBT) classifier [43] was trained and evaluated using a 5×2 cross validation scheme [44]. For each of the 5 runs, the dataset was divided into 2 folds such that all samples from a single patient were contained in the same fold and all folds maintained class balance. The PBT classifier assigns a probability value to each sample of belonging to the positive class. Altering the threshold level of the PBT classifier allows for the construction of a ROC Curve. For each ROC Curve the area under the curve (AUC) is calculated.
6.3. Experiment 1: Application of SSMM to Filtered Manifold Learning
For each dataset Q in Table 2, a manifold
 was calculated from Q using GE as described in Section 5.1.1. Similarly a filtered manifold
was calculated from Q using GE as described in Section 5.1.1. Similarly a filtered manifold
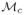 was found by FilterManifold as described in Section 5.6. The measures described in Section 6.2 were used to evaluate
was found by FilterManifold as described in Section 5.6. The measures described in Section 6.2 were used to evaluate
 and
and
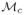 . A Student’s t-test was calculated to determine the statistical significance between
. A Student’s t-test was calculated to determine the statistical significance between
 and
and
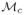 for each evaluation measure described in Section 6.2.
for each evaluation measure described in Section 6.2.
Experimental results for all datasets are reported in Table 3. Across all datasets
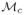 outperforms
outperforms
 in terms of SI and AUC. In the prostate histology dataset these increases in SI and AUC were statistically significant (p ≤ 0.1). Hence
in terms of SI and AUC. In the prostate histology dataset these increases in SI and AUC were statistically significant (p ≤ 0.1). Hence
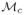 is better able to preserve object-class relationships in the datasets evaluated.
is better able to preserve object-class relationships in the datasets evaluated.
Table 3.
(a) SI and (b) AUC are reported for
 and
and
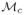 . The best value for each dataset is bolded. p-values are reported for a Student’s t-test comparing
. The best value for each dataset is bolded. p-values are reported for a Student’s t-test comparing
 and
and
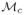 .
.
| (a) | |||
|---|---|---|---|
| Dataset |
|
|
p-value |
| Swiss Roll | 0.56 ± 0.01 | 0.57 ± 0.03 | 0.063 |
| Helix | 0.44 ± 0.05 | 0.47 ± 0.02 | 0.138 |
| Prostate | 0.02 ± 0.01 | 0.05 ± 0.03 | 0.032 |
| (b) | |||
|---|---|---|---|
| Dataset |
|
|
p-value |
| Swiss Roll | 0.876 ± 0.067 | 0.935 ± 0.065 | 0.071 |
| Helix | 0.995 ± 0.002 | 0.996 ± 0.002 | 0.240 |
| Prostate | 0.779 ± 0.075 | 0.832 ± 0.048 | 0.073 |
For the synthetic datasets, changes in SI and AUC are not always statistically significant. However, as may be noted in Figure 1 (d)
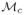 is a closer approximation to the true embedding (Figure 1 (b)) than compared to
is a closer approximation to the true embedding (Figure 1 (b)) than compared to
 (Figure 1 (c)). In Figure 1 the samples are colored according to their location on the true embedding to aid in visualization.
(Figure 1 (c)). In Figure 1 the samples are colored according to their location on the true embedding to aid in visualization.
6.4. Experiment 2: Application of SSMM to Filtered OSE
For each dataset Q in Table 2, a training set Qtr and a testing set Qte were defined so that Qte is 10% of Q and Qtr ∪ Qte = ∅. Qtr and Qte were used to construct an original manifold
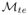 and filtered manifold
and filtered manifold
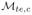 .
.
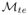 is generated by applying GE as described in Section 5.1.1 and then applying NM as described in Section 5.1.2 to Qte where
is generated by applying GE as described in Section 5.1.1 and then applying NM as described in Section 5.1.2 to Qte where
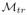 is the training manifold. The filtered manifold
is the training manifold. The filtered manifold
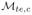 is calculated by OSE-SSMM as described in Section 5.7. The measures described in Section 6.2 were used to evaluate
is calculated by OSE-SSMM as described in Section 5.7. The measures described in Section 6.2 were used to evaluate
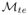 and
and
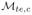 . A Student’s t-test was calculated to determine the statistical significance between
. A Student’s t-test was calculated to determine the statistical significance between
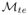 and
and
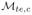 for each evaluation measure described in Section 6.2.
for each evaluation measure described in Section 6.2.
Experimental results for all datasets are reported in Table 4. For the histopathology dataset
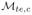 outperforms
outperforms
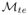 in terms of SI and AUC. The synthetic datasets, the Swiss Roll and Helix, do not show a significant improvement in performance.
in terms of SI and AUC. The synthetic datasets, the Swiss Roll and Helix, do not show a significant improvement in performance.
Table 4.
(a) SI and (b) AUC are reported for
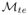 and
and
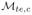 . The best value for each dataset is bolded. p-values are reported for a Student’s t-test comparing
. The best value for each dataset is bolded. p-values are reported for a Student’s t-test comparing
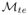 and
and
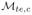 .
.
| (a) | |||
|---|---|---|---|
| Dataset |
|
|
p-value |
| Swiss Roll | 0.57 ± 0.01 | 0.58 ± 0.01 | 0.061 |
| Helix | 0.47 ± 0.01 | 0.47 ± 0.01 | 0.77 |
| Prostate | −0.04 ± 0.01 | −0.02 ± 0.02 | 0.005 |
| (b) | |||
|---|---|---|---|
| Dataset |
|
|
p-value |
| Swiss Roll | 0.997 ± 0.003 | 0.999 ± 0.002 | 0.102 |
| Helix | 0.994 ± 0.002 | 0.996 ± 0.002 | 0.089 |
| Prostate | 0.779 ± 0.054 | 0.834 ± 0.051 | 0.032 |
7. Concluding Remarks
In this paper we presented a statistical shape model of manifolds (SSMM) which is a novel integration of statistical shape models (SSMs) with ensemble learning for regularizing low dimensional data representations of high dimensional spaces. New, related manifolds may then be constrained by the SSMM to only those shapes statistically most likely to occur.
The SSMM may be utilized for several applications including (a) identification of noisy samples based on their deviation from the SSMM. Removing these samples from the dataset may result in higher area under the receiver operator characteristic (ROC) curve (AUC). (b) A classifier could be trained on the SSMM allowing for (i) classifier decision boundaries to be applied to a new related manifold without retraining the classifier or (ii) new, related samples to be classified by projection of the samples onto the SSMM. (c) identification of regions on a new, related manifold which deviate the SSMM. Identifying these regions may aid in determining meaningful differences between the dataset and SSMM.
To construct the SSMM we (1) generate a set of manifolds
 for a dataset O, (2) align manifolds in
for a dataset O, (2) align manifolds in
 , and (3) calculate the maximum likelihood estimate (MLE) of the manifold shape and its primary modes of variation. The SSMM allows for constraining a new, related manifold instance to only those shapes statistically most likely to occur.
, and (3) calculate the maximum likelihood estimate (MLE) of the manifold shape and its primary modes of variation. The SSMM allows for constraining a new, related manifold instance to only those shapes statistically most likely to occur.
We have demonstrated in this work that SSMM can improve AUC in the context of Gleason grading of prostate histopathology utilized quantitative morphologic features of glands. For the dataset considered, the tissue samples corresponded to either Gleason pattern 3 or pattern 4. Improvements in AUC via the SSMM were demonstrated for two applications:(a) We demonstrated that outlier samples within a manifold can be identified as those samples which deviate from the SSMM via FilterManifold. Removal of outlier samples increased AUC and SI. (b) We demonstrated via OSE-SSMM that manifold regularization by the SSMM improves SI and AUC when performing OSE on never before seen samples onto the SSMM.
In future work we intend to explore the ability of the SSMM to identify regions of a new, related manifold which deviate from the SSMM. These regions will then be further investigated to determine subtle difference between the dataset and the SSMM. Secondly, we plan on investigating the effects of dataset size on the SSMM by evaluating how accurately the mean manifold shape and primary modes of variation of the manifold shape are represented for SSMMs trained on different dataset sizes.
Highlights.
Statistical shape model of manifold (SSMM) constructs an ensemble of manifolds.
SSMM constrains the shape of a manifold resulting in a more stable low dimensional space.
The SSMM improves area under the receiver operator characteristic (ROC) curve (AUC) in the context of Gleason grading of prostate histopathology.
The SSMM can project new samples into a low dimensional space with high accuracy.
Acknowledgments
This work was made possible via grants from the National Cancer Institute (Grant Nos. R01CA136535-01, R01CA14077201, and R21CA167811), and the Department of Defense (W81XWH-11-1-0179). We would like to thank Dr. J. E. Tomaszewski from the University at Buffalo School of Medicine and Biomedical Sciences as well as Drs. M. D. Feldman and N. Shi from the Hospital of the University of Pennsylvania for providing prostate histology imagery and annotations.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Contributor Information
Rachel Sparks, Email: rsparks@eden.rutgers.edu.
Anant Madabhushi, Email: axm788@case.edu.
References
- 1.Epstein JI, Walsh PC, Carmichael M, Brendler CB. Pathologic and clinical findings to predict tumor extent of nonpalpable (stage t1 c) prostate cancer. JAMA: The Journal of the American Medical Association. 1994;271:368–374. [PubMed] [Google Scholar]
- 2.Bostwick D. Grading prostate cancer. American Journal of Clinical Pathology. 1994;102:S38–56. [PubMed] [Google Scholar]
- 3.Gleason DF. Classification of prostatic carcinomas. Cancer Chemotherapy Reports. 1966;50:125–128. [PubMed] [Google Scholar]
- 4.Epstein JI, Allsbrook WC, Amin MB, Egevad LL. The 2005 international society of urological pathology (ISUP) consensus conference on Gleason grading of prostatic carcinoma. American Journal of Surgical Pathology. 2005;29:1228–1242. doi: 10.1097/01.pas.0000173646.99337.b1. [DOI] [PubMed] [Google Scholar]
- 5.Epstein JI. An update of the gleason grading system. The Journal of Urology. 2010;183:433–440. doi: 10.1016/j.juro.2009.10.046. [DOI] [PubMed] [Google Scholar]
- 6.Epstein PCWJI, Sanfilippo F. Clinical and cost impact of second-opinion pathology: Review of prostate biopsies prior to radical prostatectomy. The American Journal of Surgical Pathology. 1996;20:851–857. doi: 10.1097/00000478-199607000-00008. [DOI] [PubMed] [Google Scholar]
- 7.Allsbrook WC, Mangold KA, Johnson MH, Lane RB, Lane CG, Epstein JI. Interobserver reproducibility of Gleason grading of prostatic carcinoma: General pathologist. Human Pathology. 2001;32:81–88. doi: 10.1053/hupa.2001.21135. [DOI] [PubMed] [Google Scholar]
- 8.Thompson I, Thrasher J, Aus G, Burnett A, Canby-Hagino E, Cookson M, D’Amico A, Dmochowski R, Eton D, Forman J, Goldenberg S, Hernandez J, Higano C, Kraus S, Moul J, Tangen C. Guideline for the management of clinically localized prostate cancer: 2007 update. The Journal of Urology. 2007;177:2106–2131. doi: 10.1016/j.juro.2007.03.003. [DOI] [PubMed] [Google Scholar]
- 9.Madabhushi A. Digital pathology image analysis: Oppurtunities and challenges. Imaging in Medicine. 2009;1:7–10. doi: 10.2217/IIM.09.9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Jafari-Khouzani K, Soltanian-Zadeh H. Multiwavelet grading of pathological images of prostate. IEEE Transactions on Biomedical Engineering. 2003;50:697–704. doi: 10.1109/TBME.2003.812194. [DOI] [PubMed] [Google Scholar]
- 11.Naik S, Doyle S, Madabhushi A, Tomaszeweski J, Feldman M. Gland segmentation and gleason grading of prostate histology by integrating low-, high-level and domain specific information. Workshop on Microscopic Image Analysis with Applications in Biology. [Google Scholar]
- 12.Tabesh A, Teverovskiy M, Pang H, Kumar V, Verbel D, Kotsianti A, Saidi O. Multifeature prostate cancer diagnosis and Gleason grading of histological images. IEEE Transaction on Medical Imaging. 2007;26:1366–1378. doi: 10.1109/TMI.2007.898536. [DOI] [PubMed] [Google Scholar]
- 13.Veltri RW, Marlow C, Khan MA, Miller MC, Epstein JI, Partin AW. Significant variations in nuclear structure occur between and within gleason grading patterns 3, 4, and 5 determined by digital image analysis. The Prostate. 2007;67:1202–1210. doi: 10.1002/pros.20614. [DOI] [PubMed] [Google Scholar]
- 14.Huang PW, Lee CH. Automatic classification for pathological prostate images based on fractal analysis. IEEE Transactions on Medical Imaging. 2009;28:1037–1050. doi: 10.1109/TMI.2009.2012704. [DOI] [PubMed] [Google Scholar]
- 15.Doyle S, Monaco J, Feldman M, Tomaszewski J, Madabhushi A. An active learning based classification strategy for the minority class problem: application to histopathology annotation. BMC Bioinformatics. 2011;12:424. doi: 10.1186/1471-2105-12-424. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Tambasco M, Costello BM, Kouznetsov A, Yau A, Magliocco AM. Quantifying the architectural complexity of microscopic images of histology specimens. Micron. 2009;40:486–494. doi: 10.1016/j.micron.2008.12.004. [DOI] [PubMed] [Google Scholar]
- 17.Sparks R, Madabhushi A. International Conference on Medical Image Computing and Computer-Assisted Intervention (MICCAI); pp. 658–665. [DOI] [PubMed] [Google Scholar]
- 18.DiFranco MD, Hurley GO, Kay EW, Watson RWG, Cunningham P. Ensemble based system for whole-slide prostate cancer probability mapping using color texture features. Computerized Medical Imaging and Graphics. 2011;35:629–645. doi: 10.1016/j.compmedimag.2010.12.005. [DOI] [PubMed] [Google Scholar]
- 19.Ali S, Madabhushi A. Active contour for overlap resolution using watershed based initialization (acorew): Applications to histopathology. IEEE International Symposium on Biomedical Imaging (ISBI); pp. 614–617. [Google Scholar]
- 20.Duda RO, Hart PE, Stork DG. Pattern Classification (2nd Edition) 2. Wiley-Interscience; 2001. [Google Scholar]
- 21.Roweis S, Saul L. Nonlinear dimensionality reduction by locally linear embedding. Science. 2000;290:2323–2326. doi: 10.1126/science.290.5500.2323. [DOI] [PubMed] [Google Scholar]
- 22.Tenenbaum J, de Silvia V, Langford J. A global framework for nonlinear dimensionality reduction. Science. 2000;290:2319–2323. doi: 10.1126/science.290.5500.2319. [DOI] [PubMed] [Google Scholar]
- 23.Shi J, Malik J. Normalized cuts and image segmentation, Pattern Analysis and Machine Intelligence. IEEE Transactions on. 2000;22:888–905. [Google Scholar]
- 24.Golugula A, Lee G, Master S, Feldman M, Tomaszewski J, Speicher D, Madabhushi A. Supervised regularized canonical correlation analysis: Integrating histologic and proteomic measurements for predicting biochemical recurrence following prostate surgery. BMC Bioinformatics. 2011;12:483. doi: 10.1186/1471-2105-12-483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Belkin M, Niyogi P. Laplacian eigenmaps for dimensionality reduction and data representation. Neural Compuation. 2003;15:1373–1396. [Google Scholar]
- 26.Belkin M, Niyogi P, Sindhwani V. Manifold regularization: A geometric framework for learning from labeled and unlabeled examples. Journal of Machine Learning Research. 2006;7:2399–2434. [Google Scholar]
- 27.Chang H, Yeung D. Robust locally linear embedding. Pattern Recognition. 2006;39:1053–1065. [Google Scholar]
- 28.Breiman L. Bagging predictors. Machine Learning. 1996;24:123–140. [Google Scholar]
- 29.Cootes TF, Taylor CJ, Cooper DH, Graham J. Active shape models their training and application. Computer Vision & Image Understanding. 1995;61:38–59. [Google Scholar]
- 30.Dietterich TG. Ensemble methods in machine learning. International Workshop on Multiple Classifier Systems; Springer-Verlag; 2000. pp. 1–15. [Google Scholar]
- 31.Fred AL, Jain AK. Combining multiple clusterings using evidence accumulation. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2005;27:835–850. doi: 10.1109/TPAMI.2005.113. [DOI] [PubMed] [Google Scholar]
- 32.Viswanath S, Madabhushi A. Consensus embedding: theory, algorithms and application to segmentation and classification of biomedical data. BMC Bioinformatics. 2012;13:26. doi: 10.1186/1471-2105-13-26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Bengio Y, Paiement J, Vincent P, Delalleau O, Roux NL, Ouimet M. Out-of-sample extensions for LLE, Isomap, MDS, Eigenmaps, and spectral clustering. Advances in Neural Information Processing Systems. :177–184. [Google Scholar]
- 34.Li T, Zhang C, Ogihara M. A comparative study of feature selection and multiclass classification methods for tissue classification based on gene expression. Bioinformatics. 2004;20:2429–2437. doi: 10.1093/bioinformatics/bth267. [DOI] [PubMed] [Google Scholar]
- 35.Park JH, Zhang Z, Zha H, Kasturi R. Local smoothing for manifold learning. Computer Vision and Pattern Recognition, 2004. CVPR 2004; Proceedings of the 2004 IEEE Computer Society Conference on, volume 2; pp. II–452–II–459. [Google Scholar]
- 36.Geng B, Xu C, Tao D, Yang L, Hua X-S. Ensemble manifold regularization. 2009. pp. 2396–2402. [DOI] [PubMed] [Google Scholar]
- 37.Hou C, Zhang C, Wu Y, Nie F. Multiple view semi-supervised dimensionality reduction. Pattern Recognition. 2010;43:720–730. [Google Scholar]
- 38.Jia J, Xiao X, Liu B, Jiao L. Bagging-based spectral clustering ensemble selection. Pattern Recognition Letters. 2011;32:1456–1467. [Google Scholar]
- 39.Tiwari P, Rosen M, Madabhushi A. Consensus-locally linear embedding (c-lle): Application to prostate cancer detection on magnetic resonance spectroscopy. Medical Image Computing and Computer-Assisted Intervention MICCAI 2008. 2008;5242:330–338. doi: 10.1007/978-3-540-85990-1_40. [DOI] [PubMed] [Google Scholar]
- 40.Wang C, Mahadevan S. Manifold alignment using procrustes analysis. Proceedings of the 25th international conference on Machine learning; pp. 1120–1127. [Google Scholar]
- 41.Fowlkes C, Belongie S, Chung F, Malik J. Spectral grouping using the Nyström method. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2004;28:214–225. doi: 10.1109/TPAMI.2004.1262185. [DOI] [PubMed] [Google Scholar]
- 42.Rousseeuw P. Silhouettes: a graphical aid to the interpretation and validation of cluster analysis. Journal of Computational Applied Mathematics. 1987;20:53–65. [Google Scholar]
- 43.Tu Z. Probabilistic boosting-tree: learning discriminative models for classification, recognition, and clustering. Computer Vision, 2005. ICCV 2005; Tenth IEEE International Conference on; pp. 1589–1596. [Google Scholar]
- 44.Dietterich TG. Approximate statistical tests for comparing supervised classification learning algorithms. Neural Computation. 1998;10:1895–1923. doi: 10.1162/089976698300017197. [DOI] [PubMed] [Google Scholar]



 is a neighborhood parameter.
is a neighborhood parameter.