Seeing the forest through the trees: comprehensive inference on individual mating patterns in a mixed stand of Quercus robur and Q. petraea

Abstract

Background and Aims

Sexual reproduction is one of the most important moments in a life cycle, determining the genetic composition of individual offspring. Controlled pollination experiments often show high variation in the mating system at the individual level, suggesting a persistence of individual variation in natural populations. Individual variation in mating patterns may have significant adaptive implications for a population and for the entire species. Nevertheless, field data rarely address individual differences in mating patterns, focusing rather on averages. This study aimed to quantify individual variation in the different components of mating patterns.

Methods

Microsatellite data were used from 421 adult trees and 1911 seeds, structured in 72 half-sib families collected in a single mixed stand of Quercus robur and Q. petraea in northern Poland. Using a Bayesian approach, mating patterns were investigated, taking into account pollen dispersal, male fecundity, possible hybridization and heterogeneity in immigrant pollen pools.

Key Results

Pollen dispersal followed a heavy-tailed distribution (283 m on average). In spite of high pollen mobility, immigrant pollen pools showed strong genetic structuring among mothers. At the individual level, immigrant pollen pools showed highly variable divergence rates, revealing that sources of immigrant pollen can vary greatly among particular trees. Within the stand, the distribution of male fecundity appeared highly skewed, with a small number of dominant males, resulting in a ratio of census to effective density of pollen donors of 5·3. Male fecundity was not correlated with tree diameter but showed strong cline-like spatial variation. This pattern can be attributed to environmental variation. Quercus petraea revealed a greater preference (74 %) towards intraspecific mating than Q. robur (36 %), although mating preferences varied among trees.

Conclusions

Mating patterns can reveal great variation among individuals, even within a single even-age stand. The results show that trees can mate assortatively, with little respect for spatial proximity. Such selective mating may be a result of variable combining compatibility among trees due to genetic and/or environmental factors.

INTRODUCTION

Sexual reproduction is one of the most important moments in a life cycle, determining the genetic composition of individual offspring. The way that genetic information is transferred from generation to generation underlies not only individual genotypes but also the distribution of genetic diversity within and among populations. Furthermore, mating patterns have an effect on adaptability potential of populations and, ultimately, the rate of species evolution (Schoen and Brown, 1991; Barrett and Harder, 1996). In wind- and animal-pollinated plants, outcross mating encompasses the processes of gene dispersal within and gene flow among populations (Ward et al., 2005; Ashley, 2010).

Mating patterns within populations are typically far from random. The mechanics of pollen transport alone can constrain the probability of pollination between plants, probably regardless of the pollen vector used. Most often, the probability of pollen dispersal decreases with distance from a source plant (Levin and Kerster, 1974; Ashley, 2010). This implies the existence of a ‘mating neighbourhood’ (although not a discrete spatial sub-unit, cf. Rousset, 2007) with dimensions scaled by a pollen dispersal distribution. However, proximity between potential mates does not ensure mating because, for example, flowering asynchrony (involving timing of pollen shedding and female receptivity) can limit mating opportunities (El-Kassaby and Ritland, 1986). Furthermore, successful pollination itself also does not guarantee fertilization and thus mating. This is because individual plants may produce pollen whose abilities to germinate on different pistils differ because of incompatibility reactions or variable pollen tube growth rates (Harder and Routley, 2006). In animal-pollinated species, specific foraging behaviour can lead to non-random mating patterns, such as increased geitonogamy (Finer and Morgan, 2003). In the case of wind-pollinated plants, temporal directionality of wind flow can result in an anisotropic distribution of mating probabilities (Shen et al., 1981; Burczyk et al., 2004). Among other factors, differences in male fecundity strongly influence mating probabilities (Burczyk et al., 2004; Klein et al., 2008).

Controlled pollination experiments often show high variation in mating system parameters at the individual level (Aas, 1991; Steinhoff, 1998), suggesting a persistence of individual variation in natural populations. Individual variation in self-fertilization can arise from, for example, a variable amount of outcross pollen being available to different individuals (Mimura and Aitken, 2006; Restoux et al., 2008). This can be due to flowering asynchrony, which in turn may reveal seasonal fluctuations or be genetically determined lifetime stable characteristics. However, in many species, a genetically driven compatibility system may lead to important interindividual variation in mating system preferences. Individual variation may have significant implications for a population and for the entire species. For example, individual variation in self-fertilization can lead to unpredictable oscillations in inbreeding rates (Coelho and Vencovsky, 2003) and thus may be a basis for stronger (positive or negative) inbreeding effects than predicted by simple models. Therefore, identifying individual mating parameters is a first step towards understanding the diversity of mating system variation.

Mating patterns also have implications for gene flow, and thus for genetic structure at a landscape level. One useful measure of gene flow is the rate of pollen immigration (Ashley, 2010). It is often argued that high immigration rates are synonymous with high gene flow rates (e.g. Streiff et al., 1999). Existing methods regularly assume a random pool of pollen gametes immigrating from outside a local population (Burczyk et al., 2002; Klein et al., 2005; Chybicki and Burczyk, 2010a). However, in real populations, immigration patterns may differ individually for reasons similar to those described above. For example, a female with extremely early or late stigma receptivity may be exposed to a male pollen pool different from that of a female of an average phenology (El-Kassaby and Ritland, 1986). Thus, it may not be reasonable to summarize immigration levels and pools of immigrating pollen by a single parameter.

Contemporary mating patterns can be assessed through so-called ‘indirect’ or ‘direct’ approaches (Sork et al., 1999). Relying upon theoretical models, indirect methods provide summary parameters, such as inbreeding coefficients (Chybicki et al., 2009) or effective density of pollen donors (Austerlitz and Smouse, 2002), which are informative about mating patterns in general. Nonetheless, indirect methods do not allow for in-depth understanding of the processes behind the summary measures. Specifically, indirect methods are not well suited to study individual variation, and to disentangle the effects of different factors, such as pollen dispersal, fecundity and mate compatibility, among others. Therefore, mating patterns are usually studied using direct approaches often referred to as paternity analysis. In the simplest case, mating patterns are inferred from categorically assigned pollen donors (see review by Ashley, 2010). This detailed information should in theory provide a comprehensive network of mating patterns upon which to base inferences about the determinants of mating. While the information on individual paternity is usually of little interest, it is often used to frame mating patterns into a series of parameters describing different components of mating, such as self-fertilization level, mean pollen dispersal distance, dispersal kernel parameters, variance of male fertility or the covariance between male fertility and phenotypic characters. In an idealized situation, one could identify explicitly a male parent of any individual offspring. However, although highly polymorphic genetic markers (e.g. microsatellites) theoretically allow for categorical paternity inference, multiple (and therefore uncertain) paternity assignments are often problematic in the analysis of real data. Furthermore, extensive pollen dispersal in wind- and animal-pollinated plants means that many actual fathers are not found in the local population (Ashley, 2010). Genotyping problems (including null alleles, mutations or just genotyping mistakes) may also cause type I or type II errors in paternity assignments, unpredictably confounding the inference on mating patterns (Slavov et al., 2005). As a consequence, errors in paternity assignments bias inferences about mating parameters. On the other hand, the lack of certainty of paternity assignment is inherently accounted for in more advanced approaches, here called ‘paternity modelling’. These use fractional paternity assignments (Devlin et al., 1988) in the framework of a dedicated probability (mixture) model to estimate directly the parameters (components) of mating that are defined arbitrarily during model construction (Burczyk et al., 2002; Oddou-Muratorio et al., 2005; Klein et al., 2008). However, there is a need for further statistical developments because the existing implementations of ‘paternity modelling’ tools do not take into account individual variation in mating system parameters.

This study aimed to investigate comprehensively individual mating patterns within a mixed stand of Quercus robur and Q. petraea. Interspecific mating is possible in this species complex (Bacilieri et al., 1996; Curtu et al., 2007; Gugerli et al., 2007; Lepais and Gerber, 2011), challenging us to incorporate hybridization parameters into paternity modelling. In particular, we focused on inferring the distribution of individual selfing vs. outcrossing vs. pollen immigration rates as well as a differentiation of immigrating pollen pools at the individual female level. Male fecundity, pollen dispersal and individual intra- vs. interspecific mating preferences were also of interest. These permit detailed testing of the null model of random mating. To make the underlying model more realistic, we used a Bayesian approach that adopts the methods introduced previously by Burczyk et al. (2002) and Klein et al. (2008) to the system under study. The main refinements of the model are (1) accounting for typing errors; (2) a differentiation among immigrant pollen pools received by individual mother plants; and (3) a multispecies (or groups) scheme for different mating rates.

MATERIALS AND METHODS

The study site and genotyping

The study was conducted within a 5 ha mixed stand of Quercus robur and Q. petraea located in Jamy near Grudziądz, Poland (18°55′41″E, 53°32′8′'N). The stand was previously used for studying patterns of seed and pollen dispersal based on naturally regenerated seedlings (Chybicki and Burczyk, 2010a). The 135-year-old stand originated from planting, probably using locally collected seed material. The distribution of individuals is almost uniform, while the distribution of species is nearly random (Fig. 1). Taxonomical assignment was conducted based on leaf morphology (A. Boratyński, Institute of Dendrology, Polish Academy of Sciences, Poland, unpubl. res.), and no additional (e.g. genetic) tests were undertaken to verify species identity. Therefore, the term ‘pure species’ when used here means ‘putatively pure species’, allowing for some uncertainty about the actual taxonomic identity. The study site Jamy is located at the north-eastern margin of the natural range of Q. petraea. It is fenced to prevent free penetration of larger animals (such as wild boar, roe deer, etc.) to protect natural oak regeneration. The stand is a part of a forest mosaic composed of beech, oak and pine. Pine is the most abundant tree species in the closest neighbourhood.

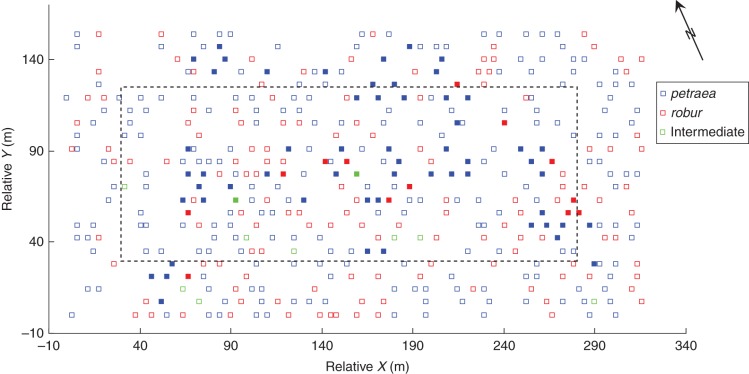
Fig. 1.

A map of the distribution of adult trees in the study site (Jamy, near Grudziądz, Poland). Mother trees are marked by filled squares.

Here we made use of data collected previously for all 421 adult individuals of both species. These include genotypes at five (out of six available in the original data set) unlinked, and highly polymorphic simple sequence repeat (SSR) loci (MSQ 4, ssrQrZAG 7, ssrQrZAG 20, ssrQpZAG 9 and ssrQpZAG 110), XY co-ordinates and diameter at breast height (DBH) measurements (Chybicki and Burczyk, 2010a). To study mating patterns, 72 trees were sampled for acorns. From these, 1911 seeds were successfully genotyped in total with 7–81 seeds per maternal family. The mother trees were selected to cover as much as possible of the total area of the stand (Fig. 1). However, due to variable female fecundity (the material was collected in a non-mast year), some regions remained under-represented. We arbitrarily classified mother trees as peripherally located (vs. centrally) if they were located <35 m from the border of the stand.

The model

Mating patterns were investigated with the aid of a probabilistic mating model (see Burczyk et al., 2002; Burczyk and Chybicki, 2004; Burczyk and Koralewski, 2005; Klein et al., 2011; Chybicki, 2013), originally referred to as the neighbourhood model (Adams and Birkes, 1991). In the neighbourhood model, in addition to genetic data, paternity is modelled through taking simultaneously into account spatial positions of trees as well as their fecundities, either in terms of fixed effects (Burczyk et al., 2002) or as random variables (Klein et al., 2008). These features make the neighbourhood model clearly different from the methods based on paternity inferred solely from genetic markers.

Total probability of an offspring genotype

The core of this model is the equation for total probability for an offspring genotype:

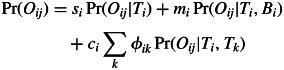(1)

where O_ij is a multilocus genotype of the j-th offspring in a family group mothered by the i-th adult tree, T_i is a multilocus genotype of the i-th adult tree, B_i is the allele frequency in an immigrant pollen pool of the i-th adult tree, {s_i, m_i, c_i} are per-family mixture rates corresponding to self-fertilization, pollination with immigrant pollen and local outcrossing (note that s_i + m_i + c_i = 1), and φ_ik is the rate of mating between the i-th and the k-th adult tree (note that Σ_k φ_ik = 1). Conditional probabilities for offspring genotype Pr(O_ij|.) follow Mendel's laws. As in the previous neighbourhood models (e.g. Burczyk et al., 2002; Klein et al., 2008), φ_ik is not a true parameter but instead it refers to a function of parameters describing a process of pollen dispersal, a distribution of individual fecundity and a rate of inter- vs. intraspecific fertilization. Here, φ_ik takes the form

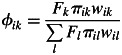(2)

where F_k is the fecundity of the k-th adult tree, π_ik is the probability of pollen dispersal at the distance between the k-th and the i-th adult tree, and w_ik is the probability of fertilization of an egg of the i-th plant with a sperm of the k-th plant as a function of species status of both parents.

Pollen dispersal

Here we assumed that pollen dispersal follows an exponential-power kernel (Austerlitz et al., 2004) of the form

(3)

where r is the distance of pollen dispersal (i.e. the distance between a point of pollen emission and the point of pollen deposition), a is a parameter of scale, b is a shape parameter of a dispersal kernel and Γ( … ) is the standard gamma function. An exponential-power kernel can take various shapes, which is useful to model various modes of dispersal. If b = 1, then dispersal follows simple exponential decay. If b > 1, then dispersal is concentrated around an emission point in a normal-like fashion (i.e. a light-tailed kernel). On the other hand, if b < 1, then the probability of dispersal decreases very slowly except for very short distances (i.e. a heavy-tailed kernel). Given the assumed dispersal kernel, then π_ik = f(d_ik; a, b) (eqn 2), where d_ik is the distance between the i-th and the k-th tree, and a and b are parameters of dispersal kernel. However, instead of a scale parameter, a theoretical average distance of (forward) pollen dispersal δ = a Γ(3/b)/Γ(2/b) was of direct interest, so the equation [eqn (3)] was rearranged appropriately to be a function of b and δ.

Fecundity

We used a model of individual fecundity distribution introduced by Klein et al. (2008). Briefly, fecundity of the i-th male F_i is assumed to follow log-normal distribution with variance Σ² and the mean fixed arbitrarily at 1. Klein et al. (2008) showed that under the assumed distribution of fecundity, Σ² + 1 equals a theoretical ratio of observed to effective density of pollen donors, i.e. Σ² + 1 = d_p/d_ep, which hereafter will be referred to as the relative effective density of pollen donors (REDP). In other words, REPD reflects the level of variation in pollen production within a population in terms of census to effective number of males.

Intra- vs. interspecific fertilization

In order to account for possible limitation of inter- vs. intraspecific mating, we used a vector of parameters corresponding to probabilities that the i-th individual can be successfully fertilized with pollen of the z-th species {ω_iz} (z = 1, 2, … , Z; where Z is the number of taxonomic groups identified in the study plot). Note that all ω_iz for the i-th individual sum up to 1. As a consequence, for a pair of individuals, of which the i-th is a mother tree and the k-th is a pollen donor belonging to the z-th species, a function w_ik = ω_iz. Because three taxonomic types were identified in the study site, we arbitrarily set z = 1 for Q. petraea, z = 2 for Q. robur and z = 3 for the intermediate type.

Typing errors

The conditional probabilities for an offspring genotype [eqn (1)] were computed assuming a possibility of random typing errors, occurring at a locus-specific rate ɛ_l. Here, ɛ_l denotes the probability that a random allele at the l-th locus has been incorrectly typed as one of the remaining alleles at the locus. Thus, the model for typing errors resembles the K-Allele Model of mutation (Crow and Kimura, 1970). All conditional probabilities were derived in an unpublished manuscript (I. J. Chybicki and J. Burczyk, unpubl. res.) and are described in detail in the manual of NM+ software ver. 1.1 (Chybicki and Burczyk, 2010b) available at the web site http://www.ukw.edu.pl/pracownicy/strona/igor_chybicki/software_ukw/.

Immigrant pollen pool

Immigrant allele frequencies (B_i) were modelled individually for each half-sib family. Although it is possible that all mother trees receive pollen from a common immigrant pollen pool (B_i = B_j = … = B), here we assumed B_i to be subjected to random drift that causes differentiation of immigrant pollen captured by different mother trees. In the simplest scenario, the random drift can occur as an effect of non-random sampling of pollen gametes from a background population. For this purpose, we used the so-called F-model of allele frequencies (Gaggiotti and Foll, 2010), in which allele frequencies in different sub-populations follow a Dirichlet distribution with parameters {p_tl1, … , p_tlM} (1/θ_i – 1), where p_tlm is the frequency of the m-th allele (out of M in total) at the l-th locus in the total population, and θ_i is the scaled variance of allele frequencies within a sub-population. Balding (2003) showed that, under Dirichlet distribution, θ_i can be interpreted as the probability that two genes drawn from a sub-population are identical by descent through shared ancestry within a sub-population. Thus, θ_i is an analogue of the classical Wright's F_ST. However, because here θ_i describes a rate of divergence of an immigrant pollen pool for the i-th mother, θ_i can be treated as an analogue of the Φ_ft parameter used in the TwoGener method (Austerlitz and Smouse, 2001; Smouse et al., 2001). Therefore, the parameter θ_i is approximately the probability of identity of two random pollen gametes drawn from an immigrant pollen pool for the i-th mother tree. It is worth mentioning that recent simulation tests confirmed the usefulness of the F-model in the analysis of pollen pool structure based on the similar Bayesian framework (Chybicki, 2013).

Inferential procedures

Because the above model depends on a large number of parameters, to estimate them we used a Bayesian approach that is conceptually similar to that proposed by Klein et al. (2008). Due to non-zero typing error rates, every candidate parent (regardless of its genotype) has a non-zero probability of being a father. Also, because error rates {ɛ₁, … ,ɛ_L} as well as allele frequencies in background populations {B_i, … ,B_N} were set as estimable, transition probabilities [eqn (1)] were no longer constants but depended on current values of ɛ_l and B_i. These two technical issues severely slow the computation of the likelihood function, making the MCMC (Markov chain Monte Carlo) algorithm as proposed in Klein et al. (2008) practically unmanageable. Therefore, to address this issue, we made use of auxiliary (latent) variables that depend on the data and the current parameter values. This allows analyses to be carried out in a reasonable time using a personal computer, even for large samples (as in this study). As explained below, the auxiliary variables store the results of paternity assignments conducted cyclically based on eqn (1) and conditioned on the current values of the parameters (see ‘Algorithm’ section). Therefore, the algorithm used here is in part analogous to that used in Hadfield et al. (2006) and Moran and Clark (2011).

Auxiliary variables

We also introduced additional variables which were not of direct interest but which facilitated the estimation of the goal parameters. These auxiliary variables are somewhat redundant as they are all deduced from assigned paternities. However, to show clearly which information is used to estimate a given parameter, we decided to avoid more complex representation. First, we introduced n_ik to represent the number of offspring in the i-th family sired by the k-th adult individual. Additionally, x_i, y_i and z_i were used to store the number of progeny in the i-th family which were a result of self-fertilization, outcrossing with locally produced pollen and outcrossing with immigrant pollen, respectively. To store the number of progeny in the i-th family sired by an adult belonging to the z-th species, we used g_iz. Finally, a_ilm was used to store a number of copies of the m-th allele at the l-th locus carried by immigrant pollen in the pool of the i-th family (i.e. in B_i).

For simplicity, we will use {n_ij} to denote multiple variables {n_i1, … ,n_iK} falling into the same category. A set of {n_i1, … ,n_iK} consists of variables which were assumed to follow a multinomial distribution with parameters {φ_ik} [see eqn (1)], i.e. {n_ik} ∼ Multinomial({φ_ik}). Similarly, {x_i, y_i, z_i} ∼ Multinomial(s_i, c_i, m_i), {a_ilm} ∼ Multinomial({p_ilm}) and {g_is} ∼ Multinomial({ω_is}). Assuming independence across offspring genotypes, all the auxiliary variables were inferred given the current parameter values, using a Bernoulli scheme based on eqn (1). First, with probability

(4)

the j-th offspring in the i-th family was a result of self-fertilization, so that after a positive outcome of a Bernoulli scheme x_i = x_i + 1. Alternatively, y_i = y_i + 1 and z_i = z_i + 1 were results of a Bernoulli scheme with probability

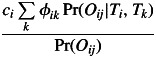(5)

and

(6)

respectively. Given an outcome of the above Bernoulli scheme, the remaining auxiliary variables were deduced in a nested scheme as follows. If the j-th offspring was deduced to be a result of outcrossing with locally produced pollen, then n_ik = n_ik + 1 with probability

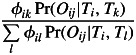(7)

Simultaneously it results in g_iz = g_iz + 1, with z corresponding to the taxonomic status of the k-th adult assigned as the father. If the j-th offspring was deduced to be a result of outcrossing with immigrant pollen, a_ilm = a_ilm + 1, where the m-th allele at the l-th locus was deduced at random under the assumption of Mendelian transmission given the maternal genotype and the current B_i.

Prior distributions

In the case of parameters referring to proportions that are directly related to the auxiliary variables, we used the Dirichlet distribution Dirichlet({α_i}) as a prior distribution. In particular, (s_i, c_i, m_i) ∼ Dirichlet(α_s, α_c, α_m) and {ω_iz} ∼ Dirichlet({1})(i.e. a uniform distribution). As mentioned earlier, in the case of immigrant pollen allele frequencies at the l-th locus in the i-th family {p_ilm} ∼ Dirichlet({p_tlm}[1/θ_i – 1]). Furthermore, because individual fecundity was assumed to follow log-normal distribution, it resulted in log(F_i) ∼ Normal(–σ²/2,σ ²), where σ² = log(Σ² + 1) was a (estimable) hyperparameter (Klein et al., 2008).

Typing error rates at the l-th locus ɛ_l as well as the hyperparameter θ_i were assumed to follow an exponential distribution truncated at 1, with the scale parameters β_ɛ and β_θ, respectively. On the other hand, {p_tlm} were assumed to follow Dirichlet({1}), i.e. the uniform distribution. The parameters taking real positive values, including parameters of dispersal kernel b and δ as well as hyperparameters σ, θ_i, α_s, α_c, α_m, β_ɛ and β_θ, were assumed (as in Klein et al., 2008) to follow an improper prior distribution proportional to 1/b, 1/δ, 1/σ, 1/θ_i, 1/α_s, 1/α_c, 1/α_m, 1/β_ɛ and 1/β_θ, respectively. In the case of the δ parameter, to avoid an uncontrolled drift towards extremely large values (Moran and Clark, 2011), we used a prior distribution truncated at 100 000 m.

Empirical estimates

Along with parameters of the model at any hierarchical level, we estimated additional quantities of interest. All these quantities were estimated in the same manner, i.e. by computing a specified function of values of current parameters during MCMC sampling, in order to obtain an empirical posterior distribution of this function. In this way, we estimated the empirical (observed) REDP_O as a function of the variance in inferred fecundity (Klein et al., 2008). REPD_O was of interest because the theoretical REDP can be biased because of the assumed prior distribution (Klein et al., 2011). To assess if there was any association between male fecundity and tree size, we estimated the empirical distribution of Spearman rank correlation between the DBH and F_i. In the same way, we assessed whether there was any relationship between the rate of local mating (c_i) and a preference towards intraspecific mating (ω_i1 and ω_i2, for petraea- and robur-type, respectively). To compare mating preferences between the two pure species, we estimated the empirical posterior distribution of the mean difference of ω_i1 between the two species:

(8)

where 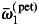and 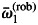correspond to averages over individual ω_i1 values, computed separately for petraea and robur sub-groups. The quantity d_i1 was expected to take values > 0, if there is positive overall skew towards intraspecific mating. Generally, similar procedures were employed whenever we wished to test a difference between two defined groups. Also, we estimated cumulative probability (CDF) of pollen dispersal distance based on the integral ₀∫^L 2πr f(r; a, b) dr, computed for a discrete set of upper limits (L). [Note that f(r; a, b) is defined in eqn (3).] Because the hyperparameters α_s, α_c and α_m were set as estimable, we were able to assess the level of over-dispersion among individual proportions, i.e. whether s_i, c_i, m_i exhibit multinomial or extramultinomial variation among mother trees. To measure an overall over-dispersion, we used a single summary parameter γ = (1 + α_s + α_c + α_m)⁻¹, estimated during MCMC. The parameter γ takes 0 if proportions follow pure multinomial variation and >0 if there is some extramultinomial variation among individuals. Although there is a boundary issue, i.e. α_s,α_c,α_m ∈ (0, + ∞), that makes it impossible to test formally for γ = 0, still the highest posterior density (HPD) set for γ can inform whether substantial over-dispersion occurs.

Algorithm

To approximate posterior distributions, a class of the MCMC approach was used called the Gibbs sampler. First, each cycle started by inferring new values for the auxiliary variables, given current parameter values. Then, for {s_i, c_i, m_i}, {ω_is} and {p_ilm}, new values were sampled directly from the posterior multinomial–Dirichlet distribution (the Gibbs sampling), given auxiliary variables inferred in the current cycle. For the remaining parameters, the Metropolis–Hastings procedure was used, which needs to define a proposal distribution. For parameters and hyperparameters that take positive real numbers, i.e. b, δ, σ², α_s, α_c, α_m, β_ɛ and β_θ, as in Klein et al. (2008), we used a proposal constructed by multiplying the current value by the random deviate drawn from log-normal distribution with a mean 1 and variance 0·1. In the case of parameters distributed continuously within the 0–1 interval, including {θ_i}, {p_tjk} and {ɛ_l}, we propose a new value using a random walk algorithm with reflection, with the additive distortion uniformly distributed between –0·1 and 0·1. Because allele frequencies must sum up to unity, in the case of {p_tjk} we used the approach of updating simultaneously frequencies for two randomly chosen alleles (cf. Falush et al., 2003). Estimation procedures were implemented in the NM2F computer program written in Pascal (the version running under Microsoft Windows is freely available at http://www.ukw.edu.pl/pracownicy/strona/igor_chybicki/software_ukw/). Estimates were derived with 50 000 MCMC samples, rejecting the first 10 000 updates. To weaken autocorrelation of subsequent updates due to Metropolis steps, only every 25th update was saved. Due to the large sample size as well as non-zero (and simultaneously estimable) genotyping errors, the estimation of all parameters in the full model took approx. 3 d on an average-speed PC unit (Intel Core 2 Duo E6750 @ 2·66 GHz).

RESULTS

Marker polymorphism

While adults had no missing genotypes (Chybicki and Burczyk, 2010a), 52 single-locus genotypes (0·5 %) were missing in progeny. The number of alleles per locus detected in progeny ranged from 24 to 30. However, due to apparent non-uniform allele frequency distributions, the effective number of alleles was low, ranging from 3·5 to 6·2. Observed heterozygosity in progeny was 78·4 % and did not deviate significantly from the panmictic expectation (77·8 %). The theoretical cumulative multilocus probability of paternity exclusion equalled EP = 0·9994, so that the probability of excluding all except the actual father (estimated as EP²⁴⁰) reached roughly 87 %. However, this proportion seemed to over-estimate the actual value, given that non-trivial typing error rates were found (see the next section).

Genotyping errors

Genotyping error rates were estimated individually for each locus assuming the exponential prior distribution. The posterior average error rates spanned from 1·4 to 8·1 %, with the grand average being 5·4 %. The scale hyperparameter of the prior distribution was slightly higher, reaching 0·066, with the 95 % credible interval (also known as Bayesian confidence interval, CI_B) between 0·024 and 0·164.

Mating patterns

Composition of progeny

In total, average rates of self-fertilization, outcrossing with a local tree and outcrossing with immigrant pollen were 0·5 % (from 0 to 7·4 %), 49·8 % (from 11·9 to 87·5 %) and 49·7 % (from 12·4 to 88·0 %) (Table 1), respectively. Interestingly, only a single Q. petraea tree (Family 11) exhibited a significant proportion of selfed progeny (7·4 %), while the others were classified as pure outcrossers. On average, robur-like mother trees experienced slightly, but significantly (P < 0·05), more outcrossing with immigrant pollen (56·7 %) than petraea-like trees (48·6 %). We also noted that mother trees (regardless of taxonomic assignation) in the periphery of the stand received significantly greater proportions of immigrant pollen than centrally located trees (60·5 % vs. 45·1 %).

Table 1.

Characteristics of half-sib families

Family	ni	Putative species	Location	X	Y	si	ci	mi	θi	Mating preference	Mating system
1	9	petraea	Central	89·9	70	0·002	0·738	0·260	0·091	petraea	Outcrossing
2	44	petraea	Central	72·5	70	0·001	0·420	0·579	0·036	petraea	Outcrossing
3	10	petraea	Central	66·7	91	0·002	0·668	0·329	0·061	Any	Outcrossing
4	7	petraea	Central	75·4	77	0·003	0·613	0·384	0·103	Any	Outcrossing
5	20	petraea	Central	66·7	77	0·002	0·327	0·672	0·046	Any	Outcrossing
6	24	petraea	Peripheral	81·2	133	0·001	0·313	0·686	0·082	Any	Outcrossing
7	14	petraea	Peripheral	142·1	133	0·003	0·475	0·523	0·038	Any	Outcrossing
8	16	petraea	Central	159·5	119	0·002	0·435	0·563	0·113	Any	Outcrossing
9	69	petraea	Central	150·8	91	0·001	0·854	0·146	0·184	petraea	Outcrossing
10	31	petraea	Central	147·9	77	0·001	0·875	0·124	0·106	petraea	Outcrossing
11	54	petraea	Central	121·8	91	0·074	0·691	0·235	0·046	petraea	Mixed
12	37	petraea	Central	110·2	77	0·001	0·682	0·317	0·060	petraea	Outcrossing
13	7	petraea	Peripheral	168·2	126	0·030	0·515	0·456	0·102	Any	Outcrossing
14	7	petraea	Peripheral	205·9	140	0·007	0·352	0·641	0·062	Any	Outcrossing
15	10	petraea	Peripheral	179·8	126	0·002	0·629	0·369	0·054	Any	Outcrossing
16	9	petraea	Central	185·6	119	0·003	0·753	0·244	0·098	petraea	Outcrossing
17	8	petraea	Peripheral	203	133	0·003	0·353	0·644	0·125	Any	Outcrossing
18	7	petraea	Central	171·1	119	0·003	0·540	0·457	0·222	Any	Outcrossing
19	23	petraea	Central	208·8	119	0·001	0·293	0·705	0·092	Any	Outcrossing
20	46	petraea	Central	220·4	119	0·001	0·580	0·419	0·150	petraea	Outcrossing
21	12	petraea	Central	214·6	105	0·003	0·199	0·799	0·228	Any	Outcrossing
22	19	petraea	Central	208·8	91	0·001	0·410	0·588	0·075	Any	Outcrossing
23	12	petraea	Central	220·4	84	0·002	0·520	0·477	0·200	Any	Outcrossing
24	14	petraea	Central	200·1	77	0·002	0·744	0·254	0·210	petraea	Outcrossing
25	79	petraea	Central	220·4	77	0·036	0·581	0·383	0·070	petraea	Outcrossing
26	25	petraea	Central	176·9	91	0·001	0·144	0·855	0·428	Any	Outcrossing
27	73	petraea	Central	179·8	77	0·000	0·842	0·157	0·058	petraea	Outcrossing
28	20	petraea	Central	182·7	84	0·002	0·686	0·313	0·105	petraea	Outcrossing
29	21	petraea	Central	211·7	77	0·002	0·581	0·417	0·045	robur	Outcrossing
30	64	petraea	Central	263·9	49	0·001	0·558	0·441	0·160	petraea	Outcrossing
31	14	petraea	Central	255·2	49	0·002	0·691	0·307	0·071	Any	Outcrossing
32	37	petraea	Central	272·6	49	0·001	0·730	0·269	0·048	petraea	Outcrossing
33	11	petraea	Central	261	56	0·002	0·659	0·339	0·068	petraea	Outcrossing
34	39	petraea	Central	255·2	84	0·001	0·354	0·645	0·076	petraea	Outcrossing
35	17	petraea	Central	269·7	42	0·002	0·401	0·597	0·077	Any	Outcrossing
36	77	petraea	Central	249·4	91	0·000	0·570	0·430	0·058	petraea	Outcrossing
37	21	petraea	Central	261	77	0·002	0·624	0·375	0·089	petraea	Outcrossing
38	19	petraea	Peripheral	287·1	49	0·002	0·607	0·391	0·057	Any	Outcrossing
39	12	petraea	Peripheral	290	28	0·003	0·404	0·593	0·061	Any	Outcrossing
40	11	petraea	Central	165·3	35	0·002	0·338	0·660	0·169	Any	Outcrossing
41	81	petraea	Central	174	35	0·001	0·530	0·470	0·053	petraea	Outcrossing
42	41	petraea	Central	171·1	63	0·001	0·707	0·293	0·044	petraea	Outcrossing
43	7	petraea	Central	165·3	63	0·002	0·498	0·500	0·069	Any	Outcrossing
44	9	petraea	Peripheral	52·2	7	0·002	0·188	0·810	0·114	Any	Outcrossing
45	22	petraea	Peripheral	58	28	0·003	0·301	0·696	0·051	Any	Outcrossing
46	19	petraea	Central	63·8	63	0·021	0·355	0·624	0·050	Any	Outcrossing
47	16	petraea	Central	75·4	63	0·002	0·426	0·572	0·115	Any	Outcrossing
48	30	petraea	Peripheral	69·6	140	0·002	0·526	0·472	0·064	petraea	Outcrossing
49	34	petraea	Central	130·5	63	0·001	0·672	0·327	0·059	petraea	Outcrossing
50	31	petraea	Peripheral	87	140	0·002	0·451	0·547	0·061	petraea	Outcrossing
51	13	petraea	Peripheral	110·2	133	0·002	0·465	0·533	0·050	Any	Outcrossing
52	13	petraea	Peripheral	84·1	147	0·002	0·456	0·542	0·125	Any	Outcrossing
53	8	petraea	Peripheral	188·5	147	0·003	0·416	0·581	0·055	Any	Outcrossing
54	15	petraea	Peripheral	174	140	0·002	0·543	0·455	0·075	Any	Outcrossing
55	16	petraea	Peripheral	46·4	21	0·002	0·119	0·880	0·057	Any	Outcrossing
56	41	petraea	Peripheral	55·1	21	0·001	0·238	0·761	0·195	Any	Outcrossing
57	7	petraea	Central	261	91	0·003	0·422	0·575	0·126	Any	Outcrossing
58	68	robur	Central	153·7	84	0·001	0·476	0·524	0·358	petraea	Outcrossing
59	26	robur	Central	142·1	84	0·001	0·597	0·402	0·094	petraea	Outcrossing
60	30	robur	Central	118·9	77	0·023	0·628	0·349	0·045	Any	Outcrossing
61	7	robur	Peripheral	214·6	126	0·003	0·275	0·723	0·162	Any	Outcrossing
62	12	robur	Central	240·7	105	0·002	0·186	0·812	0·195	Any	Outcrossing
63	46	robur	Central	188·5	70	0·001	0·735	0·264	0·034	petraea	Outcrossing
64	21	robur	Central	278·4	63	0·001	0·483	0·516	0·039	Any	Outcrossing
65	25	robur	Central	266·8	84	0·001	0·530	0·469	0·180	Any	Outcrossing
66	40	robur	Peripheral	281·3	56	0·001	0·295	0·705	0·029	robur	Outcrossing
67	40	robur	Central	275·5	56	0·001	0·365	0·634	0·048	petraea	Outcrossing
68	23	robur	Central	176·9	63	0·026	0·296	0·678	0·193	robur	Outcrossing
69	11	robur	Central	66·7	56	0·003	0·422	0·575	0·050	Any	Outcrossing
70	7	robur	Peripheral	66·7	21	0·003	0·274	0·723	0·034	Any	Outcrossing
71	29	intermediate	Central	159·5	77	0·001	0·443	0·556	0·068	Any	Outcrossing
72	74	intermediate	Central	92·8	63	0·001	0·798	0·201	0·182	petraea	Outcrossing

n_i, number of progeny in the i-th family; putative species, species assignation of the mother tree; X and Y, relative co-ordinates (in metres); s_i, posterior average self-fertilization rate; c_i, posterior average outcrossing rate with local trees; m_i, posterior average outcrossing with an immigrant pollen; θ_i, divergence of an immigrant pollen pool of the i-th mother tree from the total background population (alternative paternity identity within immigrant pollen); mating preference, preference towards mating with trees of a given (if any) species, inferred based on a test of whether the rate of acceptance of conspecific pollen is >0·5 (see text for details); mating system, preference towards purely outcross pollination or mixed self- and outcross pollination, inferred based on a test of whether a rate of self-fertiliztion is >0 (see text for details).

In addition to model parameters, the hyperparameters of the Dirichlet prior distribution were also estimated (Table 2). The posterior averages (95 % CI_Bs) were rather low, reaching 0·034 (0·006–0·082), 2·307 (1·406–3·681) and 2·322 (1·399–3·634) for α_s, α_c and α_m, respectively. The posterior average of the over-dispersion parameter γ equalled 0·183 (median = 0·182, mode = 0·181), with 95 % HPD between 0·116 and 0·251. Thus, the results provided strong support for significant over-dispersion in individual rates {s_i, c_i, m_i} among mother trees.

Table 2.

Estimates of empirical averages of individual rates of self-fertilization (s), outcrossing with local pollen (c) and outcrossing with immigrant pollen (m) together with estimates of hyperparameters of the Dirichlet distribution (see text)

Parameter	s	c	m	αs	αc	αm
Mean	0·005	0·498	0·497	0·034	2·307	2·322
Median	0·004	0·498	0·497	0·030	2·233	2·251
Mode	0·003	0·496	0·498	0·021	2·037	2·094
Q2·5 %	0·001	0·462	0·462	0·006	1·406	1·399
Q97·5 %	0·010	0·534	0·534	0·082	3·681	3·634

Mean, median and mode are point estimates given the posterior distribution, while Q values are quantiles of the posterior distribution that limits the 95 % credible interval.

Pollen dispersal kernel

Joint estimation of pollen dispersal kernel parameters with the remaining model parameters proved difficult. In particular, we found the estimate of average pollen dispersal distance (δ) to float occasionally towards extremely large values. Hence, the posterior distribution for δ was strongly right-skewed (Fig. 2A), resulting in substantial differences between posterior mean and median estimates, 3366 and 283 m, respectively. Using a default kernel density estimation procedure available in the R package (CRAN), we obtained (after log-transformation) a rough assessment of the mode equal to 121 m. In spite of a large number of offspring, we obtained a very wide 95 % HPD interval for δ, ranging between 38 and 20 189 m. The posterior mean and median for shape parameter b equalled 0·166 and 0·143, respectively. Similarly to δ, the posterior distribution of b was apparently right-skewed (Fig. 2B), resulting in the mode estimate (approximate) of 0·106. The 95 % HPD around b ranged between 0·020 and 0·366. Thus, the observed dispersal kernel was classified as ‘heavy-tailed’ with strong confidence. Based on the estimated CDF (Fig. 2C), the expected mean rate of pollen flow from outside 150 m (the mother-edge average distance) was equal to 33 % (CI_B 9–65 %), and thus did not deviate significantly from the estimated average pollen immigration rate.

Fig. 2.

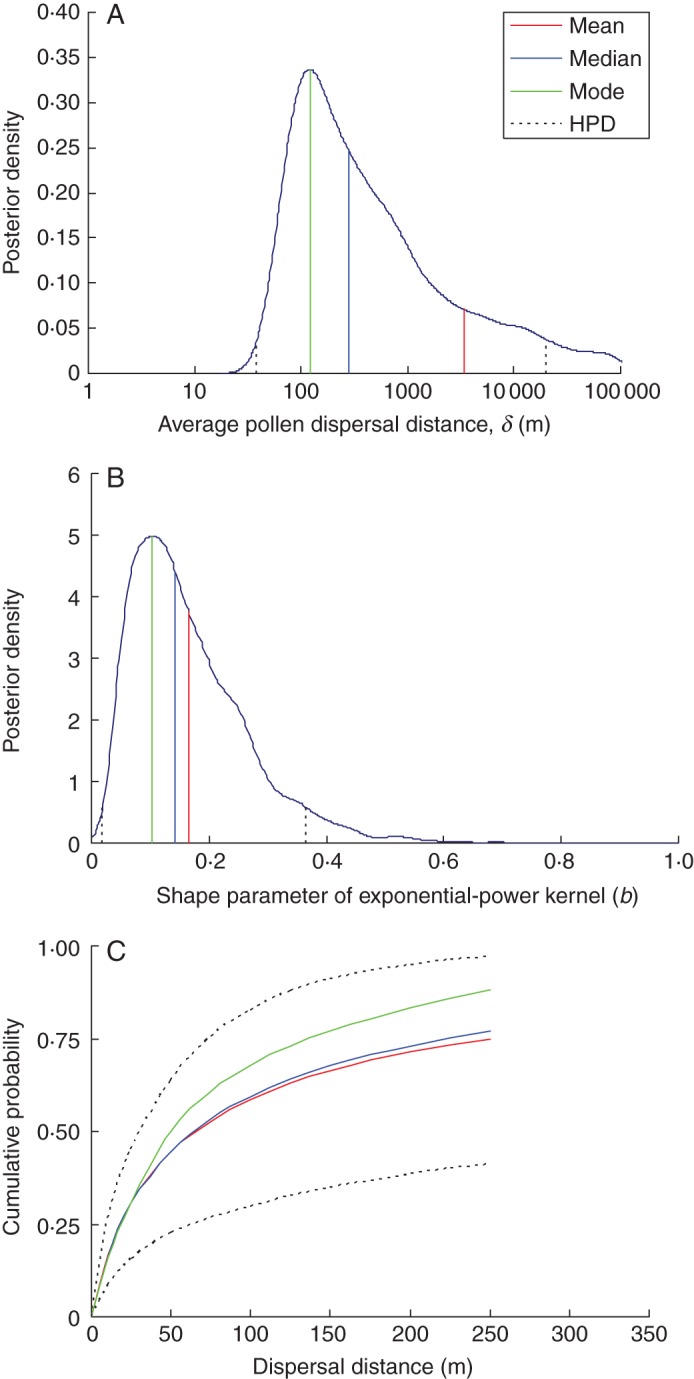
The posterior distributions of parameters of the exponential power kernel for pollen dispersal (A, B) together with corresponding pollen dispersal cumulative probability distribution (C). The three curves in (C) correspond to three point estimates of dispersal kernel parameters, i.e. mean, median and mode (see text). Note that the x-axis in (A) is given in a logarithmic scale.

Intra- and interspecific mating preferences

Generally, mother trees revealed great variability in mating preferences (Fig. 3). In order to summarize the results for pure species, we focused on rates of accepting conspecific pollen gametes. In the case of petraea-type mother trees, the average ω_i1 equalled 0·735 (95 % CI_B 0·698–0·772), spanning from 0·158 to 0·961. In the case of robur-type mother trees, the average ω_i2 was apparently lower, reaching 0·363 (95 % CI_B 0·278–457), and spanned between 0·043 and 0·783. The mean difference (d_i1) of ω_i1 between the two species equalled 0·217, with a 95 % CI_B of between 0·120 and 0·311. Thus, on average, petraea mother trees had a significantly higher preference for mating with petraea trees rather than robur mother trees. We employed CI_Bs that were significantly greater than 0·5 for ω_i1 and ω_i2 (for petraea- and robur-types, respectively) as criteria for specificity of the mating process at the individual level. Using these criteria, 23 out of 57 (40 %) petraea-type mother trees were classified as preferring to mate intraspecifically. On the other hand, only two out of 13 (15%) robur-type mother trees appeared to prefer receiving pollen gametes of the same species. Interestingly, among the remaining robur-type mother trees, four preferred to mate interspecifically (i.e. with petraea-type trees), while seven had no apparent mating preferences. In comparison, only one petraea-type mother tree was found to mate preferentially with robur-type trees, while the remaining 33 mother trees had no specific preferences. It is worth mentioning that both intermediate mother trees revealed a preference towards backcrossing with Q. petraea, with one exhibiting ω_i1 close to 1 (and significantly >0·5).

Fig. 3.

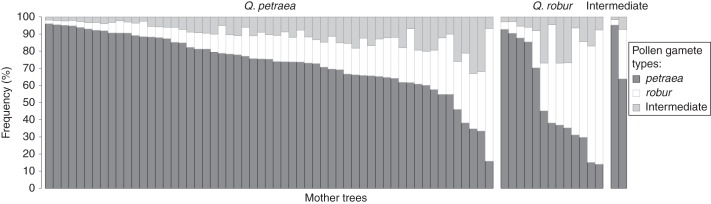
Individual per-mother tree distributions of the probability of accepting a pollen gamete of petraea, robur or intermediate type. Each bar represents a single mother tree. Mother trees were grouped according to putative species assignation.

Using the Spearman correlation coefficient (r), we also measured the relationship between the rate of local mating (c_i) and the preference towards intraspecific mating (ω_i1 and ω_i2, for petraea- and robur-type trees, respectively). In the case of petraea-type trees, we observed a positive and highly significant relationship. In this case, the normal-like posterior distribution was centred on an average r = 0·42, with a confidence interval (CI) between 0·24 and 0·58. On the other hand, for robur-type trees, the relationship was negative yet insignificant, with an average r = –0·23 and 95 % CI between –0·60 and 0·17.

Male fecundity

The hyperparameter σ of log-normal prior distribution for fecundity was concentrated on a 95 % CI_B between 1·080 and 1·504, with a mean of 1·272 and median 1·264. It resulted in the theoretical REDP being equal to 5·32, with a 95 % CI_B between 3·21 and 9·60. The empirical REDP_O appeared slightly lower than the REDP, with a posterior mean and median equal to 4·25 and 4·11, respectively. The 95 % CI_B was between 3·01 and 6·19. At the individual level, male fecundy showed high variance, with individual posterior averages ranging from 0·079 to 14·71. Because fecundity was assumed to follow a log-normal distribution with a mean equal to 1, to examine how many outliers were in the stand due to extreme fecundity values we searched for individual values significantly different from 1. We found that six trees had fecundity significantly greater than 1, while 22 had fecundity significantly lower than 1. The average fecundity of those sub-sets of superior and inferior trees was equal to 8·84 and 0·25, respectively. We found that the correlation between DBH and fecundity was positive but not significant (r = 0·072, 95 % CI_B –0·008–0·153).

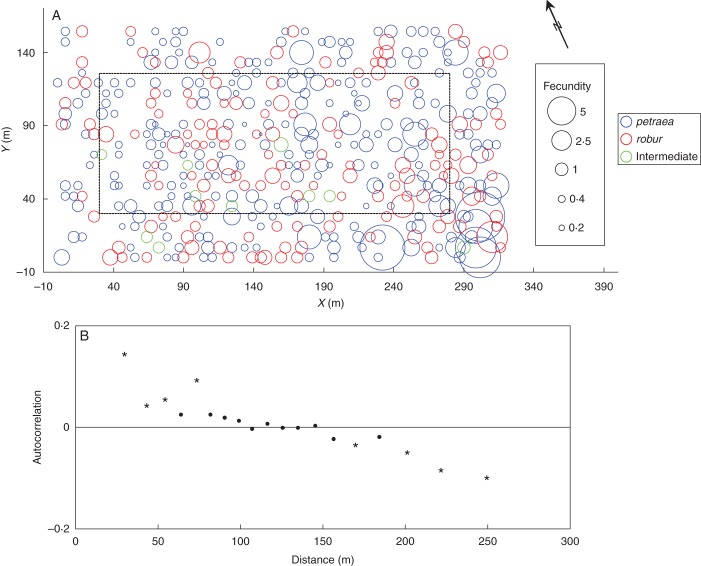
At the taxonomic level, fecundity did not differ between the three groups, taking on average 0·95 (95 % CI_B 0·76–1·16), 0·91 (95 % CI_B 0·70–1·17) and 0·85 (95 % CI_B 0·29–1·98) for petraea-type, robur-type and intermediate trees, respectively. However, inspection of the spatial distribution of individual male fecundity revealed that the most fecund trees were located in the southern corner of the stand (Fig. 4A). Using a spatial autocorrelogram (Moran's I), with posterior means as data, we revealed significant clustering (P < 0·001) of trees having a similar fecundity up to 70 m (the extent of positive autocorrelation), and significant repulsion of trees located >160 m apart (the extent of negative autocorrelation) (Fig. 4B). Thus, the autocorrelogram confirmed the presence of a strong cline-like distribution of fecundity within the stand.

Fig. 4.

Relative male fecundity in the stand. (A) Distribution of fecundity in the stand: Q. petraea, Q. robur and intermediate trees as indicated in the key. The dashed line shows the border of the central zone. (B) Spatial autocorrelogram summarizing a spatial structure of fecundity: significant autocorrelation coefficients are marked with asterisks.

The genetic structure of immigrant pollen

The average differentiation (θ_i) over all mother trees equalled 0·101, with a 95 % CI between 0·085 and 0·119. Individual values spanned from 0·029 to 0·428. On average, petraea-type mother trees had slightly lower θ_i than robur-type trees (0·098 vs. 0·112). However, the difference appeared not to be significant. Also, peripheral mother trees had lower average θ_i than central trees (0·079 vs. 0·111), but, again, the difference was not significant. We also did not observe significant correlation between m_i and θ_i.

DISCUSSION

The present study concentrated on mating patterns by using comprehensive analysis of paternity. We attempted to account for all major factors influencing paternity, including non-random pollen dispersal, uneven male fecundity and non-random interspecific mating, as well as some more technical issues such as genotyping errors or uncertainty about immigrant pollen pools. Our approach allowed us to identify detailed patterns present at the level of individual females, which would remain cryptic if mating patterns were assessed with the use of the classical neighbourhood model (Adams and Birkes, 1991; Burczyk et al., 2002).

Mating system

Oaks are mostly allogamous species (Bacilieri et al., 1993; Dow and Ashley, 1998a; Streiff et al., 1999; Nakanishi et al., 2004; Curtu et al., 2009; Chybicki and Burczyk, 2010a; Lepais and Gerber, 2011). Nonetheless, experiments based on controlled pollination showed that there might be a significant variation in ability to self-fertilize among oak trees (Aas, 1991; Steinhoff, 1993, 1998). Possible causal mechanisms may include genetically driven self-incompatibility that inhibits fertilization with selfed pollen (Hagman, 1975; Yacine and Bouras, 1997; Buschbom et al., 2011). In natural conditions, poor flowering synchrony between male and female flowers of the same individual (Bacilieri et al., 1995) and biased sex allocation (see Ducousso et al., 1993) can additionally influence the chance of self-fertilization. Our results seem to support the above opinion, as significant over-dispersion was identified. However, detailed examination revealed that only a single tree (out of 72) showed occasional (and significant) self-fertilization, with 7·4 % or about four seeds being produced through self-fertilization. Thus, to a great extent, the statistical effect of over-dispersion in selfing rates can be attributable to the exceptional behaviour of a single tree. Moreover, our previous study (Chybicki and Burczyk, 2010a) in the same stand showed some preference towards self-fertilization in another tree (Family 68), that is no longer the case here. Therefore, any furhter in-depth conclusions should be drawn with caution.

Pollen flow

In wind-pollinated tree species, pollen dispersal usually follows a leptokurtic, heavy-tailed distribution (Streiff et al., 1999; Austerlitz et al., 2004; Goto et al., 2006; Shimatani et al., 2007; Chybicki and Burczyk, 2010a). Our results conform to this pattern. In particular, the probability distribution of dispersal was apparently more heavy-tailed than a simple exponential kernel. In other words, the dispersal probability decreases very slowly at long distances, suggesting a relatively high likelihood of long-distance dispersal. These findings are concordant with the previous estimates (Dow and Ashley, 1998a; Streiff et al., 1999; Nakanishi et al., 2004; Chybicki and Burczyk, 2010a; Craft and Ashley, 2010), which generally suggest a great potential for long-distance pollen dispersal in oaks. Unfortunately, the average and the cumulative probability distribution of dispersal distance estimated in this study showed unsatisfactorily wide confidence intervals, preventing the precise predictions of patterns of pollen dispersal. In our opinion, this was mainly due to the inability to capture nuances of different heavy-tailed models (within a range of confidence intervals for b) at the spatial scale of the study plot (<300 m). A solution in this case would be to link immigration rates with the dispersal kernel (e.g. Shimatani et al., 2007; Chybicki and Burczyk, 2010a; Moran and Clark, 2011). However, it requires a reasonable model of forest landscape at least in the neighbourhood of the study plot, which is not readily available in our case. Nonetheless, the cumulative probability distribution is strongly dependent on the assumed dispersal kernel (see Gérard et al., 2006; Goto et al., 2006), and thus it has low overall confidence. The same warning is also valid for the estimates of the average (forward) dispersal distance obtained in this study. However, although this information is generally interesting, the estimate of the average dispersal distance is less important for predicting essential features of gene flow patterns (Klein et al., 2006).

Estimates of pollen immigration rates are generally very sensitive to the presence of typing errors (Gérard et al., 2006), the assumed frequencies in the pollen source background population (Burczyk and Chybicki, 2004) and the presence of unsampled local fathers. In our study, all these issues were accounted for, so it is our belief that the estimated immigration rates were nearly unbiased. Interestingly, they appeared to be about 20 % lower than our previous estimates for the same stand based on procedures ignoring typing errors (m = 0·623; Chybicki and Burczyk, 2010a); however, in that case, the analyses were conducted based on established seedlings. Moreover, if we assume that the edge effect, as detected in this study, did not affect our previous results (due to the apparently central location of potential mother trees), the difference may increase even further (i.e. 45·1 % vs. 62·3 %). It seems that the present approach effectively removed the upward bias, expected under naïve transition probabilities. Nonetheless, still about 50 % of pollination events were due to immigrant pollen, which is quite comparable with previous studies on oaks in general (Dow and Ashley, 1998a; Streiff et al., 1999; Nakanishi et al., 2004; Chybicki and Burczyk, 2010a; Craft and Ashley, 2010). Surprisingly, the mean pollen immigration rate corresponded quite well to the prediction based on the estimated (posterior average) CDF for pollen dispersal. This might suggest that there is no obvious heterogeneity between the modes of local vs. long-distance pollen dispersal, i.e. that pollen dispersal follows roughly a single monotonic probability function. This would be in opposition to the opinion that, for wind-borne pollen, long-distance and local movements are based on different aerodynamic processes (Di-Giovanni et al., 1996; Williams, 2008). However, our conclusion should be treated with caution, because estimates of dispersal kernel parameters were characterized by low precision.

Generally, the probability of paternal identity decreases together with the extent of pollen flow (Austerlitz and Smouse, 2001). Therefore, one might expect θ_i to decrease together with pollen immigration (Nakanishi et al., 2004, 2005; Craft and Ashley, 2010), because immigrant pollen can be assumed to come from a large background population. However, in our study, some trees that received a lot of pollen from outside the stand also revealed a very high level of homogeneity in immigrant pollen (e.g. Family 25, Table 1). Given that 2θ_i approximates the proportion of full-sibs among offspring produced with immigrant pollen (Hardy et al., 2004), our results indicated the presence of correlated mating among trees located further than 150 m apart. In the case of animal-pollinated species, such a correlation can be readily explained (Schoen and Clegg, 1984) as an effect of long-distance transportation of a pollen load from one plant to another (Hardy et al., 2004). However, in the case of wind-pollinated species, it is not obvious how this phenomenon could actually occur. Here, correlated mating over long distances seems extremely unlikely, because it requires that pollen gametes can travel between two particular trees structured as a homogeneous cloud. In our opinion, a possible explanation, that would lead to high genetic identity among immigrant pollen gametes, could be high mating compatibility (e.g. flowering synchronization) between particular oak trees located within the stand and near to the border of the stand. Alternatively, our estimates of θ_i may have been subject to positive bias. Although the simulation studies did not suggest any strong bias in indirect estimates of paternal identity probability (Hardy et al., 2004; Chybicki, 2013), Abraham et al. (2011) warned that the probability of paternal identity can be over-estimated (up to 4-fold) with indirect approaches when the proportion of full-sibs is very low. Nonetheless, even if this is the case in our study, the proportion of full-sibs among half-immigrant progeny would be quite high in the most extreme cases (see Table 1). Despite this speculation, our results demonstrated that a high proportion of immigrant pollen in the total pollen cloud of a single tree does not necessarily imply high pollen gene flow in certain cases, although this can be generally true (Nakanishi et al., 2004, 2005; Craft and Ashley, 2010).

Intra- vs. interspecific mating

Multispecies oak populations are often the scene of interspecific mating that leads to hybridization and introgression (Whittemore and Schaal, 1991; Bacilieri et al., 1996; Curtu et al., 2007; Gugerli et al., 2007; Peñaloza-Ramirez et al., 2010; Lepais and Gerber, 2011). Our study revealed non-random interspecific mating between Q. robur and Q. petraea. In particular, we detected asymmetric mating proportions, with Q. petraea acting generally as a donor while Q. robur acted as a recipient of interspecific pollen. However, we need to recall here that the taxonomic status of some trees in the study stand may have been incorrectly assigned. Problems with taxonomic discrimination between the studied oaks have been discussed often (e.g. Kremer et al., 2002; Curtu et al., 2007). Generally, using a multivariate approach, one is able to discriminate between the two species quite easily. However, because hybrids can manifest the phenotypes of a pure species (Gugerli et al., 2007), genetic markers are needed to improve discrimination. Unfortunately, our marker set has poor discrimination power for this purpose (as a comparison, see, for example, Lepais et al., 2009; Neophytou et al., 2010; Chybicki et al., 2012). Nevertheless, the observed asymmetric mating proportions could be due, hypothetically, to Q. petraea being a more invasive species (Petit et al., 2004). Yet controlled crosses did reveal asymmetric rates of interspecific fertilization, with Q. robur being more successful as female than Q. petraea (Steinhoff, 1998). These findings were confirmed in a few field studies (Bacilieri et al., 1996; Curtu et al., 2009; Lepais and Gerber, 2011). A hypothesis of species succession through genome invasion (Petit et al., 2004) seems very attractive in our case, especially because in the study area Q. petraea reaches the north-eastern limit of the natural distribution. However, because the stand originated artificially from planting, any in-depth interpretation should be made with caution.

Also, we detected a positive relationship between the rate of local mating (c_i) and the preference towards intraspecific mating in Q. petraea. A possible explanation could be that flowering times of the two oak species are not synchronized (Williams et al., 2001). If so, those Q. petraea trees which are more synchronized with Q. robur, as compared with the species average, could receive local pollen mostly from Q. robur. However, because the overall rate of successful interspecific fertilization (in a direction from Q. robur to Q. petraea) is low, much of the fertilization is due to immigrant, putatively conspecific, pollen. Unfortunately, we have no data on flowering phenology in the stand. Scarce published data do not support the hypothesis about significantly asynchronous flowering between Q. robur and Q. petraea (Bacilieri et al., 1995; Chesnoiu et al., 2009). However, because a similar hypothesis has already been formulated (Curtu et al., 2009), it would be an attractive subject for future studies.

Fecundity

Plant size is often considered as a proxy of fecundity. In the simplest case, fecundity (sexual function) increases allometrically with size, because larger individuals have more branches and therefore more reproductive organs (Enquist and Niklas, 2002). Also, larger plants have a larger energetic budget than smaller plants. Theoretically, in wind-pollinated hermaphrodites, such as oaks, larger plants tend to be more male-biased than smaller plants (Sakai and Sakai, 2003). The prediction holds true especially when the fecundity of larger plants in relation to smaller plants is higher than their relative seed dispersal area. This evolutionary prediction stems from the fact that larger (taller) wind-pollinated plants can disperse their pollen more extensively, achieving higher male reproductive success when compared with smaller plants. However, in natural conditions, microhabitat quality is a proximate factor of fecundity because plants that grow in a richer microhabitat are potentially larger and more fecund. However, in real-world studies, tree size was found to be unrelated to male reproductive success in the wind-pollinated tree species Quercus macrocarpa (Dow and Ashley, 1998b) and Fagus crenata (Shimatani et al., 2007). In contrast, Asuka et al. (2005) found a positive correlation between the proportion of fertilizations and the tree diameter in one of the two studied populations of F. crenata. In our case, estimated male fecundity was spatially structured, with a clinal distribution. This was not dependent on species identity and did not co-vary with tree size. Thus, it seems that male fecundity was related to resources that do not influence tree size. Better exposure to wind and/or insolation seems a possible cause because the southern corner of the stand is slightly elevated. Another explanation could be that, among size-related variables other than the tree diameter, the crown volume is a better predictor of male fecundity (Dow and Ashley, 1998b). However, in the area of high male fecundity (see Fig. 4A), trees grow in high density, so that their crown volumes probably do not deviate from the stand average.

Our study has demonstrated that the relative effective density of pollen donors is about 5. In other words, if there are approx. 100 individuals ha⁻¹, the estimated distribution of male fecundity translates into about 20 pollen donors ha⁻¹ effectively contributing to the local pollen production. One possible consequence of the uneven contribution of individuals to the next generation is a decrease of the effective population size resulting in genetic drift within populations (Wilson and Levin, 1986). Obviously, the present results describe contemporary mating patterns and thus they provide little evidence of the overall reduction of effective population size during the life time of the population. However, a previous study revealed that effective population size can be relatively stable across different seed collection years (Dering and Chybicki, 2012). Paternity data for future seasons would help in reaching a final conclusion.

In order to capture the finest details of mating patterns from the perspective of individual females, we have developed a complex mating model and used a Bayesian approach to estimate parameters of interest. Consequently, we have demonstrated that mating patterns in oaks are far from being random. This applies to all mating components: self-fertilization; outcross mating within a local population; and mating with distant males through pollen immigration. On the other hand, male features such as proximity to focal females or male size (here DBH) appeared to be poor proxies of male mating success. Therefore, the question remains: why is a given female more likely to mate with a particular male? Is the number of mates per female genetically or environmentally determined? As sexual selection by female choice has not been excluded in oaks (Dow and Ashley, 1998a), besides flower phenology, there might be additional cryptic mechanisms determining the potential of females to mate with few or many males. Temporal data on mating patterns should shed more light on these issues. Nevertheless, the long-term evolutionary implications of assortative vs. random mating in oaks are yet to be understood (Soularue and Kremer, 2012).