Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2013 Jul 22.
Published in final edited form as: Phys Med Biol. 2011 Jan 17;56(3):N39–N51. doi: 10.1088/0031-9155/56/3/N01

In Vivo Quantification of Lead in Bone with a Portable X-ray Fluorescence (XRF) System – Methodology and Feasibility

LH Nie 1, S Sanchez 1, K Newton 2, L Grodzins 3, RO Cleveland 4, MG Weisskopf 2
PMCID: PMC3718311  NIHMSID: NIHMS492533  PMID: 21242629

Abstract

This study was conducted to investigate the methodology and feasibility of developing a portable XRF technology to quantify lead (Pb) in bone in vivo. A portable XRF device was set up and optimal setting of voltage, current, and filter combination for bone lead quantification were selected to achieve the lowest detection limit. The minimum radiation dose delivered to the subject was calculated by Monte Carlo simulations. An ultrasound device was used to measure soft tissue thickness to account for signal attenuation, and an alternative method to obtain soft tissue thickness from the XRF spectrum was developed and shown to be equivalent to the ultrasound measurements (Intraclass Correlation Coefficient, ICC=0.82). We tested the correlation of in vivo bone lead concentrations between the standard KXRF technology and the portable XRF technology. There was a significant correlation between the bone lead concentrations obtained from the standard KXRF technology and those obtained from the portable XRF technology (ICC=0.65). The detection limit for the portable XRF device was about 8.4 ppm with 2 mm soft tissue thickness. The entrance skin dose delivered to the human subject was about 13 mSv and the total body effective dose was about 1.5 μSv and should pose a minimal radiation risk. In conclusion, portable XRF technology can be used for in vivo bone lead measurement with sensitivity comparable to the KXRF technology and good correlation with KXRF measurements.

Keywords: x-ray fluorescence (XRF), bone lead, lead toxicity

1. INTRODUCTION

Human exposure to lead has been reduced dramatically over the last two decades largely due to the removal of lead from gasoline. Nevertheless, lead exposure and toxicity remains a significant public health issue as certain populations still experience high exposures and increasing evidence indicates that lead has adverse health effects even at low exposure levels experienced by the general population (Canfield et al., 2003; Navas-Acien et al., 2007; Navas-Acien et al., 2008; Schaumberg et al., 2004; Shih et al., 2007; Weisskopf et al., 2009). Blood lead is the most commonly used biomarker for lead exposure assessment. However, blood lead has a short half-life of about 30 days, which means it only reflects short-term exposure (Rabinowitz, 1991). Bone lead, on the other hand, has a half-life of several years to decades, making it a better marker of cumulative or long-term exposure (Leggett, 1993). X-ray fluorescence (XRF) has been used to measure lead in bone for over two decades. The conventional XRF bone lead measurement system utilizes lead K-x rays (KXRF). Although bone lead data has been found to be a better biomarker than blood lead to predict many health effects related to long-term lead exposure (Hu et al., 1996; Gonzalez-Cossio et al., 1997; Needleman et al., 1996; Weaver et al., 2005; Shih et al., 2007; Bandeen-Roche et al., 2009), only a few research institutions possess this technology, largely because of infrastructure demands for the detection system—including radioisotope regulation issues—and the demand for a specialist in this particular technology to operate the system. A more accessible technology to measure bone lead would have important benefits for studies of health effects of lead exposure. In this study, we investigated the methodology and feasibility of a portable XRF technology for in vivo bone lead quantification. The XRF device used in this project has an energy span up to 50keV, and therefore makes use of lead L-x rays since the energy is not sufficient to produce lead K-x rays. We conducted phantom experiments to determine the sensitivity of the portable device, human cadaver experiments to measure tissue thickness overlying bone from the XRF spectrum, as well as in vivo tests to estimate the correlation of bone lead concentrations between KXRF and portable XRF.

2. MATERIALS AND METHODS

2.1 KXRF bone lead measurement system

KXRF technology was used as a standard method to validate the portable XRF technology. The physical principles and laboratory set up of this instrument have been described elsewhere (Chettle et al., 1991; Gordon et al., 1993; Aro et al., 1994). In summary, the system consists of a 51 mm diameter Canberra HpGe detector with 20 mm thickness, one feedback resistive pre-amplifier, one analog signal processing system, and a computer. The lead K x-rays are produced by irradiating tibia bone with a 109Cd source. The measurements site on the tibia was washed with a 50% solution of isopropyl alcohol and a 30-minute bone lead measurement taken. Interaction signals, which include characteristic lead K x-rays, were collected by the HpGe detector and processed by the analog electronics. The spectra were analyzed with an in-house peak fitting program based on Marquardt least-square algorithm and the final lead concentrations were calculated (Chettle et al., 1989; Bevington and Robinson, 2003).

2.2 Portable XRF device

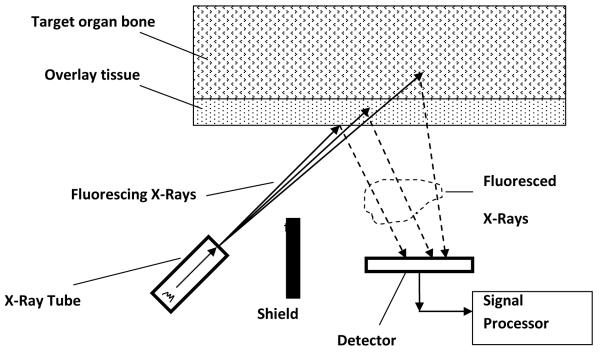
The portable XRF device (XL3, Thermo Fisher Scientific Inc., Billerica, MA) is designed for elemental quantification of industrial and environmental samples. It has an energy span up to 50 keV. It is equipped with a thermoelectric cooled Si PIN diode with 8 mm2 area and 1 mm thickness. For our experiments the x-ray tube voltage was set to 50 kV, the current set to 0.25 μA. A silver (Ag) anode was employed, and a combination of silver and iron (Fe) filters were chosen which were found to provide the best detection limit for bone lead quantification. An internal camera images the sample onto an LCD display, which is used for positioning the instrument. The image is stored along with the data for each measurement. Figure 1 shows a schematic plot of the measurement configuration for the portable XRF device. The portable XRF makes use of the lead L-x rays produced by interaction between the x-ray beam and lead in bone. Lead L-x rays have energies much lower than lead K-x rays produced by the KXRF system. Hence, portable XRF samples the surface of the bone (with a mean free path of L-x ray in bone of about 0.2-0.3 mm), while the KXRF method samples deep into the bone (with a mean free path of K-x rays in bone of about 20 mm). As for the sampling area, portable XRF samples about 1 cm2 of the skin and hence bone surface, while KXRF samples about 1-3 cm2 of the bone surface depending on the distance between the source and the skin surface.

Figure 1.

Figure 1

Open in a new tab

A schematic diagram of an in vivo bone lead quantification set up with portable XRF

2.3 Phantom measurements with portable XRF

Phantoms were used to assess the performance of the portable XRF device. Lucite phantoms were employed to simulate the soft-tissue overlying the bone. The thickness of the Lucite phantoms ranged from 0.5 mm to 5 mm, with an increment of 0.5 mm. Lead doped phantoms made of plaster of Paris were used to simulate bone. The lead concentrations in bone-equivalent phantoms ranged from 0 to 100 ppm (0, 5, 10, 15, 20, 30, 50, 75, 100 ppm). One animal bone with 0 ppm lead concentration was also used to determine the correlation between soft tissue thickness and Compton peak count rate. The effect of Compton scattering is material-dependent, with the lower atomic number materials scattering more strongly than the higher atomic numbered materials. The higher atomic number elements are also more likely to absorb x-rays than the lower atomic number materials. The soft tissue consists of elements with lower atomic numbers than those for the elements in bone. Hence, more Compton scattering will be detected from soft tissue than from bone. As we increase the Lucite thickness or soft tissue thickness over bone, we expect to see an increase of Compton peak counts.

Phantom measurements were performed for three purposes: first, to calibrate the system; second, to find the correlation between soft tissue thickness and the Compton peak counts in order to determine how well soft tissue thickness can be measured directly by the portable XRF device; and third, to calculate the detection limit of the system.

2.4 Ultrasound measurements

In order to correct for signal attenuation, the thickness of the soft tissue overlying the bone needs to be monitored. We used a diagnostic ultrasound scanner (Terason 2000, Teratech, Burlington, MA) with a 7.5 MHz linear array probe (10L5, Teratech, Burlington, MA) to measure the soft tissue thickness. The ultrasound system was operated in the default musculoskeletal imaging mode with the transmit focus set at 0.6 cm. The lateral resolution of the ultrasound system was 1 mm through the range of depths investigated here. The axial resolution was less than 0.1 mm. The soft tissue thickness was determined by manually locating the reflection from the bone in the image and using the caliper function included in the ultrasound software. The ultrasound measurement served two purposes: first, to find a spot with the thinnest soft tissue thickness overlying the bone so the signal attenuation would be minimal, which increases the sensitivity of the x-ray measurements; second, to measure the thickness of the soft tissue.

2.5 Cadaver experiments with portable XRF and ultrasound

The study protocol was approved by the institutional review boards of Harvard School of Public Health and Brigham and Women’s Hospital for cadaver experiments and in vivo testing. Measurements with the portable XRF were conducted at the Harvard Medical School Anatomy Laboratory on 6 embalmed cadavers of people who donated their bodies for scientific research.

A heavy stand made of stainless steel was manufactured to fix the portable XRF device at a given position. Three to six sites were selected on the cadaver’s leg and measured with the ultrasound probe. A lead free marker pen was used to mark the locations and then XRF device was positioned with the marker located at the center of the beam, as observed through the internal camera installed on the portable XRF device. When multiple measurements at the same site were taken, the portable XRF was not repositioned.

2.6 Study population and in vivo measurements

The population we used to test the correlation of bone lead concentrations between KXRF measurement and portable XRF measurement in vivo was the Harvard Cooperative Program on Aging cohort (HCPOA), a program of the Harvard Older Americans Independence Center, the Massachusetts Alzheimer’s Disease Research Center and the Hebrew SeniorLife Institute for Aging Research. HCPOA is a large ethnically diverse cohort of over 1300 Boston area community-dwelling older adult volunteers. Among 144 HCPOA participants with prior bone lead measurements, 9 of them with the highest tibia lead concentrations returned to be measured with both the KXRF and portable XRF machines. For these measurements the ultrasound was first used to identify a site on the tibia bone with minimal overlying tissue thickness and this spot was marked in order to center all measurements on the same site. A two-minute portable XRF measurement was made, followed by a 30 minute KXRF measurement, and then a second two-minute portable XRF measurement.

2.7 Spectrum analysis

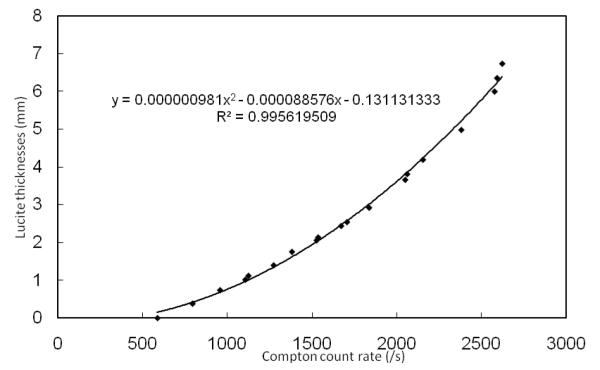
The standard method to convert the characteristic x-ray signal to bone lead concentrations for an x-ray fluorescence in vivo bone lead measurement is peak fitting coupled with traditional calibration. In this standard method, both x-ray Lα and Lβ peaks are fitted with an arbitrary function which consists of a Gaussian distribution to represent the net x-ray peak and an exponential distribution to represent the background. The count of the net x-ray peak for in vivo measurement is calculated and the lead concentration is interpolated from a calibration line created with lead doped phantoms (Nie et al., 2004). In this paper, a novel method for data analysis was developed called background subtraction. We have demonstrated that the soft tissue thickness and hence the soft tissue attenuation is correlated with Compton peak (Figure 2). So the background can be calculated as a function of Compton peak. Because soft tissue thickness and hence the net x-ray peak count rate attenuation is a function of Compton peak count rate, we can also conclude that the x-ray net count rate for a specific phantom with known lead concentration is also a function of Compton peak count rate. The new calibration procedure is illustrated as follows with lead Lα x-ray as an example.

Figure 2.

Figure 2

Open in a new tab

Lucite thicknesses versus Compton count rate for phantom measurements with portable XRF

a) Run a set of 0 ppm phantom measurements with different Lucite thicknesses to determine the relationship of the count rates between the background of the lead Lα peak and the Compton peak.

Lα,bkg=A1×c+B1

Where Lα,bkg is the background count rate in the lead L α peak area, c is the count rate of the Compton peak. A1 and B1 are coefficients determined by fitting the data to a linear line.

The function obtained from our experiments is listed below with an R2 of 0.964:

Lα,bkg=(2.0e−4±0.6e−4)×c+(0.35±0.07)

b) Run a set of 100 ppm phantom measurements with different Lucite thicknesses to determine the relationship of the count rates between the net lead L α peak and the Compton peak. The net count rate was calculated by subtracting the background count rate estimated by the 0 ppm phantom measurements from the gross count rate estimated by the 100 ppm phantom measurements.

Lα,100ppm=A2×c2+B2×c+C2

Where Lα,100ppm is the net count rate of the lead Lα peak, c is the count rate of the Compton peak. A2, B2, and C2 are coefficients determined by fitting the data to a second order polynomial function.

The function obtained from our experiments is listed below with an R2 of 0.984:

Lα,100ppm=(6e−7±1e−7)×c2−(3.6e−3±0.5e−3)×c+(5.4±0.5)

The net count rate per unit concentration will be Lα,100ppm divided by 100 ppm.

For an in vivo measurement, the net count rate of lead L α peak can be calculated by subtracting the estimated background count rate determined from the previous procedure a).

Lα,net=Lα,total−(2e−4×c+0.35)

Where L α,net and L α,total are the net and total count rates of the lead L α peak for the in vivo measurement.

The lead concentration and uncertainty in bone for the in vivo measurement can then be calculated by converting the net counts to concentration with the ratio determined from procedure b).

Concentration=Lα,net×100ppm∕Lα,100ppmσ=2×concentration×Lα,total+Lα,bkgtliveLα,net

Where tlive is the detector live time for the in vivo measurement. The final concentration is a weighted mean of the values calculated from both Lα and Lβ x-ray signals where the inverse of the variance is used for the weighting.

We note that it is different from standard peak fitting algorithm that has been employed previously (Bevington and Robinson, 2003). We were not able to apply the standard method here because the lead Lα and Lβ x-ray peaks for 2 minute measurements are very small and it is difficult to fit them into arbitrary functions. This new method is advantageous in that it does not rely on the counts of the peaks. In addition, this method can only be used for a rigid geometry, i.e. the source to skin surface distance, as well as the detector to skin surface distance have to be fixed, which is the case in our portable XRF measurement because the window of the device is always in touch with the skin.

2.8 Radiation dose assessed with Monte Carlo simulations and TLDs

Monte Carlo simulations were performed to calculate the skin dose and the total body effective dose delivered to a subject during an in vivo measurement. Monte Carlo N-Particle (MCNP4C2) transport code distributed by Radiation Safety Information Computational Center (RSICC) was used to simulate the energy delivered to the irradiated spot and the dose was calculated by assuming a 5mm skin thickness and flat skin and bone surface.

Thermoluminescent dosimeters (TLDs) from Global Dosimetry Solutions (GDS) were used to measure the dose at the skin surface and bone surface. For the dose measurement at skin surface, seven TLD chips (dimension 3.2 mm*3.2 mm*0.9 mm) were placed at the window surface of the portable XRF device, with a 2 mm Lucite plate placed on top of the window to represent the soft tissue, and a blank plaster of Paris phantom placed on top of the Lucite plate to represent the bone. For the dose measurement at bone surface, another seven TLD chips were placed on the surface between Lucite plate and the bone phantom, with the chips again cover the window area. Two sets of measurements were made at each setting for 10 minutes. The 28 chips were then mailed back to GDS, together with 28 background TLD chips, for dose reading.

2.9 Data analysis

Intraclass correlation coefficients (ICC) were calculated to determine correlations between multiple readings or between readings by different devices (Shrout and Fleiss, 1979). ICC is preferred over Pearson correlation when the sample size is relatively small and the ICC can accommodate more than two measurements. The calculations were done using mixed models with random intercepts with SAS version 9.2.

3. RESULTS

3.1 Spectrum (or Compton peak count rates) to determine soft tissue thickness

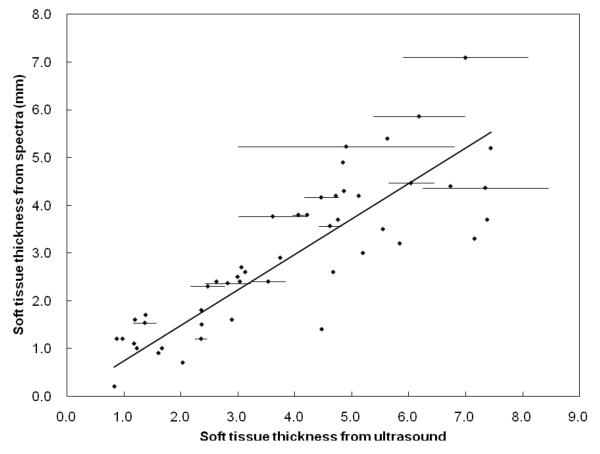
We obtained portable XRF measurements for different Lucite thicknesses over real bone and plotted the Lucite thicknesses vs. Compton count rates (Figure 2). Six cadavers were measured with portable XRF and with ultrasound at 49 different sites—up to two times per site by portable XRF and up to three times per site by ultrasound. The soft tissue thicknesses were calculated from the XRF spectra using the equation derived from Fig. 2, and from the ultrasound images by using the caliper function in the ultrasound software. We did not consider sites with skin thickness of 8 mm or more because the Compton peak becomes saturated at these thicknesses. The minimum thicknesses measured by ultrasound for the six cadavers were between 0.2 and 4.1 mm while for the portable XRF they were between 0.8 and 4.9 mm. Figure 3 plots the soft tissue thickness obtained from the spectra versus the soft tissue thicknesses obtained from ultrasound measurements. Average values were used for sites with multiple measurements and error bars for these sites were plotted; the error bars for the thicknesses obtained from the spectrum of repeat portable XRF measurements were too small to see. The ICC calculated from the 14 sites with multiple measurements was 0.83 for the ultrasound and >0.99 for the portable XRF. The mean difference between repeat measures with the portable XRF was 0.06 mm (sd=0.09 mm). There was very good agreement between the ultrasound and portable XRF measurements at the 49 different sites, with an ICC of 0.82.

Figure 3.

Figure 3

Open in a new tab

Soft tissue thicknesses calculated from the spectra vs. those measured by ultrasound (error bars were plotted for the sites with multiple ultrasound measurements; error bars for the soft tissue thicknesses from the spectra are too small to see)

3.2 Detection limit of the portable XRF device for bone lead quantification

The measurements with Lucite covered lead doped plaster of Paris phantoms were used for the calculation of the detection limit. The detection limit was calculated as:

DL=2×σ0ppm=2∗11σα,0ppm2+1σβ,0ppm2

Where

σ(α,β)0ppm=2×100ppm×BKG0∕120secGROSS100ppm−BKG0

Where BKG0 is the background count rate under Lα or Lβ peak for the 0 ppm phantom, and GROSS100ppm is the total count rate under Lα or Lβ region for the 100 ppm phantom. Table 1 lists the detection limit of portable XRF to quantify lead in bone with different tissue thicknesses.

Table 1.

Detection limit for bone lead measurement by portable XRF at different soft tissue thicknesses

Soft tissue
thickness		 Detection
limit (ppm)
0 mm 3.3
1 mm 5.4
2 mm 8.4
3 mm 10.8
4 mm 20.1
5 mm 28.9
Open in a new tab

3.3 Correlation of bone lead concentration between KXRF and portable XRF

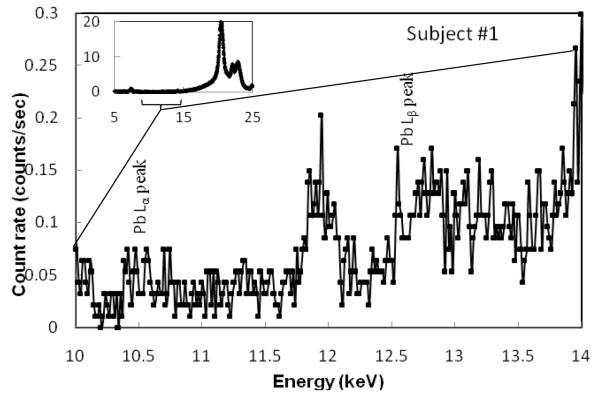
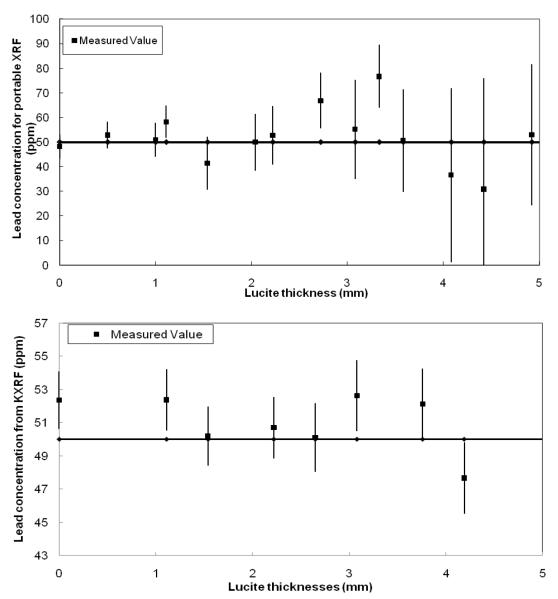
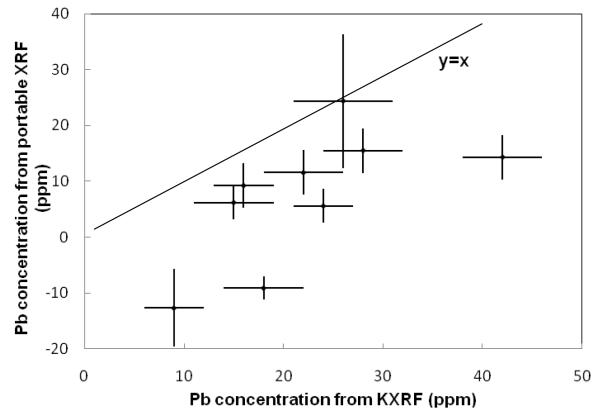
Bone lead was measured in 9 subjects. First, ultrasound was used to determine a location with the least overlying soft tissue, then a portable XRF measurement was made (2 minutes), followed by a KXRF measurement (30 minutes) and finally a second portable XRF measurement (2 minutes) in order to assess the reproducibility of these measurements. The minimum overlying skin thicknesses found for these 9 participants ranged from 1.3 to 2.6 mm (two were over 2 mm). Figure 4 shows the portable XRF spectra for bone lead measurement for one of the subjects, including the spectrum with the Compton region and an expanded spectrum for lead L-x ray region. Lead Lα and Lβ were clearly visible. The sensitivity of the portable XRF system is strongly dependent on the thickness of the soft tissue over the bone, while this dependence is much less significant for KXRF system (Figure 5). Figure 6 plots the correlation of the lead concentrations between portable XRF and KXRF. Although the results from the portable XRF were lower than those from the KXRF, the ICC between the two measurements was high (ICC=0.65). Moreover, the lead concentration results from the two in vivo portable XRF measurements (one was performed before the KXRF measurement, and one was performed after) indicate a significant correlation between these two measurements with a correlation coefficient of 0.42 (the coefficient increases to 0.80 when one set of data with the highest uncertainty is removed). The strong and significant correlation between two measurements demonstrates good reproducibility of the portable XRF even for the in vivo situation.

Figure 4.

Figure 4

Open in a new tab

Portable XRF spectrum for the bone lead measurement of one of the subjects

Figure 5.

Figure 5

Open in a new tab

Measured lead concentration of 50 ppm phantom against Lucite thickness for portable XRF and KXRF systems

Figure 6.

Figure 6

Open in a new tab

Lead concentration obtained from portable XRF system vs. lead concentrations obtained from KXRF system (ICC=0.65)

4. DISCUSSION

This study investigated three critical issues regarding the methodology and feasibility of developing a portable XRF technology for in vivo quantification of lead in bone: soft tissue thickness determination, the detection limit of the system, and the correlation of the bone lead concentrations obtained from KXRF and portable XRF.

Soft tissue thickness is usually determined by ultrasound. The accuracy of the result obtained by this method with respect to the actual tissue thickness overlying the bone at the position that the portable XRF measurement is made, however, can be hindered by two issues: a) the difficulty of locating with the ultrasound the exact position of the site that was measured with the portable XRF (in our experience, tissue thickness overlying tibia is very sensitive to site, especially along the mediolateral axis); and b) differences in thickness related to differences in pressure applied to the tissue when measuring with the ultrasound vs. portable XRF. Despite these differences, we observed excellent agreement between the soft tissue thicknesses obtained by the ultrasound and those calculated from the XRF spectra (ICC=0.82). The portable XRF did appear to give slightly thicker measurements than the ultrasound, which may be related to greater pressure applied to the tissue when measuring with the ultrasound or it could suggest that Lucite is not exactly equivalent to skin and soft tissue, and hence there is a discrepancy for the Compton cross-sections. Overall, given a) the close correlation between measurements with the two devices, b) the greater variation in measurements with the ultrasound than the portable XRF, and c) the fact that the portable XRF is by definition measuring thickness at exactly the same position—indeed from the same spectrum—from which the bone lead measurement is being made, the portable XRF may provide a better tissue thickness measurement for use in the bone lead measurement algorithm.

The detection limit for the portable XRF at 2 mm soft tissue thickness was 8.4 ppm, which is comparable to the detection limit of around 10 ppm for the KXRF bone lead measurement systems installed in most of the KXRF labs, and much better than the detection limit obtained from previous LXRF bone lead measurement systems with a detection limit of 57 ppm for 2 mm soft tissue thickness (Todd et al., 2002). One significant disadvantage for LXRF bone lead measurement is that the low energy x-rays are easily attenuated by soft tissue, so the detection limit increases significantly with the increase of the soft tissue thickness and it is difficult to obtain a reasonable value at soft tissue thickness greater than 5 mm. However, in every case tested—cadavers and human subjects—we were able to find a tibia site with less than 5 mm of overlying tissue. For 7 of the 9 participants measured in in vivo test we could find a tibia measurement site with 2 mm or less of tissue overlying the bone, and the thickest overlying tissue was only 2.6 mm. Another study reported an average soft tissue thickness over tibia of 4.8 mm for 10 subjects (Pejovic-Milic et al., 2002), which may indicate a reduced soft tissue thickness due to less fat tissue in older adults.

We observed excellent correlation between the lead concentrations obtained from KXRF and portable XRF (ICC=0.65). The bone lead concentrations obtained from portable XRF were lower than those obtained from KXRF, which could reflect a suboptimal analysis algorithm. One concern with the algorithm is that the derived functions used for calculation are based on the same set of bone-equivalent phantoms. Since the Compton scatter peak originates both from bone and soft tissue, the Compton scatter peak counts will depend on bone density as well as soft tissue thickness. However, this is not likely to make a substantial difference to the in vivo measurements for people with healthy bones. Moreover, such variability would reduce the correlation with the KXRF, which we empirically still found to be quite good. Another issue that could lead to the difference in bone measurements is that the portable XRF and KXRF do not assess exactly the same parts of the bone. Because the x-rays used by the portable XRF are low energy they will sample only the surface of the bone with a mean free path of 0.2 mm and 0.3 mm for Lα and Lβ x-rays respectively. In comparison, higher energy K-shell x-rays will sample about 20 mm into the bone. Differences in lead concentrations at the tibia surface compared to concentrations deeper in the bone may contribute to the different readings from the portable XRF and KXRF. Indeed, Parsons et al. observed an inhomogeneous distribution of lead over the cross-sectional surface of the tibia (Bellis, 2009). Nonetheless, it is important to note that for the purposes of studies relating bone lead to health outcomes, the correlation between the portable XRF and KXRF is the more critical comparison, and the high correlation suggests that the portable XRF would be very useful in such studies.

The entrance skin dose for one measurement with the portable XRF device used for the in vivo measurements reported here was calculated to be 13 mSv to 1 cm2 skin area; the total body effective dose is estimated to be about 1.5 μSv. The doses measured with the TLDs were 26.5 mSv 1 cm2 skin area and 26.0 mSv to 1 cm2 bone surface area. The difference between the simulated and the measured dose could be due to the difficulty of simulating the x-ray output from the x-ray tube with MC simulations. Compared with the annual dose limit set by National Council on Radiation Protection and Measurements (NCRP) to extremities for radiation workers (no official dose limit set to extremities for general public) of 500 mSv per year (which means 500 mSv to the whole hands and feet, as opposed to the 26 mSv to the 1 cm2 skin surface in our application), the risk of radiation exposure to the 1 cm2 skin surface induced by the portable XRF to the subject is minimal. Compared with the annual background radiation dose of 3.6 mSv to the U.S. general population, a total body effective dose of 1.5 μSv is negligible. As a comparison, the total body effective dose for the KXRF system used for this study is about 40 nSv (Todd et al., 1992).

The main advantages of the portable XRF system are that it is portable, fast, and user-friendly. In addition, the variation in the x-ray source of the portable XRF is negligible and the source does not decay as the 109Cd source used in the KXRF system. Thus, the device could be particularly valuable for epidemiologic studies with large populations, for pediatric populations (because of the shorter measurement time), and for lead surveys in the field, e.g. occupational settings and other high risk populations. One caveat for the pediatric population, is that the lead concentration and its distribution in bone may change over a short period of time due to the quick growing bones of this population. This will affect both KXRF and portable XRF methods. However, the portable XRF may be more severely affected because it samples a smaller amount of the bone (near the surface of the bone) compared to KXRF. On the other hand, this may be a benefit to understanding the more rapid dynamics of lead in bone with serial measures on children.

Future work on technique improvement includes: redesigning the instrument to include a clover-leaf geometry with four detector, with the x-ray tube mounted at the center (Nie et al., 2006), and improving the spectrum and data analysis algorithms. The clover-leaf system has already been shown to decrease the minimum detection limit of a conventional KXRF device by a factor of 3-4, and the same technological advancements could be used to improve the portable XRF device. The ‘cloverleaf’ four detector design may not be as conveniently portable as the existing commercial unit, but the increase in sensitivity should outweigh the disadvantages. Another very important research direction is to apply this technique to detect other metals in human organs in vivo. Future work on application of the technology includes introducing the technique to the metal epidemiology and toxicology society and establishing collaborations between the technique developers and metal epidemiologists and toxicologists.

5. CONCLUSION

We have shown that it is feasible to employ a portable XRF device to measure lead in bone in vivo in two minutes, and that the measurements of lead concentration show excellent correlation with the standard KXRF technique. The calculated detection limit for bone lead measurement by a portable XRF device is about 10 ppm with 2 mm soft tissue thickness, which is essentially the same as the detection limit for KXRF systems. Future improvements in detector technology could reduce the detection limit for the portable XRF even further. This device could vastly facilitate the use of bone lead exposure assessment in clinical and research settings.

ACKOWLEDGEMENT

The research described in this paper was supported primarily by NIEHS P20-MD000501. ROC acknowledges financial support of the Bernard M. Gordon Center for Subsurface Sensing and Imaging Systems under the Engineering Research Centers Program of the National Science Foundation (Award number EEC-9986821). The authors would like to acknowledge ThermoFisher Scientific for the loan of the portable XRF device (XL3). The authors would like to thank James Brute at Thermo Fisher Scientific for his help on calculating and confirming the radiation dose delivered to the subjects. The contents of this manuscript are solely the responsibility of the authors and do not necessarily represent the official views of the NIEHS and NSF.

Footnotes

The authors declare they have no competing financial interests.

References

  1. Aro AC, Todd AC. Amarasiriwardena C and Hu H 1994 Improvements in the calibration of 109Cd K x-ray fluorescence systems for measuring bone lead in vivo. Phys Med Biol. 39:2263–71. doi: 10.1088/0031-9155/39/12/009. [DOI] [PubMed] [Google Scholar]
  2. Bandeen-Roche K, Glass TA, Bolla KI, Todd AC, Schwartz BS. Cumulative lead dose and cognitive function in older adults. Epidemiology. 2009;20:831–9. doi: 10.1097/EDE.0b013e3181b5f100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Bellis D, Li D, Chen Z, Gibson WM, Parsons PJ. Measurement of the microdistribution of strontium and lead in bone via benchtop monochromatic microbeam X-ray fluorescence with a low power source. Journal of Analytical Atomic Spectrometry. 2009;24:622–6. doi: 10.1039/B820067J. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Bevington PR, Robinson DK. Data reduction and error analysis for the physical sciences. McGraw-Hill; Boston: 2003. [Google Scholar]
  5. Canfield RL, Henderson CR, Jr., Cory-Slechta DA, Cox C, Jusko TA, Lanphear BP. Intellectual impairment in children with blood lead concentrations below 10 microg per deciliter. N Engl J Med. 2003;348:1517–26. doi: 10.1056/NEJMoa022848. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Chettle DR, Scott MC, Somervaille LJ. Improvements in the precision of in vivo bone lead measurements. Phys Med Biol. 1989;34:1295–300. doi: 10.1088/0031-9155/34/9/014. [DOI] [PubMed] [Google Scholar]
  7. Chettle DR, Scott MC, Somervaille LJ. Lead in bone: sampling and quantitation using K X-rays excited by 109Cd. Environ Health Perspect. 1991;91:49–55. doi: 10.1289/ehp.919149. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Gonzalez-Cossio T, Peterson KE, Sanin LH, Fishbein E, Palazuelos E, Aro A, Hernandez-Avila M, Hu H. Decrease in birth weight in relation to maternal bone-lead burden. Pediatrics. 1997;100:856–62. doi: 10.1542/peds.100.5.856. [DOI] [PubMed] [Google Scholar]
  9. Gordon CL, Chettle DR, Webber CE. An improved instrument for the in vivo detection of lead in bone. Br J Ind Med. 1993;50:637–41. doi: 10.1136/oem.50.7.637. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Hu H, Aro A, Payton M, Korrick S, Sparrow D, Weiss ST, Rotnitzky A. The relationship of bone and blood lead to hypertension. The Normative Aging Study. JAMA. 1996;275:1171–6. [PubMed] [Google Scholar]
  11. Leggett RW. An age-specific kinetic model of lead metabolism in humans. Environ Health Perspect. 1993;101:598–616. doi: 10.1289/ehp.93101598. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Navas-Acien A, Guallar E, Silbergeld EK, Rothenberg SJ. Lead exposure and cardiovascular disease--a systematic review. Environ Health Perspect. 2007;115:472–82. doi: 10.1289/ehp.9785. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Navas-Acien A, Schwartz BS, Rothenberg SJ, Hu H, Silbergeld EK, Guallar E. Bone lead levels and blood pressure endpoints: a meta-analysis. Epidemiology. 2008;19:496–504. doi: 10.1097/EDE.0b013e31816a2400. [DOI] [PubMed] [Google Scholar]
  14. Needleman HL, Riess JA, Tobin MJ, Biesecker GE, Greenhouse JB. Bone lead levels and delinquent behavior. JAMA. 1996;275:363–9. [PubMed] [Google Scholar]
  15. Nie H, Chettle D, Luo L, O’Meara J. In vivo investigation of a new 109Cd gamma-ray induced K-XRF bone lead measurement system. Phys Med Biol. 2006;51:351–60. doi: 10.1088/0031-9155/51/2/011. [DOI] [PubMed] [Google Scholar]
  16. Nie H, Chettle DR, McNeill FE, O’Meara JM. An investigation of the 109Cd gamma-ray induced K-x-ray fluorescence (XRF) bone-lead measurement calibration procedure. Phys Med Biol. 2004;49:N325–34. doi: 10.1088/0031-9155/49/19/n02. [DOI] [PubMed] [Google Scholar]
  17. Pejovic-Milic A, Brito JA, Gyorffy J, Chettle DR. Ultrasound measurements of overlying soft tissue thickness at four skeletal sites suitable for in vivo x-ray fluorescence. Med Phys. 2002;29:2687–91. doi: 10.1118/1.1513569. [DOI] [PubMed] [Google Scholar]
  18. Rabinowitz MB. Toxicokinetics of bone lead. Environ Health Perspect. 1991;91:33–7. doi: 10.1289/ehp.919133. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Schaumberg DA, Mendes F, Balaram M, Dana MR, Sparrow D, Hu H. Accumulated lead exposure and risk of age-related cataract in men. JAMA. 2004;292:2750–4. doi: 10.1001/jama.292.22.2750. [DOI] [PubMed] [Google Scholar]
  20. Shih RA, Hu H, Weisskopf MG, Schwartz BS. Cumulative lead dose and cognitive function in adults: a review of studies that measured both blood lead and bone lead. Environ Health Perspect. 2007;115:483–92. doi: 10.1289/ehp.9786. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Shrout PE, Fleiss JL. Intraclass correlations: uses in assessing rater reliability. Psychol Bull. 1979;86:420–8. doi: 10.1037//0033-2909.86.2.420. [DOI] [PubMed] [Google Scholar]
  22. Todd AC, Carroll S, Geraghty C, Khan FA, Moshier EL, Tang S, Parsons PJ. L-shell x-ray fluorescence measurements of lead in bone: accuracy and precision. Phys Med Biol. 2002;47:1399–419. doi: 10.1088/0031-9155/47/8/312. [DOI] [PubMed] [Google Scholar]
  23. Todd AC, McNeill FE, Palethorpe JE, Peach DE, Chettle DR, Tobin MJ, Strosko SJ, Rosen JC. In vivo X-ray fluorescence of lead in bone using K X-ray excitation with 109Cd sources: radiation dosimetry studies. Environ Res. 1992;57:117–32. doi: 10.1016/s0013-9351(05)80073-8. [DOI] [PubMed] [Google Scholar]
  24. Weaver VM, Lee BK, Todd AC, Jaar BG, Ahn KD, Wen J, Shi W, Parsons PJ, Schwartz BS. Associations of patella lead and other lead biomarkers with renal function in lead workers. J Occup Environ Med. 2005;47:235–43. doi: 10.1097/01.jom.0000155971.10111.6d. [DOI] [PubMed] [Google Scholar]
  25. Weisskopf MG, Jain N, Nie H, Sparrow D, Vokonas P, Schwartz J, Hu H. A prospective study of bone lead concentration and death from all causes, cardiovascular diseases, and cancer in the Department of Veterans Affairs Normative Aging Study. Circulation. 2009;120:1056–64. doi: 10.1161/CIRCULATIONAHA.108.827121. [DOI] [PMC free article] [PubMed] [Google Scholar]

RESOURCES