A Mechanism for Frequency Modulation in Songbirds Shared with Humans

Abstract

In most animals that vocalize, control of fundamental frequency is a key element for effective communication. In humans, subglottal pressure controls vocal intensity but also influences fundamental frequency during phonation. Given the underlying similarities in the biomechanical mechanisms of vocalization in humans and songbirds, songbirds offer an attractive opportunity to study frequency modulation by pressure. Here, we present a novel technique for dynamic control of subsyringeal pressure in zebra finches. By regulating the opening of a custom-built fast valve connected to the air sac system, we achieved partial or total silencing of specific syllables, and could modify syllabic acoustics through more complex manipulations of air sac pressure. We also observed that more nuanced pressure variations over a limited interval during production of a syllable concomitantly affected the frequency of that syllable segment. These results can be explained in terms of a mathematical model for phonation that incorporates a nonlinear description for the vocal source capable of generating the observed frequency modulations induced by pressure variations. We conclude that the observed interaction between pressure and frequency was a feature of the source, not a result of feedback control. Our results indicate that, beyond regulating phonation or its absence, regulation of pressure is important for control of fundamental frequencies of vocalizations. Thus, although there are separate brainstem pathways for syringeal and respiratory control of song production, both can affect airflow and frequency. We hypothesize that the control of pressure and frequency is combined holistically at higher levels of the vocalization pathways.

Introduction

The fundamental frequency of human vocalizations depends on subglottal pressure (Titze, 1989). The variation of fundamental frequency with pressure differs depending on the regimen of phonation (e.g., see van den Berg, 1957; Lieberman et al., 1969; Rothenberg and Mahshie, 1986). Given that pressure is the primary variable for control of vocal intensity, it is evident that amplitude and frequency are not independently controlled in the human vocal system. As the tension in the vocal folds can also modify the fundamental frequency of vocalizations, it has been difficult to directly quantify the synergistic interaction between vocal fold tension and subglottal pressure in humans.

The physical mechanism for sound production in the songbird syrinx shows analogies to that in the human larynx (Mindlin and Laje, 2005; Riede and Goller, 2010), such that both can be characterized as myoelastic-aerodynamic sound sources. This encourages the exploration of a mechanism for pressure/frequency interactions in songbirds. Song production involves precise motor control of the vocal organ, the syrinx (Suthers et al., 1999; Suthers and Zollinger, 2004). Critical features of motor control are related to the tension of the syringeal membrane and the subsyringeal air sac pressure that acts to force air through the syrinx and drives membrane oscillations (Amador et al., 2013). The activity of the syringeal muscles is thought to regulate both membrane tension and to provide fine control of airflow, affecting acoustic structure and temporal features of vocalizations, respectively (Goller and Suthers, 1996a, b). For example, in brown thrashers (Toxostoma rufum), the activity of the ventral syringeal muscle is correlated with the fundamental frequency of the vocalization. In this way, a possible mechanism for controlling fundamental frequency would be controlling the labial tension via syringeal muscles. Recent results, however, raise the possibility that air sac pressure could also regulate fundamental frequency in birds. In great kiskadees (Pitangus sulfuratus), fundamental frequency was modulated through subsyringeal pressure alone, as the same modulation was obtained after removing all active muscle control (Amador et al., 2008). Whether this mechanism, observed in a suboscine species, exists in oscine birds remains unresolved. In zebra finches (Taeniopygia guttata), there has been some evidence of correlation between air sac pressure (or vocal amplitude) and fundamental frequency (Riede et al., 2010; Ritschard and Brumm, 2011), but as the resection of the tracheo-syringeal nerve resulted in large-scale disruption of acoustic features of song (e.g., see Vicario, 1991; Williams and McKibben, 1992), it has been difficult to elucidate any interplay between air sac pressure and fundamental frequency during singing.

Here, we test the hypothesis that air sac pressure helps to regulate fundamental frequency during song production by developing a technique that allows for fine manipulation of air sac pressure during otherwise normal vocal gestures. We evaluate a possible biological mechanism for this effect using a mathematical model for vocal production (Amador and Mindlin, 2008; Perl et al., 2011). The general framework of the model is applicable to human vocal production, as well as for songbirds.

Materials and Methods

All procedures were in accordance with a protocol approved by the University of Chicago Institutional Animal Care and Use Committee.

Animals and surgery.

Experiments were performed in adult male zebra finches (N = 11), bred and reared in our colony. A few days before the experiment, a bird was transferred from a general flight aviary to an individual sound isolation box. The bird was maintained on a 14/10 light cycle until sufficient numbers of baseline songs were recorded using in-house software. The bird was anesthetized for surgery by inhalation of isoflurane with lidocaine used as a local anesthetic in the incision region. A cut was performed through the skin on the ventral midline of the neck just rostral and ventral to where the trachea enters the chest cavity. Connective tissue was moved aside by blunt dissection until the air sac membrane was located. The membrane was then picked up with fine forceps and cut to reach the diameter needed to insert a chronic catheter tube designed to minimize clogging (MicroRenathane Implantation Tubing, MRE-050 OD = 0.050 in., ID = 0.040 in.; Braintree Scientific). For tubing sterilization, the tubing was soaked in benzalkonium chloride (0.01%) aqueous solution for 15 min before the surgery. Once the tubing was inserted, the air sac was sealed using veterinary tissue adhesive (3M Vetbond Tissue Adhesive, n-butyl cyanoacrylate, 3M), and the tubing was fixed to the clavicle with suture and tissue adhesive to provide an anchorage. (It was important to achieve a good seal between the air sac and the tubing.) The skin was closed with interrupted sutures and tissue adhesive. After implantation, a miniature valve (see below) was attached at the free end of the tubing to control its opening and closing. The valve was positioned on the back of the animal attached to a Velcro backpack slipped over the wings.

We achieved a surgery success rate of ∼50%. Several aspects of the procedures were challenging. Proper positioning of the tubing in the interclavicular air sac requires some dexterity as the tubing is very close to the syrinx. We think that, in less favorable cases, the tubing physically impeded the normal functioning of the syrinx, resulting in the disrupted song we sometimes observed. In addition, in some cases, there was rapid clogging of the tube, perhaps also related to its placement. The limiting factor for the duration of recordings from a given bird was tubing clogging, which occurred between 4 and 10 d. We developed an approach to unclog the tubing, but this was of only minor help in extending the viability of an implant.

In two birds, a second cannula was used to monitor air sac pressure. Measuring air sac pressure provided an independent measure as to the action of the valve, which was useful for detailed manipulation of the song, but the procedure further complicated the already challenging surgery and added weight to the backpack. In this procedure, a Silastic cannula (ID = 0.03 in., OD = 0.065 in., length 6 cm) was inserted through the abdominal wall just posterior to the last rib so that it extended a few millimeters into the cranial thoracic air sac. The cannula was fixed to the rib with suture and tissue adhesive, and the free end was connected to a miniature piezo-resistive pressure transducer (Fujikura model FPM-02PG) on the bird's backpack. After surgery, the bird was returned to its cage where it was free to move about on the end of a tether composed of fine wires for operating the valve and measuring pressure.

Miniature valve and operating system.

To open and close the end of the tube inserted in the air sac system, we developed a miniature valve. The valve has two ports: the input port where the tubing is connected and the output port to vent the air sac system to the atmosphere. The opening or closing of the output port was performed by passing current through a manually wound solenoid (40AWG copper wire, 600 turns, total resistance = 40 Ω) that moved a rare earth magnet (Machinable Neodymium-Iron-Boron Disc Magnet, diameter = 0.078 in., pull = 0.3 lb, part 5902K41; McMaster-Carr). The direction of movement depended on the direction of the current flow (Fig. 1A). A positive current moved the magnet to the center of the solenoid opening the output port, and negative current moved the magnet toward the output port blocking the hole. A small piece of silicone rubber was glued to the end of the magnet to achieve a good seal in the closed position. The output hole was formed in a metallic disc so that valve closing was maintained by magnetic forces between the metallic disc and the magnet. In this way, no holding current was needed to keep the valve closed. The body of the valve was a natural polypropylene T-connector (ID = 0.125 in.; Cole Parmer) shaped to fit the solenoid, the metallic disc, and cut to the desired length of the input port. The valve weight was 0.9 g, which could be readily carried by zebra finches.

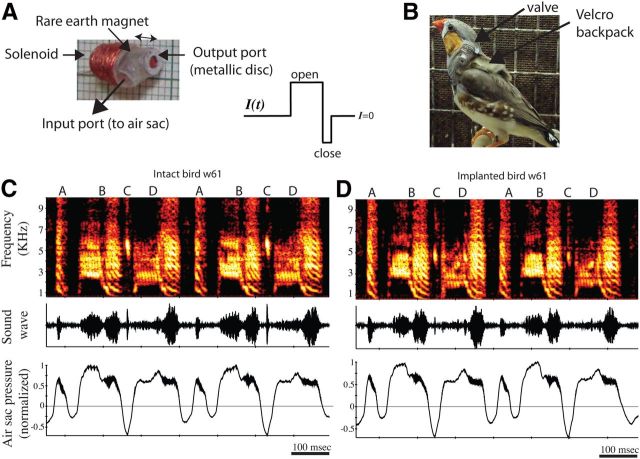
Figure 1.

Novel method for manipulation of vocal output. A, The miniature valve. Current through a solenoid rapidly moves a magnet to open or close a hole that connects the air sac system with the atmosphere. The direction of the current flow sets the direction of movement of the magnet. Absent any current, the valve is closed (i.e., the air sac system is sealed). B, Implanted bird carrying a backpack with the valve attached. C, D, Spectrograph, sonograph, and air sac pressure of a bird before (C) and after (D), valve implantation. Zero pressure represents atmospheric pressure, and the pressure values were normalized to the maximum value. The pressure patterns and song acoustics, including harmonic stacks, rapid trills, and inspiratory syllables, remain unchanged after device implantation.

We used a current source connected to a frequency to voltage converter to convert the frequency signal delivered by a computer DAC into a current signal used to control the valve (Electronics Laboratory, James Frank Institute, University of Chicago). The valve could be manually activated or using a syllable detection program (developed by E.-G. Manderscheid and C.D. Meliza). We used the latter for systematic alteration of the vocal production targeting a specific syllable. The accuracy of the syllable detection was between 90 and 98%.

We defined two types of syllables. An expiratory syllable was defined as the sound from an expiratory pressure pulse between two inspirations. An inspiratory syllable occurred during an inspiration between two expiratory pulses during. For inspiratory syllables, the absolute value of the inspiration was much larger than during silent inspirations (including breathing and mini-breaths during singing) (Goller and Daley, 2001).

Mathematical model for song production.

Many descriptions of voiced sound production are based on the seminal work by Titze (1988, 1994), who described a model to account for the vocal folds motion in humans. Given the anatomical and functional similarities between the vocal apparatus of humans and birds (Riede and Goller, 2010), this description helps to capture essential features of birdsong production. Direct endoscopic observation showed that phonation was initiated in the songbird syrinx when two soft tissue masses, the medial and lateral labia, were pushed into the bronchial lumen (Goller and Larsen, 1997). Also, vibrations of the labia were identified as the principal sound source. Therefore, a description of flow-induced oscillations in opposite labia is adequate for describing the mechanisms involved in birdsong production (Mindlin and Laje, 2005).

The mathematical model used for this study assumes that, for high enough airflow values, the labia enter a dynamic regimen of self-sustained oscillations. The labial wave motion is modeled in terms of two basic modes: a lateral displacement of the tissues and a flapping-like oscillation responsible for an out-of-phase oscillation of the top and bottom parts of the membranes. If an appropriate phase difference between these modes exists, there will be an energy gain that will allow the existence of self-sustained oscillations (Amador and Mindlin, 2008; Perl et al., 2011). The equations that describe the dynamics of the medial position x(t) of one of the opposing labia are as follows, with x(t) = 0 representing the resting position as follows:

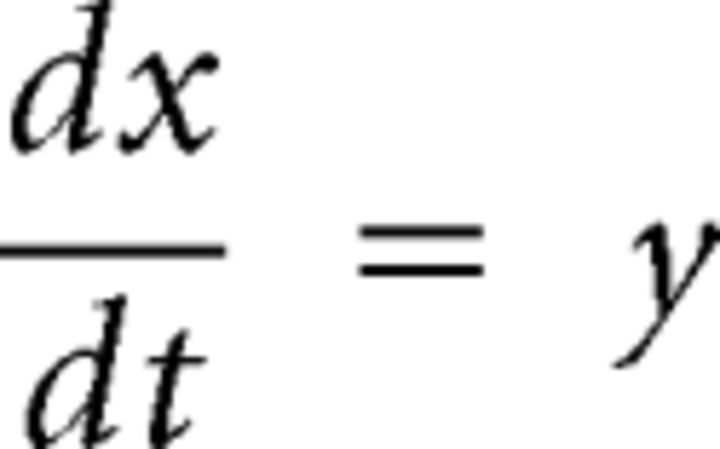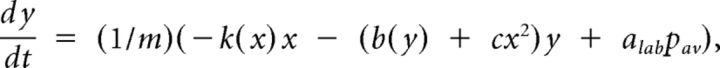where k(x) = k₁ + k₃*x² is a nonlinear restitution term (appropriately, the restitution force k(x)x only contains odd exponents of the displacement); b(y) = b₁ + b₃*y² accounts for a nonlinear dissipation; cx²y is a position-dependent nonlinear dissipation term that serves to model collisions between labia or with containing walls as this term becomes relevant as x takes large values, corresponding to large departures from the rest position. The parameters k₁, k₃, b₁, b₃, and c are all free parameters of the model. The last term describes the force resulting from the interlabial pressure. This set of equations are a form of the usual equations to describe a forced oscillator: mẍ + b(x,ẋ)ẋ + κ(x)x = F(x,ẋ). The average pressure p_av can be written in terms of the displacement of the upper and lower edges of the labia and its velocity (Amador and Mindlin, 2008; Perl et al., 2011). A detailed dynamic analysis can be found elsewhere (Amador and Mindlin, 2008). We have observed that this system is characterized by bifurcation lines that separate qualitatively different dynamic regimens. The dynamic analysis of the original set of equations leads to a minimal mathematical description with the same bifurcation diagram as the original model. This is known as a normal form (Guckenheimer and Holmes, 1997) and for the syringeal model is described by the following equations (Sitt et al., 2008; Perl et al., 2011):

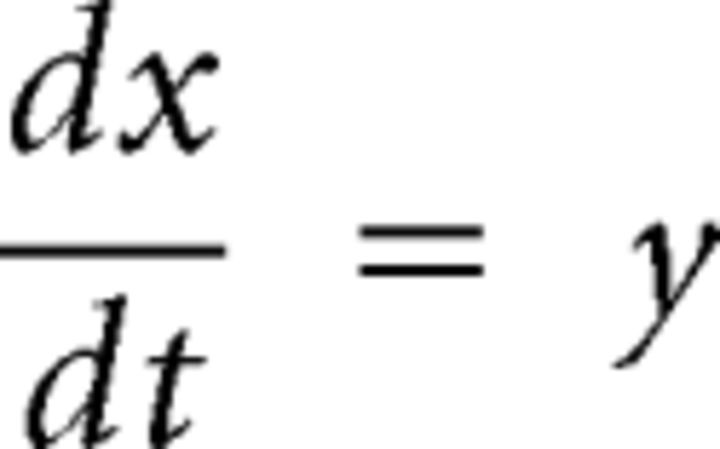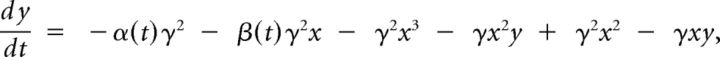where α(t) is proportional to the air sac pressure, β(t) is proportional to the labial tension, and γ is a scaling factor. The time scale parameter γ is a fixed value. In this way, once γ is fitted, there are just two variables that define the sound source output. This represents significant dimensionality reduction that has proven valuable in relating syringeal mechanics to neuronal activity (Amador et al., 2013).

Assuming the sound source and the vocal tract are dynamically uncoupled, the fundamental frequency does not depend on the filter details. Nevertheless, to produce syllables with realistic timber (e.g., Fig. 6), a vocal tract model is required. In our biomechanical model, the trachea is modeled as a tube and the oroesophageal cavity is modeled as a Helmholtz resonator (Riede et al., 2006; Perl et al., 2011). Two equations for the tube and glottis and three linear ordinary differential equations account for the dynamics of the airflow and pressure of the vocal tract (Perl et al., 2011), resulting in the final output pressure. The vocal tract acts to emphasize those frequencies that match the resonant frequencies of each device (tube or Helmholtz resonator). In this way, the fundamental frequency is generated in the sound source (the syrinx) and filtered afterward by the vocal tract. In this work, the parameters for the vocal tract were maintained as constant values, assuming that there was no dramatic changes in the filtering conditions during the time course of each syllable.

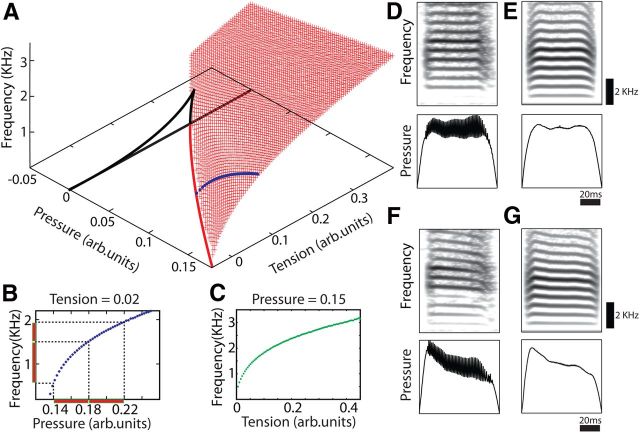
Figure 6.

Mathematical model for song production. A, The region of the parameter space where oscillations occur is shown with its corresponding value of fundamental frequency displayed with red dots. The black and red lines indicate bifurcations in the parameter space (Hopf and SNILC bifurcations, respectively). The blue line in the red surface indicates a possible path where tension is maintained constant while the pressure is changing, resulting in a frequency modulation. B, A path in parameter space where tension is constant and frequency of the oscillations is set through pressure. Red bars highlight that frequency modulation through pressure is more important for low-frequency sounds. C, This model also allows a change in frequency through changes in tension. D, F, The measured air sac pressure during singing was smoothed and fed as a parameter of the mathematical model (see Materials and Methods). E, G, The synthetic syllables generated with the mathematical model are very similar to the recorded ones. An intact singing bird is shown in D and E, and the same type of syllable with a depressurization of air sac system is shown in F and G. The pressure drop generates a frequency drop, more clearly observed in the upper harmonics of the sonogram.

Analysis of experimental data.

In the mathematical modeling of our experimental results, we focused on harmonic stacks (e.g., syllable C, Fig. 3), where the fundamental frequency remains relatively constant throughout the syllable and there is considerable power in the harmonics. To generate synthetic syllables, we used as input to the model the recorded air sac pressure. The recorded signal was smoothed using a fourth degree Savitzky-Golay algorithm (Press et al., 2007). This filter performs a local polynomial regression to determine the smoothed value for each point while preserving the relative maxima, minima, and widths. The smoothed pressure signal was scaled to get α(t). The same scale factor was used for all the syllables synthesized to mimic any given harmonic stack.

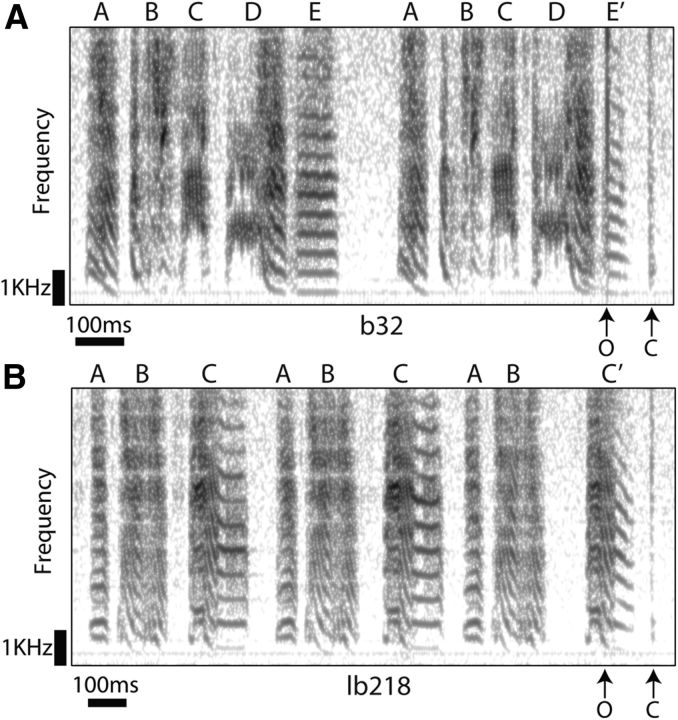
Figure 3.

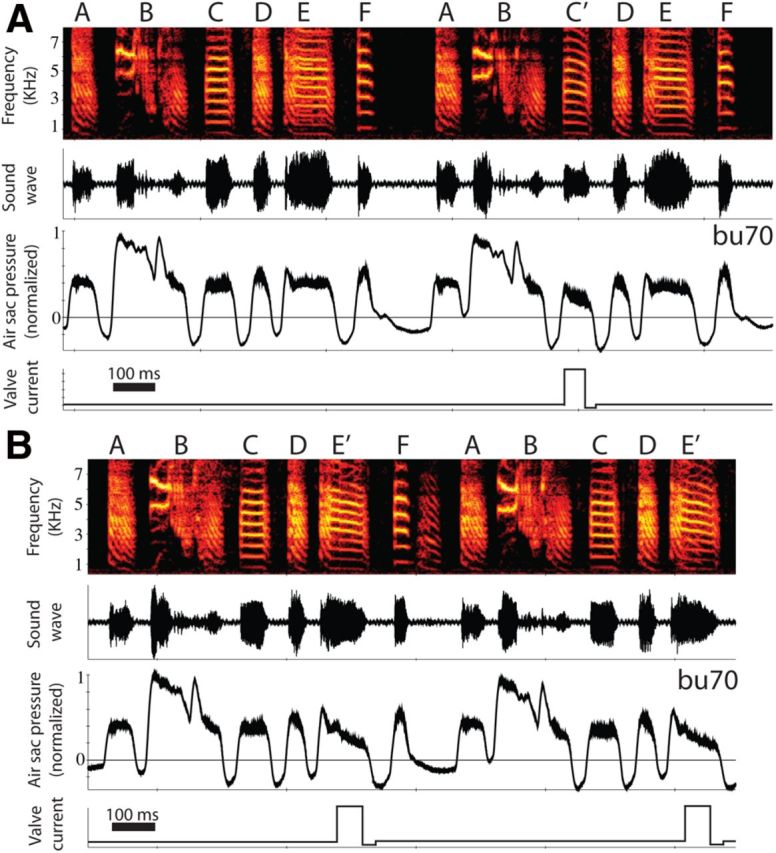
Acoustic changes driven by pressure changes. A, A decrease in the air sac pressure during vocalizing the second syllable C (harmonic stack) results in a decrease of the fundamental frequency. During intact vocalizations, when the first syllable C was not detected by the computer program, the pressure and fundamental frequency remain constant. B, The same effect is shown for syllable E, a different harmonic stack in the same bird. The panels follow the same organization as in Fig. 2.

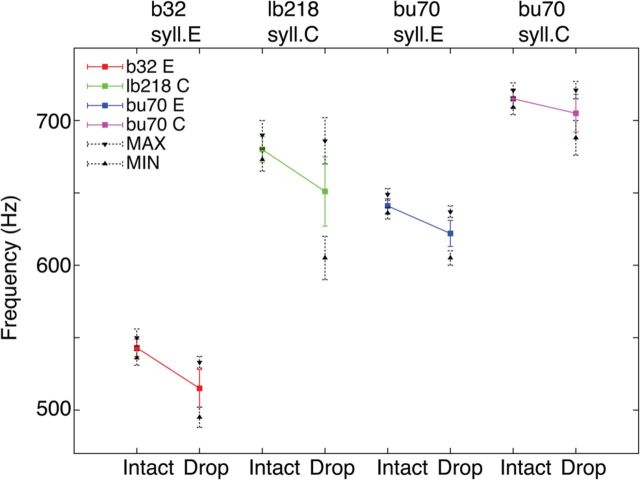
The fundamental frequency of a syllable could depend, in principle, on the labial tension and the subsyringeal pressure. During the harmonic stack components of syllables, the fundamental frequency and the air sac pressure remain constant (e.g., Fig. 3, syllables C and E). But air sac pressure can be relatively constant during frequency modulations (e.g., Fig. 3, syllable A). Therefore, the more parsimonious hypothesis is that during harmonic stacks the labial tension remains constant, too. This is the rational for assuming the parameter β(t) to be constant across the syllables synthesized (β(t) = β). The value of β was adjusted to achieve a match with the fundamental frequency of the syllable. As we wanted to study the acoustic effects of changes in pressure alone, without concurrent changes in labial tension that could generate fundamental frequency changes by itself, the same value of β(t) was used for each pair of synthetic syllables generated (with and without pressure drop). A slightly different value of β was chosen to synthesize syllable C and E as they have different values of fundamental frequency (Table 1; average fundamental frequency of intact syllables). The same scaling factor for α(t) was used for both pairs of syllables.

Table 1.

Effect of venting the subsyringeal air sac on syllable frequency and duration^a

Bird	N	Average frequency (Hz)		Maximum frequency (Hz)		Minimum frequency (Hz)		Duration (ms)		Absolute maximum frequency (Hz)	Absolute minimum frequency (Hz)
		Intact	Modified	Intact	Modified	Intact	Modified	Intact	Modified
b32 syllable E	6	543 ± 6	515 ± 13	550 ± 6	533 ± 4	536 ± 5	495 ± 7	63 ± 6	27 ± 5	7318 ± 110	475 ± 14
lb218 syllable C	9	680 ± 9	651 ± 24	690 ± 10	686 ± 16	673 ± 8	605 ± 15	58 ± 6	41 ± 9	3753 ± 57	452 ± 15
bu70 syllable E	5	641 ± 5	622 ± 9	649 ± 4	637 ± 4	636 ± 4	605 ± 5	44 ± 16	35 ± 2	6198 ± 168	462 ± 11
bu70 syllable C	108	715 ± 6	705 ± 11	721 ± 5	721 ± 6	709 ± 5	688 ± 12	41 ± 6	29 ± 4

^aThe average, maximum, and minimum values of the fundamental frequency ± SD of the intact harmonic stack (Hz), and the corresponding values of the modified syllable (Hz), the syllable duration (ms), and the number of observations for both conditions. For all comparisons (unpaired t test), the differences are significant (p < 0.001), except for bu70 syllable E duration (p > 0.05). The range of phonation for intact birds is the frequency range between the absolute maximum value of fundamental frequency of all uttered syllables and the absolute minimum.

Results

Manipulation of vocal output

Zebra finch song is typically a stereotyped sequence of four to eight distinct syllables (a “motif”), with motifs repeated a variable number of times in a song bout. To directly manipulate song production, we developed a miniature valve (Fig. 1A,B) that controlled the opening of a tube inserted in the air sac system (see Materials and Methods). In favorable cases, after implanting the device a bird could sing normally and the air sac pressure patterns remained unchanged (Fig. 1C,D). Thus, we could manipulate song at specific moments while allowing the bird to sing normally during the rest of the song. The song in Figure 1C has syllables produced both by expiration and inspiration, and both types were well preserved with this method. Birds usually recovered very rapidly from surgery, and some were able to sing during the same day.

In favorable cases, it was possible to completely mute one or several syllables, or even specific parts of a syllable. When the valve opened the end of the tube inserted in the air sac system of the bird, a rapid depressurization occurred. In some cases, this resulted in muting of a syllable. For example, in one case, a bird sang a normal syllable A twice. The local maximum of the normalized pressure of each utterance of syllable A was as follows: 0.75 ± 0.01 and 0.73 ± 0.01 (note the repetitive pattern of subsequent vocalizations). Before the start of a third syllable A, a positive current through the solenoid opened the valve. This induced a rapid depressurization of the air sac system reducing the local maximum of the normalized pressure of syllable A′ to 0.45 ± 0.01 (Fig. 2A). The resultant pressure was insufficient to induce self-sustained oscillations in the syringeal labia; therefore, no sound was produced (the pressure fell to subthreshold levels). The rapid opening of the valve produced a click sound, observed as vertical lines in the sonograph and in the sound waveform trace (Fig. 2A,B). A lower intensity sound was produced when the valve closed. In later experiments with an improved device design, the click sound was reduced, and the same behavioral outcome was observed.

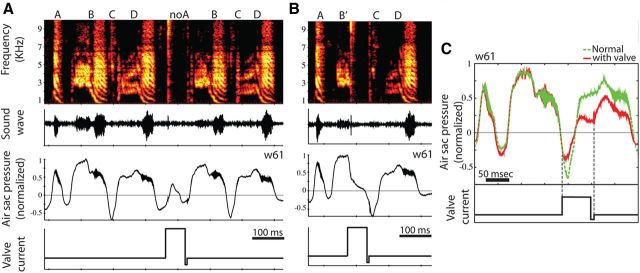
Figure 2.

Complete muting of syllables. A, Effects on acoustics of syllable A (top) when a positive current step is applied, opening the tube. The air sac pressure is measured simultaneously using a pressure sensor connected to the abdominal air sac. When muting syllable A, only the magnitude of the pressure pattern is modified, leaving the shape unchanged. The bird is able to repressurize after muting syllable A and sing syllable B immediately after the current step finishes, closing the tube. B, Muting part of a syllable, followed by rapid repressurization permitting singing of the following syllable (an inspiratory syllable in this case). C, Inspiratory syllables can also be muted with this method. When the valve is closed, a rapid repressurization occurs (final dotted line).

The valve operated quickly, with an opening time of 11 ± 4 ms a closing time of 9 ± 3 ms. The closing time was smaller because the magnet was moving in the same direction of the airflow. This allowed selective manipulation of syllable segments. For example, in Figure 2B, the initial part of syllable B (intact: 106 ± 3 ms duration) was sung normally (compare the sound and pressure patterns with the syllables B in Fig. 2A). When the valve was opened at ∼54 ms, during the second half of the syllable, the pressure rapidly dropped close to atmospheric levels and no sound was produced (Fig. 2B). The ability to phonate recovered very rapidly. For example, after modified syllable B′, the following inspiratory syllable C was produced relatively normally (Fig. 2B), and the pressure shape and maximal value also were normal (compare syllable C in Fig. 2B with syllables C in Fig. 2A). In general, after the valve was closed, birds were able to vocalize in <8 ms.

We were able to mute syllables produced during inspiration as well as syllables produced during expiration. An example of muting an inspiratory syllable is shown in Figure 2C. We quantified the magnitude of the pressure drop for one bird (Fig. 2). The pressure drop was syllable dependent. The pressure value for muted syllable A was 43 ± 5% of the pressure value for the original syllable (N = 4), for syllable B was 17 ± 2% (N = 3), for syllable C was 55 ± 2% (N = 7), and for syllable D was 38 ± 7% (N = 7). Syllable C was an inspiratory syllable. The small variance in pressure values for muted syllables indicates that the valve worked in a consistent fashion.

Two observations suggested that birds were not altering their motor output when the valve was open briefly. First, the sound and pressure patterns immediately after closure of the valve were similar to normal patterns (e.g., Figs. 2A,B, syllable C). Second, when the valve was opened during the entire duration of the syllable, the pressure pattern changed in magnitude but not in shape (Fig. 2C; Fig. 2A, muted syllable A). This suggests that the bird was following a fixed motor pattern to create the same pressure pattern but achieving a lower overall pressure magnitude because the valve was open.

Cessation of vocal output

To perform experiments with systematic muting of a targeted syllable, we used a syllable detection program to automatically trigger the valve (see Materials and Methods). Because a significant portion of a syllable was needed for detection, we detected a syllable that preceded the target syllable to be muted. For this protocol, we took advantage of the regularity of the zebra finch song: syllables were uttered in the same order and with little temporal variation for virtually every repetition. (Some zebra finches exhibit some variations of the song, but they were excluded from this study.) Using automatic syllable detection (n = 8 birds), we observed two types of behavior when muting entire syllables, which depended on the duration of the muted syllable. For syllables <60 ms, muting the syllable did not alter the singing pattern (i.e., the birds continued to sing the normal syntactic sequence without showing stuttering or any song degradation; n = 5). Auditory and somatosensory feedback was altered during this manipulation, but this change was insufficient to generate changes in the vocal sequencing.

When the valve was opened for >110 ms, to mute syllables of 130–150 ms duration, birds interrupted the song after the muted syllable (n = 3 birds). (In one bird, we superimposed playback of the recorded syllable to the muted syllable, so that the bird received something akin to normal auditory feedback and disrupted somatosensory feedback. This manipulation did not rescue the bird from stopping to sing, and we did not attempt this manipulation in other birds.) When muting these long duration syllables, we adjusted the timing such that the valve was closed at least 15 ms before the end of the syllable. This allowed for repressurization of the air sac system through a normal inspiration. Nevertheless, none of the birds under this protocol continued to sing after the long-duration syllables were muted. In the best case, for one bird, we were able to maintain systematic muting for 5 d using the syllable detection program, achieving 98% accuracy in detecting the syllable. The abnormal behavior of resetting the song after syllable muting (n = 1269 ± 546 trials per day, with a maximum of 2241 trials in one day and a minimum of 973) was uniformly maintained. In all cases, when the syllable detection program failed, however, a syllable with normal morphology was produced and the song continued. Also, when the experiment was concluded, the bird recovered normal singing immediately. These results suggest that, remarkably, the bird never modified the motor program associated with that syllable over the 5-day period. Although all these birds experienced abnormal auditory and/or somatosensory feedback, in each and every case, our data indicate that there was no compensatory plastic response in the motor program for song (see Discussion).

Frequency manipulation through subsyringeal pressure

Our approach also allowed us to perform more subtle modifications of air sac pressure while a bird was singing. To this end, we used a smaller hole in the valve opening, allowing the air sac system to depressurize at a slower rate. In this way, the system remained in the phonating region while the pressure was decreasing. For this set of experiments, we targeted “harmonic stack” syllables, which had a well-defined and constant fundamental frequency (values between 500 and 900 Hz).

A consistent result was that, when the opening of the valve reduced the air sac pressure, the fundamental frequency of the harmonic stack was also reduced. The changes in frequency were of sufficient magnitude to be readily observable graphically by examining sound spectrographs. Examples from one bird with manipulations of two different harmonic stacks are shown in Figure 3. Simultaneous measurements of abdominal air sac pressure were achieved for this bird (see Materials and Methods). In this bird, syllable B was detected in real time, allowing the targeting of either the following syllables C (Fig. 3A), or E (Fig. 3B) or combinations thereof. Comparing the pressure and frequency of unaltered syllables with the values from modified syllables, there was a clear drop in pressure and frequency (the frequency drop is more evident graphically in the upper harmonics; Fig. 3). In some cases, the pressure decreased, resulting in a continuous frequency drop until the pressure crossed the phonation threshold, terminating the syllable. Examples of this effect for two birds are shown in Figure 4, where it is clear that the modified syllables are shorter than usual.

Figure 4.

Acoustic and timing differences resulting from depressurization of the air sac system. A, The second syllable E of Bird b32 is modified in duration and fundamental frequency when the tube connected to the air sac system is opened. The opening and closing of the valve (“O” and “C” arrows, respectively) generate a click sound, shown in the sonogram as vertical lines. B, The same effect is shown for syllable C of Bird lb218.

Opening or closing the valve produced “click” sounds. For example, in Figure 4, the vertical lines in the sonograph correspond to clicks resulting from the opening and closing of the valve. Operationally, we used these sounds to confirm that the valve was functioning with precise timing. Given that we detected the sounds in our microphone recordings, however, this implies that the bird also heard the clicks and raises the possibility that the clicks acted to modify the bird's singing behavior (e.g., if the clicks acted as distractors). The evidence argues against this caveat. First, we saw a consistent pattern of rapid changes in song after actuating the value. The very brief interval (a few milliseconds) between valve opening or closing (inducing a click) and changes in vocal output indicates that these changes could not be driven by central evaluation of auditory feedback. Second, as reported above, we significantly reduced the amplitudes of the clicks by modifying the valve mechanism (these sounds were effectively removed for Bird bu70 shown in Fig. 3). Yet either with or without click sounds from the valve present, all the birds presented the same effect, a drop in frequency tightly associated with a drop in pressure (compare Figs. 3 and 4; Table 1). These observations argue against the hypothesis that the clicks acted as distractors that affected the bird's singing.

To quantify the frequency drop, the fundamental frequency of each syllable was obtained using Praat software (P. Boersma and D. Weenink; www.praat.org). This provided an accurate pitch-extraction algorithm to measure the fundamental frequency with high accuracy. The fundamental frequency drop associated with opening the valve was in all cases significant, measured either as the average fundamental frequency of the syllables or the minimum frequency value (Fig. 5; Table 1). Figure 3 shows an example where the syllable detection program was used, allowing a systematic acoustic change in the targeted syllable. In this bird, 108 syllables C were targeted, and in all of them a drop was observed, both in pressure and frequency. For the other targeted syllables, fewer exemplars were obtained, but in all the cases a significant acoustic change driven by a pressure change was observed (Table 1; Fig. 5). Quantitative analyses of the fundamental frequency values for intact and modified syllables are shown for the three birds and four syllables in Table 1. To assess the potential biological relevance of the frequency modulations through pressure during singing, we also calculated the range of phonation of each bird. Interestingly, the decrease of frequency resulting from venting the air sac system was included in the normal range of phonating for all the birds (Table 1).

Figure 5.

Frequency modulations in harmonic stacks resulting from pressure modulations. The average fundamental frequency is calculated for each harmonic stack in the intact and modified condition (pressure drop), identified by bird, syllable, and line color (e.g., Bird b32, syllable E, red). For each syllable, the maximum and minimum values of the fundamental frequency are also shown with black dotted lines (mean ± SD).

Mathematical model for song production

To explore possible mechanisms involved in the relationship between fundamental frequency and subsyringeal pressure, we worked with a mathematical model for vocal production (see Materials and Methods) (Amador and Mindlin, 2008; Perl et al., 2011). The parameter space (pressure, tension) = (α(t), β(t)) is characterized by bifurcation lines. In Figure 6A, the Saddle Node in Limit Cycle (SNILC) bifurcation is indicated as a red line that divides the parameter space in oscillatory and nonoscillatory regimens (phonating and nonphonating regimens, respectively). In regions where phonation occurs, each point (pressure, tension) defines the fundamental frequency and the spectral content of the syllable. Fig. 6A (red dots) shows fundamental frequency for each (pressure, tension) value. Modeling the syrinx as a nonlinear oscillator with nonlinear restitution force allows a particular behavior near the bifurcation line (Fig. 6A, red line): the frequency of the oscillations is determined by both pressure and tension values. In this way, the fundamental frequency can be modified by changing the pressure values while keeping the tension value constant (Fig. 6B). The increase in frequency resulting from an increase in pressure is a nonlinear relationship. Figure 6B (red bars) indicates that, for a given increase in pressure, the increase in frequency is most noticeable for low fundamental frequencies. Fundamental frequency modulations can also be achieved by changes in labial tension alone (Fig. 6C), presumably controlled by the syringeal muscles, which is in agreement with previous reports (Goller and Suthers, 1996a; Gardner et al., 2001).

We used this modeling framework to characterize the results of our experimental manipulations by creating synthetic copies of modified syllables that were recorded simultaneously with air sac pressure: Bird bu70, syllable C and C′ (Fig. 3A,B) and syllable E and E′ (data not shown). One of the advantages of the model is that physiological parameters can be related directly with mathematical parameters. To achieve this, the measured air sac pressure was smoothed and scaled, and the tension was assumed to be constant (see Materials and Methods). In this way, we generated synthetic copies of harmonic stacks uttered in normal conditions (e.g., Fig. 6D,E). We then used the model to synthesize the same syllable emitted during a pressure drop. A pressure drop was generated by opening the tube connected to the interclavicular air sac while recording in the abdominal air sac (see Frequency manipulation through subsyringeal pressure and Materials and Methods). The corresponding frequency drop was observed in the recorded song (we show an example of syllable C′ from Fig. 3A in Fig. 6F). To generate a synthetic copy of the syllable C′, we used the same scaling factor for the pressure parameter and the same tension value that we used to generate Figure 6E. The results demonstrate a clear frequency drop resulting from pressure drop (Fig. 6G). In this way, we could generate a frequency modulation through an air sac pressure modulation while maintaining the tension of the syringeal labia in a constant value. Thus, the physical model for song production could reproduce the observed behavior having as an input the value of the air sac pressure recorded during singing.

Discussion

The experiments and the mathematical modeling presented here demonstrate that the fundamental frequency of harmonic stacks in zebra finches is determined both by the subsyringeal air sac pressure and syringeal tension values achieved during singing. Considering the critical role of syringeal muscles for vocal control during singing in zebra finches (Vicario, 1991; Williams and McKibben, 1992; Goller and Suthers, 1996a, b; Riede et al., 2010), our results suggest that respiratory and syringeal muscle activity are coordinated during singing, such that the appropriate labia tension and pressure magnitude are achieved to generate the desired sound. This dependency of the fundamental frequency with the pressure could be used as a mechanism of frequency control contributing to the activity of the syringeal muscles in a synergistic way. This mechanism could explain the functionality of the complex modulations found in the pressure pattern of expiratory pulses during singing (see Goller and Daley, 2001; Franz and Goller, 2003). It would also explain some interesting findings regarding pressure structure and vocal learning in zebra finches: when air sac pressure patterns of tutored and untutored zebra finches were studied, it was observed that the respiratory effort was similar in both groups, but the expiratory pulses of song in tutored birds contained more modulations and temporal complexity (Mendez et al., 2010). Another study showed that tutees adopted the amplitude of each song element from the tutor, so that the amplitude modulation patterns were very similar (Ritschard and Brumm, 2011). Tutors and tutees also have similar mean song amplitudes. These complex pressure modulations could emerge as a fine-tuning of syringeal and respiratory musculature to control fundamental frequency, and it would be adaptive for birds imitating songs to attend to details of the amplitude waveform.

The dependency of the fundamental frequency with pressure emerges naturally from the nonlinear dynamics of the syrinx, recently modeled in the nonlinear dynamic systems framework (Amador and Mindlin, 2008; Sitt et al., 2008; Perl et al., 2011). Using this mathematical model of song production, it was possible to generate the whole range of frequencies and dynamic regimens observed in the zebra finch song; and to further validate the model, it has been shown that the bird's own song and its synthetic copy elicited similar patterns of activity from cortical HVC neurons (Amador et al., 2013). Moreover, the mathematical parameters of the model can be related to physiological parameters that can be measured in a singing bird. This model accounts for the two well-defined regimens of zebra finch vocalizations: tonal sounds with high fundamental frequencies (>2 kHz) and sounds with high spectral complexity and low fundamental frequencies (<1.2 kHz) following the description described previously (Sitt et al., 2008). This “frequency gap” that separates the two phonating regimens has also been reported by Ritschard and Brumm (2011), who found no vocal elements with pitch between 1200 Hz and 1700 Hz. In the model, these two regimens emerge when oscillations originate through two different bifurcations: Hopf and SNILC (Strogatz, 1994).

The dynamic organization of the model predicts that the dependence of frequency with pressure is more noticeable for low-frequency notes than high-frequency notes. A more abrupt change in fundamental frequency results from changes in pressure in the vicinity of the SNILC bifurcation resulting from the nonlinear relation between the fundamental frequency of the oscillations and the parametric distance to the bifurcation point (Fig. 6A, red line; B). Consistent with the prediction of the model, we observed a frequency modulation resulting from pressure in harmonic stacks that belong to the group of low fundamental frequency syllables in the zebra finch repertoire. For modulation of high-frequency notes, the prediction is that the syringeal muscles would play the more dominant role, as a noticeable effect of frequency modulation through pressure would require an extremely large variation in pressure. Therefore, frequency modulation for high-frequency notes is more parsimoniously achieved with variations in the parameter β(t), related to syringeal tension controlled by muscle activity. These predictions of the model fit recent results showing a positive correlation between amplitude (directly related with air sac pressure) and pitch, for syllables with fundamental frequency <1200 Hz, whereas this correlation was lost for notes with fundamental frequencies >1700 Hz (Ritschard and Brumm, 2011). Another study (Riede et al., 2010) reported a correlation between fundamental frequency and air sac pressure in zebra finch calls after resection of the tracheosyringeal nerve (all muscular control of the syrinx removed). With loss of muscle tone, the specific effect of air sac pressure on fundamental frequency may be different in the denervated syrinx; nevertheless, these results are informative of purely pressure-driven effects on phonation.

The similarities regarding physical mechanisms for phonation in humans and songbirds are remarkable. In both cases, flow-induced oscillations in opposing membranes modulate the airflow generating sound. Also, voiced sounds in humans have a similar acoustic structure to harmonic stacks: almost constant fundamental frequency with rich harmonic content and vocal tract modulations. Considering these similarities, it emerges naturally that humans and songbirds share mechanisms of frequency modulation through pressure. Several studies in humans have determined that speech produced in noise shows an involuntary increase in intensity, known for >100 years as the Lombard effect (Brumm and Zollinger, 2011). This reflex-like response to an increase in background noise is correlated with an increased pitch, among other changes in phonetics (Gramming et al., 1988; Garnier et al., 2010; Brumm and Zollinger, 2011). The same effect has been reported in several songbirds and budgerigars (Brumm and Zollinger, 2011). In budgerigars, changes in vocal intensity resulting from noise presentation were accompanied by changes in call fundamental frequency (Osmanski and Dooling, 2009). Also, a decrease in vocal amplitude (in response to an increase in perceived vocal loudness achieved by altered auditory feedback through headphones) was accompanied with a decrease in the fundamental frequency of the uttered calls (Osmanski and Dooling, 2009). These findings in budgerigars and humans further demonstrate the influence of pressure in fundamental frequency, giving support to our experimental results and motivating the prediction that an analogous dependency of amplitude and pitch under the Lombard effect will take place in zebra finches. The effect of frequency modulation through subglottal pressure has been studied in humans for several years (Titze, 1989), but the use of more invasive experiments in songbirds could shed light on the physiological mechanisms underlying this effect. The mathematical model used here to generate synthetic syllables in songbirds could also be use to generate synthetic vowels and further explore mechanisms for sound generation in humans.

The technique presented in this study for manipulating vocal output in singing birds provides a flexible method for studying altered auditory feedback. It is well established that, in many species of songbirds, auditory feedback is necessary to achieve and maintain adult song (Konishi, 1965; Nordeen and Nordeen, 1992). The mechanisms underlying the role of auditory feedback, however, remain largely unknown despite intensive study over many decades. Prior studies of the role of auditory feedback in song control in normal hearing birds have relied either on noise playback or delayed syllable playback (Leonardo and Konishi, 1999; Sober and Brainard, 2009). These have the disadvantage of superimposing external sounds onto feedback from the bird's singing. This complicates distinguishing between internal error representation and actual modification of auditory input. The method presented here would allow a better experimental control of the auditory feedback during singing.

Systematic muting of short syllables did not change the singing pattern. This is an indication that the error message perceived by auditory or somatosensory feedback is insufficient to induce song modification. It has been reported that short burst of stroboscopic light can stop song (Cynx, 1990) and that zebra finches exposed to delayed auditory feedback of their own song promptly produced anomalies, such as stutters, omissions, and novel sounds (Cynx and von Rad, 2001; Fukushima and Margoliash, 2007). This indicates a dynamic feedback loop between ongoing song perception and production in adult zebra finches. We have shown that the absence of a short syllable is not perceived as a strong negative feedback, in the sense that the bird continues to sing and maintains a normal singing pattern. In contrast, abnormal pressure conditions for >110 ms disrupted song. As there was no auditory feedback, the cessation of singing was probably related to somatosensory feedback. This could be the accumulation of errors or the action of an overriding control signal indicating insufficient air available to continue singing. Additional experiments, especially real-time modulation of the valve based on measurements of subsyringeal pressure, could help to explore this behavior.

In conclusion, the maintenance of the normal motor program in the presence of a targeted, highly reliable muting of a specific syllable over days suggests that assessment of a global signal (over the entire song) is important for maintenance of syntax. The ability of continuous high gain delayed auditory feedback to rapidly change syntax (Fukushima and Margoliash, 2007) is consistent with this hypothesis.