Abstract
In a complex auditory scene, a “cocktail party” for example, listeners can disentangle multiple competing sequences of sounds. A recent psychophysical study in our laboratory demonstrated a robust spatial component of stream segregation showing ∼8° acuity. Here, we recorded single- and multiple-neuron responses from the primary auditory cortex of anesthetized cats while presenting interleaved sound sequences that human listeners would experience as segregated streams. Sequences of broadband sounds alternated between pairs of locations. Neurons synchronized preferentially to sounds from one or the other location, thereby segregating competing sound sequences. Neurons favoring one source location or the other tended to aggregate within the cortex, suggestive of modular organization. The spatial acuity of stream segregation was as narrow as ∼10°, markedly sharper than the broad spatial tuning for single sources that is well known in the literature. Spatial sensitivity was sharpest among neurons having high characteristic frequencies. Neural stream segregation was predicted well by a parameter-free model that incorporated single-source spatial sensitivity and a measured forward-suppression term. We found that the forward suppression was not due to post discharge adaptation in the cortex and, therefore, must have arisen in the subcortical pathway or at the level of thalamocortical synapses. A linear-classifier analysis of single-neuron responses to rhythmic stimuli like those used in our psychophysical study yielded thresholds overlapping those of human listeners. Overall, the results indicate that the ascending auditory system does the work of segregating auditory streams, bringing them to discrete modules in the cortex for selection by top-down processes.
Introduction
Normal-hearing listeners possess a remarkable ability to disentangle competing sequences of sounds from multiple sources. This phenomenon is known as “stream segregation,” where each perceptual stream corresponds to a sequence of sounds from a particular source (Bregman, 1990). Multiple sound features can contribute to stream segregation, including fundamental frequency, spectral or temporal envelope, and “ear of entry” (for review, see Moore and Gockel, 2002).
Differences in the locations of signal and masker sources have long been thought to contribute to hearing in complex auditory scenes (Cherry, 1953). Recently, a study in our laboratory tested in human listeners an objective measure of spatial stream segregation that required listeners to discriminate between two rhythmic patterns in the presence of competing sounds (Middlebrooks and Onsan, 2012). The task was impossible when signal and masker were colocated. As little as 8° of separation of signal and masker, however, resulted in perceptual stream segregation of signal from masker that permitted reliable rhythm discriminations.
Normal function of the auditory cortex is well known to be necessary for sound localization (Jenkins and Merzenich, 1984; Malhotra et al., 2004). Recordings of the spatial sensitivity of single cortical neurons, however, demonstrate surprisingly broad spatial tuning (for review, see King and Middlebrooks, 2011). Identification of sound-source locations based on the responses of cortical neurons can approach psychophysical levels of accuracy only by combining information across sizeable neural populations (Furukawa et al., 2000; Miller and Recanzone, 2009; Lee and Middlebrooks, 2013). It is difficult to imagine how the broad spatial sensitivity that has been observed in the cortex could account for the high-acuity spatial stream segregation that is seen in psychophysics.
We tested the hypothesis that individual neurons in the primary auditory cortex (area A1) in anesthetized cats segregate sound sequences from sources that are separated in the horizontal plane. Consistent with the hypothesis, neurons synchronized preferentially to one of two broadband sound sources that alternated in location. The neurons showed spatial acuity much finer than one would have anticipated based on previous accounts of spatial sensitivity. The results cause us to revise our view of spatial sensitivity in the auditory cortex in that the presence of a competing sound sharpened the spatial tuning of neurons to levels that have not been seen using single sound sources. Also, we observed a previously unknown dependence of spatial sensitivity on neurons' characteristic frequencies, which was especially prominent under conditions of competing sources.
We measured responses to sound sequences identical to those used in our psychophysical “spatial rhythmic masking release” study (Middlebrooks and Onsan, 2012). A linear-classifier analysis of those single-neuron responses yielded spatial thresholds overlapping those of the human listeners. Under stimulus conditions in which human listeners report hearing discrete auditory streams, we find activity segregated among discrete modules of cortical neurons.
Materials and Methods
Animal preparation.
All procedures were done with approval from the University of California at Irvine Institutional Animal Care and Use Committee. Data presented here were obtained from 12 purpose-bred male cats, 3.4–6 kg in weight (median 4.5 kg); use of animals all of the same gender facilitated group housing. Anesthesia was induced with ketamine (25 mg/kg), maintained during surgery using isoflurane, and then transitioned to α-chloralose for the period of data collection. The α-chloralose was given intravenously, 25 mg/ml in propylene glycol, initially ∼40 mg/kg, and then was maintained with an intravenous α-chloralose drip (∼3 mg/kg/h), supplemented as needed to maintain an areflexive state during the physiological recordings. During the recording, the animal was suspended in a heating pad in the center of a sound-attenuating booth. Its head was supported from behind by a bar attached to the skull, and its external ears were held in a natural-looking forward position with thin wire supports. The cat was supplied with oxygen in a rebreather circuit. Pulse and respiratory rates, pedal-withdrawal and palpebral reflexes, rectal temperature, and oxygen saturation were checked at half hour intervals. Experiments lasted 18–48 h (median 36 h) from induction of anesthesia to euthanasia.
Experimental apparatus, stimulus generation, and data acquisition.
Stimulus presentation and physiological recording were conducted in a double-wall sound-attenuating booth (Industrial Acoustics; inside dimensions 2.6 × 2.6 × 2.6 m) lined with SONEXone absorbent foam. A circular hoop, 1.2 m in radius, supported 8.4 cm coaxial loudspeakers in the horizontal plane aligned with the cat's interaural axis, 1.2 m above the floor. The loudspeakers were spaced at 20° increments from left to right 80° relative to the cat's midline plus additional loudspeakers at left and right 10°. Left and right loudspeaker locations are given as contralateral (C) and ipsilateral (I), respectively, relative to the recording sites, which were all in the right hemisphere.
Stimulus generation and data acquisition used System 3 hardware from Tucker-Davis Technologies, controlled by a personal computer. Custom MATLAB scripts (MathWorks) controlled the stimulus sequences, acquired the neural waveforms, and provided on-line monitoring of responses at 32 recording sites. Sounds were generated with 24-bit precision at a 100 kHz sampling rate. Loudspeakers were calibrated using a precision 1/2” microphone (ACO Pacific) positioned at the usual location of the center of the cat's head, 1.2 m from the speakers. Calibration for broadband sounds used Golay codes (Zhou et al., 1992) as probe stimuli. The broadband frequency responses of the loudspeakers were flattened and equalized such that for each loudspeaker the SD of the magnitude spectrum across the 0.2–25 kHz calibrated pass band was <1 dB. The responses rolled off by 10 dB at 40 kHz. The calibration procedure yielded a 1029-tap finite-impulse-response correction filter for each speaker. Calibration for pure tones used pure-tone probe stimuli. A look-up table with tone responses in 1/6 octave (oct) intervals was stored for each loudspeaker.
Extracellular neural spike activity was recorded with silicon-substrate multisite recording probes from NeuroNexus Technologies. Probes had 16 recording sites spaced at 150 μm intervals or 32 recording sites spaced at 100 μm intervals. Waveforms were recorded simultaneously from 32 sites using high-impedance headstages and multichannel amplifiers from Tucker-Davis Technologies. Waveforms were filtered, digitized at a 25 kHz sampling rate, and stored to computer disk for off-line analysis.
Experimental procedure.
Recording probes were placed in cortical area A1, guided by the posterior and suprasylvian sulci as visual landmarks, and confirmed by recording of characteristic frequencies (CFs) of neurons. An on-line peak-picking procedure was used to detect spikes needed to estimate CFs and thresholds during the experiments. Sharp frequency tuning and a caudal-to-rostral increase in CFs measured at two or more locations were taken as the signatures of area A1 (Merzenich et al., 1975). The 16-site probes were placed two at a time, four pairs of placements in each of two cats (total of 16 probe placements). The 32-site probes were placed one at a time, one to six in each of 10 cats (median three per cat, total of 30). All of the 16-site placements and 11 of the 32-site placements were aimed approximately orthogonal to the cortical surface, parallel to cortical columns. After off-line spike sorting, 23 of those placements showed CF ranges spanning ≤0.83 oct, suggesting that they were aligned reasonably closely with isofrequency contours, whereas 4 showed CF ranges spanning 1.0–1.3 oct, suggesting that they were somewhat more oblique. Nineteen of the 32-site placements intentionally were oriented obliquely down the anterior bank of the posterior ectosylvian sulcus, where low-CF neurons commonly are found. Those penetrations consistently encountered a progression from high CFs at the superficial recording sites to lower CFs at deeper sites. The CFs encountered on those penetrations spanned ranges of 1.5–4.8 oct (median 2.8 oct). The range of CFs across the entire sample was 0.28–28.5 kHz (median 5.0 kHz); the distribution of CFs in 1 oct bins is given in Figures 2, 9, and 15. After each probe or pair of probes was in position, the cortical surface was covered with a warmed 2% solution of agarose in Ringer's solution, which cooled to a firm gel that reduced brain pulsations and prevented drying of the cortical surface.
Figure 2.
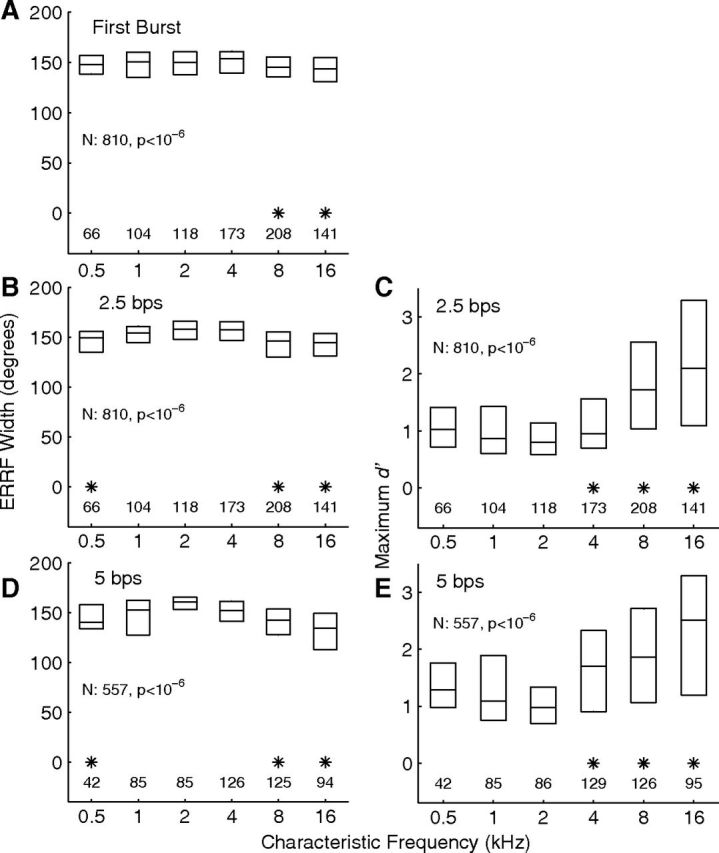
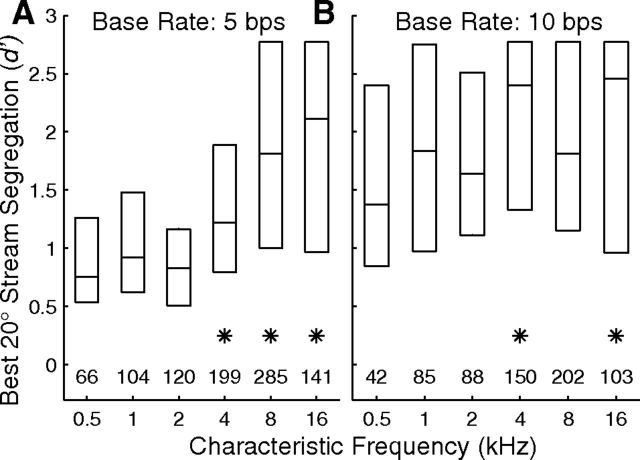
Distributions of spatial-tuning metrics as a function of units' CFs. The left column (A, B, D) indicates distributions of widths of ERRFs, (see Materials and Methods), and the right column (C, E) indicates distributions of maximum d′, which is the discrimination index for discrimination of trial-by-trial spike counts between the maxima and minima of RAFs. The maximum-d′ measure was not used for the first-burst condition because responses to one sound-burst per trial gave poor statistical strength compared with the 14 bursts per trial used for the synchronized conditions. A–C and D and E represent first-burst and 2.5 and 5 bps synchronized responses, respectively. Data are binned in 1 oct bands of CF centered at 1 oct intervals. The 12 CFs falling below the 0.5 kHz bin and the 20 CFs falling above the 16 kHz bin were combined with the adjacent bins. Each box indicates the median and interquartile range of each 1 oct bin. The row of numbers above each horizontal axis indicates the number of units represented in each bin. Asterisks indicate bins in which the median was significantly lower (left) or higher (right) than the maximum (or minimum) median in each panel (p < 0.05 after Bonferroni correction).
Figure 9.
Distributions of d′ as a function of unit CF. A, B, Represent base rates of 5 and 10 bps, respectively. Each d′ in the distributions represents for one unit the greatest magnitude for discrimination of A and B sources across B locations 20° to the left or right of A sources at C 40°, 0°, and I 40° (i.e., the maximum across 6 A/B locations, all with 20° between A and B). Data are binned in 1 oct bins of CF-centered 1 oct intervals. The rows of numbers above the abscissae indicate the number of d′ values in each bin. Asterisks indicate bins in which the medians were significantly higher than the medians in the 0.5 kHz bins (p < 0.05, corrected for multiple comparisons).
Figure 15.
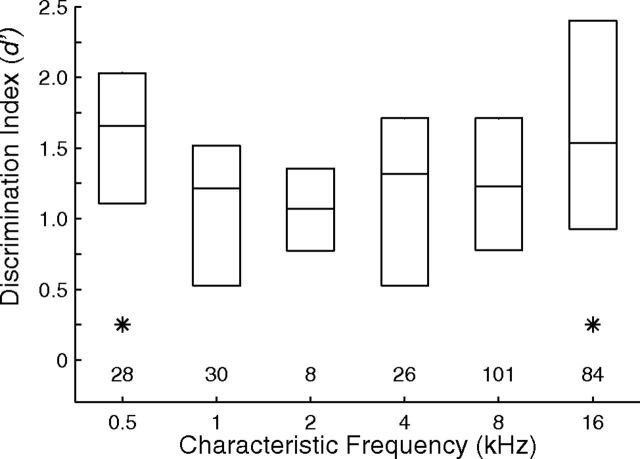
Dependence of rhythmic masking release performance on CF. Plotted are distributions of d′ for discrimination of rhythms. Signals were fixed at 0°, and the distributions represent for each unit the better of performance for masker locations at C 20° or I 20°. Boxes indicate 25th, 50th, and 75th percentiles. Asterisks indicate 1 oct bins for which medians were significantly higher than those for one or more intermediate frequencies (N = 277 single and multiple units, p < 0.05, corrected for multiple comparisons).
Study of responses at each probe position consisted of measurements of frequency response areas, of excitation thresholds for broadband noise bursts, and (in varying order) of stream segregation and spatial rhythmic masking release. Frequency response areas were measured using pure tones, 80 ms in duration with 5 ms cosine-squared on and off ramps, at a repetition rate of 1/s, presented from the C 40° loudspeaker. Tones were varied in 1/6 oct steps of frequency and 10 dB steps of sound level. Every combination of frequency and level was repeated 10 times. The frequency showing the lowest threshold was taken as the CF. Noise thresholds were measured using 80 ms Gaussian noise bursts at a 1/s repetition rate from the C 40° loudspeaker, varied in 5 dB steps of level, with 20 repetitions per level; a silent condition also was included. The distribution of noise thresholds along each recording probe was estimated on-line, and a modal value was selected. Stimulus levels for subsequent measurements were set 40 dB or more above that modal value. Off-line, noise thresholds were measured using a receiver-operating characteristic (ROC) procedure (see below, Data analysis), and stimulus levels were computed relative to those thresholds. Across 915 single- and multiple-unit recordings, the distribution of stimulus levels relative to threshold had a median of 38.9 dB and 5th and 95th percentiles of 22.9 and 47.6 dB.
The stimulus conditions for the study of stream segregation were inspired by the work of Fishman and et al. (2001, 2004), although their “A” and “B” stimuli varied in frequency and ours varied in source location. In our “competing-source” conditions, stimuli consisted of sequences of independent (i.e., nonfrozen) Gaussian noise bursts, 5 ms in duration with 1 ms cosine-squared on and off ramps. Sequences alternated between A and B sources in an ABAB… pattern comprising 15 A and 15 B bursts. Aggregate “base rates” of 5 and 10 bursts per second (bps) were tested, such that the difference in onset times between an A burst and that of the following B burst (and vice versa) was 200 or 100 ms for base rates of 5 or 10 bps, respectively. The order of testing of the two base rates varied among probe placements. Depending on the base rate, the duration of sequences was 3000 or 1500 ms, with a silent period of ≥1700 ms between the offset of one sequence and the onset of the next. The A bursts were presented from C 40, 0, and I 40°, and the B bursts were presented from C 80 to I 80° in 20° steps plus C 10 and I 10°; the set of locations included conditions of A and B colocated at C 40, 0, and I 40°. In nearly every case, a B-alone condition (i.e., silent A) also was included in which the stimulus rate was half the stated base rate. Sequences beginning with A or B were presented an equal number of times. Every combination of A location (or A silent), B location, and A or B leading was tested once in a random order, then every combination was tested again in a different random order, and so on until every stimulus combination was tested 10 times. As shown in the Results, no significant difference in stream segregation was observed between A- and B-leading conditions. For that reason, A- and B-leading conditions were combined, resulting in 20 repetitions of each pair of A and B locations.
Spatial rhythmic masking release was tested with two temporal patterns (rhythms) of signal (S) and masker (M) that were identical to the patterns used in our psychophysical study (Middlebrooks and Onsan, 2012). Rhythm 1 was SSMMSSMM (repeated four times without interruption) and Rhythm 2 was SSMMSMSM (also four times). The base rate was fixed at 5 bps, the signal location was fixed at 0°, and the masker varied among all the locations. Again, signal- and masker-leading conditions were combined, resulting in 20 repetitions of Rhythm 1 and 20 of Rhythm 2 at each masker location.
Data analysis.
Data analysis began with off-line identification of neural action potentials (“spike-sorting”), as described previously (Middlebrooks, 2008). Well-isolated single units were characterized by a discrete mode in the distribution of peak-to-trough amplitudes, no more than a small number of interspike intervals that were <1 ms, and by uniform waveform appearance in visual inspection. Multiple-unit recordings consisted of spikes from two or more neurons that could not be discriminated consistently. Neural waveforms from a total of 1216 recording sites yielded single- or multiple-unit responses at 1055 sites. Those responses then were screened to eliminate the ∼13% of units that failed to show synchronized response to our lowest rate stimulus, a 2.5 bps sequence. We were left with 205 well isolated single units, and 710 multiple-unit recordings, a total of 915. Well isolated single units are referred to as such, whereas “unit activity” or simply “units” refers to single- and/or multiple-unit recordings from a single recording site. All of the statistics include combined single- and multiple-unit responses except when stated otherwise. Not all of the stimulus sets were tested for all of the units, so the number of tested units (given as N) often was smaller than 915. In particular, eight of the probe placements were not tested at the 10 bps base rate, and many units did not synchronize to that faster rate. For that reason, the sample at the 10 bps base rate always was smaller than that at the 5 bps rate.
Rate-azimuth functions (RAFs) expressed mean rates of spikes per 5 ms noise burst as a function of loudspeaker location; note that “rate” here indicates the rate of spikes per burst, not spikes per second. Spikes tended to fall in a compact burst ≥10 ms after each noise-burst onset. We counted spikes in the 8–58 ms poststimulus-onset interval, which captured essentially all the spikes driven by each noise burst. In that way, spikes were attributed to A or B noise sources. Synchronized RAFs included responses synchronized to the last 14 of the 15 noise bursts from each source on each trial. Mean spike rates and SEM were computed over 14 bursts × 20 trials = 280 bursts. “First-burst” responses gave the response to the first noise burst in each stimulus sequence and were interpreted as comparable to the responses to single noise bursts seen in the literature; most often, such tests have used bursts 80 ms or longer in duration, but there also are examples of spatial tuning studied with transients (Reale and Brugge, 2000). We combined first-burst responses over 20 repetitions of B-source alone conditions and over the 10 repetitions of competing A/B stimuli in which the A source was at C 40, 0, or I 40° and the B stimulus was the first in the sequence. That yielded 1 burst × 50 trials collected over the same block of time in which the B-alone and various A-location conditions were interleaved trial by trial.
The preferred stimulus location of each neuron was given by its centroid. The centroid was computed from an RAF by finding the peak range of one or more contiguous sound-source locations that elicited spike rates ≥75% of a neuron's maximum rate plus the two locations on either side of that range. All the locations within the peak range were treated as vectors weighted by their corresponding spike rates. A vector sum was formed, and the direction of the resultant vector was taken as the centroid. The breadth of spatial tuning of a neuron was represented by the width of its equivalent rectangular receptive field (ERRF) (Lee and Middlebrooks, 2011). The ERRF width was computed by computing the area under a neuron's RAF, reshaping that area as a rectangle having a height equal to the maximum spike rate of the RAF, and measuring the width of that rectangle. The location of the greatest location-dependent modulation of spike rates was found by taking each RAF in 20° increments, smoothing it by convolution with a 3-point Hanning window, and then finding the stimulus location showing the steepest slope in the smoothed function. That procedure yielded steepest-slope locations lying midway between data points at 20° increments.
Discrimination of sound levels and sound-source locations by trial-by-trial neural spike counts was quantified using a procedure derived from signal detection theory (Green and Swets, 1966; Macmillan and Creelman, 2005; Middlebrooks and Snyder, 2007). The spike count on a single trial was compiled over the single 80 ms duration of noise bursts that were used for estimates of detection threshold or over the responses synchronized to a succession of 14 5-ms noise bursts. We formed an empirical ROC curve based on the trial-by-trial distributions of spike counts elicited on 20 trials by each of two stimuli. The area under the ROC curve gave the probability of correct discrimination of the stimuli, which was expressed as a z-score and was multiplied by √2 to obtain the discrimination index, d′. In cases in which 100% of the spike rates elicited by one stimulus were greater than any of those elicited by the other stimulus, d′ was written as ±2.77, which corresponds to 97.5% correct discrimination. Given N = 20 trials, that corresponds to the 1/2N procedure for dealing with extreme values described by Macmillan and Kaplan (1985). The sign convention was such that d′ was positive when the more intense or more contralaterally located sound elicited more spikes.
The ROC procedure was used for several purposes. We quantified excitation thresholds for noise bursts by computing d′ for discrimination of noise levels increasing in 5 dB steps compared with a silent condition. The interpolated level at which the plot of d′ versus level crossed d′ = 1 was taken as the threshold. We quantified the magnitude of stream segregation in conditions of interleaved A and B noise bursts by computing d′ for spikes synchronized to the A versus the B bursts. Values of d′ then were plotted as a function of B-source location. We quantified discrimination of locations of single sound sources by computing d′ based on spike counts elicited by sounds presented from one location compared with counts elicited on different trials by a source at another location. “Maximum single-source d′” was the d′ for discrimination of the locations that elicited maximum and minimum mean spike counts across all sound-source locations.
Permutation analysis was used to test for nonrandom cortical distribution of neurons having similar response properties. In single-source conditions, we compared hemifield versus omnidirectional or other spatial tuning. We counted along 16- or 32-site recording probes the number of adjacent pairs of recording sites at which units showed hemifield tuning at both sites. A run of four consecutive sites, for example, would be counted as three matched pairs. In competing-source conditions, we compared preference for the A versus B source. We considered only the sites at which units showed a significant preference for the A or B source, indicated by a magnitude of d′ ≥ 1. Among just those sites, we counted pairs of consecutive sites having units both preferring the A source or both preferring the B source. In the permutation analysis, we counted across the entire sample the total number of hemifield versus non-hemifield units or A-preferring versus B-preferring units. In each permutation, we distributed all those units randomly across virtual probes having the same number of sites as the actual recording probes, and we counted the number of matching adjacent pairs of units. That permutation was repeated 100,000 times, each with a different random distribution of unit classes among probes. If the actual recorded number of matching pairs was larger than the maximum value obtained across all the random permutations, the probability of obtaining that actual number by chance was said to be <10−5, and the measured response-specific distribution of neurons was said to be nonrandom.
A linear-classifier analysis was used to measure the accuracy with which the responses of neurons could distinguish between two rhythms of noise bursts. As described above (see Experimental procedure), each signal rhythm consisted of 4 bursts interleaved with 4 masker bursts, all repeated four times, yielding 32 bursts. We restricted the analysis to the last three repetitions (24 bursts) for the purpose of omitting the relatively nonselective response to the first sound burst in a sequence. Poststimulus spike times were folded on the 1600 ms duration of each rhythm, so that the analysis was done on spike counts within eight time bins totaled over three repetitions of the rhythm. We used least-squares multiple linear regression to classify neural responses. The spike counts in the eight time bins were the regressors, and the linear equation was solved for appropriate values of 1 or 2 when the spike counts were elicited by Rhythm 1 or 2. A one-out validation procedure was used in which spike counts from 439 of the 440 trials (2 rhythms × 11 masker locations × 20 repetitions) were used to find a set of regression coefficients, and counts from the 440th trial were used to generate a test value. That procedure was repeated, acquiring test values for each of the 440 trials. An ROC analysis of test values on Rhythm 1 or 2 trials yielded d′. Values of d′ were plotted as a function of masker location.
Statistical procedures used the MATLAB Statistics Toolbox. Post hoc comparisons used the Bonferroni correction for multiple comparisons. Error bars in the illustrations indicate SEM.
Results
Spikes rates synchronized to single sources showed broad azimuth sensitivity
Consistent with most previous studies, neurons in area A1 generally responded to single sound sources with broad spatial sensitivity. Examples of RAFs from three isolated single units are shown in Figure 1; colors indicate responses synchronized to the first sound burst in each sequence (black), and to the last 14 bursts of sequences at 2.5 (green), 5 (gray), and 10 (magenta) bps. The unit in Figure 1A responded nearly as strongly to 2.5 bps as it did to the first burst, whereas the units in Figure 1, B and C, showed a decrease in spikes per burst in all the synchronized conditions. These three examples are representative of the entire sample in that their synchronized response rates decreased systematically with increasing noise-burst rate. Across 204 units tested at both 2.5 and 5 bps in the same blocks of interleaved trials, maximum spikes per burst at stimulus rates of 10 bps averaged 45.5% of those at 5 bps. Further increases in stimulus rate, from 5–10 bps, consistently resulted in a more severe drop in spikes per burst. We do not characterize spatial tuning at 10 bps further because a relatively small number of units was studied in that condition and because many units did not respond reliably to the 10 bps stimulus rate.
Figure 1.
Single-source RAFs of three well isolated single units. Plotted are the rates of spikes per 5 ms sound burst averaged across 20 trials and 1 (first-burst condition) or 14 (synchronized conditions) bursts per trial. Error bars indicate SEM. Rates are plotted as a function of sound-source location in azimuth, which is expressed as degrees contralateral (C) or ipsilateral (I) relative to the recording sites in the right hemisphere. A, B, and C each correspond to one unit. Black lines indicate responses to the first burst in each sequence of 15 sound bursts, and green, gray, and magenta indicate responses synchronized to sound bursts at rates of 2.5, 5, and 10 bps, respectively. Units 1204.3.10 (A), 1204.5.8 (B), and 1202.2.26 (C).
The majority of units were like that in Figure 1A in showing “omnidirectional” azimuth sensitivity to single sound sources, meaning that they responded with ≥50% of their maximum spike rate for all tested sound locations. By that definition, omnidirectional tuning was seen in the first-burst responses of 73.7% of 810 units, and in the synchronized responses of 76.50% of 810 units tested at 2.5 bps and 68.6% of 557 units tested at 5 bps. The remainder of units was spatially tuned in that the spike rates were modulated ≥50% by sound-source location. Of the spatially tuned units, the most common spatial sensitivity was like that of the “contralateral hemifield” unit shown in Figure 1B in that responses were strong for most sound sources in the half of space contralateral to the recorded site, responses fell more or less sharply across source locations near the frontal midline, and responses were ≤50% of the maximum spike rates for ipsilateral locations; 12.6, 15.2, and 20.3% of all units showed hemifield tuning in their first-burst and 2.5 and 5 bps synchronized responses, respectively. A smaller number of units showed midline tuning, as in Figure 1C, or ipsilateral tuning (data not shown); midline and ipsilateral groups totaled 2.6, 1.9, and 4.5% of all units for the three response types. The remainder of units did not fit clearly into any of the listed classes.
Among the units that showed ≥50% modulation of their spike rates by stimulus location, preferred stimulus locations were given by “centroids” (see Materials and Methods). The majority of centroids were located near C 45°, which is approximately the location of the acoustic axis of the cat's contralateral pinna (Middlebrooks and Pettigrew, 1981): 67.0, 69.1, and 68.9% of centroids of first-burst, 2.5 and 5 bps responses, respectively, fell in the 45° segment of azimuth centered on C 45°. The distribution of centroids was biased somewhat away from peripheral locations in this study because we did not test sound-source locations behind the head; previous studies of area A1 that sampled 360° of azimuth have shown a sizeable population of units with centroids near C 90° (Harrington et al., 2008). If we set aside the requirement for 50% modulation of responses by source location and classify with 20° resolution the locations of RAF peaks of all units, 71.0–77.4% of RAFs peaked between C 80 and C 20°, 5.8–11.0% peaked at 0°, and 16.8–18.0% peaked between I 20 and I 80°. Across all units, steepest slopes of RAFs were distributed with a median at I 10° and interquartile range of C 10 to I 30°.
Spatial sensitivity typically varied little among first-burst and synchronized responses. We represented the breadth of spatial tuning by the widths of ERRFs (see Materials and Methods). Median ERRF widths for multiple units were 147.7, 150.9, and 148.7° for first-burst and 2.5 and 5 bps synchronized responses, respectively. Those differences were statistically significant (χ2(2,2174) = 12.3, p = 0.0022, Kruskal–Wallis) but, we think, of little practical importance. The depths of modulation of spike rates by stimulus location also showed small but statistically significant differences: medians were 36.0, 34.1, and 35.3% for first-burst and 2.5 and 5 bps synchronized responses, respectively (χ2(2,2174) = 8.4, p = 0.015). The differences in ERRF widths and modulation depths among first-burst and synchronized responses were not statistically significant for isolated single units (N = 182 isolated single units, first-burst and 2.5 bps synchronized responses; N = 118, 5 bps synchronized responses; p = 0.21 for ERRF widths and p = 0.30 for modulation depths).
An unexpected observation was that spatial sensitivity varied significantly with the CFs of units. Figure 2 shows distributions of ERRF widths (left column in each part) and of maximum single-source d′ as a function of CF in 1 oct bins; maximum single-source d′ is a measure of depth of modulation by sound-source location that accounts for trial-by-trial variance in responses (see Materials and Methods). ERRF widths were broadest and maximum d′ was weakest among units with CFs ∼2 kHz. Median maximum d′ for ∼16 kHz CFs was more than double that for ∼2 kHz CFs. Each of the conditions shown in the figure exhibited a significant dependence on CF (see Table 1). In Figure 2, asterisks mark the 1 oct CF bins that showed significantly stronger spatial sensitivity than the bin showing the weakest sensitivity in each condition (p < 0.05, Bonferroni corrected).
Table 1.
CF dependence of spatial tuning metrics
| Minimum Median | Maximum Median | N | Df | χ2 | p | |
|---|---|---|---|---|---|---|
| ERRF widths | ||||||
| Multiple units | ||||||
| First burst | 144 | 153.5 | 810 | 5,804 | 27.09 | =0.000055 |
| 2.5 bps | 146.1 | 158.3 | 810 | 5,804 | 109.11 | <0.000001 |
| 5 bps | 135.2 | 160.5 | 557 | 5,551 | 81.57 | <0.000001 |
| Single units | ||||||
| First burst | 138.7 | 142.2 | 182 | 5,176 | 0.44 | =0.99 |
| 2.5 bps | 135.9 | 148.5 | 182 | 5,176 | 15.64 | =0.0079 |
| 5 bps | 125.9 | 155.9 | 118 | 5,112 | 32.17 | =0.000006 |
| Maximum d′ | ||||||
| Multiple units | ||||||
| 2.5 bps | 0.8 | 2.07 | 810 | 5,804 | 156.07 | <0.000001 |
| 5 bps | 0.98 | 2.33 | 563 | 5,557 | 68.16 | <0.000001 |
| Single units | ||||||
| 2.5 bps | 0.93 | 1.72 | 182 | 5,176 | 22.88 | =0.00036 |
| 5 bps | 1.01 | 2.14 | 120 | 5,114 | 19.74 | =0.0014 |
Single neurons segregated competing sound sequences
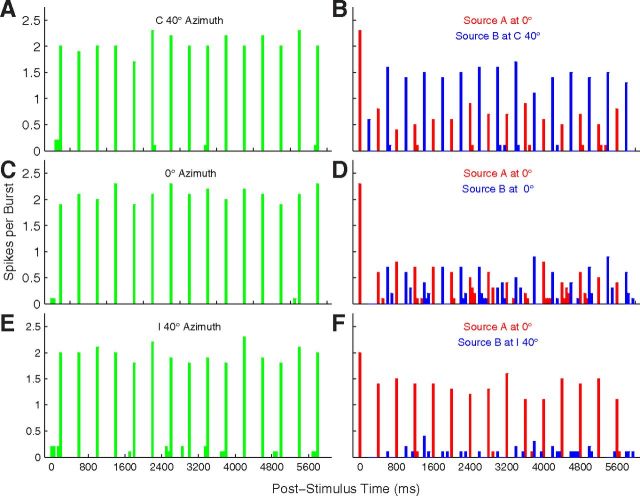
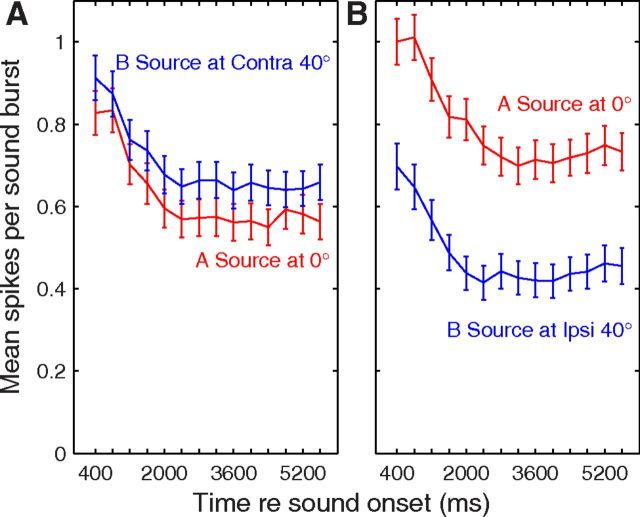
When presented with sound bursts alternating from two locations, neurons tended to synchronize preferentially to sounds from one or the other location. We tested the pattern ABABAB…, where A and B represent sound bursts from differing source locations. Poststimulus time histograms (PSTHs) from an isolated single unit in response to such stimuli are shown in Figure 3; this is the omnidirectional unit also shown in Figure 1A. The “base rate” in this example was 5 bps, referring to the aggregate of A and B rates. Figure 3, A, C, and E, shows conditions in which B was presented in the absence of A; this is equivalent to the 2.5 bps single-source condition. The unit synchronized reliably to all of these stimuli, with nearly all the spikes falling within the 50 ms time bin after the onset of each sound burst. The single-source conditions showed little difference among responses to sources located at C 40° (Fig. 3A), 0° (Fig. 3C), or I 40° (Fig. 3E). The competing sound-source condition is represented in Figure 3, B, D, and F. When an A source was added at 0° (Fig. 3D), the unit responded reliably only to the first sound burst, showing much weaker responses to subsequent A (responses coded by red) or B (blue) bursts. That condition, with A and B colocated, is equivalent to the 5 bps single-source condition. A shift of the B source to I 40° (Fig. 3F) resulted in nearly complete capture of the response of the unit by the A source. Conversely, a shift of the B source to C 40° (Fig. 3B) resulted in robust responses synchronized to the B source, with the response to A approximately equal to that in the colocated 0° condition.
Figure 3.
PSTH of a well isolated single unit. This is the unit represented in Figure 1A. Plotted are responses to sound sequences from a single-source location (left column) or to competing sequences from two locations (right). Responses are spikes per sound burst in 50 ms bins, averaged over 20 trials. In the left column, the sound source was located at C 40° (Fig. 3A), 0° (Fig. 3C), and I 40° (Fig. 3E). In the right column, colors indicate spike rates synchronized to the A source (red) or B source (blue). In all cases, the A source was fixed at 0°, whereas the location of the B source varied from C 40° (Fig. 3B), to 0° (Fig. 3D), to I 40° (Fig. 3F). Unit 1204.3.10.
Neurons generally responded with highest probability to the first noise burst in a sequence, regardless of whether the first burst came from the A or B source, and often showed suppression of the response to the second burst, as is seen in Figure 3D. For that reason, our analysis omitted responses to the first burst in each 15 burst A and B sequence. There was some concern that capture of the response of a neuron by A or B might be biased toward the first in an alternating sequence. For that reason, we tested each unit with an equal number of sequences in which an A or B sound burst was presented first. Comparison of the magnitude of d′ for discrimination of spike counts synchronized to A or B, across all units and across six pairs of A and B locations separated by 20°, demonstrated no significant difference between A- and B-leading conditions (5 bps: t(5489) = 1.24, p = 0.21, N = 915 units × 6 A and B locations; 10 bps: t(4019) = 1.38, p = 0.17, N = 670 × 6, paired t tests). For that reason, we combined data from A- and B-leading conditions for all subsequent analysis.
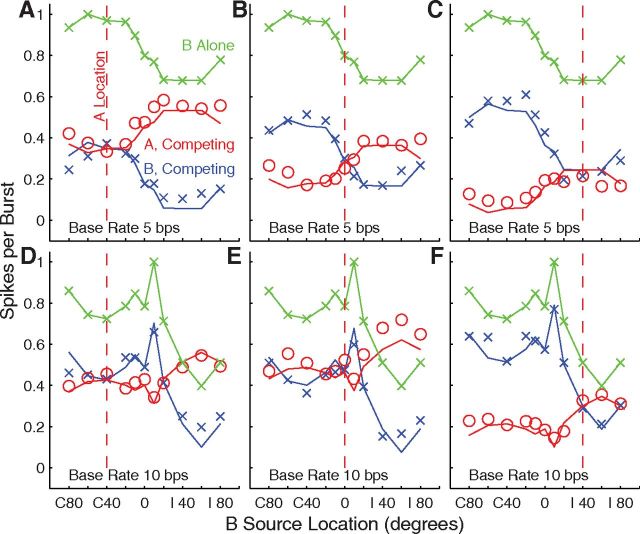
Synchronized spike counts from the same unit as in Figure 3 are quantified for a full range of A and B locations in the left column in Figure 4. Figure 4C shows the same condition as in Figure 3, with source A fixed at 0°, and Figure 4, A and E, show conditions with A fixed at C 40° and I 40°, respectively; in each part, the abscissa indicates the B-source location and the vertical dashed red line indicates the A-source location. As seen in Figure 3, the sensitivity of this unit to the location of a single sound source (green and black lines, redrawn in Fig. 4A,C,E) was quite weak. In contrast, spikes synchronized to B (blue lines) or the fixed-location A (red lines) varied markedly with B location. For each A location, spike counts synchronized equally, and relatively weakly, to A and B when A and B were colocated. As A and B sources were moved apart, typically the response to one of the sources increased and the other decreased such that responses of the neuron segregated one or the other sound source from the competing source.
Figure 4.
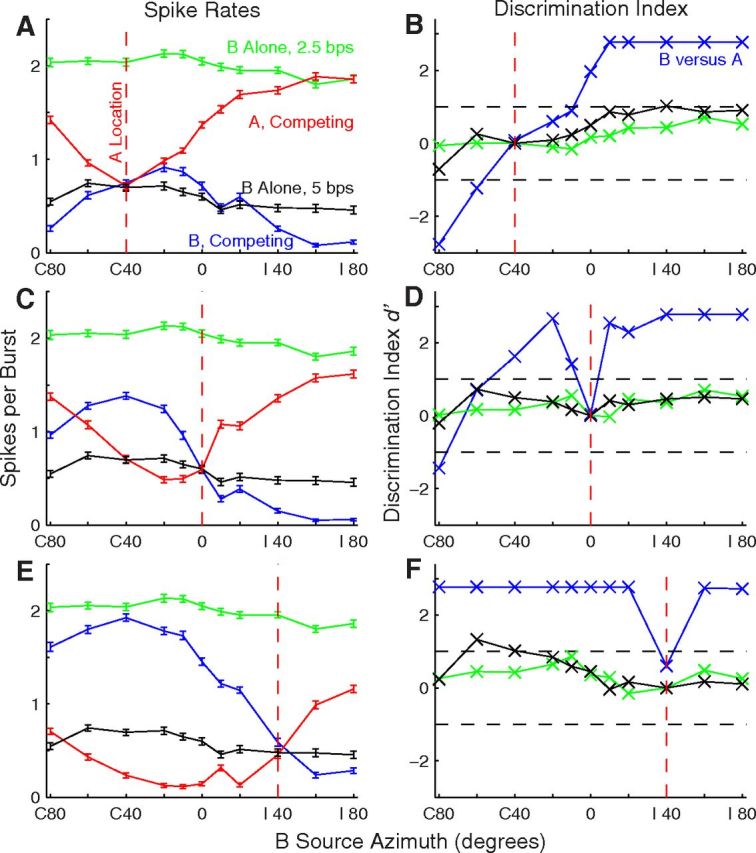
Stream segregation by an isolated single unit. This is the unit for which RAFs were shown in Figure 1A and PSTHs were shown in Figure 3. The left column (A, C, E) shows mean spike rates (with SEM) as a function of B-source location. Green and black indicate spike rates in Sync2.5 and Sync5 single-source conditions, respectively. Red and blue indicate responses synchronized to A and B sound sources, respectively, in competing-source conditions; the base rate was 5 bps. B-source locations were as plotted, whereas A sources were fixed at the locations indicated by the vertical dashed red lines. Variation in A responses reflects the effect of changing B-source locations. The right column (B, D, F) shows the d′ for discrimination of trial-by-trial spike rates elicited by A versus B sources (blue lines), or for discrimination of spike rates elicited from the plotted location versus those elicited in separate trials from the fixed location indicated by the vertical dashed red line; green and black indicate 2.5 and 5 bps single-source rates, respectively. Unit 1204.3.10.
We quantified with a discrimination index, d′, the accuracy with which spike counts discriminated between A and B sources (Fig. 4B,D,F). The blue line indicates discrimination between the more contralateral and ipsilateral sources. Many of the data points are at a ceiling of d′ = 2.77, indicating that the response to the more contralateral source on each of 20 trials was greater than any of the responses to the more ipsilateral source. We took d′ = ±1 (indicated by dashed lines) as the threshold for significant discrimination of A and B sources. In five of the six illustrated cases, significant source segregation was achieved at the minimum spatial separations that were tested (i.e., 10° around the midline or 20° around C or I 40°). The green and black lines show discrimination of single-source locations, where each data point represents discrimination of spike counts at the plotted location compared with counts on separate trials in which the single source was at the fixed A location (indicated with the vertical dashed red line). The magnitude of d′ in the single-source condition was ≤1 for nearly all of the single-source locations.
Responses of another isolated single unit are shown in Figure 5; this is the hemifield unit shown in Figure 1B. In this example, responses of the unit in the single-source conditions (green and black lines) showed a clear preference for contralateral source locations. In the competing-sound conditions, the spatial sensitivity of B responses (blue) largely paralleled the 2.5 bps single-source responses (green). Again, the d′ plots (right column) showed significant discrimination of responses to A and B for most nonzero A/B separations. In this example, the magnitudes of d′ for single-source location discrimination (green and black lines) approached the d′ magnitude for A/B discrimination (blue line).
Figure 5.
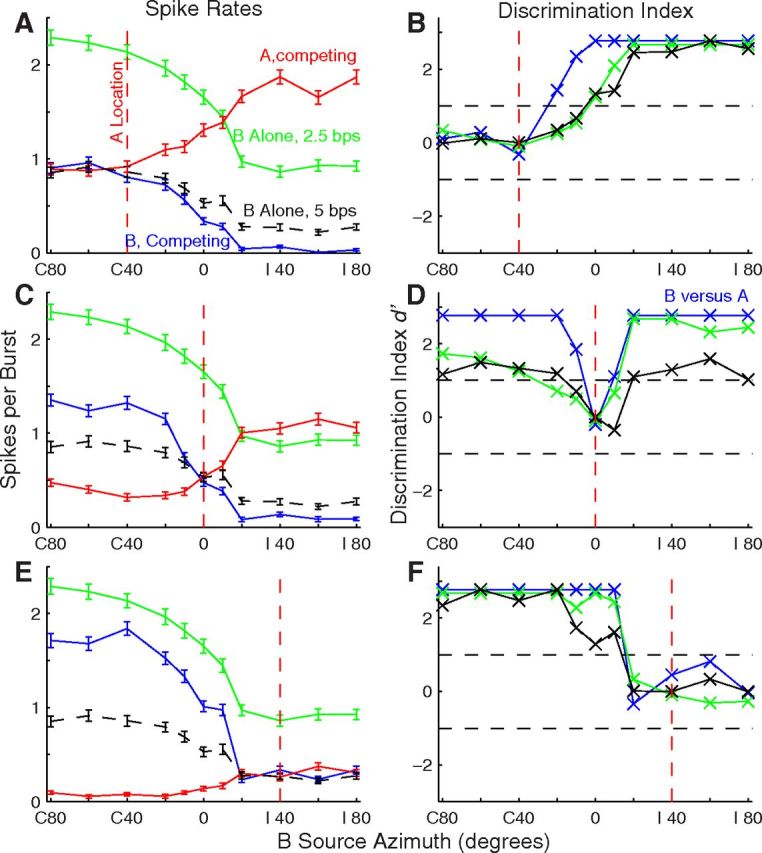
Stream segregation by an isolated single unit. This is the unit shown in Figure 1B. All conventions as in Figure 4. Unit 1204.5.8.
As noted above, neurons typically responded strongly to the first burst in each sound sequence and then showed a depressed response to the second burst. Typically, after the first pair of sound bursts, spike rates showed an additional adaptation over the next ∼2 s followed by fairly constant spike rates over the remainder of the sequence. Average spike rates per sound burst for 205 well isolated units are shown in Figure 6 for two pairs of A- and B-source locations; responses to the 2nd through 15th bursts in sequences from A and B sources are shown. Responses to A and B sources tended to adapt in parallel, so there was little or no consistent change in discrimination of A and B responses. We computed d′ for discrimination of A and B sources for sliding 1600 ms poststimulus-onset time windows and took the averages across the 206 units. Only 3 of 30 A/B-source location pairs (excluding A = B conditions) showed slight but significant post onset-time dependence (p < 0.05 after Bonferroni correction); those consisted of a decrease in d′ in one case and an increase followed by decrease in two other cases.
Figure 6.
Spike rates synchronized to the 2nd through 15th bursts from A (red lines) and B (blue) sources as a function of time after onsets of competing sound sequences. Plotted are mean and SEM averaged over 206 well isolated single units. A and B burst times are shown as temporally coincident, although in reality B bursts led and lagged A bursts by 200 ms an equal number of times. The A source was fixed at 0°, and the B source was at C 40° (A) or I 40° (B).
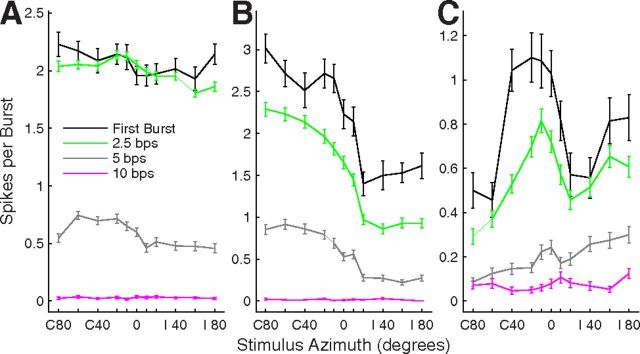
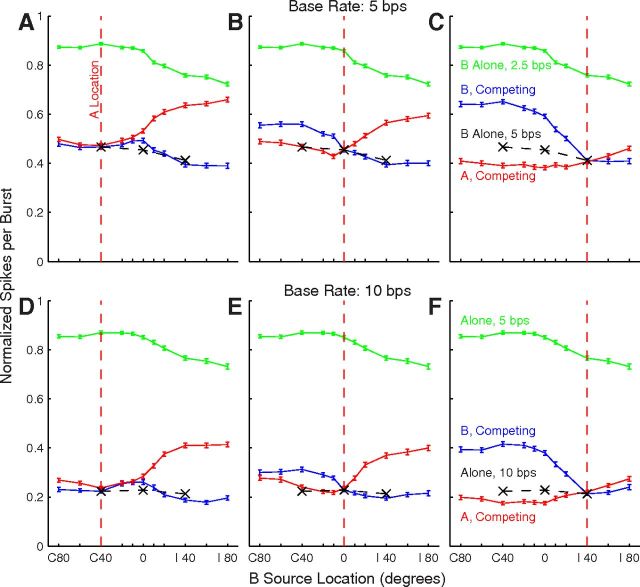
The normalized responses of all the tested units are summarized as grand-mean spike rates in Figure 7, with line colors representing rates synchronized to single sources (green) and to competing A (red) and B (blue) sources. Grand means are shown for three A-source locations (columns) and base rates of 5 and 10 bps (rows). The three black Xs in each plot indicate the grand means in conditions in which A and B sources were colocated, equivalent to the single-source condition at double the burst rate represented by the green line. The single-source mean data showed a weak contralateral preference, but indicate that there would be a sizable response of most units for any source throughout the tested (frontal) half of space. In the competing-source condition with the A source at 0° (Fig. 7B,E) shifts of the B source into the ipsilateral or contralateral hemifield resulted in varying degrees of capture of the grand-mean response by A or B, respectively. When the A source was at C 40° (Fig. 7A,D) or I 40° (Fig. 7C,F), B locations closer to the midline and into the opposite hemifield generally resulted in greater differences in synchrony to A or B than did B locations more peripheral than the A source. The difference in synchrony between A and B for any particular pair of source locations was approximately equal between the 5 and 10 bps base-rate condition when expressed as normalized spikes per burst. The overall spike counts were lower for the 10 bps rate; however, so the proportional differences between spike counts synchronized to A and B generally were greater at the 10 bps rate. These grand means of spike counts suggests that spatial acuity, in the sense of the spatial dependence of the difference in neural synchrony to A versus B, was greater around A locations at midline or ipsilateral locations than for contralateral A sources. These qualitative observations are explored quantitatively below. Also, we note that the grand means combine data across discrete neural populations having differing spatial preferences, which we consider below.
Figure 7.
Grand means of spike rates of 716 (top) or 402 (bottom) units. Plotted are grand-mean response rates (with SEM) for responses to single sources (green), and for responses synchronized to the A (red) or B (blue) source. Black Xs indicates spike counts in conditions in which A and B sources were colocated. The single-source and B-source locations were as plotted on the abscissae, whereas the A sources were fixed at the locations indicated by the vertical red lines: C 40 (A, D), 0 (B, E), and I 40 (C, F). Data from each unit were normalized before averaging according to the peak of each unit's single-source RAF. The peak value of the green line is <1 because the peaks of individual RAFs were not all mutually aligned.
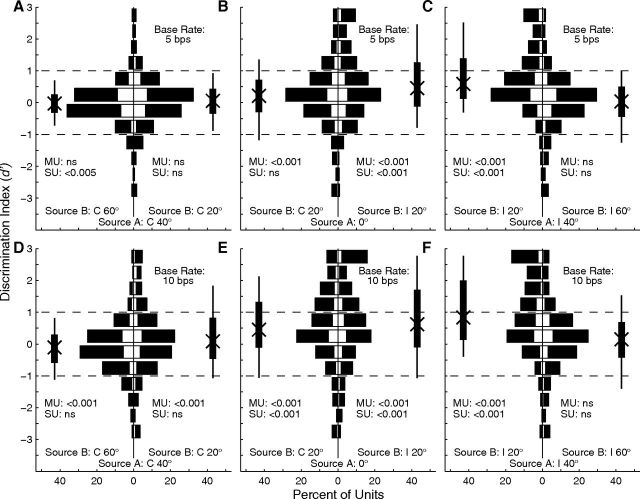
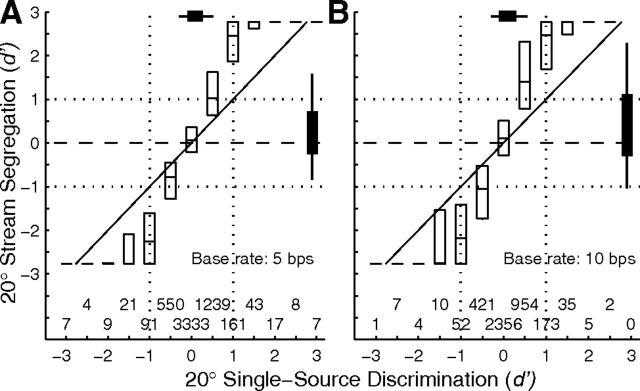
Spatial segregation for various A locations and base rates was quantified by computing the d′ for discrimination of trial-by-trial spike counts synchronized to A or B sources that were separated by 20°. Each part of Figure 8 contains two histograms representing one combination of A location (C 40, 0, or I 40°) and base rate. Bars extending to the left or right represent the distribution of d′ for B locations 20° contralateral or ipsilateral to the target, respectively; open portions of each bar represent isolated single units and filled portions represent multiple units. Positive values of d′ indicate that that unit synchronized more strongly to the more contralateral of A and B sources. The Xs, thick vertical lines, and thin vertical lines indicate the medians, interquartile ranges, and 10th to 90th percentile ranges of each distribution, respectively. Stream segregation generally was strongest around locations on the midline or in the ipsilateral hemifield (Fig. 8B,C,E,F). Specifically, >25% of units showed significant stream segregation (i.e., d′ ≥ 1) for all four of the configurations in which A and B sources both were in the range 0° to I 40°.
Figure 8.
Distributions of d′ for discrimination of A and B sources. Left (A, D), middle (B, E), and right (C, F) columns correspond to A sources at C 40°, 0°, and I 40°, respectively. Rows represent 5 bps (top) and 10 bps (bottom) base rates. Each part shows two histograms. Bars extending to the left indicate d′ for discrimination of the A source at the stated location from the B source located 20° to the left of (i.e., contralateral to) the source, and bars extending to the right indicate d′ for discrimination from B sources located 20° to the right of the source. Positive values of d′ represent greater spike rates elicited by the more contralateral source. Open and filled portions of bars indicate single and multiple units, respectively. Vertical thick and thin lines indicate interquartile ranges and 10th to 90th percentile ranges, respectively. The Xs on those lines indicate medians. The p values written in each half of each part indicate results of a t test for a mean different from 0, corrected for multiple comparisons (Bonferroni); MU and SU indicate statistics from multiple- and single-unit recordings.
Qualitative impressions from the grand mean (Fig. 7) and from the d′ histograms in Figure 8 were confirmed by an ANOVA on the magnitude (i.e., absolute value) of d′ for every combination of 5 or 10 bps base rate and B-source location 20° to the left or right of A sources at C 40°, 0°, and I 40°. There were significant main effects of base rate (multiple units: F(1,9503) = 117.1, p < 10−6; isolated single units: F(1,2045) = 25.6, p < 10−6) and A/B location (multiple units: F(5,9503) = 135.5, p < 10−6; isolated single units: F(5,2045) = 19.4, p < 10−6). Spatial stream segregation was stronger for the 10 bps than for the 5 bps base rate: across all the 20° A-B separations that were tested, magnitudes of d′ averaged 0.84 d′ units for the 5 bps base rate and 0.93 d′ units for the 10 bps rate. Comparison of various pairs of A/B locations demonstrated that d′ magnitudes were significantly greater for configurations involving locations within 40° ipsilateral of the midline (i.e., A at 0°, B at I 20° and A at I 40°, B at I 20°) than for any other A/B combinations. In contrast, d′ magnitudes were significantly lower than any others when both A and B were in the contralateral hemifield (i.e., A at C 40°, B at C 60° and A at C 40°, B at C 20°) or both were far in the ipsilateral hemifield (i.e., A at I 40°, B at I 60°). All significant pairwise comparisons showed p < 0.001 after Bonferroni correction.
The distributions of signed values of d′ in Figure 8 were significantly biased away from a mean of 0 in 8 of 12 A/B/base-rate configurations (for multiple units; 6/12 for single units); the p values for multiple units and single units are given in the panels (t tests with Bonferroni corrections). The positive biases indicated higher spike counts synchronized to the more contralateral sound source. Despite the general contralateral bias, there also were sizeable populations of units in most conditions that synchronized significantly to the more ipsilateral sound. In 6 of the 12 conditions shown in Figure 8, both the thin vertical lines representing the 10th and 90th percentiles intersect the d′ = 1 or −1 lines. That means that for those six conditions, >10% of the units synchronized significantly to sounds from one source while a different >10% synchronized to the competing sound.
The accuracy of spatial stream segregation by cortical units tended to increase with units' CFs (Fig. 9). We evaluated d′ for discrimination of neural synchrony to A versus B sources and, for each unit, identified the greatest d′ magnitude across all A/B separations of 20° in 20° increments from contralateral to ipsilateral 60°. The CF dependence was more conspicuous for the 5 bps base rate (Fig. 9A) than the 10 bps rate (Fig. 9B), but both base rates showed a significant dependence of d′ on CF: for 5 bps, χ2(5,909) = 145.0, p < 10−6; for 10 bps, χ2(5,664) = 16.8, p = 0.0049 (Kruskal–Wallis). Asterisks indicated the CF bins in which the median d′ was significantly higher than that in the 0.5 kHz CF bin (p < 0.05, pairwise comparison). For this 20° spatial-stream-segregation measure at the 5 bps rate, d′ averaged 1.1 among units with CFs ≤ 2 kHz, whereas d′ averaged 1.8 among units having CFs ≥ 4 kHz. A two-way ANOVA demonstrated significant main effects of CF (F(5,1578) = 24.2, p < 10−6) and of base rate (F(1,1578) = 78.8, p < 10−6).
Spatial tuning sharpened in competing-sound conditions
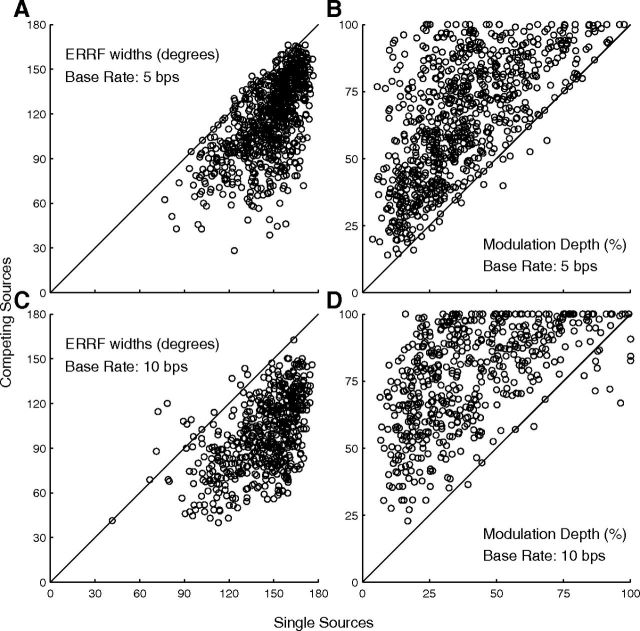
Addition of a competing source sharpened markedly the spatial tuning of units. Individual examples can be seen in Figures 4 and 5 by comparison of B-source RAFs (blue lines) with single-source RAFs (green lines), and summary data are plotted in Figure 10. Breadth of spatial tuning, represented by median ERRF widths, narrowed by approximately a third in some conditions (150.9 to 118.9° at 5 bps, Fig. 10A; 148.7 to 98.6 at 10 bps, Fig. 10C), and the depth of modulation by changes in B-source location could nearly double (34.1 to 53.2% at 5 bps, Fig. 10B; 35.3–68.9% at 10 bps, Fig. 10D). Comparisons of median ERRF widths and modulation depths across conditions of single source and competing A source at C 40, 0, and I 40° showed significant sharpening in every condition of single- and multiple-unit recording and 5 and 10 bps base rates (Friedman test: χ2 = 166.7–1025.11 depending on condition, p < 10−6, all conditions).
Figure 10.
Spatial-tuning metrics for single-source (horizontal axis) and competing-source (vertical axis) conditions. Left and right columns show ERRF widths and modulation depths, respectively, and top and bottom rows correspond to base rates of 5 and 10 bps, respectively. ERRF widths below or modulation depths above the diagonal lines indicate sharper spatial tuning in the presence of a competing sound. N = 810 single and multiple units tested at 5 bps and N = 556 tested at 10 bps.
Addition of a competing source also sharpened discrimination of pairs of source locations. We computed d′ for discrimination of various pairs of A- and B-source locations (i.e., A at C 40, 0, and I 40°; B at all other locations), and then interpolated to find the threshold source separation at which d′ ≥ 1. In single-source conditions (i.e., comparison of spike rates synchronized to sounds from two sources tested independently), the median discrimination thresholds were 115.5° at the 5 bps base rate (i.e., a single-source rate of 2.5 bps) and 49.6° at the 10 bps base rate. In contrast, median thresholds for discrimination of sources of interleaved A and B sources were 23.1 and 12.1° at base rates of 5 and 10 bps, respectively. The differences between single- and competing-source thresholds were significant (multiple units: N = 809 and 550 for 5 and 10 bps rates, respectively, p < 10−6 for both rates; single units: N = 181, p = 0.0080 for 5 bps, N = 117, p < 10−6 for 10 bps; signed rank test). Figure 11 plots d′ for discrimination of spike counts in the competing-source compared with the single-source condition at base rates of 5 and 10 bps (Fig. 11A,B, respectively); these data represent all combinations of A source at C40°, 0°, or I40°, with B positioned 20° to the left or right of the signal (i.e., six A-B configurations per neuron). The competing-source values consistently were greater in magnitude than the single-source data. The best-fitting regression line through the 5 bps data had a slope of 1.99, and intercept of 0.081 (r2 = 0.68, p < 10−6), meaning that d′ in the competing-source condition was approximately twice that in the single-source condition. At 10 bps, the results were slope = 2.34, intercept = 0.15, r2 = 0.59, and p < 10−6. The data in Figure 11 tended to fall in the upper right and lower left quadrants, meaning that, despite the generally lower spatial sensitivity in the single-source condition, the single-source tuning tended to predict whether source A or B would capture the response of the neuron.
Figure 11.
Comparison of d′ for discrimination of two competing sounds separated by 20° (vertical axis) versus d′ for discrimination of two single sources with the same separation (horizontal axis). A, B, Represent 5 and 10 bps base rates. Single-source data are binned in half-d′ intervals. The two staggered rows of numbers above the abscissa indicate the number of d′ values in each bin. Each unit is represented by 6 d′ values, for B sources 20° to the left and right of A sources at C 40°, 0°, and I 40°. N = 915 units (i.e., 5490 comparisons) at 5 bps and 670 units (4020 comparisons) at 10 bps. Boxes represent medians and interquartile ranges. Median lines without boxes drawn at vertical positions ±2.77 indicate instances in which >75% of the distribution was at d′ = 2.77 or d′ = −2.77. Note that ±2.77 single-source values fall in the ±3-d′ bins.
Neurons showing differing spatial sensitivity tended to occupy discrete cortical modules
We often encountered sequences of units at multiple sequential recording sites that showed similar spatial sensitivity, such as all omnidirectional or all contralateral hemifield tuning in the case of sensitivity to single-source locations or all preferring source A or all preferring B in competing-source conditions. This is suggestive of a columnar or modular distribution of units having particular patterns of spatial sensitivity. We examined 810 units along 38 multisite probe placements in the condition of responses synchronized to a single 2.5 bps source. We tallied the number of times that units at two adjacent sites separated by 100 or 150 μm both showed contralateral hemifield tuning; 12.3% of those 810 units showed contralateral hemifield tuning. Of 772 pairs of sites, 65 pairs (8.4% of pairs) showed matching hemifield tuning, substantially larger than the expectation of 1.5% of pairs based on a 12.3% occurrence of contralateral hemifield units randomly distributed. Along the 38 recording-probe placements, there were 13 runs of 3–24 consecutive hemifield units including 3 runs of 11 or more units spanning 1200–3000 μm. A permutation test (see Materials and Methods) demonstrated significant nonrandom distribution at the level of p < 10−5.
Preference of units for the A or B sound source also showed a nonrandom distribution along recording tracks. We tested for runs of units that all showed the same A- or B-source preference (“equal-preference runs”). We limited the analysis to units for which the magnitude of d′ was ≥1 for segregation of sources separated by 20°. Of 915 total units, 105–342 units had d′ magnitudes ≥1, depending on A and B locations covering C 60° to I 60° in 20° steps. Full statistics are given for the configuration of the B source at C 20° and A source at 0°, which had a relatively balanced number of A- and B-preferring qualifying units: 60.2% of 259 qualifying units had d′ ≥ 1 and 39.8% had d′ ≤ −1. On 34 probe placements having two or more qualifying units, 89.3% of 225 pairs of qualifying units had both units in the pair favoring the same sound source. That is substantially more than the expectation of ∼52% based on an assumption of a random distribution of the same number of A- and B-preferring units. Median lengths of equal-preference runs were 1650 μm (interquartile ranges: 638–2250 μm). In each source configuration (i.e., each of the six pairs of A- and B-source locations at base rates of 5 and 10 bps), the permutation test demonstrated a probability <10−5 that that many unit pairs with matching preference could have arisen by chance.
We tested whether response-specific sequences of units extended beyond cortical iso-frequency columns by examining the ranges of CFs corresponding to runs of constant A- or B-source preference. Permutation analyses that were limited to 10–20 probe placements spanning CF ranges <0.34 oct (i.e., presumably along a vertical cortical column) or to 3–11 probe placements spanning CF ranges >1 oct (presumably crossing columns) both yielded more equal-preference pairs of units than would be predicted by chance (p < 10−5). The ranges of CFs that were encountered depended on the orientation of recording probes, and therefore are not random samples, but it is noteworthy that 7 of 35 equal-preference runs having two or more units with magnitudes of d′ ≥ 1 spanned CF ranges of 1.7–3.5 oct.
A linear model of spatial stream segregation by A1 neurons
Plots of the spatial sensitivity of B spike counts typically resembled vertically shifted copies of the single-source spatial sensitivity (i.e., source-B RAFs tended to lie parallel to single-source RAFs), and plots of A spatial sensitivity as a function of B-source location (source-A RAFs) resembled inverted, scaled, and vertically shifted single-source RAFs. That can be seen in the examples of the hemifield unit in Figure 5, in the grand mean shown in Figure 7, and to a lesser degree in the example of an omnidirectional unit in Figure 4. In this section, we explore the hypothesis that spike counts synchronized to the A and B sound sequences could be predicted by a linear model based on the spatial sensitivity for single sources combined with a term that represented the amount of attenuation of responses by addition of a competing sound source.
We began by testing the hypothesis that the spatial sensitivity of spike counts in competing-source conditions tended to lie parallel to that of single-source spike counts. For each unit, we computed the regression of the B-source RAF as a function of the single-source RAF. For the 5 bps base rate, the median slope of the regression was 0.90, and the interquartile range was 0.54–1.28 (N = 719 units), which encompassed the expected slope of 1.0. The goodness of fit, represented by r2, averaged 0.58. For the 10 bps base rate, corresponding percentiles of the slope distribution were 0.26, 0.66, and 1.14, and the r2 averaged 0.48 (N = 402). We interpret these generally good fits as confirmation that, for most units, the spatial sensitivity of responses to competing noise bursts resembles downward-shifted versions of the single-source spatial sensitivity. We emphasize that by “downward shift” we mean subtraction of a constant from spike rates, not scaling by a constant. Scaling by a constant <1 would have reduced the maximum values of B RAFs relative to single-source RAFs, which we did see: maximum values of B RAFs when A sources were fixed at C 40, 0, and I 40° were 62, 67, and 75%, respectively, of the maxima of single-source RAFs. Scaling by a constant, however, also would have decreased the difference between maximum and minimum values in each B RAF relative to the maximum-minus-minimum differences in the single-source RAF, which we did not see: the maximum-minus-minimum differences of BRAFs when A sources were fixed at C 40, 0, and I 40° actually increased, to 104, 114, and 130%, respectively, of the maximum-minus-minimum differences in single-source RAFs.
We attempted to predict spike counts synchronized to A and B sources in the competing-source condition based on a linear combination of the single-source response at A and B locations; the single-source RAF, in effect, was taken as a surrogate for the spatial sensitivity of the inputs to the recorded A1 units. We estimated A and B responses in competing-source conditions as follows:
where RA and RB are the spike counts synchronized to A and B sources, respectively, as a function of A and B locations, θA and θB, RSgl(θ) is the spike count elicited by a single source at stimulus location θ, and Atten is an attenuation factor computed for each unit. The expressions state, essentially, that the predicted spike count synchronized to A (or B) is just the single-source spike count at the A (or B) location attenuated by a scalar times the single-source spike count at the location of the competing sound. We found the value of Atten for each unit by filling in the measured spike counts for the three A-B location conditions for which A and B were colocated (at −40, 0, and 40°), solving for Atten, and averaging Atten across the three conditions. Across just the 393 units that were tested with both 5 and 10 bps sound sequences, Atten was significantly greater at the 10 bps base rate (0.68 ± 0.16, mean ± SD) than at the 5 bps rate (0.42 ± 0.24); t(1,393) = 24.6, p < 10−6. Examples of the model fit are shown in Figure 12 for one unit tested at 5 bps (top row) and for another unit tested at 10 bps (bottom row). The goodness of fit of the model was assessed across the dataset by analysis of a regression on the model predictions of the empirical data. We restricted model testing to the units that showed significant stream segregation (i.e., a d′ magnitude ≥1 in the competing-sound conditions). For N = 382 units tested at 5 bps, r2 averaged 0.64 ± 0.25 (mean ± SD), the slope averaged 1.04 ± 0.62, and the intercept averaged −0.054 ± 0.33. Similarly, 295 units tested at 10 bps showing d′ magnitudes ≥1 yielded r2 = 0.46 ± 0.28, slope = 0.70 ± 0.52, and intercept = 0.059 ± 0.16. Overall, these results demonstrate rather satisfying predictions of neural responses by a simple parameter-free linear model.
Figure 12.
Model predictions of spike rates synchronized to A and B sources. Red and blue symbols indicate measured spike rates synchronized to A (red) and B (blue) sources in competing-source conditions. Red and blue lines indicate corresponding spike rates predicted from the linear model described in the text. The green line and symbols indicate the single-source RAF, which plots spike rates elicited by single sources at rates of 2.5 (A–C) or 5 (D–F) bps. Upper and lower rows represent responses of 2 units: unit 1204.5.22 tested at a base rate of 5 bps (upper row), and unit 1102.4.21 tested at a base rate of 10 bps. Columns represent conditions of A source at C 40° (left), 0° (middle), and I 40° (right).
We considered the possibility that the weaker spatial stream segregation seen among low-CF units (Fig. 9) might have resulted from CF-dependent differences in the strength of attenuation among those units. Within the unit population tested at both base rates, we compared attenuation for the 121 units with CF ≤ 2 kHz versus the 179 units with CF ≥ 4 kHz. Contrary to the hypothesis, there was no significant difference in attenuation between low- and high-CF groups at the 5 bps base rate (t = 1.66, df = 298, p = 0.10), and a slight but significant increase of attenuation in the lower CF group at the 10 bps rate (t = 2.35, df = 398, p = 0.019).
Little-to-no contribution of cortical post discharge adaptation to attenuation of responses to successive sounds
The attenuation observed in the competing-source conditions might have represented post discharge adaptation in which an action potential on one cortical neuron would reduce the probability of the same neuron firing in response to the next sound burst. Alternatively, some or all of the attenuation might have been due to some other form of forward suppression occurring in the auditory pathway previously than at the particular neurons from which we were recording. We tested the post discharge adaptation hypothesis using only recordings of well isolated single units (N = 205 at 5 bps and 137 at 10 bps). We studied only stimulus conditions in which A and B sources were colocated at −40°, 0°, or 40°, so that A and B sound bursts were equivalent. Further, we limited analysis to individual trials in which the probability of one or more spikes elicited by any burst ranged from 0.25 to 0.75; trials having very low or very high spike probabilities tended to bias the estimates of contingent probabilities.
The cortical adaptation hypothesis predicts that the probability of one or more neural spikes in response to sound A, P(A), would be reduced by the presence of one or more spikes in response to preceding sound B, occurring with probability P(B); that is, the hypothesis predicts that the probability of a spike to A contingent on a preceding spike on B, P(A|B) would be lower than the probability of a spike on A contingent on no preceding spike on B, P(A|0). Contrary to that hypothesis, we found in the 5 bps condition that P(A|B) was (nonsignificantly) 2.9% higher than P(A|0) (F(1,840) = 0.016, p = 0.90, ANOVA). In contrast, there was some indication of weak but significant intracortical adaptation at 10 bps: P(A|B) was 9.0% lower than P(A|0): F(1,366) = 18.55, p = 0.000021. The greater intracortical adaptation in the 10 bps condition presumably reflects the shorter (100 ms) intervals between sound bursts at that rate.
Single neurons exhibit spatial rhythmic masking release comparable to that of human listeners
A recent human psychophysical study in our laboratory used a spatial “rhythmic masking release” procedure to quantify spatial stream segregation (Middlebrooks and Onsan, 2012). Listeners attempted to discriminate between two rhythms of noise bursts. Performance was at chance levels when the signal bursts were interleaved with bursts from a colocated masker, and criterion performance was achieved when the signal and masker were separated in azimuth by a median value of 8.1°. At signal-masker separations at or greater than the threshold, the listeners reported hearing two discrete streams. In the present study, we tested the responses of cortical units to similar rhythms and measured the accuracy with which a linear classifier could identify the (masked) rhythms on the basis of temporal patterns of spikes.
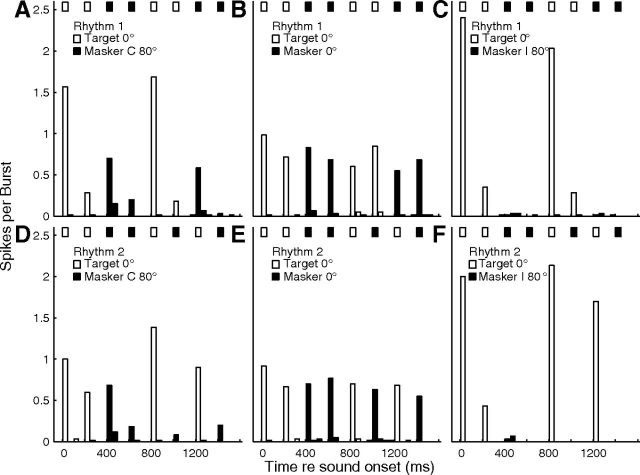
Examples of PSTHs from one well isolated single unit in response to Rhythm 1 (top row) and Rhythm 2 (bottom row) are shown in Figure 13. In this example, when the signal and masker were colocated at 0° (Fig. 13B,E), there was a fairly uniform response to signal and masker. When the masker was moved to the ipsilateral hemifield (Fig. 13C,F), however, there were reliable spike counts restricted to two signal time bins per rhythm (for Rhythm 1, Fig. 13C) or three (for Rhythm 2, Fig. 13F). The PSTHs compare well with the stimulus rhythms represented by the rows of boxes across the tops of each part. When the masker was in the contralateral hemifield (Fig. 13A,D), the responses to the masker increased somewhat, but the largest spike counts were those in two or three signal time bins per rhythm.
Figure 13.
Unit synchrony to rhythmic stimuli. Plotted are PSTHs for an isolated single unit in response to rhythmic masking-release stimuli (described in the text). Rows of bars at the top of each part indicate rhythms of signal (open) and masker (filled) noise bursts. Open and filled PSTH bars indicate spike rates synchronized to those bursts. The time axis is folded on the 1600 ms rhythm duration, so that each part represents the average across 20 trials × 3 repetitions of the rhythm per trial. Upper and lower rows represent Rhythms 1 and 2, respectively. The signal location was fixed at 0°. Columns represent conditions of masker locations as C 40° (left), 0° (middle), and I 40° (right). Unit 1204.3.25.
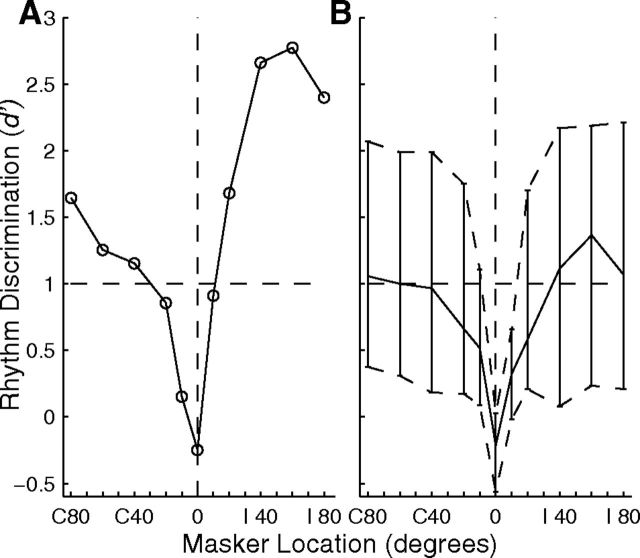
Hypothetically, if the responses of a unit could segregate signal from masker, a linear classifier should be able to discriminate the stimulus rhythms on the basis of spike counts elicited by various bursts. For each unit, we counted spikes in time bins corresponding to each of the noise bursts in each of 20 trials for each of the two rhythms. We conducted a multiple linear regression on spike counts in the eight time bins, solving for the coefficients that yielded outputs of 1 or 2, indicating the appropriate rhythm; details of the procedure and of the one-out cross validation are given in Materials and Methods. Values of d′ as a function of masker location are plotted in Figure 14A for the unit whose spike rhythms were shown in Figure 13. One can see the expected chance performance (i.e., d′ near 0) when signal and masker were colocated at 0° and performance rapidly improving with 10 or 20° shifts of the masker.
Figure 14.
Discrimination of rhythms by cortical units. The d′ indicates performance of a linear classifier in discriminating between two rhythms of sound bursts based on the responses of cortical units. The signal was fixed at 0°, and the masker location is plotted on the abscissae. A plots d′ from the same isolated single unit shown in Figure 13 (Unit 1204.3.25). B plots the distribution of d′ across 57 isolated single units. The contours show 25th, 50th, and 75th percentiles of the distributions.
The distributions of d′ for the rhythm discrimination for N = 57 isolated single units are shown in Figure 14B; the lines show the medians and interquartile ranges as a function of masker location. Between 25 and ∼50% of units exhibited performance better than a criterion of d′ = 1 for all signal-masker separations ≥20°. For each unit, we computed the interpolated threshold signal/masker separation at which d′ was ≥1. The median threshold across the 57 isolated units was 14.3°, and the 25th percentile was 8.5°, which is close to the median thresholds of 8.1° in our human psychophysical study (Middlebrooks and Onsan, 2012). Performance varied with the CFs of units. We found the greater of the d′ values measured for each unit for masker locations of C 20 and I 20°, and plotted the distribution of those values in 1 oct bins of CF (Fig. 15). Values of d′ varied significantly with CF (F(5,271) = 2.82, p = 0.017). Pairwise comparisons identified CF bins, marked with asterisks, showing significantly higher distributions of d′ than other CF bins (p < 0.05). As seen for other measures of spatial sensitivity and spatial stream segregation, spatial release from masking in this rhythm discrimination was best for the lowest and highest CFs.
Discussion
Under stimulus conditions in which human listeners hear sequences of sounds from spatially separated sources as segregated streams, single cortical neurons synchronized preferentially to sounds from one or the other of two sources. Of course, a neuron (or a listener) has no independent time reference by which to assess synchrony to a sound source. Neurons that synchronize to a common stimulus, however, necessarily synchronize with each other. The present results demonstrate that stimuli that are heard as segregated streams activate discrete mutually synchronized populations of neurons in A1.
A revised view of cortical spatial sensitivity
Previous studies of spatial sensitivity of cortical neurons have demonstrated spatial tuning that seems far too broad to account for psychophysical localization performance (for review, see King and Middlebrooks, 2011). Ensembles of 16 or more neurons are needed to approach behavioral levels of localization performance (Furukawa et al., 2000; Miller and Recanzone, 2009; Lee and Middlebrooks, 2013). In contrast, the competing-sound conditions in the present study yielded distributions of spatial acuity by single neurons (medians ∼6–10°) that overlapped those shown by human listeners in a spatial stream segregation task (median of 8.1°) (Middlebrooks and Onsan, 2012).
Neurons having similar spatial properties showed a conspicuous nonrandom distribution in the cortex. That accords with previous reports of columnar or banded organization of binaural or spatial sensitivity (Imig and Adrian, 1977; Middlebrooks and Pettigrew, 1981). The present results offer a picture of multiple cortical modules, spanning cortical layers and extending beyond cortical isofrequency columns, which comprise neurons responding specifically to one or another of multiple competing sound sources.
We observed for the first time a significant CF dependence of spatial sensitivity. Spatial acuity in all conditions of single and competing sources was sharpest among units having the highest CFs, declined to a minimum for units having CFs around ∼2 kHz, and in some tests improved significantly at even lower CFs. The CF dependence of spatial tuning likely was missed in previous studies because most (in the cat, at least) have tested only units with CFs ≥2 kHz (Harrington et al., 2008) or ≥5 kHz (Imig et al., 1990). Also, the CF dependence was rather weak in first-burst responses, which are most like the single bursts that have been studied previously. The CF dependence was greater in responses synchronized to 2.5 and 5 bps sequences and was obvious in competing-sound conditions.
Stream segregation and the auditory cortex
Previous intracortical studies have demonstrated stream segregation based on tonotopic differences (Fishman et al., 2001, 2004,2012; Micheyl et al., 2005). Analogous results have been obtained from the forebrain of the European starling (Bee and Klump, 2004; Bee et al., 2010). A number of human auditory-cortex studies using noninvasive methods have demonstrated stream segregation based on pure-tone frequencies or on the pitches of harmonic complexes (for review, see Micheyl et al., 2007). In particular, stream segregation based on interaural time differences (ITDs) has been demonstrated with both magnetoencephalography (MEG; Carl and Gutschalk, 2013) and functional magnetic imagery (Schadwinkel and Gutschalk, 2010). Because ITD is an important spatial cue, this could be taken as a demonstration of cortical spatial stream segregation.
The present results bear some similarity to observations of a neural correlate of stream segregation in the forebrain of a songbird (Maddox et al., 2012). A spike-distance classification scheme was used to discriminate neural responses to two conspecific songs in the presence of an energetic masker consisting of song-spectrum noise. As in the present study, spatial separation of signal and masker sources enhanced neural synchrony to the signal and, consequently, improved signal discrimination.
Stream segregation based on source location was prominent in the present single-unit recordings. Segregation generally was strongest when one of the sources was located in the ipsilateral hemifield. Analysis of single-source spatial sensitivity showed that the steepest slopes of RAFs of the majority of units also were located ipsilateral to the midline. Intuitively, one can see how discrimination of two interleaved sources would be greatest when the source locations straddle the most location-dependent portion of a response function. Conversely, discrimination tended to be weakest when both A and B sources were in the contralateral hemifield, where responses of most units tended to be uniformly strong, as shown by the grand-mean RAFs in Figure 7.
We presented (see Results) a quantitative model that accounted for around half of the stimulus-specific variance in neural responses. The model assumes that a neuron receives a (typically small) bias favoring one of the two sound sources and that the bias is amplified by forward suppression. For instance, a cortical neuron or its subcortical inputs might respond more strongly to a sound from the A source. That response would elicit forward suppression of the already weaker response to the subsequent B sound. The weak B response would elicit a relatively weak forward suppression of the subsequent A response, and so on, resulting in magnification of the difference in responses to A and B sources. Our quantitative model shares several features with qualitative “peripheral channeling” models of stream segregation by frequency or laterality, which posit that perceptually segregated streams correspond to partially nonoverlapping populations of neurons that are segregated by tonotopic locus and/or “ear of entry” (van Noorden, 1975; Hartmann and Johnson, 1991; Moore and Gockel, 2002). That channeling is thought to be amplified by forward suppression that occurs in the cortex itself (Fishman et al., 2001) and/or in subcortical pathways. In our case, peripheral channeling would be replaced by location sensitivity derived from binaural computations within the brainstem.
The forward suppression in our model was computed from the single-source spike rate at the location of the competing source multiplied by a measured neuron-specific scalar. The suppression was a uniform downward shift of the single-source RAF (i.e., a subtraction of spike rates). That had a disproportionately greater effect on low spike rates than on high rates, thereby increasing the ratio of maximum-to-minimum spike rates and increasing sharpness of tuning. Subtraction of spike rates contrasts with a scaling (or “gain control”) of RAFs, which would have scaled maximum and minimum rates proportionately, resulting in no change in proportional sharpness of tuning. Forward suppression observed at the cortex could reflect multiple subcortical and cortical components. The present results argue against a major contribution of one such component: post discharge adaptation of cortical neurons. That is, we found that the probability of a spike elicited by a given sound burst tone was independent of the occurrence of a cortical spike elicited by the preceding burst at the 5 bps base rate, and the probability was only weakly reduced at the 10 bps rate. Similarly, Calford and Semple (1995) and Brosch and Schreiner (1997) demonstrated cortical forward suppression having a duration comparable to the 100–200 ms interburst times in our study, and they showed that forward suppression could take place even when the masker did not elicit a cortical spike. Also, in a study of forward suppression in rat auditory cortex, Wehr and Zador (2005) found that inhibitory postsynaptic potentials elicited by maskers “rarely last longer than 50–100 ms,” indicating that forward suppression on a 100–200 ms timescale could not result from synaptic inhibition of those neurons. Those authors concluded that forward suppression in their system reflects synaptic depression and/or an inheritance from subcortical inputs.
Cortical neurons are limited in the rate at which they can synchronize to modulated waveforms. For instance, in anesthetized guinea pigs, cortical neurons phase lock to amplitude-modulated waveforms only up to ∼20 Hz compared with ∼100 Hz for neurons in the medial geniculate body (MGB; Creutzfeldt et al., 1980). That comparison demonstrates a low-pass modulation filter between MGB and A1, perhaps at the level of thalamocortical synapses. Our interpretation is that low-pass modulation filtering is an essential component of spatial stream segregation as we have seen it in the auditory cortex. For that reason, we would not expect to see spatial stream segregation in the MGB, at least not at the 5 and 10 bps rates that we have used in cortex and that produce perceptual streaming in humans. Moreover, a brief study of the inferior colliculus showed no evidence of spatial stream segregation at rates of 5–40 bps (Shackleton et al., 2012). Based on the available results, we hypothesize that spatial stream segregation arises first at the level of the auditory cortex, presumably reflecting a low-pass filter operation occurring at the level of thalamocortical synapses.
There is some evidence suggestive of tone-frequency-based stream segregation even at the level of the cochlear nucleus (Pressnitzer et al., 2008). In particular, segregation by frequency tended to build up over the course of up to 10 s. That contrasts with the absence of location-based stream segregation at the level of the inferior colliculus (Shackleton et al., 2012). The discrepancy in results might reflect a difference between streaming by frequency compared with streaming by location. In a recent human psychophysical study of spatial stream segregation (Middlebrooks and Onsan, 2012), there was little or no indication of “buildup” of streaming over time, aside from the benefits of listening to multiple repetitions of the test rhythms. Also, the cochlear-nucleus results might reflect differences in long-term neural adaptation between responses to on- and off-CF stimuli. In the present cortical study, we observed adaptation of response over the course of ∼2 s, but responses to favored and less favored locations adapted in parallel, resulting in no consistent change in location discrimination.
Bottom-up and top-down processes in stream segregation
The spatial stream segregation seen in the cortex in anesthetized conditions presumably is dominated by processing at subcortical and thalamocortical-synaptic levels of the auditory pathway. Similar bottom-up mechanisms likely underlie the psychophysical results in humans. Previous event-related potential studies in human have demonstrated the pre-attentive, bottom-up, nature of stream segregation, albeit in nonspatial tasks (Sussman et al., 1999; Nager et al., 2003).
What might be left for top-down processing in our simple spatial stream-segregation task? It appears that the ascending pathway does the work of segregating sounds from various sources within discrete cortical neural populations. Perhaps the contribution of top-down processing is to focus attention on the activity of one or another active cortical modules. A good listening strategy, for instance, would be to attend to cortical modules in the cortical hemisphere ipsilateral to a masker location, which the present results suggest would enhance signal/masker segregation and signal recognition. Examples of perceptual selection among multiple auditory objects are well known in psychophysics (Ihlefeld and Shinn-Cunningham, 2008) and MEG studies (Xiang et al., 2010). The present results suggest that “selection of auditory objects” corresponds to “selection of cortical modules.” We hope to explore that hypothesis in future experiments.
Footnotes
This work is supported by National Institute on Deafness and Other Communication Disorders Grant RO1 DC000420. We thank Elizabeth McGuire for technical support and Zekiye Onsan for help in making the illustrations. Chen-Chung Lee, Alana Kirby, Lauren Javier, and Justin Yao helped with data collection.
The authors declare no conflict of interest.
References
- Bee MA, Klump GM. Primitive auditory stream segregation: a neurophysiological study in the songbird forebrain. J Neurophysiol. 2004;92:1088–1104. doi: 10.1152/jn.00884.2003. [DOI] [PubMed] [Google Scholar]
- Bee MA, Micheyl C, Oxenham AJ, Klump GM. Neural adaptation to tone sequences in the songbird forebrain: patterns determinants, and relation to the build-up of auditory streaming. J Comp Physiol A Neuroethol Sens Neural Behav Physiol. 2010;196:543–557. doi: 10.1007/s00359-010-0542-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bregman AS. Auditory scene analysis: the perceptual organization of sound. Cambridge, MA: MIT; 1990. [Google Scholar]
- Brosch M, Schreiner CE. Time course of forward masking tuning curves in cat primary auditory cortex. J Neurophysiol. 1997;77:923–943. doi: 10.1152/jn.1997.77.2.923. [DOI] [PubMed] [Google Scholar]
- Calford MB, Semple MN. Monaural inhibition in cat auditory cortex. J Neurophysiol. 1995;73:1876–1891. doi: 10.1152/jn.1995.73.5.1876. [DOI] [PubMed] [Google Scholar]
- Carl D, Gutschalk A. Role of pattern, regularity, and silent intervals in auditory stream segregation based on interaural time differences. Exp Brain Res. 2013;224:557–570. doi: 10.1007/s00221-012-3333-z. [DOI] [PubMed] [Google Scholar]
- Cherry CE. Some experiments on the recognition of speech, with one and two ears. J Acoust Soc Am. 1953;25:975–979. doi: 10.1121/1.1907229. [DOI] [Google Scholar]
- Creutzfeldt O, Hellweg FC, Schreiner C. Thalamocortial transformations of responses to complex auditory stimuli. Exp Brain Res. 1980;39:87–104. doi: 10.1007/BF00237072. [DOI] [PubMed] [Google Scholar]
- Fishman YI, Arezzo JC, Steinschneider M. Auditory stream segregation in monkey auditory cortex: effects of frequency separation, presentation rate, and tone duration. J Acoust Soc Am. 2004;116:1656–1670. doi: 10.1121/1.1778903. [DOI] [PubMed] [Google Scholar]
- Fishman YI, Reser DD, Arezzo JC, Steinschneider M. Neural correlates of auditory stream segregation in primary auditory cortex of the awake monkey. Hear Res. 2001;151:167–187. doi: 10.1016/S0378-5955(00)00224-0. [DOI] [PubMed] [Google Scholar]
- Fishman YI, Micheyl C, Steinschneider M. Neural mechanisms of rhythmic masking release in monkey primary auditory cortex: implications for models of auditory scene analysis. J Neurophysiol. 2012;107:2366–2382. doi: 10.1152/jn.01010.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Furukawa S, Xu L, Middlebrooks JC. Coding of sound-source location by ensembles of cortical neurons. J Neurosci. 2000;20:1216–1228. doi: 10.1523/JNEUROSCI.20-03-01216.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Green DM, Swets JA. Signal detection theory and psychophysics. New York: Wiley; 1966. [Google Scholar]
- Harrington IA, Stecker GC, Macpherson EA, Middlebrooks JC. Spatial sensitivity of neurons in the anterior, posterior, and primary fields of cat auditory cortex. Hear Res. 2008;240:22–41. doi: 10.1016/j.heares.2008.02.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hartmann WM, Johnson D. Stream segregation and peripheral channeling. Music Percept. 1991;9:155–184. doi: 10.2307/40285527. [DOI] [Google Scholar]
- Ihlefeld A, Shinn-Cunningham B. Disentangling the effects of spatial cues on selection and formation of auditory objects. J Acoust Soc Am. 2008;124:2224–2235. doi: 10.1121/1.2973185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Imig TJ, Adrián HO. Binaural columns in the primary field (A1) of the cat auditory cortex. Brain Res. 1977;138:241–257. doi: 10.1016/0006-8993(77)90743-0. [DOI] [PubMed] [Google Scholar]
- Imig TJ, Irons WA, Samson FR. Single-unit selectivity to azimuthal direction and sound pressure level of noise bursts in cat high-frequency primary auditory cortex. J Neurophysiol. 1990;63:1448–1466. doi: 10.1152/jn.1990.63.6.1448. [DOI] [PubMed] [Google Scholar]
- Jenkins WM, Merzenich MM. Role of cat primary auditory cortex for sound-localization behavior. J Neurophysiol. 1984;52:819–847. doi: 10.1152/jn.1984.52.5.819. [DOI] [PubMed] [Google Scholar]
- King AJ, Middlebrooks JC. Cortical representation of auditory space. In: Winer J, Schreiner C, editors. The auditory cortex. New York: Springer; 2011. pp. 329–341. [Google Scholar]
- Lee CC, Middlebrooks JC. Auditory cortex spatial sensitivity sharpens during task performance. Nat Neurosci. 2011;14:108–114. doi: 10.1038/nn.2713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee CC, Middlebrooks JC. Specialization for sound localization in fields A1, DZ, and PAF of cat auditory cortex. JARO. 2013;14:61–82. doi: 10.1007/s10162-012-0357-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Macmillan NA, Creelman CD. Detection theory: a user's guide. Ed 2. Mahwah, NJ: Lawrence Erlbaum; 2005. [Google Scholar]
- Macmillan NA, Kaplan HL. Detection theory analysis of group data: estimating sensitivity from average hit and false-alarm rates. Psychol Bull. 1985;98:185–199. doi: 10.1037/0033-2909.98.1.185. [DOI] [PubMed] [Google Scholar]
- Maddox RK, Billimoria CP, Perrone BP, Shinn-Cunningham BG, Sen K. Competing sound sources reveal spatial effects in cortical processing. PLoS Biol. 2012;10:e1001319. doi: 10.1371/journal.pbio.1001319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malhotra S, Hall AJ, Lomber SG. Cortical control of sound localization in the cat: unilateral cooling deactivation of 19 cerebral areas. J Neurophysiol. 2004;92:1625–1643. doi: 10.1152/jn.01205.2003. [DOI] [PubMed] [Google Scholar]
- Merzenich MM, Knight PL, Roth GL. Representation of cochlea within primary auditory cortex in the cat. J Neurophysiol. 1975;38:231–249. doi: 10.1152/jn.1975.38.2.231. [DOI] [PubMed] [Google Scholar]
- Micheyl C, Tian B, Carlyon RP, Rauschecker JP. Perceptual organization of tone sequences in the auditory cortex of awake macaques. Neuron. 2005;48:139–148. doi: 10.1016/j.neuron.2005.08.039. [DOI] [PubMed] [Google Scholar]
- Micheyl C, Carlyon RP, Gutschalk A, Melcher JR, Oxenham AJ, Rauschecker JP, Tian B, Wilson E. The role of auditory cortex in the formation of auditory streams. Hear Res. 2007;229:116–131. doi: 10.1016/j.heares.2007.01.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Middlebrooks JC. Auditory cortex phase locking to amplitude-modulated cochlear-implant pulse trains. J Neurophysiol. 2008;100:76–91. doi: 10.1152/jn.01109.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Middlebrooks JC, Onsan ZA. Stream segregation with high spatial acuity. J Acoust Soc Am. 2012;132:3896–3911. doi: 10.1121/1.4764879. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Middlebrooks JC, Pettigrew JD. Functional classes of neurons in primary auditory cortex of the cat distinguished by sensitivity to sound location. J Neurosci. 1981;1:107–120. doi: 10.1523/JNEUROSCI.01-01-00107.1981. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Middlebrooks JC, Snyder RL. Auditory prosthesis with a penetrating nerve array. J Assoc Res Otolaryngol. 2007;8:258–279. doi: 10.1007/s10162-007-0070-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller LM, Recanzone GH. Populations of auditory cortical neurons can accurately encode acoustic space across stimulus intensity. Proc Natl Acad Sci U S A. 2009;106:5931–5935. doi: 10.1073/pnas.0901023106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moore BCJ, Gockel H. Factors influencing sequential stream segregation. Acta Acustica. 2002;88:320–332. [Google Scholar]
- Nager W, Teder-Sälejärvi W, Kunze S, Münte TF. Preattentive evaluation of multiple perceptual streams in human audition. Neuroreport. 2003;14:871–874. doi: 10.1097/00001756-200305060-00019. [DOI] [PubMed] [Google Scholar]
- Pressnitzer D, Sayles M, Micheyl C, Winter IM. Perceptual organization of sound begins in the auditory periphery. Curr Biol. 2008;18:1124–1128. doi: 10.1016/j.cub.2008.06.053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reale RA, Brugge JF. Directional sensitivity of neurons in the primary auditory (AI) cortex of the cat to successive sounds ordered in time and space. J Neurophysiol. 2000;84:435–450. doi: 10.1152/jn.2000.84.1.435. [DOI] [PubMed] [Google Scholar]
- Schadwinkel S, Gutschalk A. Activity associated with stream segregation in human auditory cortex is similar for spatial and pitch cues. Cereb Cortex. 2010;20:2863–2873. doi: 10.1093/cercor/bhq037. [DOI] [PubMed] [Google Scholar]
- Shackleton T, Middlebrooks J, Palmer A. Spatial position related adaptation in the inferior colliculus of anesthetized guinea pigs. Abs Assoc Res Otolaryngol. 2012:35. [Google Scholar]
- Sussman E, Ritter W, Vaughan HG., Jr An investigation of the auditory streaming effect using event-related brain potentials. Psycho Phys. 1999;36:22–34. doi: 10.1017/S0048577299971056. [DOI] [PubMed] [Google Scholar]
- van Noorden L. Eindhoven: University of Technology; 1975. Temporal coherence in the perception of tone sequences. PhD thesis. [Google Scholar]
- Wehr M, Zador AM. Synaptic mechanisms of forward suppression in rat auditory cortex. Neuron. 2005;47:437–445. doi: 10.1016/j.neuron.2005.06.009. [DOI] [PubMed] [Google Scholar]
- Xiang J, Simon J, Elhilali M. Competing streams at the cocktail party: exploring the mechanisms of attention and temporal integration. J Neurosci. 2010;30:12084–12093. doi: 10.1523/JNEUROSCI.0827-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou B, Green DM, Middlebrooks JC. Characterization of external ear impulse responses using Golay codes. J Acoust Soc Am. 1992;92:1169–1171. doi: 10.1121/1.404045. [DOI] [PubMed] [Google Scholar]