Heterogeneous Attractor Cell Assemblies for Motor Planning in Premotor Cortex

Abstract

Cognitive functions like motor planning rely on the concerted activity of multiple neuronal assemblies underlying still elusive computational strategies. During reaching tasks, we observed stereotyped sudden transitions (STs) between low and high multiunit activity of monkey dorsal premotor cortex (PMd) predicting forthcoming actions on a single-trial basis. Occurrence of STs was observed even when movement was delayed or successfully canceled after a stop signal, excluding a mere substrate of the motor execution. An attractor model accounts for upward STs and high-frequency modulations of field potentials, indicative of local synaptic reverberation. We found in vivo compelling evidence that motor plans in PMd emerge from the coactivation of such attractor modules, heterogeneous in the strength of local synaptic self-excitation. Modules with strong coupling early reacted with variable times to weak inputs, priming a chain reaction of both upward and downward STs in other modules. Such web of “flip-flops” rapidly converged to a stereotyped distributed representation of the motor program, as prescribed by the long-standing theory of associative networks.

Introduction

Motor planning relies on the concerted activity of distributed neuronal assemblies in different brain areas. Among them, dorsal premotor cortex (PMd) of primates is involved in building motor programs suitable for executing reaching movements (Weinrich and Wise, 1982; Wise, 1985; Crammond and Kalaska, 2000; Churchland et al., 2010b), after transformation of visuospatial information about target location into joint-angle changes and forces needed to reach those targets (Hoshi and Tanji, 2000; Wallis and Miller, 2003; Nakayama et al., 2008). PMd plays a role in selecting potential options (Ohbayashi et al., 2003; Wallis and Miller, 2003; Cisek and Kalaska, 2005), even when actions are observed but not performed (Cisek and Kalaska, 2004), and it is also involved in more abstract cognitive functions such as time coding (Lebedev et al., 2008; Genovesio et al., 2009), inhibitory control (Mattia et al., 2010, 2012; Mirabella et al., 2011), and set-related working memory (Ohbayashi et al., 2003; Cisek and Kalaska, 2005; Hernández et al., 2010). All these evidences clearly show that this area provides an ideal framework to study how information is integrated, transformed, and stored in cortical networks.

Theoretical descriptions of cortical computation in motor cortices have been proposed (Kalaska and Crammond, 1992; Georgopoulos et al., 1993; Houk and Wise, 1995; Erlhagen and Schöner, 2002; Cisek, 2006; Sussillo and Abbott, 2009; Churchland et al., 2010b), but a full understanding of neuronal mechanisms behind motor planning is still lacking. Reliable and stereotyped movements, needed to minimize errors or to compose frequently repeated motor patterns, require network dynamics capable to attract inner representations of ongoing actions to low-dimensional subspaces of suited collective variables (Schöner and Kelso, 1988; Shenoy et al., 2011). Supporting evidence of such attractor dynamics is accumulating, and both dimensional reductions of the explored state space and decreases of trial-by-trial variability of neural activities coding output behaviors have been reported in motor cortices (Abeles et al., 1995; Churchland et al., 2006a) and other frontal areas (Balaguer-Ballester et al., 2011). Nevertheless, more direct footprints of such nonlinear dynamics have proven to be elusive, leaving open issues like whether attractor behavior of recorded neural activity is the result of a local network activity or is the echo of a remote neuronal machinery (Ganguli et al., 2008).

Here we try to fill this gap investigating the cortical computation underpinning motor plan maturation in PMd. We report evidence about the existence of diverse degrees of meta-stable dynamics in local cell assemblies. They seem to be hierarchically organized in time as a web of heterogeneous cortical modules capable to produce fast transitions toward distributed and stereotyped representations of motor-related programs.

Materials and Methods

Task description and data acquisition.

We trained two male monkeys (Macaca mulatta) weighing 6–7 kg using general procedures described recently (Mirabella et al., 2011). Monkeys were trained to perform a reaching version of the stop-signal task (Fig. 1A, left; Logan and Cowan, 1984; Mirabella et al., 2006, 2011). On each trial, after a variable holding time (500–800 ms), cue disappeared (Go) and simultaneously a peripheral target appeared at one of two opposite positions with respect to the center (movement conditions). In No-stop trials, the monkey had to reach the target within a maximum allowed time [reaction time (RT) of 600 ms for one animal and 750 ms for the other one]. On a randomized fraction of trials (33%; Stop trials), central cue reappeared during RT, instructing the monkey to inhibit movement initiation. At least 480 trials were performed per countermanding block, equally separated for the movement condition. Stop signal delays (SSDs) varied randomly to allow the animals to inhibit about half of the Stop trials (Correct-stop trials), by adapting, accordingly, the average movement onset timing. No reward was delivered, and target disappeared, when the monkey started the movement despite the Stop signal (Wrong-stop trials). One of the two monkeys also performed a standard delayed reaching task (Fig. 1A right; Weinrich and Wise, 1982; Crammond and Kalaska, 2000), where Go signal occurred after a random delay (800–1600 ms) since the target appearance.

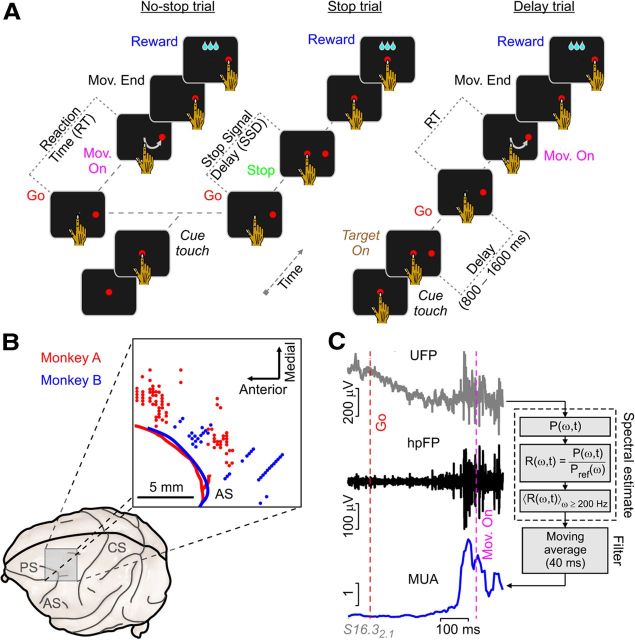
Figure 1.

Behavioral task, recording sites, and signal extraction. A, Temporal sequence of the visual displays and required motor behavior for stop-signal and delayed reaching tasks. Go, Cue disappearance; Mov. On, movement onset; Mov. End, movement end' (see Results for further details). B, Recording sites in the left PMd for the two monkeys magnified in the square (red, monkey A; blue, monkey B). AS, Arcuate sulcus; PS, principal sulcus; CS, central sulcus. C, UFPs (raw signal) were sampled at 24.4 kHz from intracortical recordings using arrays of seven platinum–tungsten electrodes. Left, A No-stop trial with UFP, high-pass filtered UFP (hpFP), and MUA for comparison. Right, Postprocessing steps to extract MUAs from high Fourier frequency spectrum P(ω,t) of UFPs on 5 ms sliding windows. MUA was the average relative spectrum R(ω,t) in a high-ω band ([0.2, 1.5] kHz), finally smoothed by a moving average (40 ms sliding window). The reference spectral density P_ref(ω) to obtain R(ω,t) was the average P(ω,t) during intertrial intervals.

Animals were cared for and housed in accordance with European guidelines (European Community Council Directive 86/609/ECC) and with Italian national law (DL 116/92) on the use of animals in research. At the start of the training period, a head-holding device was implanted on each monkey, and a scleral search coil was inserted subconjunctivally to monitor eye movements (Remmel Labs). The connector leads of the coil were embedded in a dental acrylic implant positioned to firmly anchor the head-holding device to the skull. After training, a chronic recording chamber (18 mm diameter) was stereotaxically implanted over the left frontal lobe centered around the arm representation in left PMd. There, a linear array of seven quartz-insulated platinum–tungsten electrodes (80 μm diameter; impedance, 0.8–2.5 MΩ) were inserted transdurally to acquire unfiltered electric field potential (UFP; the raw signal) simultaneously sampled at 24.4 kHz from each of the seven probes (Tucker Davis). The location of the neural recording sites (Fig. 1B) was confirmed by structural MRI on one monkey and by visual inspection of the anatomical landmarks on the second monkey after surgically opening the dura.

Data analysis.

Multiunit activity (MUA) was extracted by computing the time-varying power spectra P(ω,t) from the short-time Fourier transform of UFPs in 5 ms sliding windows. Relative spectra R(ω,t) were then obtained normalizing P(ω,t) by their average P_ref(ω) across the first 400 ms of the intertrial intervals. Our spectral estimated MUAs were the average R(ω,t) across the ω/2π band [0.2, 1.5] kHz (Fig. 1C), extending a previous approach based on the moving variance of high-pass filtered UFPs (Stark and Abeles, 2007). Our estimate relies on two hypotheses. The first one is that high-ω components of UFPs result from the convolution of firing rates ν(t) of neurons close to the electrode tip with a stereotyped single-unit waveform (Martinez et al., 2009; Miller et al., 2009; Rasch et al., 2009). R(ω,t) allows to eliminate the Fourier transform K(ω) of such unknown waveform, making R(ω,t) a good approximation of the ratio of firing rate spectra |ν(ω,t)|²/|ν_ref(ω)|². Second, high-ω power |ν(ω,t)|² is proportional to the firing rate ν(t) itself (Mattia and Del Giudice, 2002), such that our MUA estimate is proportional to ν(t). Logarithmically scaled MUAs were smoothed by a moving average (40 ms sliding window).

Recordings with task-related activity were those with a significant difference in average log(MUA) between the 50 ms before Go of reaching trials and either the interval 100–150 ms after Go (ν_down) or 50 ms before the movement onset (ν_up) (t test, p < 0.001). We looked for sharp upward transitions (SUTs) among task-related recordings showing a significant increase in activity during RT: ν_up > ν_down (t test, p < 0.001). SUT occurred at the first crossing time of a threshold MUA at 60% between ν_down and ν_up starting from 100 ms after target display. Only those crossings with MUA above threshold for >80 ms were considered. This allowed us to filter fast MUA fluctuations out, thereby reducing the rate of false positives in SUT detection below 2%. SUT times were refined by fitting the log(MUA) time course around the detection threshold with a cubic polynomial and carrying out its crossing time. SUT duration was the time needed to go from ν_down to ν_up assuming the slope resulting from a linear fit of average MUA around the SUT threshold.

Off-line analyses were implemented in MATLAB (The MathWorks).

Theory, models, and simulations.

We used both a minimal rate model and a neural network model of integrate-and-fire (IF) neurons. The minimal rate model had dynamics determined by the gain function Φ (Wilson and Cowan, 1972) as follows: τ dν/dt = Φ(ν,Δν_ext) − ν, with instantaneous firing rate ν(t) converging asymptotically to one of the fixed-points ν = Φ(ν,Δν_ext). A dependence on Δν_ext appeared explicitly since we were interested in the reaction of the model to external stimuli. We introduced intrinsic fluctuation by adding a finite-size correction to the firing rate (Mattia and Del Giudice, 2002) such that ν = ν_∞ + Γ(t) and τ dν_∞/dt = Φ(ν,Δν_ext) − ν_∞, where ν_∞ was the firing rate in the limit of an infinite number of neurons in the network, Γ(t) was a Gaussian white noise with zero mean and variance ν_∞η, and η was adjusted to reproduce time scales similar to those observed in our in vivo recordings. τ was an arbitrary time constant set to 5 ms. We numerically integrated the model dynamics with a first-order Euler approach with a time step of 0.1 ms. Our typical module included multiple interacting neural populations (both excitatory with different selectivity and inhibitory); therefore, the mean-field dynamics would be described by a multidimensional gain function. Our gain function Φ was computed as an “effective” gain function, along the lines proposed by Mascaro and Amit (1999): this approximation allows the reduction of the multidimensional mean-field problem (Amit and Brunel, 1997) to a one-dimensional one corresponding to the dynamics of the firing rate of the population of interest, still keeping trace of the effects of the interaction with the others. Under stationary conditions, for activities fluctuating around fixed points of the minimal rate model, ν(t) had power spectrum P(ω) = ην (1 + ω²τ²)/[(1 − Φ′)² + ω²τ²], where ν was the rate averaged in time and ω = 2πf with f the Fourier frequency. High- and low-ω limits for P(ω) were P(0) ∝ ν/(1 − Φ′)² and P(∞) ∝ ν.

Cortical modules we modeled were composed of 20,000 IF excitatory (80%) and inhibitory (20%) neurons with strengthened synaptic couplings between cells responsive to the same input stimuli (Amit and Brunel, 1997). Membrane potential V(t) of IF neurons evolved according to the following: dV(t)/dt = − V(t)/τ_{α +} I_syn(t) − I_AHP(t), where I_syn(t) was the synaptic incoming current and τ_α was the membrane decay constant (τ_E = 20 ms and τ_I = 10 ms). Point-like spikes were emitted when V(t) crossed a 20 mV threshold, after which a 15 mV reset potential was set for an absolute refractory period of 2 ms (1 ms) for excitatory (inhibitory) neurons. I_AHP(t) was the activity-dependent afterhyperpolarizing K⁺ current acting as a fatigue mechanism for spiking activity of excitatory neurons: dI_AHP(t)/dt = −I_AHP(t)/τ_AHP + g_AHP Σ_k δ(t − t_k), with τ_AHP = 50 ms and g_AHP = 0.11 mV/s. The δ(t − t_k) were the point-like spikes emitted by the neuron.

Synaptic transmission was instantaneous, and I_syn(t) = Σ_j J_j Σ_k δ(t − t_jk − δ_j) + Σ_k J_ext,k δ(t − t_ext,k). The kth spike emitted at t = t_jk by the local presynaptic neuron j affected the postsynaptic membrane potential with a synaptic efficacy J_j after a transmission delay δ_j. Synaptic efficacies were randomly chosen from a Gaussian distribution with mean J_αβ and SD ΔJ_αβ depending on the type of presynaptic (β ∈ {E, I}) and postsynaptic (α ∈ {E, I}) neurons. In unstructured networks where excitatory neurons had no preferred connections coding selectivity to an external stimulus, we set J_EE = 0.35 mV, J_IE = 0.47 mV, J_EI = −1 mV, and J_II = −0.8 mV, whereas ΔJ_αβ = 0.25 J_αβ for any α and β. Connectivity was sparse, and two neurons were synaptically connected with probability c_αβ = 5%, for any α and β, unless otherwise specified. Transmission delays were chosen to match the typical time scales of excitatory and inhibitory synaptic transmissions. In particular, for excitatory synapses delays were drawn from the sum of two exponential distributions with the average delay 3 and 40 ms, mimicking AMPA and NMDA conductances, respectively. Inhibitory spike delays were sampled from an exponential distribution with a 3 ms average aiming to mimic, in this case, GABAergic synaptic transmission.

For each target neuron in the module, spike trains {t_ext,k} coming from neurons outside the cortical module were collectively modeled as a Poisson process with average spike frequency ν_ext = 2.4 kHz. Synaptic efficacies J_ext,k were randomly chosen from a Gaussian distribution with the same moments as the local ones (J_αE and ΔJ_αE, with α = E, I). Sensorial inputs were modeled by increasing ν_ext to stimulus-selective neurons by a fraction Δν_ext. Intermodule connectivity was set only for excitatory neurons with the same stimulus selectivity (c = 2%), modeling corticocortical long-range synaptic connections. Intermodule spike delays were sampled from an exponential distribution with a 21 ms average. To keep spontaneous firing frequencies almost unchanged, neurons receiving spikes from other modules had a ν_ext reduced by 120 Hz.

We embedded selectivity to eight abstract stimuli in each cortical module, by strengthening the synapses inside eight corresponding, not overlapped, neuron pools. Assuming such selectivity to emerge from a Hebbian learning, synapses connecting neurons with same selectivity were potentiated by a factor w₊ > 1, whereas connections between cells with different selectivity were depressed by a factor w_- < 1 (Amit and Brunel, 1997; Wang, 2002). Depending on w₊, a mean-field approach (Amit and Brunel, 1997) was used to compute w_- to keep the firing rate of the asynchronous spontaneous state at 3 and 6 Hz for excitatory and inhibitory pools, respectively.

We also performed simulations of three-module networks in which one of the downstream modules displayed a sudden downward transition (SDT) from Up (high-firing) to Down (low-firing) states. In these networks, neuronal pools with SUTs in the upstream module were connected directly to inhibitory neurons of the downstream SDT module (c = 2% and c = 2.5% for modules with strong and weak self-excitation, respectively). Neuronal pools showing SDTs were set in the Up state, increasing ν_ext by 560 Hz and 1.04 kHz for strongly and weakly self-coupled modules, respectively.

In silico UFPs for modeled cortical modules were a linear transform of spike trains discharged by all excitatory neurons and a random subset of inhibitory cells (20%). As transform we used the convolution of emitted spikes with a stereotyped single-unit waveform K(t), because of well approximating high-ω components of UFPs (Martinez et al., 2009). For K(t), we adopted a waveform similar to the impulsive response of a bandpass (ω/2π ∈ [0.3, 1.7] kHz) Butterworth filter of second order, whose shape qualitatively fitted the single-unit waveforms usually obtained from in vivo recordings.

Results

Upward MUA transitions anticipate movements at single-trial level

We selected recordings with task-related activity (n = 267 of 340; see Materials and Methods) in at least one movement condition during No-stop trials. A subset of task-related recordings (n = 112, 42%) showed a significant growth of MUA during the RT. Among these, we found activity showing SUTs at the single-trial level. Figure 2A shows an example recording (blue circle represents the time when SUTs were detected by a thresholding algorithm, as detailed in Materials and Methods). For this recording, by plotting MUA profiles aligned to the movement onset and grouping trials with different average RTs, a stereotyped and sharp neuronal activity growth appeared, the shape of which was independent of the RT (Fig. 2B). Furthermore, a strong linear correlation between RTs and SUT occurrence times emerged, such that SUT times were predictive of RTs at the single-trial level (Fig. 2C). For population analysis, we selected recordings (61%, n = 68 of 112) with SUTs detected in at least two-thirds of the trials and having high correlation with RTs (R > 0.3). A fraction of them (43%, n = 29 of 68) showed a selective response for only one of the two movement conditions. This fraction increased to 60% (n = 41 of 68) if the selectivity criterion required a significantly different SUT detection rate in the two conditions (Fisher's exact test, P_F < 0.05). Across the selected recordings/conditions, the degree of correlation between RTs and SUT times had a population average of R = 0.67 ± 0.21 (mean ± SD, n = 107, two conditions for 39 recordings and one for the remaining 29), and all cases resulted to be significantly correlated (p < 0.001). In these recordings, we found a narrow distribution of the time needed for MUAs to rise from low to high levels of activity (Fig. 2D; see Materials and Methods for details), with an average transition duration of 92.9 ± 6.8 ms (mean ± SEM): a relatively brief time compared with RTs, which ranged between 300 and 650 ms across all recording sessions. These fast transitions of activity occurred well before arm movement onset (Fig. 2E; 110.8 ± 4.4 ms, mean ± SEM before movement onset).

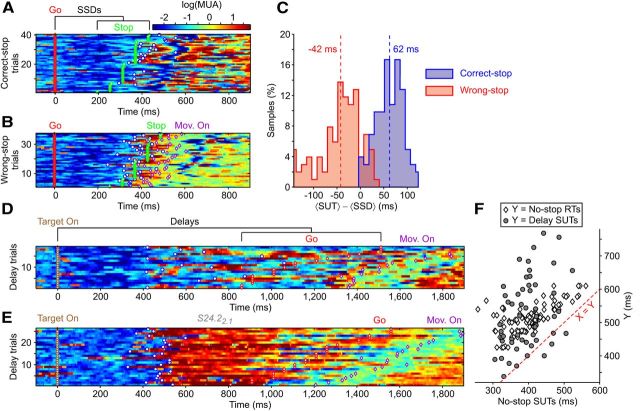
Figure 2.

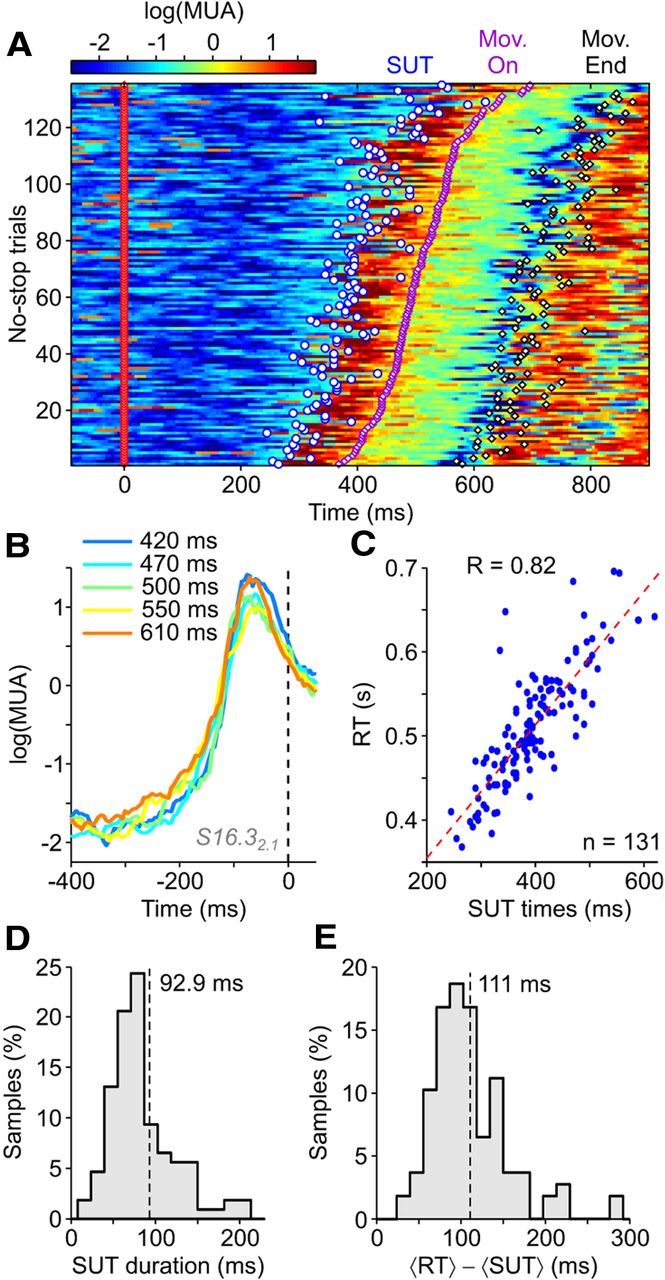
MUA sharp upward transitions predict movement onset at single-trial level. A, Trial-by-trial time course of color-coded log(MUA) from a representative extracellular recording, sorted by RT, for one of the two movement conditions, for reaching trials aligned to the Go signal (red diamond). Superimposed events are detected SUTs (white circle), movement onsets (magenta diamond, Mon. On.), and movement ends (black diamond, Mon. End). B, The trials in A are subdivided into five groups of equal size according to RT, and for each group, the time courses of log(MUA) are aligned to the movement onset (dashed line) and averaged. Inset, Average RT within each group of trials. C, Correlation between RTs and SUT times detected at the single-trial level in A. The dashed red line indicates linear regression. D, E, Histograms of average SUT durations (D) and average time lags between SUTs and RTs (E) (n = 107 recordings/conditions). The black dashed lines indicate population averages.

We also recorded saccadic movements in 45 recording sessions to analyze the relationship between SUT times and saccadic reaction times (SRTs). No-stop trials with SUTs were selected to have both monkey eyes fixating on the central cue at the target onset and a saccade occurring within the RT. Detected eye movements were those with angular velocity higher than 30°/s. The number of recordings/conditions with significant hand RT–SUT time correlation was a large majority (n = 37 of 45) compared with those with correlated SRTs and SUT times (n = 6 of 45) (Fisher's exact test, p < 0.001). This evidence suggests a modest oculomotor involvement in the arm movement planning coded in PMd, in agreement with previous findings (Cisek and Kalaska, 2002).

Hence, in 25% of the PMd's task-related recordings, SUTs were well represented. These stereotyped rapid activations were detectable at the single-trial level, extending previous evidence based on MUA (Stark and Abeles, 2007). SUTs were also consistent with rapid onsets of single-unit activities (SUAs) observed in multitrial spike-density profiles during visually guided motor tasks (Weinrich and Wise, 1982; Weinrich et al., 1984; Crammond and Kalaska, 2000; Churchland et al., 2006a, 2010b; Nakayama et al., 2008; Rickert et al., 2009; Afshar et al., 2011).

SUTs underlie maturation of motor programs

Now a question arises: Are SUTs the neural substrate of what? SUTs might represent the neural substrate of the forthcoming motor act or, instead, underlie the planning of intended movements. We addressed this issue by focusing on the neuronal population activity recorded in Stop trials, in which an imperative Stop signal required the inhibition to reach displayed targets. For correctly withheld movements, motor programs could normally be implemented in the brain after target appearance, but their translation into an overt action needs to be blocked. In a large fraction of Correct-stop trials, when no overt movements were performed, we continued to observe SUTs (Fig. 3A) with a similar shape and distribution of occurrence time as those in No-stop trials (Fig. 2A). In Wrong-stop trials, when the monkey failed to cancel the movements, the overall time structure of the MUA raster plot in Figure 3B appeared almost overlapping with Figure 2A, as expected.

Figure 3.

SUTs code motor programs and not movement execution. A, B, Trial-by-trial time course of log(MUA) aligned to Go for Correct-stop (A) and Wrong-stop (B) trials with Stop signal (green diamond) for the same recording/condition of Figure 2, A and C. Trials were sorted by SSDs. C, Histograms of the average latency between SUTs and SSDs for Correct-stop (blue) and Wrong-stop (red) trials from recordings/conditions with SUTs during No-stop trials (n = 107 recordings/ conditions). The dashed lines indicate population averages. D, E, Raster plot of log(MUA) centered around Target on (brown diamond) for Delay trials from two different example recordings/conditions. The recording/condition in D is the same as in A and B. Other symbols are as in Figure 2A. F, Correlation between average SUT times and average RTs during No-stop trials (white diamond, n = 107 recordings/conditions) and average SUT times in Delay trials (gray circle, the subset n = 54 of recordings/conditions showing SUTs both in stop-signal and delayed reaching tasks).

Interestingly, SUT latencies with respect to SSDs were predictive of the behavioral outcome of Stop trials. For the large majority of the Correct- and Wrong-stop trials in Figure 3, A and B, SUTs followed and preceded the SSDs, respectively. The same timing was confirmed at the population level: the distributions of the average latency between SUT times and SSDs for each recording/condition showed only a small amount of overlap and were clearly distributed over positive or negative values for Correct- or Wrong-stop trials, respectively (Fig. 3C). As SUTs occur also on trials when monkeys successfully vetoed the reaching movement, they likely represent a neural correlate of motor plans of intended arm movements.

Such evidence suggested a prediction: SUTs should be found also during instructed delays of reaching tasks, when PMd is known to participate in motor plan encoding well before movement execution (Weinrich et al., 1984; Riehle and Requin, 1993; Crammond and Kalaska, 2000; Hoshi and Tanji, 2000; Cisek and Kalaska, 2004, 2005; Churchland et al., 2006b). Figure 3D confirms this intuition. In fact, in the Delay trials from the previous recording/condition MUA raster, SUTs were detected during delays well before Go signals. A different example recording/condition reported a less prominent SUT time variability (Fig. 3E), together with a stably persistent high firing rate after SUTs. SUTs in Delay trials were identified selecting recordings/conditions with a detection rate during the Delay period no less than two-thirds; correlation with the next RTs was not required (n = 79). The majority of such recordings/conditions had SUTs also in No-stop trials (68%, n = 54 of 79). Furthermore, average SUT times in Delay trials were more widely distributed compared with those of No-stop trials (Fig. 3F, Levene's test for equality of variances, p < 0.001) and occurred later in time than average SUT times of No-stop trials (above red dashed line in Fig. 3F; Wilcoxon rank sum test, p < 0.001). These task-dependent differences in the properties of stereotyped MUA transitions could further confirm the ability of PMd to code set-related information during motor planning (Hoshi et al., 1998; Wallis and Miller, 2003; Cisek and Kalaska, 2005; Nakayama et al., 2008).

Footprints of a possible local origin of SUTs

The observed SUTs could represent the reaction to a strong change in the synaptic input from remote neurons. Under this view, recorded neuronal pools would be mere relay stations with a marginal role in the computation of a movement plan. A more intriguing hypothesis is to consider the local, recurrent synaptic coupling as a critical ingredient for pool dynamics. A minimal rate model (see also Material and Methods) can help to gain insights into the computational machinery and basic components of the network generating SUTs. In this model, the discharge rate ν(t) of the pool is driven by incoming synaptic current via a gain function Φ (Wilson and Cowan, 1972): τ dν/dt = Φ(ν,Δν_ext) − ν.

Gain functions depend on both local (ν, recurrent) and external (Δν_ext, i.e., from other neuronal pools) activity. Their sigmoidal shape increases in steepness for larger Δν_ext, making more excitable the neuronal pool (Fig. 4A). Nonlinearity of network dynamics allows the existence of two preferred states where the output rate is driven to equal the local incoming input [Φ(ν,Δν_ext) = ν and Φ′ = ∂Φ/∂ν < 1; Fig. 4A, circles]. The Down (low-firing) and Up (high-firing) attractor states (Amit and Brunel, 1997) are apparent in the numerical integrations of ν(t) (Fig. 4B). An intrinsic noise for ν(t) was introduced (see Materials and Methods) to recover the effect of the spike count fluctuation caused by the finite-size of simulated pools (Zipser et al., 1993; Mattia and Del Giudice, 2002). We modeled the processing of the stimulus-related input by a gradual and moderate increase of Δν_ext at a fixed latency of 100 ms after stimulus onset signal (t = 0), as depicted in Figure 4B. Activity dynamics from simulations with different intrinsic noise clearly show how ongoing fluctuations of ν(t) contribute to cause a sudden and stereotyped increase in the firing rate at random times, similarly to what we observed in in vivo recordings (Figs. 2, 3). These dynamics could be better understood by referring to the effective energy landscape [the integral of Φ(ν,Δν_ext) − ν, the “force” field] in Figure 4C, which shows two equilibrium states (right and left wells are the Up and Down state, respectively) both before and after the stimulation onset. By increasing Δν_ext, the attractive force toward the Down state reduces. The shallower well facilitates transitions, i.e., the rapid rolling down toward the Up state (Amit and Brunel, 1997; Wang, 2002), as sketched by the circles representing the activity distribution during the four stages marked by the numbered dashed lines in Figure 4B.

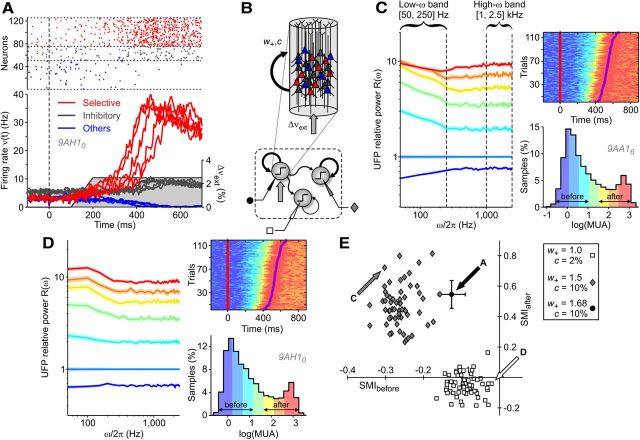
Figure 4.

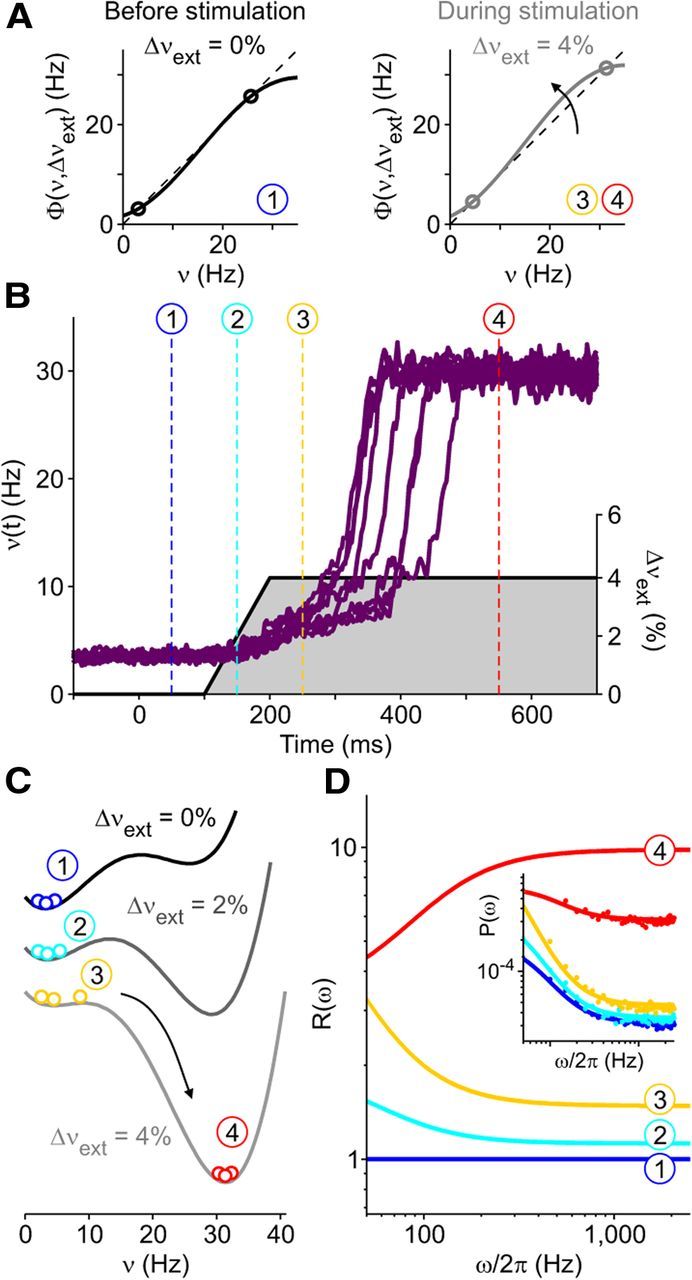
Spectral modulation of activity in a bistable minimal model showing SUT. A, Example gain functions Φ(ν,Δν_ext) driving the minimal rate model dynamics when different additional external inputs Δν_ext are delivered (solid curves). The dashed black line indicates where input and output rates are equal. Circles, Stable fixed points of the dynamics where input equals output firing rate (Φ(ν) = ν) and Φ′ = ∂Φ/∂ν < 1. B, Numerical integration of the minimal model dynamics around stimulation onset. Activity ν(t) fluctuates to mimic the intrinsic variability of a finite number of interacting neurons. Purple traces, ν(t) of 10 simulated trials (left axis); right axis, gray shaded Δν_ext modulating Φ and modeling the target-related input. Dashed vertical lines show four reference dynamical stages of modeled trials defined by the activity level and the Δν_ext value. C, Effective energy landscapes obtained integrating the “restoring” force Φ(ν,Δν_ext) − ν in the different reference stages. Bistability of the system is determined by the coexistence of two wells separated by an energy barrier. Colored circles represent ν(t) distribution in the reference periods in B. D, Relative power spectra R(ω) = P(ω)/P_ref(ω) of ν(t) at different stages (P_ref(ω), spectrum at stage 1). Inset, Power spectra P(ω) estimated from simulations (colored dots) and theoretical predictions (solid lines). Power spectral densities in Figure 4D were estimated from 5-s-long simulations of the rate model.

Different strengths of attraction to the energy minima affect the dynamic time scales of the network, and modulations of the power spectrum P(ω) (ω/2π, Fourier frequencies) of ν(t) reflect such variations (Fig. 4D; see Materials and Methods). Before upward transitions (from stage 1 to stage 3), relative spectra R(ω) display a higher increase of power at low ω with respect to asymptotic high-ω components, confirming a dominance of slow time scales in the destabilized Down state. The opposite happens when the system falls in the Up state (stage 4), where the landscape curvature is higher than at stage 1. In this minimal rate model P(0) ∝ ν/(1 − Φ′)², hence the slope Φ′ governs slow time scales. Therefore, the sigmoidal shape of Φ determines both the bistability and spectral modulations shown in Figure 4. This suggests detectable measures to reveal the dynamics of attractor switching in our recordings and to prove that in vivo SUTs primarily originate in local neuronal pools.

A local synaptic reverberation hypothesis for SUTs

The minimal rate model provides quantitatively reliable hints for more detailed networks of IF neurons, once a good approximation for Φ is taken into account (Gigante et al., 2007; Linaro et al., 2011; Ostojic and Brunel, 2011). This is apparent in Figure 5A, where firing rates ν(t) of a stimulus-selective subset of IF neurons in a wider network show SUTs as in Figure 4B. Here the same stimulation was delivered, and microscopic parameters were set to have, under mean-field approximation (Amit and Brunel, 1997; Mascaro and Amit, 1999), the same Φ as in Figure 4A. A neuronal population (cortical module) was composed of both excitatory and inhibitory neurons differently selective to the two conditions (Amit and Brunel, 1997) (Fig. 5B, top; see Materials and Methods). Synaptic couplings between excitatory neurons with similar selectivity were strengthened by a factor w₊ with respect to synapses among nonselective cells. Connectivity was sparse, and two neurons were synaptically coupled with probability c. Stimulus-related input was modeled by a relative increase in Δν_ext of incoming spike rates from neurons outside the module. Similar models have been suggested as substrates for working memory and decision making (Amit and Brunel, 1997; Wang, 2002; Martí et al., 2008).

Figure 5.

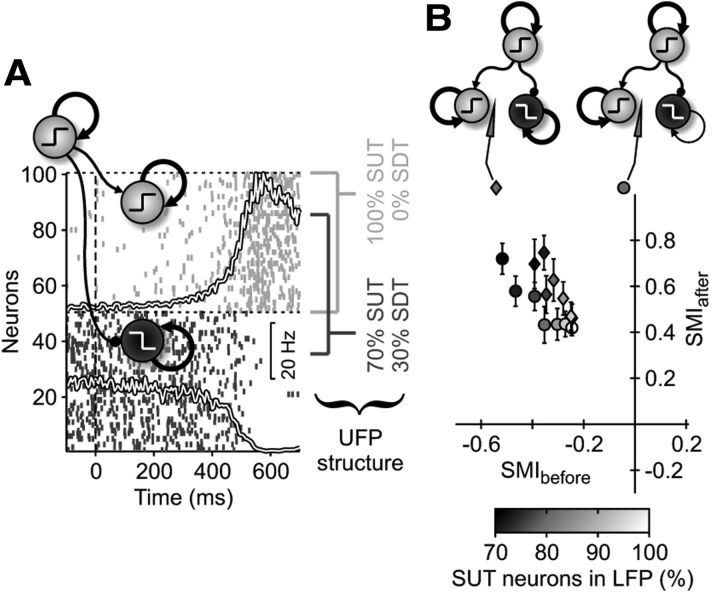
In silico spectral modulations of UFPs around SUTs depend on synaptic reverberation strength. A, Sample simulations of a cortical module. Network arrangement is as in B. Firing rates of excitatory subpopulations with different target selectivity (red and blue) and of inhibitory neurons (dark gray), centered around stimulus onset (t = 0 ms) for 10 simulated trials. Gray area (right axis), Increase of incoming spike rate Δν_ext delivered to selective neurons (red) modeling target-related input. Top, Raster plot of spikes emitted by a subset of neurons in a single simulated trial from different subpopulations. B, Simulated network (bottom) of modules (circles) showing SUTs with intramodular and intermodular synaptic connections (arrows) with different strengths (arrow thickness). Each cortical module had 20,000 IF neurons (top). Synaptic excitatory feedback among neurons with similar selectivity had relative strength w₊ (black arrow) and average connectivity c. Gray arrows stand for Δν_ext. C, D, Spectral analysis of in silico UFPs extracted from two of the output modules with large and small self-excitation (white square and gray diamond in B, respectively). Top right, Raster plots of in silico MUAs from 20 ms time windows. Symbols are as in Figure 2A. Simulated RTs are randomly generated from SUT occurrences. Bottom right, Histograms of log(MUA) during RT epochs (first 100 ms not considered). Seven activity levels with the same size define color codes for other panels. Left, Relative power spectra R(ω) in silico UFPs computed on the same 20 ms time windows, averaged depending on activity level. Color shades are SEM of R(ω). Relative spectra are estimated from simulations 10 times longer than those represented on the right. E, Scatter plot across different simulations (n = 70 networks of 3 modules) of the SMIs (see Results) before and after SUT onsets (periods with colors labeled accordingly on the histograms). Symbols refer to the different modules as in B (marks next to the sketched electrodes). Simulations differ only in the initial condition and the realization of the synaptic connectivity (same connectivity c). For the upstream module in A, only average and SD (black circle and error bars, respectively) across simulations were plotted.

Up to now, we considered only a single isolated pool of neurons. To test a more realistic scenario, we performed simulations of three synaptically connected (and individually recurrent) modules of IF neurons (Fig. 5B, bottom). This in silico experiment allowed us to investigate whether the modulation of self-excitation w₊ is crucial to shape Φ and hence to establish the spectral footprint suggested by Figure 4D. From simulated activity, we modeled in silico UFPs by convolving emitted spikes with a single-unit waveform (Martinez et al., 2009; Mattia et al., 2010) (see Materials and Methods) to map simulations onto in vivo recordings. In Figure 5, C and D (top right), extracted in silico MUAs display raster plots looking like the in vivo ones, within simulated RTs that we randomly assigned as Gaussian distributed time lags from the detected SUTs. We considered log(MUA) samples, within the RT of all trials, starting from the time when Δν_ext increases. Such MUAs were averaged on moving time windows of 20 ms and pooled in seven groups with logarithmically spaced levels of activity, shown as different colored stripes in the histograms of Figure 5, C and D. Then we worked out the power spectra P(ω) of in silico UFPs within the selected 20 ms time windows, grouping and averaging them in the same log(MUA) intervals as in the histograms. Finally, we computed relative spectra R(ω) as ratios of P(ω), taking as reference the average spectrum of the log(MUA) interval representative of the Down state before SUTs (Fig. 5C,D, left). This activity-driven analysis was approximately equivalent to monitor the changes of P(ω) in time, as in Figure 4D, because during RTs, ν(t) had a roughly monotonic increase. The advantage of such analysis was to be insensitive to nonstationary UFPs and variable RTs, like in in vivo recordings.

We performed the analysis for each of the three cortical modules (Fig. 5B, bottom), considering that they have different external input (Δν_ext), recurrent activity (w₊ and c), and intermodular connectivity. Here only one module (Fig. 5A, black circle) received external sensory-related input (gray arrow), had high w₊, and provided excitatory synaptic input to the other two modules, which had, respectively, strong (Fig. 5C, gray diamond) and weak (Fig. 5D, white square) recurrent synaptic excitation.

In Figure 5C (left), when intra-modular feedback was strong, spectral modulation was qualitatively similar to that in Figure 4D. Before SUTs (MUA levels from light blue to green), R(ω) showed a stronger increase of power in the low-ω band (LFB; ω/2π < 250 Hz) than at high frequencies [high-ω band (HFB); ω/2π > 1 kHz], signaling the destabilization of the Down state. After SUTs (from yellow to red levels), local spike reverberation primed a chain reaction capable to attract selective pool activity to the high firing Up state, which in turn damps changes of R(ω) at low ω. This spectral modulation was not observed in Figure 4D, where no changes of firing rate ν in Up states was taken into account. Here no changes in the LFB were observed going from yellow to red MUA levels, where HFB power increased. This can be still explained in terms of the gain function Φ. The reduction of R_LFB(ω)/R_HFB(ω) across these activity levels can be interpreted as a lowering of Φ slope around the fixed point corresponding to the Up state. This led to a more stable high-firing state with increased attractive forces (narrow energy well), making the system faster. On the other hand, for weak self-couplings (Fig. 5D, left), R(ω) was uniformly modulated across the full frequency range. This module would not be capable of generating SUTs on its own, and the reaction to the SUTs that occurred in the input module did not provoke changes in the dynamics time scales: observed SUTs were merely the echo of the activity changes in the module shown in Figure 5A. The absence of a strong feedback straightens the gain function Φ and only one attractor is available, which is being shifted to higher firing rates by increasing input spike rates. Interestingly, although similar bimodal histograms of MUAs were observed in both neuronal pools, they did not imply a locally generated bistability, which occurred only for modules with high w₊.

Modulation of R(ω) would seem to reliably predict the strength of the excitatory synaptic feedback w₊. To investigate such a relationship, we computed a spectral modulation index (SMI), SMI = (ΔR_HFB − ΔR_LFB)/(ΔR_HFB + ΔR_LFB), where ΔR_LFB (ΔR_HFB) is the ratio between the average values of R(ω) for two levels of activity, in the low-ω (high-ω) band. The two levels of activity were chosen to be representative of the period just before (SMI_before) and just after (SMI_after) SUTs. We performed simulations (n = 70) of our multimodular network choosing random connectivity matrices and the same set of c and w₊. In Figure 5E, the SMIs before and after SUTs (see details in Fig. 5, C and D, bottom right) were plotted for each module and simulation. When recurrent excitation was strong (gray diamonds and black circle modules), an anticorrelation between SMIs clearly emerged, whereas for almost uncoupled modules, flat relative spectra kept SMIs close to zero (white square). We, therefore, generate the expectation that almost uniform spectral modulation in vivo should be observed for remotely driven modules with small self-excitation, whereas locally generated SUTs in strongly self-excited modules typically should show the peculiar modulation in Figure 5C.

Cortical modules with heterogeneous self-excitation underlie in vivo SUTs

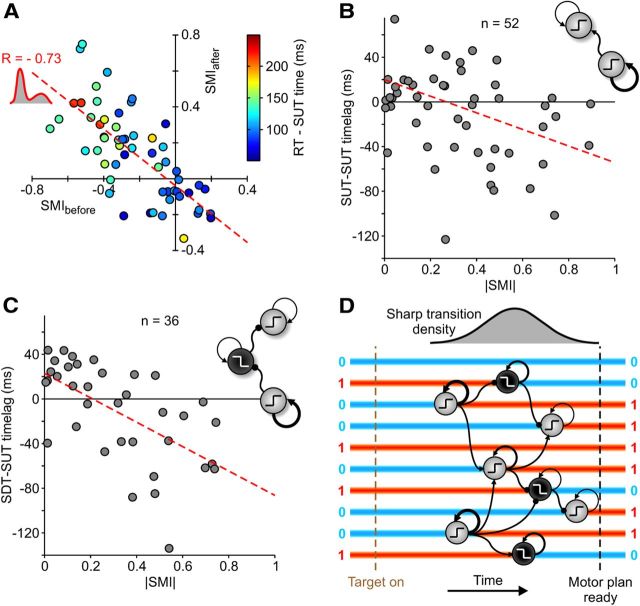
We tested the predictions of both the minimal and detailed models performing the same analysis on in vivo recordings. Figure 6A displays the SMIs for the selected recordings/conditions with SUTs described in Figure 2. At first glance, the distribution spread without any order, but a deeper inspection allowed us to uncover a clear organization. We marked each recording/condition with the likelihood to correctly consider the distribution of log(MUA) during RTs as unimodal. Half of them showed a bimodal distribution (white circle; n = 57 of 107; Hartigan's dip test on log(MUA) histograms, p < 0.05; Hartigan and Hartigan, 1985), and a clear anticorrelation between their SMI_before and SMI_after emerged (dashed red line; r = −0.73, p < 0.001), confirming theoretical expectation (Fig. 5E). Like in the model, we observed different degrees of UFP spectral modulations ranging from the ones possibly attributable to intense self-excitation (compare Figs. 6B, 5C) to those expected for almost uncoupled networks (Fig. 6C, to be compared with Fig. 5D), possibly driven by other modules with SUTs.

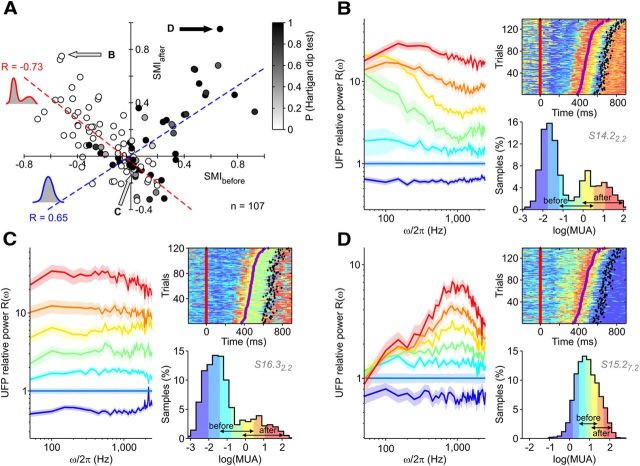
Figure 6.

Spectral modulations of in vivo UFPs confirm the theoretical attractor picture. A, SMIs for the selected recordings and conditions with predictive SUTs (n = 107, as in Fig. 2, D and E). SMIs are computed as in Figure 5, with activity levels before and after SUTs as labeled on the histograms. The dashed red line indicates linear regression (r = −0.73, p < 0.001) for recordings with bimodal activity histogram during RT (red circle; p < 0.05, Hartigan's dip test; n = 57 of 107; see also Fig. 9A). The dashed blue line indicates linear regression (r = 0.65, p < 0.001) for recordings/conditions with unimodal activity histograms (black circle; dip test, p ≥ 0.05; n = 50 of 107). B–D, Spectral modulations as in Figure 5, C and D, for representative recordings/conditions marked by arrows in A. Other conventions and symbols are as in Figures 2, 3, and 5.

The other half of recordings/conditions, those with unimodal distribution of log(MUA) in Figure 6A (black circle; n = 50 of 107; dip test, p ≥ 0.05), displayed a positive SMI correlation (dashed black line; r = 0.65; p < 0.001). The apparent paradox of detecting SUTs when log(MUA) distribution did not show separated peaks for Up and Down states can be explained recalling that MUAs in this spectral analysis were estimated at low temporal resolution (from sliding windows of 20 ms) without any smoothing in time. Such noisy estimates blurred histograms of log(MUA) that appeared bimodal at higher resolution (Figs. 2, 3). This effect turned bimodal into unimodal those distributions with small differences Δν between Up and Down firing rates (Δν = ν_up − ν_down; see Materials and Methods). In fact, histograms of Δν for unimodal recordings/conditions had a significantly lower median than for bimodal ones (Wilcoxon rank sum test, p < 0.001). The example recording/condition with unimodal activity distribution in Figure 6D captured another interesting feature: MUAs before transitions started consistently from a high level compared with activities after movement ends (black diamond). This was compatible with a cortical module residing in an Up state well before SUT occurrences, in which an Up-to-Up shift in firing rates reflected a SUT generated by an upstream module. Small MUA changes underlying unimodal distributions would also explain the absence of low-ω modulation of R(ω). In fact, additional excitatory input to modeled cortical modules further stabilized the Up state by lowering Φ slope around upper fixed point. As explained before, this results in a faster dynamics, hence a mild modulation of R(ω) at low-ω. Compatibly with such a hypothesis, we found median SMI_before negative for bimodal distributions and positive for unimodal ones (Wilcoxon rank sum test, p < 0.001). On the other hand, the histograms of SMI_after for bimodal and unimodal distributions were not statistically different (Kolmogorov–Smirnov test, p = 0.3). Therefore, SUTs with unimodal and bimodal MUAs differed in the initial state of the cortical modules, but not in the final Up state.

Overall, we argued that the above heterogeneity of module excitability found in vivo resulted from the diversity of recurrent connectivity, determined in turn by strength and density of local synaptic couplings. Gradients in the anatomical and functional organization of PMd are known to exist (Johnson et al., 1996), hence we looked for a possible topographic counterpart of this heterogeneity but no ordered spatial arrangement of the module with different degrees of excitability emerged.

Downward MUA transitions complement motor plan coding

Relying on a reasonable principle of a limited global activation of cortical areas, SUTs should likely be compensated by transitions from Up to Down states. We looked for such MUA changes during RTs, finding a phenomenon that mirrored SUTs: SDTs were detected at the single-trial level, reliably predicting forthcoming movements, as shown in Figure 7A. Methods for SDT and SUT detection and analysis were identical, with the only exception to consider as transition times for SDTs those when MUAs downward crossed a threshold set at 40% between ν_down and ν_up. Within the subset of task-related recordings showing a MUA reduction during RT (n = 110 of 267), a fraction of 42% (n = 64 of 110) displayed SDTs in more than two-thirds of the trials at times correlated with movement onsets (R > 0.3). Like SUTs, SDTs were movement selective, occurring only for one task condition in 70% of the recordings (n = 45 of 64). Even in this case, such fraction grew to 80% (n = 51 of 64) considering as selective those recordings with SDT detection rates significantly different in the two conditions (Fisher's exact test, P_F < 0.05). SDTs and SUTs were often (n = 16 of 54) observed in the same multielectrode recording session in different electrodes. When detected, MUA decreases displayed a stereotyped time course independent from the RT (Fig. 7B). This is supported, at a population level, by the narrow distribution of SDT durations (Fig. 7C). Besides, SDT times were highly and significantly correlated with RTs: R = 0.63 ± 0.17 (mean ± SD; n = 83; two conditions for 19 recordings, and one for the remaining 45; in all cases, p < 0.001). Time lags between SDT times and movement onsets were large (Fig. 7D; 90.6 ± 3.2 ms; mean ± SEM), although 20 ms smaller than the average latency between SUTs and RTs. Finally, we found only unimodal distributions of log(MUA) during RTs when SDTs occurred (data not shown), suggesting that Up states before SDTs and after SUTs could be different. As for SUTs, unimodal distributions were caused by a small difference Δν between Up and Down firing rates.

Figure 7.

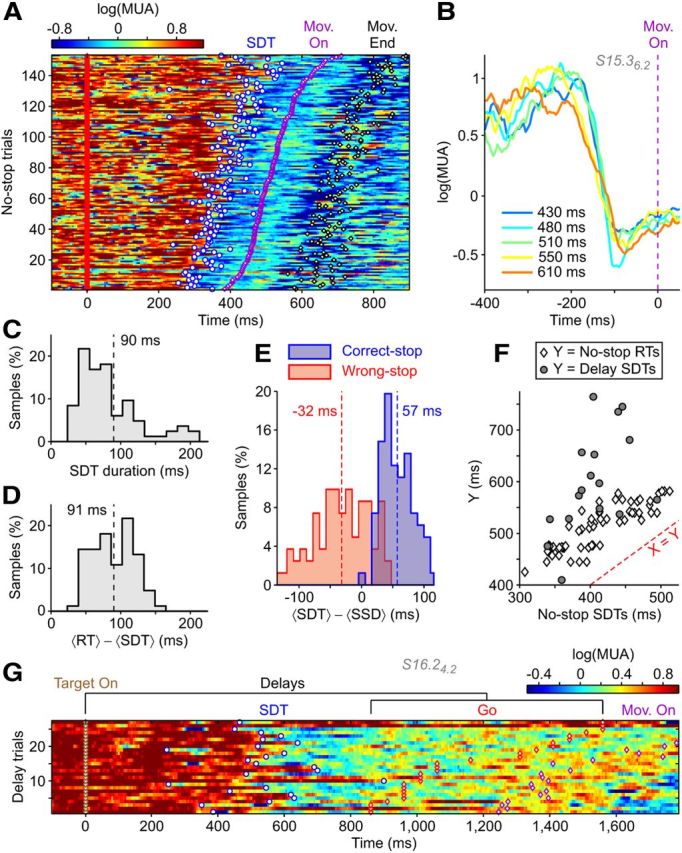
Sharp downward transitions also code motor plans at the single-trial level. A, Raster plot of log(MUA) as in Figure 2A from a representative extracellular recording and target position showing SDTs (circles) from Up (reddish) to Down (bluish) states in No-stop trials. B, Average of log(MUA) across trials in A grouped by RT (inset, average RT in each group) and aligned to movement onsets (dashed line). C, D, Histograms of the average SDT durations (C) and average time lags between SDT and RT end (D) (n = 83 recordings/conditions). E, As in Figure 3C, histograms of average latencies between SDTs and SSDs for Correct-stop (blue) and Wrong-stop (red) trials in the same recordings/conditions (n = 83). Dashed lines show population averages. F, Correlation between average SDT times and average RTs during No-stop trials (white diamond, n = 83) and average SDTs in the Delay trials (gray circle, the subset n = 17 of recordings/conditions showing SDTs both in stop-signal and delayed reaching tasks). G, Raster plot of log(MUA) aligned to Target on (brown diamonds) for Delay trials from an example recording/condition showing SDTs. Mov. On, movement onset; Mov. End, movement end.

As for SUTs, fast downward transitions were observed also in the absence of overt movements. In Stop trials, SDTs were detected also when animals successfully withheld movement. In Figure 7E, average latencies of SDTs, with respect to SSDs, had the same distribution pattern reported for SUTs: transitions in Wrong-stop trials occurred before Stops, whereas in Correct-stop trials, SDTs where later detected. Coherently with the picture of sharp transitions (STs) underlying motor plan maturation and not a merely motor-related activity, we found SDTs also during preparatory periods of Delay trials (n = 23 recordings/conditions; as for SUTs, the adopted criterion was to have SDTs in at least two-thirds of the trials without considering the correlation with the RTs). In the recording subset showing SDTs also in No-stop trials (n = 17 of 23), a wider distribution of times was found for the instructed delay task (Fig. 7F; Levene's test for equality of variances, p < 0.05). As for SUTs, average SDT times in Delay trials occurred later than SDTs in No-stop trials of the same recording/condition (Wilcoxon rank sum test, p < 0.001).

Robustness of UFP spectral modulation as self-excitation indicator

The existence of both SUTs and SDTs in PMd raised a question on the reliability of the relationship between SMI anticorrelation and self-excitation strength of cortical modules (Fig. 5E). Indeed, recorded UFPs could, in principle, sample mixed activities of neuronal pools showing SUTs and SDTs. Assuming the mixture is such as to observe a SUT anyway, for this “blended” UFP we asked: Are SMIs around SUTs still predictive of local synaptic strength? To answer this question, we devised three-module network simulations (as in Fig. 5) in which one of the downstream modules displayed SDTs driven by inhibitory projections from the upstream module (Fig. 8A; see Materials and Methods). In Figure 8B, we tested two multimodular networks with different SDT modules: (1) one with strong self-excitation (top left, as in Fig. 5C) and (2) another with weak self-excitation (top right, as in Fig. 5D). Increasing the proportion of SUT versus SDT neurons in the composition of UFP (white to dark gray shadings, respectively), anticorrelation between SMIs was still apparent in both network configurations. Although this allowed us to exclude possible false negatives (strongly self-excited module ending up with small SMIs), SMIs moved toward large values when the fraction of SDT neurons was increased in the UFP composition, giving rise to possible false positives. To rule out such a hypothesis, we realized that such SMI shift was mainly because of the reduction of the gap Δν in the firing rate between Up and Down state (see above). Indeed, the smaller Δν, the smaller R(ω) changes, and hence the denominator in the SMI definition, which means higher absolute values of SMIs.

Figure 8.

Robustness of relationship between SMI anticorrelation and synaptic self-excitation in silico. A, Single-trial simulation of a three-module network with strong self-excitations. Upstream and downstream modules are as in Figure 5, A and C, respectively. One of two downstream modules (black) was set in the Up state injecting an additional external current. Its inhibitory synaptic input from an upstream module determined SDT whenever a presynaptic SUT occurs. Raster plots show spikes emitted by a subset of excitatory neurons in the two downstream modules (dark and light gray, respectively). Solid curves indicate firing rates of the two whole pools. B, SMIs for different configurations of in silico UFPs and network composition. UFPs were reconstructed using different fractions of SUT and SDT neurons from downstream modules (represented by different gray shadings). Two network configurations were tested in which the SDT module had strong (top left, diamond) and weak (top right, circle) synaptic self-excitation (parameters as in Fig. 5, C and D, respectively). Symbols indicate average across 10 simulations with randomly extracted synaptic connectivity. Vertical and horizontal (not visible) bars show SDs.

To test such possibility in the experimental data, first we defined |SMI|, the distance from the circle projections on the linear regression and the axis origin, and we checked that |SMI| and measured Δν were not correlated (ρ_pearson = 0.01, p = 0.95) for the recording/conditions with SUTs and bimodal activity distribution. For the simulations in Figure 8, we set the maximum fraction of SDT neurons in the mixed UFP at 30%, the one for which the relative reduction of Δν, with respect to the pure SUT case, equals the coefficient of variation of the Δν distribution in the data. Such changes in UFP composition produced only a limited spread of SMIs (Fig. 8B), which cannot explain the whole range of in vivo SMIs (Fig. 6A). This further ruled out the possibility that Δν underlay SMI anticorrelation, confirming that it was a robust indicator for the self-excitation strength in modules with SUTs and bimodal activity distribution.

Motor plans as an avalanche of orderly sharp transitions

As we found that, on average, SUTs occurred earlier than SDTs with respect to movement onsets, an orderly sequence of upward and downward transitions could be hypothesized. Besides, from the theoretical framework we introduced, a tight relationship between module excitability and SUT timing had to be expected. Given that bistable in vivo cortical modules (Fig. 6A, red circle) with larger self-excitation were those with larger SMI values, we predicted a gradient of time gaps between SUTs and RTs along the linear regression (Fig. 6A, red dashed) line. Accordingly, in Figure 9A, the same subset of recordings/conditions displayed small time gaps (bluish circle) around SMI = 0, whereas larger latencies (green to red circle) could be found only for large SMI values. Here we grouped together recordings from experimental sessions with different RTs. To test more precisely such time–excitability relationships, we compared ST times occurring in simultaneous recordings from the seven-electrode array for the same experimental condition. We labeled each in vivo module in Figure 9A with its level of self-excitation measured as the |SMI| (see above). In Figure 9B, the |SMI| of each cortical module was plotted with the average time lag between SUTs it performed and those simultaneously detected in the other electrodes. A clear anticorrelation resulted (r = −0.35; Pearson one-tailed test, p < 0.01), such that modules with higher self-excitation (high |SMI|) had SUTs earlier, whereas late transitions followed in less excitable modules (low |SMI|). In other words, as shown in Figure 9B (inset), the former drove the latter. The same analysis comparing SUT and SDT timing (this time |SMI| of modules with SUTs were plotted against average latency with SDT times simultaneously detected) showed an even stronger anticorrelation correlation (Fig. 9C; r = −0.60; Pearson one-tailed test, p < 0.001). This indicated that SDTs occurred at intermediate time lags compared with those of SUTs in low and high |SMI| modules (Fig. 9C, inset).

Figure 9.

Motor programs mature as sequences of MUA STs in PMd. A, Correlation plot between SMIs as in Figure 6A for recordings/conditions with only bimodal distribution of MUA during RTs (dip test, p < 0.05; n = 57 of 107). Circle colors indicate average time lags between RTs and SUT times (see color bar). B, Average latency between SUT times in each recording/condition in A and SUTs simultaneously detected in other channels of the multielectrode array used (n = 52 of 57; those with SUTs in at least two electrodes and two outliers not shown). The dashed line indicates linear regression (y = −74x + 20 ms, p < 0.01). Inset, Cortical modules with larger |SMI|, and hence larger self-excitation, are likely activated earlier. C, As in B, the average latency between SUT times and SDTs simultaneously detected (n = 36 of 57). The dashed line indicates linear regression (y = −109x + 23 ms, p < 0.001). Inset, Graph depicting a possible ordered inhibitory chain of cortical modules in which SUTs in modules with larger |SMI| prime SDTs and then SUTs in other modules. D, A possible scenario of motor plan maturation. Before target onset, PMd stays in a stable state with active (1) and inactive (0) cortical modules. After a random delay, some modules with strong self-excitation have SUTs priming a chain reaction of STs in other modules and ending in a different stable multimodular activity pattern, the motor plan.

Discussion

Half of our task-related recordings (n = 132 of 267) displayed either SUTs or SDTs of MUAs before the end of the RT of a reaching movement. This widespread phenomenon in PMd underpinned the motor plan development. STs reflected the collective dynamics of spatially confined cortical modules, as confirmed by the fact that MUAs, the pooled activity of thousands of neurons nearby the electrode tips (Buzsáki, 2004), displayed different modulations even when sampled from close recording electrodes. The subset of these modules showing SUTs and two preferred high- and low-firing states during RTs was also characterized by a heterogeneous degree of self-excitability (Fig. 9A). Their excitability level was determined by the amount of spectral modulation of UFPs during MUA transitions within RTs, consistently with models of neuronal networks in which the strength of recurrent synaptic couplings determines the nonlinearity of the module response. More excitable modules, likely so because of stronger synaptic self-excitation, were those capable to produce autonomously SUTs as stimulus-triggered transitions from Down to Up local attractor states (Fig. 6B). These state switches were facilitated by endogenous noise in the firing dynamics, which in turn determined the variability of SUT occurrences, as suggested by models of other cognitive functions (Okamoto and Fukai, 2001; Wang, 2002; Kitano et al., 2003; Mongillo et al., 2003; Martí et al., 2008). Other cortical modules had SUTs exogenously driven by sudden changes in the synaptic input, possibly attributable to either an insufficient excitability (Fig. 6C) or a highly stable state trapping the module activity (Fig. 6D).

Uncovering compelling evidence of local attractor dynamics in vivo is one of our main findings. Evidence of a variability decrease of neural representations, likely resulting from the convergence toward stable activity patterns, has been reported previously (Abeles et al., 1995; Churchland et al., 2006a; Balaguer-Ballester et al., 2011). Nevertheless, we know of no attempts in vivo to tell a local origin of such nonlinear dynamics from the possibility that variability decline is attributable to fluctuation dampening in the received input, as it happens throughout the cortex after stimulation (Churchland et al., 2010a). Yet, even when bimodal distributions of discharge rates result from single-unit recordings (Zipser et al., 1993; Okamoto et al., 2007), the locality issue remains unsolved. In fact, as shown in Figures 5 and 6, both modules with high and low excitability levels display bimodal MUA distributions.

Heterogeneity in module excitability seems to be a key ingredient in the maturation process of macroscopic activity patterns across PMd. Indeed, action plans developed as a chain reaction (Fig. 9D) primed by SUTs in more excitable modules, eliciting, in turn, SUTs and SDTs in other cortical modules. In about 100 ms, such hierarchically cascade ended, and a new stereotyped configuration of active and inactive cortical modules emerged. Like steps of a staircase, ordered STs were allowed to climb the slopes of an effective energy landscape of the whole network by changing a few bits at a time of binary “words,” which represents a large part of the task-related activity patterns found in PMd. Such fine structure of global transitions between one macroscopic state preceding the target onset and another corresponding to a mature motor program highlights an effective strategy in the coordination of multimodular networks to go over reliable pathways linking different state space regions. This picture extends the standard views contrasting reservoir computing with attractor-based neural computation (Rabinovich et al., 2008; Buonomano and Maass, 2009). If neural computation is the result of the itinerant dynamics between metastable patterns of distributed cortical activities (Tsuda, 2001; Durstewitz and Deco, 2008), our findings provide an alternative implementation of such itinerancy that is neither the result of generic chaotic dynamics of a high-dimensional dynamical system (Skarda and Freeman, 1987; Tsuda, 2001) nor the stochastic hopping between global and stable attractor states (Okamoto and Fukai, 2001; Mongillo et al., 2003; Durstewitz and Deco, 2008; Martí et al., 2008; Miller and Katz, 2010). Here a heterogeneous reservoir of “flip-flops” (Abeles et al., 1995; Shu et al., 2003) allows to compose specific trajectories that tightly constrain the cortical dynamics of PMd once suited pivotal modules are primed by an exogenous stimulation. Such trajectories are stereotyped also because each ST composing the sequence of module flips has well reproducible MUA time courses across trials (Figs. 2B, 7B). As a result, a reduction in the variability of cortical activity across trials during motor planning is expected, similarly to the compelling evidence recently found in SUA from the same motor area during action planning (Churchland et al., 2006a).

Together, these results depict a rather general “cortical processor” that exploits a multimodular and heterogeneous architecture extending implementations of motor plans as associative maps in premotor cortex (Kalaska and Crammond, 1992; Houk and Wise, 1995; Nakayama et al., 2008). Indeed, the long-standing theory of associative networks (Amari, 1972; Hopfield, 1982; Amit, 1989) here is further extended by linking metastable states through constrained sequences of mesoscopic events, suggesting an effective combination of attractor- and trajectory-based computation. Because of such generality, a reasonable expectation is that premotor cortex is not the unique area to implement this computational strategy. Best candidates should be those cortices involved in functions like cognitive control, which, through the development of inner representations of goals and plans, allows them to flexibly guide thoughts and actions (Miller and Cohen, 2001; Badre and D'Esposito, 2009). Implementation of such functions would benefit from a versatile nonlinear dynamical system capable to hold information as metastable states and to integrate multiple sources of inputs as stimulus-driven state transitions (Tanji and Hoshi, 2001; Rigotti et al., 2010). Consistently with this hypothesis, sudden changes in multitrial spike densities promoted by stimuli, but not temporally locked to them, have been found in temporal (Naya et al., 2001), parietal (Maimon and Assad, 2006), and frontal (Seidemann et al., 1996) [but see Figs. 6 and 7 of Brody et al. (2003)] cortex of monkeys performing tasks that rely on working memory and planning.

In motor and premotor cortical areas, local field potentials (LFPs) are modulated in the frequency domain during both movement execution and planning (Sanes and Donoghue, 1993; Rickert et al., 2005; O'Leary and Hatsopoulos, 2006; Mattia et al., 2010). The physiological mechanisms underlying such modulations are still debated, although synaptic inhibition appears to play a key role in generating LFP power spectra resonances in neuronal networks and, more in general, in excitatory–inhibitory loops (Wang, 2010). Although we embodied synaptic inhibition in our modeling framework, we cannot exclude additional contributions to UFP spectral modulation during SUTs, like those that might emerge from the interactions between PMd and other cortical areas. Notice, however, that resonances and amplitude modulations of LFP-relative spectra in motor areas have been observed only at frequencies below 65 Hz (Rickert et al., 2005; O'Leary and Hatsopoulos, 2006). This should be contrasted with the focus of our spectral analysis on the high-ω components of UFPs (ω/2π ≥ 50 Hz and up to the kilohertz range), which favors our hypothesis of a major role played by changes in the energy landscape. On the other hand, the shape of the energy landscape is determined by the gain function Φ, and physiological mechanisms not included in our model might contribute, in principle, to shape Φ. For instance, dopaminergic neuromodulation has been argued to affect robustness of attractor states modeling working memory (Durstewitz et al., 2000; Brunel and Wang, 2001), and in vitro, dopamine modulates the input–output response properties of pyramidal neurons (Thurley et al., 2008). The widespread diffusion of dopamine across neocortex (Robbins and Arnsten, 2009) poses some limits on this alternative hypothesis, making it difficult to reconcile with the heterogeneity of module self-excitability we observed on the short spatial scale of our multielectrode recordings. Nevertheless, to confirm the critical role of synaptic self-excitation in shaping Φ, more focused experiments are needed.

Although rapid SUA changes are expected to underlie STs of MUA, more general SUA patterns could be associated with fast onsets of metastable activity patterns. In fact, trial-by-trial variability in transition times may underlie smooth time courses of average spike densities (Okamoto and Fukai, 2001; Mongillo et al., 2003; Miller and Wang, 2006; Okamoto et al., 2007; Martí et al., 2008). Pooled spike trains showing jittered STs across trials may compose decaying or raising ramps of average firing rates [for example, Fig. 5B of Mirabella et al. (2011)], similar to those found to be also associated with action planning in motor areas (Tanji and Evarts, 1976; Georgopoulos et al., 1989; Riehle and Requin, 1989; Bastian et al., 2003). This could reconcile our observation of abrupt maturations of motor programs with the hypothesis that slow changes of firing rates underlie preparatory activity, eventually determining action executions when a threshold value is reached (Hanes and Schall, 1996; Erlhagen and Schöner, 2002).

However, STs in Delay trials are not correlated to RTs (data not shown), and hence movement preparation and execution are, in general, two independent processes. This supports the view that motor plans are metastable states of premotor cortex establishing the initial conditions of the dynamical system that, when requested, will instruct other areas to implement planned actions (Churchland et al., 2010b).

On the other hand, completion of the motor plan is a necessary condition for the movement execution, and this accounts for the strong correlation between STs and RTs observed in No-stop trials. Only when a plan in premotor cortex has matured can the above “dynamical machine” guide the execution of a well formed movement. Under this hypothesis, PMd should be monitored by other brain structures [e.g., basal ganglia (Houk and Wise, 1995] to evaluate whether a cascade of STs is ending or not, thereby informing whether a motor program is available. Hence, the occurrence time of such transient dynamics may act as a trigger for movement initiation, eventually controlling RTs and other behavioral outputs. In PMd, we showed that the plan development is initiated by more excitable cortical modules, for which SUT times are governed by the stability of the low-firing Down state (Okamoto and Fukai, 2001; Miller and Wang, 2006; Martí et al., 2008) modulated, in our case, by an external input (Fig. 4). Local and global factors affecting Down-state stability, like synaptic self-excitation and neuromodulation (Durstewitz et al., 2000), make intrinsic activity fluctuations more or less effective in eliciting SUTs (Fig. 4C) and modulate their time scales. Depending on task demands, Down-state stability of pivotal modules may be adjusted to advance or delay the onset of ST chain reaction, without changing the resulting final metastable state. This could explain why in No-stop trials similar STs of the same cortical modules occur systematically earlier than in Delay trials (Figs. 3F, 7F). Indeed, RTs in the stop-signal task have to be adapted to SSDs (Logan and Cowan, 1984; Mirabella et al., 2011), a constrain absent in delayed reaching tasks.