CLASSIFYING PROCESSES: AN ESSAY IN APPLIED ONTOLOGY

Abstract

We begin by describing recent developments in the burgeoning discipline of applied ontology, focusing especially on the ways ontologies are providing a means for the consistent representation of scientific data. We then introduce Basic Formal Ontology (BFO), a top-level ontology that is serving as domain-neutral framework for the development of lower level ontologies in many specialist disciplines, above all in biology and medicine. BFO is a bicategorial ontology, embracing both three-dimensionalist (continuant) and four-dimensionalist (occurrent) perspectives within a single framework. We examine how BFO-conformant domain ontologies can deal with the consistent representation of scientific data deriving from the measurement of processes of different types, and we outline on this basis the first steps of an approach to the classification of such processes within the BFO framework.¹

1. The Background of Applied Ontology

1.1 Applied Ontologies in Biology

In the wake of the successful sequencing of the human genome, contemporary biology has been transformed into a discipline in which computer processing of genomic data plays an essential role. But genomic data processed by computers are useful to our understanding of, say, animal behavior, or human health and disease, only if some way can be found to link these data to theoretical assertions using terms that are intelligible to biologists. Such links are created by means of what biologists call ‘ontologies’, which are classifications of biological and other phenomena used to annotate (or ‘tag’) genomic and other experimental data in a systematic way that enables computers to gain consistent access even to data that has been collected in highly heterogeneous ways.²

When scientists are collecting data, this still frequently happens in a poorly coordinated fashion, and this is so even where the scientists in question are working in the same field. The data are in consequence difficult to aggregate in ways that might be useful in testing hypotheses or in drawing comparisons. In former times the needed connections were drawn through manual intervention by human beings familiar with the subject-matter. The indispensability of computers to the processing of data in information-intensive areas of science, however, has brought the recognition that ways need to be found to establish such connections computationally. The rise of science-based ontologies³ is one product of this recognition.⁴

We shall focus in what follows on those ontologies that are being developed on the basis of the assumption that, to create an ontology that brings benefits to scientists working with data in a given domain, the ontology should employ classifications that are based on the established scientific understanding of the entities and relations in this domain.⁵ An ontology of this sort comprises theoretical terms used to represent the types or classes of entities in some given domain together with relational expressions representing the relations between these entities. It thereby extends into the terminology of scientific theories some of the advantages brought by the International System of Units to the consistent representation of experimental data expressed in quantitative terms.

Each ontology can be conceived as a set of terms (nouns and noun phrases) which form the nodes of a directed acyclical graph, as in Figure 1. We can think of the nodes in such a graph as representing types or universals,⁶ which are the sorts of entities represented by the general terms used in formulating scientific theories such as ‘cell’ or ‘electron’ and which have instances which are the sorts of entities that are observed in scientific experiments. The nodes in the graph are joined by edges representing relations between the types, of which the most important (illustrated in Figure 1) are is_a (abbreviating ‘is a subtype of’) and part_of.⁷

Figure 1.

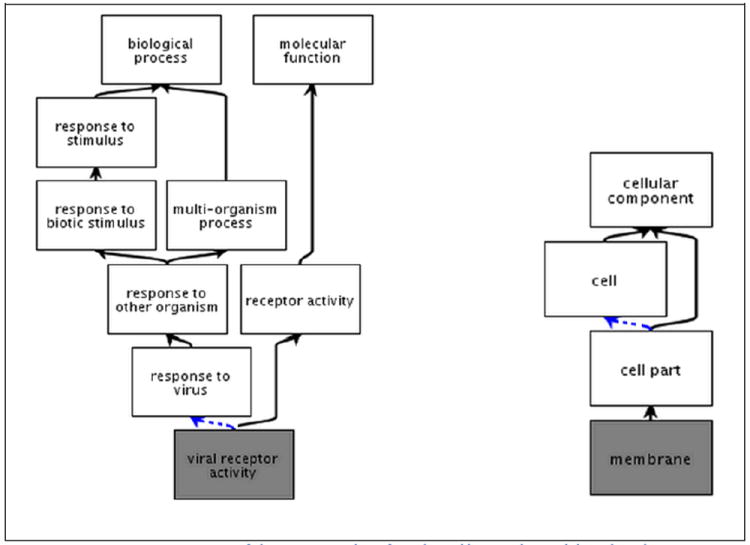
Fragments of the Gene Ontology from http://www.ebi.ac.uk/QuickGO/.

Nodes in the graph represent types in reality; edges represent is_a and part_of relations.

When two nodes are joined together by the is_a relation, as for example in:

• (1)receptor activity is_a molecular function

then this represents an assertion to the effect that all instances of the first type are also instances of the second type.

When two nodes are joined together by the part_of relation, as in

• (2)viral receptor activity part_of response to virus

then this represents an assertion to the effect that every instance of the first type is a part of some instance of the second type. (Here ‘part of’ in the unitalicized form represents the familiar instance-level parthood relation holding between, for example, your finger and your hand, or between the first half of a football match and the whole match.⁸)

1.2 The Common Logic Interchange Format and the Web Ontology Language

Ontological axioms such as (1) and (2), together with accompanying definitions of terms and relations, are formulated using logical languages – typically fragments of first-order logic – developed to facilitate the representation and interchange of information and data among disparate computer systems.⁹ Prominent examples are the (CLIF) Common Logic Interchange Format¹⁰ and the (OWL) Web Ontology Language¹¹. Common Logic is an ISO Standard family of languages with an expressivity equivalent to that of first-order logic. OWL-DL is a fragment of the language of first order logic belonging to the family of what are called Description Logics. While OWL-DL is marked by severe restrictions on its expressivity, the theories formulated in its terms have desirable computational properties. Because logical languages such as CLIF or OWL are used in their formulation, ontologies themselves can be viewed as simple first-order theories. Providing care is taken to use terms, definitions and relational expressions in consistent ways in different ontologies, such theories can be merged at will to create larger ontologies and, at least in the case of ontologies formulated using a language like OWL, the consistency of such mergers can be checked automatically using dedicated software applications called ‘reasoners’.¹²

1.3 The Gene Ontology

It is the Gene Ontology (GO), portions of which are illustrated in Figure 1, which is the most successful ontology currently being used by scientists in reasoning with experimental data.¹³ The GO consists of three sub-ontologies, together comprehending some 30,000 terms representing types and subtypes of biological processes, molecular functions, and cellular components. The GO is used by researchers in biology and biomedicine as a controlled vocabulary for describing in species-neutral fashion the attributes of genes and gene products (for example proteins) identified both in experiments on model organisms such as mouse or fly and in clinical studies of human beings. The GO offers a set of terms, such as ‘membrane’ or ‘viral receptor activity’ or ‘meiosis’, which are defined in ways which reflect the usage of biologists. It thereby provides a means of computationally associating humanly intelligible descriptions of biological phenomena with the massive quantities of sequence data being made available through genomic experimentation. Because the GO is species neutral, it provides a means of comparing data pertaining to different organisms in a way which allows results gained through experimentation on non-human organisms to be exploited in studies of human health and disease.¹⁴

1.4 The Gene Ontology and the Unification of Science

The GO is described by its originators as a ‘tool for the unification of biology’, and we can see how it is being used, in conjunction with other ontologies such as the Protein¹⁵ and Cell Ontologies¹⁶, to realize at least a part of the old logical empiricist vision of a logical unification of scientific knowledge.¹⁷ One aspect of this realization – not clearly anticipated by the logical empiricists – is the degree to which not only do theoretical assertions need to be unified through use of common logically structured ontologies, but so also do experimental data (for example gene or protein sequence data) compiled in databases processed by computers. In addition, bioinformaticians have discovered that additional ontology resources are needed to unify both of these with assertions about the experimental and computational procedures used to generate the data. This aspect of the unification of science is addressed by the Ontology for Biomedical Investigations (OBI),¹⁸ which comprehends a set of terms which can be used to describe the attributes of experiments in biological and related domains. The goal is a logically well-structured set of preferred terms and logical definitions that can be used to support common access to, and computational reasoning over, data about experiments in order to address the problems which arise at the point where experimental methods (or protocols or statistical algorithms or sample processing techniques or software or equipment used) have become so complex as to cause problems for the interpretation and comparison of the results achieved with their aid. The underlying idea is that use of the OBI vocabulary to annotate results obtained through experimentation would make these results not only more easily interpretable by human beings but also more reliably processable by computers.

2. Basic Formal Ontology

As will by now be clear, the principal concerns of applied ontologists are highly practical in nature. Just occasionally, however, they still face problems of a recognizably philosophical sort, and one such problem – relating to the treatment of process measurement data – is the topic of this essay.

Basic Formal Ontology (BFO) is a domain-neutral resource used by biologists and others to provide a top-level ontology that can serve as a common starting point for the creation of domain ontologies in different areas of science.¹⁹ BFO provides a formal-ontological architecture and a set of very general terms and relations that are currently being used by more than 100 ontology development groups in biology and other fields.²⁰

BFO is, by the standards predominant in contemporary ontology, very small, consisting of just 34 terms (see Figure 2), including both familiar terms such as ‘process’, ‘object’, ‘function’, ‘role’ and ‘disposition’, and less familiar terms such as ‘generically dependent continuant’ and ‘continuant fiat boundary’. Each of these terms must either be declared primitive and elucidated by examples and accompanying axioms, or it must be defined in a logically coherent way in terms of these primitives.

Figure 2.

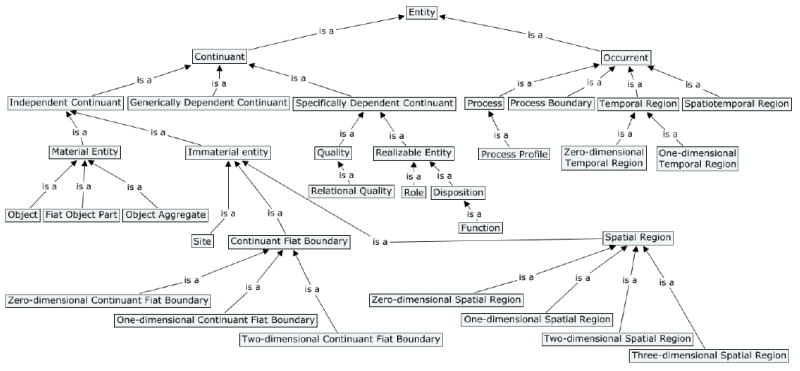
Draft BFO 2.0 is_a Hierarchy²¹

2.1 Continuants and Occurrents

BFO takes as its starting point a familiar distinction between two sets of views, which we can refer to as four-dimensionalist and three-dimensionalist, respectively. Four-dimensionalists (in simple terms) see reality as consisting exclusively of four-dimensional entities (variously referred to as processes, events, occurrents, perdurants, spacetime-worms, and so forth). They thereby regard all talk of entities of other sorts – for example, of three-dimensional things such as you and me – as a mere locution, to be eliminated in favour of some ultimate four-dimensionalist translation. (A four-dimensionalist might hold, for example, that only processes exist, and that talk of continuously existing things pertains rather to special kinds of processual entities, for example to continuous series of processes of a bill-clintonizing sort.²²) The three-dimensionalists who embrace positions at the opposite extreme see reality as consisting exclusively of entities extended along the three spatial dimensions, and they view all change in terms of the different attributes truly predicable of such entities at different times. Talk of processes, from this perspective, is a mere locution to be eliminated in favour of some ultimate three-dimensionalist translation.

Both families of views bring benefits of their own. In the field of medical ontology, for example, four-dimensionalism provides a natural framework for the ontological treatment of processes of, say, drug interaction or immune response, while three-dimensionalism provides a similarly natural framework for the treatment of the chemical, histological and anatomical structures which participate in such processes.

Unfortunately, the two sets of views are standardly formulated in a way which forces a choice between one or the other. BFO, in contrast, is founded on a bicategorial approach which seeks to combine elements of both the three-dimensionalist and four-dimensionalist perspectives.²³ Thus it incorporates an ontology of continuants and an ontology of occurrents within a single framework in a way that seeks to reconcile the contrasting logico-ontological orders reigning in each.

2.2 Zemach’s ‘Four Ontologies’

BFO’s treatment of the dichotomy between continuants and occurrents is adapted in part from the strategy proposed by Zemach in his ‘Four Ontologies’²⁴ for distinguishing between continuant and non-continuant entities, which Zemach calls ‘things’ and ‘events’, respectively. The former, for Zemach, are defined by the fact that they can be sliced (in actuality, or in imagination) to yield parts only along the spatial dimension – for example those parts of your table which we call its legs, top, nails, and so on.²⁵ The latter, in contrast, can be sliced to yield parts along any spatial and temporal dimensions. For example: the first year of the life of your table; the entire life of your table top (as contrasted with the life of your table legs); and so forth. As Zemach puts it:

An event is an entity that exists, in its entirety, in the area defined by its spatiotemporal boundaries, and each part of this area contains a part of the whole event. There are obviously indefinitely many ways to carve the world into events, some of which are useful and interesting (e.g., for the physicist) and some of which – the vast majority – seem to us to create hodge-podge collections of no interest whatsoever. (‘Four Ontologies’, pp. 233 f.)

Zemach notes that it is the ontology of continuants that comes most naturally to normal persons:

We normally regard almost every object we come across as a [continuant entity]: this chair, my pencil, my friend Richard Roe, the tree around the corner, the fly that crawls on the page. [The names we give to chairs and dogs] in our language, obey a grammar which is fundamentally dissimilar to the grammar of names of events. (‘Four Ontologies’, p. 240)

You, for example, are a continuant; your arms and legs are parts of you; your childhood, however, is not a part of you; rather, it is a part of your life. Continuants are entities which have no parts along the time axis; that is, they may be extended along the three spatial dimensions, not however along the temporal dimension.

It will be important for what follows that BFO generalizes Zemach’s idea of a continuant entity by allowing not only things (such as pencils and people) as continuants, but also entities that are dependent on things, such as qualities and dispositions such as solubility and fragility.²⁶ The solubility of a given portion of salt requires a dissolving process in order to be realized or manifested. A quality, for BFO, is a dependent continuant that does not require such a process of realization of this sort.

BFO departs from Zemach also in its account of occurrent entities. What Zemach refers to as ‘events’ are in every case the whole content of a spatiotemporal region. As we shall see, however, what BFO ‘processes’ are conceived in such a way that multiple processes are able to occupy the same spatiotemporal region, as for example when a process of your running down the street is co-located with a process of your getting warmer.

The distinction between continuants and occurrents is for BFO categorical. All the parts of continuants are continuants, and any whole to which a continuant belongs is also a continuant. Similarly, all the parts of occurrents are occurrents, and any whole to which an occurrent belongs is also an occurrent. This division flows from two essentially different ways of existing in time. For each continuant, there is some temporal interval during which it exists. For each occurrent there is some temporal interval during which it occurs. Certainly there are manifold connections between continuants and occurrents, but they are secured in BFO not through parthood relations, but rather through relations of participation.²⁷

2.3 The Ontological Square

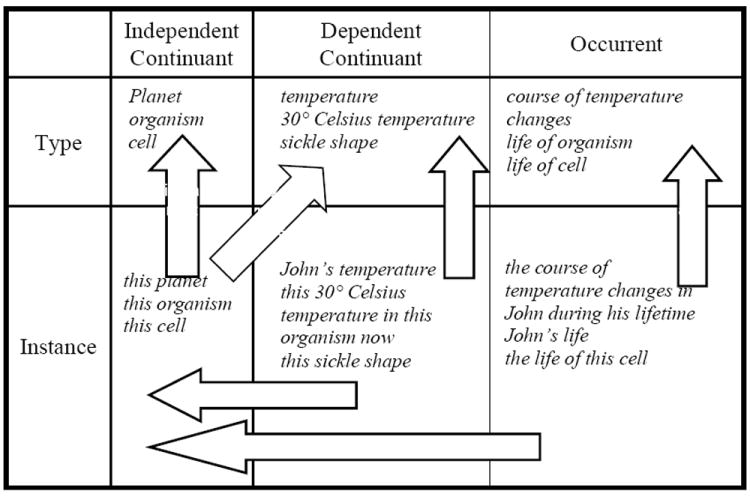
In allowing not only things but also entities that are dependent on things as continuants, BFO draws on Aristotle’s ideas concerning the division of substances and accidents, which reappears in BFO as the division between independent and dependent continuants. Given that BFO accepts also the distinction between universals and particulars, it thus recapitulates Aristotle’s ontological square,²⁸ as represented in Table 1.

Table 1.

Aristotle’s Ontological Square in BFO form

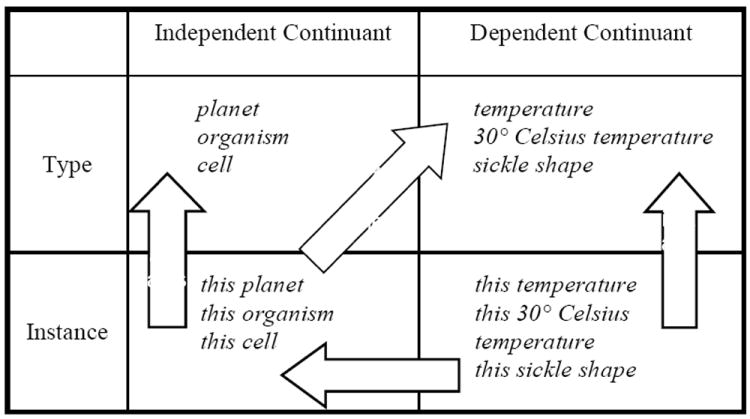
2.4 Determinable and Determinate Quality Universals

Qualities are first-class entities in the BFO ontology (of the sort referred to elsewhere in the literature as ‘tropes’, or ‘individual accidents’). They are entities which are dependent on the independent continuant entities (such as molecules, organisms, planets) which are their bearers. Qualities instantiate quality universals, which are divided into determinable (such as temperature, length and mass) and determinate (such as 37.0°C temperature, 1.6 meter length, and 4 kg mass).²⁹

Determinable quality universals are rigid in the sense that, if a determinable quality universal is exemplified by a particular bearer at any time during which this bearer exists, then it is exemplified at every such time.³⁰ John’s temperature (a certain quality instance inhering in John from the beginning to the end of his existence) instantiates the same determinable universal temperature throughout John’s life, even while instantiating different determinate temperature universals from one moment to the next, as illustrated in Figure 3.

Figure 3.

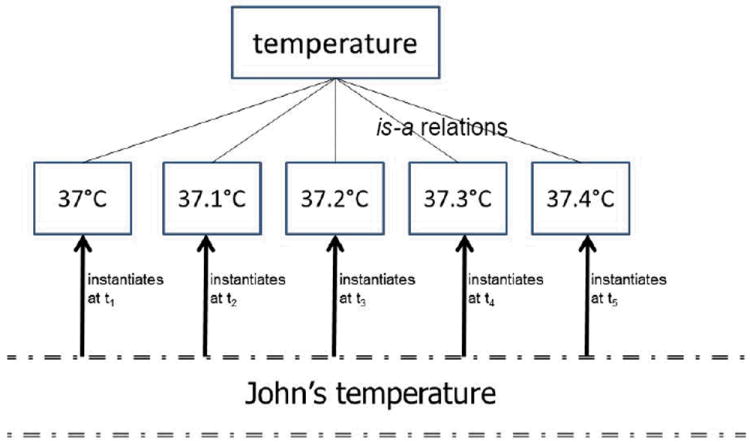
John’s temperature and some of the determinable and determinate universals it instantiates at different times

We note in passing that the determinate temperature universals are independent of whatever system of units is used to describe them. The universals here referred to in terms of degrees Celsius would be instantiated even in a world in which the Celsius or any other system of units had never been proposed. We note also that for certain families of determinate qualities we can draw a distinction between what we can think of as absolute and relative values, respectively. The Kelvin scale is a scale of absolute temperature values in this sense.

We can acknowledge also a second sense of ‘relative’ for determinate qualities that is involved for example when clinicians speak of temperatures as falling within some ‘normal’ range. A single person has a normal temperature in this sense only relative to (the temperature qualities of) persons in one or other larger population (for example healthy persons at rest in an indoor environment, persons recovering from pneumonia, persons sharing a certain genetic mutation in common, and so on).

3. Processes in BFO

Our primary concern in the remainder of this essay is with BFO’s treatment of occurrents, which include processes, process boundaries (for example beginnings and endings), spatiotemporal regions, and temporal intervals and temporal instants. BFO uses ‘occupies’ to refer to the relation that holds between an occurrent and the spatiotemporal region which it exactly fills. Processes and process boundaries occupy spatiotemporal regions and they span temporal intervals and temporal instants, respectively. Processes are thus distinguished from process boundaries in that the former, but not the latter, are temporally extended.

The assertion that one entity is an occurrent part of a second entity means simply that both are occurrents and that the first is a part – for example a sub-process – of the second. The sum of all processes taking place in your upper body during the course of your life is a proper occurrent part of the sum of processes taking place in your whole body during the same period. There is however a narrower relation which holds between occurrents a and b in the case where a is exactly the restriction of b to a temporal region that is a proper part of the temporal region spanned by b. When this relation holds, we shall say that a and b stand in the relation of temporal parthood, defined as follows:³¹

a temporal_part_of b =Def.
 a occurrent_part_of b
  & for some temporal region r (a spans r
   & for all occurrents c, r′
    if (c spans r′ & r′ occurrent_part_of r)
     then (c occurrent_part_of a iff c occurrent_part_of b)))

The first quarter of a game of football is a temporal part of the whole game. The process of your heart beating from 4pm to 5pm today is a temporal part of the entire process of your heart beating throughout your life. The 4th year of your life is a temporal part of your life, as is the process boundary which separates the 3rd and 4th years of your life. The process of a footballer’s heart beating once is an occurrent part, but not a temporal part, of the whole game (because when this heart beat occurs many other things are occurring which are also occurrent parts of the whole game).

3.1 BFO’s Treatment of Quality Measurement Data

When BFO is used to annotate the results of measurements of qualities, then in a typical case, for example in the case where your height is being measured, the following elements can be distinguished:

• (1)the BFO:object that is you,
• (2)the BFO:quality that is your height,
• (3)the BFO:one-dimensional spatial region, stretching at some time t between the top of your head and the base of your feet, that is measured when we measure your height at t.

The result of this measurement is expressed by means of

• (4)the BFO:generically dependent continuant expression: ‘1.7 m tall’.

Each item on this list is unproblematically identifiable as instantiating a BFO category. (4) is an information artifact.³² It can be stored, for instance, as a record in some file on your laptop. The record is said to be generically dependent upon its bearer since it can be transferred to another laptop through a process of exact copying. The temperature of your laptop, in contrast, is specifically dependent on the laptop, since a temperature (a specific instance of the universal temperature) cannot migrate from one body to another.

3.2 Ontological Treatment of Process Measurements

What happens, now, when we attempt to develop a corresponding analysis in BFO terms of the data resulting from measurements of processes? In the case of a body moving with constant speed, for example, we can here distinguish at least the following elements:

• (1)the BFO:object that is moving (changing its spatial location),
• (2)the BFO:process of moving (change of spatial location),
• (3)the BFO:spatiotemporal region occupied by this process (the path of the motion),
• (4)the BFO:temporal region spanned by this process (the temporal projection of (3)),
• (5)the speed of the process (rate of change of the spatial location of (1)),

where (5) is represented by means of

• (6)the BFO:generically dependent continuant expression: ‘3.12 meters per second’.

Each of the items (1)-(4) and (6) instantiates a readily identifiable BFO category. For item (5), on the other hand, there is no candidate category in the BFO ontology, since there is no counterpart on the occurrent side for BFO’s qualities of independent continuants.³³

3.3 Why Processes Do Not Change

To see why not, we need to understand the reason why qualities of independent continuants are accepted by BFO as first class entities. This turns on the fact that independent continuants can change from one time to the next by gaining and losing qualities. No counterpart of such change can be accepted by BFO on the occurrent side, since it follows trivially from BFO’s four-dimensionalist account of occurrents that occurrents cannot change.

Processes, in particular, cannot change on the four-dimensionalist view, because processes are changes (they are changes in those independent continuant entities which are their participants).³⁴ Certainly we have ways of speaking whose surface grammar suggests that processes can change. But when we say, for example, let’s speed up this process, then what we mean (in four-dimensionalist terms) is: let’s ensure that some on-going process is one which will be quicker than the process that would have occurred had we not made some specific extra effort.

Continuants may change not only through change in qualities but also in other ways. For example they may gain and lose parts over time, as for example when you gain and lose cells from your body. To address such changes, BFO’s instance-level continuant parthood relation is indexed by time. The counterpart relation on the side of occurrents, in contrast, holds always in a non-indexed way.³⁵ If a process p₁ occupying temporal interval t₁ is a part of a second process p₂ occupying temporal interval t₂, then p₁ is timelessly a part of p₂ just as t₁ is timelessly a part of t₂.

A second way in which continuants, but not occurrents, may change is by instantiating non-rigid universals. We saw examples of this in our discussion of dependent continuant universals such as temperature above. But examples can be found also among independent continuant universals such as larva or fetus. If some organism a instantiates the universal larva at t, for example, then it does not follow that a instantiates larva at all times at which a exists. Universals on the side of occurrents, in contrast, are always rigid, so that if an occurrent instantiates a universal at some time, then it instantiates this universal at all times.³⁶

An apparent analogue of the phenomenon of non-rigidity in the realm of occurrents is illustrated by a case such as the following. Suppose John, half way through some 20 minute running process p, increases his running speed from 6 to 7 mph. Could we not then say that the process p instantiates the determinate universal 6 mph running process in the first 10 minute interval and the determinate universal 7 mph running process in the second? On the four-dimensionalist view, the answer to this question is ‘no’: p never instantiates the universal 6 mph running process, any more than the front half of my rabbit instantiates the universal rabbit. What we can more properly assert is that p, timelessly, has a sub-process p₁ (a temporal part of p), which instantiates the universal 6 mph running process, and a subsequent sub-process p₂ (a second temporal part of p) which instantiates the universal 7 mph running process.

3.4 First Approximation to a Solution of the Problem of Process Measurement Data

How, then, do we respond to the need on the part of the users of BFO to annotate data deriving from measurements which have processes as their targets?

Our response is, in first approximation, very simple: when we predicate, for instance, ‘has speed 3.12 m/s’, of a certain process of motion, then we are asserting, not that that the process in question has some special quality which the same process, in another scenario, might conceivably have lacked. Rather, we are asserting that this process is of a certain special type. Thus an assertion to the effect that

• (1)motion p has speed v

is analogous, not to:

• (2)rabbit r has weight w,

but rather to:

• (3)rabbit r instance_of universal rabbit.

(1), in other words, should be interpreted as being of the form:

• (4)motion p instance_of universal motion with speed v.

where the universal motion with speed v is a specification of the universal motion.³⁷

This treatment of attribution in terms of instantiation reflects what is standard policy in other parts of BFO in accordance with its goal of remaining ontologically simple. There are no qualities of occurrents, in BFO, just as there are no qualities of qualities, and also no qualities of spatial or temporal regions. Leaving aside the single case of qualities of independent continuants, attributions in BFO are quite generally treated in terms of the relation of instantiation, as in Table 2:

Table 2.

Examples of attributions in BFO

spatial region r has volume w	r instance_of universal region with volume w
height quality q has value 2 meters at t	q projects onto a one-dimensional spatial region r at t and r instance of universal 2 meter long one-dimensional spatial region
temporal region t has duration d	t instance_of universal temporal region with duration d
temperature quality q has value 63° Celsius	q instance_of universal 63° Celsius temperature quality
process p has duration d	process p spans temporal region t and t instance_of universal temporal region with duration d
motion p of object o has trajectory with shape s	the sequence of locations occupied by object o at successive instants of time forms a spatiotemporal region t and t instance_of universal spatiotemporal region with shape s

3.5 Processes as Dependent Entities

Processes themselves stand to the independent continuants which are their participants in a relation that is analogous to that in which qualities stand to the independent continuants which are their bearers. In both cases we have to deal with the relation of what BFO calls specific dependence. ³⁸ This means that we can extend the ontological square in Table 1 with a representation of the relation between instances and universals on the side of occurrents to create an ontological sextet, as follows:³⁹

Our strategy, now, is to use the instantiation relation captured in the rightmost column of Table 3 as basis for an account of the truthmakers of process attributions. But to make an approach along these lines work, certain problems still need to be addressed.

Table 3.

The Ontological Sextet

4. Process Profiles

We note, first, that a single running process p might be an instance of multiple determinable universals such as:

• running process

• constant speed running process

• cardiovascular exercise process

• air-displacement process

• compression sock testing process

as well as of multiple determinate universals such as

• running process of 30 minute duration

• 3.12 m/s motion process

• 9.2 calories per minute energy burning process

• 30.12 liters per kilometer oxygen utilizing process

and so on.

How, given the complexity of this list and of the many similar lists which could be created for many other types of process, are we to create classifications of the process universals instantiated in different domains in the sort of principled way that will be necessary to ensure consistency and interoperability when classifications are needed for the annotation of data in domains such as physiology or pathology?

To see the lines of our answer to this question, consider Figure 4, which illustrates the cardiac events occurring in the left ventricle of a human heart. This figure tells us that each successive beating of the heart is such as to involve multiple different sorts of physiological processes, corresponding to measurements along the six distinct dimensions of aortic pressure, atrial pressure, ventricular pressure, ventricular volume, electrical activity, and voltage⁴⁰, respectively.⁴¹

Figure 4.

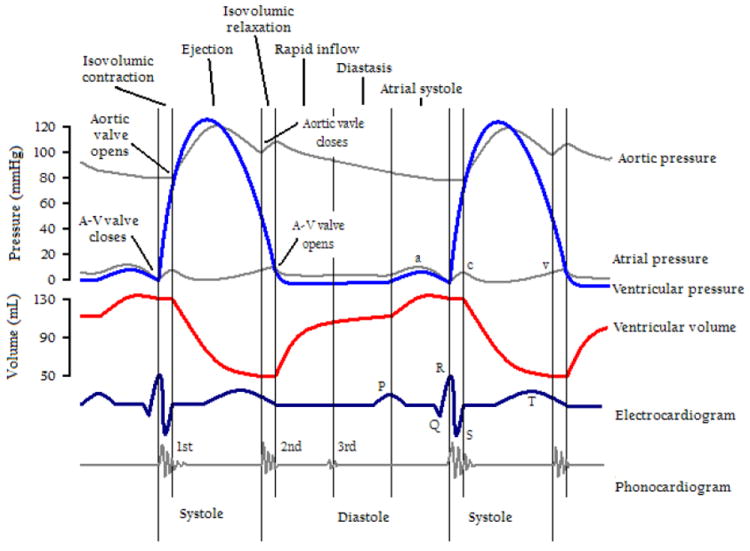
A Wiggers diagram, showing the cardiac processes occurring in the left ventricle ⁴²

These structural dimensions are, equivalently, different dimensions along which processes can be compared. When comparing two heart beating processes as being for example of the same rate, or when comparing two games of chess as consisting of the same series of moves, then there is something in each of the two processes which is – not numerically but qualitatively – ‘the same’. This something which the two processes share in common we shall refer to in what follows to as a process profile.

What they share in common more precisely is that each contains an instantiation of the same process profile universal. The figure illustrates multiple instantiations of multiple process profile universals reflecting the fact that we can measure and compare cardiac processes along multiple different axes, each of which corresponds, in our proposed terminology, to a different determinable process profile universal.

In the running case, similarly, we can measure and compare along different structural dimensions pertaining to speed of motion, energy consumed, oxygen utilized, and so forth. In each case we focus on some one structural dimension and thereby ignore, through a process of selective abstraction, all other dimensions within the whole process.

Not every dimension of comparison between processes corresponds to a determinable process profile universal in the sense here intended. When we compare processes as to their duration, for example, or as to the time at which they occur or their trajectory in space and time, then we can advert simply to the temporal or spatiotemporal regions which the processes occupy (see again Table 2 above). We can compare processes also for example in terms of whether they involve the same participants, or take place in the same spatial regions. Process profiles enter into the picture only where it is something (thus some occurrent entity) in the processes themselves that serves as fundamentum comparationis.

4.1 Quality Process Profiles

The simplest example of a process profile is that part of a process which serves as the target of selective abstraction focused on a sequence of instances of determinate qualities such as temperature or height. When we measure, for example, the process of temperature increase in patient John, then there is a sequence of determinate temperature qualities whose values when measured on some scale are recorded on John’s temperature chart. Process profiles of this simple sort can very often be represented by means of a graph in which measures of a certain quality are plotted against time.

4.2 Rate Process Profiles

On a somewhat higher level of complexity are what we shall call rate process profiles, which are the targets of selective abstraction focused not on determinate quality magnitudes plotted over successive instants of time, but rather on certain ratios between these magnitudes and associated intervals of elapsed time. A speed process profile, for example, is represented by a graph plotting against time the ratio of distance covered per unit of time. Since rates may change, and since such changes, too, may have rates of change, we have to deal here with a hierarchy of process profile universals at successive levels, including:

speed profile
 constant speed profile
  2 mph constant speed profile
  3 mph constant speed profile
acceleration profile (increasing speed profile)
 constant acceleration profile
  32ft/s2 acceleration profile
  33 ft/s2 acceleration profile
 variable acceleration profile
  increasing acceleration profile

and so on.

The types and subtypes listed here are in some respects analogous to the determinable and determinable types and subtypes of qualities recognized by BFO-conformant ontologies on the continuant side discussed already in our discussion of Figure 3 above. And here, too, the reader must bear in mind that the determinate process profile universals in question – while they need to be referred to in reporting results of measurement acts using specific units of measure – are in and of themselves unit-specification independent.

Measurement data representing rates are often expressed in terms not of the process profile instantiated across a temporal interval, but rather of what holds at some specific temporal instant. The latter is then defined in terms of the former in the following way:

• (1)John is moving with speed v at time instant t

asserts, roughly, that there is some temporal interval (t₁, t₂), including t in its interior, in which the speed v process profile universal is instantiated. More precisely (in order to take account of the fact that John may be moving with a continuously changing speed in the neighborhood of t), (1) must be formulated in something like the following terms:

• (2)Given any ε, however small, we can find some interval (t₁, t₂), including t in its interior, during which the speed w at which John is moving is such that the difference between w and v is less than ε.⁴³

4.3 Cyclical Process Profiles

One important sub-family of rate process profiles is illustrated by cyclical processes, for example the 60 beats per minute beating process of John’s heart, or the 120 beats per minute of his drumming process, and so on.

Cyclical process profiles are a subtype of rate process profiles in which the salient ratio is not distance covered but rather number of cycles per unit of time. Here again we find a variety of more specialized universals at lower levels of generality, including for example:

rate process profile
 cyclical process profile
  regular cyclical process profile
   3 bpm cyclical process profile
   4 bpm cyclical process profile
  irregular cyclical process profile
   increasing cyclical process profile

and so on.

In the case of a regular cyclical process profile, a rate can be assigned in the simplest possible fashion by dividing the number of cycles by the duration of the temporal region occupied by the process profile as a whole. Irregular cyclical process profiles, for example as identified in the clinic, or in a morse code transmission, or in readings on an aircraft instrument panel, may be of specific interest because they are of diagnostic or forensic significance.

5. Conclusion: Towards an Ontology of Time Series Graphs

We have dealt in the foregoing with only a small selection of the ways in which processes can be classified through division into types and subtypes. One important next step will deal with the ways in which such classification is complicated by the fact that processes are embedded within a series of larger process wholes, each nested within yet larger process wholes. Thus when a billiard ball is moving across a table, we can focus on the ball’s motion relative to the table, but we can also focus on the larger process which is the motion of the body-table system relative to the motion of the earth; or we can focus on the motion of the body-table-earth system relative to the movement of the sun; and so forth.

Human physiological processes, too, are embedded within series of larger wholes in this way. When studying the heart, for example, physiologists may investigate processes within the interior of the left ventricle, interactions between the left ventricle and other parts of the cardiovascular system, interactions between this system and other bodily systems, and so on. Physiologists may be interested in the processes involving multiple organisms; for example they may be interested in some given organism as part of one or other larger whole which includes some population of organisms of a relevant similar type (all humans, all human babies of a given birth weight, all athletes, and so on). Normal processes are defined for this larger population (as normal qualities were defined above), and deviations from this norm are defined for the single organism relative thereto.

A further application of the theory of process profiles will include the development of an ontology of time series graphs in terms of a view of process profiles as the truthmakers for such graphs. On this basis we will then explore how the ontology of process profiles might throw light on the semantics of differential equations and of the various mathematical models of dynamic systems in physics, biology and other disciplines constructed on their basis.⁴⁴

We will investigate also how the theory can be applied not merely to quantitative information artifacts but also to other sorts of symbolic representations of processes, as for instance when a chess game is represented in one or other of the standard chess notations, or when a symphony performance is represented in a score. Interestingly, this score itself serves also to provide the set of instructions for the unfolding performance, and we shall explore also ways in which the idea of process profiles may help to throw light on how such planned processes depend on, and are at the same represented by, the plans or protocols which define them.