Development of a model to simulate infection dynamics of Mycobacterium bovis in cattle herds in the United States

Abstract

Objective

To develop a mathematical model to simulate infection dynamics of Mycobacterium bovis in cattle herds in the United States and predict efficacy of the current national control strategy for tuberculosis in cattle.

Design

Stochastic simulation model.

Sample

Theoretical cattle herds in the United States.

Procedures

A model of within-herd M bovis transmission dynamics following introduction of 1 latently infected cow was developed. Frequency- and density-dependent transmission modes and 3 tuberculin-test based culling strategies (no test-based culling, constant (annual) testing with test-based culling, and the current strategy of slaughterhouse detection-based testing and culling) were investigated. Results were evaluated for 3 herd sizes over a 10-year period and validated via simulation of known outbreaks of M bovis infection.

Results

On the basis of 1,000 simulations (1000 herds each) at replacement rates typical for dairy cattle (0.33/y), median time to detection of M bovis infection in medium-sized herds (276 adult cattle) via slaughterhouse surveillance was 27 months after introduction, and 58% of these herds would spontaneously clear the infection prior to that time. Sixty-two percent of medium-sized herds without intervention and 99% of those managed with constant test-based culling were predicted to clear infection < 10 years after introduction. The model predicted observed outbreaks best for frequency-dependent transmission, and probability of clearance was most sensitive to replacement rate.

Conclusions and Clinical Relevance

Although modeling indicated the current national control strategy was sufficient for elimination of M bovis infection from dairy herds after detection, slaughterhouse surveillance was not sufficient to detect M bovis infection in all herds and resulted in subjectively delayed detection, compared with the constant testing method. Further research is required to economically optimize this strategy.

Tuberculosis caused by Mycobacterium bovis infection is currently at historically low levels in cattle in the United States, with an estimated prevalence of 0.0006% herds in 2007¹ and 51 states, zones, and territories with accredited free status (herd prevalence of 0 for bovine tuberculosis in cattle and bison, with no more than 1 detected herd outbreak within a 24-month period, and all detected herds depopulated and investigated within 90 days of confirmation and associated herds investigated within 120 days²) at the end of 2010.³ The cost of surveillance is high, with 1,275,815 live cattle and 10,914 granulomas from slaughtered cattle tested in 2010.³ Between 2001 and 2009, approximately $342 million was spent on national bovine tuberculosis surveillance and control.⁴ Since 1994, more than 1.8 million cattle have been tested in over 38,000 whole-herd surveillance tests in Michigan alone, detecting M bovis infection in 150 cattle from 50 herds.³ In Nebraska, trace-out and trace-back testing in 2009 detected 1 infected beef cow out of > 31,000 tested and no infected dairy cattle out of > 16,000 tested, at a cost of $450,000.³ As the proportion of dairy herds with > 100 head of cattle increased from 0.115 in 1991 to 0.233 in 2006, costs of indemnity attributable to depopulation also increased.⁵ For these reasons, Veterinary Services, a branch of the USDA APHIS, recently recommended changes to the national bovine tuberculosis control program, including a need to prioritize animal removal and develop test-and-removal protocols.⁴ Current testing protocols require herds to have 8 negative whole-herd test results, with a testing interval of 60 days between each of the first 4 tests, 180 days between the fourth and fifth test, and 12 months between remaining tests, to be declared clear of M. bovis after slaughterhouse detection. Under the current plan, all whole-herd tests prior to negative results for 2 consecutive whole-herd tests require postmortem inspection of all cattle that have positive CFT results.²

Several models have been developed to predict within-herd spread of M bovis infection in well-managed dairy cattle in other countries, including New Zealand,^6,7 Ireland,⁸ and Argentina.⁹ However, no models exist for the US dairy system, in which animals are generally intensively managed in high-density environments. Overall, the United States lacks a nationwide sylvatic source of infection, as caused by brushtail possums in New Zealand and badgers in the United Kingdom and importation of M bovis–infected animals in Argentina.⁹ Portions of the United States do have potential wildlife reservoirs of M bovis infection such as white-tailed deer⁴ or a potential for transboundary introduction via the approximately 1 million cattle introduced annually from Mexico.⁴ The majority of these imported animals are beef cattle intended for slaughter, and importation has been shown to have a role in infection of dairy herds in the western and southwestern United States, where feeder herds have been known to share premises with herds under the management of professional heifer growers.¹⁰ Although uncommon, shipment of exposed cattle throughout the country should be considered the primary source of infection in most states. Hence, we suggest that a model of within-herd transmission of M bovis for the US cattle industry should account for within-herd spread after a single introduction event; importation and infectious pressure from wildlife as sources of repeat introduction should be considered separate elements that can be added in future analyses for specific regions.

The objective of the study reported here was to develop a mathematical model to simulate infection dynamics of M bovis in cattle herds in the United States and predict efficacy of the current national strategy for control of M bovis infection in cattle. A secondary objective was to provide a framework that can be used to study the financial impact of bovine tuberculosis outbreaks in US cattle herds. We used a mathematical model to predict the probability of disease spread within herds, the number of infected animals, and the time required to clear a herd of the disease following introduction of 1 M bovis–infected cow.

Materials and Methods

Model Development

A model for transmission and progression of M. bovis in a typical US cattle herd was designed on the basis of existing models,⁷ knowledge of the biology of the pathogen, and the structure of typical US cattle herds (Figure 1). The model was defined by the following 4 differential equations:

$$\begin{array}{l}\frac{ds}{dt}=\mu N-({\mu }_d+{\delta }_{FP}+\beta I)S\\ \frac{dE}{dt}=\beta SI-({\mu }_d+{\delta }_{FP}+\gamma )E\\ \frac{dR}{dt}=\gamma E-({\mu }_d+{\delta }_{TP}+\eta )R\\ \frac{dI}{dt}=\eta R-({\mu }_d+{\delta }_{TP})I\end{array}$$

where N is the current herd size and S, E, R, and I represent the number of cattle classified as susceptible to M bovis infection; latently infected (ie, noninfectious [not shedding the organism] and having negative test results); noninfectious, test-positive reactors (ie, cattle with positive CFT or CCT results); and infectious [shedding M bovis], respectively. The change in category X over time is expressed as dX/dt. The rate at which cattle susceptible to infection are born into the herd as replacements is designated as μ. The effective contact rate of M bovis infection in density-dependent models is represented by β, and the rate at which susceptible cattle develop latent M bovis infection following exposure to infectious animals is designated βI. The variable γ represents the rate at which latently infected cattle become (noninfectious) reactors, and the rate at which these reactors become infectious is designated η. The variables δ_TP and δ_FP represent culling rates on the basis of true-positive and false-positive test results, respectively, and μ_d is the general culling rate for all cattle. This variable is related to the birth rate and current herd size and is scaled to the target herd size (N*, the optimal size of the herd) according to the following equation: μ_d = μN/N*. Modeling simulations included variables that were user defined or obtained from other sources. These were summarized (Appendix).

Figure 1.

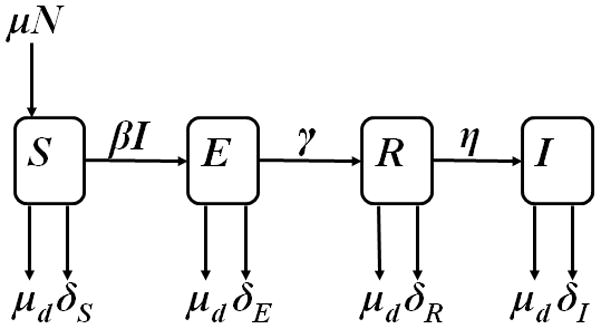
Schematic diagram of the full state-transition model for dynamics of the spread of Mycobacterium bovis infection in a theoretical US cattle herd. Animals susceptible to M bovis infection (S) enter a herd of size N at a replacement rate of μ, become latently infected at rate βI through contact with cattle shedding M bovis (termed infectious [I]). Latently infected cattle (E) become noninfectious, test-positive reactors (R) at rate γ, which become infectious at rate η. Cattle in each category k are removed on the basis of CFT and CCT results at rate δ_k, which is based on the testing interval as well as sensitivity and specificity of the skin tests. From all categories, cattle are culled (or die for any reason) at a general rate μ_d.

Because it was unknown if M bovis transmission among cattle would be better explained by frequency-dependent or density-dependent transmission, both methods were used and the results were compared. In density-dependent transmission, β was set as a constant (Appendix), which allowed the rate of infection, βI, to change with the number of susceptible and infected animals, which in turn could change with herd size. In frequency-dependent transmission, the term β′ was population size-dependent, and defined at time t as follows:

$${\beta }^{\prime }(t)=\frac{\beta }{N(t)}$$

where β is the previously described effective contact rate and N(t) is the number of cattle in the herd at time t. This allowed the rate of infection, calculated as βI/N, to scale only with the proportion of cattle susceptible to infection. Because the proportion of susceptible animals remained stable with changes in herd size, the rate of infection remained the same for herds with different sizes.

Three versions of test-based culling were used in the model: no test-based culling (base model), constant testing and test-based culling, and the current slaughterhouse detection-based testing and culling strategy. According to the slaughterhouse detection-based strategy, no test-based culling was implemented unless an M bovis–infected animal was detected via postmortem inspection; the probability of detecting an infected animal removed from the herd through general culling was termed Se_pm; this term does not appear in the model development equations, as the system of ordinary differential equations was not used to determine detection. Under the constant testing strategy, whole-herd tests were performed annually unless an infected animal was detected via testing or slaughterhouse surveillance. In both the current and the constant testing versions, test-based culling was implemented at 3-month intervals (user-defined on the basis of the minimum testing interval of 2 months) after detection through slaughterhouse surveillance or whole-herd testing.

Cattle in the reactor and infectious categories were subject to test-based removal (culling) on the basis of true-positive test results at rates δ_R and δ_I, respectively, whereas those in the susceptible and latently infected categories were removed on the basis of false-positive test results at rates δ_S and δ_E, respectively. The test-based removal rates were calculated according to the following equations, which were adapted from the culling rates derived in a previous study¹¹ by our group:

$$\begin{array}{l}{\delta }_{TP}={\delta }_R={\delta }_I={\left(T_{tt}+\left[\frac{1}{Se+\{1-Sp\}-S{e}^{·}\{1-Sp\}}-\{1-\nu \}\right]T_{ti}\right)}^{-1}\\ {\delta }_{FP}={\delta }_S={\delta }_E={\left(T_{tt}+\left[\frac{1}{\{1-Sp\}}-\{1-\nu \}\right]T_{ti}\right)}^{-1}\\ Se={{Se}_{\mathit{CFT}}}^{·}{Se}_{\mathit{CCT}}\end{array}$$

where T_tt is the test turnaround time, T_ti is the testing interval, v is the proportion of the testing interval during which an animal recently categorized as a reactor could be identified with the tests performed (set at 0.5, the midpoint of the period, as a conservative estimate), Se_CFT is sensitivity of the CFT, Se_CCT is sensitivity of the CCT, Se is the combined sensitivity of both tests, and Sp is specificity of the CCT.

The basic reproduction ratio for M bovis infection, R₀ (a threshold value), was derived using the next generation method¹² for the model without test-based culling and the reproduction ratio R_0t was derived for the model with constant test-based culling by use of the previously defined variables as follows:

$$\begin{array}{l}{R}_0=\left(\frac{\gamma }{\gamma +\mu }\right)\left(\frac{\eta }{\eta +\mu }\right)\left(\frac{\beta N}{\mu }\right)\\ R_{0t}=\left(\frac{\gamma }{\gamma +\mu +{\delta }_{FP}}\right)\left(\frac{\eta }{\eta +\mu +{\delta }_{TP}}\right)\left(\frac{\beta N}{\mu +{\delta }_{TP}}\right)\end{array}$$

If R₀ was < 1, no endemic infection would be expected even without control strategies. If R_0t was < 1, no endemic infection would be expected in herds managed with test-and-removal strategies.

In the frequency-dependent model, the herd size term (N) was cancelled out by use of the effective contact rate term (β′) in place of the density-dependent effective contact rate term (β). At introduction of the first infected animal into a herd that was not subject to test strategies, herd infection dynamics were defined by R₀, whereas under a testing program, infection dynamics at introduction in a naïve population were defined by R_0t. Thus, the system’s dynamics were dependent on the sensitivity of slaughterhouse detection, which was not captured in either reproduction ratio and which drove the transition from the calculation of R₀ to the calculation of R_0t.

A stochastic realization of the full model was developed using the τ-leap methodology¹³ with 1-month time steps; the order of actions was infection, disease stage progression, death or general culling, birth, and test-based culling. These actions were defined by a series of equations, in which t is the time point, t−1 is the period immediately preceding time t (in this model, the previous month), and Poi(x) is a Poisson distribution with a rate of x. All random selections were made using a default random number generator supplied with the software, and were given an upper limit of the number of cattle in the category from which they were removed.

Infection was modeled as follows:

$$\begin{array}{l}\mathit{Number}of\mathit{Cattle}\mathit{Infected}=\mathit{Poi}({\beta }^{\prime }S{[t]}^{\prime }I[t])\\ S(t)=S(t-1)-\mathit{Number}of\mathit{Cattle}\mathit{Infected}\\ E(t)=E(t-1)+\mathit{Number}of\mathit{Cattle}\mathit{Infected}\end{array}$$

The number of cattle infected at time t was randomly selected on the basis of infectious pressure (βSI). These animals were then moved from the susceptible category to the latently infected category.

Disease Progression was calculated according to the following equations:

$$\begin{array}{l}{R}_{\mathit{new}}=\mathit{Poi}({\gamma }^{·}E[t])\\ I_{\mathit{new}}=\mathit{Poi}({\eta }^{·}R[t])\\ E(t)=E(t-1)-R_{\mathit{new}}\\ R(t)=R(t-1)+R_{\mathit{new}}-I_{\mathit{new}}\\ I(t)=I(t-1)+I_{\mathit{new}}\end{array}$$

where R_new and I_new represent the number of cattle newly categorized as reactors and infectious, respectively. The number of cattle newly categorized as reactors at time t was randomly selected and moved from the latently infected category to the reactor category. The number of cattle newly categorized as infectious at time t was then randomly selected and moved from the reactor category to the infectious category.

Death, including culling for general purposes, was modeled for cattle in each category with the following equations:

$$\begin{array}{l}S(t)=S(t-1)-\mathit{Poi}({{\mu }_d}^{·}S[t])\\ E(t)=E(t-1)-\mathit{Poi}({{\mu }_d}^{·}E[t])\\ R(t)=R(t-1)-\mathit{Poi}({{\mu }_d}^{·}R[t])\\ I(t)=I(t-1)-\mathit{Poi}({{\mu }_d}^{·}I[t])\end{array}$$

In each category, the number of cattle undergoing culling or other death at time t was randomly selected and removed from that category.

Birth of cattle was calculated as follows:

$$S(t)=S(t-1)+\mathit{Poi}({\mu }^{·}N[t])$$

The number of calves born at time t was randomly selected and added to the susceptible category.

Finally, culling of cattle in each category for positive CFT and CCT results was calculated with the following equations:

$$\begin{array}{l}S(t)=S(t-1)-\mathit{Poi}({{\delta }_{FP}}^{·}S[t])\\ E(t)=E(t-1)-\mathit{Poi}({{\delta }_{FP}}^{·}E[t])\\ R(t)=R(t-1)-\mathit{Poi}({{\delta }_{TP}}^{·}R[t])\\ I(t)=I(t-1)-\mathit{Poi}({{\delta }_{TP}}^{·}I[t])\end{array}$$

In each category at time t, the number of cattle removed for a positive test result was randomly selected and removed from that category.

Modeling was initiated with the introduction of 1 latently infected animal and implemented for a period of 10 years or until no cattle categorized as infectious remained in the herd (ie, herd clearance of M bovis, termed fadeout), whichever occurred first. The number of infected cattle and the number of cattle culled because of a positive test result in each category were tracked, and the time at which fadeout occurred was recorded where applicable. Results were produced separately for small, medium-sized, and large herds (comprising 40, 276, and 3,000 adult cattle, respectively) with typical replacement rates for dairy (0.33 cows/y)¹⁴ and beef herds (0.17 cows/y)¹⁵ to identify effects of various herd sizes and replacement rates. Any outputs in which the ranges failed to overlap were considered to be statistically significantly different. The model and all analyses were programmed with commercially available software.^a The program was accessed through an analytic software interface.^b

Validation of base model results

To determine the validity of the base model results, the model was run to simulate a reported outbreak in a US beef herd with well-established introduction, final outcome, and timeline.¹⁶ In that outbreak, 26 Red Devon cattle were purchased in a short period of time and added to a beef ranch where 1 animal remained from the previous owner. This animal was believed to be exposed to M bovis. After purchase of the 26 cattle, the herd was closed except for purchase of breeding bulls. All introduced cattle (26 plus bulls) were tested for M bovis infection at the time of purchase with negative results. After 15 years of farm operation, the bovine tuberculosis outbreak was detected through slaughterhouse surveillance; of 331 cattle on the farm, 193 (58%) randomly selected animals were tested via CCT and 52 had positive results. Of the 52 cattle with positive CCT results, 32 had visible lesions at slaughter. In order to reproduce the growth of the herd, the final herd size was assumed to be the target herd size (N* = 331) and the base replacement rate was assumed to be 0.25/year. Infection dynamics of the herd were simulated as described, and the proportion of CCT reactors and cattle with detectable lesions after 15 years was recorded. Perfect sensitivity was assumed for postmortem inspection in cattle with positive CCT results (ie, it was assumed that all cattle with true-positive CCT results would have detectable lesions), as there were no further postmortem infection assessments performed for the herd. The proportion of iterations in which the number of test-positive cattle after 15 years equaled or exceeded the observed value was compared between the frequency- and density-dependent models and statistically evaluated with a Fisher exact test, with values of P < 0.05 considered significant, and 95% prediction intervals were calculated for this outcome. Validation measures were repeated with the minimum and maximum effective contact rates predicted by Barlow et al⁶ (0.004/y and 0.028/y, respectively) to test sensitivity of the results to this variable.

Validation of culling strategy model

The current slaughterhouse detection-based testing and culling strategy model was validated by simulating known outbreaks of bovine tuberculosis in 10 dairy herds with known total outbreak sizes in Texas and New Mexico.¹⁰ These herds were reported to have outbreaks detected through slaughterhouse surveillance and were subsequently managed via test-based culling. Known infected herds from Michigan, for which there was a possibility of transmission from wildlife, were omitted from the analysis as the possibility of reintroduction could bias the results. Each herd was assumed to have 1 to 4 latently infected cattle introduced, equal to the number of cattle that initially had a diagnosis of bovine tuberculosis, and the model was simulated as described for the current test-based culling strategy for the particular herd size observed. Because testing intervals were not reported, a standard testing interval of 3 months was assumed. The proportion of iterations in which the number of cattle with positive test results equaled the observed value or was greater or less than the observed value by at least 1 was compared in each herd and for all herds between the frequency-and density-dependent models with a Fisher exact test, with values of P < 0.05 considered significant. Validation measures were repeated with the minimum and maximum effective contact rates predicted by Barlow et al⁶ (0.004/y and 0.028/y, respectively) to test the sensitivity of the results to this variable.

Sensitivity Analysis

Global sensitivity analysis was performed for the base model, the current slaughterhouse detection-based testing and culling strategy model, and the constant testing and test-based culling strategy model using Latin hypercube sampling, with variables varied over the estimated range of their values (Appendix). Previously described variables included for the base model were β, γ, η, μ, and N; in the test-based models, Se_pm, Se, and Sp were also included. The base model was run for 1,000 iterations of 10 years each, and the PRCC^c was calculated for each variable with each of the following outputs: probability of fadeout in 10 years and the mean and SD of the total number of cattle infected over 10 years. The models were run for 1,000 iterations or until fadeout, and the PRCC was calculated for each variable with each of the following outputs: mean and SD of the number of months required for fadeout and mean and SD of the total number of cattle infected over 10 years. All P values < 0.10 were considered significant in these models.

Effects of testing strategies

To explore the effects of different combinations of whole-herd testing, the model was run for 1,000 iterations over each of a range of testing intervals (2 months to 1 year) and negative results for whole-herd tests required for a herd to be declared clear of M bovis (1 to 5). The number of cattle culled, number of months herds were quarantined (ie, months between the time of detection and being declared clear of M bovis), and the probability of an infected herd being declared clear of infection were recorded for each scenario.

Results

Unless otherwise stated, all results were obtained from the frequency-dependent model. These were selected because of better fit of the model to the observed data.

Model development

With the previously described base values used for model variables (Appendix), the basic reproduction ratio for M bovis infection in the model was 4.13 and the basic reproduction ratio with constant test-based culling was 0.02, indicating that the infection would spread in the absence of testing, but would be controlled by test-based culling. With the assumed effective contact rate, the reproduction ratio with constant test-based culling was < 1 when testing was performed more frequently than every 4 years. It should be noted that in the density-dependent transmission model, where both reproduction ratios scale linearly with herd size, a more frequent testing strategy would be required to eliminate the infection in large herds.

The stochastic model without test-based culling (base model) predicted that many herds (mean, 340 to 570 per 1,000) would have an outbreak of bovine tuberculosis, although in 1,000 simulations of 1,000 herds each, fadeout occurred ≤ 10 years after introduction of the first infected animal in the majority of herds with a high replacement rate (0.33/y) and in a mean of 570 per 1,000 herds with a low replacement rate (0.17/y). The mean probability of fadeout was smaller for herds with a low replacement rate than for herds of the same size with a high replacement rate; however, these differences were not statistically significant (Table 1).

Table 1.

Results of stochastic modeling to simulate outbreaks of bovine tuberculosis in herds of various sizes and replacement rates following introduction of 1 latently infected animal.

Replacement rate (1/y)	Herd size	No test-based culling		Slaughterhouse detection-based testing and culling				Constant testing test-based culling
		Probability of fadeout	Time to fadeout (mo)	Probability of fadeout	Time to fadeout (mo)	Probability of fadeout before detection	Time to detection of M bovis (mo)	Probability of fadeout
0.33	Small	0.66 (0.63–0.72)	16 (1–116)	0.99 (0.98–0.998)	24 (1–119)	0.88 (0.87–0.91)	29 (1–119)	0.999 (0.995–1)
	Medium	0.62 (0.57–0.67)	15 (1–118)	0.99 (0.98–0.998)	23 (1–119)	0.58 (0.53–0.63)	27 (1–117)	0.99999 (0.999–1)
	Large	0.53 (0.48–0.58)	12 (1–110)	0.99 (0.98–0.999)	27 (1–116)	0.58 (0.53–0.63)	30 (1–112)	0.9999 (0.999–1)
0.17	Small	0.43 (0.38–0.48)	20 (1–115)	0.96 (0.95–0.98)	39 (1–119)	0.77 (0.72–0.81)	43 (1–120)	0.999 (0.994–1)
	Medium	0.43 (0.37–0.48)	19 (1–111)	0.97 (0.95–0.99)	37 (1–119)	0.75 (0.70–0.79)	42 (1–120)	0.999 (0.994–1)
	Large	0.43 (0.37–0.47)	20 (1–117)	0.97 (0.95–0.98)	38 (1–119)	0.74 (0.70–0.79)	42 (1–120)	0.999 (0.993–1)

Small, medium and large herds comprised 40, 276, and 3,000 cattle, respectively. The time of introduction of the infected animal was considered day 0. The model was run for a 10-year period; variability was assessed by performing 1,000 simulations of 1,000 herds each for each of the 6 scenarios. In the base model, no test-based culling was performed. Under the current slaughterhouse detection-based testing and culling strategy, whole-herd tests were performed after detection of M bovis infection in an animal via postmortem inspection. Under the constant testing strategy, whole-herd tests were performed annually unless infection was detected. For both testing strategies, test-based culling was implemented at 3 month intervals after detection according to USDA recommendations. Fadeout refers clearance of M bovis infection from the herd. Probabilities of fadeout are presented as mean (range) data; time to detection and time to fadeout are presented as median (range).

When test-based culling was added to the model, the probability of fadeout was significantly higher than that for herds with no test-based culling, regardless of size (Table 1). If testing was constant throughout the simulation, fadeout occurred in close to 100% of herds ≤ 10 years after introduction of the first infected animal; if testing was initiated after detection of M bovis via slaughterhouse surveillance, the probability of fadeout within 10 years of introduction was somewhat smaller, but still > 95% in all scenarios tested. In the latter situation, fadeout was predicted to occur in > 58% of all herds before slaughterhouse detection, and the median time to detection was 27 to 30 months after the infected animal was introduced in herds with high replacement rates and 42 to 43 months in herds with low replacement rates. The probability of fadeout before slaughterhouse detection was ≥ 58% in most (5,511/6,000) herds regardless of replacement rate (i.e., 618/1,000 medium-sized herds with high replacement rates), and median time to detection for most (400/715) herds was > 2 years after introduction. Decreasing the sensitivity of slaughterhouse detection increased the median time to detection, and increasing slaughterhouse detection sensitivity decreased the time to detection (data not shown). A survival curve was generated to compare herd-level bovine tuberculosis infection in medium herds (276 adult cattle) with high replacement rates under the 3 described testing strategies (Figure 2). Analysis revealed that herds with constant testing experienced fadeout quickly, while herds with testing initiated after slaughterhouse detection experienced slow but eventual fadeout over approximately 5 years. Herds with no test-based culling had high rates of fadeout early during infection, but were unlikely to experience fadeout after 2 years of infection. Survival curves created for other herd sizes and replacement rates were similar (data not shown). Predicted distributions of the number of cattle infected and the number culled on the basis of true-positive and false-positive test results under the three testing strategies were summarized for medium-sized herds with high replacement rates (Figure 3). For large herds (3,000 adult cattle), the nonzero portions of each distribution were shifted to the right, but the shape of the distribution was similar, with a mean of 3 cattle infected with M bovis and test-based culling of 3 infected and 30 uninfected animals under the current slaughterhouse detection-based testing and culling strategy, whereas small herds (40 adult cattle) had a mean of 1.9 cattle infected and 2.5 removed through test-based culling under the same strategy; these results were similar for herds with low replacement rates (data not shown). Decreasing the sensitivity of slaughterhouse detection led to larger numbers of infected cattle, while an increase in slaughterhouse detection sensitivity decreased the numbers of infected cattle (data not shown). Constant testing and test-based culling prevented M bovis infection from spreading, but also resulted in a somewhat higher number of cattle culled because of false-positive test results (mean value, 9.2, compared with 8.0 under the current testing strategy in medium-sized herds). In a mean of 309 of 715 herds of any size in this simulation, the animal in which M bovis infection was detected at slaughter was the only infected animal in the herd, and in a mean of 319 of 1,000 (32%) of infected small herds, 272 of 1,000 (27%) of infected medium herds, and 265 of 1,000 (27%) of infected large herds with high replacement rates, the infection was never detected via slaughterhouse surveillance. Similarly, the infection was not detected in 200 of 1,000 (20%), 230 of 1,000 (23%), and 213 of 1,000 (21%) of small, medium, and large herds, respectively, with low replacement rates. For herds in which infection was detected, ≤ 5 positive results for whole-herd tests were observed after detection.

Figure 2.

Survival curves for the persistence of M bovis infection in theoretical medium-sized (276 head) US cattle herds with high replacement rates (0.33/y) managed via 3 different strategies. In the base model (dashed line), no test-based culling was performed. Under the current slaughterhouse detection-based testing and culling strategy (solid line), whole-herd tests were performed every 3 months after detection of M bovis infection in an animal via postmortem inspection. Under the constant testing strategy (dashed-and-dotted line), whole-herd tests were performed annually before detection of infection and every 3 months after detection. A herd was assumed to start with 275 susceptible cattle and 1 latently infected animal, and was followed for 10 years or until the infection was cleared from the herd, whichever timepoint occurred first.

Figure 3.

Predicted distributions of the number of cattle infected with M bovis (A), culled on the basis of true-positive CFT and CCT results (B), and culled on the basis of false-positive CFT and CCT results (C) for the same theoretical cattle herds as in Figure 2. Results for 3 different management strategies (no test-based culling [base model; gray bars], constant testing and test-based culling (white bars), and slaughterhouse detection-based testing and culling (black bars) are shown.

Validation of base model results

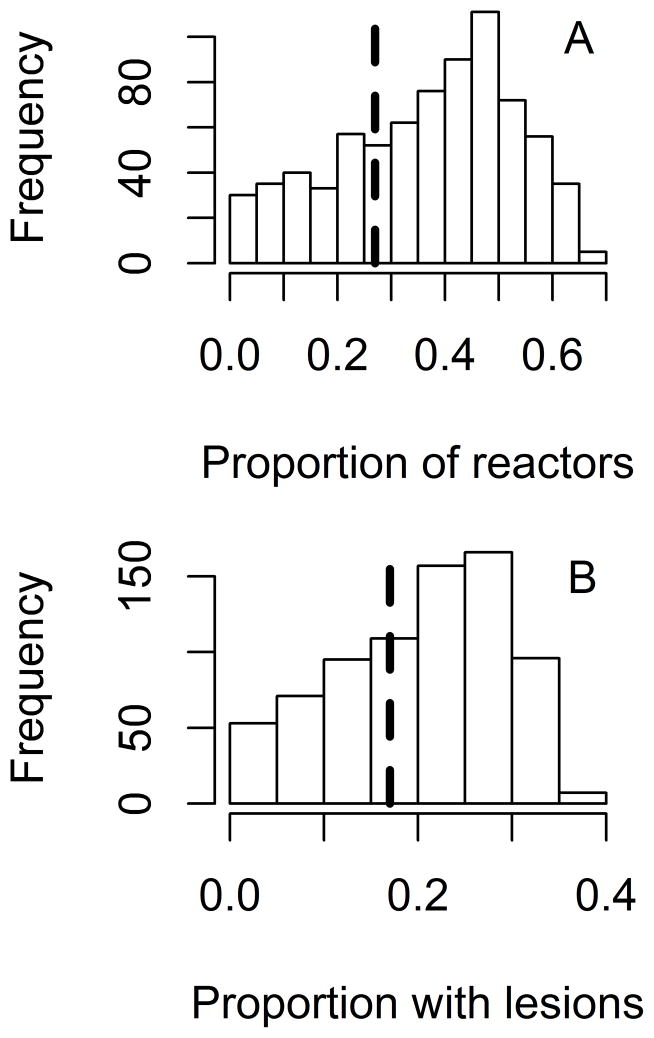
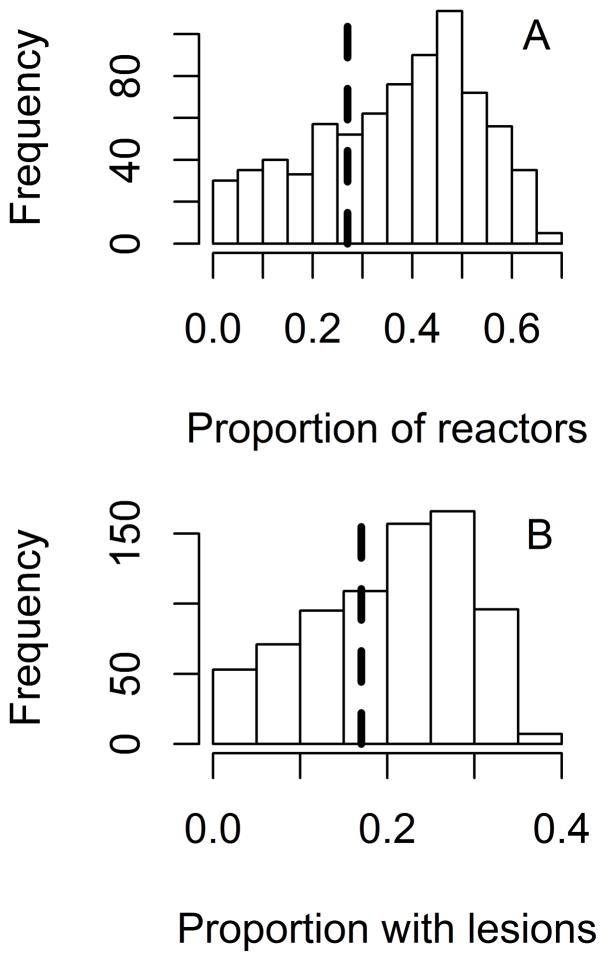
The predicted outcomes of the modeled outbreak of bovine tuberculosis were compared to known outcomes from an outbreak at a single US Red Devon beef cattle ranch¹⁶ with an effective contact rate of 0.01/y (Figure 4). Both of the outcomes evaluated (the proportion of CCT-positive reactors and the proportion of cattle with detectable tuberculosis lesions) fell within the 95% prediction interval in both the frequency- and density-dependent models; the density-dependent model accurately predicted the observed proportion of cattle with lesions significantly (P < 0.001) more often (35 vs 30 iterations for density and frequency-dependent models, respectively). Although prediction of the proportion of CCT reactors appeared to match the observed value more often in the frequency-dependent model, this difference was nonsignificant (P = 0.15). The time from introduction to detection of M bovis infection (15 years) fell within the range predicted by the model (0.17 to 19.42 years; median, 6 years). Similar results were seen with lower and higher effective contact rates (0.004 and 0.028/y, respectively; data not shown).

Figure 4.

Bar graphs showing predicted and observed prevalence of test results during an outbreak of bovine tuberculosis in a single 331-head herd of beef cattle, in which M bovis was detected 15 years after probable disease introduction.¹⁶ The analysis was used for validation of a base model created to predict various outcomes in theoretical cattle herds following introduction of 1 latently infected animal. A—Proportion of cattle with positive CCT results (ie, reactors). B—Proportion of reactors that had lesions detected at slaughter. Bars indicate predicted values, and dashed vertical lines indicate observed values.

Validation of culling strategy model

Results for the stochastic model with the current slaughterhouse detection-based testing and culling strategy were compared with observed values in outbreaks of bovine tuberculosis in 10 US dairy herds.¹⁰ With an effective contact rate of 0.01/y, the observed value fell within the 95% prediction interval of the model in all 10 evaluations. Distributions of predicted probabilities for outbreaks of various sizes were summarized (Table 2). The frequency-dependent model predicted the exact observed final outbreak size more often than the density-dependent model overall (443 vs 227 iterations; P < 0.001) and in 4 of 10 individual herds (P < 0.05 for each); the frequency-dependent model also predicted a final outbreak size greater or less than the observed outbreak size by ≤ 1 more often than the density-dependent model overall (2,279 vs 1,726 iterations; P < 0.001) and in 7 of 10 individual herds (P < 0.05 for each). The 2 largest outbreaks were accurately predicted most often by the density-dependent model (33 vs 7 iterations; P < 0.05), although the frequency of prediction was low for both model types. Similar results were seen with lower and higher effective contact rates (0.004 and 0.028/y, respectively; data not shown).

Table 2.

Distributions of predicted probabilities (%) for bovine tuberculosis outbreaks of various sizes in 10 dairy herds in Texas and New Mexico following detection of M bovis infection via slaughterhouse surveillance and clearance through test-based culling.¹⁰

Herd No.	Herd size	Transmission method	Outbreak size category (No. of infected cattle)
			0–10	11–20	21–30	31–40	≥ 41
1	160	F	95.7*	3.7	0.6	0	0
		D	96.5*	3.2	0.3	0	0
2	280	F	94.3*	5.3	0.3	0.1	0
		D	92.1*	6.6	1.2	0.1	0
3	370	F	95.4*	4.1	0.4	0.1	0
		D	89.5*	8.6	1.4	0.3	0.2
4	600	F	95.0*	4.3	0.5	0.2	0
		D	83.4*	11.5	3.1	1.7	0.3
5	1,200	F	95.8	3.4*	0.7	0.1	0
		D	79.6	13.8*	7.9	4.8	2.9
6	1,400	F	95.3	4.1*	0.5	1	0
		D	69.4	13.2*	7.9	5.3	4.2
7	1,500	F	95.2*	4.4	0.4	0	0
		D	69.0*	13.8	6.8	4.6	5.8
8	3,700	F	94.8*	4.2	1.0	0	0
		D	54.3*	10.5	8.8	7.4	19.0
9	5,000	F	94.8*	4.2	0.7	0.2	0.1
		D	54.3*	7.1	9.5	6.8	22.3
10	7,300	F	94.3*	5.2	0.5	0	0
		D	54.4*	2.9	6.0	6.3	30.4

Results for frequency-dependent (F) and density-dependent (D) transmission methods are shown.

^*Observed outbreak size category for the indicated herd.

Sensitivity analysis

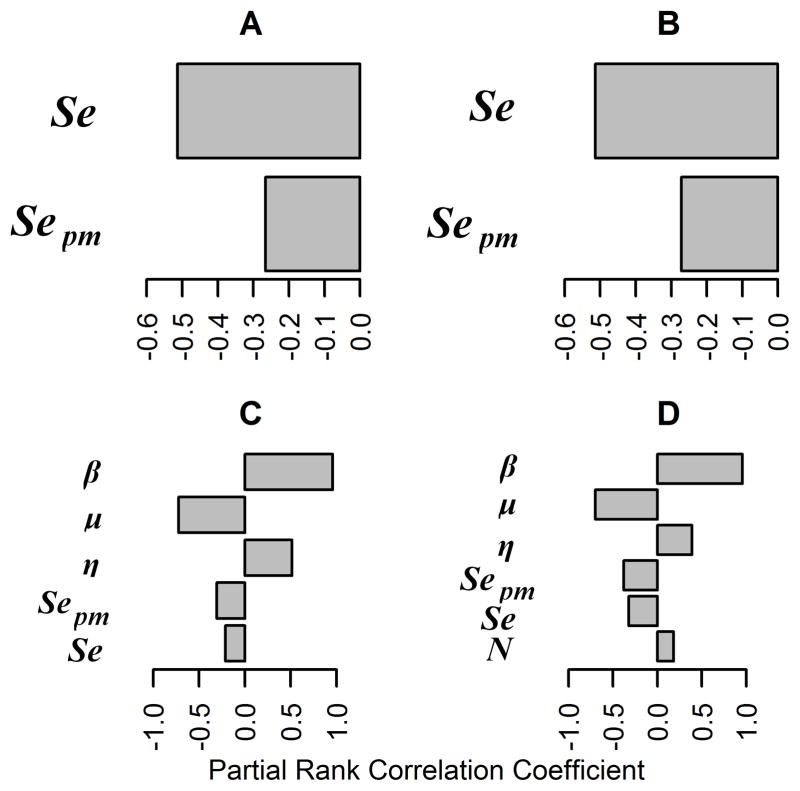
Global sensitivity analysis for the base model in large herds with high replacement rates showed that the replacement rate and the effective contact rate of M bovis infection were the only variables that were significantly associated with both the probability of fadeout and the mean number of cattle infected. Rate of transition from the latent to the reactor category was significantly associated with the probability of fadeout, and rate of transition from the reactor to the infectious category was significantly associated with the mean number of cattle infected (Figure 5). Increased effective contact rate or rate of transition from the reactor to the infectious category were associated with an increase in the mean number of cattle infected and increased effective contact rate or rate of transition from the latent to the reactor category were associated with a decrease in the probability of fadeout, whereas an increased replacement rate was associated with a decrease in the mean number of cattle infected and an increase in the probability of fadeout. In medium and large herds with low replacement rates, and in medium herds with high replacement rates, the same relationships were observed, but in small herds with low replacement rates, increased herd size was significantly associated with a decrease in the probability of fadeout and an increase in the mean number of cattle infected (data not shown).

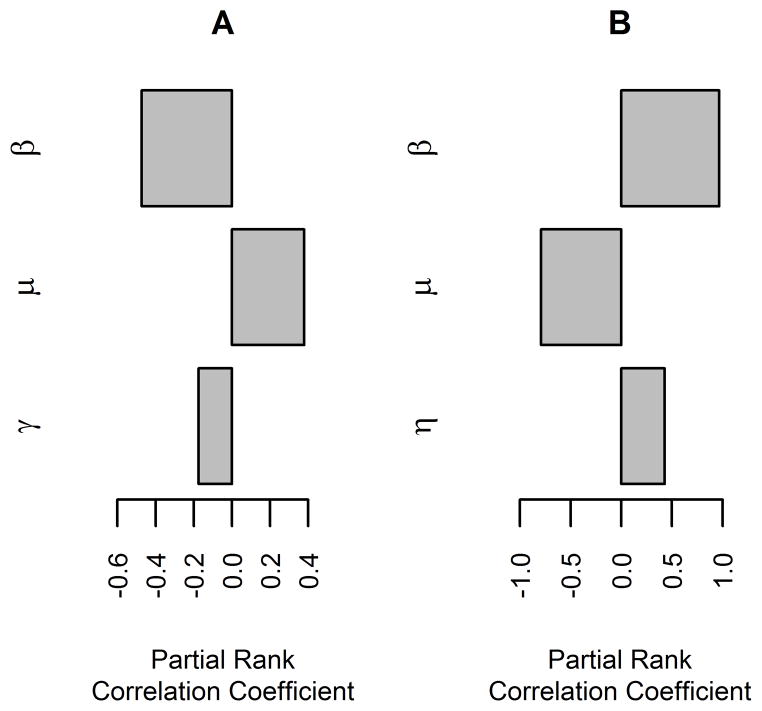
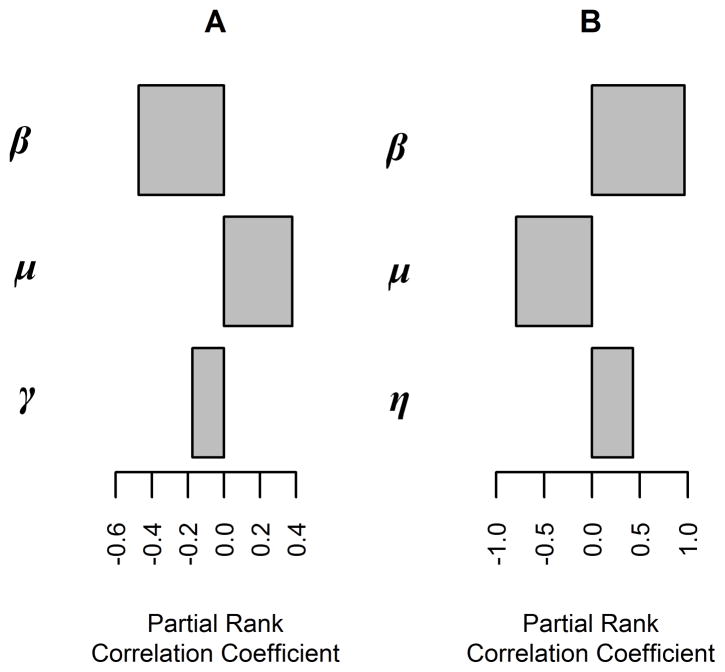
Figure 5.

Tornado graphs generated via global sensitivity analysis of the base model for within-herd spread of bovine tuberculosis in large (3,000 head) cattle herds with high replacement rates (0.33 cows/y). Partial rank correlation coefficient values for variables significantly associated with the probability of fadeout (A) and the mean number of cattle infected (B) are shown. β = Effective contact rate of M bovis infection. See Figure 1 for remainder of key.

Results of global sensitivity analysis were summarized for the current slaughterhouse detection-based testing and culling strategy model for medium-sized herds with high replacement rates (Figure 6). Mean and SD of time to fadeout were each significantly associated with the combined sensitivity of the CFT and CCT and with the sensitivity of slaughterhouse detection. An increase in either variable was associated with a decrease in mean and SD of time to fadeout. Results for the mean number of animals infected broadly resembled those of the base model (Figure 5), with the addition that an increase in combined sensitivity of the CFT and CCT or of slaughterhouse detection was associated with decreases in the mean and SD of the number of cattle infected. In large herds and in medium-sized herds with low replacement rates, the same relationships were observed for the mean and and SD of the number of cattle infected, but sensitivity of the CFT and CCT and sensitivity of slaughterhouse detection were no longer significantly related to the mean and SD of time to fadeout. In large herds, PRCCs for mean and SD of time to fadeout were 0.12 and 0.11 (for sensitivity of slaughterhouse detection) and −0.27 and −0.27 (for sensitivity of the CFT and CCT), respectively; PRCCs for mean and SD of the number of cattle infected were −0.44 and −0.54 (for sensitivity of slaughterhouse detection) and −0.44 and −0.55 (for sensitivity of the CFT and CCT), respectively. In medium-sized herds with low replacement rates, PRCCs for mean and SD of time to fadeout were 0.018 and 0.016 (for sensitivity of slaughterhouse detection) and −0.47 and −0.47 (for sensitivity of the CFT and CCT), respectively; PRCCs for mean and SD of the number of cattle infected were −0.50 and −0.67 (for sensitivity of slaughterhouse detection) and −0.40 and −0.59 (for sensitivity of the CFT and CCT). In small herds with low replacement rates, sensitivity of slaughterhouse detection was no longer significantly associated with to mean time to fadeout, but increased replacement rate was significantly associated with a decrease in mean time to fadeout (PRCC, −0.22). Global sensitivity analysis for the constant testing and test-based culling strategy model was dominated by combined sensitivity of the CFT and CCT, which significantly decreased all model outputs (mean and SD of time to fadeout, mean and SD of the number of cattle infected) regardless of herd size and replacement rate (data not shown).

Figure 6.

Tornado graphs generated via global sensitivity analysis of the slaughterhouse-detection based testing and test-based culling strategy model for within-herd spread of bovine tuberculosis in the same theoretical cattle herds as in Figure 2. Partial rank correlation coefficient values for variables significantly associated with the mean (A) and SD (B) of time to fadeout and mean (C) and SD (D) number of cattle infected are shown. Se = Combined sensitivity of the CFT and CCT. Se_pm = Sensitivity of detection of M bovis infection via slaughterhouse surveillance. See Figures 1 and 5 for remainder of key.

Effects of testing strategies

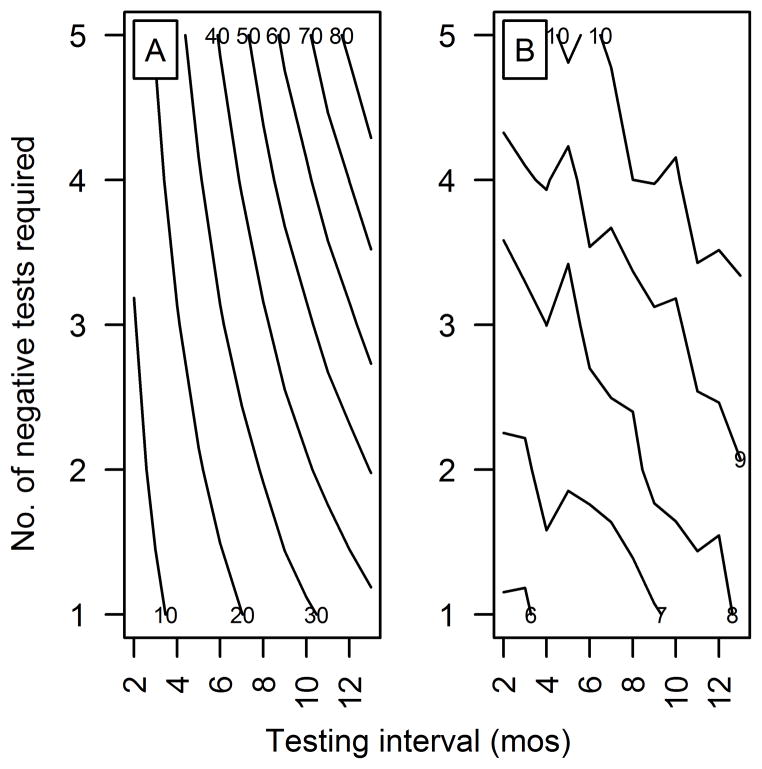
The results of scenario analysis for the test-based culling model in medium-sized herds indicated that requiring more negative whole-herd test results for a herd to be declared clear of M bovis infection resulted in a numerically greater increase in the number of cattle culled because of positive CCT results than did increasing the testing interval (Figure 7); this was true regardless of replacement rate. However, the number of months a herd spent in quarantine was more affected by increases in the testing interval. In small herds, both results were more affected by increases in the testing interval, but otherwise the relationships were similar across herd sizes and replacement rates (data not shown). For most scenarios, no infected herds were falsely declared cleared of M bovis infection; the exceptions were summarized (Table 3).

Figure 7.

Contour maps depicting the mean number of months that medium-sized cattle herds were predicted to be quarantined after detection of M bovis infection via slaughterhouse surveillance (A) and the mean number of cattle culled for positive CFT and CCT results (B) on the basis of testing interval and number of negative whole-herd test results required to declare a herd clear of infection. A herd was assumed to start with 275 susceptible cattle and 1 latently infected animal, and was followed until the infection was cleared from the herd.

Table 3.

Scenarios in which stochastic modeling of bovine tuberculosis outbreaks predicted that infected herds would be falsely declared clear of M bovis after whole-herd testing initiated by detection through slaughterhouse surveillance. The model was run for a 10-year period for each of 1,000 herds.

Replacement rate (1/y)	Testing interval (mo)	No. of tests*	No. of herds
			Small herds		Medium herds		Large herds
			Cleared	Falsely cleared	Cleared	Falsely cleared	Cleared	Falsely cleared
0.33	2	1	724	1	701	7	724	3
	2	2	714	1	717	3	713	0
	2	3	722	1	718	3	723	0
	3	1	681	0	739	3	724	1
	4	2	730	0	716	1	694	0
	6	1	707	0	727	1	720	0
	8	1	709	0	721	1	708	0
	10	1	700	0	724	0	714	1
	11	1	694	1	717	0	721	0
	12	1	709	0	708	1	715	0
	14	1	712	0	725	1	695	0
	16	1	716	0	703	1	719	0
	17	1	731	0	717	0	720	1
	18	1	723	0	717	0	704	1
	22	1	716	0	728	0	720	1
0.17	2	1	806	6	804	8	818	9
	2	2	824	1	810	1	791	2
	3	1	836	1	810	2	822	0
	3	2	825	0	829	0	812	2
	4	1	811	0	809	0	796	3
	5	1	806	0	816	1	815	1
	6	1	812	0	819	0	828	0
	7	1	780	0	810	0	816	0
	9	1	804	0	810	1	828	0
	11	1	805	0	814	1	787	0
	15	1	807	0	816	0	804	1
	16	1	809	0	821	0	806	1
	20	1	807	0	825	1	793	0
	21	1	790	1	805	0	808	0
	22	1	811	0	812	0	820	2

Data are presented as the number of herds/1,000 in which M bovis infection was detected and subsequently cleared (in total) or falsely cleared.

^*Indicates number of consecutive negative whole-herd tests required for a herd to be declared free of M bovis infection. See Table 1 for remainder of key.

Discussion

In the study reported here, we used a stochastic model to simulate the spread of bovine tuberculosis through US cattle herds, a useful step in understanding the efficacy of national control strategies for the disease. Similar models have been well-established for national control systems in other countries,^6–9 but this is the first model specifically designed to predict outcomes in the US cattle industry. The model successfully predicted outcomes for several scenarios, including results for a number of observed outbreaks.^10,16 In most scenarios, the model predicted a small outbreak or natural clearance of infection (termed fadeout) from herds, which agrees with the observed situation in a review¹⁷ of outbreaks that occurred in Europe.

The model used in the present study did not consider various sources of M bovis infection because the purpose was to study the spread of infection within a herd following introduction of 1 latently infected animal, and this included the assumption that each herd was closed to external infection during the study period. In situations in which wildlife or imported animals can reintroduce infection, this model would likely underestimate the persistence of M bovis infection in herds. In future studies, the model should be expanded to include further external sources of infection for analysis.

Both frequency- and density-dependent transmission methods were evaluated in this study. The density-dependent transmission model assumed that the number of infected cattle would be greater in larger populations than in smaller populations following exposure to 1 animal that was shedding M bovis (termed infectious). The frequency-dependent transmission model, however, assumed that the number of secondary infections would be unrelated to population size because secondary infections result from cattle having a fixed number of interactions with potentially infectious animals each day, regardless of herd size. Because the effective contact rate used was estimated for a herd size of 276 adult cattle,⁶ the models were expected to yield similar results for herds of that size because the initial rate would be 2.76/y in both models. The density-dependent model was expected to predict smaller outbreaks in smaller herds and larger outbreaks in larger herds (because the size-corrected initial effective contact rates would be < 2.76 and > 2.76/y, respectively). In the frequency-dependent model, the initial effective contact rate is unaffected by herd size.

Transmission of bovine tuberculosis is often modeled as density dependent, because transmission relies on close contact, which is more common in dense populations.¹⁸ However, unlike the situations for wildlife and humans, animal density in cattle herds is rarely related to population size.¹⁹ Cattle have been found to preferentially associate closely with only a small number of animals regardless of the population size,^20,21 rendering herd size irrelevant in calculation of transmission rates and making frequency-dependent transmission models more appropriate for the spread of infections that require close contact. This biological understanding was borne out by our model results, in which the frequency-dependent model better predicted variables for observed outbreaks in most circumstances. Results of a risk factor study²² in the United Kingdom indicated that herd size was significantly related to the risk of a bovine tuberculosis outbreak, but the effect seemed to be restricted to herds of < 200 cattle, of which there was only 1 in the observed outbreaks that were evaluated. These results are important in calculating the economic cost of a bovine tuberculosis outbreak, because frequency-dependent models were less likely to predict larger outbreaks as herd size increased.

In an infectious disease model, one of the most important components is the definition of variables. While many variables for this model are well-known (eg, sensitivity and specificity of the skin tests and the rate of disease progression), 2 are difficult to measure: transmission rate of infection and sensitivity of slaughterhouse detection.

Transmission rates are not only determined by the contagiousness of the organism, but also by the contact rate between animals. The effective contact rate used in the present study was originally calculated for herds of dairy cattle in New Zealand,⁶ which are managed in an extensive, pasture-based system. In the US system, dairy cattle are intensively managed and frequently kept within buildings; these practices are likely to increase contact rates and possibly transmission rates. Thus the predictions of the model were considered more likely to underestimate than overestimate outbreak size, which could explain the result that the frequency-dependent model accurately predicted the 2 largest observed outbreaks only rarely (7/1,000 iterations). However, in our simulations, a large number of outbreaks (618/1,000) were predicted to end because the infected animal introduced to the herd was culled before becoming infectious (while still in the latently infected or reactor categories); in this situation, the effective contact rate would not apply. Also, an effective contact rate 40 times the assumed value of 0.01/y would still result in a reproduction ratio for M bovis infection below the threshold value of 1 in the constant testing and test-based culling model with the 3-month testing interval currently in use (although this does not take into account the effect of pulsed testing, or testing the entire herd simultaneously). Because the model was able to accurately predict outbreaks for herds managed with slaughterhouse detection-based testing and culling or with no test-based culling, we concluded that the effective contact rate of Barlow et al.⁶ was acceptable for our purposes. Validation measures were repeated with the minimum and maximum predicted values of the effective contact rate from Barlow et al⁶ and produced similar results, indicating that the model validation was not sensitive to this degree of variability in transmission rates.

The current control strategy for bovine tuberculosis in the United States relies on slaughterhouse surveillance in regions considered free of the disease. For the sensitivity of slaughterhouse detection, we used a moderate value of 55%,²³ but the sensitivity of this method has been estimated to be as high as 95%²² and as low as 28.5%.¹ Such a large degree of variation could result in large changes in the predicted results for outbreaks. Although 28.5% sensitivity was associated with in longer delays in detection and a greater number of cattle infected, the same proportion of herds were able to clear infection within 10 years; likewise, 95% sensitivity simply decreased the amount of time needed for fadeout and the total number of cattle infected. Therefore, according to model predictions, the final efficacy of the control program would not be affected by the sensitivity of detection at slaughter, although the speed of detection for herd-level infection would be; thus the cost of the control program and the risk of infecting other herds would likely be increased by decreased sensitivity of this method. Another factor affecting the speed at which herd-level infection is detected is the rate at which cattle are culled. For our scenario and sensitivity analysis, we assumed replacement rates typical of well-managed dairy and cow-calf (beef) herds, in which adult cattle are presumed to spend approximately 3 years in the milking herd and 6 years in the breeding herd, respectively.^25,26 When the low replacement rate (0.17 cows/y) typical for cow-calf herds was used, median time to detection of infection at the herd level solely on the basis of culling of adult cattle was delayed by ≥ 1 year, compared with that predicted for herds of the same size when the high replacement rate (0.33 cows/y) typical for dairy herds was used. Similarly, in the outbreak used to validate the base model, the infection remained undetected for 15 years,¹⁶ whereas our model predicted a median time to detection of 6 years, with a maximum of 19.42 years. In addition, it should be noted that cattle in some small beef herds are culled at extremely low rates, resulting in fewer animals undergoing slaughterhouse inspection.¹ For such herds, detection of bovine tuberculosis would likely be delayed even longer.

Under the slaughterhouse-detection based testing and culling strategy and the no test-based culling strategy, the model predicted that small, medium, and large herds (comprising 40, 276, and 3,000 adult cattle, respectively) with low replacement rates would have a longer median time to fadeout and slightly lower mean probability of fadeout than herds with high replacement rates, although these differences were not significant. The probability of fadeout before or at the time of detection was also apparently higher for medium and large herds with low replacement rates than for herds of the same size with high replacement rates. This could lead to a different strategy being economically optimal for beef herds as opposed to dairy herds. Beef herds may also have different dynamics because of the seasonal presence of calves; the calves could increase the number of animals susceptible to M bovis infection, and latently infected calves could easily be moved or sold, thereby spreading the infection beyond the farm of origin. However, trace-back of these animals, if detected via slaughterhouse surveillance, could increase the speed at which infection is detected in the herd. Development of a model for infection dynamics of M bovis infection in beef herds that specifically accounts for the impact of the seasonal calf crop would be of value in future studies.

The predicted speed of diagnosis and control in the results of this model are of great importance for national control strategies. Although the current control method recommended by the United States Animal Health Association is predicted to be effective in eliminating M bovis infection from farms once detected, the method of detection was shown to be slow (median time to detection for most (400/714) herds was > 2 years after introduction) and incomplete (the probability of fadeout before detection was ≥ 58% in many [5,511/6,000] herds). If animals are sold from infected herds during this time period, there is a risk of spreading the infection. On the basis of these results, we would recommend that trace-back programs include up to 10 years of herd history (the maximum time to detection predicted) to improve the chances of finding both the source and any possible spread of the infection. However, the model predicted that M bovis infection in large herds was more likely to be detected, and would be detected slightly sooner, than in small herds; as herd size increased, the rate of detection and sensitivity of this surveillance method improved.

Predicted outcomes of the scenario analysis are also of importance for the national control strategy. There are economic costs related to quarantine and culling of animals.²⁵ However, there is also a potential cost and a risk involved in falsely declaring a herd to be clear of M bovis infection. Results of the present study suggest that decreasing the cost of the control program increases the possibility of falsely declaring a herd to be clear of M bovis infection. This was especially true in small herds, for which the results were very sensitive to the testing interval. Therefore, an economically optimal balance must be struck between the cost of quarantine, the cost of culling animals, and the risk of allowing the disease to remain in the herd.

Our model was able to predict dynamics of the spread of M bovis infection within US cattle herds. On the basis of these predictions, we conclude that the current national control strategy is sufficient to control bovine tuberculosis after it has been detected in a herd, but may result in a large number of infected herds escaping detection for several years.

Abbreviations

CCT

Comparative cervical tuberculin test

CFT

Caudal fold tuberculin test

PRCC

Partial rank correlation coefficient

Appendix. Values for model variables obtained from various sources in a study to evaluate dynamics of the spread of Mycobacterium bovis infection in theoretical US cattle herds

Variable	Description	Base value (range) and source
β (1/y)	Effective contact rate of M bovis infection in density-dependent models	0.01 (0.004–0.028)6
γ (1/y)	Rate at which latently infected cattle become (noninfectious) reactors	8.32 (8.32–26.07)6,7
η (1/y)	Rate at which reactors become infectious	0.347 (0.347–4.06)6,7
μ (1/y)	replacement rate	High rate: 0.33 (0.2–0.4)14 Low rate: 0.17 (0.08–0.25)15
SeCFT	Sensitivity of the CFT to detect M bovis infection	0.968 (0.632–1)26
SeCCT	Sensitivity of the CCT to detect M bovis infection	0.995 (0.551–1)26
Sepm	Sensitivity of postmortem inspection to detect M bovis infection	0.55 (0.285–0.95) 1,23,25
Sp	Specificity of the CCT	0.995 (0.888–1)26
Tti (mo)	Testing interval	3 (2–12)
Ttt (d)	Test turn-around time	10 (6–14)25
N* (No. of cattle)	Targeted (ideal) herd size	Small herd: 40 (25–50) Medium-sized herd: 276 (100–400) Large herd: 3,000 (2,500–3,500)
ν	Proportion of the testing interval during which an animal recently categorized as a reactor may be identified with the tests performed	0.5 (NA)

Base values were used for simulations, and ranges were used for sensitivity analysis. Infectious cattle were defined as cattle shedding M bovis. Values without numbered references were user-defined. NA = not applicable.