Growth Mixture Modeling: A Method for Identifying Differences in Longitudinal Change Among Unobserved Groups

Abstract

Growth mixture modeling (GMM) is a method for identifying multiple unobserved sub-populations, describing longitudinal change within each unobserved sub-population, and examining differences in change among unobserved sub-populations. We provide a practical primer that may be useful for researchers beginning to incorporate GMM analysis into their research. We briefly review basic elements of the standard latent basis growth curve model, introduce GMM as an extension of multiple-group growth modeling, and describe a four-step approach to conducting a GMM analysis. Example data from a cortisol stress-response paradigm are used to illustrate the suggested procedures.

One of the first tasks in the study of development is to describe how individuals change over time (Wohlwill, 1973). Growth curve modeling has provided a set of tools that are useful for modeling within-person change and between-person differences in change (e.g., Bryk & Raudenbush, 1987, 1992; McArdle & Epstein, 1987; Rogosa & Willett, 1985; Singer & Willett, 2003). Conventional growth modeling applications usually assume that the sample is drawn from a single population characterized by a single set of parameters (e.g., means, variances, covariances). Substantively, though, we are often interested in and deal with samples from multiple populations (e.g., we collect data from males and females, adults with pre-clinical dementia and adults without any signs of dementia). Simultaneous modeling of change for multiple observed populations can be accommodated using multiple-group growth models, wherein parameters describing growth patterns are examined to determine whether they are invariant over group (i.e., sub-sample). The multiple-group framework allows for a description of how (and possible reasons why) the groups differ in their prototypical pattern of change through formal statistical comparisons. Application of multiple-group growth models requires a priori knowledge of individuals’ group membership. In contrast, growth mixture modeling (GMM) is a method for identifying multiple unobserved sub-populations, describing longitudinal change within each unobserved sub-population, and examining differences in change among unobserved sub-populations. Stated differently, GMM methods provide a framework for post-hoc identification and description of group differences in change.

The purpose of this paper is to provide a practical primer that may be useful for researchers beginning to incorporate GMM analysis into their research. After briefly reviewing basic elements of a conventional SEM growth curve model that accommodates non-linear patterns of change we introduce GMM as an extension of a multiple-group growth model and describe a four-step approach to conducting GMM analyses. Example data are used to illustrate the procedures.

Growth Curve Modeling

The objective of growth curve modeling (a catch-all term for various similar and often identical approaches for modeling change, including multilevel models of change, latent trajectory analysis, latent curve modeling, mixed effects models of change, etc.) is to describe and test hypotheses about interindividual (between-person) differences in intraindividual (within-person) change. Comprehensive introductions to growth curve methodology can be found in Bollen and Curran (2006), Burchinal, Nelson, and Poe (2006), Duncan, Duncan, Stryker, Li, and Alpert (2006), Preacher, Wichman, MacCallum, and Briggs (2008), and Singer and Willett (2003). With an interest in modeling non-linear change (see also Grimm & Ram, in press; Ram & Grimm, 2007), our example makes use of a latent basis growth model, a model that allows for great flexibility in characterizing nonlinear patterns or shapes of change over time (McArdle & Epstein, 1987; Meredith & Tisak, 1990). In brief, this model provides an alternative representation of the change trajectories often modeled via polynomial models (e.g., quadratic, cubic, etc.) and is particularly useful for representing complex shaped trajectories in a parsimonious manner.

The model can be written as

$$Y{[t]}_n=g_{0n}·A_0[t]+g_{1n}·A_1[t]+e{[t]}_n,$$ (1)

where the observed longitudinal data (i.e., the left side of equation, individuals’ scores on variable Y repeatedly measured at times t = 0 to T) are represented or described using two latent variables, g_0n and g_1n, two corresponding basis vectors (i.e., sets of factor loadings), A₀ and A₁, and a time-specific residual (i.e., error), e[t]_n. We concentrate on three primary aspects, the pattern or shape of change (Pattern), mean change (Means), and the extent of interindividual differences in change (Covs).

The basis vectors, A₀ and A₁, describe the general pattern(s) or shape(s) of change (e.g., linear, quadratic, nonlinear). Following the usual SEM specification, A₀ is a fixed vector of 1s, (e.g., for nine occasions of measurement, t = 0 to 8, A₀= [=1, =1, =1, =1, =1, =1, =1, =1, =1] and captures aspects of stability over time. Occasion-to-occasion changes (the pattern of greatest interest) estimated directly from the data are captured by A₁. In the linear growth model, the elements of A₁ are fixed to follow a linear progression, (e.g., A₁ = [=0, =.125, =.250, =.375, =.500, =.625, =.750, =.875, =1]. Deviances from linearity are construed as residual error. In the latent basis model, though, the elements of A₁ are not predetermined. Instead, they are estimated from the data in the same way that factor loadings are estimated in a confirmatory factor analysis (e.g., A₁= [=0, α₁, α₂, α₃, α₄, α₅, α₆, α₇, =1], where two elements, =0 and =1, are fixed for purposes of model identification). The free elements of A₁ (e.g., α₁ to α₇) represent a distinctive pattern of change that best describes the data. For example, if the changes in the data followed a nonlinear pattern of change characterized at first by stability, then a quick increase, and then stability again, the elements of A₁ would reflect this pattern (e.g., A₁= [=0, .000, .472, .831, .999, .999, .999, .999, =1]. In sum, the elements of A₁ are used to represent the general pattern or shape of change.

Two other aspects of change are described by the means, variances, and covariances of the latent variables, g_0n and g_1n The means describe the prototypical amounts of change. Specifically, the mean of g_0n, μ_g0 describes the average starting point, and the mean of g_1n, μ_g1, describes the average amount of change from t = 0 to 8. In turn, the variances and covariances of g_0n and g_1n describe the extent to which the individuals in the sample differ from one another with respect to starting levels, ${\sigma }_{g0}^2$, and amounts of change, ${\sigma }_{g1}^2$, and how interindividual differences in starting level are related to interindividual differences in total amount of change, σ_g0g1. Parsimoniously representing three aspects of nonlinear change (mean change, extent of interindividual differences in change, pattern of change,), latent basis growth curve models have proved very useful in many different domains (see McArdle & Nesselroade, 2003 for an overview). More extensive discussion of this model can be found in the references above and application to the current example in Ram and Grimm (2007).

Multiple-group Growth Curve Modeling

In a straightforward manner, growth curve models can be extended to accommodate and examine differences in change among multiple groups of individuals. For instance, when examining differences in change between boys and girls, gender (a categorical grouping variable, c, with two categories) is used to divide the longitudinal data into two (non-overlapping, mutually exclusive) subsets of data. Separate growth models are specified that indicate the pattern of change, mean change, and extent of interindividual differences in amount of change for each group (e.g., boys or girls). Extending Eq. 1, a multiple-group growth model can be written as

$$Y{[t]}_n=g_{0nc}·A_{0c}[t]+g_{1nc}·A_{1c}[t]+e{[t]}_{nc},$$ (2)

where the c subscripts indicate the group to which individual n belongs (e.g., for males c = 0 and for females c = 1). The pervasiveness of the c subscripts on the right side of the equation indicates that groups can differ in all three aspects of the model highlighted above (via group-specific basis vectors, group-specific means of the latent variables, and group-specific variances of the latent variables).

Growth Mixture Modeling

We present the growth mixture model as an extension of the multiple-group growth model in which the grouping variable, c, is latent or unobserved. Just as the multiple-group model given above (Eq. 2) can be used to describe differences in how longitudinal change proceeds (mean, extent of interindividual differences, pattern,) in defined subsets of data, the objective of the growth mixture model is also to describe differences in how longitudinal change proceeds in subsamples within the data. Where the approaches differ, is in whether or not one has a priori knowledge about how to split the data. The objective of the growth mixture model is to describe, in a post-hoc manner, possible sub-groups within the data and to describe group differences in longitudinal change between and within those unobserved groups.

Practically, from this extended multiple-group perspective, we must estimate who belongs to which group/class (e.g., who is male and who is female) based on their observed trajectory. GMM provides a method by which we can develop a probable representation of unobserved group classification and group differences – based on observed information and user specified constraints. More specifically, the parameters of the model provide information about the mean change, extent of interindividual differences in change, and pattern of change for the unobserved groups we think may be in the data, and, for each individual, the probability that he or she belongs to each of those groups. Extending Eq. 2, a growth mixture model can be written as

$$\begin{array}{c}Y{[t]}_n=\sum _{c=1}^C\left({\pi }_{nc}(g_{0nc}·A_{0c}[t]+g_{1nc}·A_{1c}[t]+e{[t]}_{nc})\right)\\ \text{given}0\le {\pi }_{nc}\le 1\text{and}\sum _{c=1}^C{\pi }_{nc}=1.\end{array}$$ (3)

The portion of the equation within the inner parentheses on the right-hand side is the same as above in Eq. 2. Possible differences among groups, often called classes in mixture models, are indicated by the c subscripts. As before, our interest is in if and how the classes differ on the means, variances, and covariance of the latent variables g_0nc and g_1nc, and the basis vectors, A_0c and A_1c. Within the new part of the model, π_nc is the probability that individual n belongs to class c. As the extra conditions on the model indicate, these probabilities may range between 0 and 1 and must sum to 1. For example, with two classes, if an individual is likely to be in class 1, π_nc=1 = .80, he or she, by definition is not so likely to be in class 2, π_nc=2 = .20. In total, the observed data are represented as a function of the probability of class membership and the multiple-group growth model.

Four-Steps for Conducting a GMM Analysis

GMM can be implemented using step-by-step procedures similar to those used when fitting multiple-group growth models. As detailed in the following sections we designate these steps as (1) problem definition, (2) model specification, (3) model estimation, and (4) model selection and interpretation. For illustration we use the example data presented in Ram and Grimm (2007), a brief description of which follows. Other introductions to and procedures for applying GMM can be found in Connell and Frye (2006), Jung and Wickrama (2008), Li, Duncan, Duncan, and Acock (2001), Muthen (2004), and Wang and Bodner (2007). A “road-map” outlining our suggestions is included in Figure 1, with readers also being strongly encouraged to keep in mind the notes and cautions given in the remainder of the text.

Figure 1.

Step-by-step procedures for implementing GMM analysis. Further explanation provided in the text.

Example data

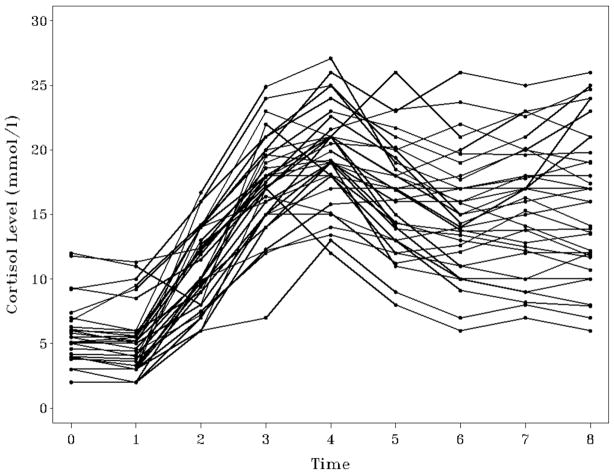
As a companion piece to our introduction to simple and complex growth curves (Ram & Grimm, 2007), we illustrate how those same data can be approached from another perspective. The data were collected, as part of the MacArthur Successful Aging Studies, during an investigation of interindividual differences in the time-course of cortisol production and dispersion in response to a stress-provoking intervention. Nine successive measurements (coded t = 0 to 8) of cortisol (mmol/l) were obtained over the course of a few hours from 34 older participants. The first two measurements (t = 0 & 1) were taken as baseline measurements, after which individuals began a driving simulation challenge task. Observations 2, 3, and 4 were taken during and directly after the challenge and are indicators of cortisol production or response. The remaining observations (5, 6, 7, & 8) were taken during a post-challenge rest period and are viewed as indicators of cortisol dissipation (see Seeman et al., 1995; Seeman, Singer, & Charpentier, 1995 for details of the experimental protocol).

As seen in Figure 2, the data are characterized by nonlinear intraindividual changes and by interindividual differences in those changes. The objective of the GMM is to determine if there are unobserved sub-groups of individuals who exhibit different patterns of change. Note that these data are used here to illustrate GMM procedures using a real-world example, but not necessarily to reach definitive substantive conclusions regarding typologies based on the time course of individuals’ cortisol responses. Further, please note that the sample size is very small, N = 34. The statistical procedures underlying SEM and GMM are large sample techniques. We do not, as a general rule, recommend using these methods with such small samples. However, there is also not a general rule regarding how large a sample is necessary. Identification and description of unobserved groups depends on many factors, including the extent of between-group differences, homogeneity of the change process, relative group sizes, reliability of measurement, and so on. In GMM, as in the determination of power in growth modeling and SEM more generally, each substantive application must be evaluated in relation to the particulars of the data, model, and theoretical underpinnings of the study.

Figure 2.

Cortisol levels obtained from 34 individuals across 9 occasions.

Problem Definition

One of the initial steps in any empirical investigation is to define the research question. Data are collected with a purpose and should be approached with one. The objectives of the problem definition step are to formalize the link between theory and method and develop an appropriate analytical plan. Two important aspects of analysis should be considered at the outset. First, researchers should formulate some initial GMM hypotheses. Using theory, previous empirical findings, and initial examinations of the data (i.e., longitudinal plots of the raw data) answers to two questions should be developed. How many unobserved groups are expected? How are these groups expected to differ with respect to mean change (Means), extent of interindividual differences in change (Covs), and pattern of change (Pattern)? Answering these questions will make explicit the perspective from which the data are being approached and help delineate a plan for how the subsequent steps of the GMM analysis should proceed. Generally, GMM is considered an “exploratory” procedure. In practice, the method should be a guided and constrained exploration of the data. It is functionally similar to cluster analysis in that decisions made during implementation (e.g., choice of distance measure) heavily affect the obtained results. Thus, it is important that the analyst has some general hypotheses and expectations about what might emerge.

Second, a baseline single-group growth curve model must be obtained. This model, designated 1-Class_Baseline, will serve as a starting point from which the exploration for unobserved groups proceeds. Following usual growth curve modeling procedures, a series of models (e.g., no growth, linear, quadratic, latent basis, etc.) are fit to the full data in order to find the best single-group representation of change (see e.g., Ram & Grimm, 2007). Proceeding from the single-group baseline model, the intent of the GMM analysis is to obtain a better and more complete representation of the data by allowing for the possibility of multiple unobserved groups.

Illustration

Cortisol is a measure of hypothalamic-pituitary-adrenocortical axis activity, and considered a marker of individuals’ stress response. The example data were collected to obtain a picture of how individuals respond when exposed to a stress-provoking event. The question relevant for GMM is, “Are there multiple phenotypes of stress-response?” A visual examination of the data (see Figure 2) indicates a nonlinear response pattern, but does not readily suggest distinct groups of individuals who respond to the stressor (introduced between t = 1 and t = 2) in substantially different ways. We do not see stark evidence of multiple groups when looking at the raw data plots. However, some theories of stress response and previous empirical findings suggest at least two phenotypes (Heim, Elhert, & Hellhammer, 2000; Miller, Chen & Zhou, 2007, p. 28). Purposefully being selective in our interpretations of the literature for our illustration, we hypothesize two sub-groups exist within our data, “typical” individuals who exhibit a down-regulation of cortisol levels shortly after exposure to stress, and “chronic-stress” individuals who, because of chronic exposure to stress throughout their lives, do not exhibit down-regulation after exposure to stress. The “typical” group’s cortisol levels are expected to rise in response to the stress event and then quickly subside. In contrast, the “chronic-stress” group’s cortisol levels are expected to rise to a similar amount in response to the stress event, but remain relatively high. Having examined the literature and formulated some general hypotheses, the data can now be approached with some purposeful ideas about what to look for. We shall use GMM to look for at least two unobserved groups that might differ with respect to mean amount of change (Means), extent of interindividual differences in change (Covs), and pattern of change (Pattern).

Model Specification

Once the research problem has been defined, a series of useful models can be specified and subsequently estimated. In multiple-group investigations where the grouping variable is known, the objective is to determine if and how the groups differ with respect to the mean amount of change, the extent of interindividual differences in change, and in the pattern of change. A Baseline model and three group difference models, Means, Means+Covs, and Means+Covs+Pattern, are fit. For instance, if examining differences in change between groups of individuals who exhibit either typical or chronic-stress type responses, comparisons would be made among four models. In the baseline (invariance) model, the typical and chronic-stress groups have identical growth patterns, means, variances, and covariances as all parameters are constrained to be equivalent across groups. In this model all typical and chronic-stress persons are, in essence, treated as a single-group.

The first group difference model, 2-Class_Means is a model where the two groups are allowed to differ with respect to mean change. Specifically, μ_g0 and μ_g1, are allowed to differ between the two groups. The next model, 2-Class_Means+Covs, additionally allows the extent of interindividual differences among no-stressed persons to differ from the extent of interindividual differences among stressed persons (stressed-out persons might be expected to exhibit a wider range of behavior – e.g., some having low levels of reaction, others being very reactive). Now, in addition to the means, the variances (and covariances) of the intercept and slope factors (e.g., ${\sigma }_{g0}^2,{\sigma }_{g1}^2$, σ_g0g1, and in some cases the residuals, ${\sigma }_e^2$) may differ among groups. Finally, 2-Class_{Means+Covs+Pattern}, also allows for differences in the shapes or patterns of change (e.g., one group linear, one group quadratic). Here the elements of the A₁ basis vector are estimated separately for the typical and chronic-stress groups. This final relaxation of the model enables the two groups to have completely different shapes or patterns of nonlinear change.

In our data, we expected such differences between typical and chronic-stress groups. However, these groups were not identified a priori. Instead, we would like to use GMM, seeking evidence for multiple patterns of change that map onto our theoretical expectations. In principle, we indicate that the grouping variable, c, is latent, indicate how many categories c has (e.g., that there are 2, or 3, or 4, …, C unobserved groups), and estimate the model parameters for each latent class and the probability that each individual is a member of each group. Starting from a baseline model, 1-Class_Baseline, models are specified to examine how two unobserved groups might differ, 2-Class_Means, 2-Class_Means+Covs, and 2-Class_{Means+Covs+Pattern}. There may, though, be more than just two unobserved groups in the data. Sets of models examining the same group differences among three unobserved groups, 3-Class_Means, 3-Class_Means+Covs, and 3-Class_{Means+Covs+Pattern}., four groups, 4-Class_Means, 4-Class_Means+Covs, and 4-Class_{Means+Covs+Pattern}., five groups, and so on may be needed. We suggest fitting sets of models that accommodate the possibility of at least one more group than the number of groups that are expected and to monitor changes in fit (e.g., BIC) and convergence as will be explained in the model selection step. This allows the possibility to reject models with additional groups and thereby provide statistical evidence that we have found an appropriate number of groups. For example, if, based on substantive theory and past findings, the data are thought to contain two unobserved groups, one should fit a baseline model with one class (1-Class_Baseline), and sets of models with two classes and with three classes – expecting that the 1-Class and 3-Class models can be rejected in favor of a 2-Class model. Comparisons among all of these models would then be used to infer the most likely number of unobserved groups in the data and how these groups differ with respect to the mean amount of change, the extent of interindividual differences in change, and the pattern of change. In sum, the goal is to specify a collection of models that allow us to identify the best possible multiple-group representations of the data.

Illustration

Considering that our 34 person sample may have been drawn from at least two sub-populations of persons (typical and chronic-stress), we fit the series of models outlined above with one, two, and three classes. Our expectation is to reject the one and three class models in favor of the two class models. Further, our expectation is that the pattern of change will differ among unobserved groups. Thus, we fit models that allow for all possible types of differences (i.e., in mean change, extent of interindividual differences in change, and patterns of change).

Following standard growth curve modeling procedures, we first specify a baseline, single-group model. Selecting among a collection of possibilities (e.g., no-growth, linear, quadratic, etc), the latent basis model was chosen as the 1-Class_Baseline model because of its simplicity, flexibility, and parsimony for representing the observed non-linear pattern of change present in the data (programming scripts and details are given in Ram & Grimm, 2007). We then specified models allowing for two unobserved groups that varied in specific aspects of change (2-Class_Means, 2-Class_Means+Covs, and 2-Class_{Means+Covs+Pattern}), and for three unobserved groups that varied in specific aspects of change (3-Class_Means, 3-Class_Means+Covs, and 3-Class_{Means+Covs+Pattern}). Importantly, the exact number of categories/groups in the latent c variable and what parameters may differ among groups is specified for each model. For the 2-Class models, c is specified to have exactly 2 categories and particular parameters (Means, Covs, Pattern) are allowed to differ between groups, invoking the assumption (hypothesis) that there are two groups underlying in the data and that they differ in particular ways. Similarly, in the 3-class models, c is specified to have exactly 3 categories (and various types of differences among groups), invoking the assumption of three unobserved groups – hypotheses we expect to reject. In total, we specify seven models to examine if and how two hypothetical groups of individuals may exhibit differential patterns of cortisol production and dispersion.

Model Estimation

As in most other types of latent variable models (e.g., SEM, multilevel models), the GMM can be estimated using maximum likelihood (ML) or Bayesian methods. Current implementations in commonly used statistical programs use either an expectation-maximization (EM) procedure (e.g., Mplus) or Markov Chain Monte Carlo procedures (e.g., AMOS), wherein the unobserved group classification variable, c, is treated as a latent variable. Both approaches, in essence, use iterative procedures to obtain parameter estimates and posterior estimates of the probability of individuals’ membership in each of the possible groups (thus the importance of specifying whether c has 2, or 3, or 4, …, C categories) to maximize the likelihood of the data given the model parameters (for ML) or to estimate the posterior mean for the parameters given the data (for Bayesian approach). Missing data on the outcome variable (i.e., Y[t]_n) are accommodated using full information maximum likelihood (or imputed directly in the Bayesian approach) under missing at random assumptions (Little & Rubin, 1987). Interested readers are referred to Muthén and Shedden (1999) for technical aspects of the EM estimation algorithms and Lee (2007) for the Bayesian approach.

Illustration

We fitted the sets of models described above to the example data using Mplus 5.0 (Muthén & Muthén, 1998–2008), wherein an EM estimation procedure is used to obtain maximum likelihood estimates of all model parameters and individual posterior probabilities (all the π_nc) are derived from those estimates. Fit statistics for all seven models are reported in Table 1. A sample programming script can be found in the Appendix (and all scripts are available at http://psychology.ucdavis.edu/labs/Grimm/personal/downloads.html). Readers are referred to the Mplus User’s Guide (Muthén & Muthén, 1998–2008) and AMOS User’s Guide (Arbuckle, 1995–2008) for details regarding how GMMs are programmed and estimated in each of these packages.

Table 1.

Fit statistics for baseline latent growth model, 2-class growth mixture models, and 3-class growth mixture models

	1-Class Baseline	2-Class Means	2-Class Means+Cov(b)	2-Class Means+Cov+Pattern	3-Class Means (b)	3-Class Means+Cov (c)	3-Class Means+Cov+Pattern (d)
Sample Size(a)
Nc=1	34	13.08	6.50	16.62	11.82	6.26	12.91
Nc=2	--	20.92	27.50	17.38	5.79	2.26	3.99
Nc=3	--	--	--	--	16.39	25.48	17.11
Fit Statistics
# of Parameters	13	16	15	26	16	18	37
AIC	1568	1573	1568	1434	1569	1569	1412
BIC	1588	1598	1591	1474	1594	1597	1469
ABIC	1547	1547	1544	1393	1541	1541	1353
Entropy	--	.544	.831	.963	.642	.866	.972
Vuong-Lo-Mendell-Rubin LRT p-value	--	.8387	.2290	.0244	.6086	.2143	.2527
Lo-Mendell-Rubin Adjusted LRT p-value	--	.8435	.2454	.0262	.6317	.2300	.2601
Parametric Bootstrap LRT p-value	--	1.0000	0.0000	0.0000	1.0000	.0128	0.0000

Notes:

^(a)Estimated counts for the latent classes based on the posterior probabilities,

^(b)intercept variance was fixed at zero for each class,

^(c)intercept variance was fixed at zero in each class and slope variance was fixed at zero for the second latent class,

^(d)slope variance was fixed to zero in class 2, estimated standard errors for this model may not be trustworthy.

Model Selection (and Interpretation)

The objective of the model selection step is to determine which of all of these models provides for the best or most reasonable representation of the observed data. Two aspects of the models must be considered, the optimal number of unobserved groups, and the type and extent of differences between and within those groups.

As in cluster analysis there is not a deterministic set of rules to follow when selecting the best model (see Hair & Black, 2000). Rather, model selection is an art – informed by theory, past findings, past experience, and a variety of statistical fit indices. To complicate matters, conventional chi-square based fit indices usually used in SEM analyses (e.g., CFI, GFI, RMSEA, etc.) are unavailable in mixture modeling (see McLachlan & Peel, 2000 for details). However, there are a number of fit statistics that may be useful when determining the best model. We suggest building a defensible judgment about the optimal model using a combination of model results, theory, and fit statistics – working through the available information in a progressive manner as outlined below.

First, researchers should carefully examine the estimation output, looking for parameter estimates that are out of bounds (e.g., negative variances) and/or problems in estimation. Given that the solutions obtained during model estimation may sometimes not be accurate or useful (cf. Hipp & Bauer, 2006), it is important to first check that the model makes sense mathematically. Further, model interpretation plays a crucial role in model selection. For instance, parameter estimates may indicate that two or more groups exhibit practically identical change patterns, particularly when working with large sample sizes. Such solutions should be considered carefully and perhaps set aside while models with fewer classes are examined more carefully. In all cases, knowledge of the substantive area regarding the distinctiveness of the obtained trajectories should inform model selection. Inadmissible or inappropriate models should be dismissed.

Second, the remaining models can be compared using relative fit information criteria such as the Bayesian Information Criteria (BIC), Akaike Information Criteria (AIC), and Adjusted BIC. Lower values on these information criteria indicate better fitting models (Muthén, 2003; Nylund, Asparouhov, & Muthén, 2007). The general principle is to select models that have the lowest information criteria, in terms of absolute value. Models that do not fit better than the baseline model can be dismissed, and a selection of the best fitting models can be carried forward and examined further.

Third, models can be evaluated with respect to the accuracy or, more aptly, confidence with which individuals have been classified as belonging to one group or another. Entropy, a statistic that ranges from 0.00 to 1.00 (as implemented in Mplus), is an increasingly used summary indicator of the conditional probabilities of individuals’ group membership (Jedidi, Ramaswamy, & Desarbo, 1993). High values of entropy (> .80) indicate that individuals are classified with confidence (i.e, the model is generally pretty sure that persons belong to a particular class) and there is adequate separation between the latent classes (see Greenbaum, Del Boca, Darkes, Wang, & Goldman, 2005; Muthén, 2004). Given the practical goal of identifying individuals’ likely group membership, we suggest that models with higher entropy are favored when selecting among models with similar relative fit indices (e.g., BIC).

Finally, comparisons can be made on an array of likelihood ratio tests that quantify specific comparisons between the model of interest and a model with one fewer class. These tests include the Vuong-Lo-Mendell-Rubin likelihood ratio test (VLMR-LRT) and Adjusted Lo-Mendell-Rubin likelihood ratio test (Adjusted LRT) and, in brief, apply a corrected likelihood-ratio distribution (a chi-square distribution is inappropriate) to compare models with C and C – 1 unobserved groups (see Vuong, 1989, Lo, Mendell, & Rubin, 2001; Muthén, 2004; Nylund, Asparouhov, & Muthén, 2007). A significance test (p< .05) of the VLMR-LRT or Adjusted LRT indicates that the model with C – 1 classes should be rejected in favor of the model with C classes. These tests can be supplemented with bootstrapping procedures that are interpreted in the same manner, but that generate and use empirical distributions of the likelihoods (see McLachlan & Peel, 2000; Muthén & Muthén, 1998–2008). Note that the likelihood ratio tests compare models that differ only in the number of classes. Thus, they can be used to select among models that only differ with respect to number of classes (3-Class_Means+Cov with 2-Class_Means+Cov), but are not appropriate for comparing models that allow for different types of between-class differences (e.g., a 3-Class_{Means+Cov+Pattern} model to either 2-Class_Means+Cov or 3-Class_Means+Cov models. Finally, group trajectories can be plotted and together with the model parameters scrutinized for their theoretical sensibility and distinctiveness.

Generally, we recommend that researchers pay attention to all of the available fit indices as well as the relevant theory and past research findings when selecting the GMM that provides the best representation of the data (see also Masyn, 2009). Our ordering is meant to provide a practical guide for systematically working through and making sense of the available information.

Illustration

The growth and growth mixture models described in the model specification step were fit to the longitudinal cortisol data of Figure 2. A latent basis growth model served as the baseline model, 1-Class_Baseline. The parameters of the basis vector A₁ were [=0, −.01, .40, .81, =1, .81,.72, .76, .79] for t = 0 to 8. For ease of interpretation we fixed the t = 4 basis coefficient to =1 as this was the time at which cortisol level was at its maximum. This identification constraint was different from the identification constraints used in our previous work. The fit, seen in Table 1, however, remains identical (see Ram & Grimm, 2007 for details). The mean of the intercept, g_0n, and slope, g_1n, were 5.19 and 14.00 mmol/l, respectively. Together, these parameters describe an overall pattern of change that begins at 5.19, shows little to no change though time 1, growth through to time 4 (to 19.16), and decline and leveling out thereafter, the percentage of decline at each time point being described by elements of A₁ (decline from =100% at t = 4 to 79% at t = 8; see also Figure 3C in Ram & Grimm, 2007).

Building from this baseline model, two series of GMMs (2-class models that allowed for differences in Means, Means+Covs, and Means+Covs+Pattern and 3-class models that allowed for differences in Means, Means+Covs, and Means+Covs+Pattern) were then fit to the data. Fit information is given in Table 1.

We began the model selection process by examining and interpreting the parameter estimates and output details of the models. We found evidence that the 3-class models should be considered cautiously, including that (a) several models encountered convergence issues including variance estimates that were negative (e.g., for the intercept) – often an indication that the model was not appropriate for the data (in such cases the offending variance and associated covariances were fixed to =0 and the re-estimated model interpreted with caution; see notes in Table 1); (b) for the 3-Class_{Means+Covs+Pattern} model very few persons were classified into one of the unobserved groups (i.e., N₂ = 3.99; the non-integer group size is the implied sample size based on probabilistic membership); (c) for 3-Class_{Means+Covs+Pattern} unobserved groups 1 and 2 had very similar mean trajectories – both following the expected typical cortisol response and diffusion process; and (d) the estimates for 3-Class_{Means+Covs+Pattern} may not be trustworthy (indicated in Mplus as a cautionary note in the output).

Next, we turned to the fit statistics. Looking for the models with the lowest information criteria (i.e., AIC, BIC, ABIC), the 2-Class_{Means+Covs+Pattern} and 3-Class_{Means+Covs+Pattern} models emerged as obvious improvements over the baseline model and as better representations of the data as compared to the other models. The 3-Class_{Means+Covs+Pattern} model had the smallest information criteria suggesting it was the more appropriate than the 2-Class_{Means+Covs+Pattern} model; however, given the problem noted above, we carried both models forward.

The 2-Class_{Means+Covs+Pattern} and 3-Class_{Means+Covs+Pattern} models both had high entropy (i.e., .963 and .972, respectively) – making them indistinguishable with regard to confidence of classification. For the 3-Class_{Means+Covs+Pattern} model, the probabilities associated with two of the three Likelihood Ratio Tests (i.e., .25, .26, and .00) were not very low – indicating that a model with one fewer class (i.e., a 2-class model) may be more appropriate. In contrast, for the 2-class_{Means+Covs+Pattern} model, all three Likelihood Ratio Tests indicated low probability (i.e., .02, .03, .00) that the data were generated by the model with one fewer latent class (i.e., baseline growth model). Given the problems with 3-Class_{Means+Covs+Pattern} noted early on in the selection process, we concluded, based on all the information about the models we fit, the 2-Class_{Means+Covs+Pattern} model was the most appropriate for these data.

Estimated parameters for this model are given in Table 2. Class 1 was estimated, based on the sum of the individual probabilities of membership to contain roughly half (N₁=16.62) of the sample. On average these individuals had a .976 probability of being assigned to this latent class (and complementary small probability of being in the other class). Plugging the basis coefficients, mean intercept (5.12), and mean slope (14.04) parameters into Eq. 1 the average trajectory was calculated to begin at 5.12, and show little change through t = 1. After this, the cortisol response began with cortisol levels increasing to 19.16 at t = 4. Then the diffusion process occurred, where cortisol levels declined to 46% of their peak growth to a final level of 11.58. Additionally, there was significant within-group variation in the intercept and slope and a non-significant covariance between the intercept and slope (converted to a correlation, r = −.21). All together, the parameter estimates for Class 1 appeared to describe the expected “typical” phenotypic cortisol response and dispersion process.

Table 2.

Parameter Estimates for the chosen model: 2-Class_{Means+Covs+Pattern}

	Group/Class 1	Group/Class 2
Sample Size	16.62	17.38
Average Probability of Class Membership	.976	.999
Latent Variable Means
Intercept Mean, μg0	5.12 (.64)	5.28 (.49)
Slope Mean, μg1	14.04 (1.11)	14.38 (.79)
Slope Loadings, A1
Time 0	=0 (fixed)	=0 (fixed)
Time 1	−.01 (.01)	−.02 (.01)
Time 2	.43 (.04)	.38 (.03)
Time 3	.91 (.04)	.79 (.03)
Time 4	=1 (fixed)	=1 (fixed)
Time 5	.66 (.03)	.93 (.04)
Time 6	.49 (.03)	.90 (.04)
Time 7	.49 (.05)	.96 (.04)
Time 8	.46 (.05)	1.03 (.04)
Latent Variable Covariances
Intercept Variance, σ2g0	4.50 (1.57)	3.54 (1.44)
Slope Variance, σ2g1	16.28 (4.25)	9.04 (3.13)
Intercept-Slope Covariance, σg0g1	−1.81 (2.55)	−1.93 (1.38)
Residual Variance, σ2e	2.83 (.45)	2.83 (.45)

Class 2 contained the other half of the sample, N₂=17.38 individuals who were, on average, assigned into this second latent class with .999 probability. This latent class was allowed to differ from the first class with respect to means of the intercept and slope variables (5.28 and 14.38), extent of interindividual differences (covariances), and pattern of change (elements of A₁). The average trajectory for this class started out at 5.28, didn’t show much change until the stress event was introduced after t = 1. Cortisol levels then increased to 19.66 at t = 4 (a similar level as Class 1), but then did not show the “typical” diffusion. Instead, the high level of cortisol was maintained through to t = 8 and a final level of 20.09. As in the first class, there was significant variation in the intercept and slope and a non-significant intercept-slope correlation (r = −.34). All together, the parameter estimates for class 2 appeared to describe the cortisol response and non-dispersion process expected of a “chronic-stress” group.

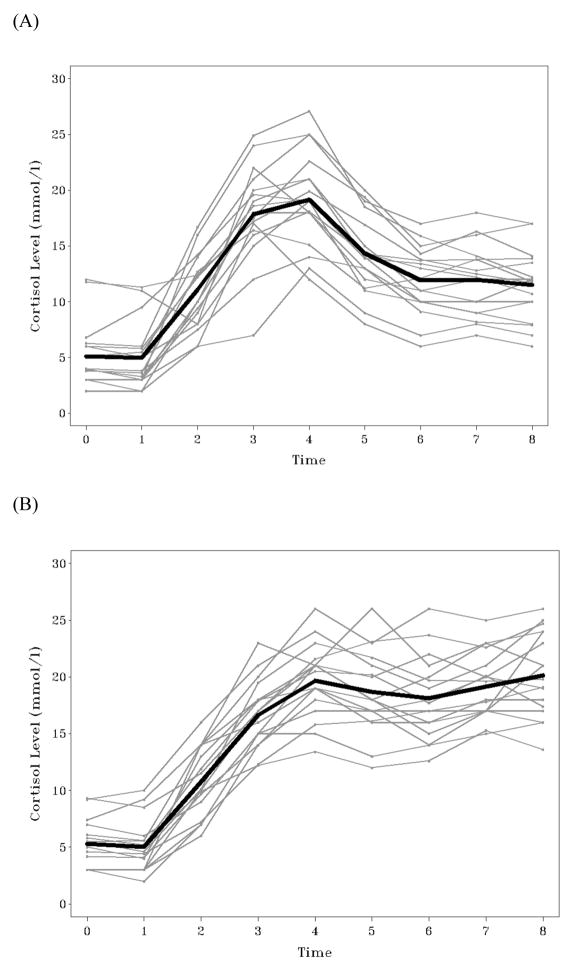
To examine the separation of latent classes and their change patterns, we plotted individuals based on their most likely class membership and the mean trends for each class. These trajectories are shown in Figure 3. Class 1 (Figure 3A) clearly describes and contains individuals who follow a “typical” response and diffusion pattern, whereas Class 2 (Figure 3B) describes and contains “chronic-stress” individuals whose cortisol levels do not dissipate following the stressor (see Miller, Chen, & Zhou, 2007 for extensive discussion of cortisol response curve possibilities). We hope the usefulness of such plots for model interpretation and presentation of results is clear.

Figure 3.

Mean and individual trajectories obtained from the 2-Class_{Means+Covs+Pattern} model. Panel A = “typical” individuals (n = 17); Panel B = “chronic-stress” individuals (n = 17).

Cautions

We characterized GMM as an extension of multiple-group growth modeling that is useful for identifying multiple unobserved sub-populations, describing longitudinal change within each unobserved sub-population, and examining differences in change among unobserved sub-populations. The beauty of the method is that, given some knowledge about the analysis problem, group differences in longitudinal change can be identified and described even when the grouping variable is latent or unobserved.

GMM is a constrained exploratory technique. It is a post-hoc analysis technique that seeks out the story the data are trying to tell – a story that is limited by the specific bounds imposed during model specification. Much can be learned about possible groups and patterns of change that exist within one’s data. However, as with all exploratory procedures, what can be learned is limited by what is entered and what is looked for. Thus, care should be taken that the set of models used in the exploration both capture and allow for the type and extent of differences in longitudinal change that are expected. Mixture models accommodate and represent non-normality in observed data. This non-normality may arise for many reasons, including true non-normally distributed outcomes, poor measurement, or the mixing of multiple groups. Given these multiple possibilities, GMM results may be misinterpreted as unobserved groups. There are real dangers of finding and identifying false groups (see Bauer & Curran, 2003a, 2004, & associated commentaries). The model estimation algorithms seek to find the best representation of the data, given the specifications of the models. Answers will be found; groups and differences among groups provided; but, whether they represent true processes that generated the data is unknown. Thus, it is important to make sure the estimates and number of classes makes sense. There is no substitute for careful definition of the research problem (Bauer & Curran, 2003b; Muthen, 2003; Rindskopf, 2003). We would suggest obtaining further evidence that the groups are real by replicating the results with new data and also confirming that the latent grouping variable is related to other measured variables in predictable ways. For instance, in our example it would be good if the two groups obtained in the GMM mapped on to a measured life stress variable. Note, however, that if such a variable was available, the GMM may not be needed, and a multiple-group model would suffice.

We have presented and illustrated GMM procedures using a growth model with a nonlinear change pattern, the latent basis growth model as a starting point. Our intent was to examine group-level differences in the pattern of change, mean change, and extent of interindividual differences in change. Researchers may not always be interested in all three of these aspects, or may have more specific hypotheses regarding how and where such differences may be manifest in the data. For example, rather than using the latent basis growth model, where the pattern of change is driven by the data, applications of GMM might rather make use of specific polynomial (e.g., linear, quadratic, cubic, etc.) or nonlinear functional forms (e.g., exponential, sigmoid, etc.) that match the developmental process being studied. That is, the models can be constructed to look for particular patterns of change. Further, we sought to implement a GMM that allowed for within-class interindividual differences in the intercept and slope, so that we could examine if and how unobserved classes differed in the extent of those interindividual differences. We also highlight another subset of GMMs, often called latent class growth analysis (LCGA; cf. Nagin, 1999, 2005). These models are the special cases of GMM that assume no interindividual differences in change within-class. That is, the extent of interindividual differences (Covs) are all constrained to zero, implying that all individuals in a particular class are homogeneous. In cases where such homogeneity exists (e.g., a class of individuals who never smoke, see also notes on our model estimation and adjustments in Table 1) LCGAs often allow for more straightforward interpretations. They are easily implemented using PROC TRAJ in SAS (Jones & Nagin, 2007; Jones, Nagin & Roeder, 2001). In sum, depending on the research problem, there is great flexibility in how one chooses to approach the research question and implement the guided exploration of group differences in change. The latent basis GMM framework we used here is but one of an infinite set of modeling possibilities.

We have only touched the surface of some of the issues surrounding the exciting possibilities of the application of GMMs to developmental inquiry. Readers are encouraged to consult the host of recent papers that consider, build upon, and extend the use of GMM as a tool that can inform and advance our understanding of developmental processes (e.g., Connell & Frye, 2006; Grimm & Ram, in press; Harring, 2005; Kelley, 2005; Muthén & Masyn, 2005; Muthén & Muthén, 2000; Stanger, 2006). The potential utility of GMM for understanding group differences in developmental processes is strong and we encourage researchers to examine the need for unobserved group differences into their research.

Appendix. Mplus programming script for 2-Class_{Means+Cov+Pattern} model. Additional scripts and programs available at http://psychology.ucdavis.edu/labs/Grimm/personal/downloads.html

TITLE: Latent Basis 2-Class Growth Mixture Model – Means+Cov+Pattern;
DATA: FILE= data.dat;
VARIABLE: NAMES = t1-t9; USEVAR= t1-t9; CLASSES = c(2);
ANALYSIS: TYPE= MIXTURE; !LRTSTARTS = 5 5 50 15; STARTS = 20 5;
! LRTBOOTSTRAP = 100;
MODEL:
%OVERALL%
!Intercept Loadings
   g0 BY t1-t9@1;
!Latent Basis Slope Loadings
   g1 BY t1@0.0
         t2* (L2)
         t3* (L3)
         t4* (L4)
         t5@1.0
         t6* (L6)
         t7* (L7)
         t8* (L8)
         t9* (L9);
!Intercept & Slope Means, Manifest Means fixed to Zero
     [g0*0] (M0); [g1*2] (M1); [t1-t9@0];
!Intercept & Slope Variances & Covariances, Residual Variances
     g0*5 (V0); g1*5 (V1);
     g0 WITH g1*0 (C01);
     t1-t9*20 (Ve1);
!Class 1 Model Statement
%c#1%
     [g0*3 g1*5]; g0 g1; g0 WITH g1;
     g1 BY t1@.0
           t2*.0
           t3*.5
           t4*.8
           t5@1.0
           t6*.8
           t7*.6
           t8*.4
           t9*.4;
!Class 2 Model Statement
%c#2%
     [g0*5 g1*15]; g0 g1; g0 WITH g1;
     g1 BY t1@.0
           t2*.0
           t3*.5
           t4*.8
           t5@1.0
           t6*1.0
           t7*1.0
           t8*1.0
           t9*1.0;
OUTPUT: STANDARDIZED TECH7 TECH11 TECH14;