Correspondence analysis is a useful tool to uncover the relationships among categorical variables

Abstract

Objective

Correspondence Analysis (CA) is a multivariate graphical technique designed to explore relationships among categorical variables. Epidemiologists frequently collect data on multiple categorical variables with to the goal of examining associations amongst these variables. Nevertheless, despite its usefulness in this context, CA appears to be an underused technique in epidemiology. The objective of this paper is to present the utility of CA in an epidemiological context.

Study Design and Setting

The theory and interpretation of CA in the case of two variables and more than two variables is illustrated through two examples.

Results

The outcome from correspondence analysis is a graphical display of the rows and columns of a contingency table that is designed to permit visualization of the salient relationships among the variable responses in a low-dimensional space. Such a representation reveals a more global picture of the relationships among row-column pairs which would otherwise not be detected through a pairwise analysis.

Conclusion

When the study variables of interest are categorical, CA is an appropriate technique to explore relationships amongst variable response categories and can play a complementary role in analyzing epidemiological data.

1. Background

In epidemiological studies, researchers often collect large amounts of data on study participants. Much of these data are collected through questionnaires in which many questions have categorical response options, either binary, ordinal or nominal. For example, “Has a doctor ever told you that you have heart disease?”, “How would you rate your health?”, “What is your marital status?”. Researchers are often interested in exploring the relationships among such sets of categorical variables. One might consider conducting separate chi-square tests; one for each pair of variables, or, in the case of binary or ordinal variables, a correlation matrix of the bivariate relationships could be viewed. For a large number of categorical variables, however, this pairwise strategy would quickly become cumbersome and render the results difficult to summarize. More importantly, such an approach would reveal only that a relationship exists but not which response categories are related [1]. Moreover, it would not provide us with a global picture of the salient relationships among these variables when taken together. An alternative approach is to employ a multivariate approach to explore these relationships simultaneously.

Commonly used exploratory multivariate techniques include principal components analysis (PCA) and factor analysis (FA) which are frequently used in the validation of scales and syndromes, e.g. metabolic syndrome [2–4]. These techniques were, however, designed for use with continuous variables and utilize the Pearson correlation coefficient as the measure of association. An extension to FA has been proposed for binary and ordinal variables by using the tetrachoric and polychoric correlation coefficient, respectively [5]. These coefficients assume that both variables are dichotomized continuous variables with underlying bivariate normal distribution [6]. Moreover, the results of the multivariate analysis do not exploit the individual response categories of the categorical variables.

One technique that is designed specifically for the analysis of categorical variables and which is not yet widely used in epidemiological research is correspondence analysis (CA). This technique preserves the categorical nature of the variables since the analysis is conducted at the level of the response categories themselves rather than at the variable level. The primary goal of CA is to illustrate the most important relationships among the variables’ response categories using a graphical representation [7]. CA is a versatile technique in part because no underlying distributional assumptions are required, thus accommodating any type of categorical variable whether binary, ordinal or nominal. The value of CA is perhaps most demonstrable in applications to nominal variables for which few alternative analytical methods exist.

In this paper, we describe the use of CA through a simple example of two nominal variables. We also illustrate the use of Multiple Correspondence Analysis (MCA), an extension of CA, using data on several binary variables from a study on frailty in the elderly. For complete MCA results in this frailty study, please see Sourial et al (2009) (MS Ref 08-216). All analyses were conducted using the PROC CORRESP procedure in SAS 9.1.3, Cary, NC, USA.

2. Description of Correspondence Analysis

In this hypothetical study we are interested in exploring the relationship between country of residence and primary language spoken. The contingency table of the frequencies is shown in Table 1. Let i=1,2,3,4,5 represent the levels of the row variable, country, and j=1,2,3,4,5 the levels of the column variable, language (Table 1). A chi-square test reveals that there is statistically significant association (p<0.0001). However, this test does not tell us how the two variables are related. Using this example, we will demonstrate the conceptual theory behind CA, the interpretation of a CA map and reveal relationships that would otherwise not be detected through a pairwise test of association.

Table 1.

Contingency table of country of residence and primary language spoken

	Language
Country	English	French	Spanish	German	Italian	Total
Canada	688	280	10	11	11	1000
USA	730	31	190	8	41	1000
England	798	74	38	31	59	1000
Italy	17	13	11	15	944	1000
Switzerland	15	222	20	648	95	1000
Total	2248	620	269	713	1150	5000

CA is based on the analysis of the contingency table through the row and column profiles (Table 2) [8]. Row profiles correspond to the relative frequencies of the different languages spoken within each country surveyed. For example, among the 1,000 fictitious respondents from Switzerland, German is the most common primary language spoken (64.8%) followed by French (22.2%), Italian (9.5%), Spanish (2.0%) and English (1.5%). The average row profile, presented in the bottom row of Table 2 is the average of the row profiles weighted by the marginal row frequencies, or equivalently, the marginal frequency distribution over the sum of the rows. In CA, the average row profile is called the “centroid” of the row variable. In our example, the average row profile shows that, when pooling across countries, English is the dominant primary language while Spanish is the least common. Analogously, column profiles are the relative frequencies of the different countries within each language. For example, among the 620 respondents who reported French as their primary language, most reside in Canada (45.2%) followed by Switzerland (35.8%), England (11.9%), USA (5.0%) and Italy (2.1%). The average column profile or column centroid is defined as the marginal frequency distribution over the sum of the columns. In our example, the average column profile shows an equal proportion in each country as a result of the equal number of respondents from each country.

Table 2.

Row and column profiles of country of residence and primary language spoken

Row Profiles
Country	Language					Total
	English	French	Spanish	German	Italian
Canada	0.688	0.280	0.010	0.011	0.011	1.000
USA	0.730	0.031	0.190	0.008	0.041	1.000
England	0.798	0.074	0.038	0.031	0.059	1.000
Italy	0.017	0.013	0.011	0.015	0.944	1.000
Switzerland	0.015	0.222	0.020	0.648	0.095	1.000
Average row profile	0.450	0.124	0.054	0.143	0.230	1.000

Column Profiles
Country	Language					Average Column Profile
	English	French	Spanish	German	Italian
Canada	0.306	0.452	0.037	0.015	0.010	0.200
USA	0.325	0.050	0.706	0.011	0.036	0.200
England	0.355	0.119	0.141	0.043	0.051	0.200
Italy	0.008	0.021	0.041	0.021	0.821	0.200
Switzerland	0.007	0.358	0.074	0.909	0.083	0.200
Total	1.000	1.000	1.000	1.000	1.000	1.000

The usual purpose in using CA is to graphically represent these relative frequencies in terms of the distance between individual row and column profiles and the distance to the average row and column profile, respectively, in a low-dimensional space [1]. Distance is measured using the chi-square metric [8]. The chi-square distance between row i and row i′ (i ≠ i′) is given by $d(i,i\text{'})=\sqrt{{\displaystyle \sum _j}\left(\frac{{(p_{ij}-p_{i^{\prime }j})}^2}{p_{+j}}\right)}$, where p_ij and p_i′j are relative frequencies for row i and i′ in column j and p_+j is the marginal relative frequency, or “mass” as it is called in CA, for column j. For example, the chi-square distance between Canada and Italy is:

$$d(\mathit{\text{Canada, Italy}})=\sqrt{\left(\frac{{(0.688-0.017)}^2}{0.450}\right)+\left(\frac{{(0.280-0.013)}^2}{0.124}\right)+\left(\frac{{(0.010-0.011)}^2}{0.054}\right)+\left(\frac{{(0.011-0.015)}^2}{0.143}\right)+\left(\frac{{(0.011-0.944)}^2}{0.230}\right)}=2.315$$

Dividing by the marginal frequency standardizes the variance and compensates for larger variances associated with high proportions and smaller variances associated with low proportions [1]. This ensures that differences between larger proportions do not dominate the distance calculation relative to smaller proportions [1].

It should be noted that distances are only defined within the countries (rows) or within the languages (columns), not across the categories of countries and languages [8].

The weighted sum of the squared chi-square distance between each row profile and the average row profile is the total variance, or “inertia” (Λ²) as it called in CA, of the row variable and is defined as follows [8]:

${\mathrm{\Lambda }}^2={\displaystyle \sum _i}{p}_{i+}{d_i}^2$, where

p_i+ is the marginal relative frequency (or mass) of row i and, $d_i=\sqrt{{\displaystyle \sum _j}\left(\frac{{(p_{ij}-p_{+j})}^2}{p_{+j}}\right)}$ is the chi-square distance between row i’s profile and the average row profile. In terms of the countries surveyed, the row profile for England was closest to the average profile with a distance of 0.714 whereas Italy was furthest with a distance of 1.697. All aforementioned equations are analogous for column profiles.

Inertia is a measure of variance or dispersion of the individual profiles around the average profile and represents a measure of deviation from independence [9]. The larger the differences are, the larger the inertia will be. Inertia is in fact directly related to Pearson’s chi-square statistic (X²):

${\mathrm{\Lambda }}^2=\frac{{\text{X}}^2}{N}$, where N is the total sample size (8).

CA decomposes the inertia by identifying a small number of mutually independent dimensions that represent the most important deviations from independence [9]. Dimension 1 represents the largest amount of explained inertia or largest deviation from independence; dimension 2, the second largest and so on. Dimensions are formed by identifying those axes for which the distance between the profiles and axes is minimized while simultaneously maximizing the amount of explained inertia. Each dimension has an eigenvalue which represents its relative importance and how much of the inertia it explains [8]. Although the mathematics involved in creating dimensions is complex, dimensions can be interpreted based on how the variables’ response categories separate on either side of the dimensions. Moreover, the further away from the origin a response category is along a particular dimension, the greater its importance on that dimension. This positioning also provides insight into the dimensionality of each response and which responses group or “load” together on a same dimension.

The following SAS code was used to carry out the analysis.

PROC CORRESP DATA=CAexp FREQOUT DIMENS=2 OUTC=outCA ALL;
        TABLES country, language;
        WEIGHT count;
RUN;

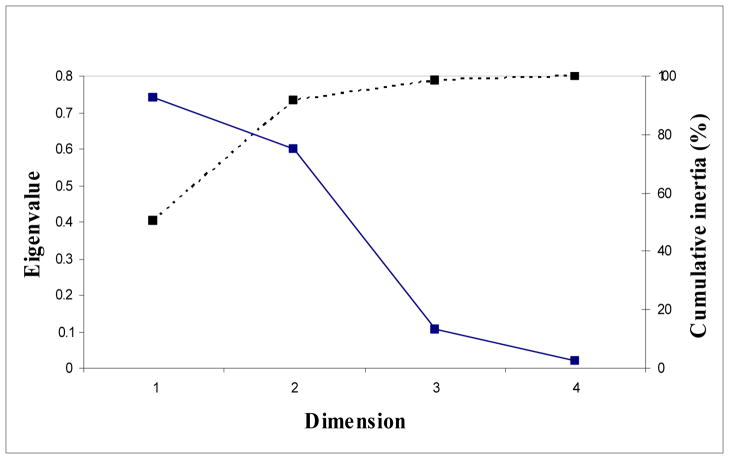
The FREQOUT and WEIGHT options specify that the input data (DATA=CAexp) are in the form of a contingency table. The row (country) and column (language) variables are listed in the TABLES statement. The option ALL requests all output to be displayed. The results of the inertia decomposition are shown in Table 3. The total number of dimensions created is equal to the minimum of (I-1, J-1), where I and J are the number of categories for each variable [8]. In our example, this corresponds to the minimum of (5-1, 5-1) or 4 dimensions. Most analyses retain two or three dimensions for interpretation. The code DIMENS=2 requests that two dimensions be retained. To decide how many dimensions to retain, rules of thumb similar to those used in PCA and FA are applied. More precisely, commonly used rules recommend that the number of dimensions retained represent >70% of the inertia [10] or correspond to the number right before the “elbow” in a plot of the eigenvalues by dimension number, called a “Scree” plot [11]. The “elbow” corresponds to the dimension where the curve begins to level off. Another recommendation specific to CA is to retain those dimensions with eigenvalues > 1/[min (I, J)-1] [1]. In our example, according to the proportion of explained inertia in Table 3, one dimension represents 50.6% of the inertia and two dimensions, 91.6%. The Scree plot (not automatically created by PROC CORRESP) shows the “elbow” occurring at three dimensions implying that two dimensions should be retained (Figure 1). Combining these rules, we chose to retain two dimensions to describe the salient relationships.

Table 3.

Inertia decomposition of country of residence and primary language spoken

Dimension	Eigenvalue	Chi-square	Percent of inertia	Cumulative percent of inertia
1	0.74304	3715.2	50.6	50.6
2	0.60177	3008.9	41.0	91.6
3	0.10393	519.6	7.1	98.7
4	0.01905	95.2	1.3	100.0
	1.46779	7338.9	100.0

Figure 1.

Scree plot of country of residence and primary language spoken

Scree plot of eigenvalues represented by the lined curve; cumulative percent of explained inertia represented by the dashed curve

Dimensions are typically plotted to visualize the relationships among the variables. In CA, this graphical representation is called a “map”. The %PLOTIT SAS macro can be used to produce the map of Dimension 1 by Dimension 2 (PLOTVARS=Dim2 Dim1) by inputting the results of the CA (DATA=outCA) from the previous CORRESP procedure. The code specifies the type of analysis performed on the data (DATATYPE = corresp) and requests a horizontal (HREF=0) and vertical line (VREF = 0) through the origin to facilitate interpretation. It should be noted that we have chosen to present the simplest and most accessible SAS code for the purpose of this introductory paper. Additional graphing options are available for the %PLOTIT macro [12] as well as other graphing methods including the %CORRESP macro [9] and ODS (output delivery system) graphics [13].

For readers with a particular interest in the R software, please see Greenacre [14].

%PLOTIT(DATA=outCA,DATATYPE=corresp, HREF=0, VREF=0,
         PLOTVARS=Dim2 Dim1, COLOR=black);

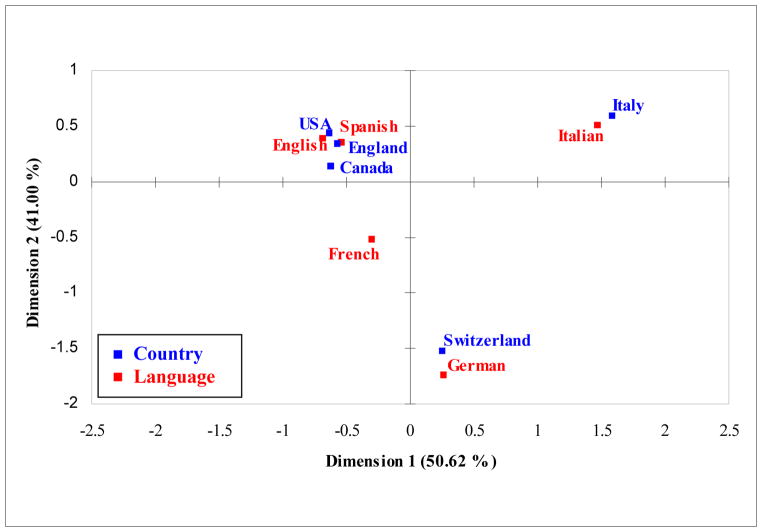
The map is presented in Figure 2. The origin on the map corresponds to the centroid of each variable. The closer a row profile’s vector location is to the origin, the closer it is to the average profile. In our example, those from England and those reporting “English” as their primary language were closest to their respective average profiles and therefore closest to the origin.

Figure 2.

Correspondence analysis map of country of residence and primary language spoken

Dimension 1 is represented by the horizontal axis; Dimension 2, the vertical axis. Along Dimension 1, we see on the map that Italy and Italian are furthest away from the origin and therefore have the most importance. Along Dimension 2, we see that Switzerland and German have the most importance. These results indicate that the most important difference or largest deviation from independence in the sample is between Italy/Italians and the other countries and languages. The second most important difference is between Switzerland/German and the other countries and languages. The other responses being closer to the origin imply that the deviations from the expected proportions are relatively small.

Although distances between categories of countries and languages are not mathematically defined, their degree of “clustering” or closeness of points on the map with regards to their angle from the origin and points in the same quadrant can be used as guidelines to interpret relationships between row and column variables [10, 15]. In the example, we see that Italy clusters with Italian, Switzerland clusters with German, and to a lesser extent French given the moderate proportion of Swiss respondents who speak French as their primary language. Similarly, Canada is associated with English and to a lesser extent French. The USA clusters with English and Spanish and England clusters with English. These clusters provide additional information beyond the simple statement that a statistically significant association exists between country and language. The clusters allow us to visualize how the countries and languages are related.

3. Extension to more than two variables: Application in frailty

Possibly the most useful epidemiological application of correspondence analysis is to explore the relationships among multiple variables (i.e. more than two variables). Multiple Correspondence Analysis (MCA) is an extension to correspondence analysis when multiple variables are being considered. We illustrate the use of MCA using an application involving multiple binary variables in the context of our research on frailty.

Frailty in the elderly population is generally acknowledged to be a state of increased vulnerability to stressors due to impairments in multiple physiological systems [16]. However, there remains debate over the operational domains of frailty.

The International Database Inquiry on Frailty (FrData) is an initiative with the goal of improving our understanding of seven candidate frailty domains: nutrition, physical activity, mobility, strength, energy, cognition, and mood. Each domain was dichotomized into the presence (coded 1) or absence (coded 0) of a frailty deficit. Bivariate correlations between each pair of variables were examined using a correlation coefficient for binary variables, the tetrachoric correlation coefficient. To explore the relationships among the variables simultaneously, we used MCA. Data from multiple studies were examined; however, to simplify the presentation of this example, the results from only one study, the System of Integrated Services for Older Persons (French acronym, SIPA) (15), are presented. Complete results are presented in Sourial et al (2009) (MS Ref JCE-08-216).

Briefly, the SIPA study participants consisted of 1,164 community-dwelling persons in Montreal, Canada, aged 65 years and over, and with a disability in at least one instrumental activity of daily living. Of the seven frailty domains, only six were used in the analysis as there was no measure of nutrition collected in the SIPA study. Among the 1,164 participants, 57.5% had deficits in physical activity, 75.0% in mobility, 74.2% in strength, 87.3% in energy, 52.8% in cognition, and 71.2% in mood.

Table 4 presents the bivariate correlation coefficients between the frailty domains. Mobility was found to be highly correlated with energy and strength. Physical activity was moderately correlated with mobility, energy and strength and energy was moderately correlated with strength. The degree of correlation between cognition and the other domains was negligible and, in some cases, slightly negative.

Table 4.

Tetrachoric correlation coefficients between frailty variables

Domain	Physical activity	Mobility	Strength	Energy	Cognition	Mood
Physical activity	1.00
Mobility	0.38	1.00
Strength	0.32	0.63	1.00
Energy	0.52	0.76	0.57	1.00
Cognition	0.07	−0.12	−0.01	−0.07	1.00
Mood	0.17	0.21	0.21	0.22	−0.04	1.00

To conduct MCA in SAS, the multidimensional contingency table of all two-way cross-tabulations across all variables, called the Burt matrix, is analyzed (Table 5) [9]. MCA decomposes the Burt matrix to find the pairwise associations which account for the greatest proportion of inertia and displays them on a reduced number of dimensions. MCA can be thought of as analogous to the decomposition of the bivariate correlation matrix in PCA or FA [9].

Table 5.

Burt matrix of frailty variables

	PA_0	PA_1	MB_0	MB_1	ST_0	ST_1	EN_0	EN_1	CG_0	CG_1	MD_0	MD_1
PA_0	495	0	182	313	174	321	114	381	246	249	175	320
PA_1	0	669	109	560	126	543	34	635	304	365	160	509
MB_0	182	109	291	0	166	125	116	175	119	172	106	185
MB_1	313	560	0	873	134	739	32	841	431	442	229	644
ST_0	174	126	166	134	300	0	92	208	141	159	113	187
ST_1	321	543	125	739	0	864	56	808	409	455	222	642
EN_0	114	34	116	32	92	56	148	0	61	87	56	92
EN_1	381	635	175	841	208	808	0	1016	489	527	279	737
CG_0	246	304	119	431	141	409	61	489	550	0	173	377
CG_1	249	365	172	442	159	455	87	527	0	614	162	452
MD_0	175	160	106	229	113	222	56	279	173	162	335	0
MD_1	320	509	185	644	187	642	92	737	377	452	0	829

PA: Physical Activity, MB: Mobility, ST: Strength, EN: Energy, CG: Cognition, MD: Mood. Suffix 1 corresponds to the presence of deficits in the domain; suffix 0 represents the absence of deficits.

Results of the MCA were generated using the following SAS code:

PROC CORRESP DATA=MCA_fmt MCA DIMENS=3 GREENACRE
OUTC=SIPAcorresp;
        TABLES phys_act mobility strength energy cognition mood;
RUN;
%PLOTIT(DATA=SIPAcorresp,DATATYPE=MCA, HREF=0, VREF=0,
         PLOTVARS=Dim2 Dim1, COLOR=black);
%PLOTIT(DATA= SIPAcorresp,DATATYPE=MCA, href=0, vref=0,
         PLOTVARS=Dim3 Dim1, COLOR=black);

The dataset MCA_fmt contains the six binary frailty variables with formatted labels concatenating the variable name with the response category to differentiate the variables on the map. Two options not shown in the Country/Language example have been added to the code. The DATATYPE = MCA instructs SAS to conduct a Multiple Correspondence Analysis. The GREENACRE option requests an adjustment to the calculation of the inertia using Greenacre’s formula [17]. Greenacre showed that, with MCA, the usual computation of explained inertia in each dimension underestimates the quality of fit and proposed an alternative calculation which results in a more precise estimate. An adjustment proposed by Benzecri [18] is also available in SAS; however, Greenacre argues that this adjustment is overly optimistic [17].

Table 6 presents Greenacre-adjusted inertia decomposition of frailty variables. The same rules of thumb as for CA can be applied to guide the choice of the number of dimensions. However, rather than using the rule 1/[min(I,J)-1], for MCA, Greenacre [14] recommends that the number of dimensions to retain correspond to those with eigenvalues > 1/Q, where Q is the number of variables. In our example Q=6, and viewing Table 6, we see that the first two dimensions have eigenvalues > 1/6, or 0.17. However, since two dimensions account for only 63.7% and three dimensions account for 77.1%, we chose to include the third dimension in our interpretations.

Table 6.

Greenacre-adjusted inertia decomposition of frailty variables

Dimension	Eigenvalue	Adjusted Inertia	Percent of inertia	Cumulative Percent of inertia
1	0.33	0.24	45.8	45.8
2	0.18	0.10	17.9	63.7
3	0.15	0.07	13.5	77.1
4	0.14	0.06	11.4	88.5
5	0.11	0.04	7.4	95.9
6	0.08	0.02	4.1	100.0
	Total	0.53	100.0

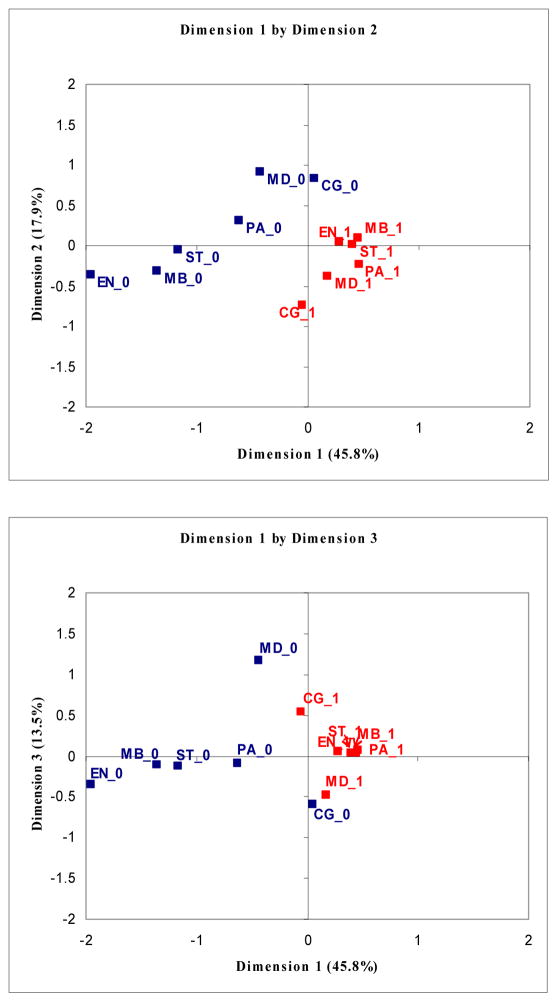
Figure 3 presents the results of the MCA. For ease of visualization, we present the results of the three retained dimensions in two graphs using separate %PLOTIT macros. Analysts may also wish to consider a dynamic 3-D display where all three dimensions may be viewed simultaneously and the image rotated at different angles (see [19] for information on dynamic 3-D capabilities in SAS). As in CA, the closer the response category’s vector location is to the origin, the more similar the response profile is to the average profile. In the map of Dimension 1 vs. Dimension 2, we see that a majority of the SIPA participants had frailty markers for energy, mobility, strength and mood and approximately half had markers for physical activity and cognition. This is in keeping with the proportions of participants with these deficits reported earlier. An artefact of CA when using binary variables is that the positive and negative point for each variable are situated 180 degrees apart from the origin on the map [9]. The interest is in seeing “which” side each point falls on relative to the other variables. In this example, we see that the response categories for presence of a frailty deficit (suffix ‘1’) are on the positive side of Dimension 1 and those for absence of a deficit (suffix ‘0’) on the negative side, in all domains except for cognition. This separation of ‘1’s and ‘0’s on either side of Dimension 1 shows that, with the exception of cognition, the most importance difference in the sample is between having and not having frailty markers. This separation also implies that domains are positively correlated except for cognition (Table 4).

Figure 3.

Multiple correspondence analysis map of frailty variables

PA: Physical Activity, MB: Mobility, ST: Strength, EN: Energy, CG: Cognition, MD: Mood. Points in red (with suffix 1) correspond to the presence of deficits in the domain; points in blue (with suffix 0) represent the absence of deficits.

Considering the relative distance of the points from the origin along each dimension, we also examined on which dimension each domain was best represented and which domains loaded on the same dimension. Separation of presence from absence of deficits in energy, mobility and strength appears to be the most important in explaining the deviation from independence in this sample given the strong representation of these domains on Dimension 1. Moreover, deficits in energy, mobility and strength appear to cluster closely together on map and are in fact the most strongly associated domains (TCC = 0.57 to 0.76). Physical activity does not contribute much information given its relatively low loading on all three dimensions, although slightly higher on Dimension 1. Cognition and mood are well represented on Dimensions 2 and 3, with Dimension 2 characterized primarily by cognition and Dimension 3 by mood. This may suggest different subgroups or pathways of frailty or, alternatively, that cognition and mood are relatively independent from the other domains.

3.1 Supplementary variables

In studying the frailty domains, we were also interested in seeing how age was related to these domains since one would naturally predict that the presence of frailty deficits is more common with increasing age [16].

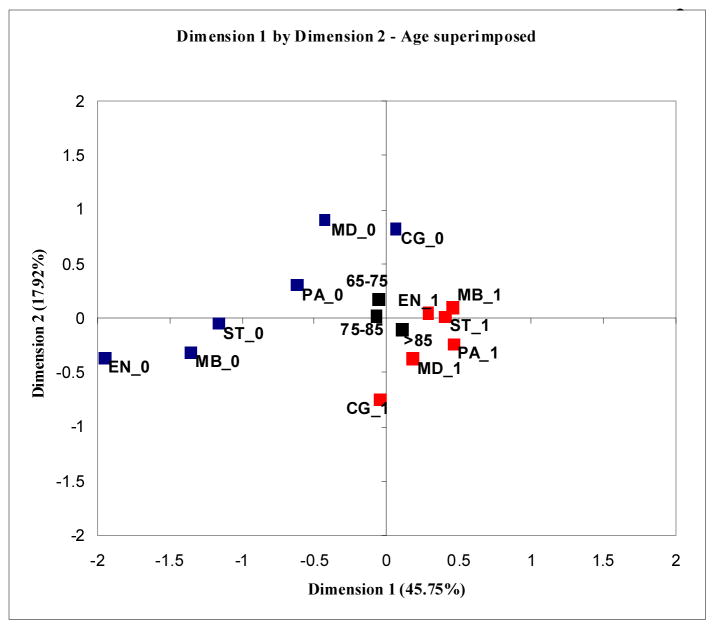
A nice feature of correspondence analysis is the ability to add supplementary variables to the map [8]. Such variables are projected onto the dimensions after the original analysis on the variables of interest is carried out. In this way, these additional variables do not contribute to the inertia nor do they affect the original results. However, their position on the graph allows us to see how the primary variables of interest (in our case, the frailty domains) relate to these supplementary variables [8]. Including the age groupings (65–74, 75–84, 85+) in the MCA, as expected (see Figure 4), we found that those 85 and over were more likely to have frailty deficits than those in the younger age groups.

Figure 4.

Relationship of frailty variables with age

PA: Physical Activity, MB: Mobility, ST: Strength, EN: Energy, CG: Cognition, MD: Mood. Points in red (with suffix 1) correspond to the presence of deficits in the domain; points in blue (with suffix 0) represent the absence of deficits.

4. Discussion

Faced with the challenge of examining the associations among several categorical variables in our frailty research initiative, we chose to use multiple correspondence analysis. The graphical display of relationships provides a user friendly overview of the salient relationships among the variable categories which are not easily captured by visual inspection of contingency tables. Correspondence analysis (CA) can be used for nominal, ordinal or binary variables [10]. In addition, unlike traditional principal components analysis (PCA) or factor analysis, which require an assumption of underlying normality, correspondence analysis makes no distributional assumptions [20].

The measure of association used in CA is the chi-square distance between the response categories [8]. The mathematical form of this measure helps to ensure that larger observed proportions do not dominate the distance calculation relative to smaller proportions [1]. CA thus provides a more precise measure of association than other multivariate techniques based on the correlation coefficient [21] for which no such standardization is performed.

Although the first mention of CA in the statistical literature can be traced to Hirschfeld in 1935 [22], the technique has only recently started to gain in popularity. In reviewing CA for our own analysis, we noted that CA has been “discovered” many times in different fields and under different names including correspondence factor analysis, principal components analysis of qualitative data, dual scaling and optimal scaling [23]. To further confuse things, a related statistical method called PRINQUAL in SAS is also referred to as principal components analysis of qualitative data. The term correspondence analysis, a translation of the French ‘analyse des correspondances’, originated from the work of Benzecri in 1973 [7]. Since that time, CA has been very popular in the French literature. In fact, the French news often includes correspondence maps in the explanation of topics such as voting behaviour [20]. However, it was only after Hill [21] and Greenacre [24] presented CA in the English literature in the 70’s and 80’s accompanied by the availability of accessible computer software that CA began to gain recognition in the English-speaking world. CA can now be easily performed with most statistical software, including SAS, R and SPSS.

A MEDLINE and EMBASE search of the medical and epidemiological journals, revealed 387 articles written in English since 1950, with correspondence analysis in the keywords, title or abstract. Of the 387, only 46 were linked to epidemiology of which two were published in the Journal of Clinical Epidemiology [25, 26]. The most common use of CA in the medical literature is in microarray analysis; for example, evaluating the presence of multiple bio-pathological disease factors and the genetic similarity/variation among different populations [27, 28]. Another major use of CA is in psychology and sociology where our quick search of the PSYCHINFO and SOCIOLOGICAL ABSTRACT databases revealed 220 articles published after 1950. Examples in this field include the exploration of segregation patterns among different communities and social status classification [29, 30].

An interesting feature of correspondence analysis is its close connection to log-linear analysis. Goodman (1981b) showed that, under certain conditions, the estimates of the multiplicative row and column parameters in the log-linear model are approximately equal to the row and column scores of the first dimension in correspondence analysis [31]. Van Der Heijden (1989) showed how CA can be used as a complementary technique to log-linear analysis for the decomposition of the residuals of specific restricted log-linear models [32]. In addition, using epidemiological data, Panagiotakos and Pitsavos (2004) showed how CA could be used to reduce the number of tested interaction terms in the final log-linear model, leading to a more parsimonious and more easily interpreted model [33]. Recent work by Greenacre has also revealed conditions under which CA could be used for inference [34]. Nevertheless, in practice, CA remains an exploratory technique.

In our own research on frailty, we found CA to be very useful in answering our research question on how frailty domains associate together. One advantage we found is that its “model-free” approach and lack of underlying assumptions make it versatile for all types of categorical data, especially nominally scaled data. It enabled us to go further than pairwise correlations or tests of association as the graphical display shows how response categories from two or more variables cluster together. We also found its analysis of rows and columns based on the decomposition of the chi-square to be intuitive and appropriate in the context of categorical data.

While we believe CA to be a very useful technique, one limitation is that distances between row and column points are not mathematically defined. One must, therefore, be cautious when interpreting relationships between row and column variables on the CA map. One can use the angle from the origin or points within the same quadrant to suggest stronger associations but the numerical output is sometimes also needed to get a sense of the dimensionality of the points [35]. As with other multivariate techniques, the more variables included in the analysis, the less inertia or variability each dimension will tend to explain. Therefore, retaining only two or three dimensions may not sufficiently describe all the salient features in the data. In this case, investigators must use judgment in deciding if the percentage of explained inertia is adequate for their purposes or may choose to rely on the numerical output to study the dimensionality of the data points. It should be noted that, as in other multivariate graphical techniques, interpretations of the graphs are in part subjective and therefore may vary somewhat from one researcher to another. Finally, the use of CA requires some initial practice in choosing the correct analytical options and in interpreting the maps.

In summary, correspondence analysis can be a very helpful tool to uncover the relationships among categorical variables, generate hypotheses for future analyses, and is easily implemented with most statistical software. Because CA explores the clustering among categorical variable responses, it can uncover how responses within and between variables are related; knowledge that may not otherwise be discovered through a pairwise analysis. We believe that correspondence analysis is an underutilized technique which can play a complementary role in analyzing epidemiological data and therefore deserves greater consideration in this field.

What is new?

Key finding

• Correspondence analysis is an underutilized multivariate technique designed specifically to explore relationships within and between two or more categorical variables.

What this adds to what was known

• Correspondence analysis analyzes binary, ordinal as well as nominal data without distributional assumptions (unlike traditional multivariate techniques) and preserves the categorical nature of the variables.

• Correspondence analysis provides a unique graphical display showing how the variable response categories are related.

What is the implication, what should change now

• Epidemiologists should include correspondence analysis in their “toolkit” of analytical techniques for categorical data.