Exsolution by spinodal decomposition in multicomponent mineral solutions

Abstract

Phase separation in a three-component system that results from the uphill diffusion of chemical components is considered. The binary decomposition model of Cahn and Hilliard is generalized to account for the interdiffusion of several chemical components with considerably different diffusion constants. Thereafter the decomposition dynamics and the phase relations of the final system state are investigated by means of finite-element modeling. Examples from a hypothetical regular solution and from ternary feldspar are addressed. Special attention is given to situations in which different diffusivities affect decomposition dynamics and the final system states. Good qualitative agreement between our modeling and petrographic observations on exsolved feldspar is achieved. Our model explains systematic deviations from equilibrium element partitioning between the two phases exsolving from an initially homogeneous ternary feldspar during slow cooling.

1. Introduction

Uphill diffusion of chemical components and the resulting spinodal decomposition of phases in alloys, polymers and minerals are usually associated with the interdiffusion of atoms. Many mineral systems may be described as ionic crystals and interdiffusion occurs by a vacancy mechanism. Provided that the concentration of vacancies is constant over time, such interdiffusion implies that the fluxes of the substitutional components in a binary solid solution take identical values and have opposite directions in the material fixed frame of reference. Therefore both moving components can be characterized by a single mobility [1] or by a single diffusivity [2] parameter. Following these lines, spinodal decomposition in a multi-component system is usually considered under the assumption of one common mobility (diffusivity) constant [3,4,2,5,6].

The proposition of nearly equal diffusivities of components in a multicomponent solution may be a reasonable approximation for spinodal decomposition in alloys and in polymers, but it definitely fails for mineral solid solutions. The latter show diffusivity parameters differing up to several orders of magnitude [7]. Investigations of phase separation in multicomponent systems with different diffusivities are relatively scarce [8,9]. These studies typically conclude that neither the newborn phases nor the morphology of the final system state is affected by possibly different mobilities of the components. This is a natural conclusion because the stationary equilibrium state, say for given pressure and temperature, is determined by equilibration of chemical potentials. As there are no fluxes, the mobilities cannot affect the uniform phases with the exception of the transition regions between the different phases. The transition regions are coined by the interplay of particle mobilities and interfacial energy [10,11].

Mineral solid solutions that are originally formed at high temperatures that are typical of the Earth’s crust and mantle are often observed far from the equilibrium state. Such transient states may get “stranded” due to successively more sluggish kinetics during cooling. Therefore the whole evolution path may be of interest. This path is of course affected by the contrasting diffusivities of the components. Spinodal decomposition in mineral solid solutions is the main topic of the present study. We first revisit the standard derivation of the Cahn–Hilliard equation (see e.g. the review by Nauman and He [2]) and carefully account for the arbitrary diffusivities of the components. The key point is that the flux j_A of a component A is not proportional solely to −∇μ_A but results from additive contributions of gradients of all chemical potentials in the spirit of non-equilibrium thermodynamics [12]. Substitutional interdiffusion is ensured by special properties of the mobility matrix. In this paper we are primarily interested in new physical effects caused by the considerably different mobilities of the components. To illustrate these new phenomena as simply and cleanly as possible, we deliberately ignore all secondary effects, e.g. contributions of the induced stresses, possible changes in the number of vacancies and possible influence of the induced electric fields on diffusion of components in ionic crystals. After the multicomponent generalization of the Cahn–Hilliard equation is derived, we consider how the final equilibrium or a long-lived quasi-stationary state is approached by the system. To this end, the generalized Cahn–Hilliard equation is solved numerically in several typical situations for a hypothetical regular solution and for ternary feldspar. Special attention is given to considerably different diffusivities and to the intermediate long-living quasi-stationary system states that may differ from those predicted by equilibrium thermodynamics. Finally, our modeling results are discussed in the light of observations on naturally exsolved feldspar from slowly cooled rocks.

2. Derivation

2.1. Interdiffusion

In this paper we consider spinodal decomposition in a multicomponent system. The latter is characterized by specifying its uniform temperature T = const and an externally applied uniform pressure P = const. We presuppose that atoms do not leave the system, occupy identical volumes and only rearrange within some fixed crystalline sublattice. The remainder of the crystal structure remains unchanged, local stresses are not created and the system volume V is a constant. The difference between the Helmholtz free energy and the Gibbs free energy is then also a constant, and both quantities are equally suitable for describing the system. In what follows, the free energy refers to the Gibbs free energy. Moreover, there is no distinction between the laboratory reference frame and the lattice reference frame because both frames are associated with the same fixed crystalline sublattice.

The local concentrations of atoms per unit volume are denoted by n_α(r, t), index α = A, B, C, … enumerates components. We consider substitutional interdiffusion, which is a special case of interdiffusion for which the total volume concentration of atoms $\mathfrak{n}$ does not change,

$$\mathfrak{n}={\displaystyle \sum _{\alpha }}{n}_{\alpha }(\mathbf{r}\text{,}t)=\mathrm{const}$$ (1)

In particular, the total flux of atoms is zero in a suitable frame of reference. To quantify the rearrangement dynamics, we have to introduce an expression for the local flux of each component j_α(r, t) such that

$${\displaystyle \sum _{\alpha }}{\mathbf{j}}_{\alpha }(\mathbf{r}\text{,}t)=0$$ (2)

in accord with Eq. (1). The flux model will be derived by incorporating Onsager’s approach [12].

2.2. Flux model

Rearrangement of the atoms pushes the system towards an equilibrium state with the smallest possible free energy. The corresponding thermodynamic forces act on atoms and are opposite to the spatial gradients of the chemical potentials. The resulting atomic fluxes are given by the Onsager-type relation

$${\mathbf{j}}_{\alpha }=-{\displaystyle \sum _{\beta }}{L}_{\alpha \beta }\nabla {\mu }_{\beta }$$ (3)

in which μ_β = μ_β(r, t) denotes the chemical potential of a component, −∇μ_β is the thermodynamic force per atom and L_αβ is the kinetic coefficient, also referred to as mobility. One naturally expects that

$$L_{\alpha \beta }>0\mathrm{for}\alpha =\beta$$ (4)

$$L_{\alpha \beta }<0\mathrm{for}\alpha \ne \beta$$ (5)

In other words, the driving force −∇μ_β in Eq. (3) yields a flux of component β in the same direction as the force and fluxes of all the other components α ≠ β in the opposite direction. The matrix L is assumed symmetric

$$L_{\alpha \beta }=L_{\beta \alpha }$$ (6)

in analogy with the reciprocal relation [12].

To address interdiffusion, we impose an additional restriction

$${\displaystyle \sum _{\alpha }}{L}_{\alpha \beta }=0\text{.}$$ (7)

Now the total flux (2) vanishes automatically because Eqs. (3) and (7) imply

$${\displaystyle \sum _{\alpha }}{\mathbf{j}}_{\alpha }=-{\displaystyle \sum _{\alpha \text{,}\beta }}{L}_{\alpha \beta }\nabla {\mu }_{\beta }=-{\displaystyle \sum _{\beta }}\left({\displaystyle \sum _{\alpha }}{L}_{\alpha \beta }\right)\nabla {\mu }_{\beta }=0$$

irrespective of the specific values of ∇μ_β.

The symmetry relation (6) and the interdiffusion condition (7) imply that Eq. (3) is equivalent to

$${\mathbf{j}}_{\alpha }={\displaystyle \sum _{\beta }}{L}_{\alpha \beta }\nabla ({\mu }_{\alpha }-{\mu }_{\beta })$$ (8)

and the particle flux actually depends only on the difference of chemical potentials. In what follows we will see that, although the expressions for the chemical potentials may be quite complicated, their differences are considerably simpler. It is therefore more convenient to deal with Eq. (8) instead of the parent Eq. (3).

Another consequence of condition (7) is that only the off-diagonal elements of the matrix L need to be specified. For instance, for a binary system with α = A, B, we have an especially simple form

$$L=\left(\begin{array}{cc}\hfill -L_{\mathit{AB}}\hfill & \hfill L_{\mathit{AB}}\hfill \\ \hfill L_{\mathit{AB}}\hfill & \hfill -L_{\mathit{AB}}\hfill \end{array}\right)$$

in which only one parameter L_AB < 0 counts. The fluxes are given by expression (8)

$${\mathbf{j}}_A=-{\mathbf{j}}_B=L_{\mathit{AB}}\nabla ({\mu }_A-{\mu }_B)$$ (9)

accounting for the fact that the positive factor −L_AB relates the flux j_A and the corresponding driving force −∇(μ_A − μ_B) for interdiffusion of unlike atoms moving in opposite directions. Cahn and Hilliard [1] considered Eq. (9) as a phenomenological definition of the diffusive mobility M = −L_AB > 0.

For a three-component system, all nine elements of matrix L are determined by only three independent negative parameters:

$$L=\left(\begin{array}{ccc}\hfill -L_{\mathit{AB}}-L_{\mathit{AC}}\hfill & \hfill L_{\mathit{AB}}\hfill & \hfill L_{\mathit{AC}}\hfill \\ \hfill L_{\mathit{AB}}\hfill & \hfill -L_{\mathit{AB}}-L_{\mathit{BC}}\hfill & \hfill L_{\mathit{BC}}\hfill \\ \hfill L_{\mathit{AC}}\hfill & \hfill L_{\mathit{BC}}\hfill & \hfill -L_{\mathit{AC}}-L_{\mathit{BC}}\hfill \end{array}\right)$$

Particle fluxes are given by the relations

$$\begin{array}{c}\hfill {\mathbf{j}}_A=L_{\mathit{AB}}\nabla ({\mu }_A-{\mu }_B)+L_{\mathit{AC}}\nabla ({\mu }_A-{\mu }_C)\text{,}\\ \hfill {\mathbf{j}}_B=L_{\mathit{AB}}\nabla ({\mu }_B-{\mu }_A)+L_{\mathit{BC}}\nabla ({\mu }_B-{\mu }_C)\text{,}\\ \hfill {\mathbf{j}}_C=L_{\mathit{AC}}\nabla ({\mu }_C-{\mu }_A)+L_{\mathit{BC}}\nabla ({\mu }_C-{\mu }_B)\end{array}$$

and the total flux automatically vanishes.

2.3. Diffusivities

Interdiffusion of unlike atoms is only possible if both types of atoms are present in a given volume element. For example, in a two-component system the mobility L_AB in Eq. (9) must be concentration dependent and must vanish if either n_A = 0 or n_B = 0. It is then useful to introduce a positive coefficient D_AB such that

$$L_{\mathit{AB}}=-\frac{D_{\mathit{AB}}}{\mathit{kT}}\frac{n_A{n}_B}{\mathfrak{n}}$$ (10)

where k is Boltzmann’s constant and $\mathfrak{n}$ is defined by Eq. (1). The parameter D_AB is referred to as the interdiffusion coefficient (this notation is justified later on in Section 3.1). Here we stress that the mobility coefficient L_AB is composition dependent whereas the interdiffusion coefficient D_AB may be constant, as discussed in Ref. [2]. This is why it is more convenient to operate with D_AB.

Following these lines, we return to the multicomponent case and define a set of positive parameters D_αβ such that

$$L_{\alpha \beta }=-\frac{D_{\alpha \beta }}{\mathit{kT}}\frac{n_{\alpha }{n}_{\beta }}{\mathfrak{n}}\mathrm{for}\alpha \ne \beta$$ (11)

The diagonal values L_αα are uniquely deduced from Eq. (7). The symmetry relation (6) immediately indicates that D_αβ = D_βα. Using definition (11), the flux model (8) can be rewritten as

$${\mathbf{j}}_{\alpha }=-{\displaystyle \sum _{\beta }}\frac{D_{\alpha \beta }}{\mathit{kT}}\frac{n_{\alpha }{n}_{\beta }}{\mathfrak{n}}\nabla ({\mu }_{\alpha }-{\mu }_{\beta })$$ (12)

where α, β = A, B, C, … enumerate all components. Eq. (12) specifies our flux model for a multicomponent interdiffusion system.

2.4. Chemical potential

To apply Eq. (12), we require explicit expressions for the chemical potentials. These are derived from the system free energy $\mathcal{G}$, the latter being defined as a spatial integral of the volume density G

$$\mathcal{G}=\int G(T\text{,}n\text{,}\nabla n)d^3\mathbf{r}$$ (13)

where n is a short notation for all particle densities and a dependence of G on ∇n is introduced in the spirit of the seminal work [1]. The integration in Eq. (13) is performed over the system volume V. In principle, the latter is a self-organized quantity determined by P, T and the total number of atoms of each component. However, V = const in our interdiffusion framework.

To determine chemical potentials, one must consider a small variation of the particle concentrations n_α → n_α + δn_α. Note that the integration volume does not change, and contributions to the particle number due to fluxes through the system boundaries are ignored. In other words, δn_α represents some internal rearrangement of atoms (and in general their chemical interconversion). The corresponding variation of the system free energy can be transformed to the form

$$\delta \mathcal{G}=\int \left({\displaystyle \sum _{\alpha }}\frac{\delta \mathcal{G}}{\delta n_{\alpha }}\delta n_{\alpha }\right)d^3\mathbf{r}$$ (14)

where partial integration was performed to eliminate terms proportional to ∇δn_α and

$$\frac{\delta \mathcal{G}}{\delta n_{\alpha }}=\frac{\partial G}{\partial n_{\alpha }}-\nabla \frac{\partial G}{\partial (\nabla n_{\alpha })}$$

denotes a variational derivative. System-interface related contributions to $\delta \mathcal{G}$ are set to zero. Now we identify the variational derivatives with the chemical potential of the components

$${\mu }_{\alpha }=\frac{\delta \mathcal{G}}{\delta n_{\alpha }}\alpha =A\text{,}B\text{,}C\text{,}\dots$$ (15)

such that variation of the system free energy in a unit volume takes the well-known form, ${\sum }_{\alpha }{\mu }_{\alpha }\delta n_{\alpha }$.

To compute μ_α, all components n_α are considered as independent quantities. In other words, definition (15) is independent of the interdiffusion condition (1). It is the relation (7) for the mobility matrix that accounts for interdiffusion.

2.5. Dynamic model

We can now specify a dynamic equation for decomposition of phases in a multicomponent system. For a given free energy density G(T, n, ∇n), the chemical potentials are first calculated using Eq. (15). Second, they are inserted into Eq. (12) to derive fluxes. The latter are then inserted into a sourceless continuity equation for the particle density

$${\partial }_t{n}_{\alpha }=-\nabla {\mathbf{j}}_{\alpha }$$ (16)

Eq. (16) is finally solved numerically to obtain n_α(r, t).

Our dynamic model can be written as

$${\partial }_t{n}_{\alpha }=\nabla \left[{\displaystyle \sum _{\beta }}\frac{D_{\alpha \beta }}{\mathit{kT}}\frac{n_{\alpha }{n}_{\beta }}{\mathfrak{n}}\nabla ({\mu }_{\alpha }-{\mu }_{\beta })\right]$$ (17)

and formally contains one equation for each component. However, these equations are not independent due to the interdiffusion condition (1), which is automatically supported by all solutions of Eq. (17). Specifically, one can always eliminate one component by reducing Eq. (17) to the equations for mole fractions $n_{\alpha }/\mathfrak{n}$ such that, for example, a two-component system is described by a single equation.

Some useful system properties can be derived prior to numerical solution of Eq. (17). For instance, let us trace the evolution of the free energy $\mathcal{G}(t)$. In accord with Eqs. (14) and (16), we obtain

$$\frac{d\mathcal{G}}{\mathit{dt}}=\int \left({\displaystyle \sum _{\alpha }}{\mu }_{\alpha }{\partial }_t{n}_{\alpha }\right)d^3\mathbf{r}={\displaystyle \sum _{\alpha }}\int {\mathbf{j}}_{\alpha }\nabla {\mu }_{\alpha }{d}^3\mathbf{r}$$

where partial integration was performed in a second step. For the flux model (3), we immediately obtain

$$\frac{d\mathcal{G}}{\mathit{dt}}=-\int \left({\displaystyle \sum _{\alpha \text{,}\beta }}{L}_{\alpha \beta }\nabla {\mu }_{\alpha }\nabla {\mu }_{\beta }\right)d^3\mathbf{r}$$ (18)

Furthermore, using Eq. (7), we transform Eq. (18) to the form

$$\frac{d\mathcal{G}}{\mathit{dt}}=\frac{1}{2}{\displaystyle \sum _{\alpha \text{,}\beta }}\int L_{\alpha \beta }{(\nabla {\mu }_{\alpha }-\nabla {\mu }_{\beta })}^2{d}^3\mathbf{r}<0$$

and conclude that $\mathcal{G}(t)$ permanently decreases because of inequality (5). In particular, stable equilibrium system states can be calculated by constrained minimization of the free energy. The constraints are derived from the condition that $\int n_{\alpha }(\mathbf{r}\text{,}t)d^3\mathbf{r}$ is conserved for each component. Specific examples are given in Appendices A and B.

3. Model equations

3.1. Two components

A simple illustration of the model (17) is given by a two-component system with α = A, B. We define the mole fraction of the component A

$$a(\mathbf{r}\text{,}t)=\frac{n_A}{n_A+n_B}$$

and introduce the following expression for the free energy density [1]

$$G=(n_A+n_B)\left[g(a)+\frac{\kappa }{2}{(\nabla a)}^2\right]$$ (19)

Here g(a) is just a free energy per particle in a uniform system. It accounts for both the configurational and the non-ideal contributions to the free energy. The gradient term with the parameter κ > 0 describes the interfacial energy associated with the phase boundaries. Using Eq. (15), one directly obtains

$$\begin{array}{cc}\hfill & {\mu }_A=g(a)+\frac{\kappa }{2}{(\nabla a)}^2+(1-a)\left(\frac{\partial g}{\partial a}-\kappa {\nabla }^{2}a\right)\hfill \\ \hfill & {\mu }_B=g(a)+\frac{\kappa }{2}{(\nabla a)}^2-a\left(\frac{\partial g}{\partial a}-\kappa {\nabla }^{2}a\right)\hfill \end{array}$$

where as expected, G = μ_An_A + μ_Bn_B. Although both chemical potentials look quite complicated, their difference is much more simple:

$${\mu }_A-{\mu }_B=\frac{\partial g}{\partial a}-\kappa {\nabla }^{2}a$$ (20)

so that, for α = A, Eq. (17) takes the form

$${\partial }_{t}a=\nabla \left[\frac{D_{\mathit{AB}}}{\mathit{kT}}a(1-a)\nabla \left(\frac{\partial g}{\partial a}-\kappa {\nabla }^{2}a\right)\right]$$ (21)

which is the well-known nonlinear Cahn–Hilliard equation for an isotropic binary system (for a recent review see Ref. [2] and references cited therein; anisotropic models for the surface free energy term are discussed in Refs. [13–17]). The dynamic equation for the second component, α = B, trivially follows from Eq. (21) and can be dropped. The quantity

$$D_{\mathrm{eff}}(a)=\frac{D_{\mathit{AB}}}{\mathit{kT}}a(1-a)\frac{{\partial }^{2}g}{\partial a^2}$$

is referred to as an effective diffusion coefficient. If the κ term can be ignored, Eq. (21) is just a nonlinear diffusion equation:

$${\partial }_{t}a=\nabla [D_{\mathrm{eff}}(a)\nabla a]$$

Moreover, for an ideal mixture with

$$g(a)=\mathit{kT}[a\ln a+(1-a)\ln (1-a)]$$

we obtain D_eff(a) = D_AB = const, which is why parameter D_AB is associated with the interdiffusion coefficient [2].

More complex behavior is possible in a non-ideal mixture where an unstable (spinodal) region of concentrations appears. This region is determined by the inequality

$$D_{\mathrm{eff}}(a)<0\mathrm{or}\frac{{\partial }^{2}g}{\partial a^2}<0$$ (22)

and physically corresponds to the uphill diffusion of components. A typical example is given by a non-ideal mixture in which

$$g(a)=\mathit{kT}[a\ln a+(1-a)\ln (1-a)+\chi a(1-a)]$$

and the uphill diffusion and spinodal phase separation are possible if the parameter χ > 2. When uphill diffusion is present, the κ term in Eq. (21) cannot be ignored; this term finally stabilizes the system.

3.2. Three components

We now formulate a closed system of two equations for a three-component system with α = A, B, C. The system is completely described by two mole fractions,

$$a(\mathbf{r}\text{,}t)=\frac{n_A}{\mathfrak{n}}\mathrm{and}b(\mathbf{r}\text{,}t)=\frac{n_B}{\mathfrak{n}}$$ (23)

where $\mathfrak{n}=n_A+n_B+n_C$. In full analogy with Eq. (19), the free energy density is presented as

$$G=(n_A+n_B+n_C)\left[f(a\text{,}b)+\frac{{\kappa }_{\mathit{aa}}}{2}{(\nabla a)}^2+{\kappa }_{\mathit{ab}}(\nabla a\nabla b)+\frac{{\kappa }_{\mathit{bb}}}{2}{(\nabla b)}^2\right]$$ (24)

where the specific expression for f(a, b) is determined by the free energy per particle for the uniform system states. (In full analogy with g(a) from the previous section, a different notation is used to avoid confusion between two- and three-component systems.) The most simple f(a, b) is given by the expression

$$\frac{f(a\text{,}b)}{\mathit{kT}}=a\ln a+b\ln b+c\ln c+{\chi }_a\mathit{bc}+{\chi }_b\mathit{ca}+{\chi }_c\mathit{ab}$$ (25)

in which c = 1 − a − b. More complicated models for f(a, b) in real materials will be considered in the numerical section.

The gradient terms in Eq. (24) should give a positive contribution for arbitrary directions of ∇a and ∇b. This implies the restrictions

$${\kappa }_{\mathit{aa}}>0\text{,}{\kappa }_{\mathit{bb}}>0\text{,}{({\kappa }_{\mathit{ab}})}^2<{\kappa }_{\mathit{aa}}{\kappa }_{\mathit{bb}}$$

In what follows, we use the short notations

$$\begin{array}{cc}\hfill & {\mu }_a=\frac{\partial f}{\partial a}-{\kappa }_{\mathit{aa}}{\nabla }^{2}a-{\kappa }_{\mathit{ab}}{\nabla }^{2}b\hfill \\ \hfill & {\mu }_b=\frac{\partial f}{\partial b}-{\kappa }_{\mathit{ab}}{\nabla }^{2}a-{\kappa }_{\mathit{bb}}{\nabla }^{2}b\hfill \end{array}$$ (26)

The chemical potentials of the components are calculated in accord with definition (15) and read

$$\begin{array}{cc}\hfill & {\mu }_A=G/\mathfrak{n}+(1-a){\mu }_a-b{\mu }_b\hfill \\ \hfill & {\mu }_B=G/\mathfrak{n}-a{\mu }_a+(1-b){\mu }_b\hfill \\ \hfill & {\mu }_C=G/\mathfrak{n}-a{\mu }_a-b{\mu }_b\hfill \end{array}$$

where, as expected,

$$G={\mu }_A{n}_A+{\mu }_B{n}_B+{\mu }_C{n}_C$$

One sees that the differences between chemical potentials are given by

$$\begin{array}{cc}\hfill & {\mu }_A-{\mu }_C={\mu }_a\text{,}{\mu }_B-{\mu }_C={\mu }_b\hfill \\ \hfill & {\mu }_A-{\mu }_B={\mu }_a-{\mu }_b\hfill \end{array}$$

The governing equations for the field variables (23) are obtained by inserting the latter differences into Eq. (17):

$$\begin{array}{cc}\hfill & {\partial }_{t}a=\nabla \left[\frac{D_{\mathit{AB}}}{\mathit{kT}}\mathit{ab}\nabla ({\mu }_a-{\mu }_b)+\frac{D_{\mathit{AC}}}{\mathit{kT}}\mathit{ac}\nabla {\mu }_a\right]\hfill \\ \hfill & {\partial }_{t}b=\nabla \left[\frac{D_{\mathit{AB}}}{\mathit{kT}}\mathit{ab}\nabla ({\mu }_b-{\mu }_a)+\frac{D_{\mathit{BC}}}{\mathit{kT}}\mathit{bc}\nabla {\mu }_b\right]\hfill \end{array}$$ (27)

where c = 1 − a − b. Similar to condition (22), the uphill diffusion of components is possible if either ∂²f/∂a² < 0 or ∂²f/∂b² < 0. More accurate conditions for spinodal decomposition are derived in Appendix B.

System (27) is the starting point for describing phase decomposition in a three-component system. It can be solved numerically after an expression for the free energy (24) and diffusion coefficients D_αβ are specified. An equation for the third component is derived in a similar manner,

$${\partial }_{t}c=\nabla \left[-\frac{D_{\mathit{AC}}}{\mathit{kT}}\mathit{ac}\nabla {\mu }_a-\frac{D_{\mathit{BC}}}{\mathit{kT}}\mathit{bc}\nabla {\mu }_b\right]$$

but does not provide new information.

3.3. Special cases

In this section we describe several special cases for the general system (27). First of all, a connection between the three- and two-component systems can be found, for example, by setting b → 0. Thereafter, the second equation in Eq. (27) is satisfied automatically, whereas the first one is simplified to the form

$${\partial }_{t}a=\nabla \left[\frac{D_{\mathit{AC}}}{\mathit{kT}}a(1-a)\nabla \left(\frac{\partial f}{\partial a}-{\kappa }_{\mathit{aa}}{\nabla }^{2}a\right)\right]$$

which is equivalent to Eq. (21).

Another special case of Eq. (27) is that, for identical diffusion coefficients, i.e. replacing D_AB, D_AC and D_BC with one common D, we obtain

$$\begin{array}{cc}\hfill & {\partial }_{t}a=\frac{D}{\mathit{kT}}\nabla \left[a(1-a)\nabla {\mu }_a-\mathit{ab}\nabla {\mu }_b\right]\hfill \\ \hfill & {\partial }_{t}b=\frac{D}{\mathit{kT}}\nabla \left[b(1-b)\nabla {\mu }_b-\mathit{ab}\nabla {\mu }_a\right]\hfill \end{array}$$ (28)

Spinodal decomposition in such systems was examined in Ref. [4], and possible morphologies are listed in Ref. [3].

In this paper we are primarily interested in systems with considerably different mobilities of components. For instance, in minerals, as opposed to alloys, such a difference may be several orders of magnitude. An extreme situation occurs when e.g. D_AB = 0, so that direct interdiffusion of the components A and B is not possible. Both components are transported due to binary exchanges with the third component. The equations in Eq. (27) are then reduced to the system

$$\begin{array}{cc}\hfill & {\partial }_{t}a=\nabla \left[\frac{D_{\mathit{AC}}}{\mathit{kT}}a(1-a-b)\nabla {\mu }_a\right]\hfill \\ \hfill & {\partial }_{t}b=\nabla \left[\frac{D_{\mathit{BC}}}{\mathit{kT}}b(1-a-b)\nabla {\mu }_b\right]\hfill \end{array}$$ (29)

Informally, one may say that Eq. (29) represents an effective two-component system in which in general D_AC ≠ D_BC.

4. Equilibrium states

If the chemical potentials of all components are constant throughout the system, the fluxes predicted by Eq. (12) vanish, and the system is in equilibrium. The equilibrium state does not depend on diffusion coefficients, the latter only determining the path to a final state. The main properties of the equilibrium states for two- and three-component systems are described in Appendices A and B. Here we stress that sometimes it is important to account for the differences in the diffusion coefficients even near to the equilibrium. This happens, for example, when the system is cooled down, such that some intermediate non-equilibrium system state becomes “frozen”. It is then critically important to reconstruct the path to which the intermediate state belongs. As we will see later, considerably different diffusion coefficients may force the system to evolve along a “wrong” conode, returning to a “correct” one only in close vicinity to the final state. Such situations will be considered later on for ternary feldspar.

5. Modeling

In this section we provide exemplary numerical solutions of the basic system (27). All solutions are obtained with the Multiphysics Modeling and Simulation Software, COMSOL [18].

5.1. Decomposition into two phases

As a first example, we consider a non-ideal three-component mixture where the free energy is given by the expression (25), in which χ_a = 2.6, χ_b = 2.5 and χ_c = 2.7. To begin with, we calculated the corresponding phase diagram. Barycentric coordinates are used, such that each point within the Gibbs triangle in Fig. 1 simultaneously represents a, b and c. Red regions indicate stable and metastable uniform system states. These regions are bounded by spinodal lines, which are calculated using Eq. (B.5). Straight black lines (conodes) indicate the directions along which the decomposition tends to occur; these lines are bounded by the binodal points. More precisely, if the initial (uniform) system state belongs to a conode, the final (uniform) phases are determined by the binodal points at the ends of the same conode. However, spinodal decomposition leads to highly non-uniform intermediate states, and compositions of the newborn phases may then temporarily leave the conode and finally return to it. Examples are given in Sections 5.3 and 5.4.

Fig. 1.

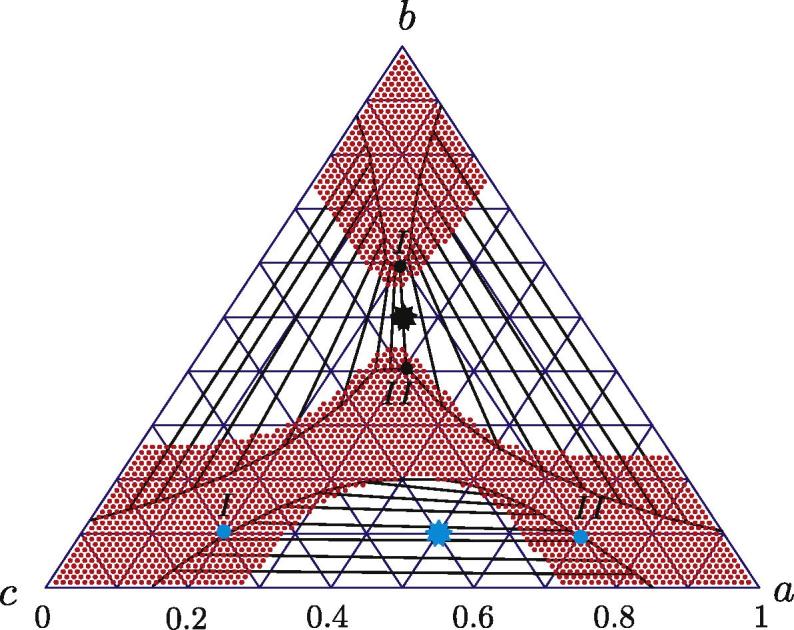
Phase diagram for a three-component system with the free energy (25) and χ_a = 2.6, χ_b = 2.5 and χ_c = 2.7. The initial system states for two exemplary calculations of phase decomposition are indicated by stars and the final decomposed phases are indicated by points.

Returning to Fig. 1, we observe three smooth binodal curves within the red regions. These curves separate the stable and metastable system states. To construct the binodal curves, we numerically build a convex hull over the free energy surface. The line at which the convex hull intersects the free energy surface is the binodal curve. The facets of “tangent planes” give the conodes.

Two exemplary initial concentrations are chosen, as shown by the black star (a₀, b₀) = (0.25, 0.5) and blue star (a₀, b₀) = (0.5, 0.1) in Fig. 1. The finally decomposed phases are shown by the black and blue points on the binodal curves on the same phase diagram. As expected, the initial stars and the final binodal points belong to the same conode.

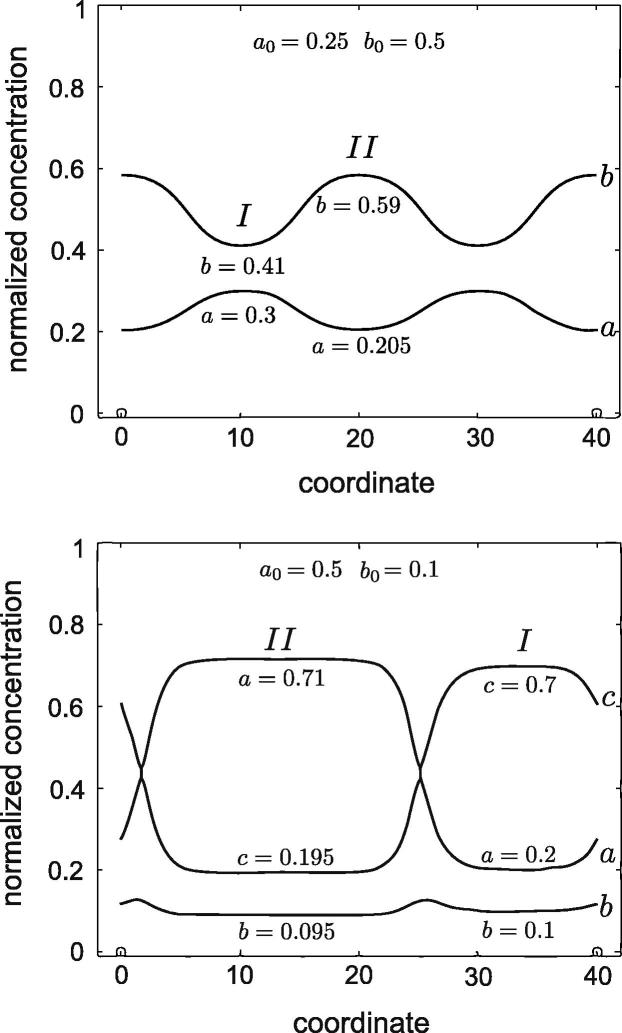
The distributions a = a₀ and b = b₀ with some small additive random perturbation are used to trigger decomposition. Periodic boundary conditions are applied. After the quick initial separation has taken place, the system evolves into a nearly stationary state. Exemplary nearly stationary spatial distributions of the mole fractions are shown in Fig. 2. Two phases are clearly observed. The corresponding values of the mole fractions agree with those taken from the phase diagram. The further evolution of such a state is extremely slow.

Fig. 2.

Nearly stationary 1-D distributions of mole fractions for Eq. (27). Free energy parameters and initial concentrations correspond to those in Fig. 1. Top: (a₀, b₀) is given by the black star in Fig. 1. In the final state, a(x) ≈ c(x); therefore only a(x) and b(x) are shown. Bottom: (a₀, b₀) is given by the blue star in Fig. 1. Here all three mole fractions are different.

In a next step we consider decomposition of phases in the same system as above, but in two spatial dimensions. Exemplary snapshots of the density distribution for a(x, y, t) are shown in Fig. 3. The initial condition is given by the blue star in Fig. 1. The snapshots demonstrate all typical features of spinodal decomposition: a quick initial separation and a much slower further coarsening. The morphology is richer than in the one-dimensional (1-D) case, e.g. labyrinths are observed for our initial condition.

Fig. 3.

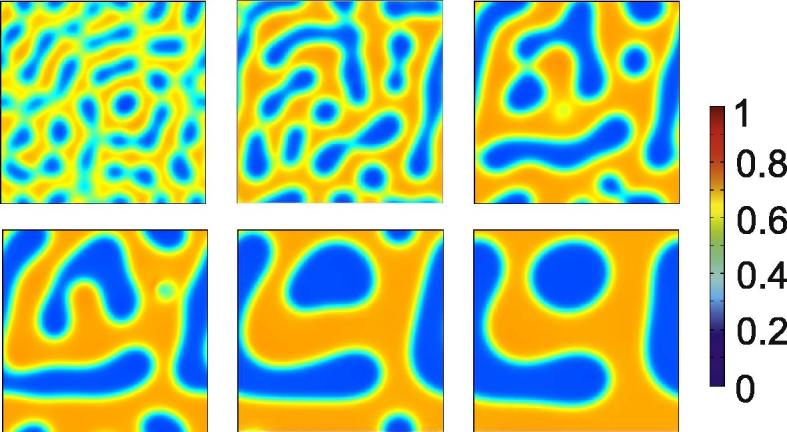
Snapshots of a(x, y, t) for numerical solution of Eq. (27) in two spatial dimensions. The initial composition is given by the blue star in Fig. 1. The snapshots are taken at times 500, 1500, 3000, 5000, 10,000 and 18,000. The simulation domain is 80 × 80.

5.2. Decomposition into three phases

In this section, spinodal decomposition into three phases is considered. The system free energy is again described by Eq. (25), in which χ_a = 2.3, χ_b = 3.0 and χ_c = 2.4. The corresponding phase diagram is calculated as in the previous section. The diagram is shown in Fig. 4 and has a new feature as compared to Fig. 1, namely in the white (unstable) domain there is a small region free of conodes. If the initial concentration lies in this region, spinodal decomposition into three phases will take place. Let us consider one such example.

Fig. 4.

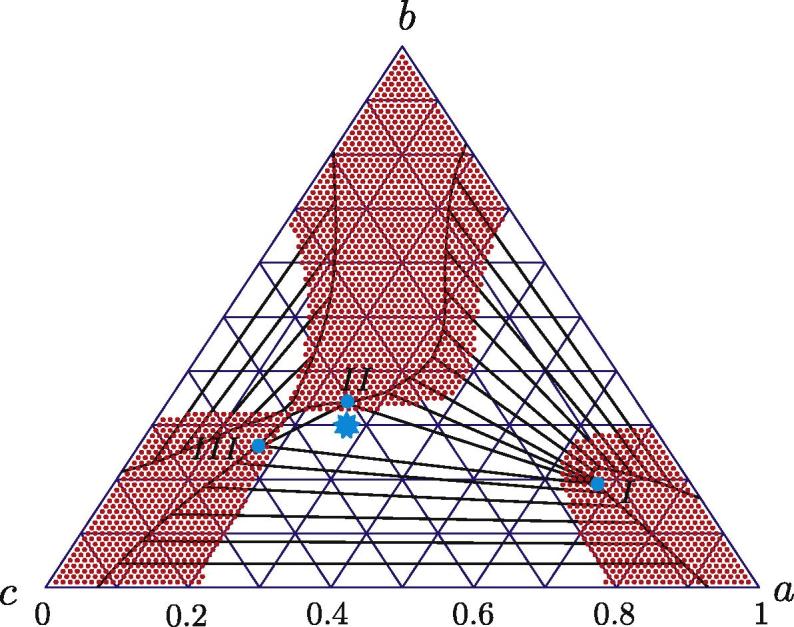
Phase diagram for a three-component system with the free energy (25) and χ_a = 2.3, χ_b = 3.0 and χ_c = 2.4. The initial system state for an exemplary calculation of phase decomposition is indicated by the star, the final decomposed phases by three points.

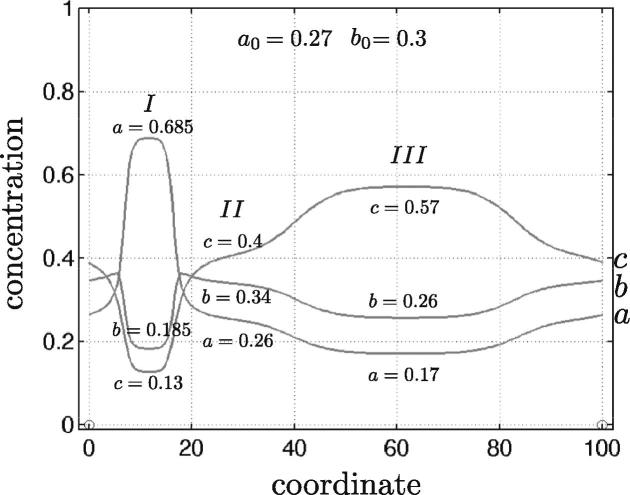
Eq. (27) has been solved twice: in one and two spatial dimensions. The initial composition (a₀, b₀) = (0.27, 0.3) is shown by a blue star in Fig. 4. A final quasi-stationary state for one spatial dimension is shown in Fig. 5. In the latter, one can clearly distinguish three phases. The final mole fractions (a_i, b_i), i = 1, 2, 3 agree well with those obtained from the phase diagram.

Fig. 5.

Nearly stationary spatial distributions of the mole fractions a(x), b(x) and c(x) for the three-component system (27) in one spatial dimension. The initial uniform concentrations correspond to system decomposition into three phases, as shown by the blue star in Fig. 4. The free energy parameters read χ_a = 2.3, χ_b = 3.0 and χ_c = 2.4.

Exemplary snapshots of the mole fraction distribution a(x, y, t) for the numerical solution of Eq. (27) in two spatial dimensions are shown in Fig. 6. Typical features of the spinodal regime of phase separation are clearly observable: at first, several individuals of the new phases appear. These grow in size and reduce in number, and the system develops into a quasi-equilibrium state. The subsequent evolution is extremely slow. Three different phases are now involved in the decomposition.

Fig. 6.

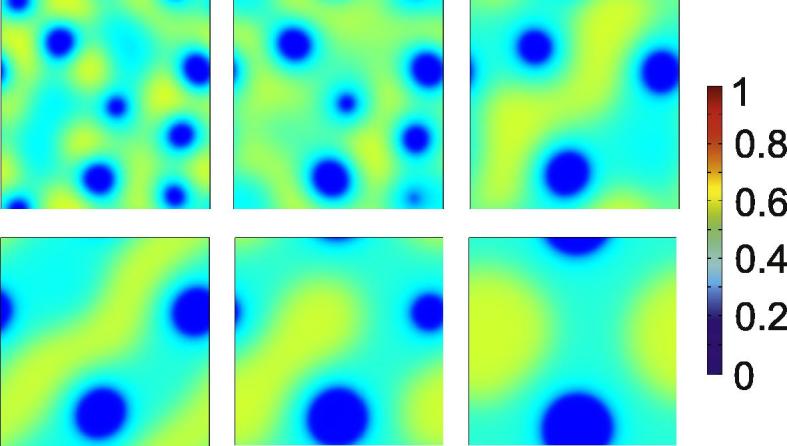
Snapshots of a(x, y, t) for a numerical solution of Eq. (27) in two spatial dimensions. The initial composition is given by the blue star in Fig. 4. The snapshots are taken at times 7000, 16000, 48000, 88000, 350000 and 8e5. The simulation domain is 80 × 80.

5.3. Ternary feldspar

We now turn to a real mineralogical example and consider the spinodal decomposition of ternary feldspar. The latter is a solid solution consisting of the three components, Or, An and Ab (orthoclase, anorthite and albite), with compositions KAlSi₃O₈, CaAl₂Si₂O₈ and NaAlSi₃O₈, respectively. In the following their mole fractions are denoted by a, b, and c such that (a, b, c) ↔ (X_Or, X_An, X_Ab). The feldspar structure consists of a 3-D framework of interlinked [SiO₄]⁴⁻ and [AlO₄]⁵⁻ tetrahedra. The Na⁺, K⁺, and Ca²⁺ ions occupy large irregular cavities in the tetrahedral framework. It is important to note that exchange of K⁺ and Na⁺ ions is considerably easier than exchange of either K⁺ or Na⁺ ions with Ca²⁺ because, due to charge balance constraints, such an exchange requires simultaneous transport of Al³⁺ and Si⁴⁺ in the tetrahedrally coordinated sites, which is exceedingly difficult. Therefore, our system consists of two mobile components (orthoclase and albite) and one less mobile component (anorthite). The dynamic model (27) accounts for different diffusivities and is thus suited for tracing decomposition dynamics. We use a realistic free energy function for the uniform states [19]

$$\frac{f(a\text{,}b)}{\mathit{kT}}=a\ln [a(1-b^2)]+b\ln \left[b\frac{{(1+b)}^2}{4}\right]+c\ln [c(1-b^2)]+w_{\mathit{ac}}\mathit{ac}\left(c+\frac{b}{2}\right)+w_{\mathit{ca}}\mathit{ac}\left(a+\frac{b}{2}\right)+w_{\mathit{ab}}\mathit{ab}\left(b+\frac{c}{2}\right)+w_{\mathit{ba}}\mathit{ab}\left(a+\frac{c}{2}\right)+w_{\mathit{bc}}\mathit{bc}\left(c+\frac{a}{2}\right)+w_{\mathit{cb}}\mathit{bc}\left(b+\frac{a}{2}\right)+w_{\mathit{abc}}\mathit{abc}$$ (30)

To specify the coefficients in the last equation, it is convenient to introduce a new index,

$$★=\{\mathit{ac}\text{,}\mathit{ca}\text{,}\mathit{ab}\text{,}\mathit{ba}\text{,}\mathit{bc}\text{,}\mathit{cb}\text{,}\mathit{abc}\}$$

Each coefficient w_★ is related to the three Margules parameters, W_E★, W_S★ and W_V★ (excess internal energy, excess entropy, and excess volume parameters respectively), by virtue of equation

$$w_{★}=\frac{W_{E★}-{\mathit{TW}}_{S★}+{\mathit{PW}}_{V★}}{\mathit{RT}}$$

where R is the gas constant. All involved Margules parameters are listed in Table 1 in accord with Ref. [19]. Exemplary phase diagrams of ternary feldspar for two temperatures are shown in Fig. 7. The straight lines indicate conodes joining points on the binodal curves that represent compositions of feldspars that coexist stably at the temperatures and pressures for which the diagrams have been constructed. The red dotted areas indicate the stable (outside the binodal regions) and metastable (inside the binodal regions) domains. The white area represents the unstable region. The boundary between the metastable and unstable regions is calculated from condition (B.5). Note that relatively orthoclase-poor feldspars with compositions close to the albite–anorthite join coexist with relatively anorthite-poor feldspars with compositions close to the albite–orthoclase join. The former pertain to the plagioclase series, the latter constitute the alkali feldspars. As expected, the difference in the compositions of the coexisting feldspars increases with decreasing temperature (compare the top and bottom diagrams in Fig. 7). In the following we consider the decomposition of ternary feldspar in a closed system, i.e. we ignore any interaction with a fluid or melt that could change the bulk composition. Given this constraint, it is noted that when going from high to low temperature alkali feldspar becomes successively more orthoclas-rich and anorthite-poor, whereas the plagioclase becomes successively more orthoclase-poor and anorthite-rich.

Table 1.

Margules parameters for feldspar [19].

★	WE (J/mol)	WS (J/(mol K))	WV (J/(mol bar))
AbOr	18810	10.3	0.394
OrAb	27320	10.3	0.394
AbAn	28226	0	0
AnAb	8471	0	0
AnOr	52468	0	−0.12
OrAn	47396	0	0
OrAbAn	8700	0	−1.094

Fig. 7.

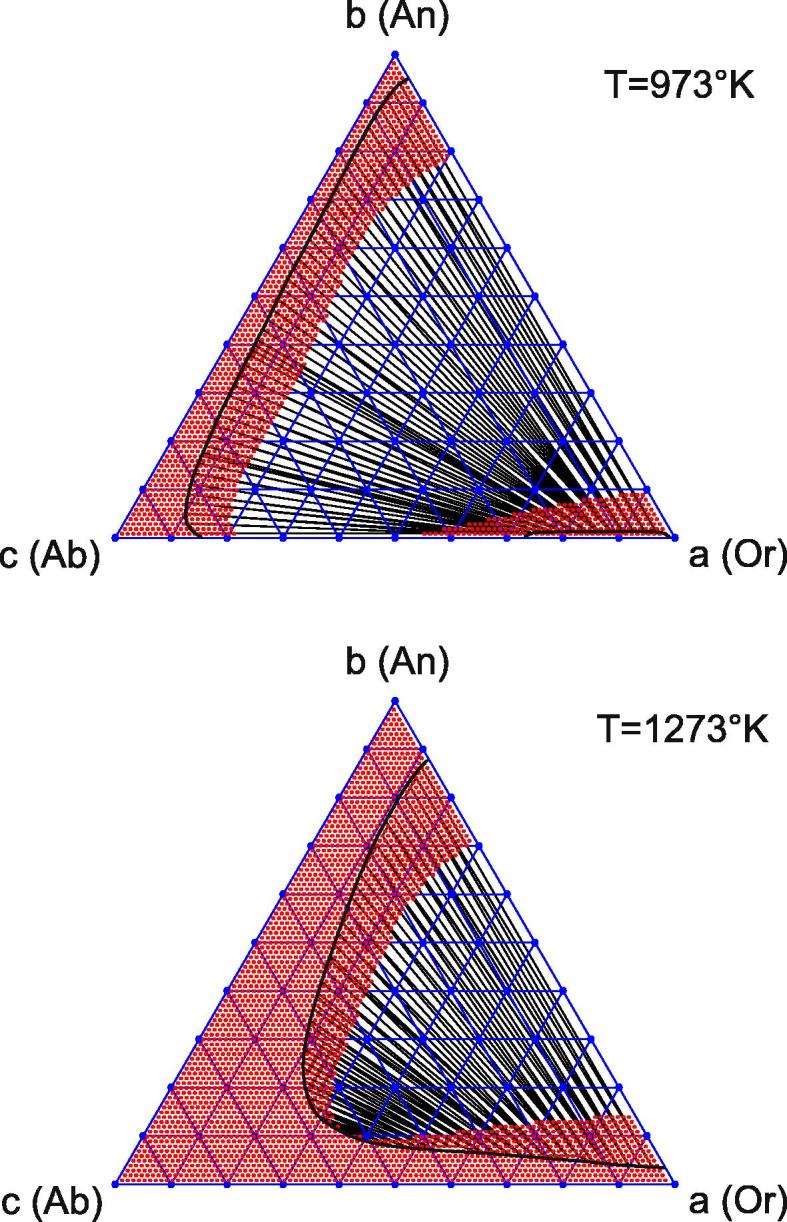
Exemplary phase diagrams of ternary feldspar for two temperatures. The binodal curves separate stable and metastable initial states (both red). The unstable (spinodal) white region is covered by conodes, which also cover metastable regions and are bounded by binodal points. The spinodal curves are calculated in accord with Eq. (B.5). The free energy model (30) follows Ref. [19].

We now consider the decomposition dynamics, taking into account that D_AB ≃ D_BC ≪ D_AC. As suggested by our numerical solutions, the flux of the b-component is initially ignorable. The main results are as follows. The system first behaves like a two-component system in which only one diffusivity D_AC is present. That is, the newborn phases evolve not along the conodes shown in Fig. 7 but along lines that are approximately parallel to the base of the Gibbs triangle, such that b ≈ const. Only when the separation of the albite and orthoclase components is nearly completed does exchange of the anorthite component become effective and the system slowly returns to a correct conode.

This effect is illustrated in Fig. 8. The initial condition corresponds to T = 973 K, P = 8000 bar and mole fractions (a₀, b₀) = (0.4, 0.07), as indicated by a green star. If all three diffusivities are similar, the system predictably evolves along the conode (Fig. 8, top). In contrast, the above-described two-stage decomposition regime is observed for realistic relations among the diffusivities (Fig. 8, bottom).

Fig. 8.

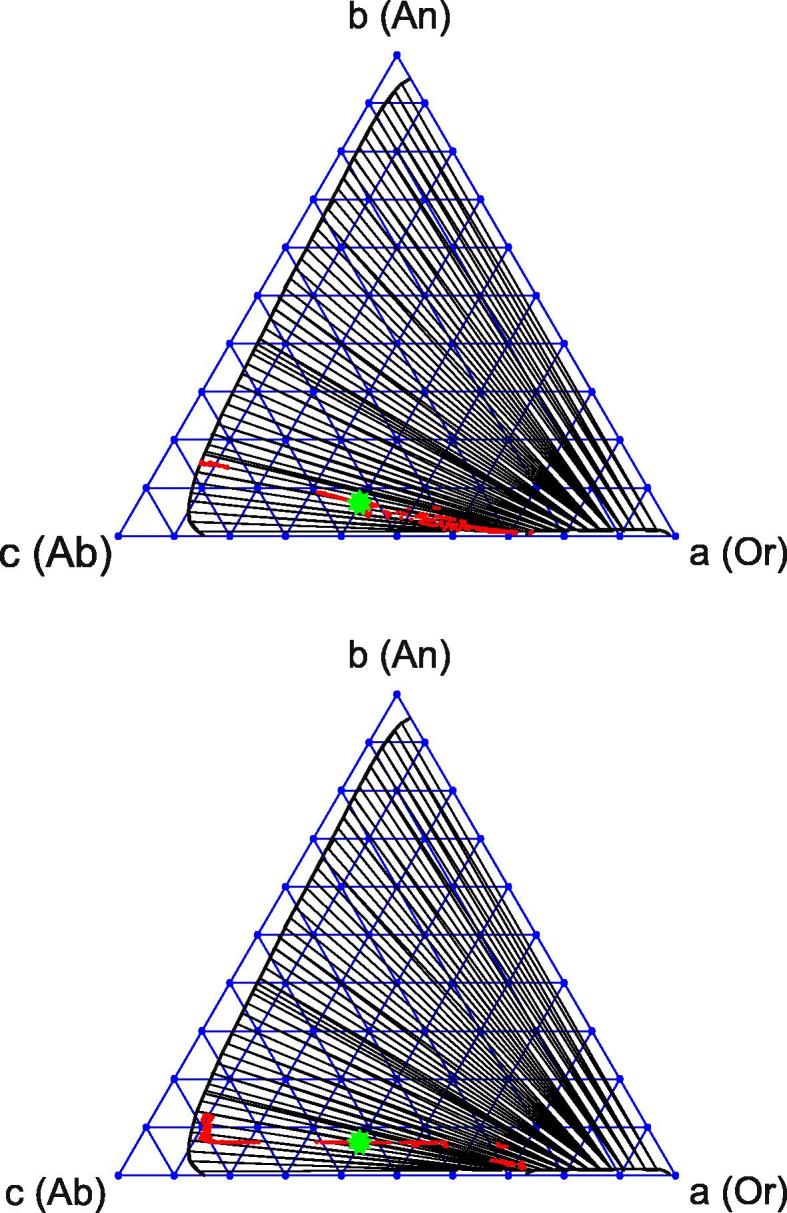
Phase decomposition of a ternary feldspar shown using paths on the Gibbs triangles. Top: diffusivities of components are artificially taken to be identical. Bottom: realistic diffusivities are taken. In the second case, the system first leaves the conode and then returns to it.

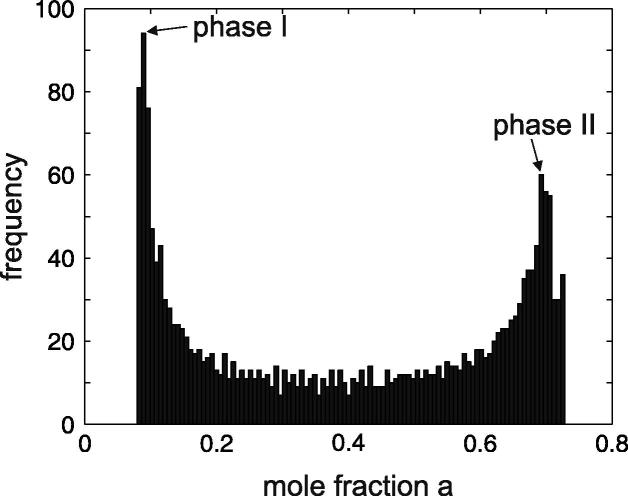
To trace the evolution of the intermediate highly non-uniform system states using the Gibbs triangle, one must permanently evaluate the instant mole fractions of the phases. For a given t, these mole fractions are obtained from a histogram indicating, for example, the probability of different values of a(t,x,y). An example is shown in Fig. 9. We observe two pronounced maxima, which are attributed to the values of a for the developing phases. The mole fractions are determined through a normal fit and are used to plot the evolution paths in Fig. 8.

Fig. 9.

An exemplary histogram of different values of a(t, x, y) observed throughout the decomposing system for a fixed t. The two maxima are associated with the compositions of the newborn phases. These compositions are used to plot the paths in Fig. 8.

5.4. Cooled feldspar

Another interesting phenomenon resulting from the different diffusion coefficients occurs in a slowly cooled feldspar. The point is that diffusivities are very sensitive to temperature, e.g. nearly identical diffusivities of components for high temperatures may be replaced by considerably different ones in the course of cooling. Thereby the decomposition dynamics changes considerably. In particular, even the final quasi-stationary system state may lay off the binodal curve.

To illustrate the effect of cooling numerically, we have chosen a ternary feldspar at P = 8000 bar. The initial mole fractions are (a₀,b₀) = (0.4, 0.2). Cooling is performed in two steps. First, the ternary system with nearly equal diffusivities of the components decomposes at T = 1273 K until two nearly stationary equilibrium phases are formed. These phases are shown by the red points in Fig. 10 (top). Note that the initial decomposition occurs along the conodes.

Fig. 10.

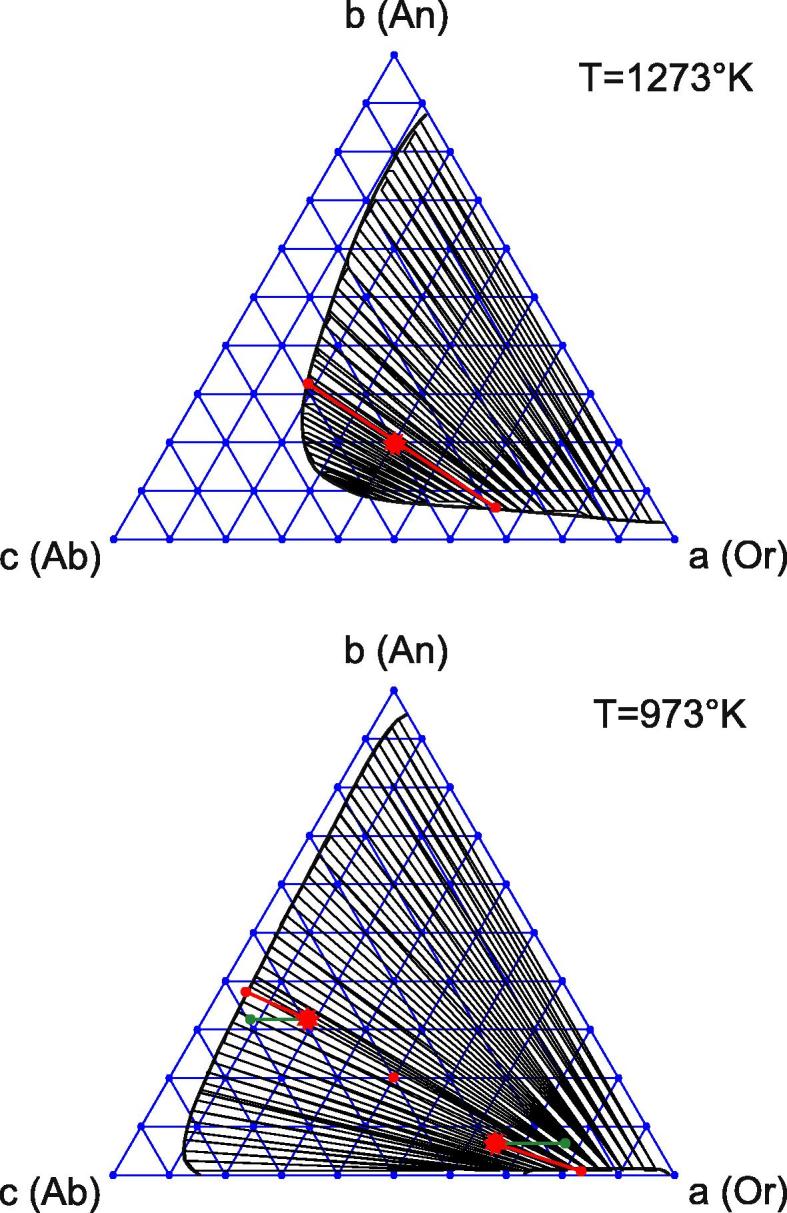
Different diffusion effects on cooling feldspar.

In a second step, the system is quickly cooled down to the temperature T = 973 K. The formerly created phases (red stars in Fig. 10, bottom) are used as a new initial condition. The less mobile anorthite component is now assumed to be “frozen”, unlike the others. Therefore D_AB and D_BC are set to zero, and further system evolution is determined by D_AC only.

The system decomposes further, the final phases being shown by the green points in Fig. 10 (bottom). As b = const for the second stage, the compositions of both phases evolve along lines which are parallel to the base of the Gibbs triangle. Notably, the final compositions do not reach the binodal curves at all. The reason for this is that in the second stage we effectively have a two-component system, which does not behave in accord with the ternary phase diagram.

For comparison, we also calculated decomposition of the system at T = 973 K, taking identical diffusivities for all three components. In this case, the final phases (red points in Fig. 10, bottom) are different and predictably correspond to the conodes on the Gibbs triangle. We see that accounting for different diffusivities may lead to system states that deviate considerably from what is predicted for thermodynamic equilibrium.

It is a common phenomenon that the compositions of the two feldspars exsolved from a homogeneous ternary feldspar precursor do not lay on a binodal curve. This has been attributed to the ease of diffusion of the mono- and divalent cations in the feldspar differing. It has been argued [20,21] that prolonged exchange of Na⁺/K⁺ at cooling stages when Na⁺/Ca²⁺ and K⁺/Ca²⁺ interdiffusion has already essentially ceased leads to further separation of Na⁺ and K⁺, whereas the Ca²⁺ contents remain constant. In such a case, the compositions of the two feldspars produced from exsolution are shifted away from the common binodal curve and, if applied in two feldspar thermometry, give systematic errors. Voll et al. [20,21] suggested that this effect could be corrected for by drawing lines parallel to the albite–orthoclase join of the Gibbs triangle through the observed compositions and then identifying the equilibration temperature by finding the binodal curve for which both phases lay on the same conode. Although slightly inaccurate, this procedure in essence reflects the effect that we obtain from our numerical simulation. This simplistic correction cannot, however, account for the complex microstructural and compositional evolution during the decomposition of a homogeneous ternary feldspar. The information from both the observable microstructures and the mineral compositions can be fully exploited based on our kinetic model. An example of such an analysis was given for exsolution of a binary alkali feldspar [22]. Such a quantitative analysis for ternary feldspar is hampered because the mobility of the anorthite component is not yet well enough constrained. The knowledge of relative component mobilities in ternary feldspar could, in principle, be better constrained from confronting mineral chemical data from exsolved feldspars with our numerical simulations, but this is beyond the purpose of this communication.

6. Conclusions

In conclusion, we investigated spinodal decomposition in a three-component system with considerably different diffusion coefficients. After deriving a suitable generalization of the Cahn–Hilliard equation, we addressed phase separation for both an idealized regular solution and ternary feldspar. In principle, the system in question must finally reach the thermodynamically stable equilibrium state, in which there are no fluxes and the differences in diffusivities are unimportant. In actual fact, the system may become frozen in a long-lived quasi-equilibrium state, which is strongly affected by the specific values of the diffusivities. This is especially true when the system is cooled down. In particular, the system evolution may occur along paths that deviate markedly from conodes. Such behavior has frequently been observed in exsolved felspar from slowly cooled rocks. Our approach reveals the intrinsic reasons for the specific phase separation path and rigorously describes it by direct numerical solution of the generalized Cahn–Hilliard equation.

Appendix A. Equilibrium states for two components

Describing stationary equilibrium states with several coexisting phases in a multicomponent system is a complicated task. Before turning to three-component systems in the second section of the Appendix, we discuss the relatively simple and well-investigated case of a two-component system.

Equilibrium states a = a(r) for Eq. (21) are described by the following relation:

$$\frac{\partial g}{\partial a}-\kappa {\nabla }^{2}a=\Lambda \text{,}\Lambda =\mathrm{const}$$ (A.1)

which is a nonlinear elliptical partial differential equation. It is associated with the constrained minimization problem

$${\displaystyle \underset{a(\mathbf{r})}{\min }}\int \left[g(a)+\frac{\kappa }{2}{(\nabla a)}^2\right]d^3\mathbf{r}$$ (A.2)

with the constraint

$$\frac{1}{V}\int a(\mathbf{r})d^3\mathbf{r}=a_0$$ (A.3)

where a₀ is the mean value of a(r) determined by the initial condition for Eq. (21). Indeed, Eq. (A.1) is nothing but an extremum condition for the combined functional

$$\int \left[g(a)-\Lambda a+\frac{\kappa }{2}{(\nabla a)}^2\right]d^3\mathbf{r}$$

where parameter Λ is the corresponding Lagrange multiplier.

From the physical point of view, by solving Eq. (A.2) we look for a system state with the minimal free energy $\mathcal{G}$ (cf. Eqs. (13) and (19)). The constraint (A.3) ensures conservation of the total particle number. Eq. (20) indicates that parameter Λ is just the difference of the equilibrium chemical potentials.

There is a trivial uniform solution a = a₀ of Eq. (A.1) with Λ = g′(a₀). It represents a stable equilibrium state for a concave g(a), e.g. for an ideal solution. If g(a) has a two-well shape, Eq. (A.1) allows for nonuniform solutions with coexisting phases. Here, two regions with almost constant a(r) are separated by a “boundary” where a smooth transition between the phases occurs. The term κ(∇a)²/2 contributes to the integral (A.2) mainly at the transition region. It describes the boundary-related part of the free energy. If the boundary energy can be ignored, we write the minimization problem (A.2) as

$$\begin{array}{cc}\hfill & {\displaystyle \underset{a_1\text{,}{a}_2\text{,}{V}_1\text{,}{V}_2}{\min }}[g(a_1)V_1+g(a_2)V_2]\hfill \\ \hfill & a_{0}V=a_1{V}_1+a_2{V}_2\text{,}V=V_1+V_2\hfill \end{array}$$ (A.4)

where the volumes occupied by the phases are denoted by V_1,2.

To solve Eq. (A.4), one may minimize a combined expression

$$g(a_1)V_1+g(a_2)V_2-\Lambda (a_1{V}_1+a_2{V}_2)-{\Lambda }_0(V_1+V_2)$$

with two Lagrange multipliers, Λ and Λ₀. Taking derivatives with respect to both pairs of variables a_1,2 and V_1,2, we obtain four equations:

$$g^{\prime }(a_1)=g^{\prime }(a_2)=\Lambda \text{,}g(a_{1\text{,}2})={\Lambda }_0+\Lambda a_{1\text{,}2}$$ (A.5)

The equilibrium chemical potentials μ_A0 and μ_B0 are defined by the relations Λ₀ = μ_B0 and Λ = μ_A0 − μ_B0. Now the extremum conditions take the form

$$\begin{array}{cc}\hfill & g^{\prime }(a_1)=g^{\prime }(a_2)={\mu }_{A0}-{\mu }_{B0}\hfill \\ \hfill & g(a_1)={\mu }_{A0}{a}_1+{\mu }_{B0}(1-a_1)\hfill \\ \hfill & g(a_2)={\mu }_{A0}{a}_2+{\mu }_{B0}(1-a_2)\hfill \end{array}$$

and indicate that the line μ_A0a + μ_B0(1 − a) on the (a, g) plane is in contact with the curve g = g(a) at two points, a = a_1,2. The specific values a₁, a₂ (binodal points) and μ_A0, μ_B0 are then determined by the common tangent rule as illustrated in Fig. 11.

Fig. 11.

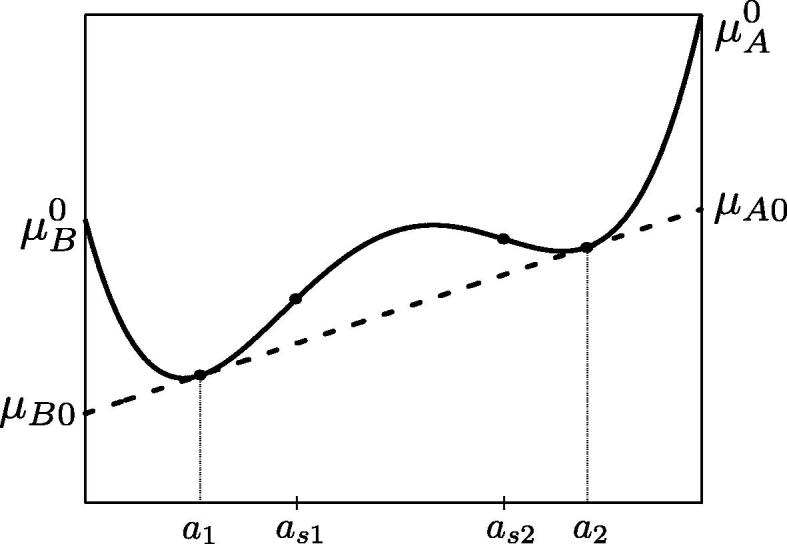
Exemplary two-well g(a) (solid line) and complement tangent line μ_A0a + μ_B0(1 − a) (dashed line); the spinodal points a_s1,s2 are the inflection points. The binodal points a_1,2 are determined by the common tangent rule. The equilibrium chemical potentials are μ_A0, μ_B0. Parameters ${\mu }_A^0\text{,}{\mu }_B^0$ denote chemical potentials of pure components.

Appendix B. Equilibrium states for three components

Eqs. (27) indicate that both μ_a and μ_b are constant for an equilibrium state. These constants will be denoted by μ_a0 and μ_b0. The equilibrium distribution of a(r) and b(r) is described by a system of two coupled nonlinear partial differential equations

$$\begin{array}{cc}\hfill & \frac{\partial f}{\partial a}-{\kappa }_{\mathit{aa}}{\nabla }^{2}a={\mu }_{a0}\hfill \\ \hfill & \frac{\partial f}{\partial b}-{\kappa }_{\mathit{bb}}{\nabla }^{2}b={\mu }_{b0}\hfill \end{array}$$ (B.1)

where for simplicity we set κ_ab = 0. Eqs. (B.1) are equivalent to the minimization problem

$${\displaystyle \underset{a(\mathbf{r})\text{,}b(\mathbf{r})}{\min }}\int \left[f(a\text{,}b)+\frac{{\kappa }_{\mathit{aa}}}{2}{(\nabla a)}^2+\frac{{\kappa }_{\mathit{bb}}}{2}{(\nabla b)}^2\right]d^3\mathbf{r}$$ (B.2)

with the constraints

$$\frac{1}{V}\int a(\mathbf{r})d^3\mathbf{r}=a_0\text{,}\frac{1}{V}\int b(\mathbf{r})d^3\mathbf{r}=b_0$$ (B.3)

A trivial uniform solution to the system (B.1) is given by the relations

$$a(\mathbf{r})=a_0\text{,}b(\mathbf{r})=b_0$$ (B.4)

where a₀ and b₀ are determined by the initial condition for Eq. (27). The uniform solution (B.4) with an additive small fluctuation is typically used as an initial condition for numerical solutions of Eqs. (27). Spinodal phase separation occurs when (B.4) is unstable. In accord with the standard minimum criteria, the uniform solution (B.4) is stable if

$${\left[\frac{{\partial }^{2}f}{\partial a^2}\right]}_0>0\text{,}{\left[\frac{{\partial }^{2}f}{\partial b^2}\right]}_0>0$$

and moreover if

$${\left[\frac{{\partial }^{2}f}{\partial a^2}\right]}_0{\left[\frac{{\partial }^{2}f}{\partial b^2}\right]}_0>{\left[\frac{{\partial }^{2}f}{\partial a\partial b}\right]}_0^2$$

where the index 0 means that derivatives are calculated at a = a₀ and b = b₀. The spinodal points are now replaced by spinodal curves, which separate stable and unstable “initial points” (a₀, b₀) on the (a, b) plane. If we start from some stable state (a₀, b₀) and continuously change the initial condition entering the spinodal region, the instability onset is completely determined by a single equation:

$$\frac{{\partial }^{2}f}{\partial a^2}\frac{{\partial }^{2}f}{\partial b^2}={\left(\frac{{\partial }^{2}f}{\partial a\partial b}\right)}^2$$ (B.5)

If the initial concentration is unstable, spontaneous decomposition takes place and the system evolves into a new equilibrium state with two or more separated phases. For instance, assume that three different phases with well-defined nearly uniform concentrations (a_i,b_i), i = 1, 2, 3 are observed and occupy volumes V₁, V₂ and V₃, respectively. If the system is large enough, the contribution of the transition regions to the integral (B.2) can be ignored. In full analogy with the two-component case, the equilibrium phases (a_i, b_i) and the corresponding volumes V_i can be found by minimizing the expression derived from Eq. (B.2):

$$\min [f(a_1\text{,}{b}_1)V_1+f(a_2\text{,}{b}_2)V_2+f(a_3\text{,}{b}_3)V_3]$$

under restrictions derived from Eqs. (B.3)

$$\begin{array}{c}{a}_{0}V=a_1{V}_1+a_2{V}_2+a_3{V}_3\hfill \\ b_{0}V=b_1{V}_1+b_2{V}_2+b_3{V}_3\hfill \\ V=V_1+V_2+V_3\hfill \end{array}$$

We denote the Lagrange multipliers corresponding to the latter three equations by μ_a0, μ_b0 and μ₀. The solution of the reformulated minimization problem

$$\min \left\{{\displaystyle \sum _{i=1\text{,}2\text{,}3}}[f(a_i\text{,}{b}_i)-{\mu }_0-{\mu }_{a0}{a}_i-{\mu }_{b0}{b}_i]V_i\right\}$$

with respect to the nine variables a_i, b_i, V_i with i = 1, 2, 3 is given by the following system (cf. Eq. (A.5)):

$$\begin{array}{cc}\hfill & {\left(\frac{\partial f}{\partial a}\right)}_{\begin{array}{c}a=a_i\hfill \\ b=b_i\hfill \end{array}}={\mu }_{a0}\text{,}{\left(\frac{\partial f}{\partial b}\right)}_{\begin{array}{c}a=a_i\hfill \\ b=b_i\hfill \end{array}}={\mu }_{b0}\hfill \\ \hfill & f(a_i\text{,}{b}_i)={\mu }_0+{\mu }_{a0}{a}_i+{\mu }_{b0}{b}_i\hfill \end{array}$$

The equilibrium chemical potentials μ_A0, μ_B0, and μ_C0 are determined by the relations

$${\mu }_{a0}={\mu }_{A0}-{\mu }_{C0}{\mu }_{b0}={\mu }_{B0}-{\mu }_{C0}{\mu }_0={\mu }_{C0}$$

Now the extremum conditions take the form

$${\left(\frac{\partial f}{\partial a}\right)}_{\begin{array}{c}a=a_i\hfill \\ b=b_i\hfill \end{array}}={\mu }_{A0}-{\mu }_{C0}$$ (B.6)

$${\left(\frac{\partial f}{\partial b}\right)}_{\begin{array}{c}a=a_i\hfill \\ b=b_i\hfill \end{array}}={\mu }_{B0}-{\mu }_{C0}$$ (B.7)

$$f(a_i\text{,}{b}_i)={\mu }_{A0}{a}_i+{\mu }_{B0}{b}_i+{\mu }_{C0}(1-a_i-b_i)$$ (B.8)

with i = 1, 2, 3.

Eqs. (B.6)–(B.8) have a simple geometrical interpretation. They indicate that the plane

$${\mu }_{A0}a+{\mu }_{B0}b+{\mu }_{C0}(1-a-b)$$

in a three-dimensional (a,b, f) space is in contact with the free energy surface f = f(a, b) at three points (a_i, b_i) with i = 1, 2, 3. In other words, a familiar common tangent-line rule is replaced by a common tangent-plane rule.

To conclude the description of the equilibrium states, we note that decomposition into two phases may also be possible in a three-component system for some initial concentrations (a₀, b₀). This happens if, for example, the minimization problem (B.6)–(B.8) results in a₂ = a₃ and b₂ = b₃. In such a case, the values V_2,3 remain unspecified and only the sum V₂ + V₃ has a physical meaning. The specific values of (a₁, b₁) and (a₂, b₂) belong to straight lines (conodes) on the (a, b) plane (see Figs. 1 and 4).

On the other hand, decomposition into four (five) phases is degenerate and occurs if the plane μ₀ + μ_a0a + μ_b0b happens to touch the surface f = f(a, b) at four (five) different points. According to the Gibbs phase rule, decomposition into four (five) phases may be expected if P and T are subject to one (or two) additional constraint(s). This may happen on some lines (points) on the (P, T) plane. Such degenerate situations are destroyed by a small variation of the free energy, e.g. by a small temperature change.