Abstract
Calculating the longitudinal extension of the average attributable fraction (LE-AAF) for many risk factors (RFs) requires a two-stage computational process using only those combinations of RFs observed in the dataset. We first screen candidates RFs in a Cox Model, and assuming piecewise constant hazards, use pooled logistic regression to model the probability of death as a function of combinations of selected RFs. We average the iterative differencing of the attributable fractions calculated for all overlapping subsets of co-occurring RFs to obtain a LE-AAF for each RF that is additive and symmetrical. We illustrate by partitioning the additive proportions of death from 10 different groupings of acute and chronic diseases, on a national sample of older persons from the US (Medicare Beneficiary Survey) over a 4-year period and compare with results reported by the National Center for Healthcare Statistics. We conclude that careful screening of RFs with analysis restricted to extant combinations greatly reduces computational burden. LE-AAF accounted for a cumulative total of 66% of the deaths in our sample, compared with the 83% accounted for by the National Center for Healthcare Statistics.
Keywords: average attributable fraction, high dimension, Cox regression, logistic regression, cause of death, medicare
1. Introduction
The epidemiological literature has widely embraced the use of the attributable fraction (AF) since its introduction by Levin in 1953 [1]. The AF is defined as the proportion by which the occurrence of a disease can be hypothetically reduced, given the whole population were to remain unexposed. Calculation of the AF for a specific risk factor combines the probability of the outcome (conditional on the risk factor), with the prevalence of the risk factor. In the case where multiple risk factors (RFs) contribute to a specific health outcome, for example death, the AF has a few notable mathematical limitations. The most important is that when calculated for a number of co-occurring conditions, the AFs for a particular outcome can add up to more than 100% [2]. This is because each AF represents the maximum, possible reduction in the outcome obtained by removing all exposure to a risk factor.
By virtue of its strong conceptual link with probability, the AF loses face validity when its values for multiple RFs add up to more than 100%. The amount by which the sum of the AFs exceeds 100% is termed the excess risk, and several methods have recently been suggested to achieve additivity of the individual AFs by a redistribution of the excess risk among the co-occurring RFs. Mc Elduff et al. (2002) estimate the contribution of individual RFs to occurrence of a disease using the AF in the exposed part of the population, that is, the attributable fraction of exposed (AFE). Their approach estimates the proportion of the attributable fraction for each RF by using a weighted mean of the excess relative risk where weights are calculated as the proportion of cases in the exposed [3]. Llorca and Rodriguez extended the approach of McElduff to the AF of the entire population [4]. It has recently been pointed out that methods involving proportional distribution of the excess risk among co-occurring RFs are not yet well developed [5]. Because the procedures of McElduff and Llorca are demonstrated using only two or three RFs, their utility for the high dimensional case is uncertain.
In a recent study we needed a statistically credible method of assigning population level fractions of death to the multiple chronic conditions that older persons in the US experience over a span of years. Because the occurrence of death among older persons can be reasonably attributed to many diseases occurring in a broad array of combinations, we desire the solution that best addresses the overlap of multiple diseases. For this reason we prefer the average attributable fraction (AAF) proposed by Eide and Gefeller [6], also referred to as partial attributable risk [7], which has the properties of additivity and symmetry. Additivity means that for a group of RFs, the sum of the individual AAFs cannot exceed 100%, whereas symmetry holds that the AAF can be uniquely calculated regardless of the order of removal of co-occurring RFs. The AAF possesses another desirable property from game theory referred to as the ‘dummy property’, which implies that its value for an irrelevant factor is zero [8].
The longitudinal extension of the AAF, that is, LE-AAF, was introduced by Lin et al. [9] and demonstrated for five diseases. The LE-AAF represents a weighted average of the AAFs calculated for each individual year (or other pertinent interval of time) in which data was collected. In Section 2 of this article, we describe a data-centric computational process for calculating the LE-AAF (or AAF) when there are a large number of RFs, that is > 10, for a particular health outcome. We illustrate our approach by applying our algorithm to a large US dataset of older persons (Medicare Beneficiary Survey data) over a 4-year period. In our demonstration we define risk factors as Clinical Classification Software [10] groupings of international classification of disease codes recorded in Medicare claims. In Section 3, we compare our LE-AAF findings with those reported by the National Center for Healthcare Statistics (NCHS) of the Centers for Disease Control and Prevention. In Section 4, we examine the strengths and limitations of the proposed approach and make concluding remarks.
2. Methods
2.1. Sequential attributable fractions: building blocks of average attributable fraction
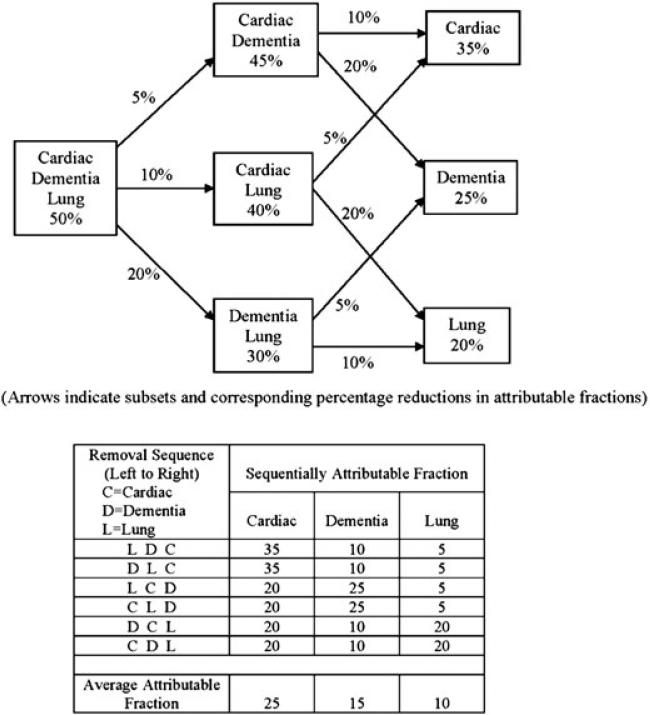
The pivotal concept is that the AAF is the average of sequentially attributable fractions (SAFs), which are reductions in AFs determined by specific removal sequences from a group of co-occurring RFs. For illustrative purposes only, Figure 1 depicts a hypothetical model with three RFs: a cardiac-related condition, (C), a lung related condition (L), and dementia (D). The top part of Figure 1 shows columnar groupings of blocks representing subsets of the full set of RFs as individual ones are sequentially removed. The lower part of Figure 1 tabulates the SAFs derived for each RF over each of the six possible removal orderings.
Figure 1.
Deriving average attributable fractions from sequentially attributable fractions in a hypothetical model with three risk factors.
The left-most block in the top part of Figure 1 indicates that the three RFs collectively account for 50% of the outcome. The three blocks in the middle column reflect AFs calculated from all two factor subsets, with arrows indicating reductions in AF corresponding to the removal of individual RFs. The right-most column of blocks gives the residual SAFs of individual RFs after all co-occurring RFs have been removed. The lower part of Figure 1 shows the six possible removal orderings of the RFs, with removal progressing from left to right. Consider the first ordering (LDC), where initially removing risk factor L results in a 5% reduction in AF, followed by removal of D, which yields in a 10% reduction in AF, leaving C with a residual SAF of 35%. These reductions and residual proportions are the SAFs for each RF in this particular removal ordering. Each removal order, that is, row, provides an SAF for each RF, which are averaged at the bottom to yield the AAF. The AAF thereby averages the SAFs from all removal orderings. Because all orderings may be possible within a large population, the AAF is best construed as a population descriptor.
2.2. Data centric approach for high dimensional calculation of AAF and LE-AAF
When considering how to best sort out the overlap in AF contributed by a large number of RFs, it is natural to approach the AAF computation from an RF perspective. That is, given a collection of RFs, structure the computation to process an enumeration of all the possible subsets of RFs, evaluating each subset of RFs in turn with respect to the study population. This conceptual approach is natural, but expensive: the memory and computational requirements grow exponentially with the number of RFs. Given the memory capacity and speed of current computers and the performance characteristics of MATLAB (The MathWorks, Inc, Natick MA, USA) [11], this approach is feasible for approximately 20 or fewer risk factors.
As illustrated in Figure 1, the calculation of AAF is the averaging of all possible SAFs, that is, the differences in values of AF yielded by different removal sequences of coexisting RFs. The evaluation of all possible SAFs, that is, the enumeration of all permutations of a combination of RFs, is by far the most burdensome computational task. The memory and computation needed for this grows as the factorial of the number of RFs, making this approach impractical for more than nine RFs.
Because we are motivated to calculate the LE-AAFs of a large group of RFs with respect to death, we needed a more efficient computational approach. The data-centric perspective makes the LE-AAF computation as efficient as possible by restricting evaluation to only those unique combinations of RFs that exist in our data. The first step is to define a design matrix consisting of all observed combinations, something easily accomplished using Microsoft Access (Microsoft Corporation, Redmond, WA, USA).
2.3. Defining a data-centric design matrix
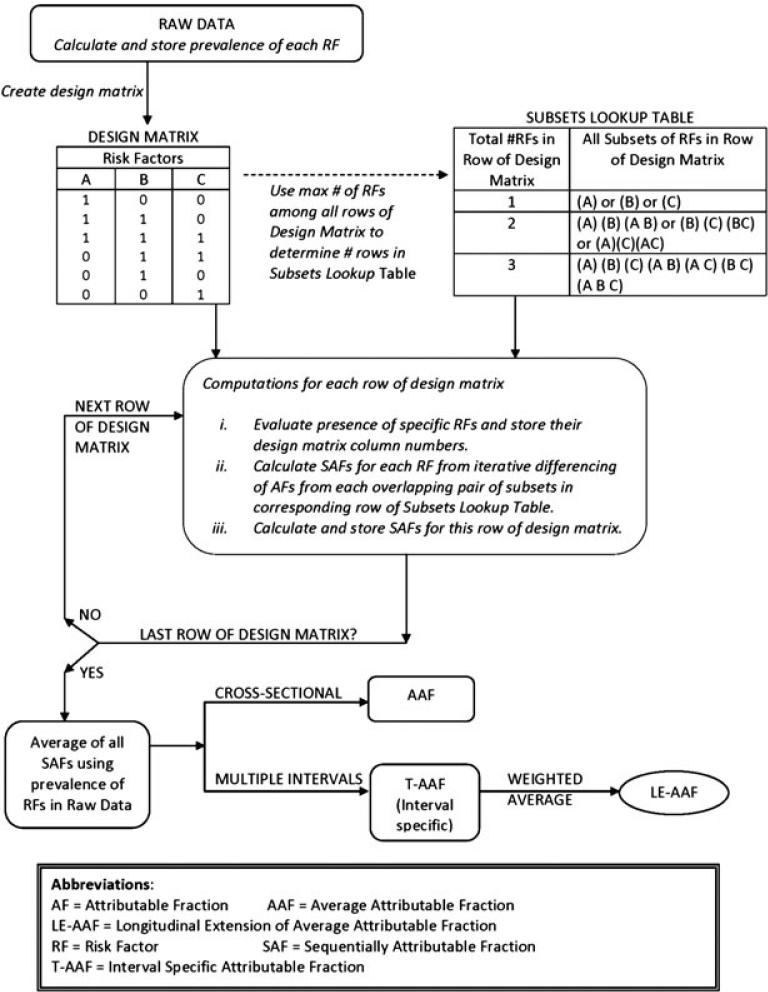
For purposes of illustration, the design matrix in Figure 2 depicts a hypothetical population where only three RFs, namely A, B, and C, are potentially present in any given data observation. Note that only 6 of the 12 possible combinations of the three RFs are contained in the design matrix, reflecting empiric rather than potential contents. Once the design matrix is formed, the largest number of RFs among all its rows determines the number of rows in the subsets lookup table. For this reason the subsets lookup table in Figure 2 consists of three rows, corresponding to rows of the design matrix containing one, two, or three RFs, respectively.
Figure 2.
High dimensional calculation of AAF/LE-AAF.
With our dataset of over 271,000 observations (person-months) and 28 RF indicators, we observed a total of < 10,000 distinct RF combinations. The use of a naïve enumeration would have resulted in 228— over 268,000,000. Because the specific RF combinations residing in each observation are merely counted for purposes of averaging, the number of observations, person-months in our example, is of much less computational importance than the number of RF combinations. In contrast the evaluation of all the SAFs derived from extant RF combinations comprises the bulk of the computational effort.
2.4. Computing sequentially attributable fractions without permutations
We exploit the fact that AAF is an average to restrict our attention to subsets without ordering of a given combination of RFs. By creating an indexing structure of RF column locations, the cell array type of MATLAB permits efficient examination of all subsets of the RFs in any given row of the design matrix. Our MATLAB program counts how many RFs are in each observation, and then considers only the subsets corresponding to that number of RFs. The subsequent iterative differencing of the AFs between each pair of overlapping subsets automatically calculates all the partial differences, that is, SAFs, that would otherwise be derived from the far more tedious process of stepping through all permutations. With only a fraction of the calculations, our order-free subsets-based process yields an average of the SAFs that is mathematically equal to that derived from stepping through all permutations. In our example the maximum number of RF indicators among all rows of our design matrix was 14, meaning that our subsets lookup Table had 14 rows respectively listing the subsets pertaining to observations with 1, 2, 3, . . . , 14 RFs. In the worst case this involves ~16,000 subcomputations, versus the 9 × 1010 required if we considered all permutations.
2.5. Dataset for demonstration of method
In the US the national program providing healthcare to over 95% of the population 65 years of age and older is called Medicare. A statistically representative sample of over 22,000 persons who filed claims within a 4-year period (2002–2005) was taken from the Medicare database maintained by The Center for Medicare and Medicaid Services per protocol approved by the Yale University Institutional Review Board.
2.6. Use of statistical models
We examined a list of time dependent medical conditions by calculating their unadjusted associations with death using Cox regression. Using Clinical Classification Software [10] groupings of international classification of disease codes recorded in Medicare claims, the acute and chronic conditions with bivariate associations of were aggregated to correspond to the ‘cause of death’ categories reported by the NCHS. Indicators for each category were set to a value of one (referent to zero) when any of their component conditions was present in any given person-month of data. Because Cox regression calculates hazards rather than probabilities, we used a pooled logistic model based on monthly observations and year-specific intercepts to estimate the probability of death conditional on the aggregate categories in the model [12]. Bootstrapping of these models allowed us to estimate confidence intervals for the estimated LE-AAFs presented in Section 3.
3. Results
Table I presents the proportions of death attributed to leading disease categories by the NCHS of the Centers for Disease Control and Prevention. LE-AAF results for our corresponding groupings of significant acute and chronic diseases are provided for comparison. Although cardiovascular disease was the unanimous leader, the proportion of deaths reported by NCHS was 30.4% in contrast with the 17.4% reported by LE-AAF. For NCHS the category of Malignancy/Cancer consisted of all cancers, whereas LE-AAF only counted the following types: bladder, bone/connective tissue, breast, colorectal, head/neck, kidney/urinary, leukemia, liver/pancreas, lung, lymphoma, and prostate. Relative to the 22% reported for this category by NCHS, only 7.6% of deaths were attributed by LE-AAF to its restricted group of cancers. Relative to NCHS, twice as many deaths were attributed by LE-AAF to chronic lung disease (13.6% versus 6%). Whereas NCHS ranked diabetes as a leading cause of death, that is, 3.1%, it was not a major contributor when evaluated with the high dimensional LE-AAF approach. The converse was true for psychiatric disease.
Table I.
Top 10 disease categories contributing to death among US persons 65 years and older by NCHS method and by LE-AAF.
| Percent of deaths attributed to the disease category (95% CI) |
||
|---|---|---|
| NCHS reported | LE-AAF | |
| Disease category‡ | Percentage of deaths | Proportional contribution (95% CI) |
| Cardiovascular | 30.4 | 17.4 (10.8, 23.0 ) |
| Malignancy / cancer | 22.0 | 7.6 (6.3, 8.9 ) |
| Cerebrovascular / stroke | 7.4 | 2.9 (1.4, 4.2 ) |
| Lower respiratory / lung | 6.0 | 13.6 (11.6, 16.3 ) |
| Alzheimer's / dementia | 3.7 | 7.1 (5.9, 8.2 ) |
| Diabetes | 3.1 | Not in top ten |
| Pneumonia, influenza | 3.0 | 4.8 (4.1, 5.8 ) |
| Renal / kidney | 2.0 | 4.8 (3.9, 5.7 ) |
| Unintentional injuries | 2.0 | 3.0 (2.1, 4.0 ) |
| Septicemia | 1.5 | 1.8 (1.4, 2.3 ) |
| Psychiatric | Not in top 10 | 3.1 (1.5, 4.5 ) |
| All other causes | 19 | 33.9 (residual) |
Aggregate disease categories evaluated with LE-AAF were as follows: Cardiovascular included heart failure, pericarditis, endocarditis, and myocarditis, pulmonary heart disease, dysrhythmias, peripheral and visceral vascular disease, atherosclerosis, valve disorders, conduction disorders, hypertension, acute myocardial infarction, and other and ill-defined heart disease. Malignancies included lung, liver, pancreas, bone, connective tissue, head and neck, lymphoma, leukemia, colorectal, kidney and other urinary organs, bladder, prostate, and breast. Lung disease included COPD, other chronic lung diseases, and asthma. Renal included chronic kidney disease and acute kidney injury. Unintentional injuries included hip fracture, other fractures, head injury, falls, motor vehicle accidents, injuries other than falls and motor vehicle accidents, and complications of medical or surgical care; Psychiatric included mood disorders including depression, anxiety disorders, schizophrenia, and other psychotic disorders.
4. Discussion
The LE-AAF method described here adjusts for the duration and time of onset for each co-occurring RF while preserving the advantageous properties of additivity and symmetry that are lacking in attributable fractions [6,9,13]. We believe the LE-AAF's ability to disentangle the overlap among many co-occurring diseases provides a significant conceptual advantage over the AF of Levin. With the data-centric approach described here, the computational burden is reduced to a manageable level, making it widely accessible to public health researchers and epidemiologists.
There are a few noteworthy limitations in our demonstration of the high dimensional LE-AAF approach. Only 66% of all deaths were ‘explained’ by the LE-AAF-based method. Because our eligibility criteria for inclusion of acute and chronic conditions in the different disease categories restricted the field of candidates, inclusion of a broader range of diseases might have accounted for a larger overall fraction of deaths. The LE-AAF is a population based method and should not be interpreted in the context of any individual participant. Finally, because our method is based on observational data, it does not in any way represent causal inference.
5. Conclusion
To prioritize the allocation of shrinking financial resources in areas of health research and policy, it is important to be able to partition the proportional contributions to an outcome of interest, such as death, among a reasonably large number of RFs. Although the LE-AAF was specifically introduced to study causes of death [9], it is appropriately applied to any nonrecurring outcome. This can be especially useful in gerontological studies that study outcomes such as first occurrence of sentinel events in the aging process such as functional disability, urinary tract infection, occurrence of a specific cancer, or fall-related injury. In this article we show that through careful model selection and detailed knowledge of the data in hand, a high dimensional calculation of the LE-AAF is computationally feasible. As our understanding of the dynamic between multiple explanatory factors and specific outcomes evolves, techniques such as the high dimensional calculation of LE-AAF make sophisticated analyses increasingly accessible. To our knowledge at this time, only the AAF and its longitudinal extension are capable of accommodating more than 10 RFs. Future work will consider empirical weighting of the temporal disease sequences when computing the LE-AAF.
Acknowledgements
This work was supported in part by the Claude D. Pepper Older Americans Independence Center at Yale University School of Medicine (P30AG021342), the National Institute on Aging (RO1 AG030109 and 1R21AG033130–01A2), and the Yale University Biomedical High Performance Computing Center (NIH grant RR19895). This publication was made possible in part by CTSA Grant Number UL1 RR024139 from the National Center for Research Resources (NCRR), a component of the National Institutes of Health (NIH), and NIH roadmap for Medical Research. Its contents are solely the responsibility of the authors and do not necessarily represent the official view of NCRR or NIH.
References
- 1.Levin ML. The occurrence of lung cancer in man. Acta Unio Internationalis Contra Cancrum. 1953;9:531–541. [PubMed] [Google Scholar]
- 2.Rowe AK, Powell KE, Flanders WD. Why population attributable fractions can sum to more than one. American Journal of Preventive Medicine. 2004;26(3):243–248. doi: 10.1016/j.amepre.2003.12.007. [DOI] [PubMed] [Google Scholar]
- 3.McElduff P, Attia J, Ewald B, Cockburn J, Heller R. Estimating the contribution of individual risk factors to disease in a person with more than one risk factor. Journal of Clinical Epidemiology. 2002;55:588–592. doi: 10.1016/s0895-4356(02)00388-8. [DOI] [PubMed] [Google Scholar]
- 4.Llorca J, Delgado-Rodriguez M. A new way to estimate the contribution of a risk factor in populations avoided nonadditivity. Journal of Clinical Epidemiology. 2004;57:479–483. doi: 10.1016/j.jclinepi.2003.10.003. [DOI] [PubMed] [Google Scholar]
- 5.Rabe C, Lehnert-Batar A, Gefeller O. Generalized approaches to paratitioning the attributable risk of interacting risk factors can remedy existing pitfalls. Journal of Clinical Epidemiology. 2007;60:461–468. doi: 10.1016/j.jclinepi.2006.06.024. [DOI] [PubMed] [Google Scholar]
- 6.Eide GE, Gefeller O. Sequential and average attributable fractions as aids in the selection of preventive strategies. Journal of Clinical Epidemiology. 1995;48(5):645–655. doi: 10.1016/0895-4356(94)00161-i. [DOI] [PubMed] [Google Scholar]
- 7.Ramsch C, Pfahlberg AB, Gefeller O. Point and interval estimation of partial attributable risks from case-control data using the R-package ‘pARccs’. Computer Methods and Programs in Biomedicine. 2009;94:88–95. doi: 10.1016/j.cmpb.2008.10.006. [DOI] [PubMed] [Google Scholar]
- 8.Land M, Gefeller O. A game theoretic approach to partitioning attributable risks. Biometrical Journal. 1997;39:777–792. [Google Scholar]
- 9.Lin HQ, Allore HG, McAvay GJ, Tinetti ME, Gill TM, Gross CP, Murphy TE. A method for partioning the attributable risk of multiple time-dependent co-existing diseases to the occurrence of an adverse health outcome. American Journal of Public Health. 2012 doi: 10.2105/AJPH.2011.300458. In Press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.CCS [October 10, 2010];Clinical Classification Software (CCS) for ICD-9-CM. www.hcup-us.ahrq/toolssoftware/ccs.jsp.
- 11.Matlab R2009a [computer program]. Version 7.8.0.347. The MathWorks Inc.; Natick, Massachusetts: 2009. [Google Scholar]
- 12.D'Agostino RB, Lee ML, Belanger AJ. Relation of pooled logistic regression to time dependent Cox regression analysis: The Framingham Heart Study. Statistics In Medicine. 1990;9:1501–1515. doi: 10.1002/sim.4780091214. [DOI] [PubMed] [Google Scholar]
- 13.Gefeller O, Land M, Eide GE. Averaging attributable fractions in the multifactorial situation: assumptions and interpretation. Journal of Clinical Epidemiology. 1998;51(5):437–441. doi: 10.1016/s0895-4356(98)00002-x. [DOI] [PubMed] [Google Scholar]