Abstract
Recent experiments to characterize the short-range stiffness (SRS) – force relationship in several cat hindlimb muscles suggested that the there are differences in the tendon elastic moduli across muscles (Cui et al. 2007a). Those conclusions were inferred from whole muscle experiments and a computational model of SRS. The present study sought to directly measure tendon elasticity, the material property most relevant to SRS, during physiological loading to confirm the previous modeling results. Measurements were made from the medial gastrocnemius (MG), tibialis anterior (TA), and extensor digitorum longus (EDL) muscles during loading. For the latter, the model indicated a substantially different elastic modulus than for MG and TA. For each muscle, the stress-strain relationship of the external tendon was measured in situ during the loading phase of isometric contractions conducted at optimum length. Young’s moduli were assessed at equal strain levels (1%, 2% and 3%), as well as at peak strain. The stress-strain relationship was significantly different between EDL and MG/TA, but not between MG and TA. EDL had a more apparent toe region (i.e., lower Young’s modulus at 1% strain), followed by a more rapid increase in the slope of the stress-strain curve (i.e., higher Young’s modulus at 2% and 3% strain). Young’s modulus at peak strain also was significantly higher in EDL compared to MG/TA, whereas no significant difference was found between MG and TA. These results indicate that during natural loading, tendon Young’s moduli can vary considerably across muscles. This creates challenges to estimating muscle behavior in biomechanical models for which direct measures of tendon properties are not available.
Keywords: Stiffness, Force, Model, Architecture, Muscle
INTRODUCTION
The fibers of most skeletal muscles insert into bone through tendon. Besides transmitting muscle fiber forces to the skeleton, tendon plays an important role in other physiological features of muscle-tendon units (MTU), such as storage and recovery of elastic energy (Alexander and Bennetclark 1977; Cavagna 1977). These functions are influenced by the material properties of tendon and knowledge of these properties is essential for understanding tendon function across muscles. Extensive studies have been conducted to assess tendon stress-strain characteristics and to calculate the Young’s modulus (i.e., the slope of the stress-strain curve) of tendons from different muscles within various species. Young’s modulus approaches an asymptotic (peak) value at high stresses, greater than 30 MPa (Bennett et al. 1986). Using in vitro tests, similar peak Young’s moduli have been reported among different mammalian tendons from seven species (1.2–1.6 GPa, Bennett et al. 1986) and from eighteen species with body masses ranging from 0.5 kg to 545 kg (0.9–1.8 GPa, Pollock and Shadwick 1994b). Also the results from in vivo studies in humans suggest that the material properties of tendons are similar between muscles (Maganaris 2002).
The Young’s modulus of a tendon also is an important contributor to whole muscle short-range stiffness (SRS) (Cui et al. 2007b; Morgan 1977). SRS is defined as the linear force response of an isometrically contracting muscle to short quick stretches and releases. It describes the initial response of a muscle to external perturbations of length, prior to changes in activation mediated through reflex or voluntary mechanisms. As SRS plays an important role in the control of limb stability (e.g., Perreault et al. 2004), we are ultimately interested in estimating this property for different human muscles based on architectural parameters that can be measured non-invasively. In a previous study, the SRS-force relationship was predicted for six different muscles of the cat hindlimb using a simple model, consisting of a force-dependent active stiffness connected in series with a constant passive stiffness (Cui et al. 2007a). The predictions for each muscle were based on its architectural parameters (i.e., muscle physiological cross-sectional area, fascicle length, tendon cross sectional area (CSA) and length) and compared to experimental data. As suggested by the studies described above, it was assumed that all muscles have uniform tendon Young’s modulus. Furthermore, since tendon properties are most critical for whole muscle SRS at higher forces, it was assumed that the stress-strain curve is linear.
The anatomical model predicted the SRS-force relationship remarkably well for all muscles (error < 5%) except for extensor digitorum longus (EDL) muscle (26% error). The model predictions for EDL improved greatly (i.e., to an error < 5%) if the Young’s modulus was optimized for this muscle. This optimization suggested that the Young’s modulus of EDL is substantially higher than the Young’s modulus of the other hindlimb muscles. Alternatively, the large error for EDL could have been the result of the simplifying assumptions of the model (e.g., uniform fascicle length throughout the muscle and a uniform CSA of the tendon) or muscle specific stiffness of the fibers.
A direct comparison of the tendon material properties of different muscles in the cat was not encountered in the literature. Therefore, the goal of this study was to measure and compare the tendon material properties of EDL to those of medial gastrocnemius (MG) and tibialis anterior (TA) muscles during conditions relevant to natural muscle activation. We tested the hypothesis that the Young’s modulus of the EDL tendon is higher than the Young’s modulus of MG and TA, as our previous study suggested. Across the group of tested muscles, there were differences in architecture (fascicle length, pennation angle, tendon length), fiber type composition (fast, slow) and function (one-joint, two-joint). The stress-strain relationship and Young’s modulus were assessed in situ for the tendons of each muscle. The use of an in situ approach was selected to allow for direct measurements of tendon force and slack length (in contrast to in vivo measurements) while preserving physiological tendon loads generated through muscle contraction (in contrast to in vitro preparations).
METHODS
Data were collected from one or two muscles in eight adult cats (weight: 2.7 – 4.1 kg; either sex). A total of ten muscles from the left and/or right hindlimb were measured, including 4 MG, 3 EDL and 3 TA. All procedures were approved by the Animal Care Committee of Northwestern University and conformed to policies set by the National Institute of Health.
Surgical Procedures
Initial surgical preparations were done under deep gaseous anesthesia (1.5–3.0 % isoflurane in a 3:1 mixture of O2 and NO2), according to standard procedures in our lab (Sandercock and Heckman 2001). The anesthesia was then switched to sodium pentobarbital (i.v.) during the rest of the experiment. The target muscle was carefully isolated from the surrounding tissues, preserving the innervation and blood supply. While the neurovascular tract can transmit force (Maas et al. 2005) this will have an insignificant effect in this study because force was measured through the tendon. For MG and TA, a piece of bone was left attached to the distal tendon to secure it to the force transducer. As there is not a single bone of insertion for EDL, the four distal tendons were tied together then cut from the insertion site, looped and attached to a stiff metal ring with surgical threads. The ring was then connected to the force transducer. As all length measurements were made directly from pins inserted into the tendon (see below), any difference in material properties was not due to this difference in fixation. The exposed muscle and tendon were kept moist by spraying warm saline. Radiant heat and a heating pad were used to maintain hindlimb and core temperatures within physiological limits.
External Tendon Length Tracking
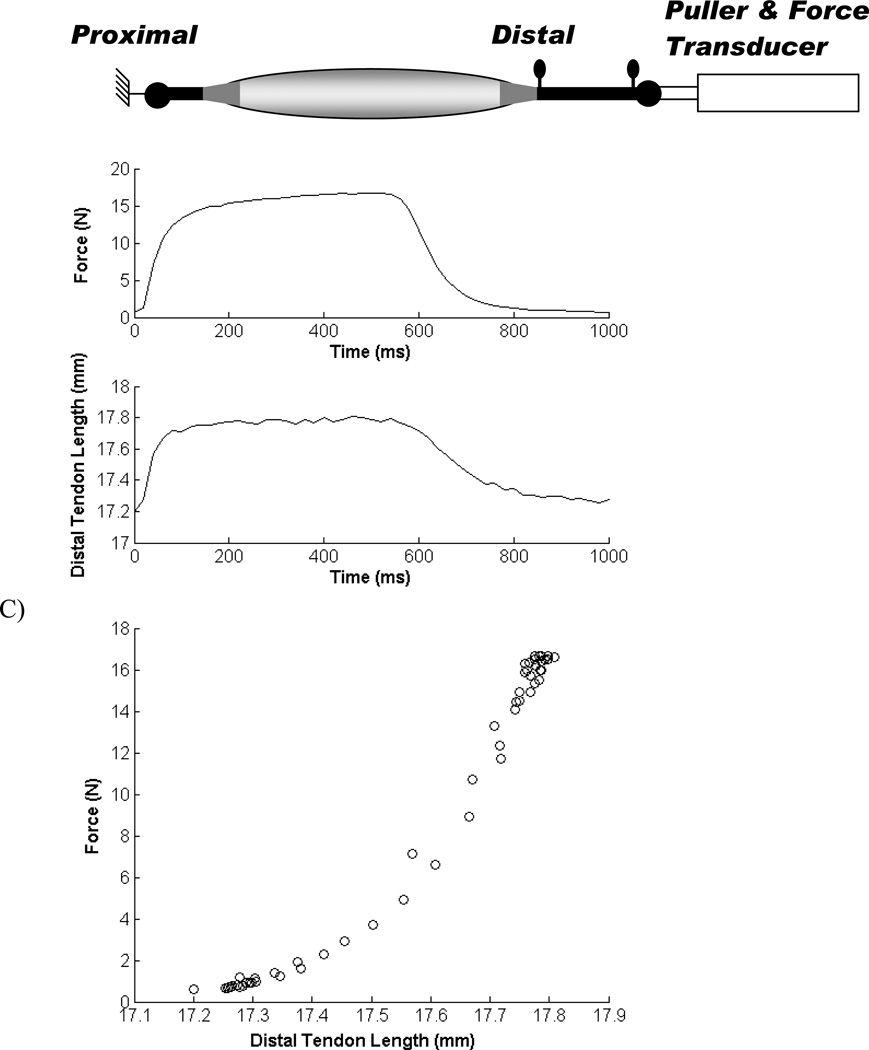
A 3D motion tracking system was used to measure the length changes of the distal external tendon in direction of stretch. Two insect pins (~ 2 mm long) with a dark marker attached to one end of each pin were used to define the external tendon length (lT). One pin was placed at the insertion site of the tendon to the bone chip (MG and TA) or next to the site where the tendon was tied to the ring (EDL). The second pin was inserted into the myotendinous junction in line with the first pin along the direction of the tendon (Fig. 1A). Both pins were positioned so that only the marker was visible on the surface of the tendon. The EDL has an unusual anatomical structure with 4 separate muscle divisions (Maas et al. 2003). The EDL pins were placed in the tendon for head V. In two experiments additional pairs of pins were placed in other tendon heads to confirm all heads showed similar strain. The locations of the pins were tracked using two high speed video cameras (Ademic-1000M, Ademic Electronic Imaging, Stoneham, MA) at 50 Hz with an accuracy of 0.05 mm/pixel. The video data were recorded and processed using 3D motion tracking software (DMAS6, Spica Technology, Maui, HI).
Figure 1.
Representative waveforms that were used to obtain the stress-strain relationship. A) Schematic representation of experimental setup. The tendon was connected to a force transducer mounted on a puller. Two insect pins were used to define the external length of the distal tendon. B) Muscle force and change in tendon length as a function of time during an isometric contraction at optimum length. C) Muscle force – tendon length relationship, which was converted to a stress-strain relationship using the tendon cross-sectional area and slack length (see methods).
Experimental Protocols
Intramuscular electrodes were used to activate the muscle supramaximally. Pulse trains at 100 Hz lasting 0.5 second were delivered to the muscle with at least 2 minutes between successive activations to prevent muscle fatigue. The optimum muscle-tendon unit (MTU) length (L0) was determined at the beginning of the experiment by measuring isometric force at various MTU lengths. A linear puller (stiffness 250 N/mm, Copley ThrustTube TB3806; Copley Controls Corp., Canton, MA) was used to control and measure (RGH24; Renishaw, Gloucestershire, UK) MTU length. A force transducer (Model 31; Honeywell Sensotec, Columbus, OH) in series with the puller was used to measure the resulting force. Force was collected at 5 kHz and, subsequently, down-sampled to 50 Hz to match the sampling frequency of the video camera used to measure tendon length.
Prior to data collection, the muscle and tendon tissues were preconditioned by passive cyclic stretches to reduce the effects of hysteresis (p. 261, Fung 1993). The muscle was stretched from L0 − 4 to L0 + 8 at a rate of 1/10 L0 s−1 and the difference between the stress-strain relationship during loading and unloading was measured. When the change between cycles was less than 1% conditioning was stopped. It usually took about 10 passive cycles to achieve this state. This is comparable to other studies (Virchenko et al. 2008).
Tendon slack length (lTS), which represents the stress-free state, is critical for calculating tendon strain. A passive loading-unloading procedure was used to determine this length. The muscle was incrementally stretched at a rate of 1 mm/s starting at L0 − 4 until the passive force reached about 0.5 N. It was subsequently shortened at the same rate back to its original length. This was repeated several times so that a linear passive force – length relationship F = k(lT − lTS) could be constructed around the zero force state, using a linear least squares fit. Tendon slack length was then determined from this relationship.
To characterize the in-situ stress-strain characteristics of each tendon, muscle force and tendon length were measured during maximal isometric contractions at L0 (Fig. 1). Only data measured during force development is presented in this manuscript. Regarding stress-strain during unloading it is noted that the relationship depended upon the duration of the tetanus but this will not be discussed further; hereafter we concentrate upon loading only.
Calculation of Stress, Strain and Young’s modulus
Tendon stress (σ) was calculated as:
| (1) |
where P is muscle force and AT is the cross-sectional area (CSA) of the external tendon. It was determined by the following equation:
| (2) |
where WT is the wet weight of the external tendon, lEXT is the external tendon length when the muscle is relaxed at L0 and ρT is the density of the tendon tissue, 1.12g×10−3 / mm3 (Ker 1981). It should be noted that we used the CSA of the tendon before deformation for calculating the stress. It is a reasonable approximation since the deformation was small (see Results). Tendon strain (ε) was calculated as:
| (3) |
An exponential relationship was used to fit (least-squares) the stress – strain data from the isometric contractions:
| (4) |
This relationship was subsequently used to calculate the Young’s modulus (E) at different strain levels (see below).
| (5) |
Because the stress-strain properties were measured during muscle stimulation the strain rate varied throughout the contraction. The rate was approximated by determining the total strain occurring during the time needed for the muscle to reach 50% of the peak tetanic tension during stimulation at 100 Hz.
Homogeneity analysis of tendon cross-sectional area
In the assessment of tendon stress and Young’s modulus it was assumed that the CSA is uniform along its length. The same assumption was used when assessing SRS from anatomical muscle parameters in our previous paper (Cui et al. 2007a). Here we tested the effect of this assumption on the calculation of peak Young’s modulus for TA, MG and EDL. This was done using a 4 element serial model to better describe the change in CSA along the length of the tendon. The CSA was measured at 5 evenly spaced locations. The CSA for each element was set to an average of the CSA measured at the ends. The stress-strain properties of the 4 element model were determined by assuming the 4 elements were in series. The material properties of each element were assumed to be identical and the stress was determined by the CSA of each element (force in each element constant). This was compared to the stress-strain properties of a single element with CSA determined by the average of all 4 elements. Young’s moduli, at the maximal muscle force, were compared.
Treatment of data and statistical analysis
To statistically compare the stress-strain characteristics across muscles, a bootstrap analysis (Politis 1998) was conducted, using the combined data for all muscles of a given type. This analysis allowed us to characterize the uncertainties associated with estimating the Young’s modulus for each muscle at fixed levels of strain without making any assumptions about the probability distribution of the errors. For each muscle type, N samples (stress-strain) were randomly selected with replacement from the original data set and used to estimate the parameters shown in Eq. 4; N equals the number of original data points available for each muscle type. This process of randomly selecting a set of experimental data points and estimating the model parameters was repeated 1000 times, yielding 1000 estimates of the stress-strain model for each muscle type. Each estimated model was used to provide an estimate of Young’s modulus at strain levels of 1%, 2% and 3% as well as at peak strain. The resulting distribution of Young’s moduli obtained at each strain level was used to estimate the mean and 95% confidence intervals for each muscle. The null hypothesis, that there was no significant difference in the Young’s modulus for each muscle, was tested by comparing the 95% confidence intervals of the Young’s moduli estimated at strain levels of 1%, 2% and 3%.
RESULTS
The error, resulting from the assumption that the tendon CSA is uniform, was found to be small. Tendon CSA was found to vary up to 28% along its length in the three muscles studied. In spite of this variation, the difference in Young’s modulus between a uniform tendon model and a 4-element tendon model was less than 5% for all three muscles (3.1 % ± 3.2, mean ± SD). Thus, using the mean CSA to calculate Young’s modulus cannot account for the previously reported differences (Cui et al. 2007a).
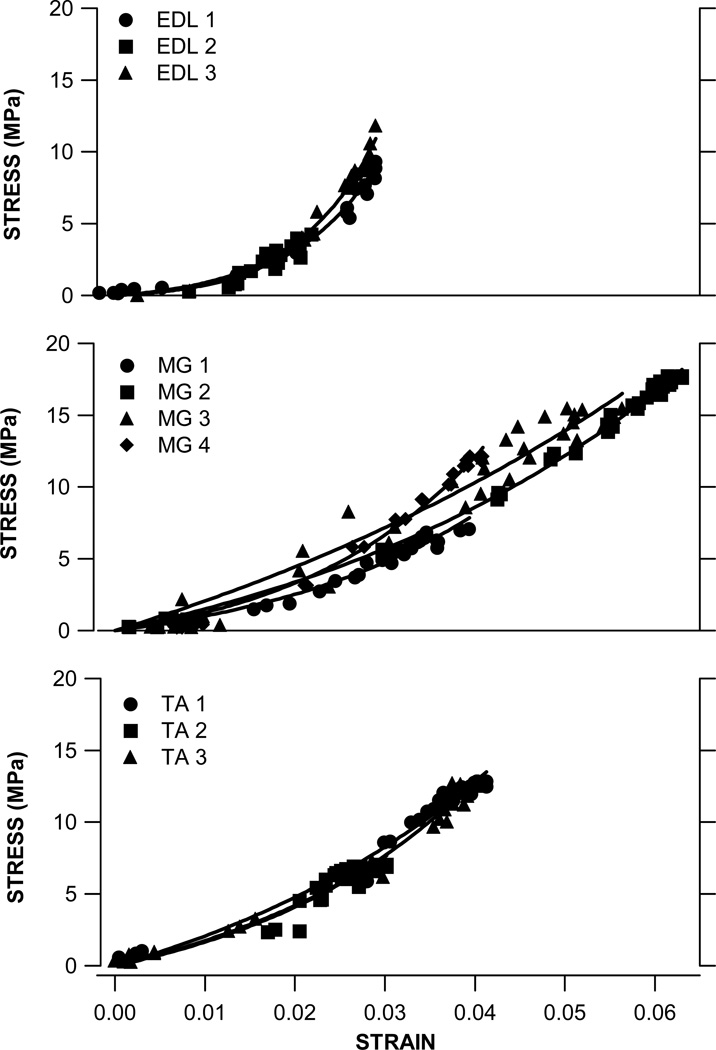
A non-linear stress-strain relationship was obtained for all muscles. Fig. 2 shows the data from all muscles plotted with the same scale for stress and strain. The proposed exponential function fit the experimental data well for all muscles. The mean R2 was 0.94 ± 0.06 (mean ± SD), 0.90 ± 0.14 and 0.98 ± 0.02 for EDL, TA and MG respectively. Although all measurements were performed at optimum MTU length, peak stresses and strains varied considerably across muscles. Peak tendon stress was 8.5 ± 3.8 MPa for EDL, 11.8 ± 1.7 MPa for TA and 13.1 ± 4.6 MPa for MG. Peak tendon strain was found to be highest in MG (5.0 ± 1.2%) and lowest in EDL (2.7 ± 0.4%), while peak strain in TA tendon was 3.7 ± 0.6%.
Figure 2.
Tendon stress–strain data for MG, TA and EDL muscles. All experimental data is plotted for 3 EDL, 4 MG and 3 TA muscles. The exponential fit to each muscle is shown with a solid line. Note that EDL has a more apparent toe region than MG and TA. However, the stress in EDL tendon increases rapidly with strain, reaching the peak at about 10 MPa. In contrast, the tendon stress – strain relationship of MG and TA is more gradual, with a peak stress of approximately 18 MPa and 13 MPa, respectively.
The anatomical and stress-strain parameters for each muscle are presented in Table 1. The parameters a and b, from the exponential fit to Eq. 4, are included. Maximum muscle force is strongly correlated with the physiological cross-sectional area (Powell et al. 1984), a measure for the sum of the cross-sectional areas of all the muscle fibers within a muscle multiplied by the cosine of the angle of pennation. Hence, in these experiments the ratio of muscle to tendon area is strongly correlated with the maximum-tendon-strain. In spite of this EDL, which had the lowest mean maximum-tendon-strain, had the largest Young’s modulus at this strain. These differences are not due to differences in the maximum strain rate achieved for each muscle. If viscous properties were significant, lower strain rates could lead to lower tendon stresses. However, the lowest strain rates also were measured in the EDL, which had the highest Young’s modulus (Table 1).
Table 1.
Anatomical and stress-strain parameters from each muscle. Par a and b were obtained by fitting the stress-strain data, measured during tension development, with Eq 4. Their mean was not presented because the parameters co-vary in a way to make the mean useless. The physiological cross sectional area (PCSA) of the muscle was determined using methods detailed in (Powell et al. 1984).
| weight muscle (g) |
par a (Mpa) |
par b | PCSA muscle (mm2) |
area tendon (mm2) |
ratio area muscle /tendon |
max. strain tendon |
E at max. strain (MPa) |
cont. time 50% force (s) |
max. strain rate (s−1) |
|
|---|---|---|---|---|---|---|---|---|---|---|
| EDL 1 | 7.61 | 0.4078 | 108.3464 | 119 | 2.81 | 42 | 0.029 | 1023 | 0.11 | 0.26 |
| EDL 2 | 5.87 | 0.2660 | 130.3831 | 116 | 2.98 | 39 | 0.022 | 595 | 0.10 | 0.23 |
| EDL 3 | 6.17 | 0.4197 | 113.6664 | 112* | 3.07 | 37 | 0.029 | 1289 | 0.10 | 0.29 |
| mean | 4.41 | 116 | 2.95 | 39 | 0.027 | 969 | 0.10 | 0.26 | ||
| MG 1 | 8.3 | 2.0937 | 39.5586 | 362 | 5.25 | 69 | 0.039 | 394 | 0.10 | 0.39 |
| MG 2 | 9.94 | 6.2371 | 21.6533 | 416 | 5.67 | 73 | 0.063 | 528 | 0.18 | 0.35 |
| MG 3 | 12.8 | 13.7923 | 13.9517 | 506* | 7.88 | 64 | 0.056 | 423 | 0.18 | 0.32 |
| MG 4 | 10.4 | 2.0040 | 48.8098 | 431* | 6.77 | 64 | 0.041 | 720 | 0.13 | 0.32 |
| mean | 10.36 | 429 | 6.39 | 67 | 0.050 | 516 | 0.15 | 0.34 | ||
| TA 1 | 4.56 | 6.9400 | 26.1681 | 132 | 2.06 | 64 | 0.041 | 535 | 0.08 | 0.54 |
| TA 2 | 4.44 | 4.5008 | 32.9374 | 108* | 3.37 | 32 | 0.030 | 401 | 0.08 | 0.39 |
| TA 3 | 4.23 | 3.5006 | 38.6960 | 112* | 2.37 | 47 | 0.040 | 647 | 0.09 | 0.46 |
| mean | 6.55 | 117 | 2.60 | 45 | 0.037 | 528 | 0.08 | 0.46 |
The asterisk denotes muscle were the fiber length was estimated (Cui et al. 2008).
Note that the maximum strain of the tendon is correlated with the ratio of muscle to tendon cross sectional area. MG has a small tendon CSA compared to its muscle PCSA. “Cont. time 50% force” is the contraction time needed for the muscle to reach half of the peak force during stimulation at 100 Hz. Max. strain rate is the average strain rate during that time.
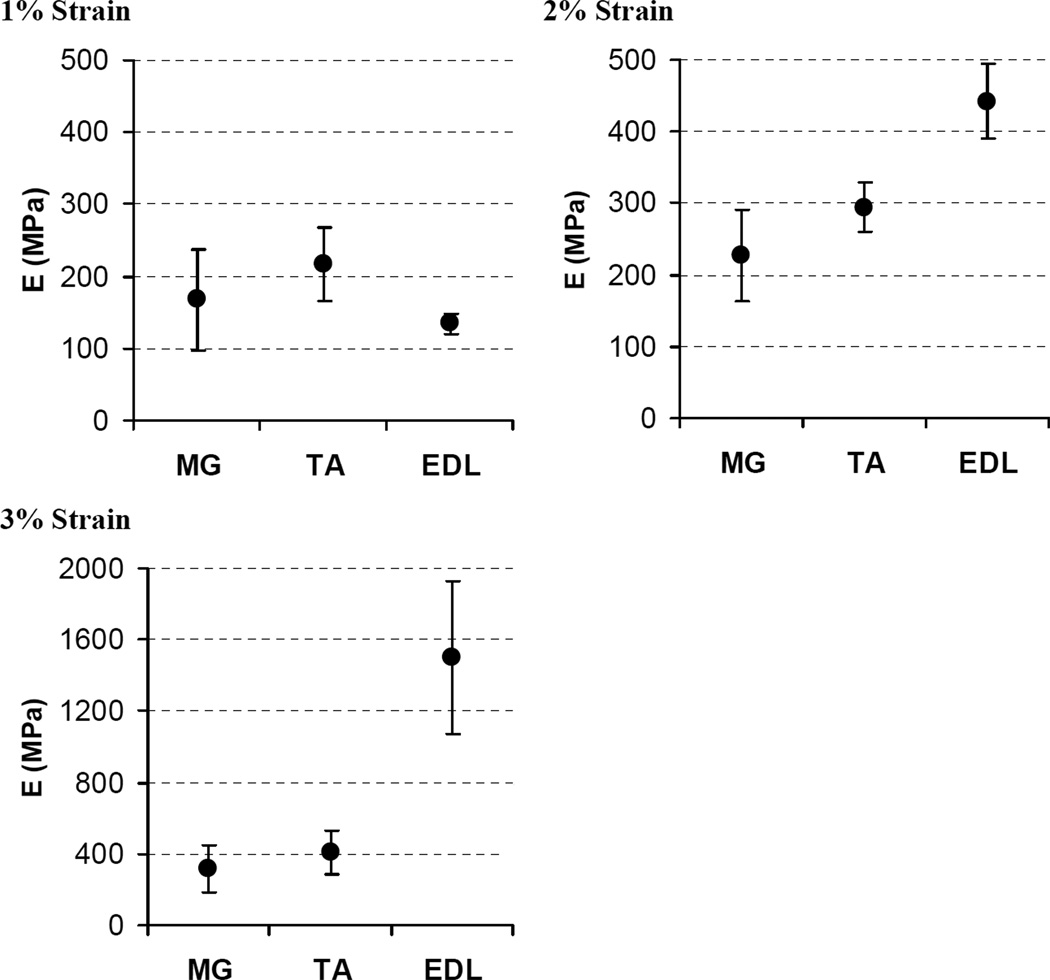
There were significant differences in the Young’s modulus between muscles at the tested strain levels (Fig. 3). At 1% strain, the Young’s modulus of the EDL tendon was lower than that of the TA tendon. This reflects the more apparent toe region of EDL muscle as shown in Fig. 2. No significant differences were found between TA and MG or between EDL and MG. At strain levels of 2% and 3%, however, the EDL tendon had a higher Young’s modulus than both MG and TA. Again, no significant differences were found between MG and TA (also true at 4% strain, data not shown). This reflects the more rapid increase in the slope of the stress-strain curve following the toe region of EDL compared to MG and TA. The Young’s modulus at the average peak measured strain for each muscle type was 987.1 ± 110.8 MPa for EDL (mean ± 95% CI at 2.7% strain), 635.7 ± 152.4 MPa for MG (at 3.7% strain) and 520.4 ± 120.9 MPa for TA (5.0% strain).
Figure 3.
Comparison of Young’s modulus (E) at different strain levels. Each plot shows the estimated mean with 95% confidence intervals. Confidence intervals were calculated using a bootstrap analysis with 1000 resamples. Note that the scale of the y-axis at 3% strain is different from the scale at 1% and 2% strain.
DISCUSSION
Our ultimate goal is to develop a muscle model that can estimate the short-range stiffness for different muscles based only on architectural parameters, as is necessary for muscles in which mechanical parameters cannot be measured directly. This may be possible if the stiffness properties of tendon (and muscle) are uniform across a wide range of muscles. However, the results of a recent modeling study suggested that the Young’s modulus of EDL is substantially higher than that of several other hindlimb muscles in the cat (Cui et al. 2007a), a finding that would confound the estimation of whole muscle stiffness based only on architectural parameters. In the present study, this Young’s modulus was measured directly in situ during the loading phase of isometric contractions. It was found that the EDL tendon has a significantly different Young’s modulus than the tendons of MG and TA, whereas no significant differences were observed between MG and TA. It should further be noted that the Young’s moduli of the present study are similar to those estimated from our previous modeling study (Cui et al. 2007a): EDL=1114 MPa, TA=414 MPa and MG=526 MPa, confirming the accuracy of those indirect estimates. This is the first study to measure tendon material properties of different muscles within the same species under in situ conditions.
Previous studies on mammalian tendons have reported a range of Young’s moduli that correspond well with the values found in this study (Bennett et al. 1986; Pollock and Shadwick 1994a). Bennett et al. conclude the Young’s moduli approaches about 1.5 GPa at stresses greater than 30 MPa, which is greater than the peak values found in the present study (i.e., 0.52–0.99 GPa). The difference probably results from the lower stresses used in this study (i.e., 8.5–13.1 MPa). Young’s moduli values reported by Bennett et al. ranged from about 0.4 to 1.4 at stresses from 6 to 20 MPa (see Fig. 3 in Bennett et al. 1986), which are similar to those observed in our work. The higher value for EDL (0.99 MPa) in our study cannot be explained by the stress at which it was measured, since EDL had the lowest stresses (8.5 MPa). It also should be noted that the tendon mechanical properties of those previous studies were assessed with an in vitro preparation. Differences in experimental methods, such as settings in moisture and temperature of the testing environment and specimen preservation may also have contributed to other values of the Young’s modulus.
This study examined tendon stress-strain properties at high strain rates (0.26 to 0.54 s−1) and moderate strains (0.22 to 0.64) produced by activation of the muscle. Rack and Westbury (Rack and Westbury 1974) demonstrated that at high strain rates and small perturbations the SRS of the MTU is primarily elastic and independent of strain-rate. This suggests that the tendon properties most relevant to SRS are also elastic and independent of strain rate. This was not tested in this study because strain rate development was dependent on muscle activation and thus difficult to control. Wu (Wu 2006) showed a strain rate dependence for the stress-strain properties of fresh chicken tendon. She studied strain rates up to 0.05 s−1, considerably lower than used here, so it is difficult to determine if the rate dependence would continue up through the higher strain rates. The stress-strain properties Wu measured at 0.05 s−1 agree well with those of the MG and TA but are lower than the EDL. Ng and colleagues (Ng et al. 2004) also reported a strain rate dependence in chicken tendon. They measured strain rates up to 1.5 s−1. They did not see much difference at low strains (less than 10%) but found it changed Young’s modulus in the linear region (strain greater than 15%). However, Ng et al. found a stress-strain relationship much lower than measured here. These results leave some doubt as to the importance of strain rate in SRS. However, because TA had a higher strain rate than EDL yet had a lower Young’s modulus (Table 1) it is unlikely that strain rate can account for the difference in EDL properties.
Our measurements of tendon strain at peak stress are also in agreement with the literature. Previous studies that measured strain in animal tendons in situ (Lieber et al. 1991; Monti et al. 2003) and in human tendons in vivo (Maganaris and Paul 2000; Magnusson et al. 2003; Muramatsu et al. 2001) have reported that tendon strain at peak muscle force ranges from 2% to 8%. The observations in the present study (i.e., strains between 2.7% in EDL and 5.0% in MG) are within this range. In addition, the study in which strains were measured in two human muscles (Maganaris 2002) reported smaller peak strain in TA (2.5%) than in GAS (4.9%), which is also similar to the results of this study (TA 3.7% vs. MG 5.0%). This suggests that in models of SRS Young’s moduli should be determined at the stresses encountered in physiological conditions. Young’s modulus is often reported at unphysiologically high stresses because the tendon stress-strain properties become linear (linear at stresses greater than 30 MPa, see Bennett et al. 1986), but these large values may lead to erroneous results within the physiological range of stresses relevant to SRS.
Since tendons are composed predominantly of type I collagen fibers, water and other proteins, which are very similar between muscles (Kjaer 2004), one might ask what causes the intrinsic material properties to be different? The answer probably lies in the roles of individual tendon components and their structural arrangements in regulating tendon material properties. It has recently been shown that the content of glycosaminoglycan (GAG) is the strongest predictor of tendon mechanical properties (Robinson et al. 2004a). A higher total GAG content may indicate a higher total collagen content and therefore increase the stiffness of tendon. In addition, the viscoelasticity of tendon is closely related to the content of proteoglycans, such as decorin, but not by collagen alterations (Robinson et al. 2004b). These studies suggest that tendon material properties can be regulated by changing the structural composition of the tendon. Therefore, a direct comparison of tendon composition between EDL and MG/TA may provide insight in the underlying mechanisms for the different material properties.
SRS of the MTU plays an important role in motor control. Young’s modulus, at the stress produced by maximal muscle activation, is an important component of SRS. This study showed, by direct measurement, that the values of Young’s modulus estimated by fitting parameters to a simple model of whole muscle SRS (Cui et al. 2008) can be quite accurate. The present results also suggest that estimating Young’s modulus at maximum physiological stress is most relevant when considering how tendon elasticity contributes to the SRS of the musculotendon structure. Furthermore, it suggests that not all muscles have identical Young’s moduli and that these differences can contribute to differences in the SRS properties across muscles, especially at higher forces. This creates challenges to estimating muscle behavior in biomechanical models for which direct measures of tendon properties are not available.
ACKNOWLEDGEMENTS
This work was supported by National Institute of Arthritis and Musculoskeletal and Skin Diseases Grant R01-AR-041531. E. J. Perreault was supported by National Institute of Child Health and Human Development Grant K25-HD-044720.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Conflict of interest statement
The authors declare no competing financial interest and personal relationships with other people or organizations that could inappropriately influence the work presented in the submitted paper entitled ‘Modeling Short-Range Stiffness of Feline Lower Hindlimb Muscles’.
REFERENCES
- Alexander RM, Bennetclark HC. Storage of Elastic Strain-Energy in Muscle and Other Tissues. Nature. 1977;265(5590):114–117. doi: 10.1038/265114a0. [DOI] [PubMed] [Google Scholar]
- Bennett MB, Ker RF, Dimery NJ, Alexander RM. Mechanical-Properties of Various Mammalian Tendons. J. Zool. 1986;209:537–548. [Google Scholar]
- Cavagna GA. Storage and utilization of elastic energy in skeletal muscle. Exerc. Sport Sci. Rev. 1977;5:89–129. [PubMed] [Google Scholar]
- Cui L, Perreault EJ, Maas H, Sandercock TG. Modeling short-range stiffness of feline lower hindlimb muscles. J. Biomech. 2007a doi: 10.1016/j.jbiomech.2008.03.024. in revision. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cui L, Perreault EJ, Maas H, Sandercock TG. Modeling short-range stiffness of feline lower hindlimb muscles. J. Biomech. 2008 doi: 10.1016/j.jbiomech.2008.03.024. In press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cui L, Perreault EJ, Sandercock TG. Motor unit composition has little effect on the short-range stiffness of feline medial gastrocnemius muscle. J. Appl. Physiol. 2007b;103(3):796–802. doi: 10.1152/japplphysiol.01451.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fung YC. Biomechanics. Mechanical Properties of Living Tissues. New York: Springer-Verlag; 1993. [Google Scholar]
- Ker RF. Dynamic Tensile Properties of the Plantaris Tendon of Sheep (Ovis-Aries) J. Exp. Biol. 1981 Aug;93:283–302. doi: 10.1242/jeb.93.1.283. [DOI] [PubMed] [Google Scholar]
- Kjaer M. Role of extracellular matrix in adaptation of tendon and skeletal muscle to mechanical loading. Physiol. Rev. 2004;84(2):649–698. doi: 10.1152/physrev.00031.2003. [DOI] [PubMed] [Google Scholar]
- Lieber RL, Leonard ME, Brown CG, Trestik CL. Frog Semitendinosis Tendon Load-Strain and Stress-Strain Properties during Passive Loading. Am. J. Physiol. 1991;261(1):C86–C92. doi: 10.1152/ajpcell.1991.261.1.C86. [DOI] [PubMed] [Google Scholar]
- Maas H, Jaspers RT, Baan GC, Huijing PA. Myofascial force transmission between a single muscle head and adjacent tissues: length effects of head III of rat EDL. J. Appl. Physiol. 2003;95(5):2004–2013. doi: 10.1152/japplphysiol.00220.2003. [DOI] [PubMed] [Google Scholar]
- Maas H, Meijer HJ, Huijing PA. Intermuscular Interaction between Synergists in Rat Originates from both Intermuscular and Extramuscular Myofascial Force Transmission. Cells Tissues Organs. 2005;181(1):38–50. doi: 10.1159/000089967. [DOI] [PubMed] [Google Scholar]
- Maganaris CN. Tensile properties of in vivo human tendinous tissue. J. Biomech. 2002;35(8):1019–1027. doi: 10.1016/s0021-9290(02)00047-7. [DOI] [PubMed] [Google Scholar]
- Maganaris CN, Paul JP. Load-elongation characteristics of in vivo human tendon and aponeurosis. J. Exp. Biol. 2000;203(4):751–756. doi: 10.1242/jeb.203.4.751. [DOI] [PubMed] [Google Scholar]
- Magnusson SP, Hansen P, Aagaard P, Brond J, Dyhre-Poulsen P, Bojsen-Moller J, Kjaer M. Differential strain patterns of the human gastrocnemius aponeurosis and free tendon, in vivo. Acta Physiol. Scand. 2003;177(2):185–195. doi: 10.1046/j.1365-201X.2003.01048.x. [DOI] [PubMed] [Google Scholar]
- Monti RJ, Roy RR, Zhong H, Edgerton VR. Mechanical properties of rat soleus aponeurosis and tendon during variable recruitment in situ. J. Exp. Biol. 2003;206(Pt 19):3437–3445. doi: 10.1242/jeb.00550. [DOI] [PubMed] [Google Scholar]
- Morgan DL. Separation of Active and Passive Components of Short-Range Stiffness of Muscle. Am. J. Physiol. 1977;232(1):C45–C49. doi: 10.1152/ajpcell.1977.232.1.C45. [DOI] [PubMed] [Google Scholar]
- Muramatsu T, Muraoka T, Takeshita D, Kawakami Y, Hirano Y, Fukunaga T. Mechanical properties of tendon and aponeurosis of human gastrocnemius muscle in vivo. J. Appl. Physiol. 2001;90(5):1671–1678. doi: 10.1152/jappl.2001.90.5.1671. [DOI] [PubMed] [Google Scholar]
- Ng BH, Chou SM, Lim BH, Chong A. Strain rate effect on the failure properties of tendons. Proc. Inst. Mech. Eng. [H] 2004;218(3):203–206. doi: 10.1243/095441104323118923. [DOI] [PubMed] [Google Scholar]
- Perreault EJ, Kirsch RF, Crago PE. Multijoint dynamics and postural stability of the human arm. Exp. Brain Res. 2004;157(4):507–517. doi: 10.1007/s00221-004-1864-7. [DOI] [PubMed] [Google Scholar]
- Politis DN. Computer-intensive methods in statistical analysis. Ieee Signal Processing Magazine. 1998;15(1):39–55. [Google Scholar]
- Pollock CM, Shadwick RE. Relationship between body mass and biomechanical properties of limb tendons in adult mammals. Am J Physiol. 1994a;266(3 Pt 2):R1016–R1021. doi: 10.1152/ajpregu.1994.266.3.R1016. [DOI] [PubMed] [Google Scholar]
- Pollock M, Shadwick RE. Relationship between Body-Mass and Biomechanical Properties of Limb Tendons in Adult Mammals. Am. J. Physiol. 1994b;266(3):R1016–R1021. doi: 10.1152/ajpregu.1994.266.3.R1016. [DOI] [PubMed] [Google Scholar]
- Powell PL, Roy RR, Kanim P, Bello MA, Edgerton VR. Predictability of Skeletal-Muscle Tension from Architectural Determinations in Guinea-Pig Hindlimbs. J. Appl. Physiol. 1984;57(6):1715–1721. doi: 10.1152/jappl.1984.57.6.1715. [DOI] [PubMed] [Google Scholar]
- Rack PM, Westbury DR. The short range stiffness of active mammalian muscle and its effect on mechanical properties. J. Physiol. (Lond) 1974;240(2):331–350. doi: 10.1113/jphysiol.1974.sp010613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robinson PS, Lin TW, Jawad AF, Iozzo RV, Soslowsky LJ. Investigating tendon fascicle structure-function relationships in a transgenic-age mouse model using multiple regression models. Ann. Biomed. Eng. 2004a;32(7):924–931. doi: 10.1023/b:abme.0000032455.78459.56. [DOI] [PubMed] [Google Scholar]
- Robinson PS, Lin TW, Reynolds PR, Derwin KA, Iozzo RV, Soslowsky LJ. Strain-rate sensitive mechanical properties of tendon fascicles from mice with genetically engineered alterations in collagen and decorin. J Biomech Eng-T Asme. 2004b;126(2):252–257. doi: 10.1115/1.1695570. [DOI] [PubMed] [Google Scholar]
- Sandercock TG, Heckman CJ. Whole muscle length-tension properties vary with recruitment and rate modulation in areflexive cat soleus. J. Neurophysiol. 2001;85(3):1033–1038. doi: 10.1152/jn.2001.85.3.1033. [DOI] [PubMed] [Google Scholar]
- Virchenko O, Fahlgren AMR, Aspenberg P. Early Achilles tendon healing in sheep. Arch. Orthop. Trauma Surg. 2008 doi: 10.1007/s00402-008-0691-x. [DOI] [PubMed] [Google Scholar]
- Wu JJ. Quantitative constitutive behaviour and viscoelastic properties of fresh flexor tendons. International J. Artificial Organs. 2006;29(9):852–857. doi: 10.1177/039139880602900906. [DOI] [PubMed] [Google Scholar]