Inattention Blindness to Motion in Middle Temporal Area

Abstract

Subjects naturally form and use expectations to solve familiar tasks, but the accuracy of these expectations and the neuronal mechanisms by which these expectations enhance behavior are unclear. We trained animals (Macaca mulatta) in a challenging perceptual task in which the likelihood of a very brief pulse of motion was consistently modulated over time and space. Pulse likelihood had dramatic effects on behavior: unexpected pulses were nearly invisible to the animals. To examine the neuronal basis of such inattention blindness, we recorded from single neurons in the middle temporal (MT) area, an area related to motion perception. Fluctuations in how reliably MT neurons both signaled stimulus events and predicted behavioral choices were highly correlated with changes in performance over the course of individual trials. A simple neuronal pooling model reveals that the dramatic behavioral effects of attention in this task can be completely explained by changes in the reliability of a small number of MT neurons.

Introduction

Appropriate expectations can dramatically improve performance. This has been most extensively studied with regard to attention, which enhances sensory processing of a specific location or attribute. Although many studies have demonstrated physiological changes with attention (McAdams and Maunsell, 1999; Seidemann and Newsome, 1999; Treue and Maunsell, 1999; Cook and Maunsell, 2002, 2004; Ghose and Maunsell, 2002; Hayden and Gallant, 2005; Womelsdorf et al., 2006, 2008; Busse et al., 2008; Cohen and Maunsell, 2009, 2010; Mitchell et al., 2009; Rao et al., 2012), there has been considerable difficulty establishing whether they can account for behavior. For example, the magnitude of these effects may not be sufficient to explain both improvements associated with expectations and decrements in performance to unattended stimuli (Cook and Maunsell, 2004; Eckstein et al., 2009; Cohen and Maunsell, 2010). Additionally, studies may analyze neuronal activity over timescales or populations that are not strictly related to behavioral choices.

Linking the physiological effects of attention to extreme behavioral consequences is particularly challenging. For example, suprathreshold stimuli can be invisible when attention is directed elsewhere (Newby and Rock, 1998; Most et al., 2001, 2005). Neurons responsible for the inattention blindness must be both responsive and effective in the attentive state and either silent or ineffective in the inattentive state. However, large changes in neuronal response that would seem necessary to explain inattention blindness have not been reported (Cook and Maunsell, 2002).

To address these issues, we studied monkeys engaged in detecting very brief pulses of motion. These pulses appeared at random times and locations but according to a fixed probability schedule. Without ever receiving explicit cues, the animals learned the pulse statistics and selectively directed their attention according to this schedule so they could detect likely pulses (Ghose, 2006; Ghose and Harrison, 2009) but largely failed to detect unlikely pulses.

We recorded from neurons in the middle temporal (MT) area, which are thought to play a critical role in motion perception (Parker and Newsome, 1998). Previous studies have demonstrated that MT neurons are modulated by attention (Seidemann and Newsome, 1999; Treue and Maunsell, 1999; Martinez-Trujillo and Treue, 2004; Womelsdorf et al., 2006) and strongly predictive of behavioral choices during motion pulse detection (Ghose and Harrison, 2009). We therefore recorded from neurons in area MT and analyzed how the timing and reliability of single-unit activity might account for the observed inattention blindness.

We found that fluctuations in the reliability with which neurons signaled pulse occurrences were highly correlated with changes in behavior resulting from attention. Changes in neuronal reliability were twofold: (1) MT neurons were both better at encoding motion pulses; and (2) their activity was better associated with behavioral choices, during periods of high behavioral performance. Moreover, in contrast to previous studies, modulations in single neurons were largely sufficient to explain changes in behavioral performance. A simple model in which behavioral decisions are completely based on the activity of sampled MT neurons suggests that the behavioral effects of expectations can be entirely explained by reliability changes in a small number of neurons.

Materials and Methods

Ethics statement.

All animal procedures conformed to guidelines established by the National Institutes of Health and were approved by the Institutional Animal Care and Use Committee of the University of Minnesota.

Task design.

In many tasks, neural activity present over large epochs of time and large numbers of neurons is potentially responsible for the transformations necessary to perceive a stimulus, make a decision, and enact a motor plan. This broad distribution of signals over time and throughout the brain makes it difficult to study the physiological basis of behavioral choices because the same action might arise from a variety of different patterns of activity. Analogously, fast or accurate performance could arise from better integration of neuronal signals at a particular stage of processing or from relatively global changes across a large population of neurons. To address these issues, we have simultaneously recorded behavior and single-neuron responses in a reaction time task in which the set of potential stimuli and motor acts in our task were strongly constrained. Specifically, we have used a detection task in which the motion pulse stimulus to be detected evokes strong activity in the neuron under study by virtue of its location and direction of movement. Upon stimulus detection, animals were required to saccade to its location. Thus, both the relevant sensory input (pulse present or absent) and the requisite action (saccade or fixate) were binary. This simplicity allowed us to quantify the relationship of neuronal activity to the full gamut of behaviorally relevant sensory inputs and behavioral choices. Moreover, because the stimuli to be detected were at specific locations in visual space and brief in duration, decisions were necessarily based on a limited pooling of signals across neurons and time.

Task schedule.

Three male monkeys (Macaca mulatta) performed a motion detection task. The animals were trained to perform a peripheral motion detection task, which required rapid responses to a pulse of coherent motion in one of two stimulus patches (see Fig. 1). Head position was stabilized by a chronic titanium head postimplant secured with orthopedic screws. Eye position was monitored by scleral eye coil or infrared eye tracker (Arrington Research) and recorded at 200 Hz.

Figure 1.

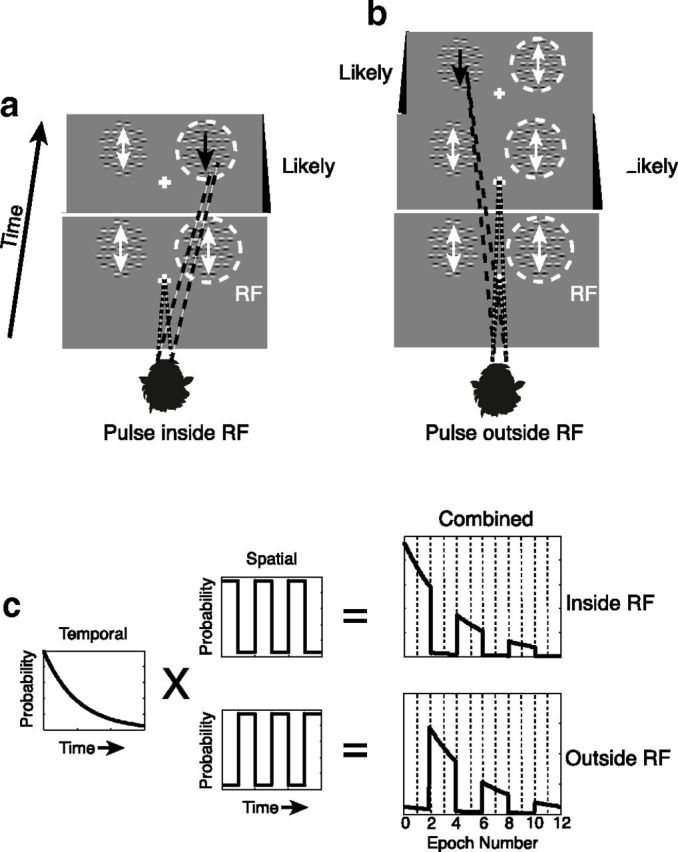
Motion pulse detection for two example trials. Animals were required to fixate on a central point while monitoring two peripherally located arrays of Gabors. One of these arrays was centered on the RF (dashed circle) of the neuron under study, whereas the other was located across the vertical meridian. At both locations, motion noise (white arrows) was presented by randomly and independently shifting the phases of the sine waves within the Gabors. A brief motion pulse was defined by consistently shifting the phases of all of the Gabors within one array in a direction consistent with the preferred direction of motion of the neuron under study (black arrows). Correct trials were defined by the monkeys breaking fixation and saccading to the location of the motion pulse immediately after its appearance. Pulse occurrence was random for every trial, but the statistics governing the timing and locations of pulses were fixed. Likely pulse location (a, b, black panels) alternated systematically over the duration of the trial. Two correct trials in which the pulse appeared at the likely location given its timing are illustrated. a, In the first trial, the monkey saccades to the array within the RF in response to motion pulse appearing within the first period of high likelihood. b, In the second trial, the monkey correctly saccades to the opposite array in response to a motion pulse appearing at that location during one of its periods of high likelihood. Statistics governing pulse likelihood were determined by multiplying the probability of pulse occurrence at a given time by the probability of it appearing at a given location (c). To analyze how the effects of attention changed with time, each pulse cycle was divided into four epochs so that the first two epochs were “Likely,” the second two, “Unlikely,” etc.

Trials began with a fixation point (0.1°) appearing at a central location of a CRT placed 57 cm in front of the animals. At 500 ms after the animals fixated upon this dot, a motion noise stimulus appeared at both locations. The animals were required to maintain fixation within a 1.5° window while these motion noise stimuli were present. Failure to maintain fixation resulted in immediate termination of the trial without reward. Correct trials were those in which the animals made a rapid eye movement to the location of a motion pulse within a reaction time window of 150–500 ms (see Fig. 1) and were rewarded with Gatorade. Failures to respond within the time window, saccades made before pulse appearance, or saccades made to inappropriate locations resulted in immediate termination of the trial without reward. To ensure vigilance, a small percentage of trials were catch trials, in which no pulse appeared and the animals were required to maintain fixation on the central fixation dot throughout the trial (∼6 s). The task was challenging because the pulse was only briefly presented (duration 67–83 ms), appeared at random times within a trial and was embedded in the high contrast background of motion noise.

Although the timing of motion pulse presentation within each trial was randomized, the statistics of pulse appearance were kept constant throughout training. For any moment of time within a trial, the pulse was likely to occur over one patch (p = 0.95–0.98), and unlikely to occur over the other patch (p = 0.02–0.05; see Fig. 1). During physiological recording sessions, the unlikely probability was increased to p = 0.05–0.10 to improve sampling of these events. The likely side is illustrated using Figure 1 (dark panels). This likelihood varied over time with a square wave modulation. In different sessions, three temporal frequencies were used for the square wave, one for each animal: 0.5 Hz (“slow”), 0.94 Hz (“intermediate”), and 1.33 Hz (“fast”). For all trials, the initial likely location of pulse occurrence was in the receptive field (RF) of the neuron under study.

The overall instantaneous probability of a pulse occurring decayed exponentially with time (mean 1.5–2.5 s; see Fig. 1c, left). The exponentially decaying instantaneous probability had important consequences for the behaviorally relevant hazard function, which is the probability that a pulse will occur at a point in time given that a pulse has not yet occurred. When the instantaneous probability is described by a decaying exponential, the hazard function is flat: encouraging a fixed level of effort (e.g., vigilance) throughout each trial (Luce, 1986). Without such a design, reaction times typically shorten for longer intervals because of the increased probability of a signal (Salidis, 2001). The combination of the exponential distribution of pulse occurrences and the spatiotemporal square wave (see Fig. 1c, middle) ensured that, at any point within the trial, the animals could not form a strong expectation about whether a pulse was going to occur or not but could form expectations about its likely location (within or outside of the RF) if it were to occur (see Fig. 1c, right).

Visual stimulus.

Stimuli were two arrays (spanning 5–7°) of small 100% contrast achromatic patches (31 Gabors, 1 cyc/deg SF, σ = 0.3–0.4°) containing luminance-modulated sine waves of identical orientation (Ghose, 2006). One array was centered on the RF of the neuron under study, whereas the other array was placed at a symmetric location (equal elevation, opposite azimuth) with respect to the vertical meridian (see Fig. 1). Although the phase of the sine wave within each Gabor was varied independently, the Gaussian envelopes of the Gabors were fixed. Sine wave phases for every Gabor were updated on each frame refresh (120 Hz, intermediate schedule monkey; 160 Hz, fast and slow schedule monkeys). Motion noise was produced by randomly and independently stepping the phase within each patch (±90° at 120 Hz, ±72° at 160 Hz; see Fig. 1, white arrow), and coherent motion was introduced by briefly (60–83 ms) enforcing a consistent phase change across all Gabor patches (motion pulse; see Fig. 1, black arrows). Local temporal frequency and velocity were constant (30°/s and 32°/s). The direction of this coherent motion was set in accordance with the preferred direction of the neuron under study.

Recording.

In two animals (fast and slow schedules), the patches were retinally stabilized to reduce the influence of small fixational eye movements on neuronal activity (Leopold and Logothetis, 1998; Snodderly et al., 2001) and behavioral performance. For the third animal, although no stabilization was done, no obvious differences in performance or physiology were observed. Eye position was continually calibrated throughout experimental sessions by randomly alternating between four fixation points separated by 1° around the center of the screen. Stabilization was accomplished by shifting the entire Gabor array, but not the fixation point, according to the most recent eye position sample after calibration. Behavioral control, visual stimulation, and data acquisition were computer controlled using customized software. We recorded well-isolated single neurons using standard extracellular recording techniques and digitized the occurrence of action potentials and CRT frame updates (1 kHz, slow animal; 10 kHz, intermediate and fast animals). Area MT was identified physiologically by the presence of audible low-frequency (<100 Hz) local field potential responses to the motion noise stimulus, a high proportion of direction selective responses, and RF mapping. At the start of each recording session, the RF of each neuron was mapped by shifting the position of the entire array while the monkey performed the task. Direction selectivity was assessed by recording responses to relatively long (167 ms) motion pulses of eight different directions while the monkey performed the motion pulse detection task. On the basis of these tuning runs, a specific stimulus location and direction were chosen for extended recording.

Analysis.

To study the physiological correlates of expectations as well as their behavioral consequences, we separately analyzed observations from different epochs within the trials. Because each epoch had a consistent motion pulse probability throughout all experiments with a given schedule, this analysis allowed us to compare how behavior and physiology were affected by probability. For each schedule, we grouped observations across different trials into bins according to when the observations relative to trial onset were made. We used four epochs per square wave cycle (see Fig. 1c, right). For the 0.5 Hz schedule, epochs were 500 ms in duration, for the 0.94 Hz schedule, epochs were 265 ms in duration, and for the 1.33 Hz schedule, epochs were 188 ms in duration.

Spike rate and variability.

Firing rates were computed in nonoverlapping 50 ms bins. For each trial, the analysis interval began at stimulus (motion noise) onset and ended when a motion pulse occurred, 200 ms before a saccade, or after 2.5 full likelihood cycles, whichever came first. Responses from all trials within a single cell were used to compute the z-score of the firing rate across time. z-scores of cells from the same schedule were then averaged to determine how pulse-likelihood affected prepulse activity levels. To determine whether pulse-likelihood was related to the variability of activity, we computed the Fano factor by dividing the variance of the firing rate at each time point by the mean at that time point. The resultant Fano factors were then averaged across cells of the same schedule.

To examine how expectations modulated responses to the motion pulse in area MT, we computed event-triggered firing rates over 50 ms bins that were aligned to the onset of motion pulses and saccades (see Fig. 3). The bins were moved by 10 ms steps, so that changes in response could be detected over the brief interval between pulse appearance and saccades. Pulse-aligned responses were computed regardless of behavior and included both successful detections and misses. Saccade aligned responses were computed regardless of the stimulus and included both false alarms and successful detections. Only stimuli within and saccades toward the neuron's RF were considered for this and all following analyses. For pulse-aligned responses, firing rates were computed separately according to the likelihood of the pulse at the time at which it was presented (see Fig. 1). For correct detections, saccade-aligned responses were also sorted according to pulse likelihood. For false alarms, in which the animals made a saccade in the absence of a pulse, pulse likelihood was inferred according to reaction time.

Figure 3.

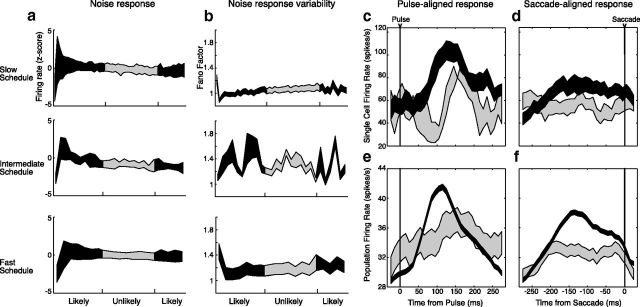
a–f, Responses to motion noise were analyzed as a function of time throughout cycles of pulse probability (a,b) and when aligned to behaviorally relevant events (c–f). For each cell, the firing rate and Fano factor during the noise stimulus were calculated within a 50 ms bin. Firing rates and Fano factors were then averaged across cells for each schedule. Black segments represent periods in which the pulse was likely, and gray represents periods of low likelihood. Motion noise responses and their variability were unaffected by pulse probability. Stimulus (c, e) and saccade (d, f) locked firing rates were also calculated for an example cell (c, d) and the population of cells recorded with all schedules (e, f). Motion pulses evoked a sharp increase in mean firing rate within 100 ms, but the increase was significantly higher when pulses were likely (black) than when they were unlikely (gray). Similarly, presaccadic activity was also significantly higher when the pulses were likely (black vs gray). Error bars for the pulse-aligned population were larger for unlikely pulses (c) because they occurred with only 5–10% probability. In all plots, line thickness represents the SEM above and below the mean.

Mutual information analysis.

The most commonly used metric for comparing the reliability of physiological responses with behavioral performance in a two alternative forced choice task is the receiver operator characteristic analysis, which quantifies the discriminability of two distributions according to the performance of an ideal observer using a single criterion threshold. Such an approach is inappropriate for our task for a number of reasons. First, because reaction times in our task are both short and narrowly distributed, comparing the temporal precision of neuronal activity and behavior is particularly important. Because receiver operator characteristic analysis (Britten et al., 1992) is based on single sampling periods, it does not directly permit such a comparison. Second, because we do not use a two alternative design, we require a metric that can accommodate biases in the task paradigm. For example, especially when analyzed on a scale of tens of milliseconds, motion pulses are far less probable than motion noise. Finally, we require a metric that allows us to predict the correlations between neuronal discharge and behavioral choices that may arise solely because of stimulus-related covariances. For example, increases in activity before saccades (see Fig. 3b,d) might simply arise from pulse-locked responses if there was a strong and consistent tendency for saccades to follow pulses.

To accomplish these goals, we applied information theory metrics to simultaneously recorded behavioral and physiological data parceled at different temporal resolutions within each epoch (Ghose, 2009). This allowed us to characterize how expectations modulated the reliability and temporal precision of both detection decisions and physiological responses with a comparable metric. Data from each epoch of every trial was parceled into equally sized temporal windows (4, 8, 16, 32, 64, and 128 ms) and the onset of the motion pulses, the initiation of saccades to the stimulus, and the number of action potentials within each bin were used to increment contingency tables between these events (see Fig. 4a,b). Both the visual stimulus and the behavioral response were treated as point processes, so that the onset of a motion pulse or a saccade anywhere within a bin incremented the corresponding location within the table. Neuronal activity was characterized according to the number of spikes within a bin.

Figure 4.

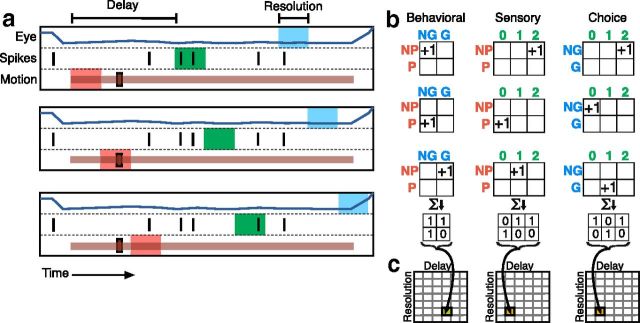
Behavioral, sensory, and choice reliability were calculated for each recording session. The events of a single trial were first parceled using bins of a certain width (resolution) separated by a fixed length of time (a, delay). Three different colors represent the variables between which pairwise mutual information is computed. The stimulus was described by a binary variable according to whether a motion pulse was present (P) or absent (NP) within the red bin. Neural response was described by the number of spikes within the green bin (b, green numbers). Finally, choice was characterized according to whether the animal made a saccade (S) or did not make a saccade (NS) within the blue bin. We used the values of pairs of these variables to update contingency tables (b). The bins were moved along the length of the trial while maintaining the same delay and resolution, and contingency tables were appropriately incremented. This process was repeated for all trials from a single recording session, resulting in three contingency tables that described the relationship between values of the variables at a given delay and resolution. In this example, sensory and choice information are being calculated for the same delay (the distance between red to green bins is the same as that of blue to green bins), but the behavioral delay is twice that length of time (the distance between red to blue bins). The contingency tables were then used to calculate mutual information rates for the specified delay and resolution. c, An information surface was created by repeating the process for different delays and resolutions.

The same analytical techniques were applied to behavioral responses, stimulus events, and neural activity. For behavioral information, each contingency table was 2 (pulse and no-pulse) × 2 (saccade and no-saccade). For neuronal information, the contingency tables were 2 × n, where n was the maximum number of spikes observed within a single bin. These contingency tables defined both the joint probability distribution between the two variables and the probability distributions of the two variables separately. The uncertainty of a particular variable or set of variables, which assumed discrete values, was quantified by entropy H as follows:

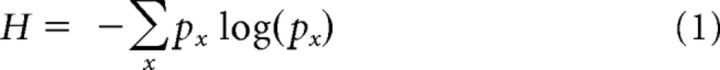where p_x is the probability of observing value x. This analysis made no assumptions concerning the underlying probability distributions of the variables. In our case, there were three relevant probability distributions regarding the task: neural activity (spike count), stimulus (pulse/no-pulse), and eye movement (saccade/no-saccade). We therefore defined three mutual information measures of how much knowledge of one variable reduced the uncertainty of the other variable as follows:

Each of the equations was specific for a particular temporal window width and delay between the variables. Thus, for each resolution and delay, we obtained the three information metrics. To examine how mutual information depended on these temporal properties, we resampled all the trials at different resolutions and delays and computed the corresponding information metrics. All information values were then converted to information rate by dividing by the resolution. The final product was an “information surface” showing how information rate changed over time (delay) and temporal resolution (precision) for each epoch (see Figs. 4c and 5). For each epoch of every neuron, we computed three information surfaces: a behavioral surface describing the correlation between pulse occurrence and saccades (behavioral information) and two neuronal information surfaces, one describing the correlation between spike count and pulses (sensory information) and one between spike counts and saccades (choice information).

Figure 5.

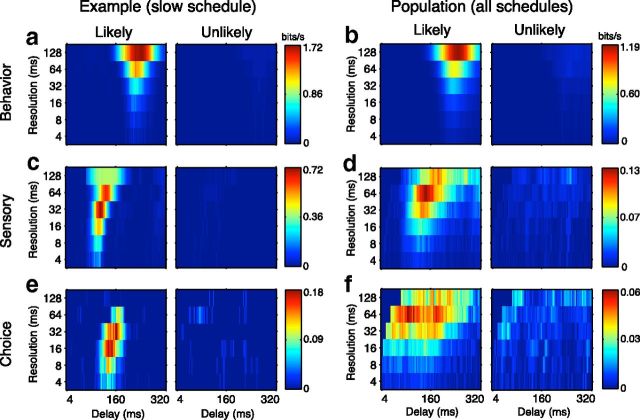
a–f, Pulse likelihood modulation of the reliability and timing of behavioral (a, b) and physiological (c–f) responses for an example neuron (a, c, e) recorded with the 0.5 Hz schedule and the population, including cells recorded with all schedules (b, d, f). Color indicates reliability (bits/s) of the relationship between pairs of variables. Color scales are consistent between conditions of high and low pulse probability but are different for different types of calculated information to emphasize the shape of the surfaces. Surfaces indicate how this reliability changed according to temporal sampling (resolution) and interval between the variables (delay). Population surfaces are the average of all surfaces from individual neurons. Behavioral information (a, b), describing the correlations between pulse occurrence and saccade initiation, is plotted as a function of delay and resolution. With regard to neuronal discharge, two types of information were computed. Sensory information (c, d) describes the mutual information between pulse occurrence and spike count, whereas choice information (e, f) describes the mutual information between saccades and spike count. Both behavioral and physiological reliabilities were strongly modulated by likelihood in both the example recording session and over the population.

Information metrics have an inherent positive bias because two sets of samples drawn from the same distribution will tend to be slightly different (Panzeri et al., 2007). We used a bootstrapping method to estimate this bias and determine significance levels. Each contingency table was resampled 100 times, keeping the probabilities for each variable category constant, to determine the information estimation when joint probabilities were assigned by chance. The significance level was specified as the 95th greatest value. Information values that did not reach significance were set to 0. The average of the bootstrapped values was subtracted from significant points. Confidence measures represent the SD of the bootstrapped information values. This bias correction tended to sharpen the peak of the information surfaces and to decrease the rates of both attended and unattended information. In particular, there was a relatively large effect of bias correction for larger resolutions, where for physiological information surfaces, there are a large number of possible spike counts that can be observed within any bin. Peak position, in terms of delay and resolution, was largely unaffected by bias correction, and differences in peak information rate associated with attention are present even in information surfaces without bias correction (data not shown).

To account for the possibility that covariances, for example, between activity and the stimulus (sensory information) and behavior and the stimulus (behavioral information) were completely responsible for observed correlations between activity and behavior (choice information), we used the behavior and sensory contingency tables to predict the choice contingency table. Similarly, we computed the sensory information that would be expected solely according to behavioral and choice information (Ghose, 2009). This procedure was applied to all resolutions and delays. For example, if p[activity = i|stim = α](t₁) describes how the probability of observing i spikes at an interval t₁ after the stimulus α, and p[eye = β|stim = α](t₂) is the probability of observing the eye movement β at an interval t₂ after the stimulus α, then probability of observing i spikes at an interval t = t₂ − t₁ before the eye movement β solely because of chance because of these relationships to stimulus α is the product of two probabilities as follows:

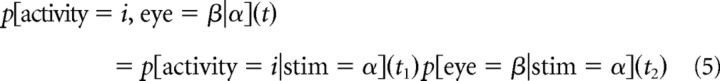and the total probability of observing i spikes before the eye movement β, taking into account all possible stimuli is as follows:

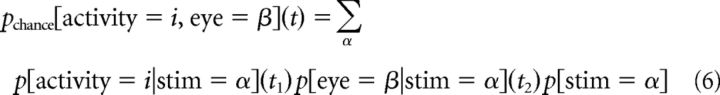By repeating this calculation for all activity levels and eye movements, we constructed a chance contingency table for the variables of activity and eye movement. For any given interval t between activity and saccade, there were a range of intervals between activity and stimulus (t₁) and corresponding stimulus/eye movement delays (t₂) that may have been responsible. Using Equations 1 and 4, we computed a chance information value for each t₁, t₂ pair for which t + t₁ = t₂.

Finally, we subtracted this “worst-case” scenario from the mutual information originally computed as follows:

In the above equations, we computed corrected choice information on the basis of behavioral and sensory contingency tables. We applied the same procedure to compute corrected sensory information on the basis of behavioral and choice contingency tables.

After these covariance and bias corrections, a single peak was observed in most cases for both physiological and behavioral information surfaces. The peak described a single combination of delay and resolution for which the relationship between the variables was the most consistent. We extracted three parameters describing this peak for each of the three information surfaces: reliability, delay, and precision. We defined reliability as the information rate at the peak regardless of its location with respect to delay and resolution. We defined delay according to the location of the peak regardless of temporal resolution. Finally, we computed precision by averaging the resolutions weighted according to the information rates observed at the optimal delay. Although these measures readily allowed a comparison between different types of information, they are not necessarily strictly analogous to traditional measures of physiological activity and behavioral performance. For example, the delay of sensory information does not strictly correspond with response latency, which is usually defined as the shortest interval after the presentation of a stimulus at which neuronal discharge significantly increases. By contrast, sensory information delay describes the interval at which pulse-related discharge is the most significantly different from the discharge evoked by motion noise. Similarly, with respect to behavior, behavioral delay does not strictly correspond with reaction time because behavioral information incorporates both false alarms and misses, and is not restricted to just correct trials.

To evaluate the effects of attention on a cell-by-cell basis, we performed a paired t test analysis of log-transformed information rates during likely and unlikely epochs. For this analysis, the minimum non-0 information rate we observed (0.01 bits/s) was added to all points. Figure 7 plots these data without that added value. When calculating the mean factor by which attention increased reliability, ratios containing a 0 were ignored. This left a sample of N = 57 for the change in sensory reliability and N = 58 for the change in choice reliability.

Figure 7.

Neuronal activity was more reliably linked to both the stimulus and behavioral choices when pulse probability was high. This was true for neurons recorded with all schedules (circles represent slow; triangles, intermediate; squares, fast). For each neuron, epochs when the pulse was likely or unlikely to occur in the neuron's RF were analyzed separately, and information surfaces (e.g., Fig. 5) were computed. Reliability was defined as the peak information rate observed in an information surface and plotted on a log scale. Histograms represent distance from unity (black represents significant; white, not significant). a, b, For most neurons, both sensory (a) and choice (b) reliabilities were higher when motion pulses were likely. c, d, The relationship between sensory and choice information within single cells was plotted for both anticipated (c) and unanticipated (d) epochs. In both attention states, sensory and choice information is correlated such that cells that most reliably signal the presence of a motion pulse are also the most predictive of the animal's subsequent behavior. e, A covariance analysis of sensory and choice information surfaces from attentive and inattentive epochs was used to generate predicted behavioral information surfaces, from which the peak predicted information rates were extracted. The responses of single cells predicted strong increases in behavioral reliability during attended epochs consistent with actual observations (Figs. 5, 6). Black shapes on the scatter plot represent the average observed behavior for each schedule.

Because unlikely pulses occurred with a probability of 0.05–0.10 during recording sessions, there was a large difference in the number of pulse responses observed between the two likelihood conditions. To ensure that the limited sampling of unlikely pulses was not affecting our results, we repeated the analysis using epochs defined according to behavior instead of pulse probability. For each cell, we sorted all of the epochs based on behavioral performance and categorized the epochs drew from the epochs with the best behavior for the “attentive” condition and the worst epochs for the “inattentive” condition such that the number of pulses occurring in each was as similar as possible. Data analyzed in this manner confirmed all major results of our analysis on epochs defined by pulse likelihood. Both sensory and choice neuronal reliability were significantly greater (p < 0.0001) in the attentive state. Cells with the highest sensory reliability were also those with the highest choice reliability, in both the attentive (r = 0.69) and inattentive (r = 0.75) states, and the correlation was not significantly different between conditions. Finally, the behavioral prediction for single cells was significantly greater for the attentive condition (p < 0.0001), and the behavioral prediction based on pooled cells was able to account for the behavior actually observed during these epochs.

Behavior prediction.

One benefit of our contingency table-based analysis is that it allows us to predict the reliability and timing of behavior if it were solely based on a single neuron's activity. Specifically, we can slightly modify the covariance analysis (Eq. 5) to predict the behavior that would be expected solely because of the correlation of a cell's activity with both stimulus and eye movement. So, for example, the predicted probability of stimulus α preceding movement β by t = t₁ + t₂ is related to sensory contingencies at delay t₁ and choice contingencies at delay t₂ as follows:

In the case of the physiological covariance correlations, we asked the question: for any given delay, what is the highest information that can be expected due to covariance between the other physiological measure and behavior? Thus, we chose the particular combination of delays, consistent with the delay we wished to predict, that maximized information (Eqs. 6 and 8). For a covariance correction of either sensory or choice information, this was the most conservative approach. However, in the case of behavior predictions, we wanted to ask a slightly different question: what was the most likely (not necessarily maximal) reliability that could be expected due to covariance between sensory and choice information? We computed this by performing a weighted average of the information across all possible delay combinations consistent with the behavioral delay whose reliability was being predicted. In this average, each delay combination was weighted according to its information on the original sensory and choice surfaces. Thus, informative sensory and choice delays (corresponding to delays at which the correlations between activity and stimulus and choice are maximal) were preferentially weighted.

Neuronal response pooling.

This same covariance-based analysis can be applied to generate behavioral predictions for any neural activity measure, including measures of activity over a population of neurons. To generate behavior predictions of pooled neuronal activity from single-unit data, however, we had to make some assumptions about how signals from multiple neurons are correlated and combined. In all of our simulations, we generated pools of neurons by randomly choosing neurons from our sample without replacement. In each recording session, the stimulus was oriented and positioned according to the preferred direction and RF location of the particular neuron under study. Despite this, many neurons had low sensory reliability. The fact that some neurons were unresponsive to the pulse is presumably because factors, such as size, speed, and spatial and temporal frequencies, were not optimized. Thus, our pooling model is essentially one in which all neuronal RFs share the same directional preference and location but likely differ in other RF properties. Because choice information reflects the correlation between behavior and a neuron, we used each neuron's peak choice information to bias our choices, such that neurons with high choice information were more likely to be chosen early rather than later. For example, for an existing pool of three neurons, a neuron whose choice information was 0.2 bits/s would be twice as likely as a neuron with choice information of 0.1 bits/s to be chosen as the fourth neuron. This process was repeated so that, for every pool size, there were 5–10 unique pools of neurons that were analyzed. For each of these pools, a behavior prediction on the basis of attentive and inattentive epochs was generated.

These predictions were generated according to pooled sensory and choice contingency tables. We assumed a linear summation of activity with equal weighting within the pool. For example, if the spike count categories for the sensory contingency table corresponding to a particular resolution and delay were 0, 1, and 2 in one neuron, and 0, 1, and 2, in another, then we added the possible spike counts to form a new set of categories with respect to a spike sum: 0–4 spikes. So to compute the probability p of a pooled spike count of i in this pool of two neurons, we summed over all the probabilities p that a total count of i can arise given the individual neurons as follows:

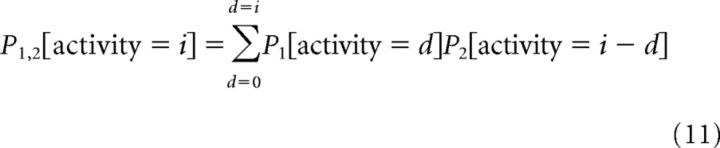To generate predictions for populations of neurons, this process was repeated iteratively by incorporating additional neurons one at a time, so that the pooled response probability for neurons 1…L is given by adding one neuron L to the previous pooled responses (neurons 1…L-1) as follows:

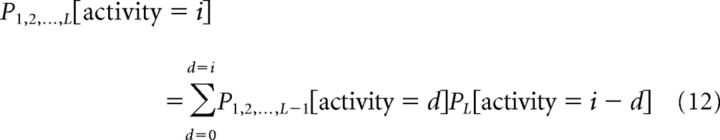How quickly information changes with the progressive addition of neurons depends on the particular neurons added. Uninformative neurons will add little to the pooled performance, whereas highly informative neurons can improve performance substantially. We therefore tested three different sequences for adding neurons to the pooled response. In the first, we use the neuron's choice information but ignored the sensory information, as a reflection of the chances that that neuron was contributing to behavior. For this sequence, the first neuron was therefore the one in our sample with the highest choice information, whereas the last neuron added was the neuron with the lowest choice information. In the second sequence, we postulated that choice information might not be an absolute determinant of a neuron's incorporation but rather might simply serve as a bias. In this model of pooling, the order of neurons selected was random but biased according to choice information, such that the first neuron in a pool is likely to be one with high choice information, but not necessarily the neuron with the highest choice information. In the final sequence, choice information was completely ignored, and the order with which neurons were incorporated into pools was completely random.

In addition to the composition of neuronal pools, another potentially critical factor in pool performance is the presence of correlations between neurons within the pool. In Equations 11 and 12, we have assumed that neurons are independent and that there is no tendency for the activity between any two neurons, for example, to covary under the same stimulus conditions. However, numerous studies suggest that this is not a valid assumption and that weak spike rate covariances can be observed (Ecker et al., 2010). Such correlations are labeled as “noise correlations” because they contribute to spike rate variance and therefore limit the ability of a spike rate decoder to identify the stimulus. Although a complete characterization of such correlations would require simultaneous multineuronal recording with our task and stimuli, we used previous studies as a guide for defining correlations within our pools. In particular, we made two assumptions on the basis of these previous studies. First, we assumed that spike rate covariance was constant over a variety of time-scales, such that the covariance observed over 128 ms is similar to the covariance observed over 16 ms (Bair et al., 2001). Second, we assumed that spike rate covariance was stimulus independent (Bair et al., 2001).

Even with these assumptions, the magnitude and distribution of covariances across nearby cortical cells remained uncertain. Whereas some studies have reported near independence between neurons (Ecker et al., 2010), other studies have reported covariances as high as 0.2. We therefore chose to implement two different models of noise correlation across our population: (1) “modest” correlation (r = 0.07) and (2) “scaled” correlation in which neurons with very similar stimulus selectivities have higher correlations (r = 0.15) than neurons with dissimilar preferences (r = 0.07) (Cohen and Newsome, 2009; Huang and Lisberger, 2009). Because we did not have quantitative stimulus tuning curves with regards to all potential stimulus parameters (speed, size, and direction of motion), we used the peak sensory information value as indication of stimulus selectivity, such that neurons with very similar sensory information are better correlated than neurons with very dissimilar sensory information rates.

To implement pairwise correlations, we generated a modified spike count probability distribution for each neuron added to the pool (Eq. 12) using the pairwise firing rate statistics of the new neuron L with each of the neurons 1…L-1 already in the pool. So the probability of observing i spikes in this new neuron (p_L) depended on the probabilities of each neuron in the pool (p_m) generating j spikes as follows:

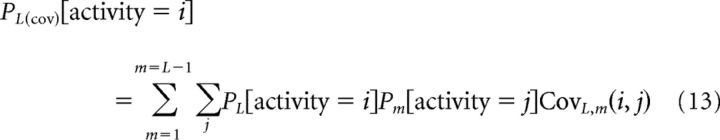For the independent model, the probability of getting any particular spike combination was simply the product of the probabilities observed in single neurons L and m, so Cov_L,m(i,j) = 1 for all spike pairs L,m with spike counts of i,j. In the previous example, if both neurons had a distribution of 50% 0 spikes, 25% 1 spike, and 25% 2 spikes, then for the sum category of 0 spikes the probability would have been 0.5×0.5 or 25%, whereas the probability of getting one spike out of their sum would have been 0.5×0.25 + 0.5×0.25. For activity covariance, the Cov matrix must be nonuniform, so that the larger the difference in activity (i-j) the smaller the likelihood. To explicitly define such a relationship, we define Cov as linearly decreasing with increasing differences in the mean-normalized firing rate of neurons L and m as follows:

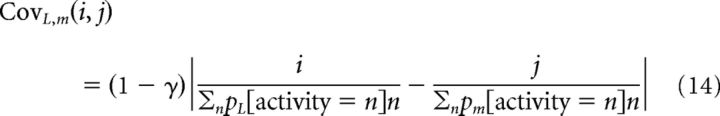Thus, the factor γ defines the tightness of the correlation. To define this probability falloff factor in accordance with experimental observations of pairwise covariance, we generated spike count probability distributions consistent with Poisson statistics, and computed pairwise correlation as a function of this factor. We found that low correlations (r = 0.07) were associated with γ = 0.2, whereas higher correlations (r = 0.15) were associated with γ = 0.5. For the low and high correlation cases, these respective factors were used for all neuronal pairs. For the scaled correlation, γ was scaled according to the stimulus response similarity of the neurons. We defined this similarity by the difference in sensory reliability between the neurons, divided by the maximum reliability difference observed over our sample. This ensured that neurons with very different sensory reliabilities, presumably because of differences in their stimulus selectivity, were less correlated with each other than neurons with very similar sensory reliabilities (Cohen and Newsome, 2009; Huang and Lisberger, 2009).

Thus, a “corrected” firing probability was generated for each cell on the basis of pairwise correlations between the individual neurons of the existing pool, and this probability is then incorporated into the pooled activity prediction (Eq. 12). All of the pooling equations (Eqs. 11–15) were applied to the spike count distributions associated with a single delay, resolution, and condition (motion pulse/noise in the case of sensory, eye fixation/saccade in the case of choice). Therefore, for every neuronal pool, pooled sensory and choice response distributions were created for each delay and resolution, and behavioral predictions generated just as they were for single neurons (Eq. 9).

Results

Motion pulse probability schedule and inattention blindness

Three monkeys were trained in a motion detection task in which the probability of a brief pulse (67–83 ms) of coherent motion varied according to specific spatiotemporal schedules (Fig. 1). Motion pulses could occur in one of two stimulus patches. One was centered on the RF of the neuron under study, whereas the other was located symmetrically across the vertical meridian. The timing of pulse presentations was randomly determined according to an exponential distribution (Fig. 1c, left), but the likely location of its appearance alternated according to a rhythmic probability schedule (Salidis, 2001) (Fig. 1c, middle), which was varied between the animals (slow = 0.5 Hz, intermediate = 0.94 Hz, fast = 1.33 Hz). The consistency of the schedule defining where pulses were likely to occur, as well as the consistency of the actual pulse used within each experimental session, enabled the animals to attend features of the pulse stimulus (Sekuler and Ball, 1977) and the likely location of its appearance (Ciaramitaro et al., 2001). The animals were trained to immediately saccade to the location of the motion pulse whenever it occurred. At no point during training were any explicit cues provided indicating where or when these pulses were likely to occur. However, because the probability of pulse occurrence varied consistently over the course of the each trial and because the pulse was difficult to detect, the task encouraged the animals to anticipate where pulses were likely to occur and consistently direct their attention to that location.

Success in this task requires continuous monitoring of the stimuli to judge whether a pulse did or did not occur. Because of this, the end result of a particular trial does not necessarily reflect performance throughout the trial. For example, a trial was immediately terminated and marked as wrong whenever an animal made an inappropriate saccade regardless of when that saccade was made. If that wrong occurred late in a trial, the animal was correctly rejecting all prior stimuli. Similarly, a failure to detect a pulse late within a trial meant that the animal was performing well until that failure. To compute performance, we divided each pulse probability cycle into four epochs (Fig. 1c, right). For each epoch, we included all trials containing that epoch, and counted both correct detections of pulses and correct rejections of motion noise in a single hemifield (Fig. 2). Correct detections were plotted as the proportion detected out of the total number of pulses presented within each interval in each hemifield (solid lines). Likewise, correct rejections were plotted as the proportion of correct rejections out of the total number of intervals containing only noise stimuli in each hemifield (dotted lines). Performance was clearly modulated in approximate accordance with the pulse probability of the three schedules. The incidence of correct detections was higher at the location where the pulse was likely for all schedules. Because no cues were provided about when and where the pulse was likely, these modulations in performance indicate the animals were using a behavioral strategy acquired during the course of training. Specifically, the animals learned the schedule of alternating motion pulse probability and attended to the stimulus where the pulse was more likely at a given point in time.

Figure 2.

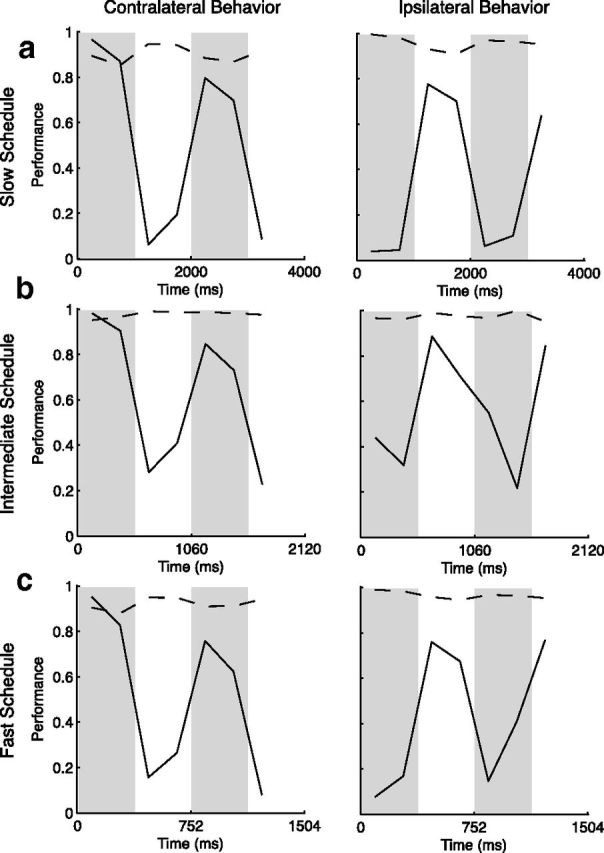
a–c, Performance for the three schedules as a function of time within the trial. Gray bars represent periods in which the likely location of pulse appearance was within the neuron's RF; white, periods during which RF pulses were unlikely. Performance is plotted according to the two types of stimulus presented: motion pulses and motion noise. In the column on the left, the proportion of pulses that were correctly detected within a cell's RF (solid) is plotted along with the proportion of motion noise epochs that were correctly rejected (dashed). The column on the right plots correct detection of pulses and rejection of noise for the stimulus patch in the visual hemifield ipsilateral to the recorded cell. For all schedules, pulse detection performance was modulated according to the schedules. Modulation of correct rejections was not as clear.

The brief and transient nature of our stimulus (Muller et al., 2001) strongly encouraged the formation of consistent temporal strategies and constant vigilance during periods of likely changes. Changes in performance occurred within hundreds of milliseconds of changes in the probability schedule (Busse et al., 2008). The magnitude and speed of these effects suggest that dynamic strategies, formed without any explicit cuing, might contribute to behavioral fluctuations and variability in any task (Ghose and Maunsell, 2002; Krug, 2004). In tasks with no pressing urgency, such as those not strongly constrained by reaction time, transient allocations of attention or intention may occur at different times within different trials (Hayden and Gallant, 2005). Similarly, for a less challenging stimulus, such as a more sustained motion pulse, brief allocations of attention might be sufficient to improve behavior (Rao et al., 2012). If the timing of transient allocations of attention varied either within trials or across trials, then analyses ignoring this variation and assuming constant attention might considerably underestimate attentional effects. Thus, the consistency of behavior with probability shifts seen in our data makes it ideal for looking at physiological correlates of attention.

Physiological correlates of inattention blindness

To detect these motion pulses, animals must encode motion information with neural activity and use that activity as the basis for a behavioral choice. Previously, we have shown that, in this task, the average firing rate of MT neurons is precisely modulated by both the stimulus and the behavioral choice (Ghose and Harrison, 2009), suggesting that MT neurons may play a role in the actual decision process. Because attention affects performance, neurons that play such a role must also be substantially modulated by attention. This modulation could take a variety of forms. For example, attention might increase responses by a constant multiplicative factor to both the background noise and the motion pulse (Cook and Maunsell, 2004), such that the difference between the two responses is on average more detectable (McAdams and Maunsell, 1999). Alternately, attention may have modest effects on mean firing rates but substantial effects on overall response variability (Mitchell et al., 2009), such that there is a more dependable difference between motion noise and motion pulse responses. Consistent with these possibilities, many physiological studies of attention have found alterations in responses before the stimulus change to be detected, including both increases in mean firing rate and decreases in response variability. To examine this possibility in our data, we analyzed mean response rates and Fano factors to motion noise preceding pulse occurrence and >200 ms before a saccade. To examine the deviation of firing rate from the mean during pulse probability epochs, we plotted the average of firing rate z-scores for all of the cells recorded with each probability schedule (Fig. 3a; gray represents unlikely; black, likely). To determine whether attention altered response variability, we also plotted the average of the Fano factors for all of the cells recorded with each probability schedule (Fig. 3a). Surprisingly, we found no substantial changes in these measures between periods in which the pulse was likely and periods in which it was unlikely, despite striking performance differences (Fig. 2).

These analyses suggest that any attentional effects on MT responses to the motion noise in our task are modest and therefore unlikely to explain behavior. However, attention might also increase detectability by selectively increasing motion pulse responses. To test for this possibility, we compared how pulse- and saccade-aligned firing rates in MT varied according to pulse likelihood. The analysis revealed a sharp low-latency increase in firing rate after pulse onset, and a similarly sharp increase before saccades (Fig. 3). Notably, both pulse- and saccade-aligned responses were higher when pulses were likely within the cell's RF (Fig. 3, black vs gray). This was true for both individual cells (Fig. 3a,b) and the average for all neurons recorded (Fig. 3c,d).

The similar dependence of performance and average firing rate on pulse likelihood suggests that these neurons might play a critical role in determining the behavioral effects of attention in this task. However, although these measures are correlated, it is not clear that even rapid changes in average firing rate are sufficient to explain the behavioral effects of attention. These averages, as well as variability measures such as Fano factor, are based on the sampling of many repetitions and therefore do not necessarily reflect the moment-to-moment variability that constrains performance in both attentive and inattentive behavioral states. For example, the detection of motion pulses embedded in noise can be formulated as a signal detection problem for the animals: how different are the sensory signals following motion pulses from the signals preceding them? If the moment-to-moment fluctuations within a trial are sufficiently large, then even neurons that on average have a higher response rate to the pulse may be insufficient to explain performance within a single trial.

Timing, especially in tasks with short reaction times, offers an additional constraint on physiological correlates of attention. For example, although firing rate differences are present over ∼150 ms periods (Fig. 3c–f), psychophysical evidence suggests that behavioral decisions were based on stimulus information acquired over tens of milliseconds (Ghose, 2006; Ghose and Harrison, 2009). Thus, firing rate changes associated with attention might persist over timescales larger than those relevant to the detection process. In this situation, one might overestimate the contribution of neurons to behavioral improvements. Even if the analysis of firing rate is restricted to the behaviorally relevant time window, it is not clear how to translate differences in firing rates to improvements in performance and reaction time. Finally, firing rate analyses are subject to potential covariances. For example, presaccadic activity might be related to saccade initiation, but if there is a strong and consistent behavioral relationship between saccades and pulses, the activity could simply reflect a pulse-locked response. Resolving these issues requires a common metric to compare neuronal discharge and behavioral performance and a means of explicitly incorporating the covariances present in this task.

Comparison of physiological and behavioral reliability

Previous work from our laboratory demonstrated that an information theoretic approach can provide directly comparable measures of behavioral and physiological responses while accommodating for the effects of covariance. The analysis computes mutual information, which quantifies how knowledge of one variable reduces uncertainty about another variable. The reduction in uncertainty per unit time is measured in units of bits/s for all pairs of variables, allowing information rates to be directly compared (Fig. 4). First, we defined three variables: motion stimulus (pulse/no pulse, red), behavioral choice (saccade/no saccade, blue), and neuronal response (spike count, green). Then we computed the mutual information rate between three pairs of these variables: one in which the relationship between the stimulus and behavioral response was analyzed (behavioral information), one in which the relationship between the stimulus and spike count was analyzed (sensory information), and one in which the relationship between spike count and behavioral response was analyzed (choice information). To fairly compare behavioral and physiological responses, analyses only considered stimuli within the RF and saccades toward the RF. A strength of our analyses is the ability to incorporate the effect of covariances. For example, high choice information could arise simply by a strong correlation of neuronal activity with the stimulus and a strong correlation between behavioral choices and the stimulus. Covariance-corrected choice information was computed by subtracting the choice information predicted by the covariance of sensory and behavioral information, whereas covariance-corrected sensory information subtracted the information predicted by the covariance of choice and behavioral information (Ghose and Harrison, 2009).

In our analysis, variables are sampled over a specific timescale and separated by a specific delay. By varying the size of the window over which variables are sampled and the intervariable delay, we obtain an “information surface,” which describes how mutual information between variables depends on these two temporal parameters (Figs. 4c and 5). Most surfaces contain a single peak whose height we define as reliability. With this analysis, we have shown that the sensory and choice information of individual neurons in MT over timescales of tens of milliseconds was similar to behavioral information (Ghose and Harrison, 2009). However, that study did not examine the effect of attention on behavioral and neuronal responses. We therefore applied these information theory metrics to observations parceled according to periods of time in which the pulse was likely and periods of time in which it was unlikely.

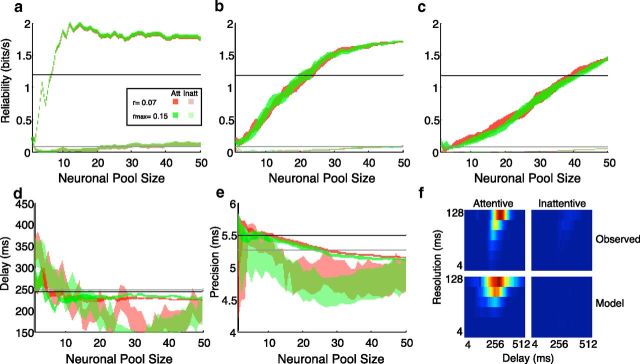
For an example recording session (Fig. 5a,c,e), we found that pulse probability had a large effect on behavioral information metrics. Consistent with measures of behavioral performance reported above, we found that, when the pulse was likely, there was a reliable correlation between motion stimuli and behavioral choice with a latency of ∼250 ms and over timescales as small as 32 ms. At this latency and a temporal resolution of 128 ms, the information rate was 1.72 bits/s. This reliability between stimulus and choice variables was nearly absent when the pulse was unlikely: the peak of the information surface was much lower (information rate = 0.05 bits/s). For all animals, behavioral reliability was much higher during periods of high pulse probability, indicating that attention can be allocated according to a variety of task schedules (fast, 1.04 vs 0.13; medium, 1.96 vs 0.39; slow, 1.28 vs 0.05 bits/s).

Physiological data recorded simultaneously with behavioral data revealed a similar pattern: pulse probability had dramatic effects on the reliability with which a single neuron's discharge reflected both stimulus events (Fig. 5c) and subsequent behavioral choices (Fig. 5e). As with the behavioral observations, reliable physiological signals at a resolution of tens of milliseconds were only present during intervals in which the pulse was likely. For an example cell, at a resolution of 32 ms, the sensory information rate was 0.72 bits/s when the pulse was likely and 0.02 bits/s when it was unlikely. Choice information, reflecting the covariance-corrected correlation between neuronal activity and behavioral choices, was similarly modulated (likely, 0.18 bits/s; unlikely, 0.04 bits/s). Analogous results were seen in the average information surface for our entire sampled population (behavioral, 1.19 vs 0.09 bit/s; sensory, 0.12 vs 0.04 bit/s; choice, 0.06 vs 0.03 bit/s; Fig. 5b,d,f). The similarity of the effect of attention on behavior and single neuron discharge in MT supports the hypothesis that MT neurons played a critical role in motion pulse detection. Moreover, because effects were seen in both sensory and choice information, it suggests that attention modulates both the encoding of sensory information and the decoding of activity associated with behavioral choice.

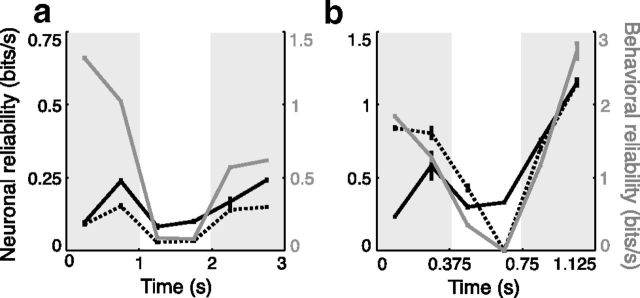
To visualize how well behavioral and neuronal reliability reflected the task schedule across time, we computed surfaces, such as those shown in Figure 5 within each epoch. For each surface (behavioral, sensory, and choice), we characterized reliability according to the maximal information rate observed, regardless of delay or temporal resolution, and plotted reliability as a function of the epoch's time after stimulus onset. Behavioral reliability was plotted on a different scale than physiological reliability to allow comparisons regarding the shape of these modulations. For example recording sessions, the analysis showed strong modulation in the time course of behavioral information, with certain epochs having almost no information (Fig. 6, gray): the stimulus change was invisible when the pulse was unexpected. Moreover, analysis of discharge from highly reliable single neurons, recorded during either the slow (Fig. 6a) or fast (Fig. 6b) pulse likelihood schedules, showed that both sensory (dashed black) and choice (black) information were also modulated with pulse probability over the course of the trial.

Figure 6.

Physiological and behavioral reliability as a function of time within the trials for two recording sessions. Reliability, the peak information rates observed over an information surface (Fig. 5), was computed for each epoch. a, b, For example, neurons recorded with the slow (a) and fast (b) schedules, behavioral (gray), sensory (dashed black), and choice (black) reliabilities were often strongly modulated over time in accordance with periods of high pulse probability (gray shading). Black numbers to the left of the plot indicate the scale for sensory and choice reliability, and gray numbers to the right of the plots indicate the scale for behavioral reliability.

To quantify the comodulation between the schedule of pulse probability, behavioral performance, and sensory and choice neuronal reliability, we examined the Spearman (rank) partial correlations between each of these variables across epochs (Table 1). In this analysis, epochs with sufficient data were not required to be contiguous and all recorded cells were used (N = 60). Consistent with the animals forming a temporal strategy on the basis of task timing, peak behavioral reliability had a significant positive correlation with the schedule (r = 0.4062, p < 0.0001). The partial correlations between the peaks of neuronal sensory reliability and the schedule, and between peak sensory reliability and behavior, were both positive and significant (r = 0.1242, p < 0.005 and r = 0.1997, p < 0.0001). Neither the partial correlations between the peaks of neuronal choice reliability and schedule nor between peak choice reliability and behavior were significant (p = 0.56, p = 0.75). However, variations in choice reliability were well correlated with variations in sensory reliability, suggesting that attention had covarying effects on the two measures (r = 0.6138, p < 0.0001). The simultaneity of physiological and behavioral modulations over time provides further evidence in support of these neurons playing a fundamental role in the decisions made by the animals.

Table 1.

Partial correlations (N = 60)

	Behavior	Sensory	Choice
Schedule	0.4062	0.1242	−0.0252
Behavior	—	0.1997	−0.0135
Sensory	—	—	0.6138

To quantify the overall effect of task schedule on sensory and choice reliability, we combined all epochs with high pulse probability as “likely” and those with low pulse probability as “unlikely” (as in Fig. 5) and plotted the peaks of these surfaces. As stated previously, behavioral information was significantly higher during likely periods in all animals (slow, 1.28 vs 0.05 bits/s; medium, 1.96 vs 0.39 bits/s; fast, 1.004 vs 0.13 bits/s). For all schedules, sensory (Fig. 7a) and choice (Fig. 7b) information rates in individual neurons were often significantly higher during periods of high pulse probability (paired t test of log values, p < 0.0001 for both sensory and choice) consistent with the observed changes in behavior.

Notably, the reliability of the relationship between MT responses and behavioral choices (choice information) was comparable to the reliability seen between motion pulses and MT responses (sensory information). This differs from previous studies where animals were required to discriminate the direction of a patch of random dots with low motion coherence, necessitating substantial spatial and temporal integration. In those studies, MT neurons exhibit only a modest ability to predict behavioral choices, whereas neurons in a higher area (lateral intraparietal area) show much better correlations with behavior (Shadlen and Newsome, 2001; Huk and Shadlen, 2005) and cue-related expectation effects (Rao et al., 2012). If training increases the behavioral weight of neurons with appropriate signals (Law and Gold, 2008), then a task such as ours that uses highly dynamic and coherent motion stimuli, well suited for MT RFs (Buracas et al., 1998; Ghose and Bearl, 2010), would result in a higher reliance on MT neurons than one involving the low coherence motion of random dot fields. This is supported by a recent study of MT neurons, which showed high correlations with behavior in a task using brief pulses of coherent motion (Smith et al., 2011).

Consistent with this task-related explanation, we found that choice information was comparable to sensory information both when the animals were performing well (likely epochs) and when the animals were performing poorly (unlikely epochs; Fig. 7). It is also possible that the high choice information values observed in some neurons are related to our task's required behavioral output. A saccade to the location of the motion, rather than a saccade to a different target or the press of a lever, may correspond better with the natural role of attention in directing eye movements to salient stimuli (Moore et al., 2003; Awh et al., 2006).

Neither sensory nor choice information was uniform across our sample population. Although we chose the location and direction of our motion pulse according the RF of the neuron under study, no effort was made to match the speed selectivity or exact spatial extent of the RF. Thus, in many cases, we were likely presenting a motion pulse of inappropriate speed and/or size for the neuron under study (Huang and Lisberger, 2009). In such cases, a minimal pulse response would likely be evoked, and the sensory information would be correspondingly low. Interestingly, and in contrast to previous studies relying of metrics, such as choice probability, neurons with poor pulse responses and low sensory information had correspondingly poor choice information. Across the population, sensory and choice information rates were strongly correlated regardless of pulse probability (Fig. 7c,d): those neurons that most reliably reflected the stimulus were also the most predictive of behavioral choice, both when the pulse was likely (Pearson's correlation of log values: r = 0.75, p < 0.0001) and when the pulse was unlikely (r = 0.63, p < 0.0001). The best fitting model of how choice information varied with stimulus information was similar for both likely and unlikely epochs and did not include an intercept term (choice = 0.48 × sensory^⋀ 0.78, likely; choice = 0.35 × sensory^⋀ 0.50, unlikely). Not only was sensory and choice information highly correlated among the population, but importantly, significant choice information was only observed for neurons with reliable sensory information, even when the animal was attentive.

Modulations in reliability associated with attention were larger than those observed in mean firing rate (Fig. 3) and often dramatic: in many cases, information rates increased by a factor of 10. Although peak choice information increased with a mean factor of 1.67 ± 0.14, sensory information increased with a mean factor of 4.7 ± 0.35. Attention had a significantly greater impact on the reliability of sensory information (paired t test of log-transformed ratios: p < 0.0001). Recent work by Masse et al. (2012) found that, in some tasks, spatial attention may increase the strength of the correlation between a cell's sensory sensitivity and its effect on behavior. However, although the strength of the correlation between sensory and choice reliability increased somewhat with attention in our task, this change was not statistically significant (two-tailed test of Fisher z transformed coefficients, z = 1.13).

These results document that the reliability of MT activity was modulated in accordance with pulse likelihood but do not reveal whether the timing of that activity was also altered. If these neurons were indeed responsible for behavior, we would expect changes in physiological timing parameters consistent with behavioral timing changes (Fig. 5). Timing parameters were quantified according to the location of the peak in the information surface. For this analysis, we only chose information surfaces with defined peaks (peak information ≥0.01 bits/s), and for each such surface compared delay and resolution as a function of pulse likelihood. We defined delay according to the location of the peak regardless of temporal resolution and computed precision by averaging the resolutions weighted according to the information rates observed at the optimal delay. Behavioral delay was shortened by attention (likely, 250 ms; unlikely, 271 ms; paired t test, p < 0.001, n = 53) and temporal precision decreased (likely, 67 ms; unlikely, 35 ms; paired t test, p < 0.001). Although no significant changes in sensory (n = 57) or choice (n = 58) delay were observed, a significant decrease in the sensory precision consistent with behavior was observed (likely, 56 ms; unlikely, 24 ms; paired t test, p < 0.001).

Behavioral predictions from physiological observations

A strong and consistent correlation between sensory and choice information among neurons, regardless of task statistics, suggested that small numbers of neurons may be sufficient to explain behavioral performance across attentive states. Those neurons that were the best at signaling stimulus events (high sensory information rates) were also the most strongly predictive of behavioral choices (high choice information rates). We therefore used our covariance analysis to produce an estimate of behavioral performance and timing under the assumption that a single cell's activity was completely responsible for behavior. In other words, we used the probability of a stimulus given a particular neuronal response and the probability of a behavioral choice given that same neuronal response to predict behavior. For both likely and unlikely epochs, we applied this analysis to the sensory and choice surfaces of individual cells (Fig. 7e). As expected given the effect of attention on both sensory and choice reliability, behavioral predictions of single cells often showed an increase in predicted behavioral reliability with attention (Wilcoxon paired-sample test on log values, p < 0.0001). Because of the combined modulations of sensory and choice reliability, for many neurons attention significantly increased the predicted behavioral reliability associated with a single cell by a factor of ≥10 (Fig. 7e, cells on the y-axis).

To estimate how a pool of these neurons might explain behavior, we combined the responses of different cells to generate pooled sensory and choice information surfaces and then used the covariance analysis to predict behavior. Responses were pooled over 4 ms (our minimum resolution). Unlike most previous attempts to quantitatively link neuronal activity to choice, this analysis made no assumptions regarding the pooling noise or motor delays because these factors were already incorporated in the choice information surface. A previous analysis using this methodology demonstrated that a small pool of independent neurons (∼5 in number) was sufficient to explain the reliability and timing of behavioral decisions in this task (Ghose and Harrison, 2009). However, the analysis did not take into account the dramatic variations in performance associated with task statistics demonstrated here, nor did they consider the potential effects of correlated activity between neurons. The effects of dynamic attention present an additional challenge to any neuronal model of behavior because, within a single trial, large and rapid behavioral changes must be explained. In particular for our task, the neuronal model must explain the near invisibility of the unexpected pulse stimulus.

We modeled behavioral predictions for pools of neurons by selecting cells from our sample without replacement and imposing small, physiologically relevant, pairwise correlations on their sensory and choice responses (Fig. 8). Pairwise correlations were assumed to be constant over different timescales, stimulus conditions, and behavioral states (Bair et al., 2001). To test the effect of such correlations, we imposed on all pools two different patterns of correlation. In the first, a relatively low and constant correlation was imposed between all neuron pairs (r = 0.07). In the second, in accordance with MT paired cell measurements (Cohen and Newsome, 2009), a variable correlation was imposed such that cells with similar sensory information values (presumably reflecting RF similarities) were more correlated (r = 0.15) than cells with very different sensory information values. Because our stimulus was always tuned to the preferred direction of each cell, we essentially modeled the behavior that would result from a population of cells with similar preferred directions, tuned to the direction of the motion stimulus, in two attentional conditions. For a single pool, we separately analyzed combined activity for epochs of high and low pulse probability.

Figure 8.

A simple population model, in which the responses from pools of sampled neurons were summed, predicted that small numbers of neurons were responsible for task performance and timing. Pools were constructed by progressively adding neurons from our sample. a–c, The order in which neurons were selected was varied three ways: (1) sorted according to their choice information (a), (2) randomly but weighted according to their choice information (b), and (3) completely random (c). For all three cases, the contingency tables from likely and unlikely epochs of different recording sessions were combined, with varying levels of pairwise correlation (red represents r = 0.07; green, r_max = 0.15), to create pooled sensory and choice information surfaces. f, Covariance analysis was applied to these pooled sensory and choice responses to create a behavioral information surface. Shaded regions indicate the SD of the random pools for information surface peak parameters of reliability (a–c), latency (d), and precision (e). Latency and precision are shown for the weighted random selection model only (b). Horizontal lines (black indicates likely; gray, unlikely) indicate behavioral observations. For all neuronal selection methods, peak information eventually exceeds actual observation of attentive reliability, although the exact number of neurons at which this happens varies (a–c). An example random pool of 17 neurons (r_max = 0.15) shows that the small neuronal numbers were capable of explaining both peak parameters (b, d, e) and the single peak nature of observed behavioral information surfaces (e) across attentive states.

In any pooling model seeking to explain behavior, the choice of which particular neurons are included can have strong effects, especially when certain neurons are highly reliable. For example, a pooling of neurons with no sensory information would be incapable of predicting how behavior is related to stimulus events. A pool of neurons with sensory information but no choice information would also be incapable of predicting behavior. To minimize assumptions regarding readout, all neurons within this pool were equally weighted. To test the effects of constructing response pools according to different rules, the sequence in which neurons were added to the response pool was varied. In the first selection algorithm, we progressively included neurons according to their ability to predict choices (i.e., choice information), such that the first neuron was the neuron in our sample with the highest choice information (Fig. 8a). In the second selection algorithm, we randomly selected neurons from our sample but biased the selection so that those neurons with high choice information were more likely to be included early on (Fig. 8b). In this algorithm, neurons that show no evidence of behavioral correlations (zero choice information) are less likely to included than neurons well correlated with choices (high choice information). Finally, in the third selection algorithm, we completely ignored choice information and randomly selected neurons from our sample (Fig. 8c). Importantly, in all of these cases, pulse information, or the strength of the correlation between response and stimulus, was never used as a basis for sorting. Thus, neurons that were highly informative about motion pulses were neither preferentially weighted in terms of their chances of being included into a neuronal pool, nor were they preferentially weighted if they were included. Similarly, the behavioral predictions from individual cells (which reflect the combination of sensory and choice information) were also not used a basis of sorting.

For each random pool, a behavioral information surface was generated on the basis on pooled sensory and choice surfaces. As previously discussed, the location of the peak on the resulting behavioral information surface was used to quantify predicted reliability, precision, and latency. We computed mean ± SD of each of these parameters across random pools of the same size for different pooling models (choice favored, choice biased, unbiased, N = 3), different correlation structures (weak constant vs variable correlation, N = 2), and different behavior states (attentive vs inattentive, N = 2).

Regardless of the exact sequence with which neurons were incorporated into a pool (Fig. 8a–c), small numbers of neurons were always sufficiently precise and reliable to explain attentive behavior. Behavior reliability (Fig. 8a–c), precision (Fig. 8d), and latency (Fig Fig. 8e) were all reproduced. This is consistent with the notion that attentive behavior can be explained by a pool containing a critical number of highly informative neurons, regardless of the exact pool composition or details of the correlations within that pool. Moreover, the effects of attention on individual neurons were so strong that, for every pooling model, the same set of neurons was also able to largely explain the invisibility of motion stimuli when attention was misdirected (Fig. 8a–c).

An example pool of 17 randomly selected neurons with variable pairwise correlation demonstrates that the model was able to accurately replicate not just peak-based measurements, but also the entire behavioral information surface (Fig. 8f). This result was not strongly dependent on preferentially including cells strongly correlated with behavior. For completely randomly chosen cell pools, the number of neurons necessary to explain behavior was larger (∼30, Fig. 8c vs Fig. 8a,b), but was also able to explain both attentive and inattentive performance. Thus, a completely random pool requires a larger number of neurons to explain performance simply because it is less likely that small pools will contain the few highly informative cells capable of predicting both attentive and inattentive performance. This is in contrast to previous models, in which performance saturates with pool sizes of hundreds of neurons (Shadlen et al., 1996; Cohen and Maunsell, 2010) and even then does not necessarily match behavior. In addition to the previously mentioned experimental differences regarding the analysis of responses and the stimulus used, the presence of a strong and consistent correlation between sensory and choice information across our sampled population is likely to be particularly important for explaining this discrepancy.

Our data highlight the potential importance of behavioral state when constructing neuronal pooling models for behavior. In our case, the physiological effects of inattention on individual neurons were so severe that increasing the size of the neuronal pool had little effect on predicted behavior. Because such a large range of pool sizes were consistent with inattentive behavior, it did not strongly constrain the size of a contributing pool of MT neurons. On the other hand, the attentive data did provide a constraint in that even modest numbers of MT neurons overpredict performance (Fig. 8a–c) and temporal precision (Fig. 8d). Thus, changes in the firing of the same small pool of neurons (∼20) can largely explain behavioral performance in terms of reliability and timing across attentive states. This is a distinguishing feature of our model, in that unlike previous ones, large numbers of neurons are actually less capable of explaining behavior.

Discussion

To study the neurophysiological basis of how strong expectations can affect performance, we trained animals to detect a brief stimulus that appeared with consistent statistics and recorded from individual neurons in area MT. We found dramatic changes in the reliability of both behavioral and neuronal responses in accordance with task statistics such that unlikely stimuli were largely invisible to both the animals and their neurons. Our results are directly relevant to the phenomena of inattention blindness where, in the absence of attention, subjects cannot perceive a suprathreshold stimulus (Newby and Rock, 1998; Most et al., 2001). Finally, we showed that reliability changes seen in small numbers of reliable MT neurons were sufficient to completely explain these behavioral variations.

Attention increased sensory reliability in individual neurons by an average factor of 4.7 (Fig. 7). This measure was based on selecting a behaviorally appropriate timescale for analysis (tens of milliseconds) and examining activity both before and after motion pulses. Attentional modulation of prechange responses need not be identical to attentional modulation of change-related responses; however, most experimental designs have solely considered activity before stimulus change (Cook and Maunsell, 2002; Ghose and Maunsell, 2002; Mitchell et al., 2009). In our study, firing rates and rate variability before pulse presentation did not vary with attention (Fig. 3a,b), whereas the actual pulse response was enhanced by attention. Analyses excluding responses during periods when decisions are actually being made (McAdams and Maunsell, 1999) would have failed to resolve these effects.

The finding that motion pulse responses were more strongly modulated by attention than motion noise responses (Fig. 3) is not consistent with a traditional gain model of attention, in which responses are multiplicatively increased regardless of the stimulus (Cook and Maunsell, 2004). However, recent data from our laboratory have suggested that attention's effects on neuronal responses are not purely linear (Ghose and Bearl, 2010). In particular, attention can increase the nonlinearity between neuronal input and output in MT neurons. A modest increase in nonlinearity would cause the effect of attention on responses to strong stimuli, such as our motion pulses, to be larger than on responses to weaker stimuli, such as our motion noise.

In most studies of attention (Seidemann and Newsome, 1999; Treue and Maunsell, 1999; Masse et al., 2012; Rao et al., 2012), it is unclear whether observed physiological changes are sufficient to explain behavioral improvements. One approach has been to quantify attentional effects in terms of an equivalent stimulus change. Using this approach, Cook and Maunsell (2002) reported that the physiological effects of attention in area MT were inconsistent with behavior. By contrast, our direct comparison of behavioral and neurophysiological reliability suggests that changes in individual neurons can explain even extreme attentional effects on behavior, such as when visibility depends on attention. Transient applications of attention and potentially incomplete measures of reliability may be responsible for previous studies' failure to explain attention effects with MT neurons.

Even if neuronal stimulus response and behavioral measures are comparable, a neuronal population affected by attention may be unrelated to the decision process. Previous studies have typically not examined whether the activity in neurons modulated by attention is correlated with behavioral choices in a trial-by-trial manner (Cook and Maunsell, 2004; Cohen and Maunsell, 2010; Rao et al., 2012). This relationship, typically quantified as choice probability, has often been measured over timescales that may not match behavior (Cohen and Newsome, 2009) and can vary substantially between tasks (Dodd et al., 2001). Recently, Smith et al. (2011) showed that individual MT neurons can exhibit high choice probability in a task using brief coherent pulses of motion similar to those used in our study. Consistent with their observations, we found that, when analysis was limited to behaviorally relevant timescales, individual MT neurons were nearly as reliable in predicting behavioral choices as they were in reflecting the onset of coherent motion.

The difference between choice probabilities as previously reported, which reflect trial-to-trial variability, and the choice information metric used here, which reflects moment-to-moment variability, is not simply a matter of analysis. The distribution of choice information across our sample is very different from what has been reported previously with choice probability. Specifically, although certain neurons in our sample had strong choice information, neurons with small sensory information tended to have very little choice information. This is in contrast to previous studies, which have reported significant choice probabilities even among relatively insensitive cells (Cohen and Newsome, 2009; Bosking and Maunsell, 2011; Masse et al., 2012). If choice information was caused solely by widespread covariation between behavior and neuronal activity (Krug, 2004; Nienborg and Cumming, 2009, 2010), we would expect it to be high regardless of a cell's sensory reliability. In such a case, choice correlations offer relatively little information about whether a neuron is actually participating in the decision process, as opposed to be simply correlated with other neurons that are. By contrast, the correlation between sensory and choice information across our neuronal population, as well as the large number of cells that show little to no choice information, suggests that only those neurons that were well suited to the task by virtue of their stimulus information were used by the animals in making their decisions.

By including a small number of cells that are informative about the stimulus and predictive of choice, we were able to explain behavioral performance. Once more than tens of neurons were included, the same model overpredicted performance. This occurs because neurons that are noisy (low stimulus information) had relatively little effect on behavior derived from pooled responses because of their small choice information. This is in contrast to models invoking a broad sampling of neurons, including those that are relatively insensitive (Shadlen et al., 1996; Jazayeri and Movshon, 2007; Bosking and Maunsell, 2011; Haefner et al., 2013). The absence of choice information among large numbers of neurons, even when the stimulus was chosen to match the preferred direction, strongly limits the number of neurons that can potentially contribute to decisions and ensures that noisy neurons are not in the pool. Because of the high correlation between choice and sensory information, we can quantify this absence on the basis of regression analysis. The best fitting regression model is on a log-log scale, log(choice) versus log(sensory), consistent with a model of choice information increasing nonlinearly with sensory information. The introduction of an intercept term into this model does not significantly improve the fit (χ² F test, nested model). However, with larger data, it is possible that a slight positive intercept would be found. If this were true, it could have significant implications regarding the size of a neuronal pool necessary to explain behavior because it would suggest that a population of purely noisy neurons may be integrated into the decision process and affect behavioral choices. Depending on the number of such cells, the noise might need to be compensated by a large pool of sensory informative neurons to create a pooled response consistent with behavioral performance.

In the absence of such noise, our data suggest that a small number of neurons could be responsible for behavior. One possible mechanism by which a small number of reliable neurons could be so influential can be imagined by a simple reaction time model in which actions are initiated as soon as a pooled sensory response reaches a criterion level. A large and reliable stimulus-evoked response would be much more likely to reach the threshold than a small or unreliable stimulus response from an insensitive neuron. Neurons with high sensory information would tend to have high choice information. A similar argument applies to attentional modulation: a strong response from an individual neuron would be more likely to trigger an action than a weak response from that same neuron (Fig. 3). Thus, we would expect a strong covariation between sensory and choice modulation by attention (Table 1). In this case, “top-down” modulations resulting from attention would be propagated in a “bottom-up” fashion to create high choice information in a select set of neurons. Our pooling models demonstrate that such a model is able to explain both the performance and timing associated with attention and inattention. Consistent with this observation, a simple threshold model suggests that pulse response modulations in a small number of neurons by attention are sufficient to explain our observations (data not shown).

Our results suggest that pooling does not significantly vary with behavioral state in our task because, for both likely and unlikely epochs of time, the neurons that most reliably signaled the stimulus were also the most strongly related to behavioral choice. The ability of attention to affect pooling (Masse et al., 2012) may be specific to tasks that require integration of a large pool of neurons over longer periods of time. Moreover, the number of neurons necessary to explain behavioral performance was similar in the two probability states, regardless of the amount of pairwise correlation.

Because we recorded from individual neurons, we assumed in our pooling simulations that MT spike rate correlations were in a range consistent with previous measures of spike count covariance (Cohen and Newsome, 2009; Huang and Lisberger, 2009). However, it is not clear that correlations in firing rates, which have usually been measured over relatively large timescales, are applicable over the short timescales relevant for our task. In addition, the correlations themselves may change with attentive state (Cohen and Maunsell, 2009; Mitchell et al., 2009), which can have substantial effects of the encoding of stimulus information and decoding of neural activity. Given our observations of strong effects in the reliability of individual neurons and that our results do not depend strongly on the level of pairwise correlation, it seems unlikely that these population effects are the sole explanation for the improvements in behavior resulting from attention, but the exact contribution of these effects will require simultaneously recording multiple neurons in area MT during task performance.

Although the small number of cells used in our model is inconsistent with the MT literature, it is largely consistent with measures of single neuron reliability during a visual search task in an area associated with saccade planning and generation. Over timescales of ∼100 ms, single neurons in the frontal eye field exhibited a consistency in their discharge between different trials that was comparable to behavioral performance (Bichot et al., 2001). The activity of just six frontal eye field neurons was sufficient to explain behavioral timing and accuracy across a variety of manipulations in task difficulty and design. However, an important distinction between these results and ours is the stimulus selectivity of neurons in MT and frontal eye field. Although frontal eye field encodes spatial salience and is relevant for potential eye movements, it has relatively limited stimulus-specific responses. By contrast, MT neurons have well-documented stimulus selectivity for parameters, such as motion direction and binocular disparity and, as evidenced by our data, can precisely encode rapid stimulus changes. Indeed, it is the coexistence of both high stimulus information and high choice information in single MT neurons that suggests their involvement in the transformation of stimulus information to behavioral choices that is central to the perceptual decisions made in our task. Our results demonstrate that attentional effects, especially strong ones as observed in our design, can serve as a powerful constraint for neural models of decision making.