Computing Steerable Principal Components of a Large Set of Images and Their Rotations

Abstract

We present here an efficient algorithm to compute the Principal Component Analysis (PCA) of a large image set consisting of images and, for each image, the set of its uniform rotations in the plane. We do this by pointing out the block circulant structure of the covariance matrix and utilizing that structure to compute its eigenvectors. We also demonstrate the advantages of this algorithm over similar ones with numerical experiments. Although it is useful in many settings, we illustrate the specific application of the algorithm to the problem of cryo-electron microscopy.

I. Introduction

IN image processing and computer vision applications, often one is not interested in the raw pixels of images used as input, but wishes to transform the input images into a representation that is meaningful to the application at hand. This usually comes with the added advantage of requiring less space to represent each image, effectively resulting in compression. Because less data are required to store each image, algorithms can often operate on images in this new representation more quickly.

One common transformation is to project each image onto a linear subspace of the image space. This is typically done using Principal Component Analysis (PCA), also known as the Karhunen–Loéve expansion. The PCA of a set of images produces the optimal linear approximation of these images in the sense that it minimizes the sum of squared reconstruction errors. As an added benefit, PCA often serves to reduce noise in a set of images.

PCA is typically computed as the singular value decomposition (SVD) of the data matrix X of image vectors or as the eigenvector decomposition of the covariance matrix C = XX^T. One then ranks eigenvectors according to their eigenvalues and projects each image onto the linear subspace spanned by the top n eigenvectors. One can then represent each image with only n values, instead of the original number of pixel values.

There are a number of applications in which each of an image’s planar rotations are interesting as well as the original images. It is usually unreasonable due to both time and space constraints to replicate each image many times at different rotations and to compute the resulting covariance matrix for eigenvector decomposition. To cope with this, Teague, [19] and then Khotanzad and Lu [10], developed a means of creating rotation-invariant image approximations based on Zernike polynomials. While Zernike polynomials are not adaptive to the data, PCA produces an optimal data adaptive basis (in the least squares sense). This idea was first utilized in the 1990s, when, in optics, Hilai and Rubinstein [8] developed a method of computing an invariant Karhunen–Loéve expansion, which they compared with the Zernike polynomials expansion. Independently, a similar method to produce an approximate set of steerable kernels was developed by Perona [14] in the context of computer vision and machine learning. Later, Uenohara and Kanade [20] produced, and Park [12] corrected, an algorithm to efficiently compute the PCA of an image and its set of uniform rotations. Jogan et al. [9] then developed an algorithm to compute the PCA of a set of images and their uniform rotations.

The natural way to represent images when rotating them is to sample them on a polar grid consisting of N_θ radial lines at evenly spaced angles and N_r samples along each radial line. The primary advantage of [9] is that the running time of the algorithm increases nearly linearly with both the size of the image (N_r below) and the number of rotations (N_θ below). The disadvantage, however, is that the running time experiences cubic growth with respect to the number of images P in the set. The result is an algorithm with a running time of O(P²N_r N_θ log(N_r N_θ) + N_θP³), which is impractical for large sets of images.

We present here an alternate algorithm that grows cubically with the size of the image, but only linearly with respect to the number of rotations and the number of images. Due to this running time, our algorithm is appropriate for computing the PCA of a large set of images with a running time of $O({PN}_{\theta }{N}_r(N_r+log(N_{\theta }))+N_{\theta }{N}_r^3)$.

Although this algorithm is generally useful in many applications, we discuss its application to cryo-electron microscopy (cryo-EM) [3]. In cryo-EM, many copies of a molecule are embedded in a sheet of ice so thin that images of the molecule of interest are disjoint when viewing the sheet flat. The sheet is then imaged with an electron microscope, destroying the molecules in the process. The result is a set of projection images of the molecule taken at unknown random orientations with extremely low signal-to-noise ratio (SNR). The cryo-EM problem, then, is to reconstruct the 3-D structure of the molecule using thousands of these images as input.

Because the images are so noisy, preprocessing must be done to remove noise from the images. The first step is usually to compute the PCA of the image set [1], [21], a step which both reduces noise and compresses the image representation. This is where our algorithm comes in, because in cryo-EM every projection image is equally likely to appear in all possible in-plane rotations. After PCA, class averaging is usually performed to estimate which images are taken from similar viewing angles and to average them together in order to reduce the noise [3], [17], [22]. A popular method for obtaining class averages requires the computation of rotationally invariant distances between all P(P − 1)/2 pairs of images [13]. The principal components we compute in this paper provide a way to accelerate this large-scale computation. This particular application will be discussed in a separate publication [18].

Other applications for computing the PCA of a large set of images with their uniform rotations include those discussed in [9]. A set of full-rotation panoramic images were taken by a robot at various points around a room. Those panoramic images and their uniform rotations were then processed using PCA. A new image taken at an unknown location in the room was then template matched against the set of images already taken to determine the location in the room from which the new image was taken. Because these images are likely to be somewhat noisy, it is important to perform PCA on them to be able to effectively template match against the training set.

The remainder of this paper is organized as follows. In Section II, we derive the principles behind the algorithms. In Section III, we describe an efficient implementation of our algorithm and discuss its space and computational complexity. In Section IV, we present a method for applying this algorithm to images sampled in rectangular arrays. In Section V, we present numerical experiments comparing our algorithm to other existing algorithms. Finally, in Section VI, we present an example of its use in cryo-EM.

II. Derivation

Consider a set of P images represented in polar coordinates. Each image is conveniently stored as an N_r × N_θ matrix, where the number of columns N_θ is the number of radial lines and the number of rows N_r is the number of samples along each radial line. Note that N_θ and N_r must be the same for all images. Then, each column represents a radial line beginning in the center of the image, and each row represents a circle at a given distance from the center. The first circle is at distance 0 from the center, and so the center value is repeated N_θ times as the first row of the matrix.

We can create a rotation of an image simply by rotating the order of the columns. Moving the leftmost column to the rightmost and cyclically shifting all other columns of the matrix, for example, represents a rotation of 2π/N_θ. In this way, we can generate all N_θ rotations of each image. Thus, let matrix I^i,l represent the lth rotation of image i, 0 ≤ i ≤ P−1, 0 ≤ l ≤ N_θ−1. Note that we may assume the average pixel value in each image is 0, otherwise we subtract the mean pixel value from all pixels.

Let J^i,l be a vector created by row-major stacking of the entries of image I^i,l, that is, $J_{N_{\theta }m+n}^{i,l}=I_{m,n}^{i,l},0\le m\le N_r-1$, 0 ≤ m ≤ N_r−1, 0 ≤ n ≤ N_θ−1. Then construct the N_rN_θ × PN_θ data matrix X by stacking all J^i,l side by side to create

$$X=\left[\begin{array}{ccc}\mid & & \mid \\ J^{0,0}& \cdots & J^{P-1,N_{\theta }-1}\\ \mid & & \mid \end{array}\right]$$ (1)

and set the covariance matrix C = XX^T. Note that C is of size N_rN_θ × N_rN_θ. The principal components that we wish to compute are the eigenvectors of C. This can be computed directly through the eigenvector decomposition of C, or through the SVD of X. We will now detail an alternative and more efficient approach for computing these eigenvectors exploiting the block circulant structure of C.

Consider Cⁱ, the covariance matrix given by just image i and its rotations, J^i,0 …J^{i, N_θ−1} as follows:

$$C^i=\sum _{n=0}^{N_{\theta }-1}{J}^{i,n}{J}^{i,n^T}.$$ (2)

Note that

$$C=\sum _{i=0}^{P-1}{C}^i.$$ (3)

Now, let C^i,αβ be an N_θ × N_θ block of Cⁱ corresponding to the outer product of row α of I^i,0, …, I^{i, N_θ−1}in J^i,0, …, J^{i, N_θ−1} with row β of I^i,0, …, I^{i, N_θ−1}.

We will now show that Cⁱ is of the form

$$C^i=\left[\begin{array}{ccc}{C}^{i,0,0}& \cdots & C^{i,0,N_r-1}\\ ⋮& \ddots & ⋮\\ C^{i,N_r-1,0}& \cdots & C^{i,N_r-1,N_r-1}\end{array}\right]$$ (4)

where each C^i,α,β is an N_θ × N_θ circulant matrix.

Because image i and its rotations comprise a full rotation of row α and a full rotation of row β, we have

$$C_{n_1,n_2}^{i,\alpha ,\beta }=\sum _{n=0}^{N_{\theta }-1}{I}_{\alpha ,n_1}^{i,n}·I_{\beta ,n_2}^{i,n}=\sum _{n=0}^{N_{\theta }-1}{I}_{\alpha ,n_1+n}^{i,0}·I_{\beta ,n_2+n}^{i,0}$$ (5)

where each row of I^i,0 is considered a circular vector, so that all indexes are taken modulo N_θ. However, due to the circular property of the vector, for any integer c, we have

$$C_{n_1+c,n_2+c}^{i,\alpha ,\beta }=\sum _{n=0}^{N_{\theta }-1}{I}_{\alpha ,n_1+c+n}^{i,0}·I_{\beta ,n_2+c+n}^{i,0}=C_{n_1,n_2}^{i,\alpha ,\beta }.$$ (6)

This means that C^i,α,β is a circulant matrix. However, this analysis applies to any rows α and β. Therefore, Cⁱ consists of N_r × N_r tiles of N_θ × N_θ circulant matrices, as in (4).

Now, the sum of circulant matrices is also a circulant matrix. Define C^α,β as

$$C^{\alpha ,\beta }=\sum _{i=0}^{P-1}{C}^{i,\alpha ,\beta }.$$ (7)

Thus, C^α,β is an N_θ × N_θ circulant matrix. Then C is of the form

$$C=\left[\begin{array}{ccc}{C}^{0,0}& \cdots & C^{0,N_r-1}\\ ⋮& \ddots & ⋮\\ C^{N_r-1,0}& \cdots & C^{N_r-1,N_r-1}\end{array}\right].$$ (8)

A known fact is that the eigenvectors V⁰, V¹, …, V^N_θ−1 of any N_θ × N_θ circulant matrix A are the columns of the discrete Fourier transform matrix [5], given by

$$V_n^k=e^{-2\pi \iota kn/N_{\theta }},0\le k,n\le N_{\theta }-1$$ (9)

where $\iota =\sqrt{-1}$. The first coordinate of any V^k is 1, so the eigenvalues λ₀, λ₁, …, λ_Nθ−1 of a circulant matrix A, for which, AV^k = λ_kV^k are given by

$$\begin{array}{l}{\lambda }_k={({AV}^k)}_0=\sum _{n=0}^{N_{\theta }-1}{A}_{0,n}{e}^{-\iota 2\pi kn/N_{\theta }}\\ ={\widehat{A}}_0(k),0\le k\le N_{\theta }-1\end{array}$$ (10)

where A₀ is the first row in matrix A, and Â₀ is its discrete Fourier transform. These eigenvalues are, in general, complex.

It follows that, for the matrix C, there are N_θ eigenvalues associated with each of its $N_r^2$ circulant tiles. We denote these eigenvalues ${\lambda }_k^{\alpha ,\beta }$ satisfying $C^{\alpha ,\beta }{V}^k={\lambda }_k^{\alpha ,\beta }{V}^k$. Note that

$$\begin{array}{l}{\lambda }_k^{\alpha ,\beta }=\sum _{n=0}^{N_{\theta }-1}{C}_{0,n}^{\alpha ,\beta }{e}^{-\iota 2\pi kn/N_{\theta }}\\ =\sum _{n=0}^{N_{\theta }-1}\left(\sum _{i=0}^{P-1}{C}_{0,n}^{i,\alpha ,\beta }\right)e^{-\iota 2\pi kn/N_{\theta }}\\ =\sum _{i=0}^{P-1}{\lambda }_k^{i,\alpha ,\beta }.\end{array}$$ (11)

Now construct a vector W^k,q of length N_rN_θ by concatenating multiples $c_{\alpha }^{k,q}$ of the vector V^k N_r times, that is,

$$W^{k,q}=\left[\begin{array}{c}{c}_0^{k,q}{V}^k\\ ⋮\\ c_{N_r-1}^{k,q}{V}^k\end{array}\right],0\le k\le N_{\theta }-1.$$ (12)

These W^k,q vectors will be our eigenvectors for C. The exact values of $c_0^{k,q},c_1^{k,q},\dots ,c_{N_r-1}^{k,q}$, as well as the index set for q, will be determined below.

Consider the result of the matrix-vector multiplication CW^k,q. Along each tile-row of C(α = α₀), each circulant submatrix C^α₀,β is multiplied by an eigenvector $c_{\beta }^{k,q}{V}^k$. Thus

$${CW}^{k,q}=\left[\begin{array}{c}\left(\sum _{\beta =0}^{N_r-1}{\lambda }_k^{0,\beta }{c}_{\beta }^{k,q}\right)·V^k\\ ⋮\\ \left(\sum _{\beta =0}^{N_r-1}{\lambda }_k^{N_r-1,\beta }{c}_{\beta }^{k,q}\right)·V^k\end{array}\right].$$ (13)

So, requiring W^k,q to be an eigenvector of C satisfying CW^k,q = μ^k,qW^k,q is equivalent to

$$\sum _{\beta =0}^{N_r-1}{\lambda }_k^{\alpha ,\beta }{c}_{\beta }^{k,q}={\mu }^{k,q}{c}_{\alpha }^{k,q},\text{for}\alpha =0,1,\dots ,N_r-1.$$ (14)

However, this in turn is equivalent to the eigenvector decomposition problem for the matrix

$${\mathrm{\Lambda }}^k=\left[\begin{array}{ccc}{\lambda }_k^{0,0}& \cdots & {\lambda }_k^{0,N_r-1}\\ ⋮& \ddots & ⋮\\ {\lambda }_k^{N_r-1,0}& \cdots & {\lambda }_k^{N_r-1,N_r-1}\end{array}\right].$$ (15)

This means that the vector W^k,q is an eigenvector of C with eigenvalue μ^k,q if the vector $c^{k,q}={(c_0^{k,q},\dots ,c_{N_r-1}^{k,q})}^T$ is an eigenvector of the matrix Λ^k, satisfying Λ^kc^k,q = μ^k,qc^k,q.

Next, we show that the matrix Λ^k is Hermitian. To that end, note that the covariance matrix C is by definition symmetric, so column γ of the N_θ × N_θ submatrix C^α,β is equal to row γ of submatrix C^β,α. Now, set γ = 0. Then, by viewing the rows of the tile C^α,β as circular vectors, the circulant property of the tiles implies that

$$C_{0,n}^{\beta ,\alpha }=C_{n,0}^{\alpha ,\beta }=C_{0,-n}^{\alpha ,\beta },\text{for}n=0,\dots ,N_{\theta }-1.$$ (16)

The eigenvalues of C^β,α, then, are

$$\begin{array}{l}{\lambda }_k^{\beta ,\alpha }={(C^{\beta ,\alpha }{V}^k)}_0=\sum _{n=0}^{N_{\theta }-1}{C}_{0,n}^{\beta ,\alpha }·e^{-\iota 2\pi kn/N_{\theta }}\\ =\sum _{n=0}^{N_{\theta }-1}{C}_{0,-n}^{\alpha ,\beta }·e^{-\iota 2\pi kn/N_{\theta }}\end{array}$$ (17)

which, by the change of variables n′ = −n, becomes

$${\lambda }_k^{\beta ,\alpha }=\sum _{n^{\prime }=0}^{N_{\theta }-1}{C}_{0,n^{\prime }}^{\alpha ,\beta }·e^{\iota 2\pi k{n}^{\prime }/N_{\theta }}=\overline{{\lambda }_k^{\alpha ,\beta }}$$ (18)

where $\overline{{\lambda }_k^{\alpha ,\beta }}$ refers to the complex conjugate of ${\lambda }_k^{\alpha ,\beta }$. Note that this property is true only because $C_{n_1,n_2}^{\alpha ,\beta }$ is real for all n₁, n₂.

Thus, Λ^k is a Hermitian matrix. As a result, all of Λ^k’s eigenvalues are real. Furthermore, these eigenvalues are the μ^k,q so q ∈ 0, 1, …, N_r −1 and the c^k,q are complex-valued.

Thus, for some fixed k₀, Λ^k₀ has N_r linearly independent eigenvectors that in turn give N_r linearly independent eigenvectors W^k,q of C, through (12). Furthermore, the vectors V⁰, V¹, …, V^N_θ−1 are linearly independent. From this, it follows that the constructed eigenvectors W^k,q are linearly independent.

Now, consider an eigenvector W^k,q, 0 ≤ k ≤ N_θ−1, 0 ≤ q ≤ N_r−1 as an eigenimage, that is, consider the eigenimage as an N_r × N_θ matrix

$$R^{k,q}=\left[\begin{array}{c}{c}_0^{k,q}{V}^{k^T}\\ ⋮\\ c_{N_r-1}^{k,q}{V}^{k^T}\end{array}\right].$$ (19)

This is of the same form as the original images, in which each row is a circle and each column is a radial line, with the first row being the center of the image. The coefficients $c_r^{k,q}$ are complex, so we may write $c_r^{k,q}=f^{k,q}(r)e^{\iota {\varphi }^{k,q}(r)}$ for 0 ≤ r ≤ N_r−1. Therefore, R^k,q is of the form

$$\begin{array}{l}{R}^{k,q}(r,\theta )=f^{k,q}(r)e^{\iota {\varphi }^{k,q}(r)}{e}^{-\iota k\theta }\\ =f^{k,q}(r)e^{\iota (-k\theta +{\varphi }^{k,q}(r))}\end{array}$$ (20)

for θ = 0, 2π/N_θ, …,2π(N_θ −1)/N_θ, r = 0, 1, …, N_r−1.

The real and imaginary parts of R^k,q are eigenimages, given by

$$\begin{array}{l}{R}_{\text{c}}^{k,q}(r,\theta )=\mathfrak{R}(R^{k,q}(r,\theta ))\\ =f^{k,q}(r)cos(-k\theta +{\varphi }^{k,q}(r))\end{array}$$ (21)

$$\begin{array}{l}{R}_{\text{s}}^{k,q}(r,\theta )=\mathfrak{J}(R^{k,q}(r,\theta ))\\ =f^{k,q}(r)sin(-k\theta +{\varphi }^{k,q}(r))\end{array}$$ (22)

for r = 0,1, …, N_r − 1, θ = 0,2π/N_θ, …, 2π(N_θ−1)/N_θ.

Thus, each eigenimage R^k,q produces two eigenimages $R_{\text{c}}^{k,q}$ and $R_{\text{s}}^{k,q}$. It may appear as though this gives us 2N_rN_θ eigenimages, which is too many. However, consider (11) for V^N−1−k = V^−k:

$$\begin{array}{l}{\lambda }_{-k}^{\alpha ,\beta }=\sum _{n=0}^{N_{\theta }-1}{C}_{0,n}^{\alpha ,\beta }{e}^{-\iota 2\pi (-k)n/N_{\theta }}\\ =\sum _{n=0}^{N_{\theta }-1}\left(\sum _{i=0}^{P-1}{C}_{0,n}^{i,\alpha ,\beta }\right)e^{\iota 2\pi kn/N_{\theta }}\\ =\sum _{i=0}^{P-1}\overline{{\lambda }_k^{i,\alpha ,\beta }}\\ =\overline{{\lambda }_k^{\alpha ,\beta }}.\end{array}$$ (23)

Therefore, ${\mathrm{\Lambda }}^{-k}=\overline{{\mathrm{\Lambda }}^k}$, Thus

$${\mathrm{\Lambda }}^{-k}\overline{c^{k,q}}=\overline{{\mathrm{\Lambda }}^k{c}^{k,q}}=\overline{{\mu }^{k,q}{c}^{k,q}}.$$ (24)

However, because Λ^k is Hermitian, μ^k,q is real, so ${\mu }^{k,q}=\overline{{\mu }^{k,q}}$. Therefore, the eigenvalues of Λ^k are the same as those for Λ^−k, and the eigenvectors of Λ^k are the complex conjugates of the eigenvectors of Λ^−k. Note also that k = −k if k = 0 or k = N_θ/2, which are also the values of k such that Λ^k has real eigenvectors. Therefore, each eigenvector from k = 0 or k = N_θ/2 contributes one real eigenimage, while eigenvectors from every other value of k each contribute two. Thus, linear combinations of the eigenvectors of the first N_θ/2 + 1 Λ^k matrices results in N_r × N_θ eigenimages.

Note also that, when N_θ is odd, eigenvectors for k = 0 each contribute one real eigenimage, while eigenvectors for every other k each contribute two. Thus, counting eigenimages for k = 0, 1, …, N_θ−1/2 produces N_r × N_θ eigenimages, as required.

III. Implementation and Computational Complexity

The first step in this algorithm is to compute the covariance matrix Cⁱ of each image Iⁱ and its rotations. However, it is not necessary to compute the actual covariance matrix. Instead, we need only compute the eigenvalues ${\lambda }_k^{i,\alpha ,\beta }$ of each circulant tile C^i,αβ of the covariance matrix. From (10) and (11), it follows that the eigenvalues are equal to the discrete Fourier transform of the top row of a tile C^i,αβ.

Note that, by (5), we have

$$C_{0,m}^{i,\alpha ,\beta }=\sum _{n=0}^{N_{\theta }-1}{I}_{\alpha ,n}^{i,0}{I}_{\beta ,m+n}^{i,0}$$ (25)

where m = 0, …, N_θ −1. Now, the convolution theorem for cross correlations states that, for two sequences f and g, if f ★ g indicates the cross correlation of f and g, then

$$\widehat{f★g}=\overline{\widehat{f}}·\widehat{g}.$$ (26)

Therefore, the eigenvalues ${\lambda }_k^{i,\alpha ,\beta }$ can be computed efficiently as

$$\begin{array}{l}{\lambda }_k^{i,\alpha ,\beta }=\overline{\left(\sum _{n=0}^{N_{\theta }-1}{I}_{\alpha ,n}^{i,0}{e}^{-\iota 2\pi kn/N_{\theta }}\right)}·\left(\sum _{n=0}^{N_{\theta }-1}{I}_{\beta ,n}^{i,0}{e}^{-\iota 2\pi kn/N_{\theta }}\right)\\ =\overline{{\widehat{I}}_{\alpha }^{i,0}}(k)·{\widehat{I}}_{\beta }^{i,0}(k).\end{array}$$ (27)

This can be computed efficiently with the dast Fourier transform (FFT). In addition, because the covariance matrix Cⁱ is symmetric, ${\lambda }_k^{i,\alpha ,\beta }=\widehat{{\lambda }_k^{i,\beta ,\alpha }}$. We can in this way compute N_θ different N_r × N_r matrices Λ^i,k and sum

$${\mathrm{\Lambda }}^k=\sum _{i=0}^{P-1}{\mathrm{\Lambda }}^{i,k}$$ (28)

so that Λ^k is as defined in (15).

Note that, in some implementations, such as in Matlab, complex eigenvectors of unit norm are always returned. As a result, real eigenvectors, which occur when k = 0 or k = N_θ/2, will have twice the norm of the other eigenvectors. One must therefore normalize these eigenvectors by dividing them by $\sqrt{2}$.

Computation of the Fourier transforms ${\widehat{I}}_{\alpha }^{i,0}$ can be performed in time O(N_θ log(N_θ)). Because we do this for every α, computation of the necessary Fourier transforms takes total time O(N_rN_θ log(N_θ)). In addition, it uses space O(N_θN_r). Computation of a matrix Λ^k has computational complexity $O(N_r^2)$, but, because we compute N_θ of them, the overall time of $O(N_{\theta }{N}_r^2)$. In addition, the space complexity of this step is $O(N_{\theta }{N}_r^2)$. Each of these steps must be repeated for each image i, and then the P matrices Λ^i,k, (i = 0,…,P −1)must be summed together for each image. Thus, the computational complexity up to this point is O(P N_θN_r(N_r + log(N_θ)))and the space complexity is $O(N_{\theta }{N}_r^2)$.

Note that the computation of Λ^k for each image i is completely independent of each other image. Thus, these computations can be performed in parallel to further improve performance. Such a parallel implementation requires space $O({PN}_{\theta }{N}_r^2)$.

At this point, we need to perform eigenvector decomposition on each Λ^k to determine the eigenvectors of C. The computational complexity of this step is $O(N_{\theta }{N}_r^3)$ and the space complexity is O(P N_θN_r). Thus, the computational complexity of the entire algorithm is

$$O({PN}_{\theta }{N}_r(N_r+log(N_{\theta }))+N_{\theta }{N}_r^3)$$ (29)

and the total space complexity is

$$max(N_{\theta }{N}_r^2,{PN}_{\theta }{N}_r).$$ (30)

The algorithm is summarized in Algorithm 1, and a comparison of the computational complexity of this algorithm with others is shown in Table I.¹

Algorithm 1.

PCA of a Set of Images and Their Rotations

Require: P image matrices I0,0, I1,0,…, IP−1,0of size Nr×Nθ in polar form.

1: Set ${\lambda }_k^{\alpha ,\beta }=0$, α, β = 0,…, Nr−1, k = 0,…, Nθ−1

2: for i = 0,…, P − 1 do

3: Compute the Fourier transforms ${\widehat{I}}_{\alpha }^{i,0}(k)$ for α = 0,…, Nr − 1, k =0,…, Nθ − 1.

4: for αβ = 0,…, Nr −1 do

5: Compute the eigenvalues ${\lambda }_k^{i,\alpha ,\beta }$ of Ci,αβ using (27).

6: end for

7: Update Λk ← Λk + Λi,k for k = 0,…, Nθ −1 as in (28).

8: end for

9: for k = 0,…, Nθ/2 do

10: Compute the eigenvector decomposition of matrix Λk to generate eigenvectors ck,q and eigenvalues μk,q for q = 0,…, Nr −1

11: for q = 0,…,Nr − 1 do

12: Construct eigenvector Wk,q as in (12), using eigenvector ck,q of Λk.

13: end for

14: end for

15: for k = 0,…, Nθ/2, q = 0,…,Nr −1 do

16: Rearrange Wk,q as an image matrix as in (19) and compute its real and imaginary parts $R_{\text{c}}^{k,q}$ and $R_{\text{s}}^{k,q}$.

17: If k = 0 or k = Nθ/2, normalize eigenimages if necessary by dividing by $\sqrt{2}$.

18: end for

19: return $R_{\text{c}}^{k,q}$ and $R_{\text{s}}^{k,q}$ as in (21) and (22).

TABLE I.

Comparison of Computational Complexities of Different PCA Algorithms

Algorithm	Computational Complexity
Ours	$O({PN}_{\theta }{N}_r(N_r+log(N_{\theta }))+N_{\theta }{N}_r^3)$
JZL	O(P2NrNθ log(NrNθ) + NθP3)
SVD	$min\{N_r{P}^2{N}_{\theta }^3,P{N}_r^2{N}_{\theta }^3\}$
Eig. Decomp.	${PN}_r{N}_{\theta }^2+{(N_r{N}_{\theta })}^3$

IV. Application to Rectangular Images

Although this algorithm is based on a polar representation of images, it can be implemented efficiently on images represented in the standard Cartesian manner efficiently and without loss of precision using the 2-D polar Fourier transform and the Radon transform.

The 2-D Radon transform of a function I(x, y) along a line ${\tau }_{\theta }^{\perp }$ through the origin is given by the projection of I(x, y) along the direction τ_θ [11]. The Radon transform is defined on the space of lines ${\tau }_{\theta }^{\perp }$ in ℝ², so we may write

$$\begin{array}{l}R(t,{\tau }_{\theta }^{\perp })={\int }_{{\tau }_{\theta }}I(x,y)ds\\ =\int {\int }_{-\infty }^{\infty }I(x,y)\times \delta (xcos(\theta )+ysin(\theta )-t)\mathit{dxdy}.\end{array}$$ (31)

The Fourier projection-slice theorem states that the 1-D Fourier transform of the projection of an image along τ_θ0 is equal to the slice of the 2-D Fourier transform of the image taken along ${\tau }_{{\theta }_0}^{\perp }$ [11]. To see this, let r ∈ ℝ² be any point on the plane, and let

$$r=u+s,u\in {\tau }_{{\theta }_0}^{\perp },s\in {\tau }_{{\theta }_0}.$$ (32)

Also, take $w\in {\tau }_{{\theta }_0}^{\perp }$. Note that r · w = u · w, since s · w = 0. Then

$$\begin{array}{l}{\widehat{R}}_{{\theta }_0}(w)={\int }_{{\tau }_{{\theta }_0}^{\perp }}{\int }_{{\tau }_{{\theta }_0}}I(u+s)ds{e}^{-\iota u·w}du\\ ={\int }_{{\tau }_{{\theta }_0}^{\perp }}{\int }_{{\tau }_{{\theta }_0}}I(u+s)e^{-\iota u·w}\mathit{dsdu}\\ ={\int }_{{\mathbb{R}}^2}I(r)e^{-\iota r·w}dr\\ =\widehat{I}(w).\end{array}$$ (33)

The Fourier projection-slice theorem provides an accurate way for computing the Radon transform by sampling the image’s 2-D Fourier transform on a polar grid and then taking inverse 1-D Fourier transforms along lines through the origin. Because the 2-D Fourier transform is discrete, performing the normal 2-D FFT and interpolating it to a polar grid leads to approximation errors. Instead, we use a nonequally spaced FFT described in [2] and [6]. This step has a computational complexity of O((mL)²log(L) + N_rN_θ log(N_rN_θ)log(1/ε)), where L is the number of pixels on the side of a square true image, N_r is the number of pixels in a radial line in polar form, N_θ is the number of radial lines, m is an oversampling factor used in the nonequally spaced FFT, and ε is the required precision.²

The Fourier transform is a unitary transformation by Parseval’s theorem. Therefore, the principal components of the normal 2-D FFT’ed images are simply the 2-D FFT of the principal component images. The 2-D polar Fourier transform, however, is not a unitary transformation, because the frequencies are nonequally spaced: they are sampled on concentric circles of N_r equally spaced radii, such that every circle has a constant number N_θ of samples instead of being proportional to its circumference, or equivalently, to its radius. In order to make it into a unitary transformation, we have to multiply the 2-D Fourier transform Î(|w|cos θ, |w| sin θ)of image I by $\sqrt{\mid w\mid }$. In other words, all images are filtered with the radially symmetric “wedge” filter $\sqrt{\mid w\mid }$ or, equivalently, are convolved with the inverse 2-D Fourier transform of this filter.

After multiplying the images’ 2-D polar Fourier transforms by $\sqrt{\mid w\mid }$, we take the 1-D inverse Fourier transform of every line that passes through the origin. From the Fourier projection-slice theorem, these 1-D inverse Fourier transforms are equal to the line projections of the convolved images, that is, the collection of 1-D inverse Fourier transforms of a given “ $\sqrt{\mid w\mid }$-filtered” image, is the 2-D Radon transform of the filtered image.

These 2-D Radon transformed filtered images are real valued and are given in polar form that can be organized into matrices as described at the beginning of Section II. We can then utilize the algorithm described above to compute the principal components of such images. Moreover, since the transformation from the original images to the Radon transformed filtered images is unitary, we are guaranteed that the computed principal components are simply the Radon transform of the filtered principal components images.

After computing all of the polar Radon principal components we desire, we must convert them back to rectangular coordinates. We cannot simply invert the Radon transform because the pixels of each eigenimage are not uniformly sampled, making the problem ill-formed. However, for the inversion we can utilize the special form of the Radon eigenimages $R_{\text{c}}^{k,q}$ and $R_{\text{s}}^{k,q}$ from (21) and (22), given by

$$R_{\text{c}}^{k,q}(r,\theta )=f^{k,q}(r)cos(-k\theta +{\varphi }^{k,q}(r))$$ (34)

$$R_{\text{s}}^{k,q}(r,\theta )=f^{k,q}(r)sin(-k\theta +{\varphi }^{k,q}(r)).$$ (35)

To compute the inverse Radon transform of such functions we utilize the projection-slice theorem. In principle, this is done by first computing the Fourier transform of each radial line, dividing by $\sqrt{\mid w\mid }$ and then taking the 2-D inverse Fourier transform of that polar Fourier image to produce the true eigenimage.

Let us first compute the 2-D polar Fourier transform by taking 1-D discrete Fourier transform along each radial line of the function in (34). Equation (34) is only defined for r ≥ 0, but we must compute the discrete Fourier transform (DFT) along an entire line through the origin. We must therefore expand this definition to allow for any real r. Let

$$g_{\text{c}}^{k,{\theta }_0}(x)=\{\begin{array}{ll}{R}_{\text{c}}^{k,q}(x,{\theta }_0),\hfill & \text{if}x\ge 0\hfill \\ R_{\text{c}}^{k,q}(-x,{\theta }_0+\pi ),\hfill & \text{if}x<0\hfill \end{array}$$ (36)

for some fixed θ₀. Note that we should really denote this function $g_{\text{c}}^{k,q,{\theta }_0}$, but since q is fixed throughout this section, we drop it for convenience of notation. Then

$$g_{\text{c}}^{k,{\theta }_0}(x)=\{\begin{array}{ll}{f}^{k,q}(x)cos(-k{\theta }_0+{\varphi }^{k,q}(x)),\hfill & \text{if}x\ge 0\hfill \\ f^{k,q}(-x)cos(-k({\theta }_0+\pi )+{\varphi }^{k,q}(x)),\hfill & \text{if}x<0.\hfill \end{array}$$ (37)

Define $g_{\text{s}}^{k,{\theta }_0}$ similarly for $R_{\text{s}}^{k,q}$. Note that $g_{\text{c}}^{k,{\theta }_0}$ and $g_{\text{s}}^{k,{\theta }_0}$ are even functions if k is even, and odd functions if k is odd. The DFT can then be defined as

$$F_{\text{c}}^{k,{\theta }_0}(r)=\sum _{n=-(N_r-1)}^{N_r-1}{g}_{\text{c}}^{k,{\theta }_0}(n)e^{-\iota 2\pi /2N_r-1rn}$$ (38)

where r =|w|. Note that

$$\begin{array}{l}{F}_{\text{c}}^{k,{\theta }_0}(-r)=\sum _{n=-(N_r-1)}^{N_r-1}{g}_{\text{c}}^{k,{\theta }_0}(n)e^{\iota 2\pi /2N_r-1rn}\\ =\overline{F_{\text{c}}^{k,{\theta }_0}(r)}\end{array}$$ (39)

because $g_{\text{c}}^{k,{\theta }_0}(n)$ is real. Furthermore, with the change of variables n′ = −n, we find that, if k is even, then

$$\begin{array}{l}{F}_{\text{c}}^{k,{\theta }_0}(-r)=\sum _{n^{\prime }=-(N_r-1)}^{N_r-1}{g}_{\text{c}}^{k,{\theta }_0}(-n^{\prime })e^{-i2\pi /2N_r-1r{n}^{\prime }}\\ =F_{\text{c}}^{k,{\theta }_0}(r)\end{array}$$ (40)

and, if k is odd, then

$$\begin{array}{l}{F}_{\text{c}}^{k,{\theta }_0}(-r)=\sum _{n^{\prime }=-(N_r-1)}^{N_r-1}{g}_{\text{c}}^{k,{\theta }_0}(-n^{\prime })e^{-i2\pi /2N_r-1r{n}^{\prime }}\\ =-F_{\text{c}}^{k,{\theta }_0}(r).\end{array}$$ (41)

Therefore, if k is even, then $F_{\text{c}}^{k,{\theta }_0}(r)$ is real and even, and, if k is odd, then $F_{\text{c}}^{k,{\theta }_0}(r)$ is pure imaginary and odd.

Then, the 2-D Fourier transform of the true image can be defined as (a proof of this formula can be found in Appendix A)

$$\begin{array}{l}{F}_{\text{c}}^k(r,\theta )=F_{\text{c}}^{k,\theta }(r)\\ =cos(-k\theta )F_{\text{c}}^{k,0}(r)-sin(-k\theta )F_{\text{s}}^{k,0}(r)\end{array}$$ (42)

and

$$\begin{array}{l}{F}_{\text{s}}^k(r,\theta )=F_{\text{s}}^{k,\theta }(r)\\ =sin(-k\theta )F_{\text{c}}^{k,0}(r)+cos(-k\theta )F_{\text{s}}^{k,0}(r).\end{array}$$ (43)

As shown above, these functions are either real or pure imaginary, depending on k.

Next we will take the 2-D inverse Fourier transform of $1/\sqrt{r}{F}_c^k(r,\theta )$ (where r = |w| and $1/\sqrt{r}$ is the filter) to obtain true eigenimages $I_{\text{c}}^k$ and $I_{\text{s}}^k$. Define $H_{\text{c}}^k$ as the order k Hankel transform of $1/\sqrt{r}{F}_{\text{c}}^{k,0}(r)$

$$H_{\text{c}}^k(s)={\int }_0^{\infty }r\frac{1}{\sqrt{r}}{F}_{\text{c}}^{k,0}(r)J_k(rs)dr$$ (44)

and define $H_{\text{s}}^k$ as the order k Hankel transform of $1/\sqrt{r}{F}_{\text{s}}^{k,0}(r)$:

$$H_{\text{s}}^k(s)={\int }_0^{\infty }r\frac{1}{\sqrt{r}}{F}_{\text{s}}^{k,0}(r)J_k(rs)dr,$$ (45)

where J_k is the Bessel function.

Then, the true real eigenimages can be described (in polar form) with the two equations (a proof of this formula can be found in Appendix B)

$$I_1^k(s,\alpha )=\beta (k)\left(cos\left(k\left(\alpha +\frac{\pi }{2}\right)\right)H_{\text{c}}^k(s)+sin\left(k\left(\alpha +\frac{\pi }{2}\right)\right)H_{\text{s}}^k(s)\right)$$ (46)

$$I_2^k(s,\alpha )=\beta (k)\left(sin\left(k\left(\alpha +\frac{\pi }{2}\right)\right)H_{\text{c}}^k(s)-cos\left(k\left(\alpha +\frac{\pi }{2}\right)\right)H_{\text{s}}^k(s)\right)$$ (47)

where

$$\beta (k)=\frac{1}{2}(1+{(-1)}^k+\iota (1-{(-1)}^k))$$ (48)

so that β(k) = 1 when k is even, and β(k) = ι when k is odd. In practice, $H_{\text{c}}^k$ and $H_{\text{s}}^k$ are computed using standard numerical procedures [4], [7], [15] and from the polar form (46)–(47), it is a straightforward manner to obtain the images’ values on the Cartesian grid.³

V. Numerical Experiments

We performed numerical experiments to test the speed and accuracy of our algorithm against similar algorithms. We performed this test on a UNIX environment with four processors, each of which was a Dual Core AMD Opteron Processor 275 running at 2.2 GHz. These experiments were performed in Matlab with randomly generated pixel data in each image. We did this because the actual output of the algorithms are not important in measuring runtime, and runtime is not affected by the content of the images. The images are assumed to be on a polar grid as described at the beginning of Section II.

We compared our algorithm against three other algorithms: 1) the algorithm described in [9], which we will refer to as JZL; 2) SVD of the data matrix; and 3) computation of the covariance matrix C and then eigenvector decomposition of C. Note that our algorithm as well as JZL compute the PCA of each image and its planar rotations, while SVD and eigenvector decomposition do not take rotations into account and are therefore not as accurate.

In Table II, one can see a comparison of the running times of various algorithms. In this experiment, images of size N_r = 100 and N_θ = 72 were used. For image counts P of at least 64 and less than 12 288, our algorithm is fastest, at which point eigenvector decomposition becomes faster. However, the goal of this paper is to work with large numbers of images, so our algorithm is not designed to compete for very small P. In addition, eigenvector decomposition does not take planar rotations into account. Thus, eigenvector decomposition only computes the principal components of P images, whereas our algorithm actually computes the principal components of P N_θ images. In addition, the calculation of the covariance matrix was made faster because Matlab makes use of parallel processors to compute matrix products.

TABLE II.

Comparison of Running Times Under Increasing Number of Images P, in Seconds N_r = 100 and N_θ = 72

P	This Paper	JZL	SVD	Eig. Decomp.
24	1.74	0.90	0.48	12.0
32	1.90	1.6	0.76	13.4
48	2.13	3.5	1.48	19.0
64	2.47	6.3	2.50	19.1
96	3.00	14.9	4.55	30.0
128	3.53	26.3	6.74	33.2
192	4.44	70.0	9.91	45.0
256	5.34	139	13.2	43.1
384	7.45	378	20.3	56.1
512	9.25	902	27.3	63.3
768	13.1	2796	43.7	73.0
1024	16.8	7926	63.1	80.2
1536	24.3	N/A	93.3	79.2
2048	31.8	N/A	137	96.8
3022	46.0	N/A	219	97.9
4096	61.9	N/A	317	122
6144	92.0	N/A	529	136
8192	122	N/A	703	151
12288	182	N/A	1116	160
16384	242	N/A	1739	197

In Table III, one can see a comparison of the running times of various algorithms as P = 500 and N_θ = 72 are held constant and N_r is increased. Even though the running time of our algorithm shows cubic growth here, it is still far faster than either JZL or eigenvector decomposition. SVD performs more quickly than our algorithm here; however, it is not considering image rotations. Note that the large jump in running time for eigenvector decomposition with N_r = 384 is due to the fact that, for large N_r, the N_rN_θ × N_rN_θ covariance matrix became too large to store in memory, causing the virtual memory to come into use, causing large delays.

TABLE III.

Comparison of Running TIMES Under Increasing Number of Pixels Per Radial Line N_r, in Seconds. P = 500 and N_θ = 72

Nr	This Paper	JZL	SVD	Eig. Decomp.
8	0.25	477	1.89	0.43
12	0.36	482	3.05	0.85
16	0.52	491	3.69	1.29
24	0.96	506	5.87	2.94
32	1.41	524	8.05	5.65
48	2.67	552	12.48	13.1
64	4.12	628	19.0	22.6
96	8.61	804	25.8	52.5
128	14.9	1027	35.1	87.8
192	34.7	1190	56.0	192
256	66.9	1520	68.9	417
384	185	2127	107	17916
512	445	3389	156	N/A
768	1751	6882	281	N/A
1024	5060	12149	386	N/A

In Table IV, one can see a comparison of the running times of various algorithms as P = 500 and N_r = 100 are held constant, and N_θ is increased. Again, our algorithm is significantly faster than any of the others.

TABLE IV.

Comparison of Running Times Under Increasing Number of Rotations N_θ, in Seconds. P = 500 and N_r = 100

Nθ	This Paper	JZL	SVD	Eig. Decomp.
8	4.84	299	3.43	0.91
12	5.21	325	4.76	2.01
16	5.64	351	5.48	3.11
24	6.27	500	8.51	6.71
32	6.77	459	11.2	12.9
48	7.78	585	18.5	26.0
64	8.70	708	23.7	47.3
96	10.7	988	40.4	104
128	12.4	1302	51.5	178
192	16.4	1859	77.4	479
256	20.1	2705	108	4022
384	27.6	3873	170	N/A
512	37.3	6976	257	N/A
768	58.9	11133	400	N/A
1024	69.6	14706	560	N/A

We now consider the numerical accuracy of our algorithm. We compare the resulting eigenvectors of SVD against those of our algorithm and eigenvector decomposition of the covariance matrix. However, these eigenvectors often occur in pairs, and any two orthonormal eigenvectors that span the correct eigensubspace are valid eigenvectors. Therefore, we cannot simply compute the distance between eigenvectors of different methods, because the paired eigenvectors produced may be different.

To measure the accuracy of the algorithms, then, we compute the Grassmannian distance between two eigensubspaces: if a subspace V is spanned by orthonormal vectors u₁, …, u_k then the projection matrix onto that subspace is defined by $P_v={\sum }_{i=1}^k{v}_i{v}_i^T$. The Grassmannian distance between two subspaces V and W is defined as the largest eigenvalue magnitude of the matrix (P_V − P_W).

In our first experiment, we artificially generated 50 projection images of the E. Coli 50-s ribosomal subunit, as described in the next section, and convert them into “ $\sqrt{w}$-filtered” radon images as described in Section IV with N_r = 100 and N_θ = 36. We then perform PCA on these Radon images and each of their 36 rotations using the four different algorithms. We then pair off principal components with identical eigenvalues, and compute the Grassmannian distance between each set of principal components and those computed by SVD.

In our second experiment, we do the same thing but using images consisting entirely of Gaussian noise with mean 0 and variance 1. The results of both experiments can be seen in Table V.

TABLE V.

Comparison of Grassmannian Distances Between SVD Eigensubspaces and Other Methods. (A)Images of Artificially Generated Projections of the E.Coli 50-s Ribosomal Subunit. (B) Images of White Noise

(A)				(B)
Princ. Comps	This Paper	JZL	Eig. Decomp.	Princ. Comps	This Paper	JZL	Eig. Decomp.
1	2.25 · 10−15	2.09 · 10−15	3.11 · 10−15	1 & 2	3.73 · 10−13	3.71 · 10−13	3.41 · 10−13
2 & 3	5.26 · 10−15	8.03 · 10−15	9.45 · −15	3 & 4	3.75 · 10−13	3.71 · 10−13	3.44 · 10−13
4 &5	6.94 · 10−15	7.17 · 10−15	7.83 · 10−15	5 & 6	9.25 · 10−13	9.27 · 10−13	1.05 · 10−12
6 &7	9.72 · 10−15	1.35 · 10−14	7.40 · 10−15	7	1.63 · 10−12	1.63 · 10−12	2.76 · 10−12
8 &9	9.45 · 10−14	9.36 · 10−14	1.87 · 10−13	8 & 9	1.60 · 10−12	1.60 · 10−12	2.74 · 10−12

Finally, in our third experiment, we compare the true eigenimages that are produced by our algorithm using the procedure described in Section IV with those produced by performing SVD on a full set of images and rotations. To do this, we produce artificially generated 75 projection images of the E. Coli 50-s ribosomal subunit and produced 36 uniform rotations of each one.⁴ We then performed SVD on this set of 2700 images and compared the results with running our algorithm on the original set of 75 images. The results can be seen in Fig. 1. Eigenimages 2 and 3 are rotated differently in our algorithm than in SVD. This is because the two eigenimages have the same eigenvalue, and different rotations correspond to different eigenvectors in the 2-D subspace spanned by the eigenvectors. Eigenimage 4 is also rotated differently, which is again due to paired eigenvalues; the fifth eigenimage is not shown.

Fig. 1.

Number above each column represents which eigenimages is shown in that column. (a) Eigenimages produced by running SVD on the original set of 75 images. (b) Eigenimages produced by running SVD on the set of 2700 rotated images. (c) Eigenimages produced by our algorithm.

VI. Cryo-EM

Cryo-EM is a technique used to image and determine the three dimensional structure of molecules. Many copies of some molecule of interest are frozen in a sheet of ice that is sufficiently thin so that, when viewing the sheet from its normal direction, the molecules do not typically overlap. This sheet is then imaged using a transmission electron microscope. The result is a set of noisy projection images of the molecule of interest, taken at random orientations of the molecule. This process usually destroys the molecules of interest, preventing one from turning the sheet of ice to image a second time at a known orientation. The goal is to then to take a large set of such images, often 10 000 or more, and from that set deduce the three dimensional structure of the molecule.

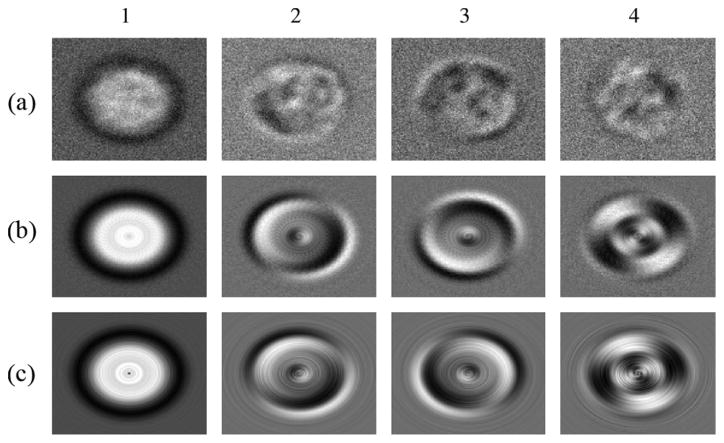
Several sample projection images are shown in Fig. 2(a). These images were artificially generated by taking projections from random orientations of the E. Coli 50-s ribosomal subunit, which has a known structure. Gaussian noise was then added to create an SNR of Var(signal)/Var(noise) = 1/5. P = 250 such images of size 129 × 129 were generated, and then transformed into radon images of size N_θ = 72 and N_r = 100. Note that, in a real application of cryo-EM, images often have much lower SNRs, and many more images are used.

Fig. 2.

(a) Artificially generated projections of the E. Coli 50-s ribosomal subunit, with Gaussian noise added to create an SNR of 1/5. (b) The first ten” $\sqrt{\mid w\mid }$-filtered” radon eigenimages. (c) The first 20 true eigenimages. Below each true eigenimage is its eigenvalue μ and frequency k, respectively.

We then applied to this set of images the algorithm described in Sections II–IV. The first 10 “ $\sqrt{\mid w\mid }$-filtered” radon eigenimages are shown in Fig. 2(b). Note that eigenimages 2 and 3 are an example of paired eigenimages. Paired eigenimages have the same eigenvalue, and occur as eigenvectors in paired Hermitian matrices Λ^k and Λ^−k, as in (21) and (22). Note that eigenimages 1 and 6 have a frequencies of k = 0, which results in only a real eigenimage and so is not paired with another.

Fig. 2(c) shows the conversion of the Radon eigenimages in Fig. 2(b) to true eigenimages. This was done with the procedure described in Section IV. Eigenimages 2 and 3 are paired with frequency k = 1, and eigenimages 4 and 5 are paired with frequency k = 2. They are described by (46) and (47). Eigenimage 1 is described by (46) only. These images can be compared in their general shape to the eigenimages shown in [19, p. 117], where the SVD was used to compute the eigenimages for all possible rotations of KLH projection images. We remark that the true eigenimages are shown just for illustrative purposes: as will be shown in [18], the principal components of the 2-D $\sqrt{\mid w\mid }$-multiplied polar Fourier transformed images are sufficient to accelerate the computation of the rotationally invariant distances [13], but the true eigenimages are not required.

Biographies

Colin Ponce received the B.S.E. degree in computer science and a certificate in applied and computational mathematics from Princeton University, Princeton, NJ, in 2010. He is currently working toward the Ph.D. degree in computer science from Cornell University, Ithaca, NY.

His current research focuses on machine learning and scientific computing.

Mr. Ponce is a member of Tau Beta Pi and Sigma Xi.

Amit Singer received the B.Sc. degree in physics and mathematics and Ph.D. degree in applied mathematics from Tel Aviv University, Tel Aviv, Israel, in 1997 and 2005, respectively.

He is an Associate Professor of Mathematics and a member of the Executive Committee of the Program in Applied and Computational Mathematics (PACM) at Princeton University, Princeton, NJ. He joined Princeton University as an Assistant Professor in 2008. From 2005 to 2008, he was a Gibbs Assistant Professor in Applied Mathematics with the Department of Mathematics, Yale University, New Haven, CT. He served in the Israeli Defense Forces during 1997–2003. His current research in applied mathematics focuses on problems of massive data analysis and structural biology.

Prof. Singer was the recipient of the Alfred P. Sloan Research Fellowship (2010) and the Haim Nessyahu Prize for Best PhD in Mathematics in Israel (2007).

Appendix A. Proof of 2-D Fourier Transform Formula

Here, we prove formulas (42) and (43). To that end, consider the operation in (38):

$$\begin{array}{l}{F}_{\text{c}}^{k,{\theta }_0}(r)=\sum _{n=-(N_r-1)}^{N_r-1}{g}_{\text{c}}^{k,{\theta }_0}(n)e^{-\iota 2\pi /2N_r-1rn}\\ =\sum _{n=-(N_r-1)}^{-1}{R}_{\text{c}}^{k,q}(-n,{\theta }_0+\pi )e^{-\iota 2\pi /2N_r-1rn}+\sum _{n=0}^{N_r-1}{R}_{\text{c}}^{k,q}(n,{\theta }_0)e^{-\iota 2\pi /2N_r-1rn}\\ =\sum _{n=-(N_r-1)}^{-1}f(-n)\\ \times cos(-k({\theta }_0+\pi )+\varphi (-n))e^{-\iota 2\pi /2N_r-1rn}\\ +\sum _{n=0}^{N_r-1}f(n)cos(-k{\theta }_0+\varphi (n))e^{-\iota 2\pi /2N_r-1rn}\\ =\sum _{n=-(N_r-1)}^{-1}f(-n)[cos(-k({\theta }_0+\pi ))cos(\varphi (-n))\\ -sin(-k({\theta }_0+\pi ))sin(\varphi (-n))]e^{-\iota 2\pi /2N_r-1rn}\\ +\sum _{n=0}^{N_r-1}f(n)[cos(-k{\theta }_0)cos(\varphi (n))\\ -sin(-k{\theta }_0)sin(\varphi (n))]e^{-\iota 2\pi /2N_r-1rn}\\ =cos(-k({\theta }_0+\pi ))\\ \times \sum _{n=-(N_r-1)}^{-1}f(-n)cos(\varphi (-n))e^{-\iota 2\pi /2N_r-1rn}\\ -sin(-k({\theta }_0+\pi ))\\ \times \sum _{n=-(N_r-1)}^{-1}f(-n)sin(\varphi (-n))e^{-\iota 2\pi /2N_r-1rn}\\ +cos(-k{\theta }_0)\sum _{n=0}^{N_r-1}f(n)cos(\varphi (n))e^{-\iota 2\pi /2N_r-1rn}\\ -sin(-k{\theta }_0)\sum _{n=0}^{N_r-1}f(n)sin(\varphi (n))e^{-\iota 2\pi /2N_r-1rn}.\end{array}$$ (49)

Note that

$$\begin{array}{l}cos(-k({\theta }_0+\pi ))\sum _{n=-(N_r-1)}^{-1}f(-n)cos(\varphi (-n))e^{-\iota 2\pi /2N_r-1rn}=cos(-k{\theta }_0){(-1)}^k\sum _{n=-(N_r-1)}^{-1}f(-n)cos(\varphi (-n))e^{-\iota 2\pi /2N_r-1rn}\\ =cos(-k{\theta }_0)\sum _{n=-(N_r-1)}^{-1}f(-n){(-1)}^{k}cos(\varphi (-n))e^{-\iota 2\pi /2N_r-1rn}\\ =cos(-k{\theta }_0)\sum _{n=-(N_r-1)}^{-1}f(-n)cos(-k\pi +\varphi (-n))e^{-\iota 2\pi /2N_r-1rn}\end{array}$$ (50)

and similarly

$$sin(-k({\theta }_0+\pi ))\sum _{n=-(N_r-1)}^{-1}f(-n)sin(\varphi (-n))e^{-\iota 2\pi /2N_r-1rn}=sin(-k{\theta }_0)\sum _{n=-(N_r-1)}^{-1}f(-n)sin(-k\pi +\varphi (-n))e^{-\iota 2\pi /2N_r-1rn}.$$ (51)

Therefore, it follows that (49) becomes

$$\begin{array}{l}{F}_{\text{c}}^{k,{\theta }_0}(r)\\ =cos(-k{\theta }_0)\sum _{n=-(N_r-1)}^{-1}f(-n)cos(-k\pi +\varphi (-n))e^{-\iota 2\pi /2N_r-1rn}\\ -sin(-k{\theta }_0)\sum _{n=-(N_r-1)}^{-1}f(-n)\\ \times sin(-k\pi +\varphi (-n))e^{-\iota 2\pi /2N_r-1rn}\\ +cos(-k{\theta }_0)\sum _{n=0}^{N_r-1}f(n)cos(\varphi (n))e^{-\iota 2\pi /2N_r-1rn}\\ -sin(-k{\theta }_0)\sum _{n=0}^{N_r-1}f(n)sin(\varphi (n))e^{-\iota 2\pi /2N_r-1rn}\\ =cos(-k{\theta }_0)\left(\sum _{n=-(N_r-1)}^{-1}{R}_{\text{c}}^{k,q}(-n,\pi )e^{-\iota 2\pi /2N_r-1rn}+\sum _{n=0}^{N_r-1}{R}_{\text{c}}^{k,q}(n,0)e^{-\iota 2\pi /2N_r-1rn}\right)\\ -sin(-k{\theta }_0)\left(\sum _{n=-(N_r-1)}^{-1}{R}_{\text{s}}^{k,q}(-n,\pi )e^{-\iota 2\pi /2N_r-1rn}+\sum _{n=0}^{N_r-1}{R}_{\text{s}}^{k,q}(n,0)e^{-\iota 2\pi /2N_r-1rn}\right)\\ =cos(-k{\theta }_0)\sum _{n=-(N_r-1)}^{N_r-1}{g}_{\text{c}}^{k,0}(n)e^{-\iota 2\pi /2N_r-1rn}\\ -sin(-k{\theta }_0)\sum _{n=-(N_r-1)}^{N_r-1}{g}_{\text{s}}^{k,0}(n)e^{-\iota 2\pi /2N_r-1rn}\\ =cos(-k{\theta }_0)F_{\text{c}}^{k,0}(r)-sin(k{\theta }_0)F_{\text{s}}^{k,0}(r).\end{array}$$ (52)

Therefore, define the 2-D Fourier transform of the true image as

$$\begin{array}{l}{F}_{\text{c}}^k(r,\theta )=F_{\text{c}}^{k,\theta }(r)\\ =cos(-k\theta )F_{\text{c}}^{k,0}(r)-sin(-k\theta )F_{\text{s}}^{k,0}(r).\end{array}$$ (53)

A similar manipulation shows that

$$\begin{array}{l}{F}_{\text{s}}^k(r,\theta )=F_{\text{s}}^{k,\theta }(r)\\ =sin(-k\theta )F_{\text{c}}^{k,0}(r)+cos(-k\theta )F_{\text{s}}^{k,0}(r).\end{array}$$ (54)

As shown above, these functions are either real or pure imaginary, depending on k.

Appendix B. Proof of the Radon Inversion Formula

Here, we show that the true eigenimages $I_1^k$ and $I_2^k$ are given by (46) and (47). To do this, we take the 2-D inverse Fourier transform of $F_{\text{c}}^{k,0}(r,\theta )$. First, let ${\stackrel{\sim }{F}}_{\text{c}}^{k,0}(w_1,w_2)=1/\sqrt{w_1^2+w_2^2}{F}_{\text{c}}^k(\sqrt{w_1^2+w_2^2},arctan{w}_2/w_2)$. Then

$$I_{\text{c}}^k(x_1,x_2)={\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }{\stackrel{\sim }{F}}_{\text{c}}^{k,0}(w_1,w_2)e^{\iota (w_1,w_2)·(x_1,x_2)}{dw}_1{dw}_2.$$ (55)

With the change of variables x₁ = s cos α, x₂ = s sin α and w₁ = r cos &thetas;, w₂ = r sin θ, we obtain

$$\begin{array}{l}{I}_{\text{c}}^k(s,\alpha )\\ ={\int }_0^{2\pi }{\int }_0^{\infty }\frac{1}{\sqrt{r}}{F}_{\text{c}}^{k,0}(r,\theta )e^{\iota (rcos\theta ,rsin\theta )·(scos\alpha ,ssin\alpha )}r\mathit{drd}\theta \\ ={\int }_0^{2\pi }{\int }_0^{\infty }\frac{1}{\sqrt{r}}(cos(-k\theta )F_{\text{c}}^{k,0}(r)\\ -sin(-k\theta )F_{\text{s}}^{k,0}(r))e^{\iota (rcos\theta ,rsin\theta )·(scos\alpha ,ssin\alpha )}r\mathit{drd}\theta \\ ={\int }_0^{2\pi }{\int }_0^{\infty }\frac{1}{\sqrt{r}}(cos(-k\theta )F_{\text{c}}^{k,0}(r)\\ -sin(-k\theta )F_{\text{s}}^{k,0}(r))e^{\iota \mathit{rs}cos(\theta -\alpha )}r\mathit{drd}\theta \\ ={\int }_0^{2\pi }{\int }_0^{\infty }\left(\frac{e^{\iota k\theta }+e^{-\iota k\theta }}{2}\right)\frac{1}{\sqrt{r}}{F}_{\text{c}}^{k,0}(r)e^{\iota \mathit{rs}cos(\theta -\alpha )}r\mathit{drd}\theta \\ -{\int }_0^{2\pi }{\int }_0^{\infty }\left(\frac{e^{-\iota k\theta }-e^{-\iota k\theta }}{2\iota }\right)\frac{1}{\sqrt{r}}{F}_{\text{s}}^{k,0}(r)e^{\iota \mathit{rs}cos(\theta -\alpha )}r\mathit{drd}\theta \\ =\frac{1}{2}{\int }_0^{\infty }r\frac{1}{\sqrt{r}}{F}_{\text{c}}^{k,0}(r)\left({\int }_0^{2\pi }{e}^{\iota (k\theta +\mathit{rs}cos(\theta -\alpha ))}d\theta +{\int }_0^{2\pi }{e}^{-\iota (k\theta -\mathit{rs}cos(\theta -\alpha ))}d\theta \right)dr\\ -\frac{1}{2\iota }{\int }_0^{\infty }r\frac{1}{\sqrt{r}}{F}_{\text{s}}^{k,0}(r)\times \left({\int }_0^{2\pi }-e^{\iota (k\theta +\mathit{rs}cos(\theta -\alpha ))}d\theta +{\int }_0^{2\pi }{e}^{-\iota (k\theta -\mathit{rs}cos(\theta -\alpha ))}d\theta \right)dr.\end{array}$$ (56)

Now, with the change of variables θ′ = α + π/2− θ, we have

$$\begin{array}{l}{\int }_0^{2\pi }{e}^{\iota (k\theta +\mathit{rs}cos(\theta -\alpha ))}d\theta =e^{\iota k(\alpha +\pi /2)}{\int }_{\alpha +\pi /2-2\pi }^{\alpha +\pi /2}{e}^{-\iota (k{\theta }^{\prime }-\mathit{rs}sin({\theta }^{\prime }))}d{\theta }^{\prime }\\ =2\pi e^{\iota k(\alpha +\pi /2)}{J}_k(rs)\end{array}$$ (57)

and, with the change of variables θ″ = θ − α + π/2, we have

$$\begin{array}{l}{\int }_0^{2\pi }{e}^{-\iota (k\theta -\mathit{rs}cos(\theta -\alpha ))}d\theta =e^{-\iota k(\alpha -\pi /2)}{\int }_{-\alpha +\pi /2}^{-\alpha +\pi /2+2\pi }{e}^{-\iota (k{\theta }^{″}-\mathit{rs}sin({\theta }^{″}))}d{\theta }^{″}\\ =2\pi e^{-\iota k(\alpha -\pi /2)}{J}_k(rs)\end{array}$$ (58)

where J_k is the Bessel function. Thus, $I_{\text{c}}^k$ becomes

$$\begin{array}{l}{I}_{\text{c}}^k(s,\alpha )=\frac{2\pi }{2}\left(e^{\iota k(\alpha +\pi /2)}+e^{-\iota k(\alpha -\pi /2)}\right){\int }_0^{\infty }r\frac{1}{\sqrt{r}}{F}_{\text{c}}^{k,0}(r)J_k(rs)dr-\frac{2\pi }{2\iota }\left(-e^{\iota k(\alpha +\pi /2)}+e^{-\iota k(\alpha -\pi /2)}\right){\int }_0^{\infty }r\frac{1}{\sqrt{r}}{F}_{\text{s}}^{k,0}(r)J_k(rs)dr\\ =\frac{2\pi }{2}\left(e^{\iota k(\alpha +\pi /2)}+e^{-\iota k(\alpha -\pi /2)}\right)H_{\text{c}}^k(s)+\frac{2\pi }{2\iota }\left(e^{\iota k(\alpha +\pi /2)}-e^{-\iota k(\alpha -\pi /2)}\right)H_{\text{s}}^k(s)\end{array}$$ (59)

where $H_{\text{c}}^k(s)$ is the order k Hankel transform of $1/\sqrt{r}{F}_{\text{c}}^{k,0}(r)$, and $H_{\text{s}}^k(s)$ is the order k Hankel transform of $1/\sqrt{r}{F}_{\text{s}}^{k,0}(r)$.

Now note that

$$e^{-\iota k(\alpha -\pi /2)}=e^{-\iota k(\alpha +\pi /2)+\iota k\pi }=e^{\iota k\pi }{e}^{-\iota k(\alpha +\pi /2)}.$$ (60)

As a result,

$$I_{\text{c}}^k(s,\alpha )=\frac{2\pi }{2}\left(e^{\iota k(\alpha +\pi /2)}+e^{\iota k\pi }{e}^{-\iota k(\alpha +\pi /2)}\right)H_{\text{c}}^k(s)+\frac{2\pi }{2\iota }\left(e^{\iota k(\alpha +\pi /2)}-e^{\iota k\pi }{e}^{-\iota k(\alpha +\pi /2)}\right)H_{\text{s}}^k(s).$$ (61)

If k is even, then e^ιkπ = −1, so

$$\begin{array}{l}{I}_{\text{c}}^k(s,\alpha )=\frac{2\pi }{2}\left(e^{\iota k(\alpha +\pi /2)}+e^{-\iota k(\alpha +\pi /2)}\right)H_{\text{c}}^k(s)+\frac{2\pi }{2\iota }\left(e^{\iota k(\alpha +\pi /2)}-e^{-\iota k(\alpha +\pi /2)}\right)H_{\text{s}}^k(s)\\ =2\pi cos\left(k\left(\alpha +\frac{\pi }{2}\right)\right)H_{\text{c}}^k(s)+2\pi sin\left(k\left(\alpha +\frac{\pi }{2}\right)\right)H_{\text{s}}^k(s).\end{array}$$ (62)

This is a real-valued function because $F_{\text{c}}^{k,0}$ and $F_{\text{s}}^{k,0}$are real when k is even.

If k is odd, then e^ιkπ = −1, so

$$\begin{array}{l}{I}_{\text{c}}^k(s,\alpha )=\frac{2\pi }{2}\left(e^{\iota k(\alpha +\pi /2)}-e^{-\iota k(\alpha +\pi /2)}\right)H_{\text{c}}^k(s)+\frac{2\pi }{2\iota }\left(e^{\iota k(\alpha +\pi /2)}+e^{-\iota k(\alpha +\pi /2)}\right)H_{\text{s}}^k(s)\\ =2\pi \iota sin\left(k\left(\alpha +\frac{\pi }{2}\right)\right)H_{\text{c}}^k(s)-2\pi \iota cos\left(k\left(\alpha +\frac{\pi }{2}\right)\right)H_{\text{s}}^k(s).\end{array}$$ (63)

While this appears imaginary, it is also real because $F_{\text{c}}^{k,0}$ and $F_{\text{s}}^{k,0}$, and therefore $H_{\text{c}}^k$ and $H_{\text{s}}^k$, are imaginary when k is odd. A similar manipulation shows that, when k is even, then

$$I_{\text{s}}^k(s,\alpha )=-2\pi sin\left(k\left(\alpha +\frac{\pi }{2}\right)\right)H_{\text{c}}^k(s)+2\pi cos\left(k\left(\alpha +\frac{\pi }{2}\right)\right)H_{\text{s}}^k(s)$$ (64)

and, when k is odd, then

$$I_{\text{s}}^k(s,\alpha )=2\pi \iota cos\left(k\left(\alpha +\frac{\pi }{2}\right)\right)H_{\text{c}}^k(s)+2\pi \iota sin\left(k\left(\alpha +\frac{\pi }{2}\right)\right)H_{\text{s}}^k(s).$$ (65)

Again, both (64) and (65) are real. However, note that (62) is a complex scalar multiple of (65). Scalar multiples of real values are unimportant, so we may combine these two into the single formula

$$I_1^k(s,\alpha )=\beta (k)\left(cos\left(k\left(\alpha +\frac{\pi }{2}\right)\right)H_{\text{c}}^k(s)+sin\left(k\left(\alpha +\frac{\pi }{2}\right)\right)H_{\text{s}}^k(s)\right)$$ (66)

where

$$\beta (k)=\frac{1}{2}(1+{(-1)}^k+\iota (1-{(-1)}^k)),$$ (67)

so that β(k) = 1 when k is even, and β(k) = ι when is odd. Similarly, (63) is a complex scalar multiple of (64), so we may combine these two into the single formula

$$I_2^k(s,\alpha )=\beta (k)\left(sin\left(k\left(\alpha +\frac{\pi }{2}\right)\right)H_{\text{c}}^k(s)-cos\left(k\left(\alpha +\frac{\pi }{2}\right)\right)H_{\text{s}}^k(s)\right).$$ (68)