Bacterial Tethering Analysis Reveals a “Run-Reverse-Turn” Mechanism for Pseudomonas Species Motility

Abstract

We have developed a program that can accurately analyze the dynamic properties of tethered bacterial cells. The program works especially well with cells that tend to give rise to unstable rotations, such as polar-flagellated bacteria. The program has two novel components. The first dynamically adjusts the center of the cell's rotational trajectories. The second applies piecewise linear approximation to the accumulated rotation curve to reduce noise and separate the motion of bacteria into phases. Thus, it can separate counterclockwise (CCW) and clockwise (CW) rotations distinctly and measure rotational speed accurately. Using this program, we analyzed the properties of tethered Pseudomonas aeruginosa and Pseudomonas putida cells for the first time. We found that the Pseudomonas flagellar motor spends equal time in both CCW and CW phases and that it rotates with the same speed in both phases. In addition, we discovered that the cell body can remain stationary for short periods of time, leading to the existence of a third phase of the flagellar motor which we call “pause.” In addition, P. aeruginosa cells adopt longer run lengths, fewer pause frequencies, and shorter pause durations as part of their chemotactic response. We propose that one purpose of the pause phase is to allow the cells to turn at a large angle, where we show that pause durations in free-swimming cells positively correlate with turn angle sizes. Taken together, our results suggest a new “run-reverse-turn” paradigm for polar-flagellated Pseudomonas motility that is different from the “run-and-tumble” paradigm established for peritrichous Escherichia coli.

INTRODUCTION

Flagellated bacteria swim in the aquatic environment by propelling their flagella (1). This swimming mechanism is best described in the Escherichia coli model, where the peritrichous cells are known to “run” and “tumble.” Flagella of a cell rotating counterclockwise (CCW) (when viewed from behind the cell) form a bundle that propels the cell to run forward, while a transient switch in the rotation direction of its flagellar motor causes the flagellar bundle to separate and the cell to tumble (2), allowing the cell to reorient its direction of motion.

In recent years, some other models have also been elucidated, including the three-step “run-reverse-flick” chemotactic response for the sodium-driven, monotrichous Vibrio alginolyticus (3, 4) and that of varying “run-and-stop” frequencies in monotrichous Rhodobacter sphaeroides (5, 6). The diversity of flagellar arrangements, flagellar motor structures (7), and chemotactic gene clusters (8) across the bacterial kingdom likely accounts for the presence of these different systems.

In the case of Pseudomonas spp., however, mechanisms of motility and chemotaxis remain unclear. Current evidence suggests that the chemosensory system and flagellar apparatus arrangement in the strains belonging to this genus are more complex than those of other bacterial species. For example, Pseudomonas aeruginosa has five gene clusters involved in chemotaxis, with 26 methyl-accepting chemotaxis proteins (MCPs) and 20 chemotaxis (che) genes, compared to E. coli, which has one gene cluster, with four MCPs and six che genes (9). Additionally, there are two sets of flagellar stators in Pseudomonas spp. compared to one set for E. coli and Salmonella enterica serovar Typhimurium (10, 11). As Pseudomonas spp. are polar flagellated, they are likely to possesses a “run-and-reverse” trajectory (12) rather than the typical “run-and-tumble” trajectory as well. Since both the Pseudomonas flagellar motor and chemosensory system present some unique features, it would therefore be interesting to study the motor dynamics of Pseudomonas spp. Notably, many members of this genus play significant roles in their environment, such as in the degradation of organic hydrocarbons, in plant growth promotion, and in nitrogen fixation. Other members, however, are pathogenic to humans, insects, or plants (13). Therefore, elucidating the motility and chemotactic mechanisms for Pseudomonas spp. can be beneficial in many studies extending to bioremediation and host-pathogen interactions. Additionally, across Pseudomonas spp., different species also exhibit dissimilar flagellar arrangements. In the plant growth-promoting rhizobium (PGPR) strain Pseudomonas putida, the flagellum is arranged in a polar multitrichous manner (14), whereas in the human pathogen P. aeruginosa, the flagellum is polar monotrichous (15). Hence, it would also be interesting to determine if there are differences in the role of each flagellum in contributing to Pseudomonas motility.

In order to study bacterial chemotaxis, various methods such as the capillary (16) and agar plate (17) assays have been previously developed to study the population movement in a macroscopic view. Tracking of a single bacterium (18) or a group of bacteria (19) in a three-dimensional environment has been used to study the response of a single bacterium to chemoattractants during swimming. As the flagellar motor is directly linked to this chemotactic response, one can study the rotation of the motor by fixing the cell body to a surface so as to observe the rotation of a bead attached to the flagella (20, 21). Alternatively, this can also be achieved by fixing (tethering) the flagella to a surface to observe the rotation of the cell body (22). The latter approach, also known as the cell-tethering method, is most widely used to study the response to stimuli of a large number of bacteria. It has been the key technique to quantitatively reveal the fundamental properties and mechanisms of E. coli chemotaxis by measuring tumbling frequency, run length, and kinetic response (23–25).

In this study, we have developed a program, which we call the bacterial tethering analysis program (BTAP), that can track large numbers of tethered cells and extract accurate and reliable rotation data. Our program dynamically adjusts the centers of the cell's rotational trajectories and applies piecewise linear approximation to the accumulated rotation curve to reduce noise and separate the motion of bacteria into phases. This is particularly useful for polar-flagellated bacteria, such as Pseudomonas spp., as they tend to give rise to unstable rotation trajectories (26). Using our program, we were therefore able to elucidate the flagellar motor properties of two Pseudomonas strains, KT2440 and PAO1, belonging to P. putida and P. aeruginosa, respectively. We show that, unlike E. coli, cells belonging to the two Pseudomonas strains spend equal amounts of time rotating in the counterclockwise (CCW) and clockwise (CW) directions. Interestingly, the Pseudomonas cells also have an additional “pause” phase that constitutes nearly 10% of the total observed time, and we propose that this pause phase allows the cells to vary their turn angle, adopting a “run-reverse-turn” trajectory. In addition, BTAP analysis of a cheY chemotaxis mutant in P. aeruginosa also revealed that Pseudomonas cells vary their run lengths, pause frequencies, and pause durations as part of their chemotactic response. By analyzing trajectories of free-swimming cells, we established a role for the pauses, where Pseudomonas cells vary their pause duration to effect different turn angle sizes.

MATERIALS AND METHODS

Growth condition.

Pseudomonas aeruginosa PAO1 wild-type and cheY cells (27) and Escherichia coli MG1655 cells from single colonies were separately cultured overnight in 10 ml Luria-Bertani (LB) broth at 37°C, 250 rpm. Cultures were diluted to an optical density at 600 nm (OD₆₀₀) of 0.1 using LB broth and grown at 37°C, 250 rpm, until the late-exponential growth phase was reached. For P. putida KT2440, cultures were grown at 30°C, 250 rpm. Cell cultures were then diluted 1:10 prior to imaging using video microscopy.

Cell tethering and video capture.

For cell-tethering assays, standard methods (22) were adapted as follows: glass coverslips were precoated with flagellar antibodies prior to use and cell chambers (2.0 cm by 1.0 cm by 150 μm) were created using three layers of double-sided tape between the microscope slide and coverslips. Flagella were sheared off by passing the bacterial cells through a 34-gauge blunt-end needle four times. Cells were loaded into the cell chamber, and nontethered cells were rinsed away using LB broth. Cells were visualized using an inverted microscope (Nikon TE2000U) under a 100× objective. Videos of tethered bacteria were taken at 120 frames per second (fps) for 1 to 5 min using a complementary metal-oxide semiconductor (CMOS) camera (Thorlabs; DCC1645). Following the convention, cells are considered to be rotating CW/CCW when viewed from the medium that they are tethered in (28). In the experiment with multitrichous P. putida, to eliminate the case where more than one filament is tethered and where the filaments do not rotate in synchrony, only cells that exhibited clear rotations were selected for analyses.

Free-swimming P. aeruginosa cells, with their intact flagellum, were loaded in cell chambers and observed in the middle of the chamber depth (away from the coverslip or microscope slide surface). Cells were visualized under a 40× objective, and videos of bacteria were taken at 25 fps. Bacterial swimming trajectories in two dimensions (2D) were captured using Image Pro Plus 6.3 (Media Cybernetics, Rockville, MD, USA), and images with cell outlines were obtained using ImageJ (NIH, Bethesda, MD, USA).

Pause detection for 2D swimming trajectories.

The instantaneous speed for free-swimming bacteria was calculated from the 2D trajectories frame by frame. Trajectories with fewer than 25 frames were discarded. A pause was identified when n (n > 3) consecutive instantaneous speeds that were below 5 μm/s appeared. The moving direction of a bacterium at a certain time was defined as the vector connecting its current coordinates to its subsequent coordinates. Accordingly, the change of angle was the angle difference between two such directions which ranged between −π and π. Additionally, to ensure that the cells swimming in the z direction did not affect the angle size tracked, only cells that were in focus, and thus swimming within the x-y focal plane, were selected for analysis.

Image extraction and data preprocessing for tethered cells.

For image processing, movies of single, tethered cells were converted to gray scale and their contrasts were adjusted (saturated pixels = 0.4, histogram stack) using ImageJ (NIH, Bethesda, MD, USA). The image of the rotating cell body was binarized to be isolated from the background for each frame in the video. Next, using the Set Measurements function in ImageJ, the coordinates of the center of mass of the rotating cell body were measured from the binarized image stack and imported into Matlab (Mathworks, Natick, MA, USA) for BTAP analyses.

RESULTS

Signal processing in BTAP.

BTAP is a code package in Matlab. BTAP has two essential components to reduce the noise from the video and separate the motion of the motor into phases. The first component of BTAP is to adjust for variations in the rotational axes of the moving trajectories of tethered cell bodies. For Pseudomonas spp., we noticed that the rotation of the tethered cell was not stable: i.e., the rotational trajectories of the cell bodies did not collapse onto a single circle but instead frequently collapsed as “clouds” (see Fig. 2B) or multiple partially overlapped circles (see inset in Fig. 3D). As this instability was not observed in tethered E. coli cells (Fig. 1B), it is likely due to the inherent location of the Pseudomonas flagellum at the cell pole, resulting in a rotating cell body that is able to vary its axis of rotation (Fig. 2F). It was, therefore, critical to adjust the axes of the rotational trajectories. If the instantaneous rotational speeds were translated directly from the positions of the cell body measured, and the rotational axes were not adjusted, large biases would be observed in data. Therefore, to perform this adjustment, we first denoted the centroid coordinates of each tethered cell at each video frame i as (x_i, y_i). To remove the impact of a changing axis on the rotational trajectory of the tethered cell, the location of the rotational axis (a_i, b_i) was identified. This was performed by fitting a circle to the trajectory as follow: a circle was fitted using the adjacent data points in the most recent 0.25 s of trajectories (30 points in our video samples taken at a frame rate of 120 fps) with the modified least-squared error method, which minimizes the sum of squared errors (SSE):

$$\mathrm{S}\mathrm{S}\mathrm{E}(a,b,r)=\sum _{i=n+15}^{i=n-15}{(r^2-{(x_i-a)}^2-{(y_i-b)}^2)}^2$$ (1)

Fig 2.

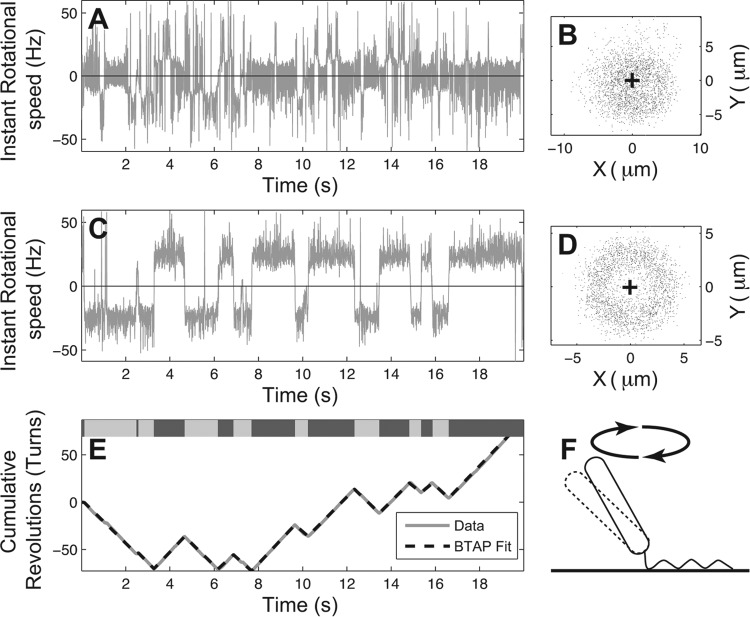
Rotation profile of a sample tethered Pseudomonas aeruginosa cell. (A and C) Instantaneous rotational speed of the tethered P. aeruginosa cell before and after BTAP adjustment, respectively. (B and D) The scattering of the centroid positions of the tethered cell before and after the BTAP adjustment, respectively. The cross indicates the assumed rotation axis. Note that the points do not fall into a smooth circle in panel B and require refitting. (E) Corresponding cumulative rotations (solid gray line) and the line fitted by BTAP algorithm (dashed black line). Top bar: labeling of rotational phases, where dark gray represents CW, light gray represents CCW, and white represents the pause phase. (F) Illustration of a tethered P. aeruginosa cell. The cell is tethered at an angle to the surface, and a small perturbation to the cell body (dashed line) largely changes its centroid positions as viewed from the top.

Fig 3.

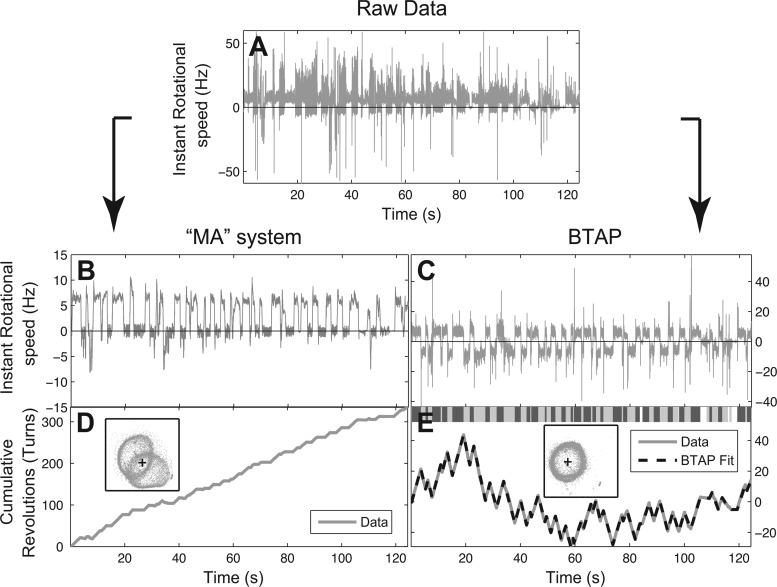
Comparison between a simple moving average system (MA) based on instant rotational speed (left panels) and BTAP (right panels). (A) Raw instantaneous rotational speed signal before MA and BTAP processing. (B) The moving average of the raw signal (without BTAP adjustment) using a window of 30 points by the MA system. (C) Raw signal after BTAP correction. (D) Cumulative revolution measured by MA. (E) Cumulative revolution and fitting measured by BTAP. Top bar: labeling of rotational phases where dark gray represents CW, light gray represents CCW, and white represents the pause phase. (Insets in panels D and E) The scattering of the centroid positions of the tethered cell. The cross indicates the assumed rotation axis. BTAP is able to refit the shifting centers of rotation in a polar-flagellated, tethered cell, in order to recover the true rotational behavior of the motor.

Fig 1.

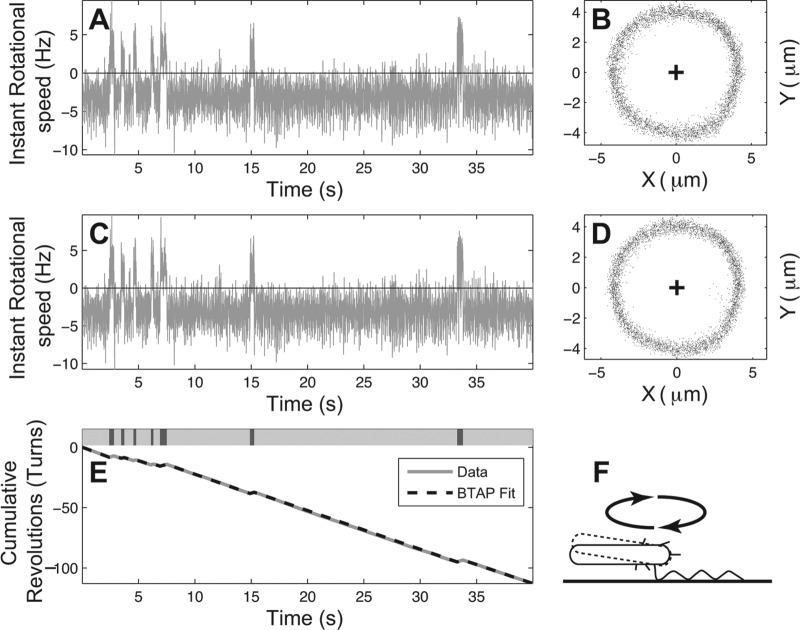
Rotation profile of a sample tethered Escherichia coli cell. (A and C) Instantaneous rotational speed of the tethered E. coli cell before and after BTAP adjustment, respectively. (B and D) The scattering of the centroid positions of the tethered cell before and after the BTAP adjustment, respectively. The cross indicates the assumed rotation axis. Note that the points fall into a smooth circle and do not require refitting. (E) Cumulative rotation of the same cell (solid gray line) and the line fitted by BTAP algorithm (dashed black line). Top bar: labeling of rotational phases, where dark gray represents CW, light gray represents CCW, and white represents the pause phase. CW and CCW phases can be clearly separated. (F) Illustration of a tethered E. coli cell. The cell is tethered parallel to the surface, and a small perturbation to the cell body (dashed line) does not change its centroid position by much as viewed from the top.

Here, x_i and y_i are coordinates of the cell body centroid at frame i and a, b, and r are the centroid coordinates and radius of the best-fitting circle, respectively. Next, the corresponding data point (x_i, y_i) was readjusted as (x_i − a, y_i − b).

The readjustment resulted in a more rounded scattering pattern for trajectories of the rotating cell body (Fig. 2D). Thus, the instantaneous rotational speeds were no longer subject to bias from the various positions of the rotation axis (Fig. 2A). In some cases, it was observed that the tethered cell body stopped rotating and the centroid oscillated near the same position, leading to a biased circle fitting. For these cases, if the radius of the fitted circle was smaller than a threshold (one-half of the global fitted circle), the center coordinates were reassigned to those of the global center of a circle (Fig. 2D, cross) fitted from all data points.

The second component of BTAP is translation of the readjusted rotational trajectories into the rotational angle θ_i = arctan (y_i/x_i) in order to measure the rotational speed (Fig. 2A). There are two considerations in this second component: to reduce the noise inherent in the rotations and to obtain the rotational phase (i.e., CCW or CW) of the motor. To accomplish these two tasks, we generated the cumulative rotations (CR) from the rotational angles of the cell bodies as $C{R}_i={\displaystyle {\sum }_{k=0}^i{\theta }_k}$ (Fig. 2E). This curve was then smoothed using a piecewise linear approximation algorithm, where the cumulative rotation curve was fitted with line segments. We used the greedy bottom-up approach (29) for the linear fitting. The curve was initially divided into many small segments, where each line segment connects only two adjacent data points. During each iteration, BTAP merges two neighboring line segments into a new segment if the benefit from the merge is the highest among all possible neighboring pairs. It reduces the computational time from O(n³) to O(n²) without any significant compromise in finding the best linear approximation. (i) The cumulative rotation curve is separated into N/2 segments (N equals total data points rounded down to even number), defined as seg_i (i = 1…N/2). So for each segment seg_i, it initially contains data points (x_{2i − 1}, y_{2i − 1}) and (x_2i, y_2i). (ii) For each iteration, two neighboring linear segments with the lowest merging cost are merged into one linear segment. The merging cost is defined as the increase of sum of squared errors (SSE) resulting from such merge: the SSE of the newly formed line segment minus the sum of SSE of the two neighboring segments before the merge. (iii) The greedy merge stops when the total number of segments reaches an arbitrary cut—in our case, this equals 4N/(frame rate).

A threshold was set at 0.5 Hz to distinguish the pause phase and rotation phases: any segment with its slope between −0.5 Hz and 0.5 Hz was considered pause; any segment with its slope higher than 0.5 Hz was considered CW; any segment with its slope lower than −0.5 Hz was considered CCW.

Speed analysis of peritrichous and monotrichous bacteria.

To determine the effectiveness of BTAP, we first applied it to peritrichous E. coli, which has been extensively studied using cell-tethering analyses (22, 25, 30). The scattering raw data of E. coli rotation follow an exact circle (Fig. 1B), which reflects the stable rotation of tethered E. coli. Because of this stability, BTAP does not drastically change the measured results (Fig. 1A and C and 1B and D). In order to reduce the noise from the instantaneous rotation speed (Fig. 1C), data were transformed into cumulative rotations, where the slopes of the curve indicate the rotational speeds (Fig. 1E). This resulted in rotational trajectories with clear rotation directions. It is also noteworthy that for each rotation phase (CCW or CW), the corresponding segment in the cumulative curve was very close to a straight line, indicating that for each phase the bacterium keeps a relatively constant rotation speed. These results agree with previous studies using tethered E. coli strains (31).

Next, we tested BTAP on the monotrichous P. aeruginosa tethered cells. Compared to E. coli, the rotation speed translated directly from the uncorrected coordinates appeared to have many pauses and fluctuations (Fig. 2A). The rotational trajectory of P. aeruginosa was also less stable (Fig. 2B). However, BTAP successfully resolved these. After BTAP correction, the high/low spike artifacts in the instantaneous speed (Fig. 2A) curve were eliminated and the true rotation of the cell was recovered, where coordinates fell into a clear circular shape (Fig. 2D), and the rotation speed also showed less noise (Fig. 2C). The readjustment, therefore, helped in representing the rotation phases in the cumulative speed curve precisely (Fig. 2E). This algorithm can, thus, separate the different rotational phases and calculate the average rotational speed for each rotation segment, yielding accurate statistics for the particular cell (Fig. 2E).

Comparison of BTAP with previous methods.

In a previous study, the moving average or weighted average method was used to reduce the noise in data of instantaneous rotational speed (5). To demonstrate the performance of BTAP, we therefore compared BTAP to a simple moving average (MA) system, which uses a 30-point moving average window to smooth the instantaneous speed. We saw that MA yielded results that were very noisy (Fig. 3B) compared with the data treated with BTAP (Fig. 3C). Although by applying the moving average one can get a smooth speed curve, it did not correct the systematic error rooted from the incorrect positioning of the rotational axis, as many of the speed time series were near zero (Fig. 3B). It was also difficult to differentiate the rotational phases (Fig. 3B and D) by using either instantaneous rotational speed or cumulative revolution curve from the MA system. However, using BTAP, cell phases that had been earlier incorrectly recognized to be in the pause phase were now identified to be in the CW rotation (Fig. 3C and E). The cumulative curve, therefore, had an increase in the CW/CCW contrast, allowing BTAP to accurately differentiate the CW/CCW/pause phases and mark the precise moment at which the motor switched its rotation direction (Fig. 3E, top bar). As a result, BTAP measured the tethering data with correction of the positions combined with noise reduction and could better capture the statistical properties of the P. aeruginosa flagellar motor.

BTAP reveals the P. aeruginosa and P. putida flagellar motor to function with an additional pause phase.

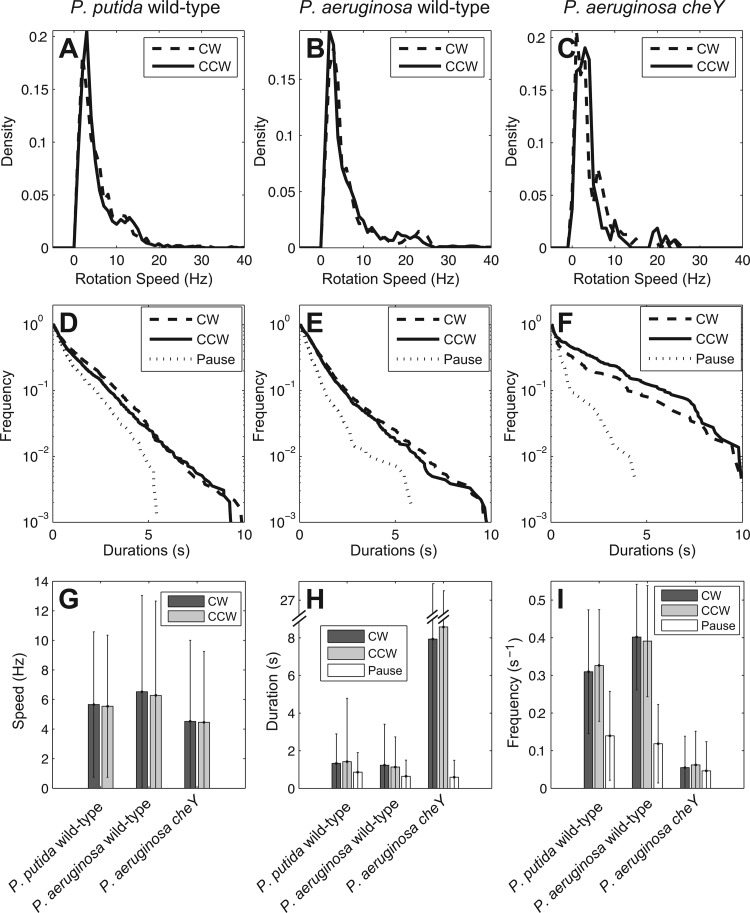
As the improved noise reduction and center adjustment system in BTAP allows for analyses of polar-flagellated bacteria, we next studied the flagellar motor function of Pseudomonas spp. in detail. First, in the analyses, we tracked the CCW and CW speed distribution of both P. aeruginosa and P. putida and showed that for the two strains, the speed distributions of both the CCW and CW rotation directions were symmetric to each other (Fig. 4A and B). In comparison of the two, P. aeruginosa had a speed distribution similar to that of P. putida (Fig. 4A and B), where the average speed was not significantly different either (Fig. 4G). In addition, the interval distributions for CCW/CW/pause followed an exponential distribution (Fig. 4D and E), with mean times of 1.30 s/1.15 s/0.85 s, respectively, for P. putida and 1.10 s/1.05 s/0.61 s, respectively, for P. aeruginosa (Fig. 4H). The average durations of CCW/CW/pause for P. aeruginosa were all lower than those for P. putida (Fig. 4D, E, and H) while the speed distribution (Fig. 4A and B) and average speed (Fig. 4G) were comparable, indicating that P. putida exhibits less switching frequency (Fig. 4I). Notably, the rotation speeds for both Pseudomonas strains (5 to 6 Hz, Fig. 6G) were also comparable to those previously reported for R. sphaeroides (∼5 Hz) and E. coli (4 to 9 Hz) under similar, unstimulated growth conditions (3, 31, 32). The interval distributions for E. coli were also exponentially distributed, but the mean time for CCW phase is considerably longer than that of CW phase (CCW/CW, 2.59 s/1.38 s, respectively). This is similar to previous reports for E. coli where the CW/CCW rotation interval of distribution was shown to follow an exponential distribution (30, 31).

Fig 4.

Speed distributions of Pseudomonas strains. (A to C) Rotational speed distributions of a P. putida (KT2440) strain and P. aeruginosa (PAO1) wild-type and cheY strains, respectively. (D to F) The corresponding cumulative distribution of interval durations from the strains in panels A to C, respectively. Solid lines denote CCW rotation; dashed lines denote CW rotation; dotted lines denote pauses. Note that the wild-type P. aeruginosa has longer pause durations than does the cheY mutant. (G, to I) The average speed, average duration of intervals, and occurrence frequency of phases for the strains in panels A to C, respectively. Error bars show standard deviations. Dark gray bars represent CW, light gray bars represent CCW, and white bars represent the pause phase. The frequencies for CW/CCW/pause in the cheY mutant were reduced compared to those for the wild type. Unlike the P. aeruginosa wild type, cheY mutants also have increased CCW and CW durations.

Fig 6.

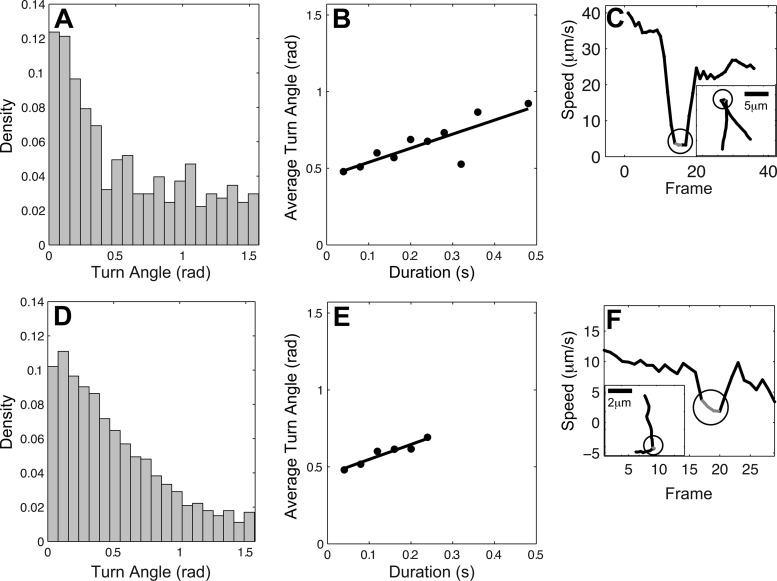
Pause durations are positively correlated with turn angles. (A and D) Distribution of the turn angles (change of direction) during pauses for P. aeruginosa wild-type and cheY strains, respectively. Angles between π/2 and π are subtracted from π as the change of cell body orientation during a pause followed by a reversal. The densities for both strains decrease as turn angles become larger. The pauses are defined when the moving speed of the cell is below 5 μm/s for at least 3 consecutive frames (frame rate = 25 fps). (B and E) The average turn angle sizes are positively correlated with pause durations. The line is a linear regression fitting of the data. The y value of each point is the average of all the turning angles at certain duration (x value). If the number of turn angles at a certain duration measured is less than two, the point will not be counted to avoid bias from data scarcity. (C and F) Speed of two sample cells from P. aeruginosa wild-type and cheY strains, respectively. The insets are their corresponding trajectories. The circles mark the section of pauses.

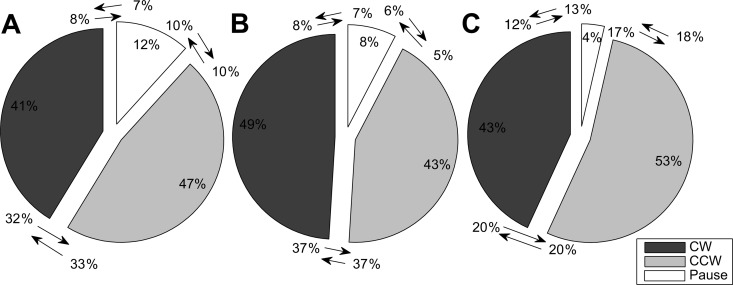
We observed that P. aeruginosa cells spent nearly equal durations of time during CW (43%) and CCW (49%) rotation and, in addition, a pause phase which consisted of 8% of the total time tracked (Fig. 5B). During this pause phase, the tethered cell body stopped rotating for a short time interval before it resumed motion. P. putida also exhibited three phases, CW (47%), CCW (41%), and pause (12%) (Fig. 5A). This rotational pattern is different from that exhibited by E. coli cells, where the total time spent in CCW phase in E. coli is 50% longer than that in CW phase and the total pause phase is short (6%) (31). There are three possible transitions for P. aeruginosa and P. putida: CW↔CCW, CW↔pause, and CCW↔pause. The transition probabilities between phases for the two strains were symmetric. For instance, in the CW↔CCW transition, the chances of switching from CW to CCW were similar (37% for P. aeruginosa and 32 to 33% for P. putida) to those for switching from CCW to CW. The transition between CW and CCW in E. coli was also shown to be symmetric (data not shown).

Fig 5.

Time spent on different phases. (A) Times spent in CW/CCW/pause phases for P. putida are 47%/41%/12%, respectively. (B) Times spent in CW/CCW/pause phases for P. aeruginosa PAO1 are 43%/49%/8%, respectively. (C) Times spent in CW/CCW/pause phases for P. aeruginosa cheY mutant are 43%/53%/4%, respectively. The transition probabilities between phases are shown as the arrows indicate. Dark gray represents CW, light gray represents CCW, and white represents the pause phase. Note the drastic decrease in time spent in pause frequency between P. aeruginosa cheY (4%) and wild-type (8%) strains.

Positive correlation of pause phase with turn angles reveals a novel run-reverse-turn mechanism.

It is noteworthy that although Pseudomonas cells pause at frequencies similar (0.12 to 0.14 Hz versus 0.16 Hz) to those of E. coli, the Pseudomonas cells spend a higher fraction of time pausing (8 to 12% versus 4.8%). While earlier reports for E. coli may have omitted this phase due to the shorter duration (33), the pause phase may be a genuine and unique feature of the bacterial flagellar motor, being particularly pronounced for the polar-flagellated Pseudomonas spp. In order to examine this phase further, we tested a cheY chemotaxis mutant of P. aeruginosa. The frequency of CW/CCW phases was lower than that for the wild-type P. aeruginosa PAO1 (0.05 s⁻¹ versus 0.4 s⁻¹) (Fig. 4I), and as expected, the duration for a CW/CCW phase was longer (∼ 8.0 s versus ∼1.5 s) (Fig. 4E, F, and H). However, in contrast, the duration of pauses did not increase as in the CW/CCW phase but decreased instead (Fig. 4E and F). This suggests that the run length of a cell and both the frequency and duration of a pause are regulated by CheY in P. aeruginosa. In addition, the cheY mutant has a suppressed CW rotation, such that the tethered cells spend slightly more time in CCW rotation phase (53% versus 43%) (Fig. 5C).

We propose that the pause phase allows the cell body to reorient and swim in a different direction, and we tested this by observing if the pause periods correlated with turn angles in trajectories of free-swimming P. aeruginosa cells (Fig. 6A and B). Speed analyses revealed that the speed of the free-swimming cells (∼5 to 40 μm/s) correlated with previous reports (∼40 μm/s) (10), and additionally, we noticed that cells also exhibited pauses in their trajectories. Notably, these cells that pause (Fig. 6C) also often turn at an angle (inset). In these examples, when cells are swimming, they often do so in a clear direction, but when cells enter the pause phase, the cell bodies appear to be reorienting their position, allowing the cells to change direction when they resume swimming. The level of reorienting can be defined as turn angles − angles of moving directions before and after pauses. As a bacterium may follow (run) or change (reverse) its moving status after a turn, the according turn angle by definition is θ and π − θ, respectively; the turn angles from population analyses of the trajectories are folded into the range of (0, π/2) (Fig. 6A). The average turn angle sizes are positively correlated with pause durations (Fig. 6B), and we hypothesize that this positive relation is due to the rotational diffusion. This positive correlation was also observed in cheY cells (Fig. 6D and E), although the overall pause durations were not as long as those in wild-type cells (Fig. 6B and E). Notably, the shorter pause durations in cheY free-swimming cells also correlated with the shorter pause durations of tethered cells than of wild-type cells.

DISCUSSION

Peritrichous bacteria such as E. coli have multiple flagella around their cell surface, while monotrichous bacteria such as P. aeruginosa have only one flagellum located at the pole. Therefore, in cell-tethering experiments, when the flagella of peritrichous bacteria are sheared off and one flagellum is tethered to the surface, the tethered flagellum stub is usually at the side of the cell body, such that the cell body is nearly parallel to the tethered surface, allowing a full rotation to be observed under the microscope (Fig. 1F). However, when polar-flagellated bacteria such as P. aeruginosa are tethered to the surface, the cell body is usually not parallel to the tethered surface (Fig. 2F), allowing the cell body to change its orientation easily because of the flexibility at the flagellar hook (34). This causes difficulty in the image analysis process, as the observed tethered cells no longer rotate in a circular trajectory but often shift around, giving rise to a noisy rotational signal.

Our new program, therefore, has several advantages (1). It reduces the position noise in the rotational tethered cell. Traditional methods translate only the centroid coordinate directly into the rotational phases, a process which is prone to error because, when the actual rotation axis is slightly deviated from the presumed axis, a rotating rod with constant radial speed will show a changing instantaneous rotational speed. By correcting the actual rotational axis, we are able to isolate the rotational data that best reflect the actual rotation of the motor from the experimental video (2). By measuring the accumulative revolution instead of instantaneous rotation, we can further reduce the rotational noise from the piecewise linear fitting. The previous method uses instantaneous speed to measure the rotation ω_i at frame i

$${\omega }_i=\frac{{\theta }_i-{\theta }_{i-1}}{t_i-t_{i-1}}$$ (2)

where θ_i is rotational angle at frame i and t_i is the corresponding time.

However, this approach results in a very noisy speed curve with a large variance. This is because tethered cells are not always rotating smoothly but exhibit fluctuations in speed within each rotation. In addition, the tethered cells in the fluidic environment are affected by other surrounding factors, such as hydrodynamic effects or Brownian force, causing the position of the cell body to have a large variance (35). The problem is more significant when the acquisition frame rate is high, such that an incidental large angle change θ_i − θ_{i − 1} between two frames can produce a spike in the instantaneous speed curve. This can be partially alleviated by introducing a (weighted) moving average window to smooth the data, but the size of the window is subjective and can have a huge impact on the result. Conversely, our approach uses the cumulative revolution to fit the curve with multiple linear segments. Although the instantaneous speed curve may be noisy and have many spikes, because the time intervals between two frames are small, the impact of such spikes on the cumulative curve would be small and thus not affect the rotation trend (the slope of the curve). These noises can be easily removed by a linear fitting in the cumulative curve (3). Through extracting the turning points on the cumulative curve, we could separate clearly the rotation phases of the tethered cell into clockwise, counterclockwise, and pause. This is difficult to achieve in the instantaneous curve because the moving average window will blur the boundary between different phases. As the smoothing result improves (i.e., the the window size increases), the ability for phase separation, in turn, weakens. However, using our approach, we were able to achieve both noise reduction and phase separation without sacrificing the accuracy of either.

As the cell-tethering experiment is one of the key techniques in quantifying the motor properties and its response in the chemotactic environment, it is important to enhance the accuracy of the data acquisition and analysis to reflect the change of motor phases in chemotaxis. Our new program, therefore, helps image processing and data analysis in research on monotrichous bacteria and gives credible results for subsequent studies.

We used our program to distinguish novel properties of the flagellar motor in Pseudomonas species, where we were able to study its flagellar rotation in a high-throughput manner for the first time. First, the Pseudomonas flagellar motor spends equal time in both CCW and CW rotations, which corroborates earlier reports for free-swimming cells, where trajectories adopt a run-and-reverse strategy (12). Additionally, speeds in the two directions are similar, suggesting that the flagellar motor is symmetric. Notably, we observed an additional pause phase, into which about 12 to 23% of cells in motion (either CCW or CW) will choose to transit. As there was a positive correlation between pause duration and turn angle sizes, our findings indicate that Pseudomonas can vary its pause duration in order to turn at different angles, resulting in a run-reverse-turn trajectory. This novel mechanism, therefore, allows the cell to swim and explore spaces more efficiently than would a typical run-and-reverse trajectory for polar-flagellated bacteria.

In polar-flagellated bacteria, cells have a limited degree of freedom in motility where they can swim only forward and backward. It appears now that there are diverse ways in which such types of bacterial cells can compensate for their limited, bidirectional movement. In the case of R. sphaeroides, cells adopt a run-and-stop motility (6) with variable speed (5), whereas in the sodium-driven V. alginolyticus, cells adopt a three-step run-reverse-flick chemotactic response (3, 4) instead. Here, in the case of Pseudomonas spp., we observe a run-reverse-turn trajectory for both monotrichous and multitrichous Pseudomonas cells. While earlier reports made brief references to these turns in free-swimming trajectories (12, 26), we have now shown that the additional pause phase in the flagellar motors allows the cells to turn at larger angles.

In addition, it is known that chemotaxis mutants of P. aeruginosa are motile but rarely change their swimming directions (36, 37). The question, therefore, arises whether the Pseudomonas chemotactic mechanism is similar to that of the peritrichous E. coli or whether the Pseudomonas motor employs a different response in general. We were able to elucidate this using BTAP, a chemotaxis mutant of P. aeruginosa, which has reduced CCW and CW frequency, and the durations in both CCW and CW directions are increased. Interestingly, there is a reduction in both the frequency and the duration of pauses as well. This suggests that the cells “turn” at a smaller angle, therefore, giving rise to trajectories that tend to be straight. Taken together, the Pseudomonas motor undergoes chemotaxis by varying its pause and switch frequencies and durations, resulting in cells that have longer runs and fewer turns. In comparison to other species, it is known that E. coli increases its run length through a decrease in switch frequency resulting in an increase in CCW rotation (28). In the case of P. aeruginosa, we show that unlike E. coli, run length is increased through a decrease in pause frequency and duration and an increase in both CW and CCW durations. In the case of the three-step run-reverse-flick V. alginolyticus, cells have decreased flicking frequency while retaining their turn angle sizes (4). Notably, while V. alginolyticus uses a flick to change its turn angle, we show here that P. aeruginosa adopts a pause mechanism to turn, and these turn angles are decreased as part of the chemotactic response. In the case of R. sphaeroides, a decrease in stop frequency was observed (38), which was a response similar to that observed in the cheY P. aeruginosa mutant. Therefore, in comparison to these three species, we show that while the details of the control of the flagellar motor differ, the outcomes of longer run lengths and reduced turn (or tumbling) frequency remain broadly conserved in P. aeruginosa. The Pseudomonas motor, therefore, adopts a combination of different properties in its chemotactic response, once again revealing the complexity of the Pseudomonas chemosensory system (9).