Geometric Metamorphosis

Abstract

Standard image registration methods do not account for changes in image appearance. Hence, metamorphosis approaches have been developed which jointly estimate a space deformation and a change in image appearance to construct a spatio-temporal trajectory smoothly transforming a source to a target image. For standard metamorphosis, geometric changes are not explicitly modeled. We propose a geometric metamorphosis formulation, which explains changes in image appearance by a global deformation, a deformation of a geometric model, and an image composition model. This work is motivated by the clinical challenge of predicting the long-term effects of traumatic brain injuries based on time-series images. This work is also applicable to the quantification of tumor progression (e.g., estimating its infiltrating and displacing components) and predicting chronic blood perfusion changes after stroke. We demonstrate the utility of the method using simulated data as well as scans from a clinical traumatic brain injury patient.

1 Introduction and Background

Image registration is based on structural similarity between a source and a target image. Similarity is often measured either by comparing image intensities directly or using indirect intensity measures like mutual information or cross correlation. However, for images with pathologies, assumptions of structural and intensity similarity may not hold.

In traumatic brain injury (TBI) cases, one clinical challenge is distinguishing permanent from transient changes in the brain in order to prescribe effective treatment and rehabilitation plans. Scans are acquired upon initial presentation in the clinic as well as after four to eight months (see Fig. 1). The geometry of the pathology, the deformation of the brain, and infiltration of the pathology into the brain change drastically between these scans. Determining the regions in which the infiltration has receded can be particularly useful in predicting long-term outcome. Similarly, in tumor cases, post-treatment assessment requires determination of changes in tumor geometry, tumor infiltration, scarring, and overall brain morphology. In stroke cases, there is a clinical need to predict chronic changes in blood perfusion from acute scans. In general, these cases are characterized by global tissue deformations, local changes in the geometry of a pathology, and local changes in the composition of the tissue and the pathology. We refer to these changes as “geometric metamorphosis.”

Fig. 1.

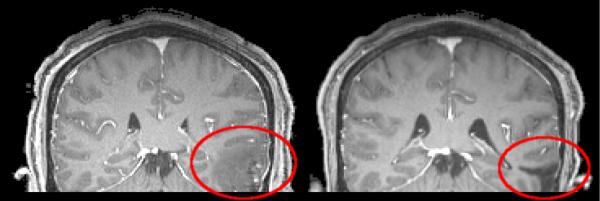
MP-RAGE, post-contrast MRI scans from TBI case. Left: Initial scan. Right: Eight months after initial scan. Rigidly registered. 1×1×1mm voxels.

While geometric metamorphosis changes may be tolerated by registration methods with low-dimensional image transformation models, direct application of a classical deformable registration method will likely produce unrealistic estimates of deformation. To address geometric metamorphosis changes, deformable registration approaches with weak and strong models of appearance change have been proposed. For example, methods having strong models of brain tumor mass effects and infiltration have been developed [4,7] and have been used to simulate tumors in atlas images to allow for spatial normalization of subjects with brain tumors [10]. While highly sophisticated, these methods are application-specific and rely on a good match of the tumor model to the observed tumor. On the other hand, image metamorphosis methods [9] use weak models to smoothly transform a source to a target image exactly. However, the transformations estimated by image metamorphosis do not explicitly model the deformation or composition of the pathologies and instead compromise between a globally smooth spatial transformation and the interpolation of image intensities along individual point trajectories. Hence, image metamorphosis models will have difficulty quantifying effects such as tumor infiltration or tissue recovery in stroke. Consider also that the approach proposed in this paper is, in spirit, related to the methods proposed in [5,8,2] in which areas that cannot be matched (because no correspondence exists) are masked out. However, in those methods registration results inside these masked-out areas are only driven by the spatial regularity terms of the deformable registration algorithms. Our method explicitly includes a deformable geometric model of the extent of the appearance change in order to capture pathology deformations in conjunction with underlying image deformations.

Sec. 2 discusses the geometric metamorphosis model. Its numerical solution method is discussed in Sec. 3. Results are presented in Sec. 5. The paper concludes with a summary and outlook on future work in Sec. 6.

2 Geometric Metamorphosis Model

Taking tumor growth as an example, changes in image appearance can be caused by a mixture of tissue deformation, tumor growth displacing healthy tissue, and tumor infiltration into healthy tissue. Tissue deformation and displacement due to tumor growth could be captured (between time-points) using a standard registration method⁶. However, infiltration does not imply spatial changes. A registration method should be able to distinguish image appearance changes arising from the composition of background deformations of the image and foreground deformations of an embedded geometric object, e.g., a tumor.

We model these transformations through a fluid-registration formulation. In large displacement diffeomorphic metric mapping (LDDMM) [6] one minimizes

$$E={\int }_0^1{\Vert v\Vert }_L^{2}dt+\frac{1}{{\sigma }^2}{\Vert I\left(1\right)-I_1\Vert }^2,\mathrm{s}.\mathrm{t}.I_t+\nabla I^{T}v=0;I\left(0\right)=I_0,$$

where v is a sought-for time-dependent velocity field which induces a spatial transformation warping the source image I₀ to the target image I₁. Typical LD-DMM formulations register from source I₀ to target I₁ on the time interval [0, 1], thus I(1) represents the warped source image. L is a differential operator (here, L = γ – α∇², α, γ > 0) controlling spatial regularity of v; σ > 0 controls the influence of the image match term. This is an inexact matching that only allows for the deformation of the source image I₀, but not for a change of its appearance. In order to explicitly model appearance changes, we augment this standard image registration model with an extra control to model foreground deformation of a geometric model (Sec. 2.1) which induces image changes through an image composition model (Sec. 2.2).

2.1 Deformation Model

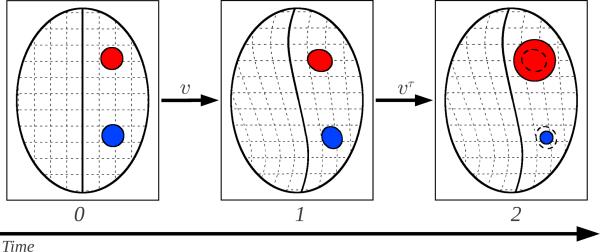
Fig. 2 illustrates the principle of the geometric metamorphosis model. Since we model geometric metamorphosis as the composition of background and foreground deformations, we introduce the (smooth) indicator functions T₁ and T₂ as models of the geometric object, T₁(x) and T₂(x) ∈ [0, 1]. We then register the background global deformation on time [0, 1] and the foreground geometry change on time (1, 2], solving for the time-dependent velocity fields v and v^τ, respectively. We define the geometric metamorphosis problem as the minimization of

$$E=(1-w){\int }_0^1{\Vert v\Vert }_L^{2}dt+w{\int }_1^2{\Vert v^{\tau }\Vert }_L^{2}dt+\frac{1}{{\sigma }_1^2}Sim(I^c(I_1,I^{\tau }\left(1\right),T_2),I^c(I\left(1\right),I^{\tau }\left(1\right),T_2))+\frac{1}{{\sigma }_2^2}Sim(I^{\tau }\left(2\right),T_2),\mathrm{s}.\mathrm{t}.I_t+\nabla I^{T}v=0;I\left(0\right)=I_0,\{\begin{array}{cc}{I}_t^{\tau }+\nabla {\left(I^{\tau }\right)}^{T}v=0,\hfill & I^{\tau }\left(0\right)=T_1,t\in [0,1],\hfill \\ I_t^{\tau }+\nabla {\left(I^{\tau }\right)}^T{v}^{\tau }=0,\hfill & t\in (1,2],\hfill \end{array}\phantom{\}}$$ (1)

where I^τ is the image of the geometric object and w ∈ (0, 1) controls the trade-off between background and foreground deformations. Note that the geometric model T₁ and its image I^τ are subject to both deformations, whereas the source image is only subjected to the background deformation. I^c(·, ·, ·) denotes the image composition model (see Sec. 2.2). Sim denotes a similarity measure of choice. For simplicity, we use the L² distance measure, Sim(I, J) = ∥I – J∥². Two similarity terms are used to assure matching of (i) the regions which correspond in both images and (ii) the geometric models.

Fig. 2.

Geometric Metamorphosis. An image is explained by a global deformation (via v) and a geometric model deformation (via v^τ). Corresponding structures in the source and target guide the estimation of v and v^τ addresses additional appearance differences at the pathology. To avoid faulty evaluation of image similarities, a suitable image composition method is required (Sec. 2.2). Regions which carry no matchable information are set to 0 in the image composition model. For a shrinking geometric model (blue) this region is specified by I^τ(1) (which already includes the background deformation) and for a growing geometric model (red) by T₂. Defining the composition model as Eq. 2 allows localized growing and shrinking simultaneously.

2.2 Image Composition Model

To accommodate local expansions and contractions of the geometric model affecting image appearance, the image composition model needs to preserve regions where the source and target image can be reliably matched. It needs to disregard areas where no matching image information can be found due to the shape change of the geometric model. The composition model

$$I^c(I,I^{\tau }\left(1\right),T_2)\left(x\right):=I\left(x\right)(1-I^{\tau }(1,x))(1-T_2\left(x\right)),$$ (2)

achieves this by zeroing out regions defined by the smoothed indicator functions I^τ(1) and T₂. Since this happens for both arguments of the similarity function in Eq. 1 the image match is effectively disregarded in these regions. This definition is reminiscent of cost function masking as for example used when registering images with and without lesions [2]. Here, we use regions in the source and target image to alter the energy function and estimate the regions which should be excluded in a joint optimization process. This allows for a combined estimation of foreground and background deformation.

3 Numerical Solution

We follow the solution method of [3] to solve the registration problem. To compute the optimality conditions, we add the dynamic constraints through the Lagrange multipliers λ and λ^τ. Note that λ^τ is allowed to be discontinuous at t = 1 due to the energy term depending on I^τ(1). After some computations we obtain the optimality conditions for t ∈ [0, 1)

$$\begin{array}{cc}\hfill 0& =2(1-w)L^{†}Lv+\lambda \nabla I+{\lambda }^{\tau }\nabla I^{\tau }\hfill \\ \hfill I_t+\nabla I^{T}v& =0,I\left(0\right)=I_0,\hfill \\ \hfill -{\lambda }_t-div\left(\lambda v\right)& =0,\lambda \left(1\right)=\frac{2}{{\sigma }_1^2}(I_1-I\left(1\right)){(1-T_2)}^2{(1-I^{\tau }\left(1\right))}^2,\hfill \\ \hfill I_t^{\tau }+\nabla {\left(I^{\tau }\right)}^{T}v& =0,I^{\tau }\left(0\right)=T_1,\hfill \\ \hfill -{\lambda }_t^{\tau }-div\left({\lambda }^{\tau }v\right)& =0,{\lambda }^{\tau }(1-)={\lambda }^{\tau }(1+)+\frac{2}{{\sigma }_1^2}{(I\left(1\right)-I_1)}^2(1-I^{\tau }\left(1\right)),\hfill \end{array}$$

and for t ∈ (1, 2]

$$\begin{array}{cc}\hfill 2w{L}^{†}L{v}^{\tau }+{\lambda }^{\tau }\nabla I^{\tau }& =0,\hfill \\ \hfill I_t^{\tau }+\nabla {\left(I^{\tau }\right)}^T{v}^{\tau }& =0,\hfill \\ \hfill -{\lambda }_t^{\tau }-div\left({\lambda }^{\tau }{v}^{\tau }\right)& =0,{\lambda }^{\tau }\left(2\right)=-\frac{2}{{\sigma }_2^2}(I^{\tau }\left(2\right)-T_2).\hfill \end{array}$$

The final conditions for λ and λ^τ in [0, 1) reflect the “don't care” areas of the registration: areas where T₂ = 1 or I^τ(1) = 1 are zeroed out. This is sensible, because the Lagrangian multipliers represent the image-matching error. We obtain a solution fulfilling the optimality conditions through the following adjoint solution method:

0) Initialize v, vτ to zero.

1) Solve It + ∇ITv = 0, I(0) = I0 and $I_{\tau }^t$, Iτ (0) = T1 forward in time in [0, 1].

2) Continue solving for Iτ for t ∈ (1, 2] but with velocity field vτ.

3) Compute the adjoint solution λ backward for t ∈ [0, 1].

4) Compute the adjoint solution λτ backward for t ∈ (1, 2].

5) Apply the jump condition to λτ at t =1.

6) Compute the adjoint solution λτ backward for t ∈ [0, 1).

5) Compute for every point and time-point the gradients

∇v (t)E = 2(1 – w)L† Lv + λ∇I + λτ∇Iτ, t ∈ [0, 1], ∇vτ (t)E = 2wL†Lvτ + λτ∇Iτ, t ∈ (1, 2].

6) Do a gradient descent step to update the velocities (using line search).

7) Repeat steps 1 - 6 until convergence.

4 Estimating Geometric Deformation

Once the foreground and background velocity fields v and v^τ have been estimated, they can be used to represent the geometric deformation modulo the background deformation. This allows for visualization and quantification, for example of tumor growth. Computing (backward in time) the mapping

$$-{\Phi }_t^r-D{\Phi }^{r}v=0,{\Phi }^r\left(1\right)=id,t\in [0,1]$$

where id is the identity map and D the Jacobian, shape change is computed as

$$S\left(0\right)=T_2\circ {\Phi }^r\left(0\right)-T_1,S\left(1\right)=T_2-I^{\tau }\left(1\right)$$

in the coordinate system of the source and the target image respectively. Here positive values indicate expansion and negative values contraction with respect to the source image.

5 Experimental Results

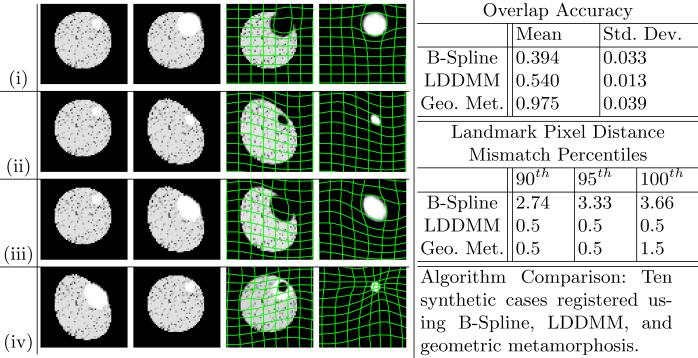
We test the geometric metamorphosis model on two sets of synthetic images, and a TBI image pair. The first synthetic set (Fig. 3) illustrates four different scenarios: (i) all change caused by infiltration, (ii) all change caused by global deformation, (iii) global deformation and local infiltration, and (iv) global deformation and local recession.

Fig. 3.

Synthetic Results. Each row, left to right: I₀, I₁, I(1) and global deformation, I^τ(2) and composite deformation. (i) Local infiltration. (ii) Image deformation. (iii) Image deformation and local infiltration. (iv) Image deformation and local recession.

The second synthetic set consists of ten different global and object warps applied to the same source image and geometric object. After registering, we compute the mean and standard deviation of the percent overlap for the geometric object as,

$$Overlap(T_2,I^{\tau }\left(2\right))=sum(\left(I_{\ge 0.5}^{\tau }\left(2\right)\right)\cap \left(T_{2,\ge 0.5}\right))∕sum\left(\left(T_{2,\ge 0.5}\right)\right),$$

where I_≥x is a binary mask of all pixels in I greater than or equal to x.

We also compute the background registration accuracy using six manually selected landmarks in the tissue region as ground truth. Landmark locations are calculated on the pixel grid and are accurate to +/− 0.5 pixels. We compare the results of our method against the B-Spline and LDDMM registration methods. Given the expected similar results in the regions of the image away from the geometric object we look at the extreme percentiles of the landmark distance mismatch values. Both LDDMM and geometric metamorphosis compute 95% of the landmarks to within 0.5 pixels of their correct location, but our method is able to achieve a significantly higher overlap accuracy (Fig. 3).

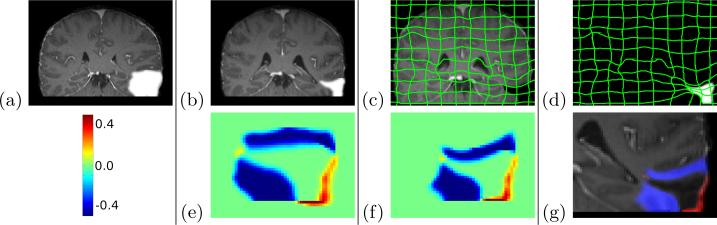
The TBI test case contains considerable deformation as well as object recession around the pathology site. To illustrate those changes, we provide manual segmentations of the pathology sites in both images (Fig. 4)⁷. Of clinical importance, Fig. 5 shows the progression of the pathology label map over the entire time solution interval [0,2].

Fig. 4.

TBI Results. Top: (a) Initial scan, T₁ overlaid. (b) Second scan, T₂ overlaid. (c) Image deformation and I(1). (d) Retraction area deformation and I^τ(2). Bottom: (e) S(0): Shape change in the source image coordinate frame (f) S(1): Shape change in the target image coordinate frame, (g) Incursion (red) and retraction (blue) in I₂.

Fig. 5.

TBI Pathology Label Map. Progression of TBI pathology label map on [0,2]. Red portion of each frame shows the change from the previous time point. Top: [0,1] Changes in global deformation. Bottom: (1,2] Changes in infiltration and recession.

6 Conclusions and Future Work

We proposed an image registration method allowing for background deformation of a source image, foreground deformation of a geometric object, and their composition to match a target image. The method can thereby account for processes causing images to change due to pathology infiltration/recession and image deformation. Since it makes minimal assumptions about the underlying change, it is generally applicable. We demonstrated its behavior for the registration of simulated data and traumatic brain injury cases. If desired, the registration framework can be augmented with an application-specific model, for example, of tumor growth, as in [4]. In future work we will investigate adaptations wherein a geometric model is only available in one of the two images and a transformed model either needs to be estimated from the image or does not exist, e.g., when registering a tumor patient to a healthy atlas. This work was sponsored in part by the following grants: NIH 1R01CA138419-01, NIH 1U54EB005149-01, NIH 1R01MH091645-01A1, NIH 2P41EB002025-26A1 and NSF EECS-0925875.