Abstract
Summary
Micro-finite element analysis applied to high-resolution (0.234-mm length scale) MRI reveals greater whole and cancellous bone stiffness, but not greater cortical bone stiffness, in the distal femur of female dancers compared to controls. Greater whole bone stiffness appears to be mediated by cancellous, rather than cortical bone adaptation.
Introduction
The purpose of this study was to compare bone mechanical competence (stiffness) in the distal femur of female dancers compared to healthy, relatively inactive female controls.
Methods
This study had institutional review board approval. We recruited nine female modern dancers (25.7± 5.8 years, 1.63±0.06 m, 57.1±4.6 kg) and ten relatively inactive, healthy female controls matched for age, height, and weight (32.1±4.8 years, 1.6±0.04 m, 55.8±5.9 kg). We scanned the distal femur using a 7-T MRI scanner and a three-dimensional fast low-angle shot sequence (TR/TE= 31 ms/5.1 ms, 0.234 mm×0.234 mm×1 mm, 80 slices). We applied micro-finite element analysis to 10-mm-thick volumes of interest at the distal femoral diaphysis, metaphysis, and epiphysis to compute stiffness and cross-sectional area of whole, cortical, and cancellous bone, as well as cortical thickness. We applied two-tailed t-tests and ANCOVA to compare groups.
Results
Dancers demonstrated greater whole and cancellous bone stiffness and cross-sectional area at all locations (p< 0.05). Cortical bone stiffness, cross-sectional area, and thickness did not differ between groups (>0.08). At all locations, the percent of intact whole bone stiffness for cortical bone alone was lower in dancers (p<0.05). Adjustment for cancellous bone cross-sectional area eliminated significant differences in whole bone stiffness between groups (p>0.07), but adjustment for cortical bone cross-sectional area did not (p<0.03).
Conclusions
Modern dancers have greater whole and cancellous bone stiffness in the distal femur compared to controls. Elevated whole bone stiffness in dancers may be mediated via cancellous, rather than cortical bone adaptation.
Keywords: 7 Tesla, Bone microarchitecture, Dancers, Micro-finite element analysis, MRI, Ultra high field
Introduction
Wolff’s Law states that bone adapts its shape and structure in response to the mechanical loads that it must endure [1]. This is well illustrated by the loss of bone mass observed in individuals who are challenged by low mechanical stress environments, such as astronauts living in microgravity [2–4] or patients who are immobilized after spinal cord injury [2, 5, 6]. It is also well illustrated by the improvements in bone density and structure observed in individuals who subject their bones to elevated mechanical stress via participation in sports including: soccer [7–9], gymnastics [10–12], fencing [13], triple jumping and sprinting [14, 15], speed skating [9, 16, 17], weightlifting [9, 15], and racket sports [18–20].
Bone strength is determined by its material composition, structure, geometry, and microarchitecture [21]. Noninvasive imaging modalities to assess these properties of bone in vivo are useful because they ultimately provide metrics or surrogate markers of bone strength or in essence, fracture resistance. Dual-energy X-ray absorptiometry (DEXA) allows assessment of areal bone mineral density, which reflects bone material composition and mass. However, because DEXA is a two-dimensional planar projection technique with low resolution, it cannot discriminate between cortical and cancellous bone compartments and cannot provide important information on bone structure, such as cross-sectional area. Quantitative computed tomography (CT) can depict bones in three-dimensions and thus allows discrimination and quantitative assessment of both cortical and cancellous bone compartments. However, it does not permit assessment of bone microarchitecture, which requires imaging with higher spatial resolution, (approximately 100–250 μm in-plane). Over the last decade, with the arrival of high-resolution peripheral quantitative CT (HRpQCT) scanners [22, 23] and the development of high-resolution, magnetic resonance imaging (MRI) techniques [24, 25], noninvasive assessment of bone microarchitecture in vivo has become possible. Numerous recent research and clinical studies have shown the value of these techniques in detecting bone microarchitectural changes in osteoporosis [23, 26–28] and in response to therapy [29, 30].
In parallel with the evolution in imaging technologies for noninvasive assessment of bone structure and microarchitecture in vivo, there has also been remarkable progress in the field of computational biomechanics [3, 31, 32]. Specifically, in recent years, high-resolution CT and MR images have been shown to be suitable for the generation of micro-finite element (μFE) models to estimate mechanical properties of bone, including bone stiffness, which is highly correlated with the ability of bone to resist fracture [23, 33, 34]. Beyond measurement of bone structure and morphology, estimation of bone mechanical properties in vivo may improve clinicians’ ability to assess fracture risk or the effects of interventions (such as altered mechanical environments) on the skeleton.
The goal of this study was to apply micro-finite element analysis (μFEA) to high-resolution MR images of bone microarchitecture and determine how whole, cortical, and cancellous bone stiffness in the distal femoral diaphysis, metaphysis, and epiphysis differ in a group of modern female dancers (n=9) compared to relatively inactive, healthy female controls (n=10) matched for age, height, and weight. We hypothesized that the dancers, because of the greater mechanical stimulation of their lower extremities due to participation in dance activity [35], would have greater whole, cortical, and cancellous bone stiffness at all three locations in the distal femur.
Methods
Subject recruitment
This study had institutional review board approval, and we obtained written informed consent from all subjects. The dancers were advanced pre-professional modern (contemporary) dance students at a school that specializes in the Limón technique and style of movement. This genre of dance involves flowing motions and changes of direction and some vertical jumping. The mean age, height, and weight of dancers were 25.7±5.8 years, 1.63±0.06 m, and 57.1±4.6 kg, respectively. The mean years of dance participation was 15.7± 6.1 years. The dancers participated in dance and training activities totaling approximately 20 h per week at the time of the study. We recruited relatively physically inactive, healthy female controls matched for age, height, and weight by placing ads around the university campus. The mean age, height, and weight for the female controls were 32.1±4.8 years, 1.6± 0.04 m, 55.8±5.9 kg, respectively. The controls did not participate in sports regularly; specifically, they were not involved in physical activities that involved weightlifting, jumping, running, or rapid changes of direction. They described their only physical activity as walking to and from class/work (less than 1 h total per day).
MRI scanning
The dominant lower extremity (the lower extremity used to kick a ball) of each subject was scanned on a whole-body 7-T MRI scanner (Siemens, Erlangen, Germany) from the level of the distal femoral diaphysis to the distal femoral articular surface using a 28 channel receive array coil (Quality Electrodynamics, Mayfield Village, Ohio). We used a three-dimensional (3D) fast low-angle shot sequence (TR/TE= 20 ms/5.1 ms, field of view=120 mm, matrix=512×512, in-plane voxel size=0.234 mm×0.234 mm, slice thickness= 1 mm, 80 axial images, parallel acceleration factor=2, acquisition time=7 min 9 s) to obtain images of bone microarchitecture as previously described [36]. The imaging parameters were chosen to reflect a balance between the need to obtain images with high resolution (which requires longer scan times) and the need to minimize patient discomfort and motion artifact (which increase with longer scan times). Kim et al. have shown that bone microarchitecture parameters derived from MR images can be preserved up to a resolution of 0.23 mm [37]. Furthermore, since trabeculae are oriented in the weight-bearing superoinferior direction, relaxation of through-plane voxel size to 1 mm should only have minor implications on the accuracy of bone microarchitectural measurements [25].
Image processing and generation of bone volume fraction map
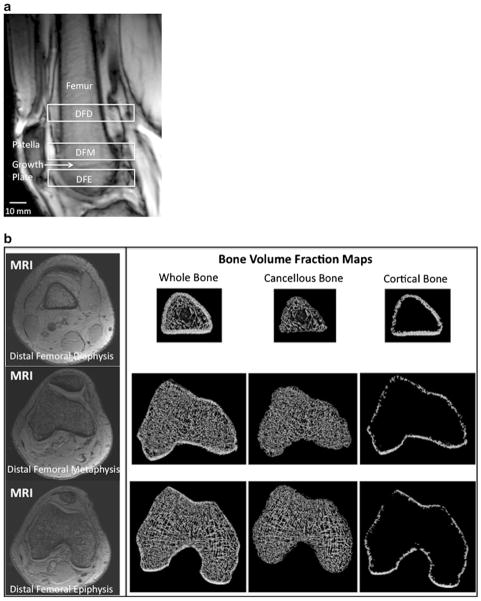
A musculoskeletal radiologist with dedicated knowledge of knee anatomy oversaw all image processing steps to ensure anatomical accuracy. We corrected all images for signal intensity inhomogeneity caused by MR coil shading using a local thresholding algorithm as previously described [38]. Furthermore, to ensure that the same relative locations were analyzed in each subject, we used anatomic landmarks (rather than absolute distance from the end-of-bone) to define the distal femoral diaphysis, metaphysis, and epiphysis (Fig. 1a). Specifically, we analyzed 10-mm-thick volumes of interest (VOIs) at the level of: the distal femoral diaphysis, with the inferior border of the VOI defined by the superior pole of the patella; the distal femoral metaphysis, with the inferior border of the VOI defined by the healed distal femoral growth plate; and the distal femoral epiphysis, with the superior border of the VOI defined by the healed distal femoral growth plate (Fig. 1a). The segmentation time per subject was approximately 15 min.
Fig. 1.
a Sagittal scout MR localizer image of the distal femur demonstrating the analysis locations for the 10-mm-thick volumes of interest (VOIs) at the distal femoral diaphysis (DFD), distal femoral metaphysis (DFM), and distal femoral epiphysis (DFE). These were defined anatomically by the superior pole of the patella (inferior margin of the DFD) and the healed growth plate (inferior margin of the DFM, superior margin of the DFE). b Representative axial MR images (left panel) at the distal femoral diaphysis (top row), distal femoral metaphysis (middle row), and distal femoral epiphysis (bottom row), and corresponding bone volume fraction maps of whole, cancellous, and cortical bone (right panel) from the same levels. In MR images of bone microarchitecture, trabeculae are represented by hypointense (dark) linear structures and marrow is hyperintense (white). For the bone volume fraction maps, MR images were inverted to create images with bone in white
For the ten slices composing each VOI at the distal femoral diaphysis, metaphysis, and epiphysis, we manually segmented the distal femur at the periosteal and endosteal boundaries to generate three datasets corresponding to whole bone, cortical bone, and cancellous bone regions (Fig. 1b). For each VOI, voxel signal intensities were linearly scaled from 0 to 100 with absolute marrow and absolute bone having minimum and maximum values, respectively [34]. This generated a 3D bone volume fraction (BVF) map, with each voxel within the BVF map representing the fractional occupancy of bone from the original MR image.
Micro-finite element analysis
We performed μFEA in the linear elastic regime to compute axial stiffness for each VOI [23, 29, 33, 34] by simulating compressive loading along the superoinferior direction [34, 38]. There is excellent correlation between MR-derived and reference standard high-resolution CT-derived (25 μm resolution) measurements of bone stiffness and bone microarchitecture [23, 34]. In brief, each voxel in the BVF map was converted into a hexahedral finite element with dimensions corresponding to the voxel size. Regarding element size, Jones and Wilcox state that there is healthy convergence for lower-resolution models; they found that element sizes of 2×2×2 mm3 appear sufficient, since error at that size is dominated by factors, such as load position, that are not improved increasing mesh-resolution [39, 40]. In addition, Crawford et al. showed that although there is an approximate 4 % difference in stiffness values calculated from low-resolution (3×3×3 mm3) and high-resolution (1×1× 1.5 mm3) finite element models, stiffness values derived from both models strongly correlate with experimentally measured stiffness values (R2≥0.92) and are suitable for cross-sectional studies [41].
The material properties of bone were chosen as isotropic and linearly elastic with Young’s modulus (YM) set to be linearly proportional to the BVF value such that YM= 15 GPa×BVF while the Poisson’s ratio was set at 0.3 for all elements [42]. Simulated compression was applied along bone’s longitudinal axis by applying a constant displacement (~1 % strain) to all finite element nodes in the proximal face of the finite element mesh while keeping those in the distal face constrained. The μFE system was solved to yield a 3D strain map for the whole bone section [33, 34]. Finally, the axial stiffness was obtained as the quotient of the applied strain on the proximal face and the resulting stress. The measurement reproducibility for μFEA of MR images of bone microarchitecture is excellent with coefficients of variation of less than 5 % [36, 43, 44].
Structural analysis
Using the same segmented VOIs at the distal femoral diaphysis, metaphysis, and epiphysis, we computed average whole, cortical, and cancellous bone cross-sectional area as the number bone-containing voxels multiplied by the voxel area in the image plane (0.0547 mm2) and divided by the number of slices in the VOI (ten slices). We also computed average cortical thickness for each VOI at the distal femoral diaphysis, metaphysis, and epiphysis. Specifically, average cortical thickness was calculated by modeling the endosteal and periosteal boundaries on each axial image as concentric circles whose radii were estimated from the respective encompassed areas [45].
Statistical analysis
We used SPSS 16.0 (Somers, New York) to perform two-tailed t-tests and analysis of covariance (ANCOVA) and compare parameters between groups (p<0.05 for statistical significance).
Results
Representative axial MR images from a dancer and a control at the distal femoral diaphysis, metaphysis, and epiphysis are shown in Fig. 2a–c. At the distal femoral diaphysis, metaphysis, and epiphysis, the dancers demonstrated 12.4 % (p=0.047), 16.9 % (p=0.002), and 8.2 % (p= 0.009) greater whole bone stiffness and 23.8 % (p=0.021), 16.9 % (p=0.029), and 11.7 % (p=0.004) greater cancellous bone stiffness compared to the controls (Table 1). At all three locations, differences in cortical bone stiffness between dancers and controls (−8.5 % at the distal femoral diaphysis, −21.1 % at the distal femoral metaphysis, −4.1 % at the distal femoral epiphysis) were not statistically significant (p>0.15 for all, Table 1).
Fig. 2.
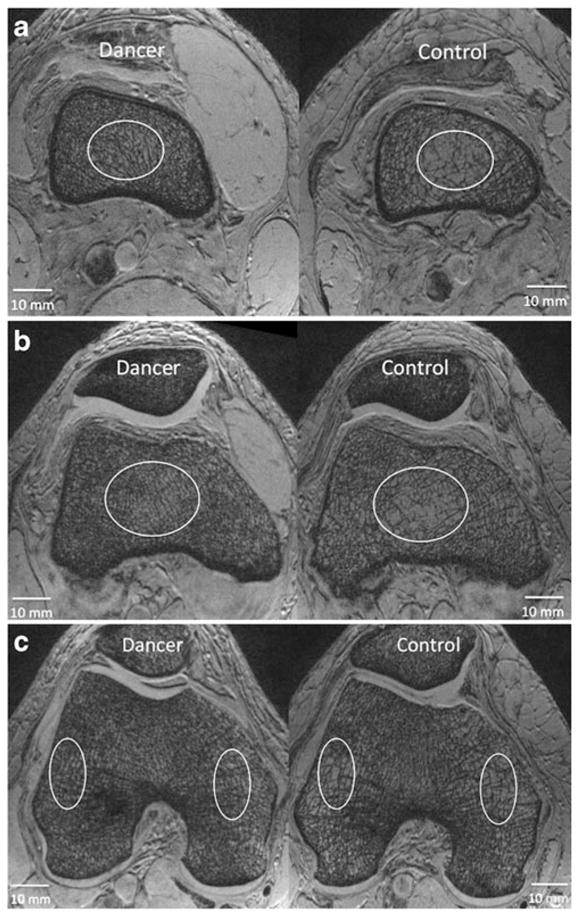
a Representative axial 7-T MR images from a dancer and a control at the level of the distal femoral diaphysis demonstrating differences in bone microarchitecture. In MR images of bone microarchitecture, trabeculae are represented by hypointense (dark) linear structures and marrow is hyperintense (white). More trabeculae are visualized in the dancer than in the control. Ovals are only placed to highlight areas with prominent differences; the entire cancellous bone compartment was analyzed to determine cancellous bone stiffness and cross-sectional area. b Representative axial 7-T MR images from a dancer and a control at the level of the distal femoral metaphysis demonstrating differences in bone microarhcitecture. In MR images of bone microarchitecture, trabeculae are represented by hypointense (dark) linear structures and marrow is hyperintense (white). More trabeculae are visualized in the dancer than in the control. Ovals are only placed to highlight areas with prominent differences; the entire cancellous bone compartment was analyzed to determine cancellous bone stiffness and cross-sectional area. c Representative axial 7-T MR images from a dancer and a control at the level of the distal femoral epiphysis demonstrating differences in bone microarhcitecture. In MR images of bone microarchitecture, trabeculae are represented by hypo-intense (dark) linear structures and marrow is hyperintense (white). More trabeculae are visualized in the dancer than in the control. Ovals are only placed to highlight areas with prominent differences; the entire cancellous bone compartment was analyzed to determine cancellous bone stiffness and cross-sectional area
Table 1.
Comparison of whole, cortical, and cancellous bone stiffness at the distal femoral diaphysis, metaphysis, and epiphysis in dancers versus healthy, relatively inactive controls
| Stiffness (kN/mm) | Dancers mean | Dancers standard deviation | Controls mean | Controls standard deviation | p value |
|---|---|---|---|---|---|
| Distal femoral diaphysis | |||||
| Whole | 481 | ±63.9 | 428 | ±43.7 | 0.047 |
| Cortical | 150 | ±18.5 | 164 | ±19.8 | 0.14 |
| Cancellous | 260 | ±42.8 | 210 | ±43.3 | 0.021 |
| Distal femoral metaphysis | |||||
| Whole | 849 | ±80.9 | 726 | ±70.7 | 0.0024 |
| Cortical | 65 | ±40.6 | 83 | ±42.1 | 0.59 |
| Cancellous | 635 | ±86.1 | 543 | ±83.8 | 0.029 |
| Distal femoral epiphysis | |||||
| Whole | 1,212 | ±40.7 | 1,120 | ±85.4 | 0.0091 |
| Cortical | 183 | ±25.8 | 191 | ±23.3 | 0.49 |
| Cancellous | 907 | ±47.8 | 812 | ±75.4 | 0.0047 |
At each location, we also evaluated the percent normalized stiffness for cortical bone and cancellous bone (ratio of segmented cortical stiffness to whole bone stiffness; ratio of segmented cancellous bone stiffness to whole bone stiffness). As described by Eswaran et al., this can be thought of as the percent of intact whole bone stiffness with a cortical bone-only model or a cancellous bone-only model [46]. At the distal femoral diaphysis, metaphysis, and epiphysis, the percent normalized stiffness for cortical bone in dancers/controls was 31.2 %/38.3 %, 10.1 %/18.2 %, and 15.1 %/23.6 %, respectively (Table 2). In all locations, these percentages were less in the dancers compared to controls (p=0.0003, p=0.002, p=0.000003, respectively). At the distal femoral diaphysis, metaphysis, and epiphysis, the percent normalized stiffness for cancellous bone in dancers/controls was 53.9 %/48.8 %, 74.7 %/74.5 %, and 74.8 %/72.5 %. In all locations, the percentages were greater in the dancer group compared to the control group, but this was only statistically significant at the distal femoral diaphysis (p=0.049, Table 2).
Table 2.
Comparison of percent normalized stiffness for cortical bone-only or cancellous bone-only (i.e., percent of intact whole bone stiffness for cortical bone alone (cancellous bone removal) or for cancellous bone alone (cortical bone removal)) at the distal femoral diaphysis, metaphysis, and epiphysis in dancers versus healthy, relatively inactive controls
| % normalized stiffness | Dancers mean | Dancers standard deviation | Controls mean | Controls standard deviation | p value |
|---|---|---|---|---|---|
| Distal femoral diaphysis | |||||
| Cortical | 31.2 | ±2.4 | 38.3 | ±3.9 | 0.003 |
| Cancellous | 53.9 | ±3.0 | 48.8 | ±6.7 | 0.049 |
| Distal femoral metaphysis | |||||
| Cortical | 10.1 | ±5.0 | 18.2 | ±8.9 | 0.0025 |
| Cancellous | 74.7 | ±7.0 | 74.5 | ±5.8 | 0.94 |
| Distal femoral epiphysis | |||||
| Cortical | 15.1 | ±1.9 | 23.6 | ±3.3 | 0.000003 |
| Cancellous | 74.8 | ±2.4 | 72.5 | ±5.1 | 0.24 |
At the distal femoral diaphysis, metaphysis, and epiphysis, the dancers demonstrated greater whole (p=0.01, p=0.002, p=0.03, respectively) and cancellous (p=0.008, p=0.002, p=0.04, respectively) bone cross-sectional area compared to the controls (Table 3), but there were no significant differences in cortical bone cross-sectional area between groups (p>0.15 for all, Table 3).
Table 3.
Comparison of whole, cortical, and cancellous bone cross-sectional area (mm2) at the distal femoral diaphysis, metaphysis, and epiphysis in dancers versus healthy, relatively inactive controls
| Cross-sectional area (mm2) | Dancers mean | Dancers standard deviation | Controls mean | Controls standard deviation | p value |
|---|---|---|---|---|---|
| Distal femoral diaphysis | |||||
| Whole | 1,143 | ±144 | 978 | ±105 | 0.01 |
| Cortical | 198 | ±16 | 193 | ±13 | 0.44 |
| Cancellous | 945 | ±132 | 785 | ±102 | 0.0085 |
| Distal femoral metaphysis | |||||
| Whole | 2,535 | ±197 | 2,165 | ±258 | 0.0028 |
| Cortical | 215 | ±14 | 204 | ±18 | 0.15 |
| Cancellous | 2,320 | ±194 | 1,961 | ±244 | 0.0026 |
| Distal femoral epiphysis | |||||
| Whole | 3,037 | ±164 | 2,832 | ±217 | 0.034 |
| Cortical | 271 | ±21 | 262 | ±17 | 0.32 |
| Cancellous | 2,766 | ±169 | 2,569 | ±214 | 0.041 |
To determine whether the greater bone stiffness in dancers compared to controls was mediated by greater bone cross-sectional area, we performed ANCOVA, adjusting for differences in bone cross-sectional area between groups (Table 4). For whole bone stiffness, at the distal femoral diaphysis, metaphysis, and epiphysis, there were no longer any significant differences between dancers and controls after adjusting for whole bone cross-sectional area (p>0.09 for all) or cancellous bone cross-sectional area (p>0.07 for all). In contrast, at all three locations, after adjusting for cortical bone cross-sectional area, the greater whole bone stiffness of dancers compared to controls remained statistically significant (p<0.03 for all). For cancellous bone stiffness, there were no longer any significant differences between groups after adjusting for cancellous bone cross-sectional area (p>0.05 for all). And finally, for cortical bone stiffness, at the distal femoral diaphysis only, a significant difference arose between dancers and controls, after adjusting for cortical bone cross-sectional area (dancers 8.5 % less than controls, p<0.01).
Table 4.
p values for comparison of stiffness in dancers versus healthy, relatively inactive controls, after adjusting for whole, cortical, and cancellous bone cross-sectional area using analysis of covariance (ANCOVA)
| P values ANCOVA (Adjusting for bone area) | Whole bone stiffness | Cortical bone stiffness | Cancellous bone stiffness |
|---|---|---|---|
| Distal femoral diaphysis | |||
| Whole area | 0.69 | – | – |
| Cortical area | 0.02 | 0.0083 | – |
| Cancellous area | 0.64 | – | 0.53 |
| Distal femoral metaphysis | |||
| Whole area | 0.17 | – | – |
| Cortical area | 0.0071 | 0.27 | – |
| Cancellous area | 0.17 | – | 0.92 |
| Distal femoral epiphysis | |||
| Whole area | 0.092 | – | – |
| Cortical area | 0.013 | 0.09 | – |
| Cancellous area | 0.072 | – | 0.054 |
After adjusting for cortical bone cross-sectional area, the greater whole bone stiffness in dancers compared to controls remained significant; in contrast, after adjusting for cancellous bone cross-sectional area, this difference was no longer significant
At all locations, there were no significant differences in cortical bone thickness (p>0.08 for all, Table 5) or bone volume fraction within the cancellous compartment between groups (p>0.41 for all, Table 6).
Table 5.
Comparison of average cortical thickness at the distal femoral diaphysis, metaphysis, and epiphysis in dancers versus healthy, relatively inactive controls
| Cortical thickness (mm) | Dancers mean | Dancers standard deviation | Controls mean | Controls standard deviation | p value |
|---|---|---|---|---|---|
| Distal femoral diaphysis | 1.73 | ±0.092 | 1.84 | ±0.15 | 0.084 |
| Distal femoral metaphysis | 1.23 | ±0.086 | 1.26 | ±0.067 | 0.32 |
| Distal femoral epiphysis | 1.42 | ±0.12 | 1.42 | ±0.09 | 0.93 |
Table 6.
Comparison of bone volume fraction within the cancellous compartment at the distal femoral diaphysis, metaphysis, and epiphysis in dancers versus healthy, relatively inactive controls
| Bone volume fraction | Dancers mean | Dancers standard deviation | Controls mean | Controls standard deviation | p value |
|---|---|---|---|---|---|
| Distal femoral diaphysis | 0.21 | ±0.014 | 0.20 | ±0.017 | 0.42 |
| Distal femoral metaphysis | 0.21 | ±0.0083 | 0.21 | ±0.0093 | 0.93 |
| Distal femoral epiphysis | 0.22 | ±0.0061 | 0.22 | ±0.0061 | 0.48 |
Discussion
We have applied μFEA to high-resolution MR images of bone microarchitecture to assess whole, cortical, and cancellous bone stiffness at the distal femoral diaphysis, metaphysis, and epiphysis in female dancers compared to relatively physically inactive, healthy female controls matched for age, height, and weight. At all three locations in the distal femur, the dancers had greater whole and cancellous bone stiffness and greater whole and cancellous bone cross-sectional area compared to the controls. This greater whole bone stiffness in the dancers appears to have been mediated by changes in the cancellous compartment, rather than cortical compartment. Specifically, after adjusting for cancellous bone cross-sectional area, there was no longer a significant difference in whole bone stiffness between groups, but after adjusting for cortical bone cross-sectional area, a significant difference in whole bone stiffness remained. In keeping with this finding (that alterations in the cancellous compartment mediated improvements in whole bone stiffness), at the distal femoral diaphysis, metaphysis, and epiphysis, the percent of whole bone stiffness remaining after cancellous bone compartment removal was lower in the dancers compared to the controls. Overall, the results suggest that participation in long-term dance activity may promote improvement in bone mechanical competence near the end-of-bone and that this improvement in bone mechanical competence, as assessed at a length scale of approximately ~0.23 mm, may be mediated by adaptation in cancellous bone, rather than cortical bone.
Ideally, we would have imaged bone microarchitecture of the proximal femur, which is a common site of fragility fracture. However, with the current level of MRI coil (antenna) technology, it is challenging to produce images bone microarchitecture of the femoral neck with high enough quality to perform 3D image analysis, such as μFEA. In 2005, Krug et al. imaged the femoral neck in the coronal plane via MRI, but concluded that only a 2D textural analysis of trabeculae was possible [47]. The main obstacle is that at the level of the hip, the MRI coil is separated from the femoral neck by several centimeters of skin, subcutaneous fat, muscle; as the distance between the MRI coil and object of interest increases, there are exponential losses in coil sensitivity, which result in lower image quality and signal-to-noise ratio (SNR). We chose to analyze the distal femur because this was an anatomic location as close as possible to the femoral neck that we could scan with enough SNR to produce high-quality images of bone microarchitecture suitable for μFEA. With improvements in MRI coil technology for the pelvis (e.g., multichannel coils, such as the new 28-channel knee coil used in this study), we expect that imaging of bone microarchitecture of the hip will eventually become feasible. Indeed when high-resolution MRI of bone microarchitecture was first described in the late 1990s [48, 49], it was performed on the distal radius and distal tibia, the most easily accessible anatomic sites.
Numerous previous studies have investigated adaptations in bone density, macrostructure and geometry in athletes from a variety of sports compared to matched controls. The sports studied include, but are not limited to: soccer [7–9], gymnastics [10–12], fencing [13], triple jumping and sprinting [14, 15], speed skating [9, 16, 17], weightlifting [9, 15], and racket sports [18–20]. In general, high-impact sports (e.g., jumping, hurdling) and odd-impact sports (e.g., squash, soccer, speedskating, where forces on bone are elevated due to lateral acceleration/deceleration, rather than vertical loading) are associated with greater bone mineral density and improved bone macrostructure and geometry. Furthermore, the types and locations of skeletal adaptations appear to be sports-specific, probably due to typical mechanical loading patterns that are associated with each sport [15]. Indeed, these findings are all supportive of Wolff’s Law, which states that bone adapts in response to the mechanical loads that it must endure.
To our best knowledge, only two previous studies have used high-resolution imaging techniques to quantitatively assess bone microarchitecture in athletes compared to matched controls. Modlesky et al. used high-resolution 1.5-T MRI to assess bone microarchitecture in the proximal tibia of female collegiate gymnasts compared to matched controls. The authors found improvements in gymnasts’ bone microarchitecture manifested by increased apparent trabecular number and decreased apparent trabecular separation [50]. Chang et al. used high-resolution 7-T MRI to assess bone microarchitecture in the distal femur and proximal tibia in members of the U.S. Olympic Fencing Team compared to matched controls [51]. Similarly, apparent trabecular number was increased and apparent trabecular separation was decreased in the athletes compared to the controls. The authors also found that markers for trabecular plate-to-rod ratio and trabecular network connectivity were also increased in the fencers. To our best knowledge, this current study in dancers is the first to apply μFEA to images of bone microarchitecture in order to assess bone mechanical competence in vivo in athletes compared to controls.
It is challenging, but not impossible to perform direct mechanical testing of bones in vivo to assess their mechanical properties. Researchers have recently described the use of a microindentation device that can be used during a minimally invasive procedure to directly test the mechanical properties of bone in subjects with osteoporosis [52]. However, μFEA represents a powerful tool to estimate the mechanical properties of bone noninvasively and in vivo. The great interest in μFEA as a tool to assess bone is illustrated by the large number of recent in vivo studies applying μFEA to high-resolution MR images or HRpQCT images to detect alterations in bone mechanical properties in subjects with osteoporosis [23, 26–28], renal disease [45], diabetes [53], or following treatment with antifracture medications [29, 30].
The dancers in this study participated in modern (or contemporary) dance, specifically Limón technique. Their specialty, abstract modern dance, involves flowing movements and changes of direction facilitated by the force of gravity, without the frequent maximal, vertical jumping as in ballet. However, it should also be noted that the dancers had an average number of years of experience of 15.7±6.1 years (including other forms of dance) and were training approximately 20 h per week at the time of the study. It remains to be determined whether such skeletal adaptations could occur in individuals who begin participation in dance after adolescence or whether such adaptations could occur in individuals who participate less frequently and for a fewer number of years.
We found that whole bone stiffness was always greater than the numerical sum of cortical bone stiffness and cancellous bone stiffness. This is not due to artifact, as whole bone cross-sectional area (calculated from the same segmented VOI used for the μFEA) at each location was always equal to the numerical sum of cortical bone and cancellous bone cross-sectional areas. Eswaran et al. previously described this result in an ex vivo microCT study of vertebral bodies [46]. In this study, the authors found that cortical bone alone had a stiffness of 9±6 % of intact whole vertebral body stiffness. However, with cortical bone removal (cancellous bone compartment alone), there was a 52 %±9 % reduction in whole bone stiffness, a direct consequence of unloading of peripheral trabeculae. Our results are consistent with those of Eswaran, who demonstrated that cortical and cancellous bone synergistically increase whole bone strength when they act in concert as one unit.
The results of this study also provide evidence that in the dancer group, greater whole bone stiffness was mediated via adaptation in the cancellous compartment, rather than in cortical bone, at least at the length scale of 0.234 mm in this study. First, we found that in the dancers, the percent of intact whole bone stiffness for cortical bone alone (i.e., percent of whole bone stiffness remaining after cancellous bone removal) was significantly lower than corresponding values in the controls (10.1±5.0–31.2±2.4 % in dancers at the distal femoral diaphysis, metaphysis, and epiphysis versus 18.2±8.9–38.3±3.9 % in controls, p<0.05 for all). Second, we also found that adjustment for cancellous bone cross-sectional area eliminated the significant differences in whole bone stiffness between dancers and controls, whereas adjustment for cortical bone cross-sectional area did not. These results do not diminish the importance of cortical bone, but suggest that near the end-of-bone, which is a cancellous-abundant location, adaptations to mechanical loading (at a length scale of 0.234 mm) appear to be mediated through the cancellous compartment.
This study has limitations. First, as a cross-sectional study, there is the possibility of selection bias. Individuals with larger or stronger bones may be more likely to participate in long-term dance activity because they are able to withstand the physical demands of the sport. Second, there are a low number of study subjects. It is possible that if we scanned more subjects, we would have enough statistical power to detect differences in cortical bone structure and stiffness between the two groups. For example, at the distal femoral epiphysis, where cortical bone stiffness was 183± 25.8 kN/mm in the dancers and 191±23.3 kN/mm in the controls, 67 total subjects would have been required to demonstrate that this difference between groups was statistically significant (for a significance level of 0.05 and test power of 0.80). At the distal femoral metaphysis, where cortical bone thickness was 1.23±0.086 mm in dancers and 1.26±0.067 mm in controls, 71 total subjects would have been needed to demonstrate that this difference was significant. Related to the low number of study subjects, it is also possible that a type I error could be committed if there are outlier values (non-normal distribution) within the small samples. When the results are also re-analyzed by a Mann–Whitney test (non-parametric test, which does not rely on normally distributed data), in only one case (cancellous bone cross-sectional area at the distal femoral epiphysis), does a statistically significant result (p<0.05) become non-significant (p<0.07). Therefore, outlier values are not responsible for the significant differences in bone stiffness that we observe between groups, and we believe that our conclusions are reasonable.
A third limitation of this study is that the image voxel size (0.234 mm×0.234 mm×1 mm) in this study is larger than that of microCT studies. Therefore, it is possible that our inability to detect differences in cortical bone structure and stiffness between groups is due to this larger voxel size. However, as mentioned above in the “Methods” section, Crawford et al. concluded that low-resolution finite element models (up to 3×3×3 mm3) are suitable for cross-sectional studies, since population variation in stiffness is greater than variation in stiffness that could be stem from differences in voxel/element sizes [41]. Fourth, due to logistical reasons and time constraints, we could not assess bone mineral density or the mid-diaphysis in the dancers and controls. Greater bone mineral density [15] and greater cortical bone thickness and cortical bone cross-sectional area [13, 54] have been demonstrated in athletes from a variety of sports. It is certainly possible that similar increases in bone mineral density or adaptations in bone geometry at the mid-diaphysis were present in dancers in this study. Finally, we have only provided bone volume fraction results and did not compute bone microarchitectural parameters, which requires special software that is not commercially sold and is only available in a few research laboratories. The higher cancellous bone stiffness in the dancers in this study is presumably due to alterations in bone microarchitectural parameters (i.e., increased trabecular number, connectivity; decreased trabecular separation). We are currently pursuing a collaboration with a laboratory with expertise in bone microarchitecture image analysis in order to address this important question.
In conclusion, we have applied μFEA to MR images of bone microarchitecture and determined that female dancers have greater whole and cancellous bone stiffness at the distal femoral diaphysis, metaphysis, and epiphysis compared to matched, relatively physically inactive, female controls. The results of this study suggest that participation in long-term dance activity may promote differences in bone mechanical competence. Furthermore, the results suggest that dancers’ greater bone mechanical competence at the distal femur, as assessed at a length scale of ~0.23 mm, is mediated predominantly by adaptation in the cancellous bone compartment, rather than the cortical bone compartment. In the future, it will be important to determine whether such adaptations can occur in adults after adolescence or even after the onset of menopause. It will also be important to determine the optimal frequency, intensity, and duration of activity necessary in order to induce such skeletal adaptations.
Acknowledgments
Grant support NIAMS/NIH K23-AR059748 (PI Chang); NIAMS/ NIH K25-AR060283 (PI Rajapakse); NIAMS/NIH RO1-AR053133 (PI Regatte); NIAMS/NIH RO1-AR056260 (PI Regatte); NIAMS/NIH RO1-AR060238 (PI Regatte)
Footnotes
Conflicts of interest None.
Contributor Information
G. Chang, Email: chang_gregory@yahoo.com, Quantitative Multinuclear Musculoskeletal Imaging Group, Center for Biomedical Imaging, NYU Langone Medical Center, 660 First Avenue, 2nd Floor, New York, NY 10016, USA
C. S. Rajapakse, Laboratory for Structural NMR Imaging, Hospital of the University of Pennsylvania, 3400 Spruce Street, Philadelphia, PA 19104, USA
M. Diamond, Department of Rehabilitation Medicine, NYU Langone Medical Center, 400 East 34th Street, New York, NY 10016, USA
S. Honig, Division of Rheumatology, NYU Langone Medical Center, Osteoporosis Center, Hospital for Joint Diseases, 301 East 17th Street, Suite 1101, New York, NY 10003, USA
M. P. Recht, Quantitative Multinuclear Musculoskeletal Imaging Group, Center for Biomedical Imaging, NYU Langone Medical Center, 660 First Avenue, 2nd Floor, New York, NY 10016, USA
D. S. Weiss, Harkness Center for Dance Injuries and Department of Orthopaedic Surgery, Hospital for Joint Diseases, NYU Langone Medical Center, New York, NY, USA
R. R. Regatte, Quantitative Multinuclear Musculoskeletal Imaging Group, Center for Biomedical Imaging, NYU Langone Medical Center, 660 First Avenue, 4th Floor, New York, NY 10016, USA
References
- 1.Wolff J. Das Gesetz der Transformation der Knochen. Verlag; Berlin: 1892. [Google Scholar]
- 2.Amin S. Mechanical factors and bone health: effects of weightlessness and neurologic injury. Curr Rheumatol Rep. 2010;12 (3):170–176. doi: 10.1007/s11926-010-0096-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Keyak JH, et al. Reduction in proximal femoral strength due to long-duration spaceflight. Bone. 2009;44(3):449–453. doi: 10.1016/j.bone.2008.11.014. [DOI] [PubMed] [Google Scholar]
- 4.Holick MF. Perspective on the impact of weightlessness on calcium and bone metabolism. Bone. 1998;22(5 Suppl):105S–111S. doi: 10.1016/s8756-3282(98)00014-3. [DOI] [PubMed] [Google Scholar]
- 5.Modlesky CM, et al. Trabecular bone microarchitecture is deteriorated in men with spinal cord injury. J Bone Miner Res. 2004;19 (1):48–55. doi: 10.1359/JBMR.0301208. [DOI] [PubMed] [Google Scholar]
- 6.McCarthy ID, et al. Changes in the structural and material properties of the tibia in patients with spinal cord injury. Spinal Cord. 2012;50:333–337. doi: 10.1038/sc.2011.143. [DOI] [PubMed] [Google Scholar]
- 7.Fredericson M, et al. Regional bone mineral density in male athletes: a comparison of soccer players, runners and controls. Br J Sports Med. 2007;41(10):664–668. doi: 10.1136/bjsm.2006.030783. discussion 668. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Ferry B, et al. Bone geometry and strength adaptations to physical constraints inherent in different sports: comparison between elite female soccer players and swimmers. J Bone Miner Metab. 2011;29(3):342–351. doi: 10.1007/s00774-010-0226-8. [DOI] [PubMed] [Google Scholar]
- 9.Nikander R, et al. Femoral neck structure in adult female athletes subjected to different loading modalities. J Bone Miner Res. 2005;20(3):520–528. doi: 10.1359/JBMR.041119. [DOI] [PubMed] [Google Scholar]
- 10.Courteix D, et al. Effect of physical training on bone mineral density in prepubertal girls: a comparative study between impact-loading and non-impact-loading sports. Osteoporos Int. 1998;8(2):152–158. doi: 10.1007/BF02672512. [DOI] [PubMed] [Google Scholar]
- 11.Taaffe DR, et al. High-impact exercise promotes bone gain in well-trained female athletes. J Bone Miner Res. 1997;12(2):255–260. doi: 10.1359/jbmr.1997.12.2.255. [DOI] [PubMed] [Google Scholar]
- 12.Ward KA, et al. Bone geometry and density in the skeleton of pre-pubertal gymnasts and school children. Bone. 2005;36(6):1012–1018. doi: 10.1016/j.bone.2005.03.001. [DOI] [PubMed] [Google Scholar]
- 13.Chang G, Regatte RR, Schweitzer ME. Olympic fencers: adaptations in cortical and trabecular bone determined by quantitative computed tomography. Osteoporos Int. 2009;20(5):779–785. doi: 10.1007/s00198-008-0730-z. [DOI] [PubMed] [Google Scholar]
- 14.Ireland A, et al. Side-to-side differences in bone strength in master jumpers and sprinters. J Musculoskelet Neuronal Interact. 2011;11(4):298–305. [PubMed] [Google Scholar]
- 15.Nikander R, et al. Cross-sectional geometry of weight-bearing tibia in female athletes subjected to different exercise loadings. Osteoporos Int. 2010;21(10):1687–1694. doi: 10.1007/s00198-009-1101-0. [DOI] [PubMed] [Google Scholar]
- 16.Heinonen A, et al. Bone mineral density in female athletes representing sports with different loading characteristics of the skeleton. Bone. 1995;17(3):197–203. doi: 10.1016/8756-3282(95)00151-3. [DOI] [PubMed] [Google Scholar]
- 17.Meyer NL, et al. Bone mineral density of olympic-level female winter sport athletes. Med Sci Sports Exerc. 2004;36(9):1594–1601. doi: 10.1249/01.mss.0000139799.20380.da. [DOI] [PubMed] [Google Scholar]
- 18.Ducher G, et al. Effects of repetitive loading on the growth-induced changes in bone mass and cortical bone geometry: a 12-month study in pre/peri- and postmenarcheal tennis players. J Bone Miner Res. 2011;26(6):1321–1329. doi: 10.1002/jbmr.323. [DOI] [PubMed] [Google Scholar]
- 19.Sanchis-Moysi J, et al. Bone and lean mass inter-arm asymmetries in young male tennis players depend on training frequency. Eur J Appl Physiol. 2010;110(1):83–90. doi: 10.1007/s00421-010-1470-2. [DOI] [PubMed] [Google Scholar]
- 20.Kontulainen S, et al. Effect of long-term impact-loading on mass, size, and estimated strength of humerus and radius of female racquet-sports players: a peripheral quantitative computed tomography study between young and old starters and controls. J Bone Miner Res. 2003;18(2):352–359. doi: 10.1359/jbmr.2003.18.2.352. [DOI] [PubMed] [Google Scholar]
- 21.Seeman E, Delmas PD. Bone quality–the material and structural basis of bone strength and fragility. N Engl J Med. 2006;354 (21):2250–2261. doi: 10.1056/NEJMra053077. [DOI] [PubMed] [Google Scholar]
- 22.Patsch JM, et al. Noninvasive imaging of bone microarchitecture. Ann N Y Acad Sci. 2011;1240:77–87. doi: 10.1111/j.1749-6632.2011.06282.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Liu XS, et al. Accuracy of high-resolution in vivo micro magnetic resonance imaging for measurements of microstructural and mechanical properties of human distal tibial bone. J Bone Miner Res. 2010;25(9):2039–2050. doi: 10.1002/jbmr.92. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Majumdar S. Magnetic resonance imaging of trabecular bone structure. Top Magn Reson Imaging. 2002;13(5):323–334. doi: 10.1097/00002142-200210000-00004. [DOI] [PubMed] [Google Scholar]
- 25.Wehrli FW. Structural and functional assessment of trabecular and cortical bone by micro magnetic resonance imaging. J Magn Reson Imaging. 2007;25(2):390–409. doi: 10.1002/jmri.20807. [DOI] [PubMed] [Google Scholar]
- 26.Melton LJ, 3rd, et al. Relation of vertebral deformities to bone density, structure, and strength. J Bone Miner Res. 2010;25(9):1922–1930. doi: 10.1002/jbmr.150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Macdonald HM, et al. Age-related patterns of trabecular and cortical bone loss differ between sexes and skeletal sites: a population-based HR-pQCT study. J Bone Miner Res. 2011;26(1):50–62. doi: 10.1002/jbmr.171. [DOI] [PubMed] [Google Scholar]
- 28.Stein EM, et al. Abnormal microarchitecture and reduced stiffness at the radius and tibia in postmenopausal women with fractures. J Bone Miner Res. 2010;25(12):2572–2581. doi: 10.1002/jbmr.152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Wehrli FW, et al. Mechanical implications of estrogen supplementation in early postmenopausal women. J Bone Miner Res. 2010;25(6):1406–1414. doi: 10.1002/jbmr.33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Burghardt AJ, et al. A longitudinal HR-pQCT study of alendronate treatment in postmenopausal women with low bone density: relations among density, cortical and trabecular microarchitecture, biomechanics, and bone turnover. J Bone Miner Res. 2010;25(12):2558–2571. doi: 10.1002/jbmr.157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.van Rietbergen B, et al. Assessment of cancellous bone mechanical properties from micro-FE models based on micro-CT, pQCT and MR images. Technol Health Care. 1998;6(5–6):413–420. [PubMed] [Google Scholar]
- 32.Newitt DC, et al. In vivo assessment of architecture and micro-finite element analysis derived indices of mechanical properties of trabecular bone in the radius. Osteoporos Int. 2002;13(1):6–17. doi: 10.1007/s198-002-8332-0. [DOI] [PubMed] [Google Scholar]
- 33.Rajapakse CS, et al. Implications of noise and resolution on mechanical properties of trabecular bone estimated by image-based finite-element analysis. J Orthop Res. 2009;27(10):1263–1271. doi: 10.1002/jor.20877. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Rajapakse CS, et al. Computational biomechanics of the distal tibia from high-resolution MR and micro-CT images. Bone. 2010;47(3):556–563. doi: 10.1016/j.bone.2010.05.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Weiss DS, Shah S, Burchette RJ. A profile of the demographics and training characteristics of professional modern dancers. J Dance Med Sci. 2008;12(2):41–46. [PubMed] [Google Scholar]
- 36.Chang G, et al. In vivo estimation of bone stiffness at the distal femur and proximal tibia using ultra-high-field 7-Tesla magnetic resonance imaging and micro-finite element analysis. J Bone Miner Metab. 2012;30:243–251. doi: 10.1007/s00774-011-0333-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Kim N, et al. Evaluation of MRI resolution affecting trabecular bone parameters: Determination of acceptable resolution. Magn Reson Med. 2012;67:218–225. doi: 10.1002/mrm.22984. [DOI] [PubMed] [Google Scholar]
- 38.Vasilic B, Wehrli FW. A novel local thresholding algorithm for trabecular bone volume fraction mapping in the limited spatial resolution regime of in vivo MRI. IEEE Trans Med Imaging. 2005;24 (12):1574–1585. doi: 10.1109/TMI.2005.859192. [DOI] [PubMed] [Google Scholar]
- 39.Jones AC, Wilcox RK. Finite element analysis of the spine: towards a framework of verification, validation and sensitivity analysis. Med Eng Phys. 2008;30(10):1287–1304. doi: 10.1016/j.medengphy.2008.09.006. [DOI] [PubMed] [Google Scholar]
- 40.Jones AC, Wilcox RK. Assessment of factors influencing finite element vertebral model predictions. J Biomech Eng. 2007;129 (6):898–903. doi: 10.1115/1.2800791. [DOI] [PubMed] [Google Scholar]
- 41.Crawford RP, Rosenberg WS, Keaveny TM. Quantitative computed tomography-based finite element models of the human lumbar vertebral body: effect of element size on stiffness, damage, and fracture strength predictions. J Biomech Eng. 2003;125(4):434–438. doi: 10.1115/1.1589772. [DOI] [PubMed] [Google Scholar]
- 42.Guo XE, Goldstein XA. Is trabecular bone tissue different from cortical bone tissue? Forma. 1997;12:185–196. [Google Scholar]
- 43.Bhagat YA, et al. Performance of muMRI-Based virtual bone biopsy for structural and mechanical analysis at the distal tibia at 7T field strength. J Magn Reson Imaging. 2011;33(2):372–381. doi: 10.1002/jmri.22439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Wald MJ, et al. Structural and mechanical parameters of trabecular bone estimated from in vivo high-resolution magnetic resonance images at 3 tesla field strength. J Magn Reson Imaging. 2010;31(5):1157–1168. doi: 10.1002/jmri.22158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Rajapakse CS, et al. Micro-MR imaging-based computational biomechanics demonstrates reduction in cortical and trabecular bone strength after renal transplantation. Radiology. 2012;262:921–931. doi: 10.1148/radiol.11111044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Eswaran SK, et al. The micro-mechanics of cortical shell removal in the human vertebral body. Comp Meth Appl Mech Eng. 2007;196:3025–3032. [Google Scholar]
- 47.Krug R, et al. Feasibility of in vivo structural analysis of high-resolution magnetic resonance images of the proximal femur. Osteoporos Int. 2005;16(11):1307–1314. doi: 10.1007/s00198-005-1907-3. [DOI] [PubMed] [Google Scholar]
- 48.Wehrli FW, et al. Cancellous bone volume and structure in the forearm: noninvasive assessment with MR microimaging and image processing. Radiology. 1998;206(2):347–357. doi: 10.1148/radiology.206.2.9457185. [DOI] [PubMed] [Google Scholar]
- 49.Majumdar S, et al. Trabecular bone architecture in the distal radius using magnetic resonance imaging in subjects with fractures of the proximal femur. Magnetic Resonance Science Center and Osteoporosis and Arthritis Research Group. Osteoporos Int. 1999;10 (3):231–239. doi: 10.1007/s001980050221. [DOI] [PubMed] [Google Scholar]
- 50.Modlesky CM, Majumdar S, Dudley GA. Trabecular bone microarchitecture in female collegiate gymnasts. Osteoporos Int. 2008;19 (7):1011–1018. doi: 10.1007/s00198-007-0522-x. [DOI] [PubMed] [Google Scholar]
- 51.Chang G, et al. Adaptations in trabecular bone microarchitecture in Olympic athletes determined by 7T MRI. J Magn Reson Imaging. 2008;27(5):1089–1095. doi: 10.1002/jmri.21326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Diez-Perez A, et al. Microindentation for in vivo measurement of bone tissue mechanical properties in humans. J Bone Miner Res. 2010;25(8):1877–1885. doi: 10.1002/jbmr.73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Burghardt AJ, et al. High-resolution peripheral quantitative computed tomographic imaging of cortical and trabecular bone microarchitecture in patients with type 2 diabetes mellitus. J Clin Endocrinol Metab. 2010;95(11):5045–5055. doi: 10.1210/jc.2010-0226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Haapasalo H, et al. Exercise-induced bone gain is due to enlargement in bone size without a change in volumetric bone density: a peripheral quantitative computed tomography study of the upper arms of male tennis players. Bone. 2000;27 (3):351–357. doi: 10.1016/s8756-3282(00)00331-8. [DOI] [PubMed] [Google Scholar]