Abstract
Many segmentation algorithms in medical image analysis use Bayesian modeling to augment local image appearance with prior anatomical knowledge. Such methods often contain a large number of free parameters that are first estimated and then kept fixed during the actual segmentation process. However, a faithful Bayesian analysis would marginalize over such parameters, accounting for their uncertainty by considering all possible values they may take. Here we propose to incorporate this uncertainty into Bayesian segmentation methods in order to improve the inference process. In particular, we approximate the required marginalization over model parameters using computationally efficient Markov chain Monte Carlo techniques. We illustrate the proposed approach using a recently developed Bayesian method for the segmentation of hippocampal subfields in brain MRI scans, showing a significant improvement in an Alzheimer’s disease classification task. As an additional benefit, the technique also allows one to compute informative “error bars” on the volume estimates of individual structures.
Keywords: Bayesian modeling, segmentation, Monte Carlo sampling, hippocampal subfields
1. Introduction
Many medical image segmentation methods perform Bayesian inference on so-called generative models to deduce segmentation labels from the available image information. The employed models commonly consist of a prior describing the spatial organization of anatomical structures in the image domain, for example via occurrence and co-occurrence statistics. They also contain a likelihood term that models the relationship between anatomical labels and image intensities.
Priors can take on different forms. Generic priors are popular in the computer vision literature, in which domain knowledge about the image content is often limited. Markov random field models, which encourage spatial regularity, are a good example of such priors (Besag, 1986; Boykov et al., 2001). In medical imaging, priors that are tailored to the anatomical structures of interest are typically more useful. These priors are often in the form of statistical atlases (Greitz et al., 1991; Thompson et al., 2001; Roland et al., 2004; Joshi et al., 2004; Yeo et al., 2008), which describe the relative frequency of labels in a reference coordinate frame, representing an “average” of the population. Image registration techniques (Brown, 1992; West et al., 1997; Maintz and Viergever, 1998; Zitova and Flusser, 2003; Pluim et al., 2003) link the reference space to the target image space, allowing the transfer of the label probabilities to coordinates of the image to be segmented.
The second component of the generative model is the likelihood term, which specifies how the different voxel labels generate the observed image intensities at each location. The likelihood models the image formation process, including artifacts such as noise and MRI bias fields (Wells et al., 1996). Many methods assume a Gaussian distribution (or a mixture thereof) for each label class present in the image (Van Leemput et al., 1999). If the parameters of these distributions are learned from the target image using Bayesian inference, rather than predefined or learned from a training dataset, the resulting segmentation method is robust against changes in modality. This is in contrast with discriminative segmentation models, which excel when the target image appearance is consistent with the training set (e.g., computerized tomography, as in Zheng et al. 2007) but falter when it is not. Appearance consistency is often not the case in MRI, due to changes in acquisition hardware and pulse sequences.
Given the prior and the likelihood terms, the posterior probability of a segmentation for a given target image can be inferred using Bayes’ rule. The posterior is a probability distribution over the possible labelings of the image, and the most likely segmentation can be computed by finding its mode. Popular methods such as (Zhang et al., 2001; Fischl et al., 2002; Van Leemput et al., 1999; Ashburner and Friston, 2005; Sabuncu et al., 2010) are based on this principle. If the ultimate goal is not to produce a segmentation, but to compute descriptors for the different structures (e.g., volume measurements), then the whole probability distribution rather than the mode can be used in the estimation.
Both the prior and the likelihood often depend on a number of unknown model parameters. In applications that use a statistical atlas, the prior is shaped by the parameters of the registration method that is used to deform the atlas towards the target image. For example, several state-of-the-art segmentation methods employ thousands or millions of registration parameters (Fischl et al., 2004b; Ashburner and Friston, 2005; Pohl et al., 2006; Van Leemput et al., 2009). The parametrization of the likelihood is usually more conventional. For example, if a Gaussian distribution is assumed for each label, two parameters (mean and variance) per class are required in the model.
In a truly Bayesian framework, unknown model parameters need to be integrated out in the computation of the segmentation posterior. However, all aforementioned segmentation methods employ point estimates for these parameters, thereby applying Bayesian inference only in an approximate sense. For example, the registration parameters are either pre-computed using metrics not necessarily related to the probabilistic framework (Sabuncu et al., 2010), or explicitly estimated to fit the segmentation model to the target imaging data (Fischl et al., 2004b; Ashburner and Friston, 2005; Pohl et al., 2006; Van Leemput et al., 2009), but in both cases only the obtained point estimate is used to generate the final segmentation result. This may lead to biased segmentation results for two different reasons. First, many reasonable atlas deformations may exist in addition to the estimated one, especially when the boundaries between the anatomical structures are poorly defined by image intensities and/or when the atlas deformation has a very large number of parameters. Second, the computed point estimate may not correspond to the global optimum of the relevant objective function, since numerical optimizers easily get trapped in local extrema in such high-dimensional spaces. Ignoring the uncertainty in the parameters of the likelihood term, as is commonly done, may further bias the results in a similar way.
Despite these issues, point estimates of the model parameters are often used in the literature due to their computational advantages: they effectively side-step the difficult integration over the model parameters that is required in a more faithful Bayesian analysis. In this paper, we propose a better approximation of the segmentation posterior that fully considers the uncertainty in the model parameters, using a computationally feasible strategy based on Markov chain Monte Carlo (MCMC) sampling. We instantiate the approach within a recently proposed Bayesian method aiming to segment hippocampal subfields in brain MRI scans (Van Leemput et al., 2009), and show that MCMC sampling yields hippocampal subfield volume estimates that better discriminate controls from subjects with Alzheimer’s disease. Moreover, the proposed approach also provides more realistic and useful “error bars” (defined as the standard deviation of the error in a measurement) on the volumes than those obtained without accounting for model parameter uncertainty.
To the best of our knowledge, integration over model parameters has not been explored before in the medical image segmentation literature. In the context of image registration, Simpson et al. (2011) proposed an approximation of the posterior distribution of deformation fields that outperforms deterministic registration when discriminating Alzheimer’s disease patients from healthy controls. Risholm et al. (2010, 2011) visualized registration uncertainty and estimated its effect on the accumulated dose in radiation therapy applications, whereas Allassonniére et al. (2007) marginalized over deformations in the context of constructing deformable models. There have been attempts to handle uncertainty estimates of spatial alignment outside the Medical Image Analysis literature, too; see for instance Pennec and Thirion (1997); Taron et al. (2009); Kybic (2010), which deal with shapes, sets of matched points and pixel data, respectively. In Tu and Zhu (2002), MCMC was used to generate a set of distinct solutions representative of the entire posterior segmentation distribution in natural images.
The rest of this paper is organized as follows. In Section 2, we briefly summarize the principles behind Bayesian segmentation models and present the baseline hippocampal subfield segmentation framework used in this paper. Section 3 details the improved inference strategy proposed in this study. Section 4 describes the experimental setup to validate the proposed approach. Section 5 presents the results of the experiments, and Section 6 concludes the paper. An early version of this work appeared in a conference paper (Iglesias et al., 2012).
2. Bayesian segmentation models and baseline method
In this section we first summarize the general theory behind Bayesian segmentation methods (Section 2.1). Then, we present the specific hippocampal subfield segmentation algorithm that we use to illustrate the methods proposed in this paper (Section 2.2).
2.1. General framework
Let y be the voxel intensities corresponding to an image, and s the underlying segmentation labels we wish to estimate. Bayesian segmentation methods aim at finding the most probable segmentation given the image using Bayes’ rule:
| (1) |
Here, p(s) encodes prior anatomical knowledge (usually in the form of an atlas), whereas the likelihood p(y|s) links the underlying anatomy with the image intensities. Both the prior and the likelihood usually depend on a number of free parameters: p(s|x) and p(y|s, θ), where x represent the parameters related to the prior and θ those related to the likelihood. Both sets of parameters have (hyper-)prior distributions p(x) and p(θ) that capture any prior knowledge we may have about them, so that:
The common practice in the literature is to first compute the most probable value {θ̂, x̂} of the model parameters in light of the image intensities:
| (2) |
and then, rather than maximize p(s|y), optimize the following expression instead:
| (3) |
This is only an approximation because a true Bayesian analysis would consider all possible values of the unknown model parameters. More specifically, Equation 3 can be interpreted as the mode approximation for the required integral over the model parameters:
| (4) |
| (5) |
Equation 5 will be accurate if the posterior probability of the model parameters given the image intensities is very sharp and therefore well approximated by a Dirac delta, i.e., p(θ, x|y) ≈ δ(θ − θ̂, x − x̂).
A large number of segmentation methods fall within this general framework, differing in the way the prior and likelihood are specified, and in the optimization algorithms that are used to solve Equations 2 and 3. Examples include Wells et al. (1996); Guillemaud and Brady (1997); Held et al. (1997); Van Leemput et al. (1999); Zhang et al. (2001); Leemput et al. (2001); Marroquin et al. (2002); Fischl et al. (2002, 2004a); Prastawa et al. (2004); Lorenzo-Valdes et al. (2004); Ashburner and Friston (2005); Pohl et al. (2006, 2007); Xue et al. (2007); Menze et al. (2010); Sabuncu et al. (2010), among others.
2.2. Baseline segmentation method
To illustrate the proposed MCMC-based method, we build on a recently developed hippocampal subfield segmentation method (Van Leemput et al., 2009), which is part of the public software package FreeSurfer1 (Fischl et al., 2002). Automatic segmentation of the subfields has recently attracted the interest of the neuroscience community because different regions of the hippocampal formation are affected differently by normal aging and Alzheimer’s disease (Mueller et al., 2010; Yushkevich et al., 2010). Here we summarize the baseline method of Van Leemput et al. (2009) within the general Bayesian segmentation framework described above.
2.2.1. Generative model
The algorithm relies on a statistical atlas of the hippocampus, in which a total of K = 11 different labels corresponding to the hippocampal subfields and surrounding brain tissue are represented: fimbria, presubiculum, subiculum, CA1, CA2/3, CA4/dentate gyrus (CA4/DG), hippocampal tail, hippocampal fissure, white matter (WM), gray matter (GM) and cerebrospinal fluid (CSF). For the likelihood term, the model assumes that the intensities of each tissue class follow a Gaussian distribution with parameters that are unknown a priori.
The statistical atlas is a generalization of the probabilistic atlases often used in brain MR segmentation (Ashburner and Friston, 1997; Van Leemput et al., 1999; Leemput et al., 2001; Zijdenbos et al., 2002; Fischl et al., 2002; Ashburner and Friston, 2005; Prastawa et al., 2004; Pohl et al., 2006; Awate et al., 2006; Pohl et al., 2007). It is automatically estimated from manual segmentations of the hippocampal formation in high-resolution MRI data from ten different subjects (Van Leemput et al., 2009). Rather than using voxel-wise statistics, the atlas is represented as a tetrahedral mesh that covers a bounding box around the hippocampus (Van Leemput, 2009). Each of its approximately 8,000 vertices has an associated set of label probabilities specifying how frequently each of the K labels occur at the vertex. The mesh is adaptive to the degree of complexity of the underlying hippocampal anatomy in each region, such that uniform regions are covered by larger tetrahedra. This yields a sparser representation than would otherwise be attainable. The position of the vertices in atlas space (henceforth “reference position”) is computed along with the label probabilities in a nonlinear, group-wise registration of the labeled training data. The atlas is displayed in its reference position in Figure 1; note the irregularity in the shapes of the tetrahedra.
Figure 1.
Tetrahedral-mesh-based atlas of the hippocampal subfields (based on the right hippocampus), showing the label probabilities with the mesh superimposed. From left to right, top to bottom: coronal slice, 3D rendering, axial slice, sagittal slice. The color map is displayed on the right. Note that the color of a voxel is a sum of the colors corresponding to the labels that might occur at that location, weighed by their prior probabilities.
The mesh is endowed with a deformation model that allows its vertex coordinates to change according to a Markov random field model. If the free parameters x related to the prior correspond to a vector representing the position of the mesh (i.e., stacked coordinates of all vertices), we have:
| (6) |
where xref is the reference position. The energy function ϕ(x, xref), which includes a term ϕt for each tetrahedron in the mesh t = 1, …, T, penalizes the deformation from the reference position. Specifically, ϕt(x, xref) follows the definition in Ashburner et al. (2000):
| (7) |
In Equation 7, λt,p, p = 1, 2, 3, represents the singular values of the Jacobian matrix of the affine mapping of tetrahedron t from reference to current position. is the volume of tetrahedron t in reference position, and F > 0 is a scalar that represents the stiffness of the mesh. The function ϕt goes to infinity if any of the singular values approaches zero, i.e., if the Jacobian determinant of the mapping goes to zero. Therefore, the energy function ϕ explicitly enforces that tetrahedra do not fold, effectively preserving the topology of the mesh. In practice, it is not necessary to explicitly compute singular value decompositions to evaluate ϕt, as explained in Ashburner et al. (2000). A movie displaying different samples from the resulting atlas deformation prior p(x) is available as part of the supplementary material.
Given the deformed mesh position x, the probability pi(k|x) that label k ∈ {1, …, K} occurs at a voxel i can be obtained by interpolating the probabilities corresponding to that label at the vertices of the tetrahedron containing the voxel. These probabilities are assumed to be conditionally independent given x. Therefore, if si ∈ {1, …, K} is the label at voxel i, the prior probability of a labeling s = (s1, …, sI)T is given by , where I is the total number of voxels in the region of interest covered by the mesh.
Finally, the likelihood model connects the labeling s with the observed image intensities y = (y1, …, yI)T. The intensities of the voxels corresponding to each class are assumed to follow a Gaussian distribution parametrized by a mean and a variance associated to that class. The probabilities are assumed to be conditionally independent given the labels. Therefore, the likelihood term is:
where the model parameters θ related to the likelihood consist of a vector grouping all the means and variances of these Gaussian distributions. In practice, to reflect the fact that there is little intensity contrast between the cerebral gray matter and the hippocampal subfields subiculum, presubiculum, CA1, CA2/3, CA4/DG and tail in our images, we consider them part of a global gray matter tissue type with a shared mean and variance. Likewise, the cerebral white matter and the fimbria are considered part of a global white matter class with a single mean and variance, and the hippocampal fissure shares Gaussian parameters with the CSF. Therefore, θ is a six-dimensional vector: . We assume the prior distribution on these parameters to be uninformative, i.e., p(θ) ∝ 1.
2.2.2. Classical inference: segmentation and volumetry
Optimizing the expression in Equation 2 is equivalent to a joint registration and intensity parameter estimation process. In the baseline segmentation method (Van Leemput et al., 2009), the variables θ and x are alternately optimized using a coordinate ascent scheme, the former with expectation maximization (Dempster et al., 1977) and the latter with the Levenberg-Marquardt algorithm (Levenberg, 1944). To reduce the computational burden of the method, the optimization of the mesh deformation is restricted to a region defined by a morphologically dilated version of the mask that the main FreeSurfer stream produces for the whole hippocampus (as in Figures 3 and 4).
Figure 3.
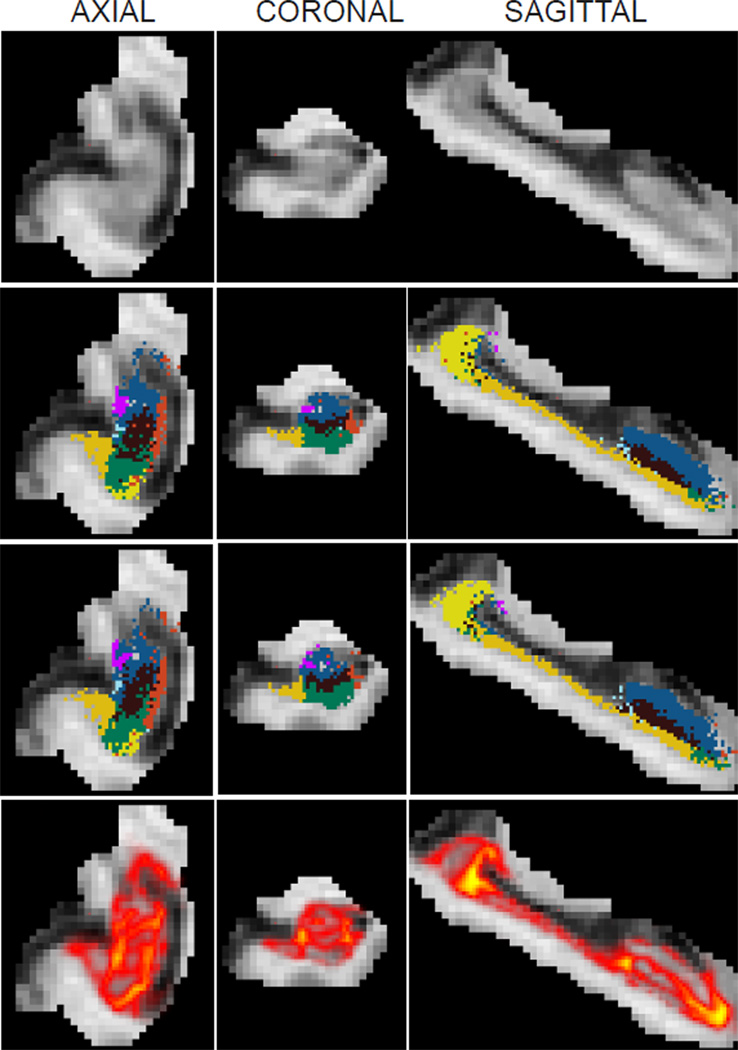
Samples from the posterior distribution of the segmentation p(s|y) when approximated by the sampling scheme, i.e., with Equation 13. The images correspond to the right hippocampus of a subject with Alzheimer’s disease. First row: axial, coronal and sagittal slices of the MRI data, cropped around the hippocampus as explained in Section 2.2.2. Rows 2–3: corresponding slices of two different samples of the segmentation; the colormap is the same as in Figure 1. Row 4: heat map representation of the label disagreement defined in Equation 19 (yellow represents most disagreement). This map highlights the regions in which the segmentation uncertainty is high. As opposed to the segmentation in Figure 2, the samples in the second and third rows of this figure do not maximize the approximate posterior probability of the labels.
Figure 4.
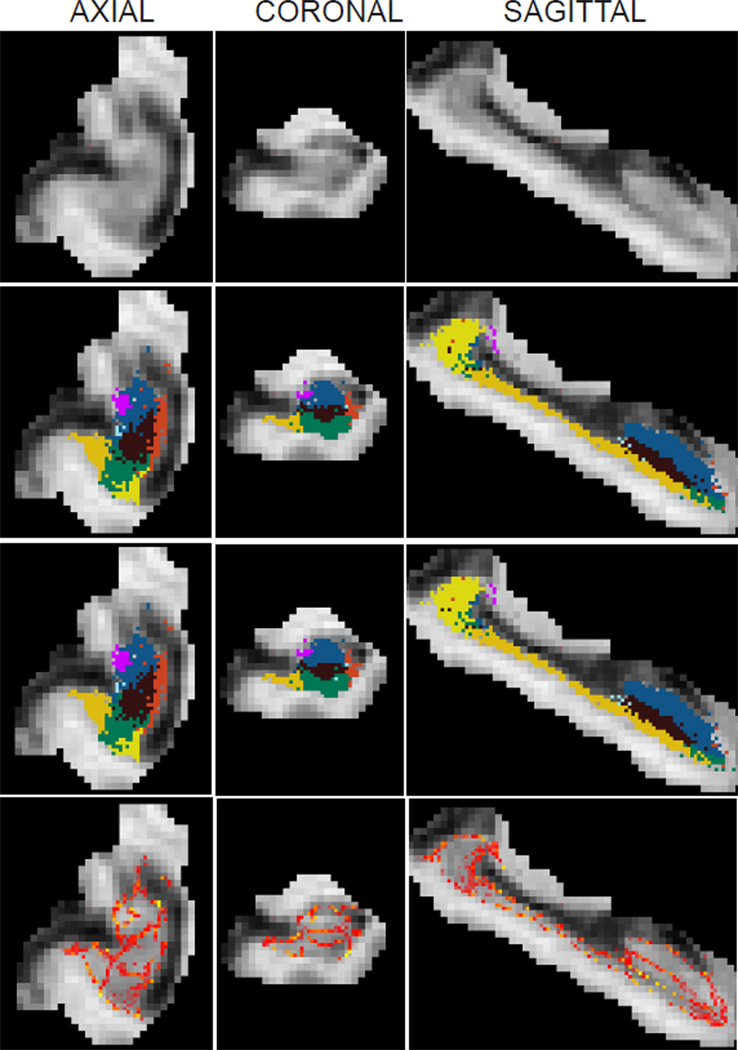
Samples from the approximate posterior distribution of the segmentation p(s|y) when the mode approximation is used in the integral over model parameters (i.e., when the posterior is approximated by Equation 5 as in the baseline segmentation method). The samples can then be obtained by independently sampling the label of each voxel from the categorical distribution in Equation 9. The images correspond to the same subject and slices as in Figure 3; please see its caption for an explanation of the illustration.
Once the most likely values of the parameters have been found, the posterior distribution of the labels given the intensities is approximately (Equation 5):
| (8) |
which factorizes over voxels because the labels are conditionally independent given x and θ. The posterior label probabilities for each voxel are given by Bayes’ rule:
| (9) |
The approximate maximum-a-posteriori (MAP) segmentation (the maximizer of Equation 3) can be computed voxel by voxel:
| (10) |
Three slices of a sample MRI scan and its corresponding MAP segmentation are displayed in Figure 2.
Figure 2.
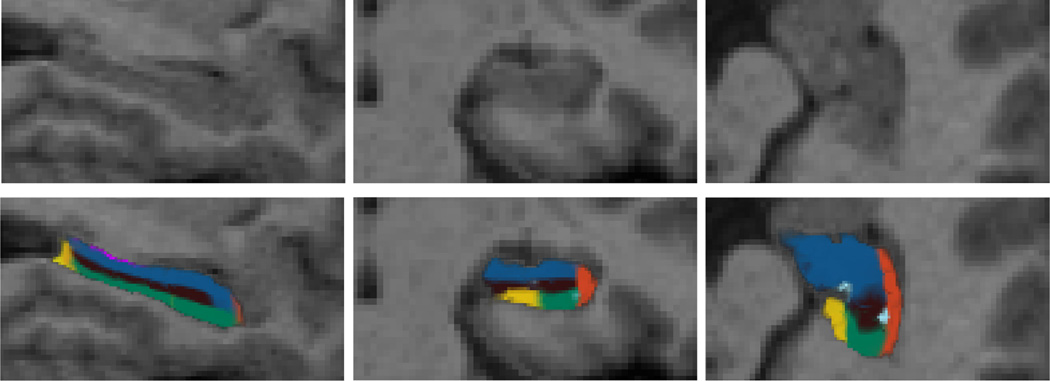
Top row: sagittal, coronal and axial slice from the left hippocampus of a sample scan from the dataset. Bottom row: corresponding MAP segmentation produced by the baseline Bayesian algorithm, i.e., computed by optimizing Equation 8. The color map for the subfields is the same as in Figure 1.
Finally, to infer the volumes of the different hippocampal subfields within the framework, we must consider that they are random variables dependent on the image data y. Under the point estimate approximation for the model parameters, the expected value vk and variance of the posterior distribution of the volume of the structure corresponding to label k are given by:
| (11) |
| (12) |
3. Considering the uncertainty in the model parameters using MCMC sampling
3.1. Parameter uncertainty
Both in segmentation and volume estimation, the framework described in Section 2.2.2 does not consider the uncertainty in the model parameters. In most medical imaging applications, including the hippocampal subfield segmentation problem, this might be a fair assumption for the likelihood parameters θ: millions of voxels are typically available to estimate a low number of parameters. In other words, it is not possible to alter θ much without largely decreasing the likelihood term of the model. However, when x is based on a nonlinear registration method, the number of parameters is much higher; as many as three times the number of voxels when nonparametric, voxel-wise deformation models are used. In that case, the mode approximation in Equation 5 may no longer be accurate. For instance, it would be relatively easy to modify the atlas warp x in areas of the image with low intensity contrast without changing the posterior probability of the model substantially.
Instead of using point estimates for x and θ, we propose to employ a computationally more demanding but also more accurate way of approximating the posterior than Equation 5. Rather than the mode approximation, which only considers a single value for the model parameters, we use Monte Carlo sampling to account for the uncertainty in {x, θ} and obtain a better approximation of the integral in the equation. Assuming that we have an efficient way of drawing N samples {θ(n), x(n)}, n = 1, …, N, from the distribution p(θ, x|y), the segmentation posterior can be approximated by:
| (13) |
which is a better approximation than Equation 5, since it considers many different values of the parameters, with more likely values occurring more frequently. The approximation can be made arbitrarily close to the true integral by allowing N to be large enough.
Within this framework, it can be shown (Appendix A) that the posterior mean v̄k of the volume corresponding to class k is:
| (14) |
where is the mean of the posterior distribution of the volume when the model parameters are set to {x(n), θ(n)} (note the analogy with Equation 11).
The expression for the variance, also derived in Appendix A, is:
| (15) |
where is the variance of the posterior distribution of the volume when the model parameters are set to {x(n), θ(n)} (very similar to Equation 12). Equation 15 has two terms: the average of the variances computed independently from each sample and the variance of the mean volumes across samples. The first term is expected to be comparable to the estimate from conventional Bayesian methods, i.e., Equation 12. However, the second term directly reflects the uncertainty in model parameters, including the atlas registration, and can potentially be much larger.
3.2. Sampling based on Markov chain Monte Carlo (MCMC)
In order to obtain the samples {θ, x} required in the proposed framework, we use MCMC techniques. Specifically, we use a Gibbs sampling scheme (Geman and Geman, 1984) that alternately draws samples of θ keeping x constant and vice versa. The sampler is initialized with the most likely model parameters as estimated by the conventional Bayesian segmentation method (Equations 2 and 3): x(0) = x̂, θ(0) = θ̂. Subsequently, samples are drawn as follows:
Since the conditional distributions p(θ|x, y) and p(x|θ, y) have different natures, we use different methods to sample from each of them. We discuss these techniques below.
3.2.1. Sampling x
To draw samples from p(x|θ, y) we use an efficient MCMC technique known as Hamiltonian Monte Carlo (HMC, Duane et al. 1987, also known as hybrid Monte Carlo). HMC belongs to the family of Metropolis-Hasting methods, in which a proposal probability distribution that depends on the current position of the sampler is used to suggest a new candidate position for the next sample. The new proposed state is then accepted or rejected using the Metropolis-Hastings equation (Metropolis et al., 1953). In traditional Metropolis-Hastings schemes, simple proposal distributions are used (e.g., a Gaussian centered on the current sample), leading to a random walk behavior that makes the exploration of the domain of the target probability distribution very slow and inefficient. In contrast, HMC is able to generate distant proposals that are still likely to be accepted by augmenting the space of the variable one is sampling from and taking advantage of the gradient of its probability distribution.
Specifically, HMC augments the state space x with a vector of momentum variables m (with the same dimensionality as x). HMC alternates two kinds of proposal: first, randomly sampling m from a zero-mean, identity-covariance Gaussian distribution; and second: simultaneously updating x and m using a simulation of Hamiltonian dynamics. The Hamiltonian is the energy of a particle with momentum m located in a potential field defined by the energy Ep(x) = − log p(x|θ, y):
where we have assumed unit mass for the particle. The two proposals are used to generate samples from the joint probability density function:
Finally, we can simply discard the momenta from the joint samples {x, m} to yield the final samples of p(x|θ, y). The details of the algorithm and of its implementation, including some modifications to improve its efficiency in our specific application, are detailed in Appendix B.
Movies illustrating atlas deformations sampled from p(x|θ, y) using the proposed method are available as supplementary material. Note that, due to the information in the image intensities y, these samples are much more similar to each other than those from the prior p(x).
3.2.2. Sampling θ
When the atlas position x is fixed, sampling from p(θ|x, y) is not straightforward because of the unknown labels s, which follow the categorical distribution in Equation 9. However, as in HMC, we can sample from the joint distribution {θ, s} ~ p(θ, s|x, y) instead and simply disregard the labelings s. To do so, we again use a Gibbs scheme, in which we alternately sample from s and θ.
Obtaining samples of p(s|θ, x, y) is immediate because it factorizes over voxels, so we can sample the labels si independently with Equation 9. Regarding θ, its conditional posterior distribution p(θ|s, x, y) = p(θ|s, y) is normal-gamma (Murphy, 2007). We can draw samples from this distribution in two steps:
| (16) |
| (17) |
where Γ(α, β) is the Gamma distribution with shape parameter α and rate parameter β, 𝒩 is the Gaussian distribution, 𝒱k(s) is the number of voxels with label k in the current sample of s, and ȳk and are the sample mean and variance of the intensities corresponding to such voxels.
In practice, generating samples of θ is much faster than drawing samples from p(x|θ, y). Therefore, we draw many samples from θ before going back to sampling a new x. The resulting sampling scheme is summarized in Table 1; note that we must draw and disregard some samples of x (burn-in period) every time we update θ and vice versa to ensure that we are actually sampling from the conditional distributions p(x|θ, y) and p(θ|x, y), respectively.
Table 1.
Algorithm to obtain samples from p(θ, x|y).
| 1. Initialize n = 1, {x, θ} = {x̂, θ̂} (optimal point estimates). |
| 2. FOR t = 1 to number of samples of x to draw: |
| 2A. FOR t’ = 1 to number of trajectories: |
| 2A-I. Sample m ~ 𝒩(0, I). |
| 2A-II. Track (x, m) with Equations B.1–B.3. |
| 2A-III. Accept move with probability given by Eq. B.4 |
| END |
| 2B. FOR t” = 1 to number of samples of θ per sample of x: |
| 2B-I. FOR t”’ = 1 to number of samples to skip: |
| 2B-Ia. Sample the image labels with Equation 9. |
| 2B-Ib. Sample the image intensity parameters with Equations 16 and 17. |
| END |
| 2B-II. Record sample: x(n) = x, θ(n) = θ. |
| 2B-III. n=n+1. |
| END |
| END |
4. Experimental setup
Ideally, we would validate the proposed method by first having a set of brain MRI scans manually labeled by an expert human rater, and then computing overlap scores with the automated segmentations. However, manually labeling the subfields in standard brain MRI scans at 1 mm resolution is extremely difficult. Therefore, we use an indirect validation method based on the fact that hippocampal volumes are known to be a biomarker for Alzheimer’s disease (AD) (Chupin et al., 2009). The volumes of the hippocampal subfields, which are automatically estimated using the Bayesian segmentation method (with and without sampling), are used to separate AD from controls using a simple classifier. The ability to separate the two classes is then a surrogate for segmentation quality that we use to assess the effect of sampling. In addition to classification accuracy, we further examine how sampling affects the error bars of the volume estimates. In this section, we first describe the MRI data used in the study, then the settings of the sampler, the classification framework used to predict AD and finally the competing approaches.
4.1. MRI data
The MRI data used in this study were obtained from the Alzheimers Disease Neuroimaging Initiative (ADNI) database (http://adni.loni.ucla.edu). The ADNI was launched in 2003 by the National Institute on Aging, the National Institute of Biomedical Imaging and Bioengineering, the Food and Drug Administration, private pharmaceutical companies and non-profit organizations, as a $60 million, 5-year public-private partnership. The main goal of ADNI is to test whether MRI, positron emission tomography (PET), other biological markers, and clinical and neuropsychological assessment can be combined to analyze the progression of mild cognitive impairment (MCI) and early AD. Markers of early AD progression can aid researchers and clinicians to develop new treatments and monitor their effectiveness, as well as decrease the time and cost of clinical trials.
The Principal Investigator of this initiative is Michael W. Weiner, MD, VA Medical Center and University of California - San Francisco. ADNI is a joint effort by coinvestigators from industry and academia. Subjects have been recruited from over 50 sites across the U.S. and Canada. The initial goal of ADNI was to recruit 800 subjects but ADNI has been followed by ADNI-GO and ADNI-2. These three protocols have recruited over 1,500 adults (ages 55–90) to participate in the study, consisting of cognitively normal older individuals, people with early or late MCI, and people with early AD. The follow up duration of each group is specified in the corresponding protocols for ADNI-1, ADNI-2 and ADNI-GO. Subjects originally recruited for ADNI-1 and ADNI-GO had the option to be followed in ADNI-2. For up-to-date information, see http://www.adni-info.org.
In this study we evaluated the proposed method with 400 baseline T1 scans from elderly controls (EC) and AD subjects available in the ADNI-1 study. The scans were acquired with sagittal 3D MPRAGE sequences at 1 mm isotropic resolution. Since ADNI is a multi-center effort, different makes and models of scanners were used to acquire the images. We refer the reader to the ADNI website for a detailed description of acquisition hardware and protocols.
The software package FreeSurfer was used to preprocess the scans. FreeSurfer produces skull-stripped, bias field corrected volumes along with a segmentation into subcortical and cortical structures, including the hippocampus. The preprocessed scans were then run through the hippocampal subfield segmentation module in FreeSurfer. This module uses the hippocampal mask to extract the bias field corrected data within a bounding box around the hippocampus, upsamples this cropped region to 0.5 mm isotropic resolution and gives it as input to the segmentation algorithm described in Van Leemput et al. (2009). The output from the hippocampal subfield module was used to initalize the sampling algorithm, which was run on the cropped, upsampled data. Throughout the experiments we used the default value in FreeSurfer for the stiffness parameter: F = 0.01. We also recorded the intracranial volumes (ICV) estimated by FreeSurfer, which are useful to correct for brain size in the volumetry. The FreeSurfer pipeline crashed in 17 subjects, which were removed from the final analysis. The demographics of the remaining 383 subjects are as follows: 56.2% EC (age 76.1±5.6 years), 43.8% AD patients (age 75.5 ± 7.6); 53.6% males (age 76.1 ± 5.6), 46.4% females (age 75.9 ± 6.8).
4.2. MCMC sampler
The Monte Carlo sampler follows the algorithm in Table 1. With the help of preliminary runs, we tuned the parameter values to the following values:
Number of iterations: 200 for x (step 2 in table), 30 samples of θ for each value of x (step 2B). This amounts to N=6000 total samples.
Number of trajectories: we simulate 100 trajectories in step 2A in Table 1) before recording each sample of x. This burn-in period ensures that we are actually sampling from the conditional distribution p(x|θ, y). In a similar way, we skip 100 samples of θ (step 2B-I in the table) for each sample that we record.
4.3. Classification, ROC analysis, and error bars of volumes
The performance when classifying AD vs. EC is used as a surrogate measure for the quality of the hippocampal subfield segmentation. It is thus desirable to use a simple classifier such that the performance is mainly determined by the input data, rather than stochastic variations in the classifier. For this reason, we choose to use a simple linear classifier (Linear Discriminant Analysis, LDA, Fisher 1936) as the base classifier in the experiments.
LDA assumes that data points (represented by a vector z) from two different classes are samples from two Gaussian distributions with different means but equal covariance matrices. In our case, the classes are AD and EC, whereas z is a vector with the hippocampal subfield volumes of a subject, left-right averaged and divided by the ICV estimated by FreeSurfer. Averaging the volumes from the left and right hippocampi enhances the power of the analysis without increasing the dimensionality of the data, whereas dividing by the ICV corrects for differences in whole brain size. The means of the the Gaussians distributions can be estimated from training data by computing the average for each class: μEC = (1/nEC) ∑j∈EC zj and μAD = (1/nAD) ∑j∈AD zj, where nEC and nAD are the number of subjects in each class in the training data. The expression for the covariance is:
When a new data point is presented to the system, the likelihood ratio is computed and compared to a threshold to make a decision:
It can be shown that this test is equivalent to:
| (18) |
which represents a linear decision function in which each subfield volume has a different weight in w = Σ−1(μEC − μAD). The threshold τ controls the compromise between sensitivity and specificity. By sweeping τ, we can build the receiver operating characteristic (ROC) curve, which depicts the true positive rate vs. the false positive rate. The area under the curve (AUROC) can be used as a measure of the performance of the classifier across all sensitivity rates. To compare AUROCs from different classifiers, we use the statistical test proposed by DeLong et al. (1988). In addition to the AUROC, we also report the maximal accuracy rate of the classification across τ. The accuracy corresponds to a single point of the ROC and is therefore a less informative measure, but is also easier to interpret.
In order not to bias the results by introducing knowledge from the test data in the evaluation, we use a leave one out scheme to compute the AUROC and the classification accuracy. For each scan s in the dataset, we build a training set 𝒯s consisting of all other available scans. From this scan-specific training set, we compute ws and use it to evaluate κs for the scan at hand. We also compute the threshold τ̂s that best separates the two classes (i.e., maximal classification accuracy) in 𝒯s. We use this value to compute a classification of the test scan by testing: κs ≶ τ̂s. After repeating these steps for all 383 scans in the dataset, we compute the ROC by thresholding {κs} at different values of τ, and the classification accuracy by comparing the automated classification given by κs ≶ τ̂s with the ground truth.
In addition to recording the AUROC and classification accuracy, we also evaluate the variance of the posterior distribution of the subfield volumes with and without sampling, i.e., with Equations 12 and 15 respectively. This allows us to quantify to what extent the error bars on the volumes are affected by the sampling.
4.4. Competing methods
We compare performance measures of LDA classifiers trained on the following volume measurements:
The whole hippocampus volume obtained by summing up the subfield volumes (computed using Equation 11) produced by the baseline method that relies on point estimates (described in Section 2.2). This benchmark allows us to quantify the additional information offered by subfield volumes. We denote these measurements as WH-PE (where WH stands for “whole hippocampus” and PE stands for “point estimate”).
The vector of subfield volumes (computed using Equation 11) produced by the baseline hippocampal subfield segmentation method that relies on point estimates. We abbreviate these measurements as SF-PE (SF stands for “subfield”).
The average subfield volumes (computed using Equation 14) obtained using the proposed MCMC sampling scheme. We abbreviate this method as SF-SP (where SP stands for “sampling”).
Finally, we use all the samples drawn with the algorithm in Table 1 to compute the decision boundary defined by w in Equation 18. In other words, each one of the N=6,000 MCMC samples computed for a subject is treated as a separate subject during training. This constitutes a richer representation of the data that allows the statistical classifier to account for the uncertainty in the volumes when learning the boundary between the two groups. When classifying a test subject, we only used the mean volumes computed over all MCMC samples of that subject (i.e., Equation 14). We denote this method as “SF-AS” (where AS stands for “all samples”).
5. Results
We first present a qualitative comparison between the proposed MCMC sampling-based segmentation framework and the baseline method that uses point estimates of the model parameters.
Both the sampling-based and baseline methods can be used to generate samples from the posterior of the segmentation. For the baseline method, this involves fixing the model parameters θ̂ and x̂ and drawing from an independent posterior distribution on labels (given by Equation 9) at each voxel. The sampling-based method produces such segmentation samples within the MCMC framework (see step 2B-Ia of Table 1). Figures 3 and 4 show examples of such segmentations for a representative subject obtained using the sampling-based and baseline methods, respectively. The two figures also show heat maps highlighting regions, in which the posterior segmentation samples disagree. Specifically, we define the disagreement ς = (ς1, …, ςI)T as the number of pairs of samples that have different labels at each voxel:
| (19) |
where δk(·) is Kronecker’s delta. This disagreement is a measurement of how confident the method is about the segmentation at a given voxel.
Table 2 summarizes the estimated uncertainty in hippocampal subfield volumes averaged across all 383 subjects. For the sampling method, this is computed using Equations 14–15. For the baseline method we used Equations 11–12. To further assess the relative impact of sampling from the Gaussian likelihood parameters θ, we computed the relative standard deviation when these are kept constant throughout the sampling (i.e., we skip step 2B-I in Table 1).
Table 2.
First row lists mean volumes of the subfields, computed with the sampling scheme, v̄k averaged across all 383 subjects. The second and third rows list the relative standard deviations of the subfield volumes (averaged across subjects), computed with the baseline (γk/vk) and sampling-based methods (γ̄k/v̄k). To quantify the relative effect of sampling the Gaussian likelihood parameters θ (compared with the registration parameters x), we also include the relative standard deviation computed based on a sampling scheme with fixed θ. We denote this alternative strategy via superscript x, i.e., the corresponding relative standard deviation is . These values are listed in the fourth row.
| Subfield | Fimbria | Presub. | Sub. | CA1 | CA2/3 | CA4/DG | Tail | Fissure |
|---|---|---|---|---|---|---|---|---|
| v̄k (mm3) | 73 | 440 | 484 | 351 | 773 | 381 | 298 | 49 |
| γk/vk (%) | 0.7 | 0.2 | 0.4 | 0.4 | 0.3 | 1.3 | 0.7 | 4.8 |
| γ̄k/v̄k (%) | 6.0 | 6.5 | 7.3 | 7.9 | 6.5 | 7.8 | 4.2 | 8.9 |
| (%) | 5.2 | 6.0 | 7.0 | 7.5 | 6.1 | 7.6 | 3.9 | 8.7 |
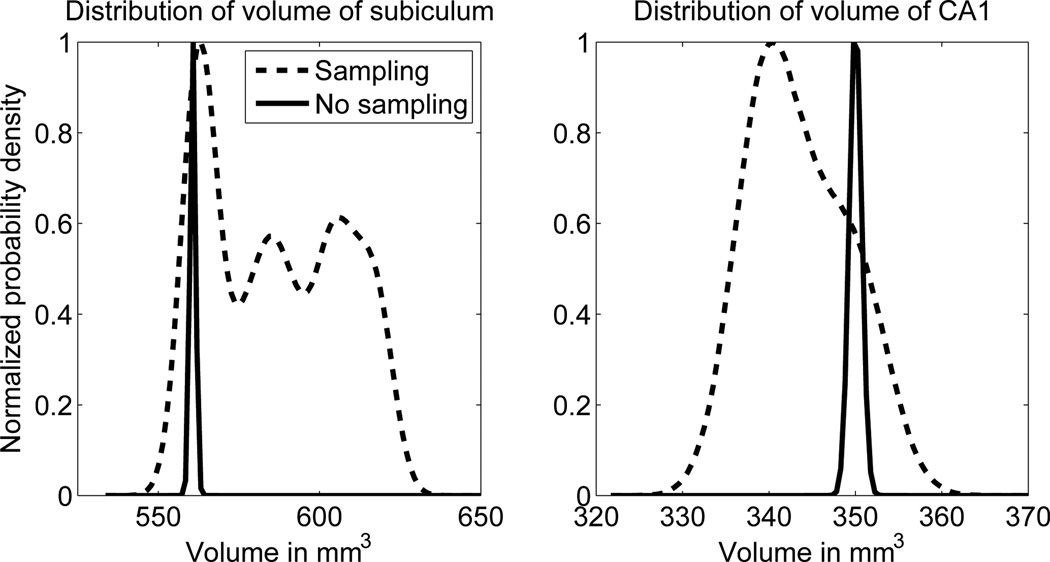
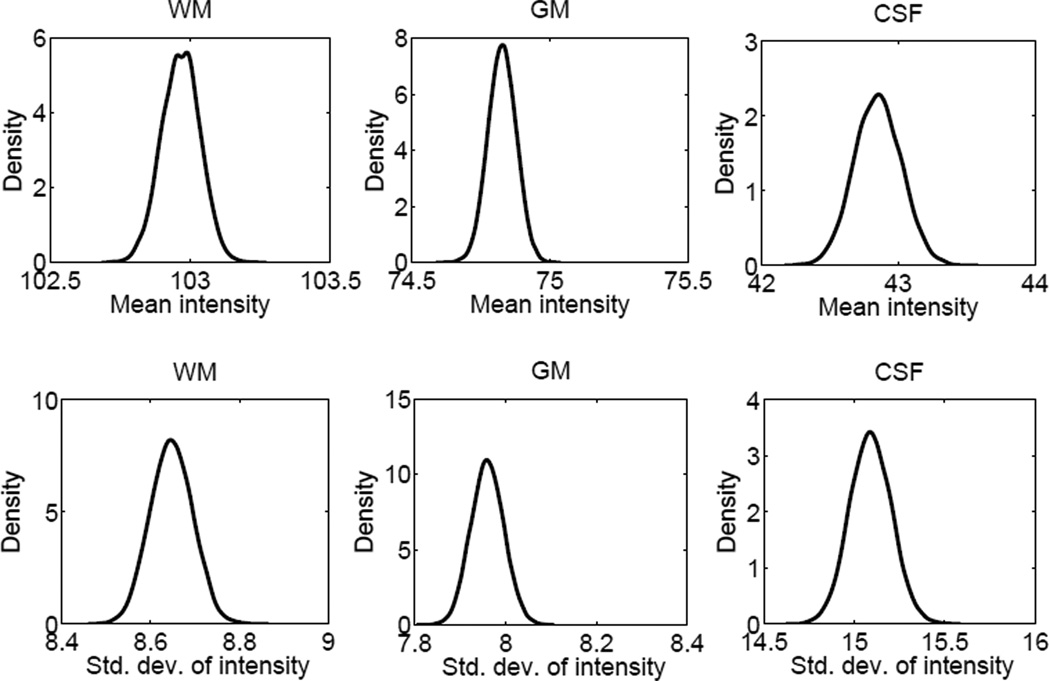
Figure 5 displays the posterior distribution of the volume measurements for two subfields (subiculum and CA1) in an example scan. For the proposed sampling scheme, these distributions were estimated using a Parzen window estimator. For the baseline method, the posteriors were approximated as Gaussians with mean and variance given by Equations 11 and 12. Here, the Gaussian assumption is reasonable thanks to the central limit theorem, since the total volume of a structure is the sum of the contributions from all the voxels, whose labels are assumed to be independent given the image and the model parameters (Equation 8). Figure 6 shows the posterior distributions of the Gaussian likelihood parameters (the mean and standard deviation of intensity values for each tissue type) computed using the sampling-based approach and Parzen window estimator on the MCMC samples.
Figure 5.
Posterior distribution of the volumes of the subiculum and CA1 for an example scan, computed with the proposed approximation of p(s|y) using sampling (Equation 13) and with p(s|x̂, θ̂, y), i.e., using point estimates of the model parameters. The former is computed using a Parzen window density estimate based on the samples recorded in step 2B-II of Table 1 with a Gaussian kernel of size σ = 4mm3, whereas the latter is approximated by a Gaussian distribution with mean and variance given by Equations 11 and 12. Both probability density functions have been normalized to [0,1] for easier visualization.
Figure 6.
Marginals of p(θ|y), the posterior distribution of the Gaussian likelihood intensity parameters for white matter, gray matter and CSF in an example scan, computed within the sampling framework. These distributions were computed using a Parzen window estimator on the samples recorded in step 2B-II of Table 1 and with a Gaussian kernel with σ = 0.01. The sharpness of the distributions (note the scale of the horizontal axis in all figures) indicates a very low uncertainty in the estimates of these parameters.
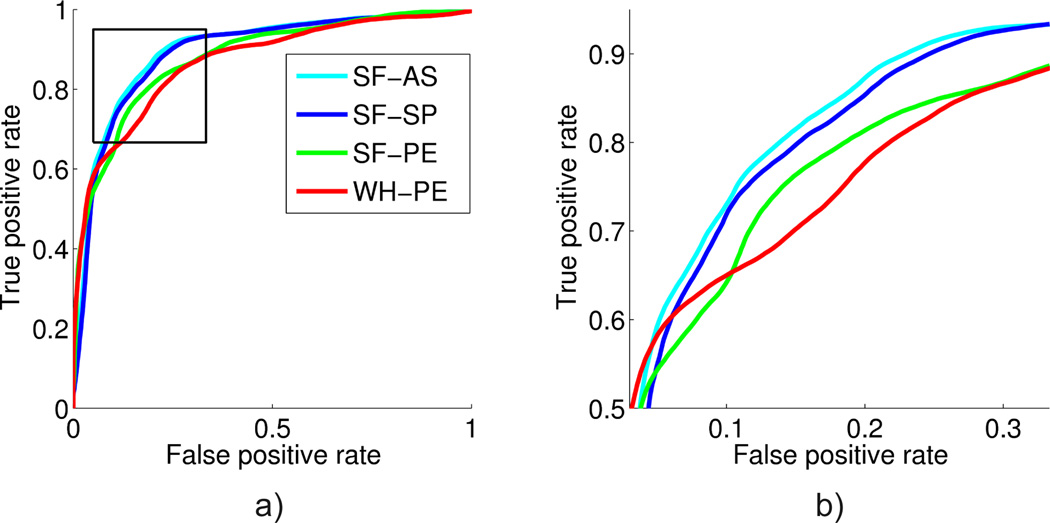
Finally, we present a quantitative evaluation of volume measurements obtained using different segmentation strategies. As we describe in Section 4.4, we use four different types of volume measurements to train a classifier to discriminate AD versus EC. Figure 7 shows the ROCs corresponding to these different measurements in the AD classification experiment. The corresponding AUROCs and accuracies are presented in Table 3. The table also displays pairwise p-values corresponding to De-Long paired statistical tests comparing the classification performance offered by the the different measurements.
Figure 7.
Receiver operating characteristic (ROC) curves for the competing methods. (a) Complete curve. (b) Detail of the top left corner (the “elbow”) of the curve, which is where the operating point would typically be located. This region is marked with a box in (a).
Table 3.
AD/EC classification accuracy at optimal threshold τ̂s, area under the ROC curve, and p-values for one-tailed DeLong statistical tests comparing the areas under the curve for all pairs of approaches. The subscripts of the p’s indicate the methods we are comparing.
| Method | Acc. | AUROC | pSF−SP | pSF−PE | pWH−PE |
|---|---|---|---|---|---|
| WH-PE | 79.9% | 0.872 | - | - | - |
| SF-PE | 82.0% | 0.878 | - | - | 0.022 |
| SF-SP | 83.8% | 0.892 | - | 0.025 | 0.013 |
| SF-AS | 84.3% | 0.898 | 0.083 | 0.018 | 0.013 |
6. Discussion
This paper investigated the use of Markov chain Monte Carlo (MCMC) sampling to approximate the segmentation posterior within a Bayesian framework. This approach is in contrast with classical Bayesian segmentation algorithms that rely on the mode approximation to integrate over the model parameters, including those describing atlas deformations. We used a database of 383 brain MRI scans and an atlas constructed for hippocampal subfield segmentation to explore the differences between the MCMC approach and a classical segmentation method (which we refer to as the “baseline”).
First we analyze the estimates of uncertainty computed by the MCMC method and the baseline. Theoretically, we expect the baseline to produce segmentation results that it is very confident about, since uncertainty in the model parameters is ignored. The MCMC results on the other hand should contain more uncertainty. Our experiments agreed with this expectation: there are more red/yellow voxels in the heat map of Figure 3 compared to Figure 4. Based on Figure 3, we observe that segmentation uncertainty for the MCMC method is higher in voxels close to boundaries between structures, and specifically between structures that belong to the same tissue type (e.g., CA4-DG and CA2/3, which are both gray matter structures). This reflects the fact that the atlas registration is not constrained by image intensities in those regions. In contrast, for the baseline algorithm (Figure 4) the only source of segmentation uncertainty is reduced atlas sharpness and/or partial voluming along structure boundaries, since uncertainties in the atlas deformation are entirely discarded.
We further explored segmentation uncertainty by computing error bars on the subfield volume measurements (see Table 2). In the baseline method, the relative standard deviation (i.e., the standard deviation divided by the volume, γk/vk) was well below 1% for most subfields, which we deem unrealistic given the poor image contrast. The values were significantly larger for the MCMC method, i.e., larger than 6% for most subfields. This difference is further highlighted in Figure 5, which displays the posterior distributions of two subfield volumes in an example subject, computed using the MCMC method and the baseline. Based on these plots, we make the observation that volume estimates obtained with the baseline method can deviate substantially from those obtained with the MCMC method, i.e., the mean of the distributions can be quite far apart. Furthermore, the uncertainty estimated by the MCMC method is dramatically higher than that computed with the baseline, which is in strong agreement with Table 2.
To examine the influence of the uncertainty in the Gaussian intensity likelihood parameters, we further computed the error bars for a modified MCMC method. In this modified version, we fixed the Gaussian intensity likelihood parameters and only sampled over the atlas deformation parameters (see last row of Table 2). These relative standard deviation values are slightly smaller than those obtained with the full MCMC implementation, which suggests that the uncertainty in the Gaussian intensity likelihood parameters has a relatively small contribution to segmentation uncertainty. Most of the segmentation uncertainty is due to the uncertainty in the atlas deformation, which contains many more model parameters. This point is further reinforced with Figure 6, which reveals the sharpness of the posterior distributions of the Gaussian intensity likelihood parameters.
Hippocampal subfields atrophy differentially in Alzheimer’s disease (Mueller et al., 2010). Thus, we utilized hippocampal subfield volume measurements to discriminate AD versus controls, using classification performance to indirectly quantify the quality of different volume measurements obtained from different segmentation schemes. Our results (illustrated in Figure 7) revealed that subfield volumes predicted AD above and beyond the total hippocampal volume: SF-PE offered ~ 2% boost in accuracy and a ~ 0.01 increase in AUROC (p = 0.022) over WH-PE. The ROC curves of these two methods might not appear very different, but there is a clear gap in the elbow (Figure 7b), which is the region with high classification accuracy, where the operating point would normally be defined. Secondly, and more importantly, subfield volume estimates obtained using the MCMC method were more predictive of AD than estimates computed using the baseline (an improvement of ~ 2% in accuracy, 0.014 in AUROC with p = 0.025). This suggests that volume measurements extracted from MCMC segmentations can be more accurate than those obtained with the baseline method. Finally, when all MCMC samples were used to train the classifier (SF-AS), a marginal improvement (though not statistically significant) was observed. This suggests that the uncertainty estimates offered by MCMC methods can be utilized to improve downstream analyses.
Overall, our empirical results are consistent with our theoretical expectations. In addition to potentially improving segmentation accuracy, the proposed MCMC method offers a strategy to obtain a more realistic quantification of segmentation uncertainty. As we demonstrated in the AD classification experiment, utilizing the uncertainty in the segmentation results might prove useful in various analyses. One immediate application would be to simply offer a quantification of the measurement confidence, as this may convey important information when these techniques are ultimately applied in clinical settings. Secondly, by examining segmentation uncertainty, one might be able to assess the effect of different parameters (e.g., the imaging modality) on segmentation quality without the necessity of ground truth. Finally, statistical power analyses commonly used to plan population studies might also benefit from accurate estimates of measurement error. For example, in a study designed to examine volume differences between two groups, one might be able to estimate the effect of improving segmentation quality on our ability to differentiate groups.
A drawback of the MCMC segmentation approach is its computational complexity. Another challenge is the fine-tuning of the sampling parameters, such as the trajectory length, step sizes, etc. Our experience suggests that these design choices can have a dramatic impact on computational efficiency. The current implementation we presented in this paper requires ~ 8 CPU hours to process an individual MRI scan, although we did not focus on optimizing run time since our main aim was to investigate the empirical advantages offered by the MCMC strategy. Note, however, that the MCMC sampling steps, which is the main computational bottleneck, is amenable to dramatic parallelization, and that the number of MCMC samples required to accurately compute the mean and variance of posterior volume distributions maybe be far less than the N = 6, 000 used in this paper.
The proposed MCMC sampling approach can also be applied to other probabilistic segmentation frameworks, such as Fischl et al. (2004b); Ashburner and Friston (2005); Pohl et al. (2006); Sabuncu et al. (2010). In doing so, one important consideration would be the number of free parameters in the models and identifying an efficient strategy to sample from the posteriors of these parameters. It is important to note that the baseline method we built on in this paper utilized a sparse atlas representation with a relatively low number of free parameters, which made it possible for us to implement an MCMC sampling strategy that was computationally practical. We are currently investigating whether similar techniques can also benefit whole brain segmentation, in which dozens of substructures are automatically segmented from brain MRI. Since the computational complexity of our atlas deformations depends mostly on the number of tetrahedra in the atlas rather than the number of voxels of the input image, we believe such an approach will be computationally feasible.
As the models used in Bayesian segmentation methods continue to grow in complexity, with a concomitant higher number of free parameters, we expect the relevance of accurate computational approximations to the true segmentation posterior to become increasingly important in the future.
Supplementary Material
Traditional Bayesian segmentation methods use point estimates (PE) for the model parameters
A more faithful analysis would marginalize over such parameters, which leads to an intractable integral.
Rather than using point estimates, we propose an improved inference method in which MCMC is used to approximate the integral.
The method beats PE at separating AD patients from controls using the volume of automatically segmented hippocampal subfields
Moreover, the proposed framework also provides informative error bars on the volume estimates
Acknowledgements
This research was supported by NIH NCRR (P41-RR14075), NIBIB (R01EB006758, R01EB013565, 1K25EB013649-01), NINDS (R01NS052585), NIH 1KL2RR025757-01, Academy of Finland (133611), TEKES (ComBrain), Harvard Catalyst, and financial contributions from Harvard and affiliations.
The collection and sharing of the data used in this study was funded by the ADNI (National Institutes of Health Grant U01 AG024904). ADNI is funded by the National Institute on Aging, the National Institute of Biomedical Imaging and Bioengineering, and through contributions from: Alzheimers Association; Alzheimers Drug Discovery Foundation; BioClinica, Inc.; Biogen Idec Inc.; Bristol-Myers Squibb Company; Eisai Inc.; Elan Pharmaceuticals, Inc.; Eli Lilly and Company; F. Hoffmann-La Roche Ltd and its affiliated company Genentech, Inc.; GE Healthcare; Innogenetics, N.V.; IXICO Ltd.; Janssen Alzheimer Immunotherapy Research & Development, LLC.; Johnson & Johnson Pharmaceutical Research & Development LLC.; Medpace, Inc.; Merck & Co., Inc.; Meso Scale Diagnostics, LLC.; NeuroRx Research; Novartis Pharmaceuticals Corporation; Pfizer Inc.; Piramal Imaging; Servier; Synarc Inc.; and Takeda Pharmaceutical Company. The Canadian Institutes of Health Research provides funds to support ADNI clinical sites in Canada. Private sector contributions are facilitated by the Foundation for the National Institutes of Health (www.fnih.org). The grantee organization is the Northern California Institute for Research and Education. The study is coordinated by the Alzheimer’s Disease Cooperative Study at the University of California, Rev. October 16, 2012 San Diego. ADNI data are disseminated by the Laboratory for Neuro Imaging at the University of California, Los Angeles. This research was also supported by NIH grants P30-AG010129 and K01-AG030514.
Appendix A
Mean and variance of the posterior distribution of the volume when sampling the model parameters
Here we derive the expressions for the mean and the variance of the posterior distribution of the volume corresponding to label k within the sampling framework (Equations 14 and 15). Let 𝒱k(s) denote the volume of class k in label map s. Then, the expected value of the posterior distribution of the volume is:
where is the expectation of the volume if the model parameters are fixed to {θ(n), x(n)}, in a similar way as in Equation 11.
For the variance, we have:
| (A.1) |
The first term in Equation A.1 is the average (over the samples) of the variances assuming that the model parameters are fixed to {x(n), θ(n)}. These variances, which we denote , can be computed in a similar way as in Equation 12:
In the second term of Equation A.1, the sum over the probability distribution is one, which simplifies the expression to . Finally, the third term is:
The final expression for the variance of the posterior distribution is therefore:
Appendix B
Hamiltonian Monte Carlo (HMC)
The details of the HMC algorithm are discussed in this appendix. Section Appendix B.1 describes how the Hamiltonian can be tracked to generate proposals, and discusses how the choice of parameters can affect the performance of the algorithm. Section Appendix B.2 discusses some modifications of the algorithm to improve its efficiency in our particular application.
Appendix B.1. Tracking the Hamiltonian using leapfrog
HMC alternates two proposals. In the first one, a new value for the momentum m is drawn from a Gaussian distribution with zero mean and identity covariance. This is a Gibbs proposal that is always accepted. The second proposal, which is the simulation of the Hamiltonian, requires tracking the change of x and m according to the equations:
In practice, these equations need to be discretized for simulation. We use the leapfrog algorithm (Hockney and Eastwood, 1988):
| (B.1) |
| (B.2) |
| (B.3) |
where ε is the step size. The proposal is generated by tracking the Hamiltonian for a predefined number of steps and, following Metropolis-Hastings, it is accepted with probability:
| (B.4) |
where Hini and Hend are the values of the Hamiltonian at the beginning and the end of the simulated trajectory, respectively. In the continuous version of the equations, the Hamiltonian is exactly preserved and the proposal is always accepted. However, the discretization introduces deviations from the continuous solution that might yield Hend > Hini and therefore ζ < 1.
There are two parameters to tune in the method: the trajectory length (i.e., the number of steps to simulate using Equations B.1–B.3) and the step size ε. Tuning ε can be difficult; very small steps keep H almost constant, producing high acceptance rates, but also render the algorithm inefficient. Large step sizes can potentially explore the space of x faster, but also lead to higher rejection rates, especially since a single component of x can already drive the Hamiltonian to infinity by collapsing a tetrahedron. Solutions to this problem are described in the next section.
We have assumed in Equations B.1–B.3 that the mass of the particle in the Hamiltonian dynamics is equal to one. This mass, which can be different for each component of m, can be set to a different value in order to match the ranges of Ep and Ek. When these are very different, very small step sizes might be required to track the Hamiltonian, decreasing the computational efficiency of the algorithm. In this study, such a correction was not necessary.
Appendix B.2. Improving the performance of HMC
To ameliorate the problems enumerated at the end of Section Appendix B.1, we use a number of modifications to the original HMC algorithm. The reason why these improvements do not undermine the proof that x ~ p(x|θ, y) can be found in Neal (1995). The modifications, all of which have associated parameters that were tuned using preliminary runs, are the following:
When the Hamiltonian deviates from its original value more than predefined threshold, the trajectory is discarded right away and the sample is rejected. This saves time by early terminating moves that are very likely to be rejected anyway. We found 5.0 to be a good value for this threshold in our application.
Rather than using a fixed trajectory length (time) and step size, we sample them from uniform distributions: the trajectory length from the interval [15, 50], and the step length from (0, 0.0025]. This allows for efficient exploration of different regions of the space, since there is always a chance that an appropriate step length is drawn. Moreover, if a large step length is used in a convoluted region of the probability density function, the error in the Hamiltonian will grow quickly and the trajectory will be early terminated without wasting too much computational time. These two factors outweigh the occasional inefficiency of using a step length that is too small.
We use the technique proposed in Neal (1992), which is based on transitions between windows of states, to improve the acceptance rate ζ. We set the window width to 7 states.
- We allow for preconditioning the space of x in order to reflect the differences in scale (size of tetrahedron) between its different components. The preconditioning can be achieved by using a different step length for each vertex of the atlas. Neal (1995) proposes the heuristic:
where xj is the jth element of x, η is a constant and x0 is a “representative” position. In our case, it is natural to use x0 = xref. Moreover, since we do not have any a priori knowledge about the image, we ignore the contribution of the likelihood to Ep. The heuristic becomes:
which, despite all the assumptions, conveys useful information about the topology of the mesh by assigning shorter step sizes to vertices associated with smaller tetrahedra. For each vertex in the mesh, we keep the smallest of the three corresponding step sizes (one for each spatial dimension); this ensures robustness against linear deformations (e.g. rotations). The constant η is set such that the median step length coincides with the desired maximum step length, which is 0.0025. We also clip the top and bottom 20% of the histogram of step lengths to aggressively remove outliers, which would lead to very large and small step sizes.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Data used in preparation of this article were obtained from the Alzheimers Disease Neuroimaging Initiative (ADNI) database (adni.loni.ucla.edu). As such, the investigators within the ADNI contributed to the design and implementation of ADNI and/or provided data but did not participate in analysis or writing of this report. A complete listing of ADNI investigators can be found at: http://adni.loni.ucla.edu/wp-content/uploads/how_to_apply/ADNI_Acknowledgement_List.pdf
References
- Allassonniére S, Amit Y, Trouvé A. Toward a coherent statistical framework for dense deformable template estimation. Journal of the Royal Statistical Society, Series B. 2007;69:3–29. [Google Scholar]
- Ashburner J, Andersson J, Friston K. Image registration using a symmetric prior – in three dimensions. Human Brain Mapping. 2000;9:212–225. doi: 10.1002/(SICI)1097-0193(200004)9:4<212::AID-HBM3>3.0.CO;2-#. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ashburner J, Friston K. Multimodal image coregistration and partitioning – a unified framework. NeuroImage. 1997;6:209–217. doi: 10.1006/nimg.1997.0290. [DOI] [PubMed] [Google Scholar]
- Ashburner J, Friston K. Unified segmentation. NeuroImage. 2005;26:839–851. doi: 10.1016/j.neuroimage.2005.02.018. [DOI] [PubMed] [Google Scholar]
- Awate S, Tasdizen T, Foster N, Whitaker R. Adaptive Markov modeling for mutual-information-based, unsupervised MRI brain-tissue classification. Medical Image Analysis. 2006;10:726–739. doi: 10.1016/j.media.2006.07.002. [DOI] [PubMed] [Google Scholar]
- Besag J. On the statistical analysis of dirty pictures. Journal of the Royal Statistical Society. Series B (Methodological) 1986:259–302. [Google Scholar]
- Boykov Y, Veksler O, Zabih R. Fast approximate energy minimization via graph cuts. Pattern Analysis and Machine Intelligence, IEEE Transactions on. 2001;23:1222–1239. [Google Scholar]
- Brown L. A survey of image registration techniques. ACM computing surveys (CSUR) 1992;24:325–376. [Google Scholar]
- Chupin M, Gérardin E, Cuingnet R, Boutet C, Lemieux L, Lehéricy S, Benali H, Garnero L, Colliot O. Fully automatic hippocampus segmentation and classification in alzheimer’s disease and mild cognitive impairment applied on data from ADNI. Hippocampus. 2009;19:579–587. doi: 10.1002/hipo.20626. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeLong E, DeLong D, Clarke-Pearson D. Comparing the areas under two or more correlated receiver operating characteristic curves: a nonparametric approach. Biometrics. 1988:837–845. [PubMed] [Google Scholar]
- Dempster A, Laird N, Rubin D. Maximum likelihood from incomplete data via the EM algorithm. Journal of the Royal Statistical Society. Series B (Methodological) 1977:1–38. [Google Scholar]
- Duane S, Kennedy A, Pendleton B, Roweth D. Hybrid Monte Carlo. Physics letters B. 1987;195:216–222. [Google Scholar]
- Fischl B, van der Kouwe A, Destrieux C, Halgren E, Segonne F, Salat D, Busa E, Seidman L, Goldstein J, Kennedy D, Caviness V, Makris N, Rosen B, Dale A, et al. Automatically parcellating the human cerebral cortex. Cerebral Cortex. 2004a;14:11–22. doi: 10.1093/cercor/bhg087. [DOI] [PubMed] [Google Scholar]
- Fischl B, Salat D, Busa E, Albert M, Dieterich M, Haselgrove C, van der Kouwe A, Killiany R, Kennedy D, Klaveness S, Montillo A, Makris N, Rosen B, Dale A. Whole brain segmentation: Automated labeling of neuroanatomical structures in the human brain. Neuron. 2002;33:341–355. doi: 10.1016/s0896-6273(02)00569-x. [DOI] [PubMed] [Google Scholar]
- Fischl B, Salat D, van der Kouwe A, Makris N, Segonne F, Quinn B, Dale A, et al. Sequence-independent segmentation of magnetic resonance images. NeuroImage. 2004b;23:S69–S84. doi: 10.1016/j.neuroimage.2004.07.016. [DOI] [PubMed] [Google Scholar]
- Fisher R. The use of multiple measurements in taxonomic problems. Annals of Human Genetics. 1936;7:179–188. [Google Scholar]
- Geman S, Geman D. Stochastic relaxation, gibbs distributions, and the bayesian restoration of images. Pattern Analysis and Machine Intelligence, IEEE Transactions on. 1984:721–741. doi: 10.1109/tpami.1984.4767596. [DOI] [PubMed] [Google Scholar]
- Greitz T, Bohm C, Holte S, Eriksson L, et al. A computerized brain atlas: construction, anatomical content, and some applications. Journal of Computer Assisted Tomography. 1991;15:26. [PubMed] [Google Scholar]
- Guillemaud R, Brady M. Estimating the bias field of mr images. Medical Imaging, IEEE Transactions on. 1997;16:238–251. doi: 10.1109/42.585758. [DOI] [PubMed] [Google Scholar]
- Held K, Kops E, Krause B, Wells W, III, Kikinis R, Muller-Gartner H. Markov random field segmentation of brain mr images. Medical Imaging, IEEE Transactions on. 1997;16:878–886. doi: 10.1109/42.650883. [DOI] [PubMed] [Google Scholar]
- Hockney R, Eastwood J. Computer simulation using particles. Taylor & Francis. 1988 [Google Scholar]
- Iglesias J, Sabuncu M, Leemput KV. ADNI. Incorporating parameter uncertainty in bayesian segmentation models: Application to hippocampal subfield volumetry. In: Ayache N, Delingette H, Golland P, Mori K, editors. MICCAI 2012. Springer Berlin / Heidelberg: 2012. pp. 50–57. volume 7512 of LNCS. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joshi S, Davis B, Jomier M, Gerig G, et al. Unbiased diffeomorphic atlas construction for computational anatomy. NeuroImage. 2004;23:151. doi: 10.1016/j.neuroimage.2004.07.068. [DOI] [PubMed] [Google Scholar]
- Kybic J. Bootstrap resampling for image registration uncertainty estimation without ground truth. Image Processing, IEEE Transactions on. 2010;19:64–73. doi: 10.1109/TIP.2009.2030955. [DOI] [PubMed] [Google Scholar]
- Leemput KV, Maes F, Vandermeulen D, Colchester A, Suetens P. Automated segmentation of multiple sclerosis lesions by model outlier detection. IEEE Transactions on Medical Imaging. 2001;20:677–688. doi: 10.1109/42.938237. [DOI] [PubMed] [Google Scholar]
- Levenberg K. A method for the solution of certain problems in least squares. Quarterly of applied mathematics. 1944;2:164–168. [Google Scholar]
- Lorenzo-Valdes M, Sanchez-Ortiz G, Mohiaddin R, Rueckert D. Segmentation of 4d cardiac mr images using a probabilistic atlas and the EM algorithm. Proceedings; Medical Image Computing and Computer-Assisted Intervention-MICCAI 2003: 6th International Conference, Montreal, Canada; November 15–18, 2003; Springer. 2004. p. 440. [Google Scholar]
- Maintz J, Viergever M. An overview of medical image registration methods. UU-CS. 1998 doi: 10.1016/s1361-8415(01)80026-8. [DOI] [PubMed] [Google Scholar]
- Marroquin J, Vemuri B, Botello S, Calderon E, Fernandez-Bouzas A. An accurate and efficient bayesian method for automatic segmentation of brain mri. Medical Imaging, IEEE Transactions on. 2002;21:934–945. doi: 10.1109/TMI.2002.803119. [DOI] [PubMed] [Google Scholar]
- Menze B, Van Leemput K, Lashkari D, Weber M, Ayache N, Golland P. A generative model for brain tumor segmentation in multi-modal images. Medical Image Computing and Computer-Assisted Intervention–MICCAI 2010. 2010:151–159. doi: 10.1007/978-3-642-15745-5_19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Metropolis N, Rosenbluth A, Rosenbluth M, Teller A, Teller E, et al. Equation of state calculations by fast computing machines. Journal of Chemical Physics. 1953;21:1087. [Google Scholar]
- Mueller S, Schuff N, Yaffe K, Madison C, Miller B, Weiner M. Hippocampal atrophy patterns in mild cognitive impairment and alzheimer’s disease. Human brain mapping. 2010;31:1339–1347. doi: 10.1002/hbm.20934. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murphy K. Technical Report. University of British Columbia; 2007. Conjugate Bayesian analysis of the Gaussian distribution. [Google Scholar]
- Neal R. An improved acceptance procedure for the hybrid monte carlo algorithm. 1992 arXiv preprint hep-lat/9208011. [Google Scholar]
- Neal R. Ph.D. thesis. University of Toronto; 1995. Bayesian Learning for Neural Networks. [Google Scholar]
- Pennec X, Thirion J. A framework for uncertainty and validation of 3-D registration methods based on points and frames. International Journal of Computer Vision. 1997;25:203–229. [Google Scholar]
- Pluim J, Maintz J, Viergever M. Mutual-information-based registration of medical images: a survey. IEEE Transactions on Medical Imaging. 2003;22:986–1004. doi: 10.1109/TMI.2003.815867. [DOI] [PubMed] [Google Scholar]
- Pohl K, Bouix S, Nakamura M, Rohlfing T, McCarley R, Kikinis R, Grimson W, Shenton M, Wells W. A hierarchical algorithm for mr brain image parcellation. Medical Imaging, IEEE Transactions on. 2007;26:1201–1212. doi: 10.1109/TMI.2007.901433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pohl K, Fisher J, Grimson W, Kikinis R, Wells W. A Bayesian model for joint segmentation and registration. NeuroImage. 2006;31:228–239. doi: 10.1016/j.neuroimage.2005.11.044. [DOI] [PubMed] [Google Scholar]
- Prastawa M, Bullitt E, Ho S, Gerig G. A brain tumor segmentation framework based on outlier detection. Medical Image Analysis. 2004;8:275–283. doi: 10.1016/j.media.2004.06.007. [DOI] [PubMed] [Google Scholar]
- Risholm P, Balter J, Wells W. Estimation of delivered dose in radiotherapy: the influence of registration uncertainty. In: Jiang T, Navab N, Pluim J, Viergever M, editors. MICCAI 2011. Springer Berlin / Heidelberg: 2011. pp. 548–555. volume 6891 of LNCS. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Risholm P, Pieper S, Samset E, Wells W. Summarizing and visualizing uncertainty in non-rigid registration. In: Jiang T, Navab N, Pluim J, Viergever M, editors. MICCAI 2010. Springer Berlin / Heidelberg: 2010. pp. 554–561. volume 6362 of LNCS. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roland P, Graufelds C, Whlin J, Ingelman L, Andersson M, Ledberg A, Pedersen J, Åkerman S, Dabringhaus A, Zilles K. Human brain atlas: For high-resolution functional and anatomical mapping. Human Brain Mapping. 2004;1:173–184. doi: 10.1002/hbm.460010303. [DOI] [PubMed] [Google Scholar]
- Sabuncu M, Yeo B, Van Leemput K, Fischl B, Golland P. A generative model for image segmentation based on label fusion. IEEE Transactions on Medical Imaging. 2010;29:1714–1729. doi: 10.1109/TMI.2010.2050897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simpson I, Woolrich M, Groves A, Schnabel J. Longitudinal brain MRI analysis with uncertain registration. In: Fichtinger G, Martel A, Peters T, editors. MICCAI 2011. Springer Berlin / Heidelberg: 2011. pp. 647–654. volume 6892 of LNCS. [DOI] [PubMed] [Google Scholar]
- Taron M, Paragios N, Jolly M. Registration with uncertainties and statistical modeling of shapes with variable metric kernels. Pattern Analysis and Machine Intelligence, IEEE Transactions on. 2009;31:99–113. doi: 10.1109/TPAMI.2008.36. [DOI] [PubMed] [Google Scholar]
- Thompson P, Mega M, Woods R, Zoumalan C, Lindshield C, Blanton R, Moussai J, Holmes C, Cummings J, Toga A. Cortical change in alzheimer’s disease detected with a disease-specific population-based brain atlas. Cerebral Cortex. 2001;11:1–16. doi: 10.1093/cercor/11.1.1. [DOI] [PubMed] [Google Scholar]
- Tu Z, Zhu SC. Image segmentation by data-driven markov chain monte carlo. Pattern Analysis and Machine Intelligence, IEEE Transactions on. 2002;24:657–673. [Google Scholar]
- Van Leemput K. Encoding probabilistic brain atlases using bayesian inference. IEEE Transactions on Medical Imaging. 2009;28:822–837. doi: 10.1109/TMI.2008.2010434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Leemput K, Bakkour A, Benner T, Wiggins G, Wald L, Augustinack J, Dickerson B, Golland P, Fischl B. Automated segmentation of hippocampal subfields from ultra-high resolution in vivo MRI. Hippocampus. 2009;19:549–557. doi: 10.1002/hipo.20615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Leemput K, Maes F, Vandermeulen D, Suetens P. Automated model-based tissue classification of MR images of the brain. IEEE Transactions on Medical Imaging. 1999;18:897–908. doi: 10.1109/42.811270. [DOI] [PubMed] [Google Scholar]
- Wells W, Grimson W, Kikinis R, Jolesz F. Adaptive segmentation of MRI data. IEEE Transactions on Medical Imaging. 1996;15:429–442. doi: 10.1109/42.511747. [DOI] [PubMed] [Google Scholar]
- West J, Fitzpatrick J, Wang M, Dawant B, Maurer C, Jr, Kessler R, Maciunas R, Barillot C, Lemoine D, Collignon A, et al. Comparison and evaluation of retrospective intermodality brain image registration techniques. Journal of Computer Assisted Tomography. 1997;21:554–568. doi: 10.1097/00004728-199707000-00007. [DOI] [PubMed] [Google Scholar]
- Xue H, Srinivasan L, Jiang S, Rutherford M, Edwards A, Rueckert D, Hajnal J. Automatic segmentation and reconstruction of the cortex from neonatal mri. Neuroimage. 2007;38:461–477. doi: 10.1016/j.neuroimage.2007.07.030. [DOI] [PubMed] [Google Scholar]
- Yeo B, Sabuncu M, Desikan R, Fischl B, Golland P. Effects of registration regularization and atlas sharpness on segmentation accuracy. Medical image analysis. 2008;12:603. doi: 10.1016/j.media.2008.06.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yushkevich PA, Wang H, Pluta J, Das SR, Craige C, Avants BB, Weiner MW, Mueller S. Nearly automatic segmentation of hippocampal subfields in in vivo focal t2-weighted MRI. NeuroImage. 2010;53:1208–1224. doi: 10.1016/j.neuroimage.2010.06.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y, Brady M, Smith S. Segmentation of brain MR images through a hidden Markov random field model and the Expectation-Maximization algorithm. IEEE Transactions on Medical Imaging. 2001;20:45–57. doi: 10.1109/42.906424. [DOI] [PubMed] [Google Scholar]
- Zheng Y, Barbu A, Georgescu B, Scheuering M, Comaniciu D. Fast automatic heart chamber segmentation from 3D CT data using marginal space learning and steerable features. Computer Vision, 2007. ICCV, 2007; IEEE 11th International Conference on, IEEE; 2007. pp. 1–8. [Google Scholar]
- Zijdenbos A, Forghani R, Evans A. Automatic” pipeline” analysis of 3-D MRI data for clinical trials: application to multiple sclerosis. IEEE Transactions on Medical Imaging. 2002;21:1280–1291. doi: 10.1109/TMI.2002.806283. [DOI] [PubMed] [Google Scholar]
- Zitova B, Flusser J. Image registration methods: a survey. Image and vision computing. 2003;21:977–1000. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.