Abstract
Collective cell invasion (CCI) through interstitial collagenous extracellular matrix (ECM) is crucial to the initial stages of branching morphogenesis, and a hallmark of tissue repair and dissemination of certain tumors. The collagenous ECM acts as a mechanical barrier against CCI. However, the physical nature of this barrier and how it is overcome by cells remains incompletely understood. To address these questions, we performed theoretical and experimental analysis of mammary epithelial branching morphogenesis in 3D type I collagen (collagen-I) gels. We found that the mechanical resistance of collagen-I is largely due to its elastic rather than its viscous properties. We also identified two strategies utilized by mammary epithelial cells that can independently minimize ECM mechanical resistance during CCI. First, cells adopt a narrow tube-like geometry during invasion, which minimizes the elastic opposition from the ECM as revealed by theoretical modeling of the most frequent invasive shapes and sizes. Second, the stiffness of the collagenous ECM is reduced at invasive fronts due to its degradation by matrix metalloproteinases (MMPs), as indicated by direct measurements of collagen-I microelasticity by atomic force microscopy. Molecular techniques further specified that the membrane-bound MMP14 mediates degradation of collagen-I at invasive fronts. Thus, our findings reveal that MMP14 is necessary to efficiently reduce the physical restraints imposed by collagen-I during branching morphogenesis, and help our overall understanding of how forces are balanced between cells and their surrounding ECM to maintain collective geometry and mechanical stability during CCI.
Introduction
Collective cell invasion (CCI) through fibrillar collagenous extracellular matrix (ECM) is a form of cohesive and guided multicellular movement that is observed in a variety of physiologic processes including tissue repair, blood vessel formation, and morphogenesis of branching organs such as lung, kidney, pancreas, salivary gland, and mammary gland.1-4 In addition, CCI is a key step in the dissemination of most solid tumors.3,5 A critical prerequisite for both physiologic and pathologic CCI is that cells employ effective strategies to overcome the physical constraints posed by structural and mechanical properties of collagenous ECM at invasive fronts.1,2,4,6,7 These constraints include space limitations due to the complex entanglement and pore distribution of the fibrillar ECM meshwork,7,8 particularly in dense ECM in which the average pore size is much smaller than the average cell size.7,9 ECM also poses mechanical resistance against the deformation caused by the compressive forces of expanding multicellular invasive front due to its viscoelastic properties.1,4 Cells predominantly employ degradative enzymes to overcome the resistance imposed by ECM during CCI.2,10,11 Of these enzymes, the family of matrix metalloproteinases (MMPs) is the most well studied.2,12 Consistently, CCI is abrogated using broad spectrum MMP inhibitors.13,14 Among the different MMPs, collagen-I is specifically degraded by both secreted collagenases (MMP-1, -8 and -13) and the cell-surface (membrane-type) collagenase MMP14 (a.k.a. MT1-MMP).14,15 However, MMP14 has proven indispensable to different invasive processes through collagen-I, including epithelial branching morphogenesis, tumor cell migration and angiogenesis.6,14,15
It has been postulated that ECM degradation at invasive fronts renders a softer, less resistant ECM, thereby facilitating invasion.1,4,7 However, direct evidence supporting this hypothesis remains unreported, and overall our quantitative understanding of how MMPs in general and MMP14 in particular compromise the structural and mechanical integrity of the ECM to facilitate CCI is still scarce.4,16 Accordingly, the goals of this study were three-fold: (i) to determine what are the mechanical barriers that dense fibrillar collagen poses to CCI, (ii) to determine what biophysical mechanisms are employed by cells to overcome these mechanical barriers, and (iii) to identify which of these mechanisms is MMP14-dependent.
To address our goals, we studied CCI in a physiological context by monitoring branching morphogenesis of phenotypically normal mammary epithelial cells (MECs) in 3D collagen-I gels.13,17 To assess quantitatively the micromechanical alterations of the ECM during branching, we used the nanotechnique atomic force microscopy (AFM),18 which can provide direct measurements of the Young’s Elastic Modulus (E)—indicative of resistance to deformation—of soft biological samples including ECM gels and cells with sub-micrometre resolution.18-20 AFM measurements demonstrated that mechanical resistance of collagen-I is reduced at invasive fronts, and genetic manipulations revealed that MMP14 is necessary for this localized reduction in ECM resistance. Additionally, theoretical modeling and morphometric analysis revealed that MECs undergoing branching morphogenesis optimize their geometries to further minimize elastic forces exerted by collagen-I fibers in order to facilitate branch formation and elongation.
Results
Tubular shapes with a thickness up to 3 cell diameters are the most frequent multicellular invasive geometries during early branching through collagenous ECM
Owing to the viscoelastic nature of collagenous gels,21 the invasion of multicellular expanding bodies is opposed by both elastic and viscous forces from the surrounding ECM. Theoretical models of contact elasticity and fluid mechanics predict that, in addition to a strong dependence of these forces on the elastic and viscous properties of the ECM, they depend also on the specific shape and size of the invasive body.22,23 Qualitative examination of MECs during early branching in 3D collagen-I gels (Fig. 1A and Supplementary Fig. 1 of the ESI†) revealed that an overwhelming majority of invasive bodies corresponded to narrow tubes, whereas few exhibited spherical shapes. Closer examination indicated that most tubular bodies could be modeled as either a truncated cone or a cylinder. We conducted a morphometric analysis on each multicellular protrusion of branching MECs consisting of: (i) measuring the width of the tip (wtip), the width of the base (wbase) of the last straight section of the protrusion, and the length of the whole protrusion (L); and (ii) labeling the protrusion as either a cylinder, cone, sphere or uncertain (i.e., commonly conical at the tip and cylindrical at the base), as illustrated in Fig. 1A. Computing the ratio wtip/wbase measured for over ~200 invasive bodies and plotting their relative frequency (%) clearly revealed two peaks centered at ~0.4 and ~0.9 (Fig. 1B). The peak at ~0.4 corresponds to the predicted value for a truncated conical body with a base thickness 2–3 cells greater than the tip thickness. The peak at ~0.9 is close to the value predicted for a cylinder. Comparing the computed wtip/wbase values with our visual geometrical labeling allowed us to score values below 0.5 as cones, and values above 0.75 as cylinders, whereas values in between were scored as uncertain. Based on this scoring, we assessed that 95% of invasive bodies corresponded to tubular sprouting, among which 47% exhibited a cylindrical shape, 31% were conical and 17% had an uncertain or mixed shape (Fig. 1B). To characterize the invasion through sharp ended tubules further, we measured the semiincluded angle (θ; see Fig. 1A) of invasive geometries scored as either cones or uncertain (wtip/wbase < 0.75). The frequency plot of θ data is shown in Fig. 1C, and revealed that ~70% of θ values fell within the narrow range of 10–20 deg, with a peak centered at 12.5 deg.
Fig. 1.
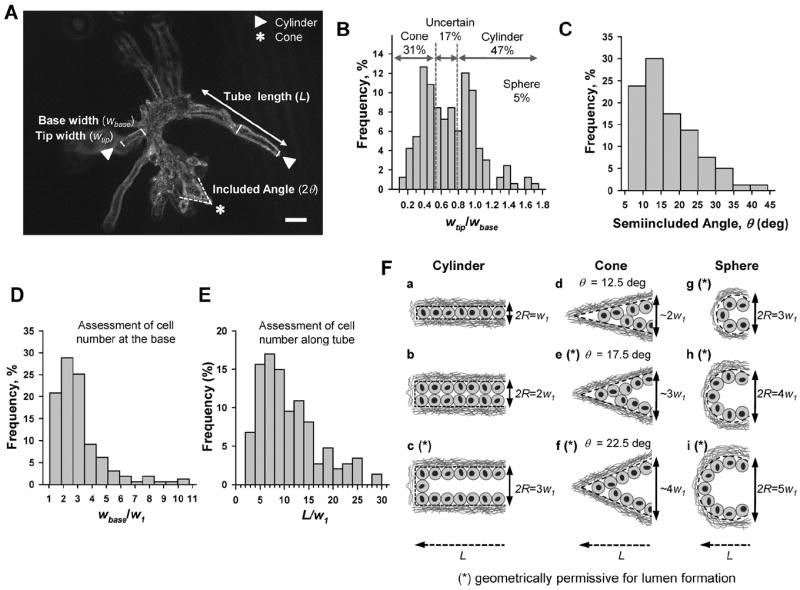
Morphometric analysis revealed the most frequent multicellular geometries during early invasion. (A) Representative phase-contrast image of a cluster of EpH4 cells in collagen-I (3 mg ml−1) induced to branch with FGF2 for 4 days. White arrow and stars point to invasive geometries labeled as cylindrical- or cone-like, respectively, by qualitative image examination. L, wbase and wtip were measured in each invasive body, whereas 2θ was measured on conical-like bodies only as shown in the image. Note that some branching structures are out of focus due to their large 3D size. Scale bar corresponds to 20 μm. (B–E) Normalized histograms of the ratio wtip/wbase (B), θ (C), wbase/w1 (D), and L/w1 (E) measured over ~200 invasive bodies. Details on the thresholds used to distinguish cones, cylinders and uncertain (mixed) geometries are given in the main text. For each image, w1 was taken as the minimum wtip. (F) Drawings illustrating the idealized most frequent cross-section invasive geometries based on combining one of the three most frequent widths (cylinder, sphere) or semiincluded angles (cone) with one of the most common and compatible tube lengths for cylinders (a–c), cones (d–f) and spheres (g–i) as found in the frequency plots (B–E). All lengths were scaled in units of the single cell width w1 to facilitate direct size comparisons. The asterisk (*) indicates those geometries theoretically permissive for lumen formation here and in Fig. 2 and 3. Likewise, the geometrical values and letters describing these idealized most frequent geometries were also used in Fig. 2 and 3.
MECs exhibit a round morphology both in vivo24,25 and in 3D culture,13,17,20 and the corresponding width or diameter of a single cell (w1) in 3D collagen-I gels has been previously determined to be within 5–10 μm, with an average value of 7 μm.26 Given the systematic round morphology of MECs and their well-defined average diameter, we assessed the most common sizes of the invasive bodies in terms of cell diameters. Because the overwhelming majority of invasive bodies had a single cell at the tip, as revealed by genomic DNA staining (Supplementary Fig. 1 of the ESI†), we first estimated w1 as the minimum wtip for each image, and used this value to assess the theoretical number of cells necessary to fill either the thickness of the base or the long axis of invasion as wbase/w1 and L/w1, respectively. The corresponding frequency plots are shown in Fig. 1D and E. The first plot exhibits a peak at 2 cells, and reveals a narrow distribution in which ~75% of invasive bodies were 1–3 cells thick at the base (Fig. 1D). The second plot shows a wider distribution in which ~50% of tubular shapes were 5–10 cells long (Fig. 1E).
Fig. 1F shows drawings illustrating the idealized invasive cross-section geometries based on the most frequent shapes and sizes found in our CCI assay after 4 days of branching induction. We considered w1 as the unit of length to facilitate direct comparison between these cross-sections. For each idealized shape (i.e., cylinder, cone and sphere) we drew three compatible combinations of the three most common values for the maximum width, length and θ (Fig. 1C–E). Furthermore, to identify those geometrical combinations potentially more permissive for lumen formation (identified with an asterisk in Fig. 1F), we used a simple theoretical approach based on drawing a monolayer of cells lining the boundary of each geometry and on considering cells as hard-spheres with equal width w1. These drawings revealed that all possible cylindrical geometries—characterized by their radius R–were compatible with all the most frequent maximum width (1–3w1) and length (~7w1) values (Fig. 1F, a–c). Unlike cylinders, the most frequent θ values restricted the width of the conical geometries to ≥ 3w1 and the length of the tube to ~5w1 (Fig. 1F, d–f). Likewise, the widths and lengths of the truncated spherical geometries characteristic of budding were restricted to ≥ 3w1 (Fig. 1E, g–h). These idealized illustrations revealed that less than half of the most common invasive geometries observed during early branching (Fig. 1E, a–e) are theoretically able to accommodate a lumen (Fig. 1E, c, e). In support of this prediction, we observed a modest appearance (<10%) of nuclei-free regions at the center of invasive bodies suggestive of lumen upon examination of nuclei distribution by confocal microscopy (data not shown). Collectively, these illustrations showed that cylindrical geometries give rise to longer tubes that are less permissive for lumen formation, whereas cones act otherwise.
Invasion through narrow tube-like geometry minimizes ECM viscoelastic resistance
The theoretical impact of the most common invasive geometries on the elastic (Fel) and viscous (Fvis) resisting forces posed by collagenous ECM in the direction of invasion (Fig. 2A) was assessed using analytical expressions reported elsewhere and described in eqn (4)-(8). To understand theoretically how cells overcome the elastic resistance imposed by the ECM during CCI, we first considered a simplified hypothetical scenario in which E of the ECM gel remains constant during invasion, which corresponds to a total absence of ECM remodeling. In this scenario, as the invasive multicellular body expands, it will cause a deformation or indentation on the surrounding ECM. Owing to its elastic properties, the ECM will oppose a force Fel against this deformation. To assess Fel, we took into account that the size of the ECM gel is much bigger than the size of any invasive body. In these conditions, Fel can be approximated by a suitable solution of the Boussinesq problem, which addresses the indentation of a semi-infinite elastic body (the ECM gel) subjected to a normal loading force imposed by an indenter of a given geometry (the invasive body).22 The solutions for the Boussinesq problem for the most frequent invasive geometries were derived elsewhere,22,27,28 and are shown in eqn (4)-(6). These solutions reveal that Fel depends on the geometry of the invasive body, the ECM indentation (δ), and E. Substituting the most common geometrical parameters reported in Fig. 1 and the average E measured with AFM on cell-free regions of collagen-I gels (E = 550 ± 80 Pa) in eqn (4)-(6) elicited the Fel vs. δ curves shown in Fig. 2B, where δ was set equal to the length of the invasive body. To facilitate the interpretation of these curves in terms of cell numbers, the δ axis was divided in units of w1 (using the average value of 7 μm here and throughout the text),26 and the maximum was set to the most common maximum length (7w1) (Fig. 1F). Fig. 2B shows that the four lowest Fel values corresponded to the two most common cylindrical and conical tubular geometries (a, b, d and e in Fig. 1F and 2B), which are non- or poorly- permissive of lumen formation. Conversely, the highest Fel values were observed with the least common geometries, which can readily accommodate a lumen (c and f–i in Fig. 1F and 2B). To analyze ECM elastic resistance to deformation further we computed the effective gel stiffness (keff) as a function of gel deformation as the first derivative of Fel with respect to δ (keff = dFel/dδ) (Fig. 2C). Consistent with Fig. 2B, the four lowest keff values for δ up to 7w1 corresponded to the two most common cylindrical and conical tubular geometries (Fig. 2C, a, b, d and e), and were on average ~3-fold smaller than keff values for spheres. Fig. 2C also revealed that keff of cylinders is largely δ independent, whereas keff of cones and spheres increases with δ as a power-law (δm), where m was 1 and 0.5, respectively. Collectively, our theoretical analysis indicated that, in the absence of ECM remodeling, the least common invasive geometries (i.e. spheres) will experience the highest resisting elastic opposition from the ECM, whereas the opposite applies to the most common geometries, which are non permissive of lumen formation.
Fig. 2.
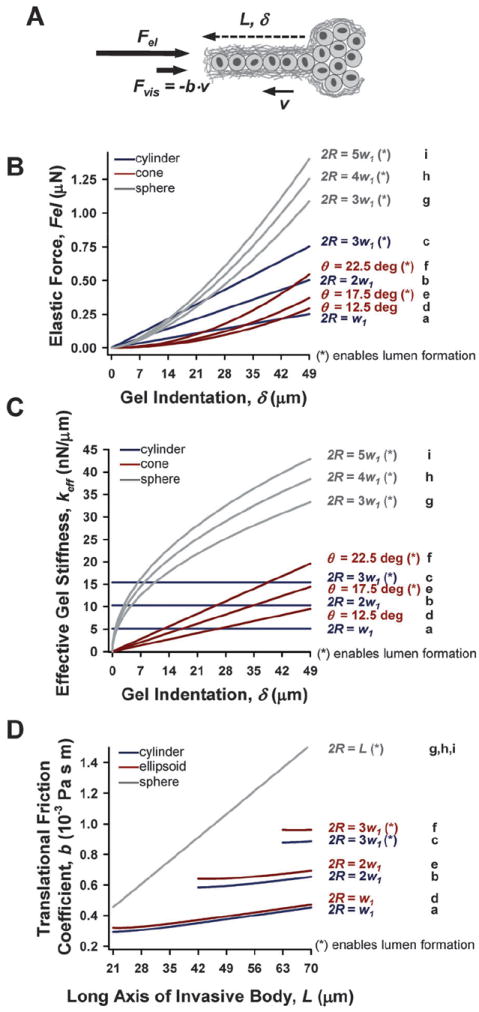
Theoretical simulations of the impact of the most frequent invasive geometries on Fel and Fvis in the absence of ECM degradation. (A) Drawing illustrating the ECM-dependent elastic and viscous forces acting on the tip of an invasive body in the direction of invasion, and the relevant geometrical parameters (L, δ and v). (B–C) Theoretical ECM elastic resistance against invasion was quantified as either Fel (B) or keff (C) as a function of gel indentation up to 7 cell diameters for the three most frequent cylindrical (blue), conical (red) and spherical (gray) invasive geometries as described in Fig. 1F. (D) Likewise, the Translational Friction Coefficient was used to assess the theoretical ECM viscous resistance for cylinders (blue), ellipsoids (red, used as surrogate for a cone), and sphere (gray) as a function of L. Note that the ticks in the x-axis are given in units of 7 μm, which corresponds to the average diameter of single MECs (w1).26 Formulas used in these simulations are shown in the main text. The letters a–i on the right side of each plot (B–D) correspond to the letters used in Fig. 1F, and are also used in Fig. 3.
Owing to the viscous properties of collagenous gels, invasive bodies will also be opposed by a viscous force Fvis, which depends largely on the geometry and velocity (v) of the invasive body, and the viscosity (η) of the collagenous gel. To assess Fvis in a first approximation, we treated the collagenous gel as a fluid. In these conditions, the specific expression for Fvis depends on the Reynolds number (Re) defined as Re = avρ/η,23 where a is the maximum width of the invasive body, and ρ is the density of the collagenous gel. Using the most common maximum L value (Fig. 1F) and the average w1 yielded v ~ 10−4 μm s−1. The average η value assessed by AFM was η ~ 2.3 Pa·s, in agreement with previous measurements in bulk.21 Combining v, η and the most common value for a from Fig. 1E elicited Re ≪ 1. In these low Re conditions, Fvis can be assessed as Fvis = −b·v, where b is the translational friction coefficient. Fig. 2D shows calculated b values as a function of L and w1 (Fig. 2A) for the most common invasive geometries. The b data were calculated using eqn (7)-(8), which correspond to a cylinder, an ellipsoid (used as a surrogate for a cone due to the non-availability of an analytical expression of b for a cone), and a sphere. Because eqn (8) is valid only for L ≫ thickness, b values for tubular geometries were plotted for L > 3w1, and up to 10w1 to enable visualizing b values for the thicker cones and ellipsoids (Fig. 2C, c and f). As in Fig. 2B–C, the four lowest b values corresponded to the most common tubular geometries, which are also non or poorly permissive for lumen formation (a, b, d, and e in Fig. 1F and 2D), whereas the highest b value corresponds to the spherical geometry (g–i in Fig. 1F and 2D). Nonetheless, irrespective of the specific invasive geometry, average values for b and v elicited Fvis ~ 10−6 μN, which is five orders of magnitude lower than theoretical values of Fel. Therefore, these theoretical calculations indicate that the mechanical resistance posed by the ECM against CCI is largely due to the elastic rather than the viscous properties of the ECM.
Tubular sprouting minimizes available surface area and enclosed volume, and maximizes the surface to volume ratio
A major physiological function of branching morphogenesis during development in vivo is to build epithelial trees that maximize the surface area of organs within a given volume to facilitate exchange of nutrients, metabolites, gases and wastes with the microenvironment.2,4 To examine whether these physiologically-dependent geometrical restrictions found in vivo were fulfilled also in our in CCI assay, we calculated the surface area (S), encapsulated volume (V) and the ratio S/V (Fig. 3B–D) of the most frequent invasive geometries for L values up to 7w1 as in Fig. 2. For this purpose, we chose the ideal shapes that capture the most common invasive geometries more faithfully by modeling tubular sprouting with either a cylinder or a truncated cone, and spherical budding with a truncated sphere, i.e. a sphere devoid of a spherical cap of height h, as described in Fig. 3A. For the truncated cone we considered R = w1/2, which corresponds to a single cell at the tip as illustrated in Fig. 1F. For the truncated sphere we used h = R/3 based on the most frequent thicknesses of our CCI assay (Fig. 1D, F), and R was calculated using the relationship 2R = L + h as illustrated in Fig. 3A. Our calculations showed that, in addition to minimize Fel and b, the four more common tubular geometries also minimized both S and V, whereas they maximized the ratio S/V (Fig. 3B–D). These calculations also point out that the narrowest cylinder (Fig. 3D, a) was particularly efficient in maximizing the ratio S/V, since it rendered a ratio after 7w1 that was three-fold larger than the average ratio of the other tubular geometries.
Fig. 3.
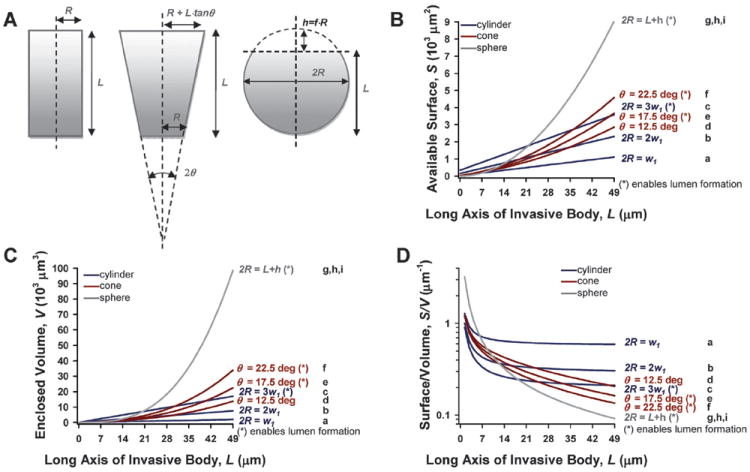
Theoretical simulations of the impact of the most frequent multicellular geometries during early invasion on their topology. (A) Drawings defining the relevant geometrical parameters used to simulate the topological parameters for a cone, a truncated cone, and a truncated sphere that best capture the most frequent invasive geometries. (B–D) Plots showing S, V and S/V as a function of L up to 7 cell diameters for the three most frequent geometries using the same color coding and x-axis ticks as in Fig. 2. The most frequent geometrical values described in Fig. 1F were considered in the topological calculations. Details on all the geometrical values and formulas used in these calculations are given in the main text. Note that only one curve is shown for the spherical geometry in B–D, since the values for L and R are not independent, but related by 2R = L + fR as shown in A. As in Fig. 2, w1 was taken as the average MEC diameter.26
MECs minimize ECM elastic resistance further through local proteolytic degradation at invasive fronts
There is solid evidence that ECM undergoes remodeling during CCI, and that ECM degradation driven by MMPs is a common key initial process in driving this remodeling.2,16,29 In the context of mammary branching morphogenesis, previous studies reported an absolute requirement for MMPs in branching of MECs in collagenous gels.2,13 Accordingly, it is conceivable that MECs could minimize Fel further by locally degrading the ECM, thereby down-regulating E of the collagenous gel at invasive fronts. To test this hypothesis, we used AFM to measure locally E of gels either at invasive fronts or > 100 μm away from cell clusters in the absence or presence of the broad spectrum MMP inhibitor GM6001 (40 μM) as illustrated in Fig. 4A. Only the closest invasive bodies to the gel surface (< 25 μm in depth) were considered to guarantee that our AFM measurements were not biased by large differences in the depth of the cell clusters within the gel (see methods and Supplementary Fig. 2 of the ESI†). We found that the average E at invasive fronts was nearly half the average E measured far from cell clusters (Fig. 4B). Furthermore, this dramatic ECM softening at the edge of invasive bodies was abrogated with GM6001, thereby supporting our hypothesis that ECM softens locally at invasive fronts, and that this softening is driven by MMP-dependent local degradation.
Fig. 4.
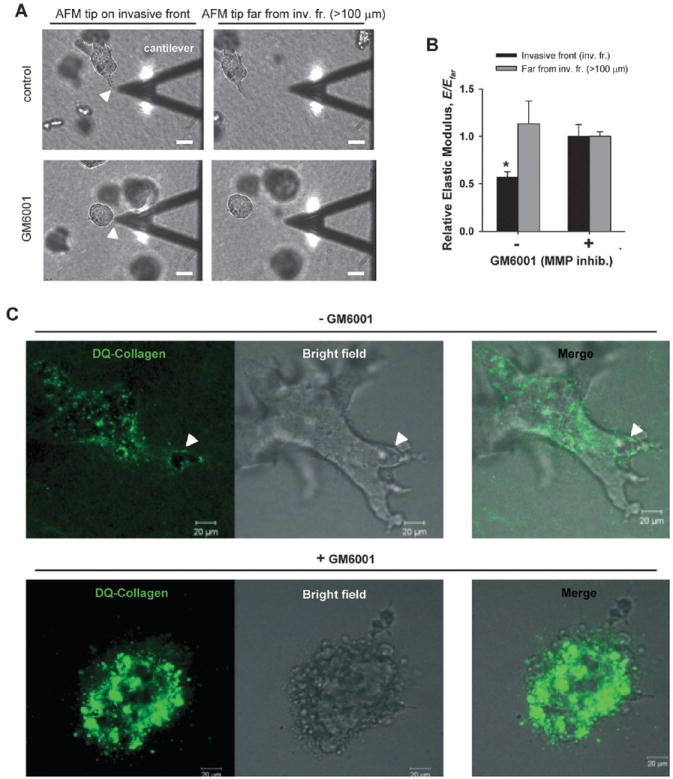
Assessment of local ECM degradation and softening at invasive fronts by AFM and confocal microscopy. (A) Representative bright-field (BF) images illustrating the spatial localization of the AFM measurements. Only the cell clusters closest to the gel surface (< 25 μm in depth) were considered, which correspond to cell clusters nearly in focus with the AFM cantilever (see methods for details). For each cell cluster, the tip of the AFM cantilever was positioned at the very edge of either an invasive tubule (top left) or a non-invasive cluster (bottom left), the corresponding E was measured, and normalized afterwards with respect to E measured far (> 100 μm) from the cell cluster (Efar) (right images). White arrow points to an invasive front (top left image) or an edge of a non-invasive cluster (bottom left image). Scale bars correspond to 40 μm. (B) Normalized E data obtained in the absence or presence of GM6001. *P < 0.05 between normalized data obtained at the cell cluster edge or far from it. (C) Confocal sections (left images) showing collagen filaments surrounding the middle of a cell cluster embedded in 3D collagen-I gel containing fluorescent DQ-Collagen and untreated (top images) or treated (bottom images) with GM6001. Corresponding BF and merged images are shown in the middle and right of each panel. The arrows (top left) point to an area void of DQ-Collagen fluorescence in the untreated cells, whereas such void areas were absent or randomly distributed in GM6001 treated cells. The full series of confocal sections are shown in Supplementary Fig. 3 of the ESI†. Scale bars correspond to 20 μm.
To analyze the extent of this local collagenous degradation, we repeated the branching experiments with cell clusters embedded in regular collagen-I mixed with dye quenched collagen (DQ-Collagen), which enables direct visualization of collagen filaments by fluorescence microscopy owing to the large number of fluorescent dyes present along the DQ-Collagen.7,30 Representative confocal images and corresponding bright field images of branching MECs are shown in Fig. 4C (the full confocal stack is available in Supplementary Fig. 3 of the ESI†). The white arrows in the left panel point to an area void of DQ signal located at the very front of an invasive body. Such areas void of DQ-signal were consistently observed at invasive fronts, whereas they were barely observed and randomly distributed in non-branching clusters or in clusters treated with GM6001 (more examples shown in Supplementary Fig. 4 of the ESI†). Morphometric analysis of the areas void of DQ-signal revealed an average width of 25–40 μm, which is slightly larger than the depth of invasive bodies probed with AFM. These findings indicate that the local ECM softening measured at invasive fronts spatially matched the appearance of areas void of fluorescent signal, which is indicative of degradation of filamentous collagens.
Relationship between elasticity and concentration of collagen gels is well captured by current models of semiflexible polymers
To understand quantitatively how local collagen degradation (i.e., reduction in concentration) leads to gel softening, we conducted two complementary experiments. First, we treated a cell-free 3 mg ml−1 collagen-I gel with exogenous bacterial collagenase up to 60 min. This enzymatic degradation induced a dramatic disappearance of collagen filaments as revealed by confocal reflection microscopy (CRM) (Fig. 5A).7 We also measured how collagenase altered the mechanics of the gel and found a five-fold decrease in E as measured by AFM (Fig. 5B). Therefore, as in our branching assay, we observed that collagenase-dependent gel softening was associated with loss of fluorescence signal indicative of degradation of collagen filaments. Second, we measured E on gels prepared at different collagen concentrations (c) (1–4 mg ml−1), and observed a marked gel stiffening with increasing c (Fig. 5C). Current models of semiflexible polymers, which were developed to describe the mechanical characteristics of filamentous proteins entangled without permanent crosslinks, predict that E depends on the average length between entanglements (Le), the average mesh size or void length between filaments (ε), and c.31 For semi-diluted polymers (Le ≫ ε), these models predict E ~ c2.2, whereas they predict the slightly stronger dependence E ~ c2.5 for densely crosslinked concentrated gels (Le ~ ε). We conducted a morphometric analysis of CRM images of cell-free collagen gels with Image J and estimated Le ~ 2 μm and ε ~ 0.8 μm, thereby suggesting that our collagen gel could be modeled as a semiflexible semi-diluted polymer. Consistently with this morphometric analysis, we found a slightly better fitting of E vs. c data for semi-diluted (r2 = 0.97) instead of concentrated (r2 = 0.94) crosslinking (Fig. 4F). These data reveal that reduction of collagen concentration by collagenolytic degradation is an efficient strategy to soften a collagenous gel, and highlight the suitability of current models of semiflexible polymers to describe E vs. c data for collagen gels.
Fig. 5.
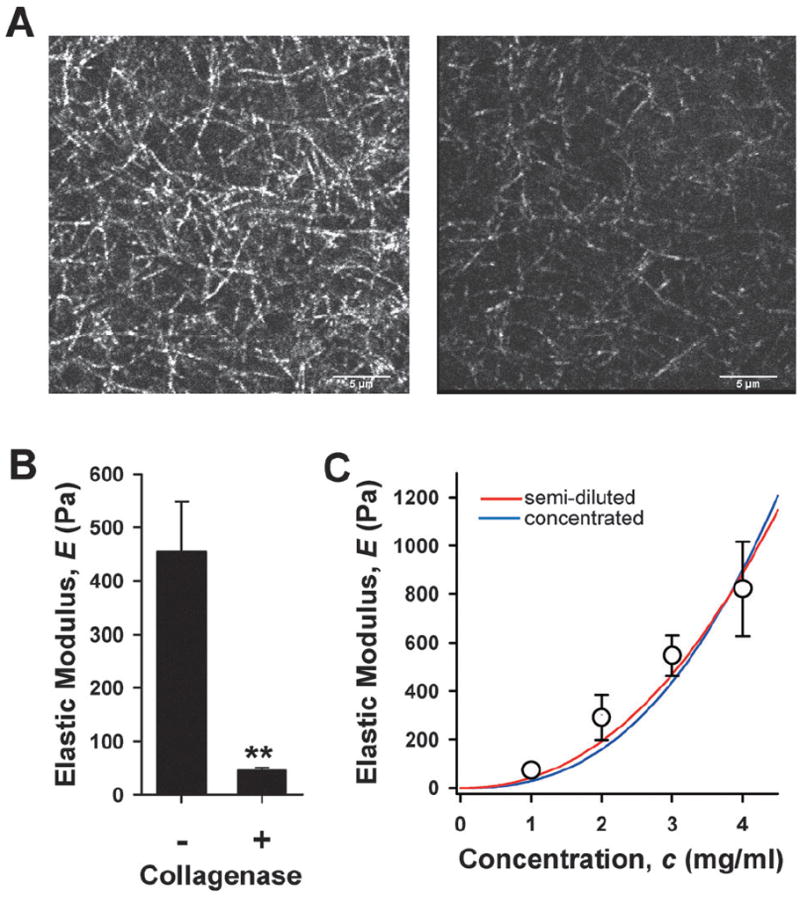
Structural and elastic properties of cell-free collagen-I gels untreated or treated with exogenous collagenase. (A) Representative confocal sections of collagen filaments obtained by CRM corresponding to an untreated or a collagenase treated (up to 60 min) 3 mg ml−1 collagen-I gel. Scale bars correspond to 5 μm. (B) E of untreated or collagenase treated collagen-I gels measured by AFM. **P < 0.01. (C) E of different concentrations of cell-free collagen-I gels measured by AFM. Data were fitted to semiflexible polymer models corresponding to semi-diluted (red) or concentrated (blue) gels.
MMP14 is required for rendering a softer collagenous ECM at invasive fronts
Previous studies reported that MMP14 is required for branching morphogenesis of normal MECs.2,17 Thus, we hypothesized that this specific MMP is necessary for the collagenase-dependent local softening observed at invasive fronts. To test this hypothesis, we used genetic manipulations to either increase or decrease MMP14 expression by infecting our mouse MEC model (EpH4 cells) with lentivirus containing cDNA for MMP14 and for shRNA against it, respectively. This genetic approach rendered two stable EpH4 cell lines that efficiently either overexpressed MMP14 (Fig. 6A) or downregulated it (Fig. 6C), as revealed by western-blotting and RT-PCR, respectively. MMP14 overexpression enhanced branching in 3D collagen gels by increasing the relative length per branching tubule (Fig. 6B and Supplementary Fig. 5 of the ESI†). Conversely, shRNA targeting MMP14 abrogated branching (Fig. 6D). In concert, we observed that MMP14 overexpressing cells rendered the collagen gel nearly 50% softer at invasive fronts than regions of the gel > 100 μm away from cell clusters, consistent with control experiments with untransfected cells (Fig. 4B) and with the elevated basal expression of MMP14 (Fig. 6A). In contrast, clusters of shRNA-treated MECs did not branch, and the E of the collagen surrounding these clusters was unaltered compared to collagenous ECM > 100 μm away (Fig. 6E). These data indicate that MMP14 is necessary to reduce the elastic resistance of pericellular collagen-I to facilitate branching.
Fig. 6.
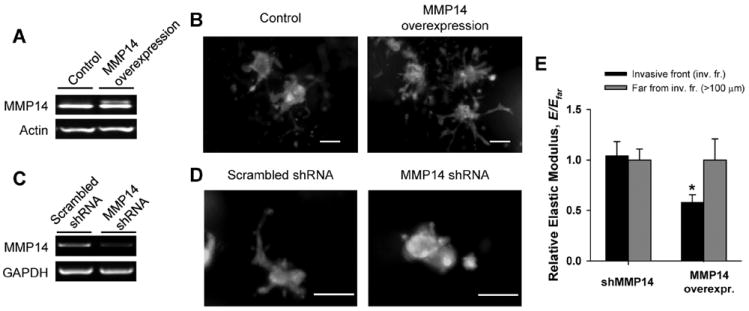
Effect of MMP14 increased or reduced expression on ECM mechanical integrity. (A–B) MMP14 overexpression experiments: EpH4 cells were stably transfected with MMP14. (A) Western-blotting showing increased MMP14 activity of transfected EpH4 cells with respect to control. (B) Representative epifluorescence images of control or MMP14 overexpressing cells stained with the live dye Calcein AM. Note that MMP14 overexpressing cells exhibited longer tubules. (C–D) Reduced MMP14 expression experiments: (C) PCR gel showing a reduction in MMP14 expression in EpH4 cells stably transfected with shRNA against MMP14 with respect to scrambled shRNA control. (D) Representative epifluorescence images of control or transfected cells stained with Calcein AM. Note the absence of branching structures in the MMP14 shRNA transfected cells. (E) Normalized E data of either MMP14 shRNA or MMP14 transfected EpH4 cells measured by AFM. *P < 0.05 between normalized E at the invasive front or far from it. All scale bars correspond to 200 μm.
Discussion
By combining morphometric analysis and theoretical modeling with AFM and confocal microscopy measurements, we found that ECM mechanical resistance is largely due to its elastic properties (as opposed to its viscous properties), and identified two strategies used by MECs to reduce ECM elastic resistance during early CCI: an optimized geometry and an MMP14-dependent local ECM softening at invasive fronts.
ECM resistance against CCI is dominated by its elastic properties
Branching morphogenesis and other types of CCI are particular manifestations of the expansion of a biological material within another, a general physical process known as a moving boundary problem (MBP). Several models are available to describe MBP based on either the laws of fluids or deformable solids.1 Previous studies on MEC branching morphogenesis suggested that this invasive process could be described using fluid-based MBP models.4 However, two pieces of evidence reported in our study and elsewhere strongly suggest that CCI should be described using the laws of deformable solids. First, branching of MECs cells through a collagenous gel is a low speed process (~10 μm day−1). In these conditions, the opposing force due to viscous properties of collagen-I gels is 5 orders of magnitude smaller than the opposing force due to its elastic properties. Likewise, similar low invasive speeds have been observed in other CCI assays in collagen-I gels7,13,16,32-35 and in other ECM gels (e.g., Matrigel and fibrin)36-38 that are known to exhibit an E within the same range of collagen-I.20 Second, the viscoelasticity of epithelial cells, collagen gels and collagenous tissues is dominated by elastic rather than viscous stresses at the relevant time-scales for CCI,19,21 even after proteolytic degradation.10,11 Accordingly, we argue that ECM mechanical opposition is largely determined by its elastic properties, whereas viscous forces are negligible in opposing CCI. In addition, these data indicate that CCI should be physically modeled as a deformable body (i.e., a multicellular structure) expanding within another deformable body (i.e., the ECM). The implications of this modeling in terms of the mechanical and shape stability of invasive bodies are addressed at the end of the discussion.
The average E of cell-free collagen gels measured with AFM (Fig. 5C) was consistent with bulk measurements reported elsewhere at similar semi-diluted concentrations,39,40 and fell within the physiological range reported for mouse mammary tissue.41 We also observed that E of cell-free gels scaled with c roughly as E ~ c2 (Fig. 5C). This dependence is well captured by current models of semiflexible semidiluted polymers in which the fibril length is larger than the pore or mesh size.31,42 In agreement with our data, similar scaling of E with c has been recently reported in bulk measurements. 30,39,40 These findings underline that molecular processes that elicit an imbalance in collagen turnover and c may be very efficient in modifying the elasticity of collageneous ECM, which is a critical aspect of the maintenance of tissue-specific function and architecture in mammary and other collagen-rich tissues.20,41
Biomechanical strategies for overcoming ECM physical resistance against CCI during early invasion
ECM poses steric obstacles against CCI owing to its entangled 3D structure that delineates pore or mesh sizes often smaller than typical cell thicknesses.7,8 In our assay, we assessed an average pore size of < 1 μm, which is smaller than the average MEC diameter.24 Likewise, previous morphometric studies of 1–3 mg ml−1 collagen gels reported pore sizes smaller than the nominal diameter of single MECs.39,43 In contrast, invasive bodies after 4 days of branching were typically 2–3 cells wide (Fig. 1D), which corresponds to a thickness of ~ 15–20 μm (i.e., twenty-fold larger than the assessed average pore size). Some poorly adhesive cells including immune, dendritic and cancer cells may be able to accommodate shape and migrate as single cells through collagenous gels without proteolytic degradation.14,44 However, shape accommodation is an unfeasible and/or inefficient strategy in CCI given the larger thicknesses of multicellular invasive bodies compared to collagen pore sizes, the increased ECM adhesion due to binding to the surrounding collagenous ECM, and the limited deformability of both mammary rudiments and single epithelial cells.20
The quantitative theoretical and experimental analysis conducted for early MEC invasion during branching morphogenesis enabled the identification of efficient strategies for overcoming ECM resistance. The identification of narrow tube-like shapes as the most frequent invasive geometries (Fig. 1) and the subsequent theoretical analysis of the impact of these invasive geometries on ECM elastic resistance (Fig. 2) revealed that they were optimal in reducing opposing mechanical forces exerted by ECM. The most frequent invasive geometries were identified as narrow cones and cylinders, and do not appear to be restricted to EpH4 cells, but they are rather ubiquitous judging by qualitative image examination of different CCI processes through collagenous gels reported elsewhere for non-malignant epithelial cells from mammary13,16,32 and other tissues,33-35,45 as well as in cancer cells.3,46 The relative abundance of both the thinnest cylinders and cones is consistent with the similarity of their respective Fel values (Fig. 2B). This similarity suggests that the probability of finding the thinnest cone or cylinder is very close, and may ultimately be modulated by small local differences in cellular and/or ECM-dependent physical processes, including: (i) the invasion depth; (ii) the spatial heterogeneity of E of gels and cells; (iii) the heterogeneity of pore size distribution, and (iv) a potential cell preference for lower keff, which is consistent with our data and with a recent observation that cells can respond directly and rapidly to changes in keff.47
In addition to reducing ECM resistance, narrow tube-like invasive geometries minimize S and V of invasive bodies, but maximize the ratio S/V (Fig. 3). We can envision functional advantages to invasion provided by these topological aspects. High S/V may facilitate cellular exchange of products with the surrounding microenvironment,2,4 whereas low V implies that invasion can proceed with a small number of cells. On the other hand, low S implies that fewer cell-cell and cell-ECM adhesions are required during early branching. Therefore, these topological features could increase the efficiency of CCI during development, repair and tumor invasion, since the required cellular resources are theoretically reduced.
In the absence of ECM remodeling, our simulations minimizing elastic ECM resistance for the most common invasive geometries yielded Fel ~ 0.25 μN for gel deformations up to 7 cell diameters (Fig. 2B). These simulations are likely an underestimation, provided the strain-hardening effect reported in collagenous gels.9,42 To put this force scale in biological perspective, previous AFM studies showed that compressive forces of ~0.1 μN applied locally on the surface of single cells with an AFM tip were sufficient to compromise the mechanical integrity of multiple cell types.48,49 Although ECM elastic resistance is distributed over the expanding body rather than acting locally within a single cell, these data suggest that ECM elastic forces in the direction of invasion can be large enough to become unbearable for invasive bodies enclosing few cells, which corresponds to the most frequent geometry of our branching assay. Accordingly, these findings strongly suggest that reduction of ECM elastic forces by an optimized geometry is not sufficient, supporting the requirement for ECM degradation during CCI. Consistently, we observed localized ECM degradation and softening at invasive fronts (Fig. 3), in agreement with a long-standing hypothesis in the field.1,4,7 In this context it is worth noting that this localized ECM remodeling may facilitate CCI through separate processes that may occur coincidentally. First, collagen degradation removes steric obstacles at invasive fronts, thereby increasing the room available to accommodate the thickness of the invasive body (i.e., a path clearing function), and/or facilitating the assembly of tracks that are filled by following cells (i.e., path-generating function).15 Second, because opposing Fel increases linearly with E of the collagen gel, a reduction of E will have a direct and proportional impact in reducing opposing elastic forces according to eqn (4)-(6). Third, local gel softening creates a stiffness gradient within the ECM, which may act as a migratory cue on its own.9,50 Finally, there is evidence that degraded fibrillar collagens per se can stimulate growth.2
Role of MMP14 in overcoming collagenous ECM physical resistance against CCI during early invasion
Our experiments revealed that MMP14 activity in EpH4 cells was necessary to efficiently reduce mechanical and structural collagen-I obstacles at invasive fronts in our branching assay (Fig. 6). This finding is consistent with the sustained elevated MMP14 expression found in EpH4 cells at the tips of engineered mammary tubules in collagenous gels,17,51 and with the fact that MMP14 is localized at the cell membrane, where it is present in its active form.6 To our knowledge, these data are the first direct experimental evidence of a previously suspected role for MMP14 in compromising the mechanical integrity of the ECM.7 Because MMP14 is elevated at the leading edge of mouse mammary and ureteric ducts in vivo,52,53 and at invasive fronts of breast cancer cells cultured in 3D collagen gels,7 we hypothesize that the efficiency of MMP14 in removing ECM physical obstacles is not restricted to EpH4 cells, but it is rather a general hallmark of epithelial CCI. In support of this hypothesis, a large body of evidence indicates that MMP14 is an essential pericellular collagenase during development, tumor growth and angiogenesis.6,12,15
Balance of forces during morphogenic CCI
The ultimate functional goal of mammary branching morphogenesis and other types of epithelial morphogenic CCI is to build a network of hollowed epithelial tubes (ducts) that transport vital fluids or gases to or from specialized spherical cavities (referred to as cysts, alveoli or acini) in an efficient manner.3,45 This is a very complex process, as it requires the concurrence of different cell types, soluble factors, ECM components, and a tight spatial and temporal control of ECM remodeling.4,12,44 In the context of mammary tissue development, primary duct elongation is driven by the formation and proliferation of spherical-like terminal end bud (TEB) structures, which elicits a tubular network that branches further within the surrounding stroma through a process of TEB bifurcation and lateral side branching.12,25 Some of these intricate structures have been partially reproduced using 3D cultures. In particular, MEC clusters invade and form duct-like structures akin to side branching in collagen-I gels when exposed to FGF2 (Fig. 1) or other morphogens of mesenchymal origin,13,17,54 while primary mammary explants invade and form alveolar structures akin to TEB bifurcation in laminin-rich ECM gels (e.g. Matrigel) when stimulated with TGFα or FGF2.25,36 In this study we focused on the influence of mechanics on the former process, and identified that the physical laws of deformable bodies are essential regulators of morphogenic CCI. A major implication of this finding is that the mechanical and shape stability of both the invasive bodies and the surrounding ECM requires the balance between cell-dependent endogenous (outwards) forces55 and ECM-dependent exogenous (inwards) resistance. This force balance requirement also implies that any increase in exogenous forces must be compensated for by an increase in cell endogenous forces and/or a reduction of the opposing exogenous forces. Conversely, any decrease in endogenous forces must be counterbalanced otherwise.
In the context of the aforementioned 3D culture assays used to study mammary branching morphogenesis, our theoretical analysis predicts that an increase in either the length or thickness of a multicellular body is penalized by an increase in the elastic resistance posed by the ECM. This elastic penalty is particularly dramatic during CCI invasion as spherical structures (Fig. 2B). Our analysis also predicts that multicellular bodies that invade as spheres or other non-optimal geometries must counterbalance the increased ECM resistance. To this aim, cells may increase proteolytic activity to degrade and remodel ECM ahead of the invasive direction even further. However, because ECM degradation must be somewhat limited to avoid compromising the mechanical integrity of the tissue altogether, it is conceivable that cells counterbalance ECM resistance largely by increasing their endogenous mechanical resistance. The latter can be accomplished through different strategies, including (i) upregulation of actomyosin contractility,25,32,51,56 (ii) increasing the number of cell layers within the invasive body,25,45,55,57 (iii) building up hydrostatic pressure within a sealed lumen,57 and (iv) strengthening the basement membrane through altered structure and/or composition.58 In support of these predictions, both increased number of epithelial layers and lumen maintenance have been observed during branching of mammary explants or organoids in Matrigel,25,36 and in TEBs or in lobulo-alveoli structures in vivo.25 Likewise, altered composition and thickness of the basement membrane have been reported at invasive fronts during mammary branching in vivo.12 In addition to mammary tissue, most of the processes that can theoretically support an increase in endogenous resistance have been observed in epithelial cells from other branching organs35,38,56,59 as well as in non-morphogenic types of CCI (i.e., tumor invasion).3,32,41,60 However, increasing endogenous resistance by raising fluid pressure appears to be restricted tomorphogenic CCI, given the requirement for a sealed cavity (i.e., lumen) capable of building up such fluid pressure,3,61 which is largely absent in tumors.3,41
Collectively, the results and analyses delineated in this work underscore that examining morphogenic CCI in terms of force balance can improve our current understanding of how epithelial cells form ducts and acini, and how the size and shape of these structures are regulated, which is a matter of much interest because defects in epithelial tubular networks are hallmarks of a variety of human diseases including cancer.
Conclusions
In this study, we analyzed the mechanical nature of ECM resistance against CCI, and sought to identify efficient strategies to overcome this resistance using a 3D culture model of mammary epithelial branching morphogenesis in collagen-I gels. We found that collagenous ECM poses exogenous mechanical resistance against CCI mainly through elastic forces that oppose ECM deformation, whereas viscous forces are negligible owing to the low invasive speed of MECs during branching. Because elastic stresses are dominant over viscous stresses in ECM gels, epithelial cells and tissues, even after ECM degradation, these findings indicate that CCI should be physically modeled as a deformable body invading another deformable body. Accordingly, any increase in exogenous ECM elastic resistance must be counterbalanced by reducing this resistance, increasing cell intrinsic forces, or both. In support of this prediction, we identified two strategies that can independently reduce the elastic resistance imposed by the collagenous ECM on cells. The first strategy is based on adopting a narrow tube-like invasive geometry, which minimizes elastic forces according to the theory of contact elasticity. The second strategy is based on locally degrading the ECM at invasive fronts, thereby inducing a local softening of the ECM gel and a concomitant reduction of at least 50% of the ECM stiffness and elastic resistance. This latter observation is of particular interest because it provides experimental evidence of a long-standing hypothesis in the field. Local ECM softening at invasive fronts was largely driven by MMP14 activity, in agreement with previous studies supporting a prominent role for thismembrane-bound collagenase in physiologic and pathologic CCI. In contrast, we discarded shape accommodation as an efficient strategy to overcome ECM barriers during CCI. In addition, our theoretical analysis revealed that invasive geometries permissive for lumen formation such as those involved in ductal formation or other forms of morphogenic CCI are subjected to increased ECM elastic resistance, and predicted that cells must employ additional strategies to compensate for this raise in ECM resistance, including increased cell layers, building up fluid pressure within a sealed lumen, or strengthening of the basement membrane. Collectively, our findings and theoretical analyses shed new light on how cells overcome ECM mechanical resistance during CCI in general, and in morphogenic CCI in particular, while maintaining their shape and mechanical integrity.
Material and methods
Preparation of 3D collagen-I gels
Acid-soluble collagen-I (Cellagen IAC-50, Koken) was neutralized on ice by mixing gently 8 volume (vol) with 10X 1 : 1 DMEM/F12 (1 vol) and 0.1N NaOH (1 vol) to obtain a 4 mg ml−1 collagen solution. Depending on the experiment, collagen solution was diluted in DMEM/F12 to obtain the desired final concentration (1–4 mg ml−1). Desired volumes of collagen solutions at final concentrations were incubated at 37 °C for 30 min to allow gelation, and immediately hydrated with DMEM/F12. In some experiments, collagen gels were incubated with 100 μg ml−1 bacterial collagenase (Sigma).
Branching morphogenesis of EpH4 cells in 3D collagen-I gels
Functionally normal EpH4 cells were propagated in growth medium as described elsewhere.20 To induce branching in 3D collagen-I gels, we followed a protocol previously published by our laboratory (schematic representation shown in Supplementary Fig. 6 of the ESI†).13 In brief, cell clusters were prepared by suspending EpH4 cells in growth medium on top of agarose-coated wells, and by incubating them at 100 rpm and 37 °C overnight. Single cells were removed by centrifugation and the clusters were washed three times with DMEM/F12. Cell clusters were embedded in a solution of 3 mg ml−1 collagen-I. Cell-containing neutralized collagen-I solution was poured on wells of a 48-well plate pre-coated with a thin layer of collagen-I gel. Wells were incubated at 37 °C for 30 min to allow gelation, and hydrated with branching induction medium containing DMEM/F12 supplemented with insulin-transferrin-selenium, penicillin/streptomycin and 9 nM FGF2 (Sigma) for 4 days. For AFM measurements, glass-bottomed culture dishes (MatTek) were used instead of 48-well plates to allow access of the AFM probe on the 3D cultures. Branching medium was replaced every two days. In some experiments, the broad spectrum MMP inhibitor GM6001 (40 μM) (Calbiochem) was added to the branching induction medium. When required, MECs in 3D cultures were stained when the live dye Calcein AM (Invitrogen).
Lentiviral shRNA
Lentivirus containing cDNA for human MMP14 or shRNA (Mission shRNA, Sigma) against MMP14 were isolated from HEK293 cells. Transfected HEK293 cells were cultured in DMEM containing 5% FBS, 100 U/ml penicillin and 100 μg ml−1 streptomycin. Culture media was replaced after 24 h with fresh media. After 48 h, recombinant lentivirus were concentrated from filtered culture media (0.45 μm filters) by ultracentrifugation at 25 000 rpm for 90 min (SW41Ti Roter, Fullerton). To infect lentivirus into EpH4 cells, 1.0 × 105 cells were plated in each well of a 6 well-plate and treated with polybrene for 30 min. For stable expression of shRNA or overexpression of MMP14, cells were selected by adding 5 μg ml−1 puromycin to growth medium for at least 4 days. Lentivirus with scrambled sequences were used as a control.
RT-PCR analysis
Total RNA was isolated from 3D cultures using the QIAGEN RNeasy Mini kit. A total of 100 ng of RNA was used to synthesize cDNA using SuperScript II First-Strand Synthesis System (Invitrogen). MMP14 was amplified with 5′-GAGATCAAGGCCAATGTTCG and 5′-GTCCAGGGCTCGGCAGAATC primers. GAPDH was amplified using commercially available primers (QIAGEN).
Western blotting
Samples were lysed using PBS containing 2% SDS. Protein concentration was determined using the BCA Protein Assay kit (Pierce) following manufacturer’s instructions. Protein samples (20 μg) were mixed with Laemmli sample buffer and heated at 95 °C for 5 min. Samples were loaded into a pre-cast 4–20% tris-glycine polyacrylamide gel (Invitrogen) using the NOVEX system (Invitrogen). Resolved proteins were transferred to nitrocellulose membrane (Whatman) and blocked in PBS containing 0.05% Tween-20 and 5% w/v non-fat dry milk for 1 h at room temperature. Membranes were incubated overnight at 4 °C in a PBS solution containing 5% BSA, 0.1% Tween-20 and specific primary antibodies against MMP14 (Chemicon) or Actin (Sigma). Appropriate secondary antibodies were incubated in PBS containing 0.05% Tween-20 and 5% bovine serum albumin (Sigma) for 1 h, and detected with the Pierce SuperSignal detection kit (Thermo Scientific). The corresponding bands were imaged with the FluorChem 8900 analysis system (Alpha Innotech).
Morphometric analysis of invasive structures during branching morphogenesis
To analyze CCI morphologies, 2–3 phase contrast microscopy images of branching cell clusters were obtained for at least 10 independent experiments using either a 10X or 20X objective. Qualitative image analysis included labeling each invasive structure as best described by a cylinder, cone, sphere or uncertain –when it was unclear the distinction between a cylinder and a cone– by visual examination. All quantitative image measurements were performed with Image J.62 For each invasive structures, the width of the tip (wtip) and the base (wbase) as well as the length of the invasive body (L) were assessed by manually drawing a straight line and measuring the corresponding length in pixels. For conical shaped structures we manually drew the opening angle 2θ and measured the corresponding semiincluded angle as θ. The frequency of each invasive geometry was assessed by computing the ratio wtip/wbase for each image and comparing the resulting ratios with the qualitative geometrical labeling. This comparison enabled scoring as cones or cylinders those ratios below 0.5 and above 0.75, respectively, whereas values in between were scored as uncertain. For each image, the width corresponding to a single cell (w1) was estimated as the minimum of wtip, and was used to assess the cell number either at the base or along the long axis of invasion of each multicellular invasive body wbase/w1 and L/w1, respectively.
Confocal microscopy
To visualize collagen remodeling during branching, EpH4 cells were seeded in No. 1.5 thickness borosilicate chamber slides (Nalge Nunc International) within 3 mg ml−1 collagen-I gels mixed with 2% (v/v) DQ-Collagen (type I Collagen; Invitrogen) of identical concentration. Images were acquired after 4 days of branching induction with a LSM 710 laser-scanning confocal microscope (Zeiss) using a LD C-Apochromat 40x water immersion objective. DQ-Collagen was excited with a 488 nm laser and emitted signal was captured from 493–582 nm. Image stacks of 50 μm total depth and 1.1 μm slice thickness were obtained, and each image was line averaged over 2 scans. Brightfield images were captured concurrently. Collagen-I fibers in cell-free gels were visualized by CRM by exciting collagen with a 488 nm laser and collecting the reflected signal at the same wavelength. To assess nuclear distribution in branching MECs, cells were fixed, permeabilized and stained with DAPI and phalloidin (Invitrogen) as previously described,20 and image stacks were collected using either the 40x or a 20x water immersion objective.
Mechanical measurements with AFM
All measurements were carried out using a stand-alone AFM (Bioscope, Veeco) adapted to an inverted optical microscope as described in detail elsewhere.19 In brief, force (F) measurements were conducted using low spring constant cantilevers (k = 0.03 N m−1) (Microlever, Veeco). For measurements on cell cluster populated gels, we first located the closest clusters to the AFM tip by identifying those clusters that were in focus with the cantilever (Fig. 3A and Supplementary Fig. 2 of the ESI†). Occasionally, focusing an invasive front rendered the tip slightly out of focus. In these conditions, we discarded cluster edges that required a vertical movement of the objective to bring the cantilever back into focus that were larger than half the cantilever height (0.5 hc), which is estimated as ~25 μm. This distance was calculated considering the actual geometry of the cantilever as hc = htip + Lc·tanβ, where htip is the height of the tip, Lc is the length of the cantilever and β is the tilting angle of the cantilever with respect to the base of the cantilever holder, which were taken as 3 μm, 220 μm and 12 deg, respectively, according to the manufacturer’s data sheet. By using these selection rules we guaranteed that the depth of the top of each cluster were <25 μm. Once a suitable cluster was identified, we approached gently the tip to the gel surface with the aid of a stepping motor either right on top of an invasive front (for branching clusters), or at the edge of the cluster, or far away (> 100 μm) from the cluster edge. For each gel location, three force vs. piezo displacement curve (F–z curves) were acquired following the initial tip contact with the gel surface at moderate loading force (~1 nN) and low speed (~5 μm s−1). In these conditions, the contribution of the hydrodynamic forces on the cantilever due to the surrounding medium can be neglected.63 For each gel location, E and sample indentation (δ) were computed as averages of the values obtained by least-squares fitting of a contact elastic model to each set of three F–z curves as described elsewhere.19 For each culture condition, we measured 4–5 clusters and 2–3 invasive fronts per cluster, and corresponding E data were screened for outliers using Chauvenet’s criterion.20 For measurements on cell-free collagen gels, a similar protocol was applied on at least 9 random gel locations. In some experiments, we measured the loss modulus G″ of cell-free collagen-I gels with AFM using low-amplitude (75 nm) and low frequency (ω = 20.4 Hz) oscillations as described elsewhere,19 and calculated the corresponding dynamic viscosity as η = G″/ω. All mechanical data are given as mean ± SE and correspond to at least 2 independent experiments.
Modeling topology and mechanical resistance
The most common branching geometries were either tube-like shapes or spherical buds.3,45 The former can be modeled as either cylinders or truncated cones, whereas the latter can be described as truncated spheres (Fig. 3A). Assuming these idealized invasive geometries –cylinder, cone and sphere–, as well as absence of ECM degradation and continuous contact between the ECM and the invasive multicellular body, we used equations reported elsewhere to assess: (i) available surface area (S) for ECM binding and corresponding volume (V) of the invasive body, (ii) elastic resisting force (Fel) opposing the expansion of the invasive body due to the deformation of the ECM, and (iii) translational friction coefficient (b) of the invasive body.
The corresponding S and V for a cylinder, a truncated cone and a truncated sphere were calculated using eqn (1)-(3) (details on how to obtain these equations are available in Supplementary Methods of the ESI†), respectively, as:64
| (1a) |
| (1b) |
| (2a) |
| (2b) |
| (3a) |
| (3b) |
where R is the smallest radius, L is the length of the invasive tubular body, θ is the semiincluded angle, and f is the height of the spherical cap normalized to R corresponding to the truncated sphere. Note that S equations exclude the surface of the base of the body, since it is not involved in cell-ECM adhesion.
Owing to the viscoelastic nature of collagenous gels,21 the invasion of multicellular expanding bodies will be opposed by both elastic (Fel) and viscous (Fvis) forces from the surrounding ECM. The contact theory of elasticity predicts the following Fel for a cylinder, a blunted cone and a sphere in the direction of invasion:22,27,28
| (4) |
| (5) |
| (6) |
where ν is the Poisson’s ratio (taken as 0.5 for collagen-I gels).20,40 These equations assume that E of the collagenous gel is much smaller than E of the expanding multicellular body, in agreement with previous mechanical measurements on EpH4 cells.20
The frictional viscous force experienced by the multicellular body along the axis of invasion at low Reynold’s number can be assessed as Fvis = −b·v, where b is the translational friction coefficient, v is the speed of the invasive body and η is the viscosity of the collagen-I gel.23 For a sphere, this coefficient can be calculated using Stoke’s law as23
| (7) |
For tube-like solid bodies, b can be assessed as23,65
| (8) |
where L is the same as in eqn (1)-(3) and γ is a correction factor that depends on the ratio between L and the maximum thickness of the invasive body in the direction of movement (2R). Eqn (8) applies for L ≫ 2R. For a cylindrical geometry, data available elsewhere65,66 predicts an average γ = −0.06. In contrast, to our knowledge there is no currently available analytical expression of b for a cone. Instead, we modeled a cone as half an ellipsoid,23,65,67 which can be described by eqn (8) and an average γ = −0.15 (details on γ values are available in Supplementary Methods of the ESI†).
Statistical analysis
Comparisons between two groups were performed using two-tailed Student’s t-test. Differences were considered significant at p < 0.05.
Supplementary Material
Insight, innovation, integration.
The interstitial collagenous extracellular matrix (ECM) acts as a physical barrier against collective cell invasion (CCI), which is an important process in branching morphogenesis, tissue repair and tumor dissemination. To obtain new insight regarding the mechanical nature of this barrier and how it is overcome during CCI, we used an innovative approach that combined morphometric analysis and mechanical modeling to predict that geometries assumed by mammary epithelial cells undergoing branching morphogenesis are optimized to reduce the mechanical resistance from the ECM. We combined this approach with atomic force microscopy to measure alterations in ECM microelasticity that occur during CCI. This integrated approach revealed that ECM mechanical resistance is largely due to its elastic properties, and that cells use at least two strategies to minimize independently the elastic resistance of the ECM during early invasion: an optimized geometry and an MMP14-dependent local ECM softening at invasive fronts.
Acknowledgments
We thank C Bustamante and D Fletcher from UC Berkeley (UCB) for the use of the AFM equipment in their laboratories, and S Smith (Bustamante Lab, UCB) and A Crow (Fletcher Lab, UCB) for technical assistance. We also thank all members of the Bissell lab and R Sunyer (UB) for helpful discussions and technical support. This work was supported by the U.S. Department of Energy (DE-AC02-05CH1123 to M.J.B.), the National Cancer Institute (R37CA064786, U54CA126552, R01CA057621, U54CA112970, U01CA143233, and U54CA143836-Bay Area Physical Sciences–Oncology Center, University of California, Berkeley, to M.J.B.), the U.S. Department of Defense (W81XWH0810736 to M.J.B.), the Ministerio de Ciencia e Innovación (SAF2009-1324 to J.A.), la Asociación Española Contra el Cáncer (to J.A.) and the Glenn T. Seaborg postdoctoral fellowship from Lawrence Berkeley National Laboratory (to C.G.).
Abbreviations
- AFM
atomic force microscopy
- CCI
collective cell invasion
- c
collagen concentration
- collagen-I
type I collagen
- CRM
confocal reflection microscopy
- E
Young’s elastic modulus
- ECM
extracellular matrix
- FGF2
fibroblast growth factor 2
- Fel
elastic force
- Fvis
viscous force
- MBP
moving boundary problem
- MEC
mammary epithelial cell
- MMP
matrix metalloproteinase
- S
surface
- TEB
terminal end bud
- V
volume
- 3D
three-dimensional
Footnotes
Electronic supplementary information (ESI) available. See DOI: 10.1039/c1ib00073j
References
- 1.Fleury V, Watanabe T, Nguyen T, Unbekandt M, Warburton D, Dejmek M, Nguyen MB, Lindner A, Schwartz L. In: Branching Morphogenesis. Davies JA, editor. Landes Bioscience; Georgetown: 2005. pp. 202–234. [Google Scholar]
- 2.Lu P, Sternlicht MD, Werb Z. J Mammary Gland Biol Neoplasia. 2006;11:213–228. doi: 10.1007/sl0911-006-9027-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Friedl P, Gilmour D. Nat Rev Mol Cell Biol. 2009;10:445–457. doi: 10.1038/nrm2720. [DOI] [PubMed] [Google Scholar]
- 4.Gjorevski N, Nelson CM. Wiley Interdiscip Rev Syst Biol Med. 2010;2:734–741. doi: 10.1002/wsbm.96. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Schedin P, Keely PJ. Cold Spring Harbor Perspect Biol. 2010;3:a003228. doi: 10.1101/cshperspect.a003228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Itoh Y, Seiki M. J Cell Physiol. 2005;206:1–8. doi: 10.1002/jcp.20431. [DOI] [PubMed] [Google Scholar]
- 7.Wolf K, Wu YI, Liu Y, Geiger J, Tam E, Overall C, Stack MS, Friedl P. Nat Cell Biol. 2007;9:893–904. doi: 10.1038/ncb1616. [DOI] [PubMed] [Google Scholar]
- 8.Zaman MH, Matsudaira P, Lauffenburger DA. Ann Biomed Eng. 2006;35:91–100. doi: 10.1007/s10439-006-9205-6. [DOI] [PubMed] [Google Scholar]
- 9.Pathak A, Kumar S. Integr Biol. 2011;3:267–278. doi: 10.1039/c0ib00095g. [DOI] [PubMed] [Google Scholar]
- 10.Stroud JD, Baicu CF, Barnes MA, Spinale FG, Zile MR. Am J Physiol Heart Circ Physiol. 2002;282:H2324–2335. doi: 10.1152/ajpheart.00711.2001. [DOI] [PubMed] [Google Scholar]
- 11.Yuan H, Kononov S, Cavalcante FS, Lutchen KR, Ingenito EP, Suki B. J Appl Physiol. 2000;89:3–14. doi: 10.1152/jappl.2000.89.1.3. [DOI] [PubMed] [Google Scholar]
- 12.Fata JE, Werb Z, Bissell MJ. Breast Cancer Res. 2004;6:1–11. doi: 10.1186/bcr634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Simian M, Hirai Y, Navre M, Werb Z, Lochter A, Bissell MJ. Development. 2001;128:3117–3131. doi: 10.1242/dev.128.16.3117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Sabeh F, Shimizu-Hirota R, Weiss SJ. J Cell Biol. 2009;185:11–19. doi: 10.1083/jcb.200807195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Friedl P, Wolf K. Cancer Res. 2008;68:7247–7249. doi: 10.1158/0008-5472.CAN-08-0784. [DOI] [PubMed] [Google Scholar]
- 16.Dhimolea E, Maffini MV, Soto AM, Sonnenschein C. Biomaterials. 2010;31:3622–3630. doi: 10.1016/j.biomaterials.2010.01.077. [DOI] [PubMed] [Google Scholar]
- 17.Mori H, Gjorevski N, Inman JL, Bissell MJ, Nelson CM. Proc Natl Acad Sci U S A. 2009;106:14890–14895. doi: 10.1073/pnas.0901269106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Alcaraz J, Nelson CM, Bissell MJ. J Mammary Gland Biol Neoplasia. 2004;9:361–374. doi: 10.1007/s10911-004-1406-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Alcaraz J, Buscemi L, Grabulosa M, Trepat X, Fabry B, Farre R, Navajas D. Biophys J. 2003;84:2071–2079. doi: 10.1016/S0006-3495(03)75014-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Alcaraz J, Xu R, Mori H, Nelson CM, Mroue R, Spencer VA, Brownfield D, Radisky DC, Bustamante C, Bissell MJ. EMBO J. 2008;27:2829–2838. doi: 10.1038/emboj.2008.206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Forgacs G, Newman SA, Hinner B, Maier CW, Sackmann E. Biophys J. 2003;84:1272–1280. doi: 10.1016/S0006-3495(03)74942-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Sneddon IN. Int J Eng Sci. 1965;3:47–57. [Google Scholar]
- 23.Howard J. Mechanics of motor proteins and the cytoskeleton 2001. Sinauer Associates; Sunderland: 1957. [Google Scholar]
- 24.Emerman JT, Pitelka DR. In Vitro. 1977;13:316–328. doi: 10.1007/BF02616178. [DOI] [PubMed] [Google Scholar]
- 25.Ewald AJ, Brenot A, Duong M, Chan BS, Werb Z. Dev Cell. 2008;14:570–581. doi: 10.1016/j.devcel.2008.03.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Emerman JT, Burwen SJ, Pitelka DR. Tissue Cell. 1979;11:109–119. doi: 10.1016/0040-8166(79)90011-9. [DOI] [PubMed] [Google Scholar]
- 27.Rico F, Roca-Cusachs P, Gavara N, Farre R, Rotger M, Navajas D. Phys Rev E: Stat Nonlinear, Soft Matter Phys. 2005;72:021914. doi: 10.1103/PhysRevE.72.021914. [DOI] [PubMed] [Google Scholar]
- 28.Rico F, Roca-Cusachs P, Sunyer R, Farre R, Navajas D. J Mol Recognit. 2007;20:459–466. doi: 10.1002/jmr.829. [DOI] [PubMed] [Google Scholar]
- 29.Williams JM, Daniel CW. Dev Biol. 1983;97:274–290. doi: 10.1016/0012-1606(83)90086-6. [DOI] [PubMed] [Google Scholar]
- 30.Raub CB, Putnam AJ, Tromberg BJ, George SC. Acta Biomater. 2010;6:4657–4665. doi: 10.1016/j.actbio.2010.07.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.MacKintosh FC, Käs J, Janmey P. Phys Rev Lett. 1995;75:4425–4428. doi: 10.1103/PhysRevLett.75.4425. [DOI] [PubMed] [Google Scholar]
- 32.Provenzano PP, Inman DR, Eliceiri KW, Keely PJ. Oncogene. 2009;28:4326–4343. doi: 10.1038/onc.2009.299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Williams MJ, Clark P. J Anat. 2003;203:483–503. doi: 10.1046/j.1469-7580.2003.00238.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Santos OF, Nigam SK. Dev Biol. 1993;160:293–302. doi: 10.1006/dbio.1993.1308. [DOI] [PubMed] [Google Scholar]
- 35.Nogawa H, Takahashi Y. Development. 1991;112:855–861. doi: 10.1242/dev.112.3.855. [DOI] [PubMed] [Google Scholar]
- 36.Fata JE, Mori H, Ewald AJ, Zhang H, Yao E, Werb Z, Bissell MJ. Dev Biol. 2007;306:193–207. doi: 10.1016/j.ydbio.2007.03.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Ghajar CM, Chen X, Harris JW, Suresh V, Hughes CC, Jeon NL, Putnam AJ, George SC. Biophys J. 2008;94:1930–1941. doi: 10.1529/biophysj.107.120774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Franzdottir SR, Axelsson IT, Arason AJ, Baldursson O, Gudjonsson T, Magnusson MK. Respir Res. 2010;11:162. doi: 10.1186/1465-9921-11-162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Yang YL, Leone LM, Kaufman LJ. Biophys J. 2009;97:2051–2060. doi: 10.1016/j.bpj.2009.07.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Gehler S, Baldassarre M, Lad Y, Leight JL, Wozniak MA, Riching KM, Eliceiri KW, Weaver VM, Calderwood DA, Keely PJ. Mol Biol Cell. 2009;20:3224–3238. doi: 10.1091/mbc.E08-12-1186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Paszek MJ, Zahir N, Johnson KR, Lakins JN, Rozenberg GI, Gefen A, Reinhart-King CA, Margulies SS, Dembo M, Boettiger D, Hammer DA, Weaver VM. Cancer Cell. 2005;8:241–254. doi: 10.1016/j.ccr.2005.08.010. [DOI] [PubMed] [Google Scholar]
- 42.Storm C, Pastore JJ, MacKintosh FC, Lubensky TC, Janmey PA. Nature. 2005;435:191–194. doi: 10.1038/nature03521. [DOI] [PubMed] [Google Scholar]
- 43.Miroshnikova YA, Jorgens DM, Spirio L, Auer M, Sarang-Sieminski AL, Weaver VM. Phys Biol. 2011;8:026013. doi: 10.1088/1478-3975/8/2/026013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Friedl P, Wolf K. J Cell Biol. 2009;188:11–19. doi: 10.1083/jcb.200909003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Lubarsky B, Krasnow MA. Cell. 2003;112:19–28. doi: 10.1016/s0092-8674(02)01283-7. [DOI] [PubMed] [Google Scholar]
- 46.Ronnov-Jessen L, Petersen OW, Koteliansky VE, Bissell MJ. J Clin Invest. 1995;95:859–873. doi: 10.1172/JCI117736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Webster KD, Crow A, Fletcher DA. PLoS One. 2011;6:e17807. doi: 10.1371/journal.pone.0017807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Henderson E, Haydon PG, Sakaguchi DS. Science. 1992;257:1944–1946. doi: 10.1126/science.1411511. [DOI] [PubMed] [Google Scholar]
- 49.Lulevich V, Zink T, Chen HY, Liu FT, Liu GY. Langmuir. 2006;22:8151–8155. doi: 10.1021/la060561p. [DOI] [PubMed] [Google Scholar]
- 50.Lo CM, Wang HB, Dembo M, Wang YL. Biophys J. 2000;79:144–152. doi: 10.1016/S0006-3495(00)76279-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Gjorevski N, Nelson CM. Integr Biol. 2010;2:424–434. doi: 10.1039/c0ib00040j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Wiseman BS, Sternlicht MD, Lund LR, Alexander CM, Mott J, Bissell MJ, Soloway P, Itohara S, Werb Z. J Cell Biol. 2003;162:1123–1133. doi: 10.1083/jcb.200302090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Kanwar YS, Ota K, Yang Q, Wada J, Kashihara N, Tian Y, Wallner EI. Am J Physiol. 1999;277:F934–947. doi: 10.1152/ajprenal.1999.277.6.F934. [DOI] [PubMed] [Google Scholar]
- 54.Oft M, Peli J, Rudaz C, Schwarz H, Beug H, Reichmann E. Genes Dev. 1996;10:2462–2477. doi: 10.1101/gad.10.19.2462. [DOI] [PubMed] [Google Scholar]
- 55.Trepat X, Wasserman MR, Angelini TE, Millet E, Weitz DA, Butler JP, Fredberg JJ. Nat Phys. 2009;5:426–430. [Google Scholar]
- 56.Moore KA, Polte T, Huang S, Shi B, Alsberg E, Sunday ME, Ingber DE. Dev Dyn. 2005;232:268–281. doi: 10.1002/dvdy.20237. [DOI] [PubMed] [Google Scholar]
- 57.Gin E, Tanaka EM, Brusch L. J Theor Biol. 2010;264:1077–1088. doi: 10.1016/j.jtbi.2010.03.021. [DOI] [PubMed] [Google Scholar]
- 58.Candiello J, Balasubramani M, Schreiber EM, Cole GJ, Mayer U, Halfter W, Lin H. FEBS J. 2007;274:2897–2908. doi: 10.1111/j.1742-4658.2007.05823.x. [DOI] [PubMed] [Google Scholar]
- 59.Bellusci S, Grindley J, Emoto H, Itoh N, Hogan BL. Development. 1997;124:4867–4878. doi: 10.1242/dev.124.23.4867. [DOI] [PubMed] [Google Scholar]
- 60.Gudjonsson T, Ronnov-Jessen L, Villadsen R, Rank F, Bissell MJ, Petersen OW. J Cell Sci. 2002;115:39–50. doi: 10.1242/jcs.115.1.39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Butcher DT, Alliston T, Weaver VM. Nat Rev Cancer. 2009;9:108–122. doi: 10.1038/nrc2544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Abramoff MD, Magelhaes PJ, Ram SJ. Biophotonics Int. 2004;11:36–42. [Google Scholar]
- 63.Alcaraz J, Buscemi L, Puig-de-Morales M, Colchero J, Baró A, Navajas D. Langmuir. 2002;18:716–721. [Google Scholar]
- 64.Spiegel MR, Liu J. Schaum’s mathematical handbook of formulas and tables. McGraw-Hill, Inc.; 1999. [Google Scholar]
- 65.Yamakawa H, Tanaka G. J Chem Phys. 1972;57:1537–1542. [Google Scholar]
- 66.Tirado MM, De la Torre JG. J Chem Phys. 1979;71:2581–2587. [Google Scholar]
- 67.Tchen CM. J Appl Phys. 1954;25:463–473. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


