Abstract
Realizing the full potential of high-resolution positron emission tomography (PET) systems involves accurately positioning events in which the annihilation photon deposits all its energy across multiple detector elements. Reconstructing the complete sequence of interactions of each photon provides a reliable way to select the earliest interaction because it ensures that all the interactions are consistent with one another. Bayesian estimation forms a natural framework to maximize the consistency of the sequence with the measurements while taking into account the physics of γ-ray transport. An inherently statistical method, it accounts for the uncertainty in the measured energy and position of each interaction. An algorithm based on maximum a posteriori (MAP) was evaluated for computer simulations. For a high-resolution PET system based on cadmium zinc telluride detectors, 93.8% of the recorded coincidences involved at least one photon multiple-interactions event (PMIE). The MAP estimate of the first interaction was accurate for 85.2% of the single photons. This represents a two-fold reduction in the number of mispositioned events compared to minimum pair distance, a simpler yet efficient positioning method. The point-spread function of the system presented lower tails and higher peak value when MAP was used. This translated into improved image quality, which we quantified by studying contrast and spatial resolution gains.
1. Introduction
High-resolution positron emission tomography (PET) requires detector modules comprising small detection elements. In these detectors, Compton scatter and other physical effects cause the annihilation photon to deposit energy in multiple interaction locations. To exploit the full potential of high-resolution PET systems, one major challenge needs to be overcome. The image reconstruction must be able to use events in which one annihilation photon deposits all its energy (511 keV) across multiple detector elements. The crystal of entrance for photon multiple-interactions events (PMIEs) is ambiguous. Hence, these events are at risk to be erroneously assigned to the wrong line of response (LOR), which, in turn, causes contrast, quantitative accuracy and spatial resolution loss (Levin et al 1997, Stickel and Cherry 2005).
Although the general formalism for interaction sequence determination derived in this work applies, in principle, to any detector, we focus on its application to a specific design under development in our lab.
1.1. A cross-strip electrode cadmium zinc telluride (CZT) detector module for PET
Unlike scintillation crystals, semiconducting detectors such as cadmium zinc telluride (CZT) directly sense the ionization signal created by the annihilation photon absorption (Levin 2008). CZT detectors have good energy and spatial resolution. In addition, they can be designed to measure the 3D coordinates of individual photon interactions. For these reasons, they constitute a prime candidate for building high-resolution PET systems with depth-of-interaction (DOI) measurement capability.
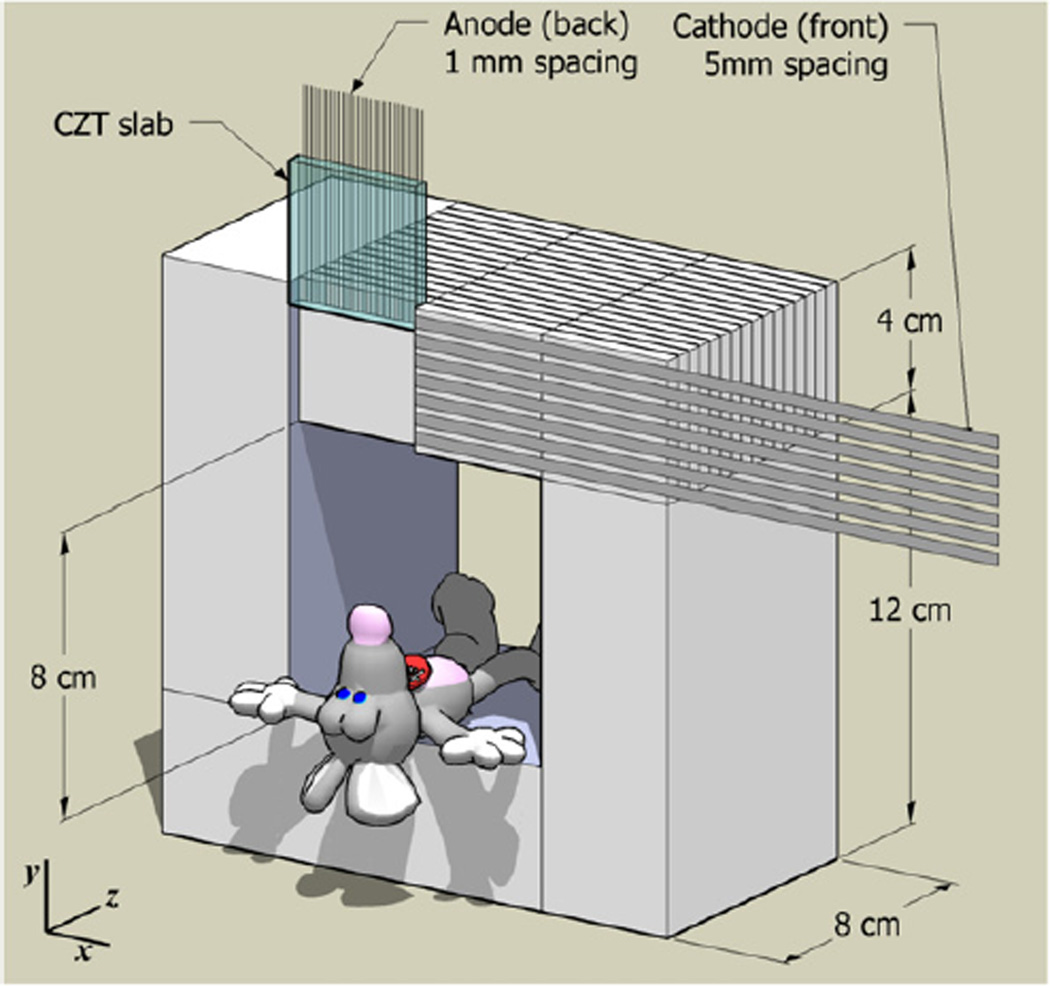
Our detector module design uses a set of parallel, thin rectangular strips for the anode and an orthogonal set for the cathode. The x–y coordinate of the interaction (as defined in figure 1) is determined by the intersection of the strips on either side of the crystal slab that record a signal above threshold. The pitch with which the electrodes are deposited determines the intrinsic spatial resolution. The z-coordinates along the direction orthogonal to the electrode planes are determined using the ratio of the cathode-to-anode signal pulse heights. In this direction, the intrinsic resolution is below 1 mm full width half maximum (FWHM).
Figure 1.
Small-animal PET scanner based on CZT detector slabs with cross-strip electrodes. The useful field of view (FOV) spans all the way to the edge of the 8 × 8 × 8 cm3 FOV. Individual interactions are read out by two sets of orthogonal electrodes. The cathodes and anode strips are deposited on the front and the back face of the CZT slab, respectively.
In a small-animal PET system we are developing (figure 1), 40 × 40 × 5 mm3 slabs of CZT are arranged edge on with respect to the incoming photons to form an 8 × 8 × 8 cm3 field of view (FOV). Due to detector’s ability to read out the 3D coordinates of individual photon interactions, the useful FOV extends all the way to the edge of the detectors. The detector voxel elements are 1 × 5 × 1 mm3 (in the coordinate system of figure 1).
CZT is a low Z material, and as a result its photo-fraction is low compared to other crystals (Levin 2008). A large fraction of all the photons undergoes Compton scatter in the detectors. Because the detection voxels are small (1 × 5 × 1 mm3), the scattered photons usually escape into adjacent crystals. On average, a 511 keV photon deposits its energy in 2.2 detector voxels (table 1). As a result, 93.8% of all recorded coincidences involve at least one PMIE. When PMIEs are used, high photon sensitivity can be reached: 17% for 800 µCi at the center (Habte et al 2007), a 16-fold increase compared to using only events that deposits all their energy in a single detector voxel. However, the ability to correctly position these events strongly determines the image quality and quantitative accuracy.
Table 1.
Distribution (%) of the events recorded in a CZT module, according to the number of interactions. Energy gating was performed on the total energy, summed over multiple interactions.
| PE Only |
1 CS +PE |
2 CS +PE |
3 CS +PE |
4 CS +PE |
5 CS +PE |
≥ 6CS +PE |
|---|---|---|---|---|---|---|
| 24.9 | 38.3 | 24.2 | 9.3 | 2.5 | 0.5 | 0.3 |
CS: Compton scatter, PE: photoelectric.
1.2. Positioning photon multiple-interactions events
The standard PET detector uses light multiplexing in the scintillation crystal array. Charge can also be multiplexed in the position-sensitive photodetector or in the associated readout circuit. This results in a few (typically four) readout channels. Such detectors estimate the photon interaction coordinates for each event by determining the weighted mean of the readout signals. Therefore, individual interaction coordinates and their deposited energies cannot be determined in the standard PET detector (Levin 2008). Fortunately, PMIEs are less frequent for standard large crystal elements which are more likely to completely absorb the energy from multiple interactions.
Some more recent PET system designs allow readout of multiple interactions (Bergeron et al 2007), Spanoudaki (2008), Braem et al (2004), Zhang et al (2007) and section 1.1). All these systems are able to distinguish the photons that deposit their energy in a single detector voxel from those which deposit their energy in multiple detector voxels. This has raised interest for ways to position PMIEs. Such methods can usually be classified in three categories.
1.2.1. Interaction selection
An estimate of the earliest interaction (EI) is selected from the finite set of all detected interactions, and used to position the PMIE. This class of methods exploits some form of correlation between the order of the interactions and properties of their energy and position. Techniques previously investigated include choosing the interaction with largest/second largest signal (Comanor et al 1996, Shao et al 1996), the smallest depth of interaction (Shao et al 1996) or the minimum distance to the other coincident photon. For sequences of more than two interactions, the order of subsequent interactions is not recovered with those methods. Several techniques have been developed specifically for positioning photons that deposit energy in exactly two detectors. Lehner et al (2004) proposed a method based exclusively on the energies, which for 511 keV photons consists of selecting the most energetic interaction. Rafecas et al (2003) investigated using both LORs in the reconstruction to describe a coincident pair in which one of the annihilation photon Compton scatters once.
1.2.2. Unconstrained positioning
The positioning problem can be relaxed by allowing the position of PMIEs to be assigned to any location within the detection volume. For example, the energy-weighted mean (EWM) scheme (Comanor et al 1996) combines the interaction locations linearly using the energy as weight. This is the only positioning method available for conventional PET systems based on four-channel block detectors.
1.2.3. Full sequence reconstruction
The crystal of entry for PMIEs can also be estimated by reconstructing the complete sequence of interactions. A number of objectives have been investigated in order to penalize sequences that violate the kinematics of Compton scatter. These techniques are based on testing the consistency of redundant information. For example, the cosine of the scatter angle can be computed using the Compton formula, provided that the order of the sequence of interactions and the annihilation photon energy are known. This quantity can also be obtained directly from the interaction locations. The sum of the squared differences of the scatter angle cosines (Oberlack et al 2000, Boggs and Jean 2000) can be used as an objective to assess that the sequence kinematics are valid. This scheme can be refined by weighting the summands by the measurement error. In a similar fashion, Schmidt et al (1999) formed the weighted sum of the absolute difference between the scatter angle computed from trigonometry and from Compton kinematics.
The objective can also be based on physical considerations, such as the probability that the annihilation photon follows a trajectory. The Klein–Nishina differential cross section is one component of the trajectory probability (Rafecas et al 2003). Other components, such as the photoelectric cross section, contribute to the trajectory probability and can be included.
Van der Marel and Cederwall (1999) proposed to reconstruct the sequence backwards. Instead of performing a full search over the combinatorial space of all the sequences, the method recovers the complete sequence of interactions sequentially by first identifying the photoelectric interaction, whose energy is assumed to be independent of the track properties, and then retracing the interaction track backwards.
2. Theory
We investigated a new sequence reconstruction technique which optimizes agreement with the measurements while also accounting for the trajectory total cross section. Bayesian estimation provides a natural framework to combine these two goals. The likelihood term can deal with the consistency of the measurements, while a prior probability distribution can describe the total trajectory cross section. The product of the likelihood with the prior distribution yields the maximum a posteriori (MAP) objective. Using a statistical framework has the advantage that measurement noise properties are rigorously characterized in the objective. In addition, the maximum likelihood (ML) estimate is asymptotically efficient and unbiased.
One issue often reported with sequence reconstruction methods is that the exact location of each interaction within the detector voxel is uncertain. It is then assumed that the interactions occur at the center of the detector voxels, which induces errors in the calculation of the objective. To mitigate this problem, we consider a stochastic Bayesian estimation approach. For every possible sequence ordering, the objective is averaged over many possible interaction paths where the interaction locations are sampled from 3D uniform distributions over the corresponding detector voxels.
2.1. Maximum likelihood
The ML criterion is used to seek the sequence of interactions that has the greatest statistical consistency with the observations. For an event comprising N interactions, N! hypotheses are tested. Each hypothesis describes a possible sequence of N interactions. The ML procedure evaluates the likelihood of all the hypotheses and selects the one that is greatest.
Due to the pixilated nature of the detector, the interaction position is quantized to the nearest detector voxel. The exact position ri of interaction i can be expressed as the sum of the detector voxel center di and the position quantization error qi (figure 2(b)):
| (1) |
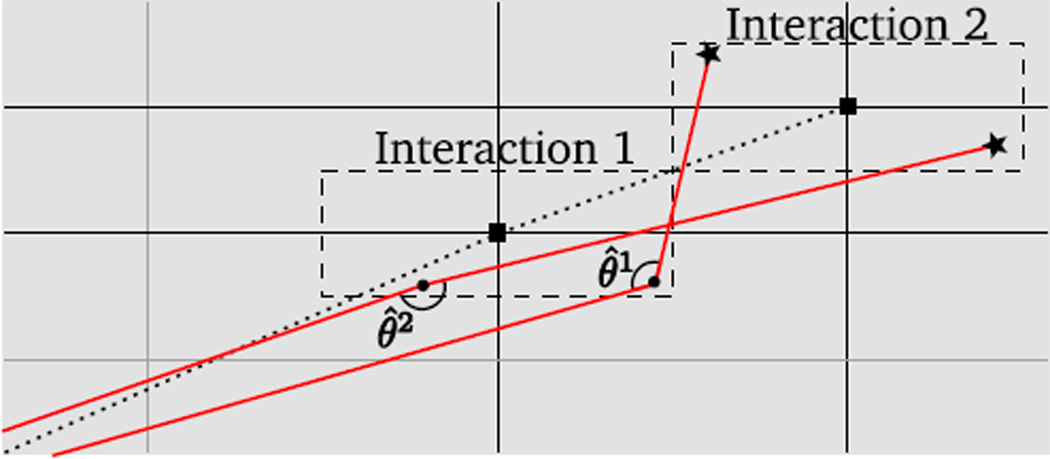
Figure 2.
Example of a coincident event recorded by a PET system based on CZT cross-strip electrodes modules (section 1.1). The solid red line represents the annihilation photon trajectory. (a) In this example, a coincident pair consists of a pure photoelectric event (left) and a PMIE (right). There are six possible sequences for the PMIE; only one of which is correct. Incorrect sequences result in mispositioning of the PMIE and misidentification of the LOR (dotted line). (b) The true interaction position ri of the energy deposition is quantized to the nearest intersection of the electrodes di. The quantization error is qi = ri − di. Electronic signals are read out from the nearest anodes and cathodes. Detector voxels are represented by dotted rectangles.
The permutations of {1, …, N} form a finite set 𝒫N, of cardinality N!. We use σ = (σ1, …, σN) to refer to an element of 𝒫N. For example, (3, 1, 2) is an element of 𝒫3. The set of all the possible sequences of N interactions can be mathematically represented by 𝒫N.
The recorded energy deposition locations are numbered j = 1, …, N. These indices are arbitrary and do not represent the true order of the interactions. The measurement Ej of the energy deposited at the j th location rj in the detector (figure 2(a)) is subject to zero-mean Gaussian noise ni, with variance :
| (2) |
where εi denotes the true energy deposition for the ith interaction. The true energy depositions are indexed by i, the true interaction number, which is related to j by an unknown permutation σ.
The key in formulating a ML objective is that it is possible to compute the energy deposited during a Compton scatter interaction analytically. Given any permutation σ in the order of the interactions, êi(σ) is the hypothetical value of the photon energy between the ith and the (i + 1)th interactions, computed from Compton kinematics. The hypothetical energy deposited by the ith interaction is denoted ε̂i(σ). Conservation of energy implies
| (3) |
The first hypothetical energy deposition can be computed using
| (4) |
where me denotes the mass of the electron and c the speed of light in the vacuum. In this expression, it is assumed that the energy e0 of the incoming photon and the position p of the other coincident photon in the pair are known. For PET, the incoming energy e0 is set to 511 keV. When the other coincident pair also involves multiple interactions, p is estimated roughly, for example, by computing the center of mass.
In a similar fashion, for i ≤ N − 1, ε̂i(σ) can be evaluated recursively for any permutation σ:
| (5) |
For i = N, the energy of the annihilation photon is fully deposited through photoelectric interaction. Therefore, the last energy deposition is
| (6) |
The correct sequence σsol satisfies ε̂i(σsol) = εi for all i. However, only a noisy measurement Ei of εi is known (2); therefore, the sequence which maximizes the likelihood that is chosen. Assuming the positions qi are known, the likelihood Lq can be expressed as
| (7) |
| (8) |
because ni is a Gaussian-distributed random variable with variance . The hypothetical energy depositions, ε̂i(σ), are computed using (4)–(6). The variance is a function of the energy deposition εi. A model of the energy resolution for the detector is used, and a hypothetical variance is computed using the hypothetical energy deposition ε̂i(σ). In the evaluation of this method, we used , where 6 keV represents the noise floor of the electronics.
In practice, the optimization parameters qi are unknown. In order to compute the objective, they can be substituted by their expected value E(qi). For a uniform distribution, E(qi) = 0; therefore, the interaction locations are assumed to be at the detector voxel center di. Because the scatter angle θi is sensitive to the precise location of the interactions, significant errors in the objective can result from position uncertainty (figure 3).
Figure 3.
The effect of detector voxel size: an interaction has occurred in each of the two detector voxels, delineated by dashed rectangles. The sub-voxel positions q1 and q2 of each interaction are unknown. If the interactions are assumed to occur at the center of the detector voxel, one obtains the average trajectory (dotted line). If sub-voxel sampling is used instead, q1 and q2 are generated randomly within the detector voxels and the objective is averaged over many possible trajectories, two of which are shown (solid red line). The scatter angle, θ, is subject to large variations depending on the position of the interaction within each detector voxel.
Stochastic optimization can deal with uncertainty in the problem parameters by seeking an optimal solution to the expectation of the objective function (which is modeled as a function of random variables). The objective expectation can be computed via Monte Carlo integration by sampling the parameters distribution. This framework was applied to sequence reconstruction by assuming that the sub-voxel interaction locations q are uniformly distributed within each detector voxel. The expectation over q of the likelihood function was calculated using Monte Carlo integration,
| (9) |
and maximized over the finite set of all possible sequence ordering. The stochastic optimization process can also be described as applying sub-voxel sampling in the calculation of the objective.
A GeForce 9800 GX2 (NVIDIA) graphics processing unit (GPU) and the CUDA library (Nickolls et al 2008) were used to accelerate the calculation of the expected value by Monte Carlo integration. Processing each PMIE involved computing the likelihood objective over 16 384 realizations. A Mersenne-twister random number generator was executed on a GPU to randomly sub-sample the detector voxels using a uniform distribution. The computation was decomposed into 32 blocks of 128 threads, resulting in a total of 4096 threads each processing four realizations. The number of realizations was chosen to maximize performance, and can be reduced for faster processing. The 16 384 objective values were subsequently averaged on the CPU.
2.2. Maximum a posteriori
The quality of the estimation can be enhanced by incorporating prior knowledge into the objective. This particularly helps when the measurements are noisy and unreliable. To estimate the order of the interactions in a PMIE, a prior probability distribution is obtained by computing the total cross section for all N! trajectories. This cross section is based on the physics of γ-ray transport. Before the energy measurements are made, the relative a priori distribution of the sequence of interactions can be inferred based on the Klein–Nishina differential cross section and the photoelectric cross section.
The prior probability distribution Pprior(σ) comprises three components: the probability Pprop(σ) that the annihilation photon travels the distance linking two successive interactions without being attenuated, the probability Pcomp(σ) that the photon Compton scatters N − 1 times, with angle θi, each interaction being localized within a small control volume δVi centered on ri and the probability Pphot(σ) that the photon is absorbed by the photoelectric effect within a small control volume δVN centered on rN.
The first component Pprop(σ) can be expressed as
| (10) |
where μtot is the linear photon attenuation coefficient in the detector material (Berger et al 1998), and ei, the energy of the photon after interaction i, is computed from Compton kinematics using (4) and (5).
The second component Pcomp(σ) can be obtained from the Compton scatter cross section:
| (11) |
where
| (12) |
| (13) |
| (14) |
is the differential Compton cross section per unit of angle, which can be computed using the Klein–Nishina formula:
| (15) |
The Compton linear attenuation coefficient, μkn(ei), is computed by integrating the Klein–Nishina scatter cross section over all angles:
| (16) |
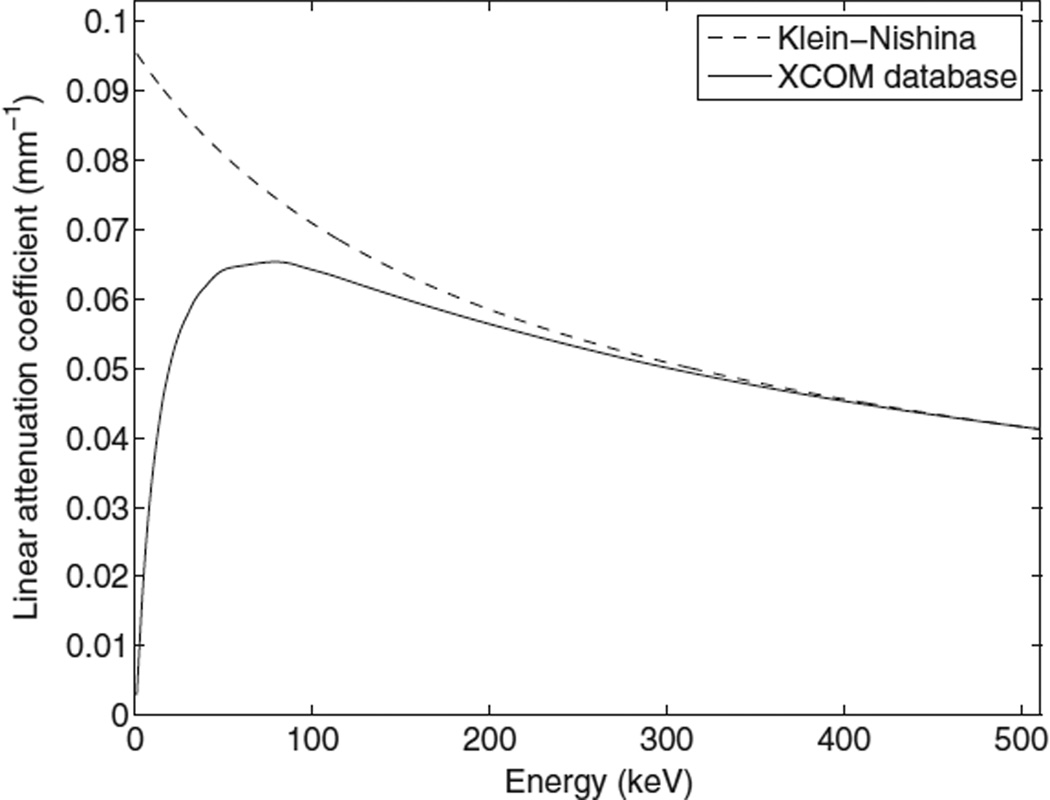
However, because the model assumes the electron is free and at rest, μkn(ei) is not accurate for low photon energy (figure 4). For this reason, (11) is rescaled using the Compton scatter attenuation coefficient μc(ei) obtained from published databases (Berger et al 1998).
Figure 4.
Linear Compton scatter attenuation coefficient as a function of photon energy for CZT. The Klein–Nishina formula does not predict accurately the Compton cross section for low (≤100 keV) energies.
The third component models the probability of photoelectric interaction, for an incoming photon energy eN−1. This prior probability is computed for an arbitrarily small control volume δVN, and is proportional to
| (17) |
The resulting prior distribution is the product of the three components:
| (18) |
The MAP objective is then formed by multiplying the likelihood objective with the a priori probability distribution:
| (19) |
where β is a parameter weighing the prior probability and the likelihood. The ML estimate is obtained when β is zero.
A simplified schematic of the complete positioning algorithm is provided in figure 5.
Figure 5.
Simplified schematics of the MAP positioning scheme.
3. Methods
3.1. Simulation of a CZT PET system
We used GRAY, a fast Monte Carlo package (Olcott et al 2006), to simulate a PET system based on CZT cross-strip electrodes modules (section 1.1). The photoelectric effect and Compton scattering are the only physical processes included in GRAY. GRAY uses published databases (Berger et al 1998) for computing the interaction cross sections. The Compton scatter angle is generated according to the Klein–Nishina formula. The accurate time, energy and position of individual interactions in the detector material are stored in list-mode.
After the simulation, the position of each event was processed to account for the limited spatial resolution of the system. Within one module, the spatial coordinates were binned to a grid of 1 × 5 × 1 mm3 detector voxels. On the rare occasion when two interactions occurred in the same detector voxel, they were merged and their energies summed up. The energy of individual interaction was blurred by additive Gaussian noise with variance . The interactions were indexed arbitrarily and the correct order of the sequence was stored for evaluation purposes. A lower-energy detection threshold of 10 keV was applied. The time stamp was blurred using 8 ns FWHM Gaussian noise. Consistent with maximizing NEC for rat and mouse phantoms (Habte et al 2007), an 8 ns time window was applied for coincidence gating. No dead time model was used in the simulation of the detectors.
3.2. Event positioning schemes
The performance of four PMIE positioning schemes was investigated:
Earliest interaction (EI): the interaction with the smallest non-blurred time stamp was selected. This ideal scheme provides the best possibly achievable performance for any positioning algorithm. It is not available in practice due to time-resolution limitations.
Maximum a posteriori : the full sequence was reconstructed using the methods described in sections 2.1 and 2.2. The event was positioned at the location of the estimated first interaction.
Energy-weighted mean: the event was positioned at the energy-weighted mean position of the interactions. This scheme is the only one available for conventional PET block detectors.
Minimum pair distance (MPD): first, both coincident events are roughly positioned (for example, using EWM). Then, the interaction closest to the rough location of the other coincident photon event is selected. This scheme is based on the preference of 511 keV photons to scatter forward. Unlike in MAP, the energy measurements are not used.
Discarding PMIEs has not been considered as one-interaction events are only a small fraction (6.2%) of all coincidence photon events.
To identify the EI with MAP, the full sequence of interactions is reconstructed. For N ≥ 5, the size of the combinatorial search space (N!) is greater than 60. Therefore, for N ≥ 5, the MPD scheme was used instead of MAP for identifying the EI. Unlike MAP, the search space size in MPD grows linearly. In addition, for N large, the energy depositions are small which means that in most interactions the photon scatters forward. Hence, MPD performs well for N ≥ 5 (table 4).
Table 4.
Recovery rate (%) for MAP and MPD positioning, as a function of the detector voxel size and energy resolution.
| Positioning Methods |
1 × 1 × 1 mm3 | 1 × 5 × 1 mm3 | ||||
|---|---|---|---|---|---|---|
| 0.5%a | 2.5%a | 12%a | 0.5%a | 2.5%a | 12%a | |
| MAP (first interaction) | 90.0 | 89.6 | 88.1 | 85.5 | 85.2 | 84.5 |
| MPD (first interaction) | 69.4b | 69.4b | ||||
FWHM at 511 keV.
The MPD scheme does not use energy information.
3.3. Positioning performance metrics
The simplest measure of the quality of the positioning is the recovery rate, defined as the fraction of all the processed single-photon events for which the first interaction is correctly identified. This figure of merit is not applicable for unconstrained positioning methods such as EWM. The recovery rate was evaluated in a variety of situations: for β varying between zero and one, for stochastic and non-stochastic optimization, for PMIEs with number of interactions varying between one and six, and for varying energy resolution (0%, 3% and 12% FWHM at 511 keV) and spatial resolution (1 × 1 × 1 and 1 × 5 × 1 mm3 detector voxels).
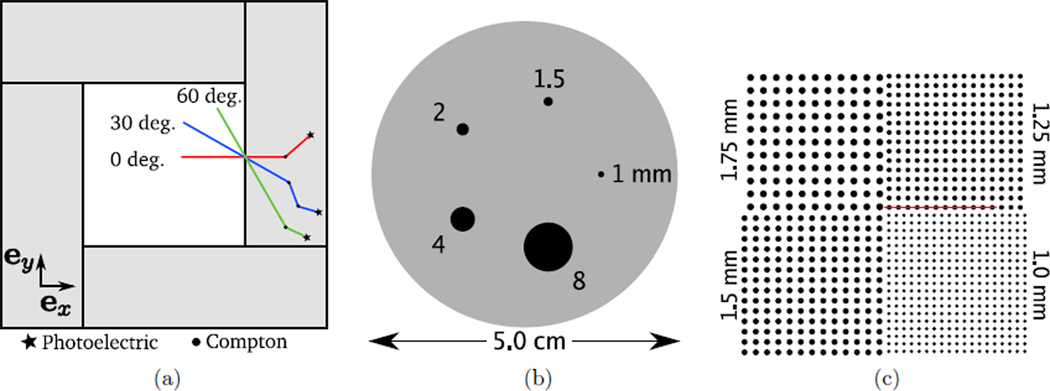
The collimated, single-photon, 1D point-spread function (PSF) was measured for three incident angles (0, 30 and 60°) and for all four positioning methods. An infinitely thin needle beam of 511 keV photons was simulated in GRAY and aimed at the center of a detector voxel in the middle of the panel (figure 6(a)). The events were positioned and their transverse coordinate (along ey) histogrammed. The axial coordinate (along ez) was also histogrammed for the normal (0°) beam. In order to assess the extent of backscatter, and investigate depth-dependant effects, 2D PSFs were also generated by histogramming the events estimated positions along both ex and ey.
Figure 6.
Depiction of phantoms used in the quantitative evaluation. (a) Three beams, with incident angles 0, 30 and 60°, were simulated. (b) A contrast phantom, consisting of a 2.5 cm radius, 6 cm long cylinder filled with a warm solution of activity, in which were placed five hot spheres of diameters 1, 1.5, 2, 4 and 8 mm. The activity was ten times more concentrated in the hot spheres than in the background cylinder. (c) A hot sphere phantom, consisting of four sphere patterns, all in the same central plane. The spheres extended to the edge of the 8 × 8 × 8 cm3 FOV, and their diameters were 1, 1.25, 1.5 and 1.75 mm. The spacing between the centers was twice their diameter.
A contrast phantom (figure 6(b)) was simulated to assess the quantitative contrast recovery. The phantom was composed of a 2.5 cm radius, 6 cm long cylinder, filled with a warm solution of activity, in which were placed five hot spheres. The spheres were centered on the central axial plane and their diameters were 1, 1.5, 2, 4 and 8 mm. The activity was ten times more concentrated in the hot spheres than in the background cylinder. The phantom had a total of 800 µCi and 5 s of acquisition were simulated, yielding 14.6 million coincident events. List-mode 3D-OSEM, with 10 million events per subset, was used for the reconstruction (Pratx et al 2009). Attenuation correction was implemented. The contrast was measured in the reconstructed image as a function of iteration number. The mean reconstructed activity was measured in the hot spheres using spherical 3D regions of interest (ROIs). The background activity was evaluated by averaging the reconstructed intensity in two cylindrical ROIs placed off of the central axial plane. The noise was approximated by the spatial standard deviation in the background ROI, normalized by the mean background intensity. The peak value of the contrast-to-noise ratio (CNR) was computed over all the iterations.
A high-resolution sphere phantom (figure 6(c)) was simulated to research the effects of the positioning algorithm on image resolution. The phantom comprised four quadrants of spheres in air, all in the central axial plane, placed all the way to the edge of the 8 × 8 × 8 cm3 system FOV. The spheres were 1, 1.25, 1.5 and 1.75 mm in diameter. Their centers were placed twice their diameters apart. The phantom had a total of 800 µCi and 5 s of acquisition were simulated, yielding 27.2 million coincident events. The reconstructed sphere FWHM was measured by fitting a Gaussian mixture with offset to 1D profiles through the reconstructed image. Note that the 1 mm spheres were too small relatively to the voxel size for a reliable measure of their FWHM.
4. Results
4.1. Recovery rate
The recovery rate is the fraction (%) of all the processed single-photon events for which the first interaction is correctly identified. All recovery rates were evaluated based on at least 10 million events, and are subject to statistical measurement error below 0.02%. Some positioning methods, such as EWM, do not identify the first interaction, but rather estimate the position directly. The recovery rate is undefined for such methods.
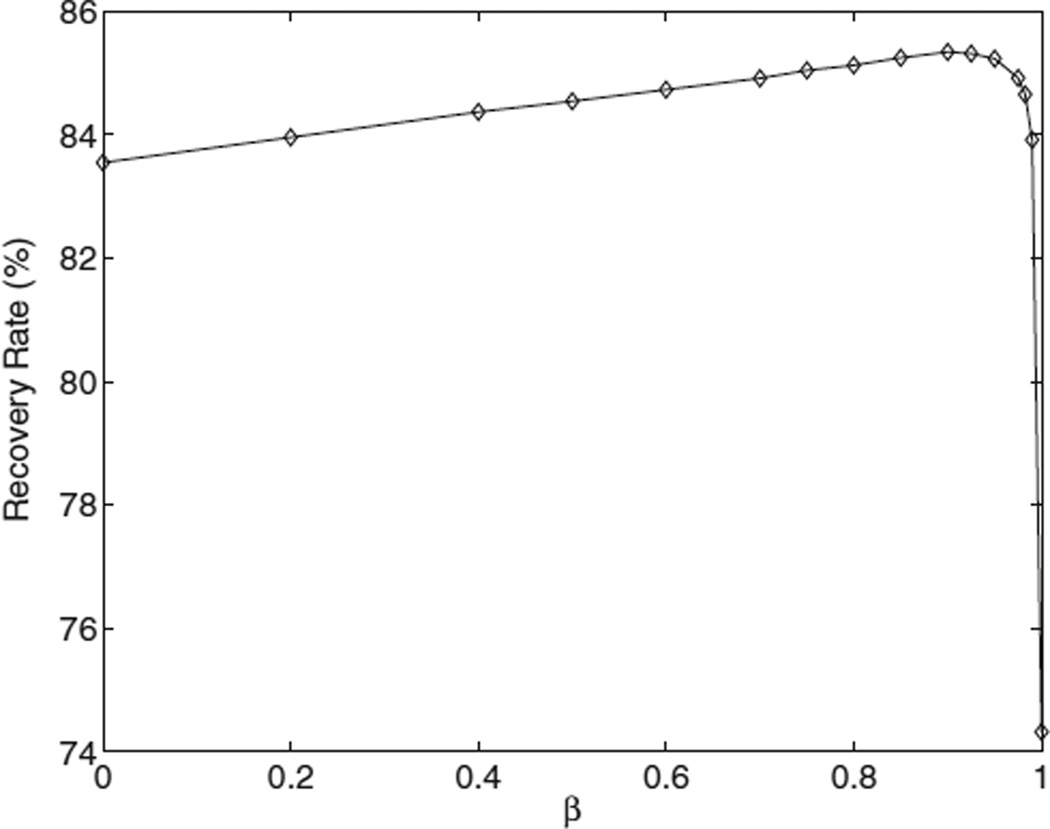
For the MAP positioning scheme, the recovery rate is shown for β varying between zero and one (figure 7). For the contrast phantom, the highest recovery rate (85.2%) is obtained for β = 0.85. The use of prior information increases the quality of the estimation: for β = 0 (no prior), the first interaction is correctly identified only in 83.5% of the single photons. The worst performance is reached for β = 1, when only the prior probability is optimized. Yet, in this case, the recovery rate (74.3%) is still larger than for MPD (69.4%).
Figure 7.
The success rate in positioning the first interaction with MAP as a function of the parameter β.
The recovery rate varies with the photon angle of incidence (table 2). MAP is most challenged by large photon incident angles (such as 60°), where the photon is more likely to interact with multiple panels. The MPD scheme performs best for photons impinging normally on the detector. For a realistic set-up (such as the contrast phantom) the number of mispositioned events with MAP is a factor of two lower compared to MPD: 30.6% versus 14.8%.
Table 2.
Recovery rate (%) for MAP and MPD positioning measured on five simulated datasets.
| Positioning Methods |
Beam 0° |
Beam 30° |
Beam 60° |
Contrast Phantom |
|---|---|---|---|---|
| MAP (first interaction) | 84.3 | 86.2 | 83.6 | 85.2 |
| MPD (first interaction) | 76.6 | 71.9 | 70.2 | 69.4 |
The recovery rate also depends upon the number of times the annihilation photon interacts with the detector (table 3). MAP’s ability to find the EI is not substantially degraded by an increasing number of interactions. PMIEs with two interactions are the most challenging to sequence for all methods. MAP has the ability to recover the full sequence of interactions which is useful in certain applications (table 3, third row).
Table 3.
Recovery rate (%) for MAP and MPD positioning as a function of the number of interactions.
| Positioning Methods |
PE Only |
1 CS +PE |
2 CS +PE |
3 CS +PE |
4 CS +PE |
5 CS +PE |
Global |
|---|---|---|---|---|---|---|---|
| MAP (first interaction) | 100 | 76.7 | 85.0 | 84.8 | – | – | 85.2a |
| MPD (first interaction) | 100 | 52.1 | 64.1 | 75.6 | 82.4 | 86.4 | 69.4 |
| MAP (full sequence) | 100 | 76.7 | 78.3 | 67.0 | – | – | 77.6b |
CS: Compton scatter, PE: photoelectric.
For N ≥ 5, the first interaction is estimated using MPD because the large size of the combinatorial search space (≥ 60) makes the identification of the correct sequence impractical.
Computed only based on events with N ≤ 4 interactions.
The specifications of the detector technology, including the energy resolution and intrinsic spatial resolution, affect the performance of the MAP scheme (table 4). For MAP, higher detector spatial and energy resolution help position correctly a larger fraction of PMIEs. Also, the recovery rate is less sensitive to the energy resolution than to the detector voxel size.
The estimation procedure uses stochastic optimization via sub-voxel sampling to account for the geometrical properties of the detector voxels. Table 5 shows that the stochastic approach results in a higher recovery rate compared to a deterministic one (where the interactions are assumed to occur at the center of the detector voxel).
Table 5.
Recovery rate (%) for MAP using stochastic and deterministic objectives.
| Interaction Position |
PE Only |
1 CS +PE |
2 CS +PE |
3 CS +PE |
Global |
|---|---|---|---|---|---|
| Sub-voxel sampling | 100 | 76.7 | 85.0 | 84.8 | 85.2 |
| Voxel center | 100 | 68.2 | 75.9 | 72.5 | 78.8 |
4.2. Point-spread function
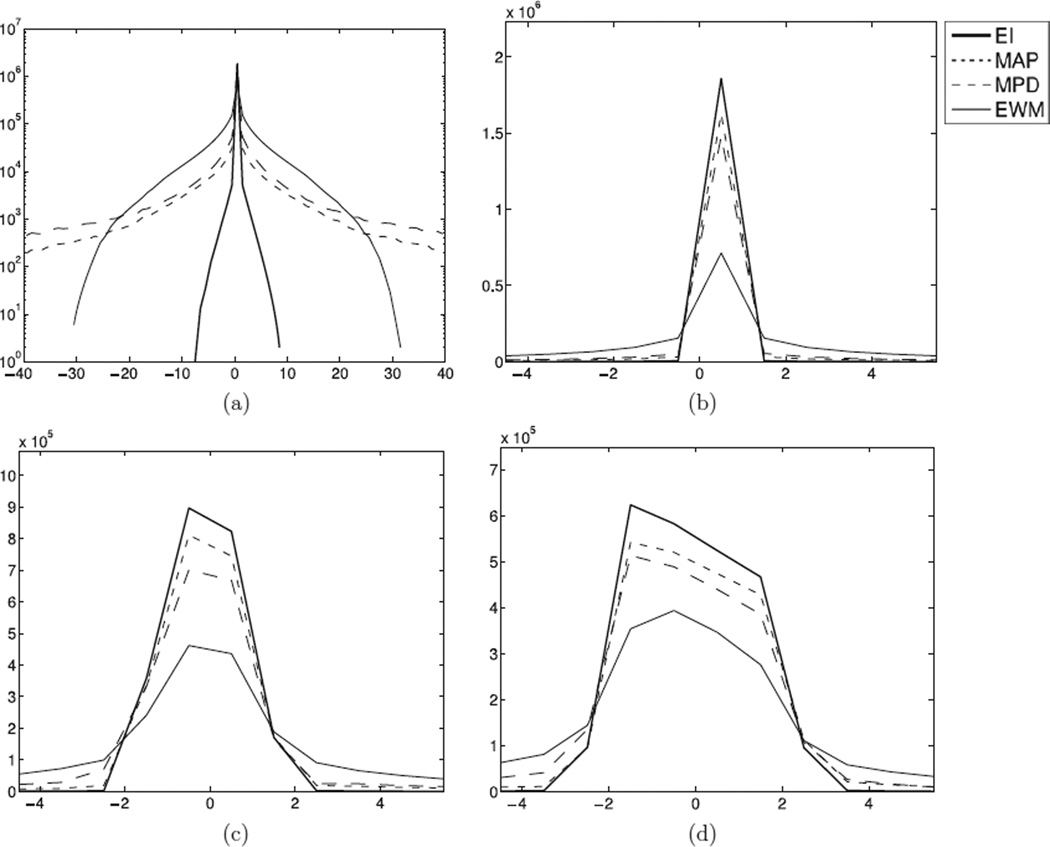
Figure 8 reports the detector coincident PSFs for all four positioning methods. For a normal beam (0°), the PSF was plotted along the axial (a) and tangential (b) dimensions. The tangential component of the PSF was also plotted for (c) 30° and (d) 60° beams. Due to the limited depth resolution of the detector design (5 mm), the PSF is wider and asymmetric for photons incoming at an oblique angle. The PSF is not normalized; therefore, a higher peak value indicates that more counts are correctly positioned at the PSF center. Note that the worst case error is smaller for EWM (≈30 mm) than for MAP or MPD (40 mm), because the EI pulls the center of mass toward itself. Nevertheless, the average error is lower for both MAP and MPD than for EWM.
Figure 8.
Point-spread functions (PSFs) for four positioning methods: earliest interaction (EI), MAP, minimum pair distance (MPD) and energy-weighted mean (EWM). (a) 1D axial PSF for a normal beam (i.e. 0° incindent angle), (b) 1D tangential PSF for the same normal beam, (c) 1D tangential PSF for a 30° beam and (d) 1D tangential PSF for a 60° beam.
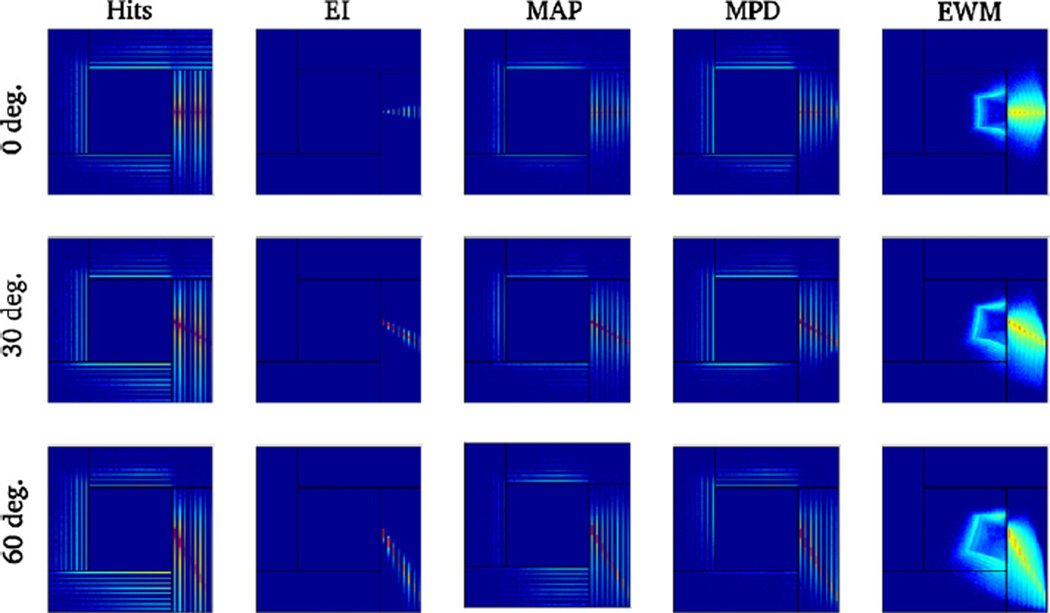
Figure 9 provides a 2D representation of the PSF for the same beam angles (0, 30 and 60°). The first column is a histogram of all the interactions as recorded by the system (raw hits). The second to fifth columns show histograms of the position estimates for the EI, MAP, MPD and EWM schemes, respectively. The histograms are shown on a logarithmic scale since PMIEs mostly affect the tails of the PSF. For the EWM scheme, some PMIEs are positioned outside of the detector volume. This occurs when the photon back-scatters and deposits energy in two opposite detector panels, which places the center of mass of the interactions toward the center of the system. These interactions have a characteristic distribution (figure 9, rightmost column) that is produced by the fixed repartition of the 511 keV between the front and back interactions for a given back-scattering angle. As a result, the distribution of the EWM locations outlines the box-shaped geometry of the scanner.
Figure 9.
Point-spread function (2D, log scale) for three beam angles (top: 0°, middle: 30°, bottom: 60°). In the first column, the histogram of all the interactions recorded by the system is shown. The second to fifth columns show histograms of the position estimate for the EI, MAP, MPD and EWM positioning schemes, respectively.
4.3. Reconstructed contrast
The system PSF affects the final image quality. Therefore, the contrast versus noise trade-off was investigated for five hot spheres in a warm background of activity (figure 6(a)). Figure 10 shows the images reconstructed using 100 sub-iterations of list-mode OSEM for all four positioning methods: (a) EI, (b) MAP, (c) MPD and (d) EWM. The four pictures are shown on the same intensity scale to facilitate the comparison. Only two spheres can be resolved for EWM. For the other positioning schemes, all but the smallest sphere are resolved. Figure 11 shows the contrast versus noise in the reconstructed images for the five spheres: (a) 8 mm, (b) 4 mm, (c) 2 mm, (d) 1.5 mm and (e) 1 mm. A total of 100 list-mode 3D-OSEM sub-iterations are displayed. The non-monotonic behavior of the noise is caused by the structural artifacts present in the early image iterates.
Figure 10.
Contrast phantom, reconstructed with 100 sub-iterations of list-mode 3D-OSEM. Ten million events were included in each subset. The phantom comprised a 2.5 cm radius, water-filled cylinder, in which were placed five hot spheres. The ratio of the activity concentration in the spheres to that in the background was 10. The sphere diameters were 1, 1.5, 2, 4 and 8 mm, respectively. Four positioning schemes were used: (a) EI, (b) MAP, (c) MPD and (d) EWM. No post-processing was performed. The images are displayed using the same intensity scale.
Figure 11.
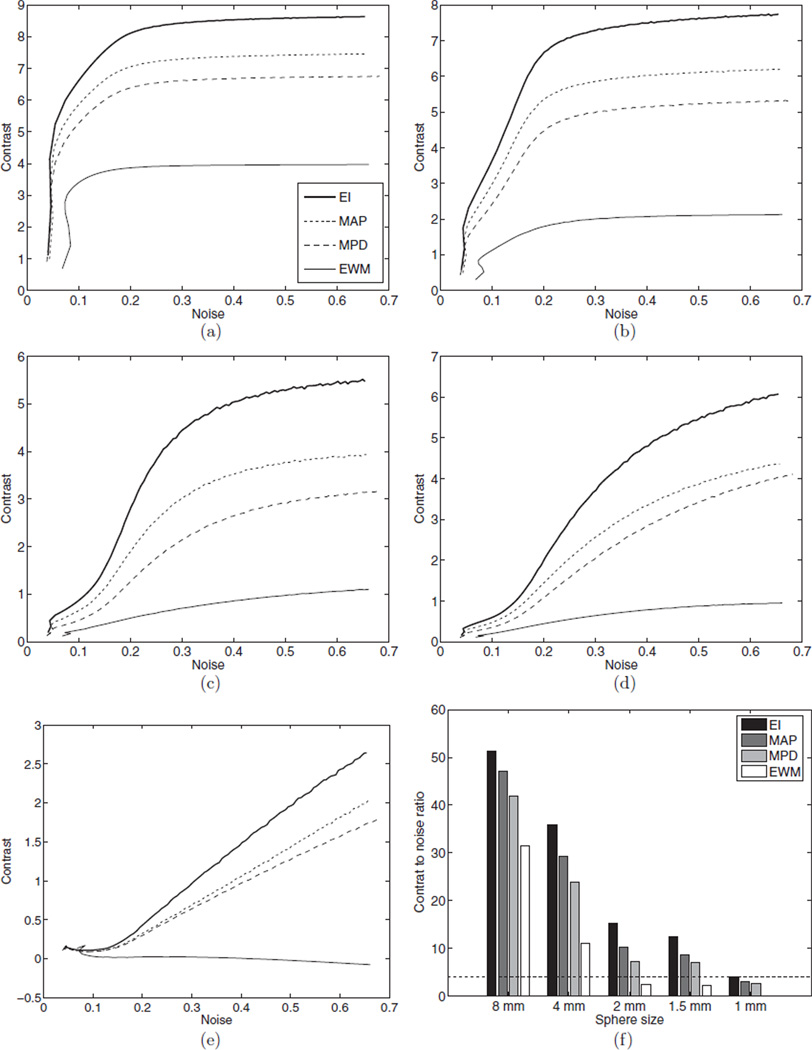
Reconstructed hot spheres contrast as a function of noise, at different sub-iteration numbers. The contrast phantom was reconstructed with list-mode 3D-OSEM using ten million events in each subset. Four positioning methods were used: EI, MAP, MPD and EWM. The resulting curves are shown for the (a) 8 mm, (b) 4 mm, (c) 2 mm, (d) 1.5 mm and (e) 1 mm spheres. (f) Peak contrast-to-noise ratio, computed between iteration number 10 and 100. The dashed line represents the threshold for Rose criterion.
Unlike the contrast recovery, the noise is not affected by mispositioning. Independently of the positioning method, the contrast is degraded by small-angle tissue scatter and by random coincidences (randoms rate is 10.6%). For this reason, it never reaches its true value (10:1), even for the ideal EI positioning scheme which provides the highest contrast recovery (8.6 to 1). For the largest sphere, the contrast is 10% higher for MAP (7.5 to 1) than for the MPD scheme (6.8 to 1). The contrast difference is even greater for the smaller spheres: for the 2 mm sphere, the contrast is 24% higher for MAP than for MPD. It should also be noted that the contrast of the smallest spheres (1 and 1.5 mm) did not converge within a hundred iterations; however, the noise prevents iterating further.
The EWM method demonstrates the worst performance for the contrast recovery task. The contrast is degraded to the extent that the small spheres (≤2 mm) cannot be resolved. The contrast of the largest sphere is 46% lower than that achieved with MAP.
The CNR (figure 11(f)) provides a rough estimate of the detectability of hot lesions in a background. Lesions with CNR greater than 4 (shown as a dashed line) are usually detectable, even though observer experience and object shape can also affect the detectability (Rose 1973). According to this criterion, the 1mmsphere can only be detected when the ideal EI positioning scheme is used. The 1.5 and 2 mm spheres are not detectable when EWM is used. The CNR is systematically higher for MAP than for MPD.
4.4. Reconstructed sphere resolution
The hot spheres phantom (figure 6(c)) was used to evaluate how the spatial resolution is affected by positioning when iterative 3D-OSEM reconstruction is used. Figure 12 shows the reconstructed images at 50 iterations for the four positioning methods (EI, MAP, MPD and EWM). The spheres are best resolved for the ideal EI scheme. MAP and MPD appear to perform similarly, but EWM shows substantial degradation of the spatial resolution.
Figure 12.
Hot spheres in an air phantom, reconstructed with 50 iterations of list-mode 3D-OSEM. Ten million events were included in each subset. The spheres extend to the edge of the 8 × 8 × 8 cm3 FOV, and their diameters are 1, 1.25, 1.5 and 1.75 mm, respectively. The spacing between the centers is twice the diameter. Four positioning schemes were used: (a) EI, (b) MAP, (c) MPD and (d) EWM. No post-processing was performed. The intensity scale was chosen to maximize the dynamic range. The intensity bar units are arbitrary.
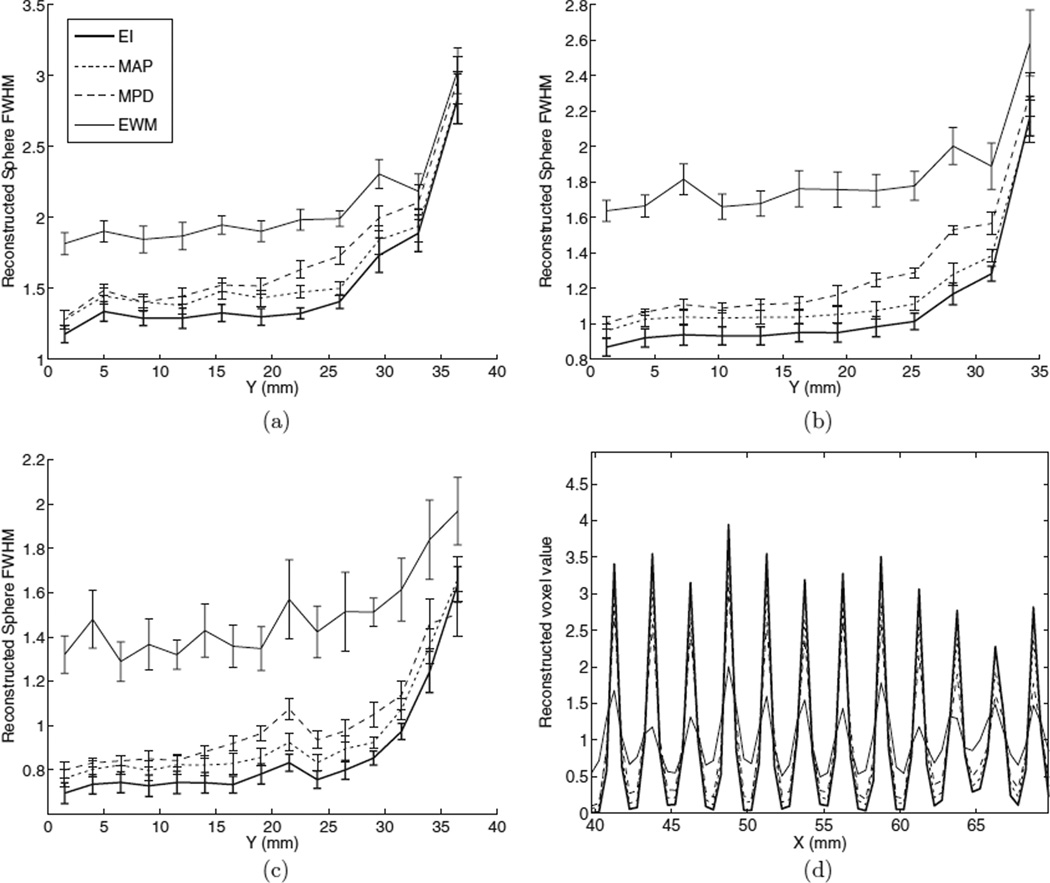
Further investigation was performed by measuring the reconstructed FWHM of the spheres (figure 13). The results of these measurements are reported in figure 13, for the (a) 1.75, (b) 1.5 and (c) 1.25 mm spheres. Since the ML estimate is nonlinear, the reconstructed sphere FWHM should be analyzed with care and should not be interpreted in terms of modulation transfer function. It is, however, an interesting figure of merit to study since it defines the ability of the algorithm to distinguish small lesions that are close to each other. It should also be noted that the reconstructed sphere FWHM is not expected to be equal to the true sphere diameter.
Figure 13.
Reconstructed sphere FWHM (mm) for the four positioning methods, measured by fitting a Gaussian mixture with offset to 1D profiles though the reconstructed volume: (a) 1.75 mm spheres, (b) 1.5 mm spheres and (c) 1.25 mm spheres. (d) A profile through the 1.25 mm spheres is shown for the four positioning methods.
Due to parallax blurring and despite 5 mm depth resolution, the reconstructed sphere FWHM is degraded for spheres near the edge of the FOV. The ideal EI scheme provides the best reconstructed FWHM, followed by MAP and MPD. Due to fewer mispositioned events, the reconstructed 1.75 mm diameter spheres were, on average, 5.6% smaller for MAP than for MPD. As demonstrated in figure 12(d), EWM adds a substantial amount of blur to the reconstructed images. The profile through the 1.25 mm diameter spheres (figure 13(d)) shows that, besides the FWHM, the contrast of the spheres is affected by positioning. A significant background is present for the EWM scheme in between the peaks.
5. Discussion
5.1. Performance of the proposed scheme
We have investigated a stochastic Bayesian method for reconstructing sequences of interactions in detectors, thereby enabling accurate identification of the first interaction in a sequence. When MAP is used, two times fewer events are mispositioned compared to MPD, a simpler algorithm. As a result, the PSF has lower tails and a higher peak value (figure 8) because more events are positioned to the correct LOR. MAP is also less likely to misposition events in which the photon undergoes back-scatter (figure 9). This directly affects the reconstructed image quality. The contrast is higher for MAP positioning than for MPD (figure 11). Mispositioning causes contrast loss because events that originate from the hot lesion are positioned in the background. The CNR is greater for MAP than for MPD and EWM, which implies that hot lesions stand a higher chance of being detected in a clinical setting. Due to event mispositioning, a significant amount of background is observed in figure 13(d) when EWM is used. MAP provides better quantitative accuracy. Images reconstructed using the MAP positioning scheme show higher spatial resolution (figure 13), which facilitate the detection of smaller hot structures.
The full sequence of interactions can also be reconstructed by optimizing the prior distribution alone (i.e. β = 1 in MAP). Like MPD, this approach has the advantage that energy measurements are not needed. Furthermore, MAP with β = 1 outperforms MPD by 4.4% (figure 7).
The size of the search space used for recovering the first interaction grows linearly with N, and so does the number of energy measurements. Therefore, the performance of the MAP scheme is maintained even as N increases (table 3, first row). When recovering the full sequence, the size of the search space increases exponentially with N; hence the recovery rate for complete sequences drops sharply for N = 4 (table 3, third row).
Uncertainty in the locations of the interactions (within the detector voxel boundaries) translates into uncertainty in the scatter angle, which, in turn, yields uncertainty on the energy deposited. Position uncertainty in 1 × 5 × 1 mm3 detector voxels causes an equivalent energy blur far greater than 12% FWHM at 511 keV (table 4). When the interactions are constrained to fixed detectors voxels, the range of energies that can be deposited is often much larger than the energy resolution of the system (figure 3). Therefore, good spatial resolution is more important than good energy resolution for estimating correctly the order of the interactions.
5.2. Limitations
The processing time is problematic when sub-voxel sampling is used in MAP. Although the algorithm was implemented on a fast GPU, it takes over 5 s to process 1000 events. MPD runs 43 times faster than MAP, mainly because MAP computes the objective over 16 384 statistical realizations. Using fewer simulation paths degrades the positioning. Hence, when the objective is computed for only one trajectory passing through the center of the detector voxels, the recovery rate drops from 85.2% to 78.8% (table 5).
The validation of the MAP scheme was carried out based on simulations performed with GRAY (section 3.1). These simulations included the standard Compton model based on the Klein–Nishina formula, the accurate linear attenuation coefficients from published databases and the standard photoelectric model. In a real system, other physical effects occur, namely characteristic x-ray production, Raleigh scattering, Bremsstrahlung and Doppler broadening. Furthermore, the electron is neither free nor at rest; therefore, the Klein–Nishina formula is not an accurate model for low (<100 keV) energy photons undergoing Compton scatter (figure 4). Therefore, we applied our method to a dataset generated using GATE (Jan et al 2004), amore detailed Monte Carlo package that incorporates all these effects (except Doppler broadening). For a point source in the center, the recovery rate dropped from 85.0% to 82.4% for MAP, and from 70.1% to 67.9% forMPD. This drop is mostly caused by the production of a characteristic x-ray that can propagate beyond the boundaries of the detector voxel, resulting in an increase in the number of interactions recorded. Doppler broadening was not modeled in any of the simulations. For 511 keV photons, Doppler broadening blur is at most 6 keV FWHM (Du et al 2001). The energy blurring remains dominated by the finite resolution of the detectors. In addition, increase in energy blur only results in a modest reduction ofMAP’s recovery rate (table 4).
5.3. Possible extensions
The effect of PMIEs has been previously compensated for by using a simple positioning method (such as EWM), and then by reconstructing the images with an accurate model of the PSF (Panin et al 2006). However, by effectively deconvolving the blur caused by PMIEs, this approach amplifies the noise. Prior to reconstruction, it is preferable to use an advanced positioning method (such as MAP) to estimate the location of the first interaction. The incorporation of the resulting PSF into the reconstruction will generate less noise amplification because such a PSF is narrower (figure 8).
In section 2.1, it is assumed that the photon incoming energy e0 and the location of the other coincident photon p are available. While true for PET, these assumptions cannot be made for other modalities such as single-photon emission computed tomography (SPECT) or Compton cameras. The method can, however, be generalized for these modalities. The incoming energy e0 can be estimated by summing the energies of all the interactions. When p is unavailable, the likelihood should not include the first interaction because the scatter angle cos θ̂1 cannot be computed (4).
The MAP objective can be readily extended to be used as criteria for rejecting tissue-scattered events and random coincidences. In its current formulation, it assumes that the incoming photon energy e0 is 511 keV and that the incident angle is given by the location p of the other photon pair. When the photon scatters in tissue or is paired up incorrectly (random coincidence), these hypotheses do not hold. As a result, no sequence might be attributed a high probability and the event can be discarded.
MAP positioning can be applied to crystals other than CZT. For instance, high-resolution detectors with depth-of-interaction capabilities can be built from lutetium oxyorthosilicate (LSO) coupled to thin position-sensitive avalanche photodiodes (Zhang et al 2007). Even though LSO’s photofraction is higher than CZT’s, small crystal elements will cause PMIEs. The MAP scheme can then be used for positioning: based on table 4, MAP is accurate even with 12% energy resolution FWHM.
6. Conclusion
The ability to correctly position PMIEs greatly affects the global performance of PET systems based on high-resolution detectors. Discarding PMIEs is not possible for the CZT system studied since these events are part of almost every recorded coincident event. Conventional positioning schemes, such as EWM, degrade both contrast and resolution, reduce the images quantitative accuracy and affect the detectability of hot lesions. Simple approaches, such as MPD, help improve the image quality, but are outperformed by MAP, a more advanced positioning scheme that uses all the information available in an optimal way.
Although inter-crystal scatter is more prevalent in smaller crystals, improved intrinsic spatial resolution will facilitate the identification of the photon crystal of entry. Bayesian sequence reconstruction methods will play a key role in ultra-high resolution systems, especially those made from materials with low photo-fraction such as CZT or germanium.
Acknowledgments
This work was supported by the National Institutes of Health (NIH) under grants R01CA119056, R33EB003283, R01CA120474 and the Stanford Bio-X graduate fellowship program.
References
- Berger MJ, Hubbell JH, Seltzer SM, Chang J, Coursey JS, Sukumar R, Zucker SS. XCOM: photon cross sections database. NIST Standard Reference Database 8(XGAM) 1998 [Google Scholar]
- Bergeron M, et al. Performance evaluation of the LabPET APD-based digital PET scanner. IEEE Nuclear Science Symp. Conf. Record. 2007;vol 6:4185–4191. [Google Scholar]
- Boggs S, Jean P. Event reconstruction in high resolution Compton telescopes. Astron. Astrophys. 2000;145:311–321. [Google Scholar]
- Braem A, et al. Feasibility of a novel design of high resolution parallax-free Compton enhanced PET scanner dedicated to brain research. Phys. Med. Biol. 2004;49:2547–2562. doi: 10.1088/0031-9155/49/12/006. [DOI] [PubMed] [Google Scholar]
- Comanor KA, Virador PRG, Moses WW. Algorithms to identify detector Compton scatter in PET modules. IEEE Trans. Nucl. Sci. 1996;43:2213–2218. [Google Scholar]
- Du YF, He Z, Knoll GF, Wehe DK, Li W. Evaluation of a Compton scattering camera using 3-D position sensitive CdZnTe detectors. Nucl. Instrum. Methods Phys. Res. 2001;457:203–211. [Google Scholar]
- Habte F, Foudray AMK, Olcott PD, Levin CS. Effects of system geometry and other physical factors on photon sensitivity of high-resolution positron emission tomography. Phys. Med. Biol. 2007;52:3753–3772. doi: 10.1088/0031-9155/52/13/007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jan CS, et al. GATE: a simulation toolkit for PET and SPECT. Phys. Med. Biol. 2004;49:4543–4561. doi: 10.1088/0031-9155/49/19/007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lehner C, He Z, Zhang F. 4π Compton imaging using a 3-D position-sensitive CdZnTe detector via weighted list-mode maximum likelihood. IEEE Trans. Nucl. Sci. 2004;51:1618–1624. [Google Scholar]
- Levin CS. New imaging technologies to enhance the molecular sensitivity of positron emission tomography. Proc. IEEE. 2008;96:439–467. [Google Scholar]
- Levin CS, Tornai MP, Cherry SR, MacDonald LR, Hoffman E J. Compton scatter and x-ray crosstalk and the use of very thin intercrystal septa in high-resolution PET detectors. IEEE Trans. Nucl. Sci. 1997;44:218–214. [Google Scholar]
- Nickolls J, Buck I, Skadron K, Garland M. Scalable parallel programming with CUDA. ACM Queue. 2008;6:40–53. [Google Scholar]
- Oberlack UG, Aprile E, Curioni A, Egorov V, Giboni KL. Compton scattering sequence reconstruction algorithm for the liquid xenon gamma-ray imaging telescope (LXeGRIT) Proc. SPIE. 2000;4141:168–177. [Google Scholar]
- Olcott P, Buss S, Levin C, Pratx G, Sramek C. GRAY: high energy photon ray tracer for PET applications. IEEE Nuclear Science Symp. Conf. Record. 2006:2011–2015. [Google Scholar]
- Panin V, Kehren F, Michel C, Casey M. Fully 3D pet reconstruction with system matrix derived from point source measurements. IEEE Trans. Med. Imag. 2006;25:907–921. doi: 10.1109/tmi.2006.876171. [DOI] [PubMed] [Google Scholar]
- Pratx G, Chinn G, Olcott P, Levin C. Fast, accurate and shift-varying line projections for iterative reconstruction using the GPU. IEEE Trans. Med. Imaging. 2009;28:435–445. doi: 10.1109/TMI.2008.2006518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rafecas M, Oning GB, Pichler BJ, Lorenz E, Schwaiger M, Ziegler SI. Inter-crystal scatter in a dual layer, high resolution LSO-APD positron emission tomograph. Phys. Med. Biol. 2003;48:821–848. doi: 10.1088/0031-9155/48/7/302. [DOI] [PubMed] [Google Scholar]
- Rose A. Vision: Human and Electronic. New York: Plenum; 1973. [Google Scholar]
- Schmidt GJ, Deleplanque MA, Lee IY, Stephens FS, Vetter K, Clark RM, Diamond RM, Fallon P, Macchiavelli AO, MacLeod RW. A γ-ray tracking algorithm for the GRETA spectrometer. Nucl. Instrum. Methods Phys. Res. 1999;430:69–83. [Google Scholar]
- Shao Y, Cherry SR, Siegel S, Silverman RW. A study of inter-crystal scatter in small scintillator arrays designed for high resolution PET imaging. IEEE Trans. Nucl. Sci. 1996;43:1938–1944. [Google Scholar]
- Spanoudaki V. Dissertation. Technische Universitt München; 2008. Development and performance studies of a small animal positron emission tomograph with individual crystal readout and depth of interaction information. [Google Scholar]
- Stickel JR, Cherry SR. High-resolution PET detector design: modelling components of intrinsic spatial resolution. Phys. Med. Biol. 2005;50:179–195. doi: 10.1088/0031-9155/50/2/001. [DOI] [PubMed] [Google Scholar]
- Van der Marel J, Cederwall B. Backtracking as a way to reconstruct Compton scattered γ-rays. Nucl. Instrum. Methods Phys. Res. 1999;437:538–551. [Google Scholar]
- Zhang J, Foudray A, Olcott P, Farrell R, Shah K, Levin C. Performance characterization of a novel thin position-sensitive avalanche photodiode for 1 mm resolution positron emission tomography. IEEE Trans. Nucl. Sci. 2007;54:415–421. [Google Scholar]