Attribution of changes in precipitation patterns in African rainforests

Abstract

Tropical rainforests in Africa are one of the most under-researched regions in the world, but research in the Amazonian rainforest suggests potential vulnerability to climate change. Using the large ensemble of Atmosphere-only general circulation model (AGCM) simulations within the weather@home project, statistics of precipitation in the dry season of the Congo Basin rainforest are analysed. By validating the model simulation against observations, we could identify a good model performance for the June, July, August (JJA) dry season, but this result does need to be taken with caution as observed data are of poor quality. Additional validation methods have been used to investigate the applicability of probabilistic event attribution analysis from large model ensembles to a tropical region, in this case the Congo Basin. These methods corroborate the confidence in the model, leading us to believe the attribution result to be robust. That is, that there are no significant changes in the risk of low precipitation extremes during this dry season (JJA) precipitation in the Congo Basin. Results for the December, January, February dry season are less clear. The study highlights that attribution analysis has the potential to provide valuable scientific evidence of recent or anticipated climatological changes, especially in regions with sparse observational data and unclear projections of future changes. However, the strong influence of sea surface temperature teleconnection patterns on tropical precipitation provides more challenges in the set up of attribution studies than midlatitude rainfall.

1. Introduction

Rainforests are not only the ecosystem with the highest biodiversity, but are also a key feature in the global carbon cycle as a sink of CO₂ and thus are crucial in the global climate system. A loss of tropical forest would not only mean a loss of biodiversity, but also amplify climate change by losing the CO₂ sink. For these reasons, Malhi & Wright [1] show that rainforests are potentially strongly affected by climate change, highlighting the need for more research on how climate change affects rainforests. Subsequent studies focus mainly on Amazonia, because IPCC projections jointly show a decrease in precipitation, whereas there are no clear projections for the African rainforest. In the study of Phillips et al. [2], it is shown that droughts in rainforests are not only stressful for the local ecosystem, but exert a strong feedback via the carbon cycle on the global climate system as a whole. However, results of studies in the Amazon region or south Asian rainforests are potentially not transferable to African rainforests in a straightforward way, since the annual precipitation is around 1000 mm per month less than in Amazonia and temperatures are much lower due to the higher elevation of African tropical forests [3]. Projections from a multi-model ensemble of temperature and precipitation changes in a warming African climate show [4] a significant increase in mean temperatures on the whole continent and in all seasons with the most pronounced warming in June, July, August (JJA), but hardly any statistically significant changes in precipitation apart from an increase in precipitation over east Africa and a pronounced drying in JJA in southern Africa. From the so-called ‘rich-get-richer effect’, convergence zones such as tropical rainforests are expected to see an increase in precipitation under global warming [5], however such an increase cannot be seen robustly in recent projections. Modelling errors aside, this shows that it is not clear which of the many mechanisms that influence African tropical precipitation dominate the response to global warming. One important feature influencing tropical rainfall in Africa is the Indian dipole oscillation which could potentially weaken under climate change (discussed by [4]). Vecchi & Soden [6] discuss the possibility of a general weakening of the tropical circulation, which seems to induce a decrease in precipitation in large parts of the tropics over land [6]. The overall picture is unclear; moreover, other factors may be important, for example, James et al. [7] discuss the possible influence of the rearrangment of zonal dynamics on precipitation anomalies. If there is a consensus, it is that most of the above effects could lead to drier and longer dry seasons (e.g. JJA) in the African tropical forests.

Despite the model disagreement on projections of precipitation changes [8], we analyse simulations of recent decades of dry season precipitation in the Congo Basin with the aim to identify changes in the precipitation and exploring whether they can be attributed to external drivers of the global climate system. Using the emerging method of probabilistic event attribution (PEA) [9], the attribution of precipitation changes to external drivers is employed, aiming at quantifying changes in the risk of extreme precipitation events. Analysing simulations of Central African precipitation in hindcast models with prescribed sea surface temperatures (SSTs) results can be robust in contrast to future predictions. Recent studies show that climate models forced with observed SSTs can actually match the observed variability of land precipitation, relating to ENSO [10], which leads to potentially high predictability of tropical forest precipitation.

Using the results from a large ensemble of global climate model simulations, we analyse the dry season in the Congo Basin as an example attribution study on tropical forest precipitation. We will show analysis for both dry seasons, JJA and December, January, February (DJF), but will concentrate in the analysis on JJA because of the clearer signal in projections as discussed earlier and a better performance of our model for JJA. By comparing the decade of the 1960s with the 2000s, and simulations of the 2000s with the anthropogenic climate signal in the driving SSTs removed, we are able to disentangle some of the drivers of anthropogenic climate forcing and find the risk of water stress has not changed significantly.

In §2, PEA is briefly introduced, followed by a description of the modelling framework and observed and reanalysis data used for the study. A time-series analysis for validation purposes is discussed. Results of applying the model in the region and the attribution study are presented in §3, which is followed by a discussion and concluding remarks in §§4 and 5.

2. Material and methods

(a). Probabilistic event attribution

The emergent science of PEA is becoming an increasingly important method of evaluating the extent to which human-induced climate change is affecting localized weather events [11–13]. The method as introduced by Stone & Allen [14] requires access to a sufficiently large number of simulations to enable sampling of the uncertainty, so that statistics of the occurrence of a rare event can be estimated with confidence. The weather@home project provides such a large ensemble using publicly volunteered distributed computing [15,16]. Studies employing PEA rely heavily on climate modelling and have concentrated on European and US American events. Hence it has been suggested that these studies make a case for natural scientific evidence as the only basis of decision-making and neglect important aspects of vulnerability. Therefore, they are claimed to have negative impacts on adaptation funding in countries with sparse data [17].

Although the main argument given in Hulme et al. [17] is unquestionably that PEA relies on the ability of climate models to represent the true statistics of extreme events, we do not come to the same conclusion. Hulme et al. [17] conclude that because models are impossible to verify, the approach is highly subjective, disguised in scientific objectivity and makes PEA seemingly misplaced in the allocation of adaptation funding. We argue, however, that attribution studies can provide a very valuable source of scientific evidence of a changing climate, especially in regions with sparse observational data and ambiguous projections of the future impacts of anthropogenic climate change. PEA is a method that identifies how climate change is affecting us now. It is not limited to attribution of extreme events that were already observed, but can assess changing risks of extreme events that may occur given current and past or counterfactual climate conditions. PEA could, therefore, provide a method to identify vulnerability in addition to socially defined capacities, potentially leading to more objective allocation of adaptation funding and allowing anticipation of extreme weather events.

(b). Observed datasets

Rainforests are regions with notoriously sparse observational data. While in recent years, several programmes have started to close this gap with satellite measurements, most prominently the joint NASA and Japan Aerospace Exploration Agency (JAXA) tropical rainfall measuring mission (TRMM), there are no reliable datasets long enough to analyse trends in precipitation over time periods longer than two to three decades. The Congo Basin, the heart of tropical African rainforest is a region where weather stations are almost absent. As a result, the African rainforest is one of the most under-researched regions in the world. Hence, analysis of changes in precipitation patterns in this region relies heavily on reanalysis data and modelling results.

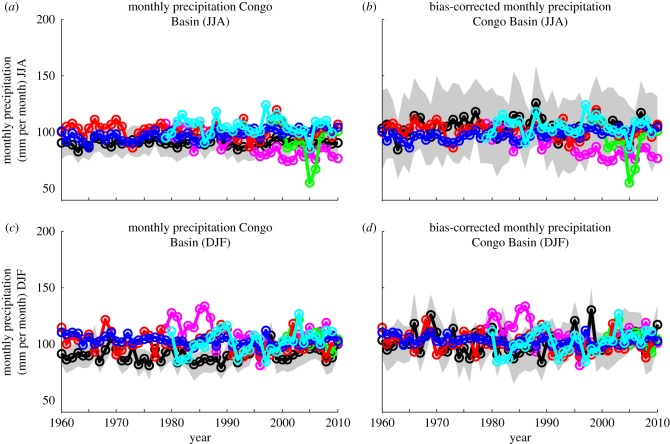
We identify the Congo Basin (10° S–9° N, 13°–30° E) as the region in the African tropical forest with two wet seasons in March, April, May (MAM) and September, October, November (SON) and two dry seasons in JJA and DJF. We concentrate in this analysis on the JJA season, additional information on the second dry season DJF can be found in the electronic supplementary material. The region has barely any weather stations [18] which renders observed datasets from rain gauge measurements especially in the pre-satellite era problematic. Figure 1a,c gives an overview of different observed and reanalysed datasets for JJA (figure 1a) and DJF (figure 1c) all of which are interpolations of few station data and satellite measurements, and so are less reliable than in other parts of the world. Figure 1 also depicts the ensemble mean (black) and 90% quantile (grey) of the modelling analysis described below. The datasets agree on the mean precipitation while the interannual variability differs across the datasets without depicting major extreme events apart from the 2005 drought in JJA, although strong precipitation anomalies are thought to have extended to the African rainforests in recent years [3].

Figure 1.

(a,c) Time series of model data (ensemble mean in black, 5–95% interval in grey), reanalysis data ERA-interim (magenta) and NCEP (blue) and observed  datasets from satellite TRMM (green), the merged dataset CMAP (cyan) and gauge dataset GPCC (red) for (a) JJA and (c) DJF. (b,d) The same time series with bias correction to match mean and s.d. of CMAP for JJA (b) and (d) DJF.

The observed datasets are based on satellite measurements in case of TRMM and CMAP. The merged analysis of precipitation (CMAP) provided by the climate prediction centre (CPC) at the National Atmospheric and Oceanic Administration (NOAA) [19] provides measurements from five different satellites using active and passive remote-sensing techniques and is thus independent from raingauge data and reanalysis products. The data obtained by the TRMM measures high and moderate precipitation roughly between 35° N and 35° S. TRMM is the only satellite additionally carrying radar measurements and is thus providing one of the first comprehensive datasets on the four-dimensional distribution of precipitation over a region with very sparse observational data. A further mission is planned to start in 2014, enabling lighter rainfall to be detected. Because of the inability of the satellite measurements to detect lighter rain, the absolute values are likely to underestimate the actual precipitation. Here, version 3B43 is used, which enhances the satellite measurements with station data to get a best estimate but is thus not independent of global precipitation climatology centre (GPCC). GPCC is a gauge-based gridded precipitation dataset provided by the Deutscher Wetterdienst [20]. Owing to the sparse station data and the need to interpolate onto a grid, the data are likely to be unrealistically smooth.

Reanalysis data, in contrast to satellite measurements, feeds observed data on pressure, winds, temperature and humidity into reanalysis climate models. Precipitation in reanalysis data is thus a model product based on observations. For regions with sparse and unreliable observational data, reanalysis models can provide good estimates of observed weather and climate events, especially for those variables used as inputs, but derived variables such as clouds and precipitation should be regarded as more like climate model data. The two reanalysis time series in figure 1, ERA-interim (an ECMWF reanalysis product) and NCEP (the reanalysis product from NOAA), differ considerably, highlighting the lack of knowledge about the region. Dee et al. [21] note in their description of ERA-interim that reanalyses data products do not balance their water budgets and suffer from data homogeneity problems, especially in Central Africa [22]. With the exception of TRMM for variability and ERA-interim in the most recent period, the model (figure 1a) simulates precipitation for JJA of similar magnitude and interannual variability to the observed datasets and thus provides a suitable tool to investigate features of mean precipitation. Precipitation for DJF seems to be biased throughout towards lower precipitation compared with all datasets and has a considerably smaller ensemble spread, represented by the 90% quantile in figure 1c.

(c). Modelling analyses

PEA relies on robust model simulations of large ensembles to account for changes in the frequency and magnitude of extreme precipitation events. The main analysis of this study is, therefore, based on a large global climate model (GCM) ensemble used to deconstruct the influence of anthropogenic climate forcing on recent changes in frequency and magnitude of extreme precipitation events in the tropical forests of the Congo Basin.

Analysing changes in magnitude and frequency of extreme events and the fraction of attributable risk due to external drivers such as anthropogenic greenhouse gas emissions, large ensembles of climate model simulations are needed to sample statistically rare events. In this study, we make use of the GCM data provided by the weather@home project.

weather@home is a volunteer distributed computing project, which uses idle computing time from a network of ‘citizen scientists’ home computers to run a regional climate model embedded within a GCM. For this analysis, we use the global model HadAM3P, an atmosphere only general circulation model with N96 resolution, (1.25° × 1.875° resolution, 19 levels), with 15 min time steps for dynamics, forced using observed SSTs and sea ice (SI) from the HadISST [23] dataset. HadAM3P is based on the atmospheric component of the Hadley Centre GCM HadCM3 [24,25], but with some major differences in the parametrizations [26] improving the representation of clouds, radiation, precipitation and the sulfur cycle. A large ensemble size is needed to provide results from which statistical significance and the shape of the distribution of key variables, which in this study is precipitation, can be assessed. Also, a sufficiently long period of time is to be simulated to evaluate model bias (figure 1), and to determine whether the model captures the observed distribution of the relevant variables (not shown). To generate a sufficiently large ensemble, the model was run for several years many hundreds of times with different initial conditions within the climateprediction.net weather@ home project [15,16] via volunteer distributed computing. Output of the global model for the region of interest provides only monthly diagnostics, which is not ideal to look at precipitation extreme events relevant for flooding, for example, however, this is no disadvantage for the study since the deficit in rainfall accumulated over months is especially important for rainforests.

Figure 1 shows a time series of precipitation in the Congo Basin from 1960 to 2010 for the global general circulation model (HadAM3P) compared with several reanalysis and observed datasets. There are no studies reporting significant trends in precipitation, however, [3] report of droughts in recent years and the satellite data depict an extremely dry JJA season in 2005. The model data do not account for this drought and neither do the reanalysis. However, the model seems to be able to simulate the mean precipitation with the ensemble average (black line) quite well for JJA but underestimates DJF precipitation.

Owing to the lack of weather stations, the satellite measurements provide arguably the best estimate of precipitation in the region, with both showing a higher interannual variability than the model in figure 1a,c, with the exception of ERA-interim for DJF, but as noted above satellites do not easily pick up on light rain and thus may underestimate precipitation. However, a recent study notes that sparse sampling in station data products may overestimate rainfall [27]. Extreme events, as the JJA drought in 2005, are not simulated in the raw model data, however, a simple bias correction to match the mean and standard deviation of the longer satellite time series (CMAP) leads to the model average closely following the variability in the satellite data for both dry seasons (figure 1b,d). However, while a straightforward bias correction matching mean and standard deviation gives very good results for the ensemble mean it increases the spread of the whole ensemble considerably as the scaling factor to match the standard deviation is applied to every ensemble member leading to unrealistic dry and wet ensemble members in JJA (see grey shading in figure 1b), while the spread in the DJF ensemble is still too low in some years to encompass the observational datasets as the spread is extremely small in the raw model data. To illustrate the impact of bias correction, the attribution analysis for the JJA season is done with raw and bias-corrected model data.

Time-series plots give a good overview of the average model behaviour and spread of the ensemble and are thus ideal to assess the suitability of a model to study changes in the mean state of climatological variables. To investigate extreme events, it would be beneficial to validate the model analysing the tails of the distribution to check whether the model simulation adequately represents extreme events in the validation time period. However, short monthly time series of observed data will probably not describe well the tails of the precipitation distribution. Hence, such a model validation exercise might not be very meaningful in this region, especially as it is unclear which observed dataset best represents reality. The latter also underlines the fact that bias-corrected data might not be better than raw model data in the Congo Basin.

For the attribution study, we follow a methodology similar to Otto et al. [13] that uses large ensembles of GCMs to assess the change in risk of a July 2010-type Russian heat wave under two different climate scenarios: observed July 1960–1969 and observed July 2000–2010. We apply this method for precipitation in the dry season, using decadal average simulations of the JJA season climate of 1960–1970 and 2000–2010, which reduces some of the effects of natural variability and allows both scenarios to be validated against observed data and the application of straightforward bias correction. Additionally, we analyse a third climate scenario [12,28]: a counter factual ensemble simulating 2000–2010 dry season precipitation forced with SSTs as might have been had anthropogenic warming not taken place.

This counter factual or natural-only forcing characterizes a climate forcing that is identical to the one we observed in the last decade, but representing greenhouse gas emissions held at a pre-industrial level, thus simulating a world that might have been without anthropogenic greenhouse gas forcing.

The attributable twentieth-century greenhouse gas warming in SSTs cannot be found directly from observations because observations also contain the signal of both natural (e.g. solar and volcanic) and other anthropogenic (e.g. sulfate aerosol) drivers, and internal variability. Instead, we obtained the pre-industrial SSTs similar to estimates in prior studies [11], using the method described in more detail in [28]. The Met Office state-of-the-art-coupled climate model HadGEM2 is used to compute SST difference fields by subtracting SSTs of a HadGEM2 ‘natural’ run without anthropogenic greenhouse gas, ozone, SO₂ and DMS forcing as provided for the coupled model intercomparison project (CMIP5, [29]) from the same model runs with ‘all forcing’. These SSTs differences are then subtracted from HadISST SSTs. To reduce noise, the SST differences are produced using decadal averages.

The counterfactual SSTs were then used to estimate the sea ice concentration for the ‘world that might have been’. All three climate scenarios of African tropical forest dry season precipitation are subsequently used to analyse changes in extreme Congo Basin precipitation events, aiming at identifying the fraction of attributable risk on global climate change.

3. Results

As described earlier, African precipitation is highly influenced by large-scale teleconnection patterns, e.g. ENSO or the Indian dipole oscillation. This is an important factor to take into consideration for attribution studies since it can make the disentangling of external drivers more difficult than in other regions with synoptic precipitation of high internal variability. In the following, the potential predictability of African precipitation owing to strong influences of external drivers is analysed as well as the coherence of precipitation in the Congo Basin. The latter is also an important precondition for an attribution analysis.

(a). Coherence and predictability of precipitation patterns

In addition to comparing model simulated time series with observed datasets, we analyse the ratio of external and internal variance of precipitation in the model as a measure of the signal-to-noise ratio, to identify the potential predictability of precipitation in the region of interest. The ratio of external to internal variance as introduced by Kumar & Hoerling [30] computes the external variance as the variance of the mean, an indicator of external variability due to external drivers and the internal variance, the mean of the variance, as an indicator of internal variability. Values are very small in midlatitudes and higher over the tropical oceans. Figure 2 shows the ratio of external and internal variance in African dry season precipitation (JJA (figure 2a) and DJF (figure 2b)). Values of the ratio are high over Central Africa in JJA with very high values at the coasts and over the oceans (not shown) and lower values over the Congo Basin and very low values in northern and southern Africa. The ratio in the Congo Basin, especially in the southwestern part of the region is still considerably higher than in most parts of the world, indicating that precipitation is strongly connected to SSTs. In DJF, values are generally lower and shifted towards the south, indicating a less strong dependency on global SST patterns in that season.

Figure 2.

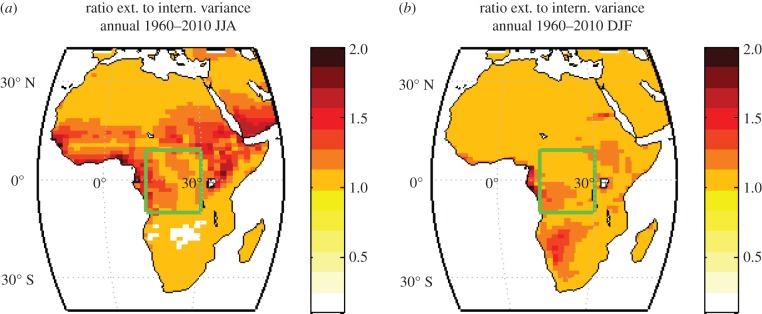
Ratio of external (variance of temporal mean dry season precipitation) and internal (mean of temporal variance of dry season precipitation) variance in African precipitation in the AGCM HadAM3P for (a) JJA and (b) DJF. The green square indicates the Congo Basin, the region used in the analysis.

Regions of high values give an estimate of the potential predictability of precipitation with respect to SSTs which in turn depend on external forcings and teleconnection patterns. High values in Central Africa indicate high predictability of precipitation from given SSTs which lends credibility to tropical precipitation in an SST-driven climate model, underlining that it is an appropriate tool for this study especially for analysing JJA precipitation. However, the variance ratio is not independent of the spatial resolution, increasing the size of the gridboxes increases the ratio. Furthermore, in an SST-driven model, it is no surprise that predictability appears to be higher at the coasts and over oceans with direct influence of ocean temperature.

The comparably high JJA values over the Congo Basin, away from the coasts leads to the conclusion that despite the deficits of the method, the potential predictability of Central African precipitation is also high in that season. Thus, interconnection of precipitation patterns and external drivers are likely to be detectable, which is integral to the attribution of identified changes in precipitation patterns to external drivers. Studies might be less reliable for DJF.

Above we identified the Congo Basin, 10° S–9° N, 13°–30° E, as the region of African tropical rainforest with two rainy (MAM and SON) and two dry seasons (JJA and DJF) per year [31]. The variance ratio earlier-mentioned (figure 2) shows the Congo Basin as a region with comparably high signal-to-noise ratio (JJA), but it also suggests that the region is not entirely coherent. Correlating the area mean precipitation of this region with global precipitation per gridbox (figure 3b,d) shows high correlation of precipitation pattern within the chosen region in both seasons, but again, a horizontal splitting of the region with less high correlation across the equator especially in JJA. Correlations in DJF are generally higher. Analysing precipitation according to the two regions of high potential predictability in JJA, the southwest Congo Basin (10°–0°S, 13°–20°E) and the north of the region (0°–9°N, 13°–30°E) reveals two very different precipitation patterns with respect to the magnitude of the rainfall; with an average precipitation of approximately 150 mm per month in the north and less than 30 mm per month in the dry season precipitation of the southwest Congo Basin. This difference shows that the identification of regions with identical seasonality and vegetation cannot be guided by similar climatological and geographical features alone. The region identified as the Congo Basin with tropical rainforest vegetation and the same seasonal paradigm of two dry and two wet seasons is not coherent in its precipitation patterns. Thus, it seems likely that the influence of external drivers on extreme precipitation events is not identical in the entire region either. We therefore analyse the two regions separately for the JJA attribution analysis and as a whole. Correlation patterns of the subseasons can be found in the electronic supplementary material.

Figure 3.

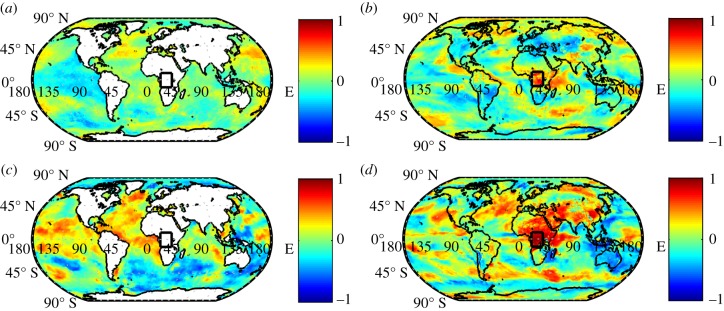
(a,c) Correlation of global SSTs with area mean dry season precipitation in the Congo Basin in HadAM3P and (b,d) correlation of global precipitation with precipitation in the Congo Basin, indicated by the black square, for (a,b) JJA and (c,d) DJF.

To identify drivers of precipitation patterns in the Congo Basin, the correlation of the area mean precipitation with SSTs is presented in figure 3a,c. The high values of the variance ratio in figure 2 lead us to expect correlations with SSTs, furthermore the correlation of JJA precipitation with global precipitation in figure 3b shows a pattern reminiscent of ENSO, with high correlations on the south American east coast and high anticorrelation values in the southern subtropical Pacific. Additionally, a correlation pattern resembling the Indian Ocean dipole oscillation pattern with high positive values close to the African coast and high anticorrelation in the eastern Indian Ocean is detectable. Correlating the period of analysis (1960–2010) Congo Basin precipitation with SSTs reveals, however, no strong correlation pattern for JJA but high correlation values for the north and tropical Atlantic and tropical Pacific as well as anticorrelation with the Southern Atlantic and Indian Oceans. The apparent anticorrelation with SSTs in the Pacific could be an indicator for an influence of ENSO but is statistically insignificant. Both the patterns resembling ENSO and IOD from the precipitation correlation are not manifest in SST patterns. Correlating the two subregions identified earlier (see the electronic supplementary material) reveals an almost identical pattern in case of the north of the Basin, with no significant interconnection; the southwest region, however, is associated with a different pattern showing a correlation with Indian Ocean SSTs with coefficients above 0.5.

Correlation patterns of DJF precipitation in figure 3d show mainly very strong correlation with precipitation patterns over eastern and Central Africa and also a pattern resembling the Indian Ocean dipole oscillation. Also for DJF the correlation of the subregions with global SSTs is similar to correlating the entire region. This underlines the assumption that the region is rather heterogeneous, especially in JJA, with respect to SST drivers, thus we analyse the southwest in addition to the entire Congo Basin in our attribution study of JJA precipitation.

(b). Attribution experiments

As described earlier [2], the first attribution experiment is a comparison of 1960s precipitation with precipitation of the last decade, under the assumption that there was no significant signal of the impact of anthropogenic greenhouse gas emissions in global mean temperature. Using the 1960s as a proxy for pre-industrial SSTs is however comparably weak due to the high anthropogenic aerosol forcing which influences temperatures and might also have an influence on circulation over Africa. Therefore, we additionally compare precipitation in the Congo Basin of the last decade (2000–2010) with simulated precipitation for the same period in a counter factual experiment, prescribing SSTs with the anthropogenic climate signal removed (§2c). This second strand of attribution analyses allow for a cleaner comparison with pre-industrial precipitation, however, it is not possible to validate the counterfactual model simulations. The two methods combined could thus lead to a robust attribution conclusion. Both extreme high and extreme low precipitation events are analysed.

A measure for droughts (extreme low precipitation events) in rainforests is the cumulative water deficit (CWD), which is accumulated in months with less precipitation than evaporation, as described by [32] for Amazonia, see also [7]. The calculation of the water deficit is based on the approximation also given by [32], that a moist tropical canopy transpires 100 mm per month. This value is derived from the mean evapotranspiration obtained by ground measurements in different locations and seasons in Amazonia [33,34]. Owing to a lack of such measurements in the Congo basin, we apply the same value for the calculation of the accumulated water deficit in the African rainforest. Zelazowski et al. [35] showed that the water deficit that assumes an evapotranspiration of 100 mm per month has reasonable skill over African forests too with the exception of western Congo where dry season cloudiness prevents application of this approach. Further studies might be needed to test the sensitivity of results using the exact value of evapotranspiration. For this study to illustrate the principle, the CWD in the dry season is calculated for African tropical forests. Measurements in Amazonia showed the water deficit to be a good indicator of meteorological water stress, following [32]. This value ignores the possibility that with a drying forest the evaporation also diminishes. Further research on the canopy will show whether this is the case. The assumption is, therefore, that the forest suffers water deficit when the monthly rainfall is less than 100 mm. The water deficit for each month within a season is calculated as follows, starting with a water deficit WD_n−1 from the previous month:

and

The water deficit is calculated for each gridbox (i, j), with ET(i, j) being the fixed evapotranspiration of 100 mm per month and P representing the monthly precipitation. Averaging the water deficit over the Congo basin and the dry season of JJA gives an indication of water stress owing to meteorological conditions without taking into account local soil conditions. The soil-moisture feedback and also plant adaptation mechanisms are thought to play a role but are poorly understood [32].

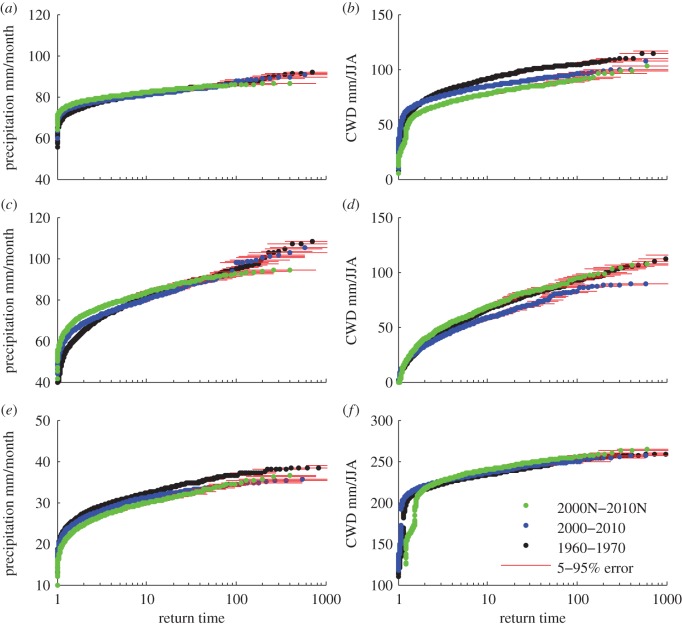
We calculate the accumulated water deficit (CWD) for the dry season (JJA) separately for each decade: the 1960s, the 2000s and the 2000s in a ‘world that might have been’. Taking the CWD defined in this way as an index for water stress in African tropical rainforests, we can assess the return period of stressful dry seasons (JJA) in the Congo Basin by plotting the CWD for the three subsequent months against the size of the sample divided by the rank of the index within the sample. Figure 4 displays the results of this analysis of water stress in the dry season in the Congo Basin area in the simulations of all three decades. The same analysis is done for DJF with figure 4a for DJF shown in the electronic supplementary material.

Figure 4.

Return periods of precipitation and CWD in the dry season (JJA) of the tropical forest in the Congo Basin for the 1960s (black), 2000s (blue) and 2000s in a counter factual world (green). The error bars give the 5–95% CI of the return periods, derived from bootstrapping several thousand times from the individual ensemble. (a) Precipitation in the Congo Basin, (b) CWD in the Congo Basin, (c) bias-corrected precipitation in the Congo Basin, (d) bias-corrected CWD in the Congo Basin, (e) Precipitation in the southwest Congo, and (f) CWD in the southwest Congo.

Dry season precipitation in the Congo Basin is on average below the 100 mm per month threshold [31], which is represented by the model simulations. While analysis of the time series shown in figure 1 would reveal trends in the mean precipitation, return time plots shown in figure 4 are means to identify changes in the return time of extreme events in different decades.

Return time plots show the chance of exceeding a threshold of any measure for a given year with the values for that measure, precipitation and CWD in figure 4, on the y-axis and the return time on a logarithmic x-axis. For example, a monthly precipitation of more than 90 mm in the JJA season in the Congo Basin is a approximately a one in a hundred years event (figure 4a), so in every given year the chances of exceeding that threshold are 1%. Comparing return time curves of different simulation ensembles are thus a good means to identify changes in the magnitude and frequency of occurrence of water deficit in the dry season. Return time plots of precipitation (figure 4a,c,e) reveal changes in magnitude and frequency of occurrence of high precipitation extreme events, while return time plots of CWD (figure 4b,d,f) depict changes on the other tail of the distribution, events of extreme dry JJA seasons.

The overall result of this attribution study is negative: there are no changes in extreme precipitation events in the dry season (JJA) of the Congo Basin that are attributable to anthropogenic climate change. Analysis of DJF precipitation shows in contrast significant changes (see the electronic supplementary material), but they differ widely between the two ensembles not representing present day conditions and are thus hard to interpret. Furthermore, figures 1 and 2 suggest a less reliable model performance for the DJF season than for JJA, therefore, all interpretation below is mainly based on JJA analysis.

Figure 4 shows the return time of (i) precipitation and (ii) CWD in the Congo Basin without applying bias correction to the simulated precipitation. While there is no change in the magnitude or frequency of occurrence of high precipitation events, a small change in low precipitation events between the 2000s and 1960s scenarios is apparent. However, this change does not occur when comparing the 2000s to a counter factual decade 2000–2010 (2000N). Applying the bias correction to match magnitude and standard deviation of the CMAP satellite observations (see §2) gives the same picture for high precipitation events (iii), but in this case the CWD return times of a 1960s scenario are almost identical to those of the 2000N scenario, with the 2000s showing slightly wetter dry seasons (iv). In figure 4a–f, the red bars are error bars representing the 5–95% CI derived from resampling the ensemble several thousand times using straight forward bootstrapping with replacement.

To account for the heterogeneity in the magnitude of precipitation in the Congo Basin, the return times of precipitation and CWD in the southwestern subregion (10°–0° S, 13°–20° E) are shown. Figure 4e is a return time plot of precipitation in that region which is not only very different in magnitude, but also shows a different return time of high precipitation in the 1960s compared with both other scenarios and compared with the return times for the entire region. Such a difference is not apparent in the return periods of extreme low precipitation events (figure 4f). The other subregion identified in the north Congo Basin reveals similar characteristics to the complete region with respect to high precipitation extremes. The CWD, however, cannot be analysed with this method: the high magnitude of dry season precipitation in the northern Congo Basin leads to very few ensemble members with CWD other than zero which renders the sample size too small to analyse return periods.

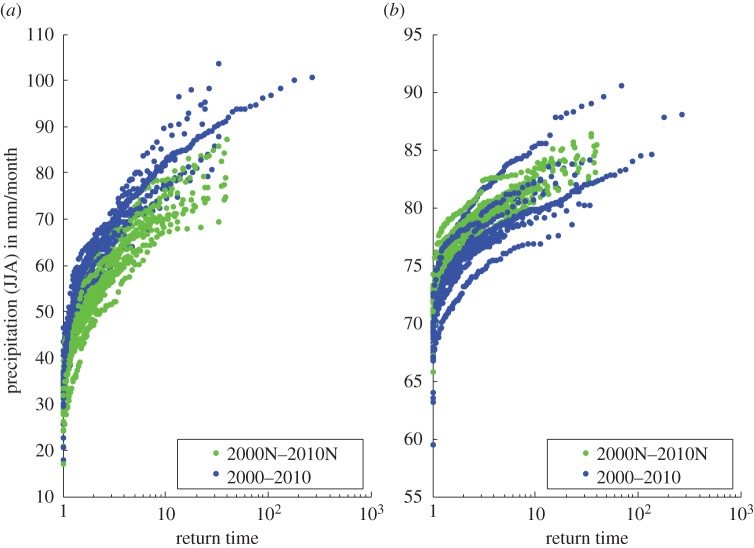
The potential predictability of tropical forest precipitation in Africa as shown in figure 2 suggests that attribution is a different challenge in this region compared with the midlatitudes, where the variance ratio is very small (not shown) because of the insignificant influence of SSTs on precipitation. It is thus possible, that the anthropogenic influence on precipitation in the Congo Basin is when small compared with SST forcing. Figure 5 shows return periods for precipitation separate for each year in the Congo Basin and in an arbitrarily chosen region of central Europe, roughly encompassing Germany and Poland (46°–54° N, 7°–25° E). The return periods in central Europe (figure 5a) in all years show shorter return times for high precipitation events in the observed 2000s compared with the counterfactual ensemble. In the Congo Basin, however, the interannual differences in return times in both ensembles are higher in most instances than the differences between blue and green curves. Reproducing figure 5 with error bars (not shown) representing 5–95% intervals of confidence, similar to figure 4, reveals that in the European case the single years could in no year be seen as statistically distinct in a decade in one but in many cases between the different ensembles, whereas the error bars do overlap in many years between the two ensembles in the Congo Basin. Although the ensemble size per year is too small to allow for yearly attribution, this finding highlights the influence of teleconnection patterns on tropical precipitation.

Figure 5.

Return periods of precipitation for each year in the decade from 2000 to 2010 in the counterfactual ensemble (green) and simulations of the observed period (blue) in (a) central Europe and (b) the Congo Basin.

4. Discussion

The aim of this paper is to investigate the applicability of the emerging science of PEA in the tropical rainforests of Central Africa. Rainforests are vulnerable to droughts as demonstrated for the Amazonian rainforests [32,18] we thus concentrate our analysis on the dry season in JJA. PEA has been successfully applied in investigating whether and to what extent anthropogenic greenhouse gas emissions have changed the probability of extreme weather events in Europe [11,12] and other midlatitude climates but never in a tropical region. The challenges for attribution in such a region differ from those in midlatitudes and are addressed in this study.

Attribution studies using PEA are only possible with large ensembles of climate model simulations and all analyses depend on the models ability to simulate the relevant climate conditions. Arguably, the greatest challenge in an almost weather station-free region such as the Congo Basin is the lack of observations, and thus a reliable dataset on which to base model validation and bias correction. The time series in figure 1a,c show the discrepancies between the datasets. The figure also shows that the average precipitation in the model is well within the range of reanalysis and observed datasets thus figure 1 gives no indication that the model gets aspects of the precipitation particularly wrong. However, other validation techniques which would be better to analyse the model's ability to simulate extreme precipitation, such as quantile–quantile plots, are not meaningful without reliable datasets.

Precipitation in the Congo Basin is strongly influenced by SST patterns, most notably ENSO and the Indian Ocean dipole oscillation. This fact can lend credibility in a SST-forced AGCM assuming that the precipitation in the region is more predictable from given SSTs than precipitation in other regions. Analysing the external variability of precipitation with respect to internal variability in the region in figure 2 indeed indicates a relatively high predictability of dry season precipitation in the Congo Basin. A correlation of the precipitation in the region with global SSTs shown in figure 3a,c shows that this high predictability is not obviously related to a specific SST pattern as no significant correlation can be detected. These two plots together add to the assumption that dry season precipitation in the Congo Basin can be reliable in a SST-driven climate model on the one hand, but on the other hand the precipitation is not strongly correlated to a specific SST pattern. Thus, changes in return times of precipitation extremes can potentially be attributed to anthropogenic climate drivers and are not necessarily disguised by a single teleconnection pattern; e.g. one could imagine that with a strong correlation to ENSO changes in precipitation due to a warming climate cannot be identified because of the larger changes driven by ENSO. Looking at decadal long calculations of return times of extreme weather events in figure 4 instead of single years furthermore decreases the influence of such patterns, rendering attribution results more robust.

Calculating return times of changes in extreme precipitation in the dry season in the Congo Basin tropical rainforest (figure 4), suggests that the risk of extreme high or extreme low precipitation has not changed. Analysis of the subregion reveals a slightly higher magnitude in high precipitation events in the 1960s compared with present day and, depending on bias correction, the magnitude of low precipitation events in the 1960s is also higher in the whole basin. However, none of these changes are also apparent in the ‘world that might have been’ scenario of the recent decade, corroborating the conclusion that there are no changes in extreme precipitation attributable to an anthropogenic climate signal. The higher aerosol concentration in the 1960s is known to have an influence on tropical precipitation, and it is thus not clear which anthropogenic signal may be driving the changes between the 1960s and 2000s, aerosols or greenhouse gas forcing though both, presumably, may be involved.

The curves in figure 4 representing the magnitude and frequency of occurrence of extreme events change considerably, especially with respect to the magnitude of precipitation in the region of tropical rainforests, dependent on bias correction and the exact layout of the region. This highlights the importance of bias correction caveats, in a region with sparse observational data; and suggests the Congo Basin to be a more heterogeneous region, with respect to precipitation patterns and drivers, in spite of its similar vegetation and seasonality. Attribution studies, however, are based on changes in magnitude and frequency of occurrence, respectively, and not absolute magnitudes and in this respect the results are robust.

Splitting the decadal long return times into individual years in figure 5 and comparing it with individual years in a midlatitude region highlights the fact that tropical precipitation might be better predictable from given SSTs, however, the interannual variability is also much higher, which renders the challenge of disentangling SST forcing from anthropogenic drivers and natural SST variability more difficult than in the extratropics. With the sampling of 11 years, we are able to sample a range of SSTs, and so believe our results to be robust especially as the last decade has not been prone to specific teleconnection patterns. However, this sampling is limited and cannot account for a large range of variability, in particular, if analysing decades with major El Niño or La Niña events. With this in mind, it may be more appropriate to prescribe forecast SSTs as opposed to observed SSTs in the model set-up, in order to allow attribution of changes in the odds of extreme precipitation events in the tropics to the anthropogenic warming signal. Such a set-up would also allow an investigation of whether the potential increase in interannual variability in precipitation suggested in figure 5b is indeed an effect of anthropogenic forcing or the specific interannual variability in the last decade. This question could also be addressed by repeating the same experiment but with counterfactual ensembles derived from different model simulations.

5. Conclusion

The non-significant change in return times in extreme high and extreme low Congo dry season precipitation as a result of this attribution study, suggests that in contrast to tropical forests in Amazonia, the risk of droughts in African rainforests in the Congo Basin has not changed. The potential high predictability of Central African precipitation in the hindcast simulations, and the fact that simulated time series are of a similar quality to reanalysis data in a highly under-researched region, underlines the fact that attribution analysis can provide a very valuable source of information in vulnerable regions. The differences in the JJA and DJF analysis, however, highlight that the reliability of analysis needs to be assessed on a case to case basis. In contrast to future projections of climate change in Africa, attribution analysis (in particular PEA) can provide more robust information to inform decision-makers. In regions with high potential predictability that allows for the deconstruction of external drivers of climatological changes, such studies are not only informative in relation to past extreme events, but also allow changing risks of extreme events in the near future to be anticipated.