Nonlinear flowering responses to climate: are species approaching their limits of phenological change?

Abstract

Many alpine and subalpine plant species exhibit phenological advancements in association with earlier snowmelt. While the phenology of some plant species does not advance beyond a threshold snowmelt date, the prevalence of such threshold phenological responses within plant communities is largely unknown. We therefore examined the shape of flowering phenology responses (linear versus nonlinear) to climate using two long-term datasets from plant communities in snow-dominated environments: Gothic, CO, USA (1974–2011) and Zackenberg, Greenland (1996–2011). For a total of 64 species, we determined whether a linear or nonlinear regression model best explained interannual variation in flowering phenology in response to increasing temperatures and advancing snowmelt dates. The most common nonlinear trend was for species to flower earlier as snowmelt advanced, with either no change or a slower rate of change when snowmelt was early (average 20% of cases). By contrast, some species advanced their flowering at a faster rate over the warmest temperatures relative to cooler temperatures (average 5% of cases). Thus, some species seem to be approaching their limits of phenological change in response to snowmelt but not temperature. Such phenological thresholds could either be a result of minimum springtime photoperiod cues for flowering or a slower rate of adaptive change in flowering time relative to changing climatic conditions.

1. Introduction

The timing of life-history events is changing in a variety of ecological systems in accordance with recent climate change [1], but phenological change is especially prevalent at high latitudes and altitudes [2]. Most species for which records are available advance their phenological events in response to warming temperatures and advancing spring snowmelt dates; at the same time, rates of change can be quite variable among taxa [2–8]. Understanding the underlying drivers of this variation in phenological shifts will contribute to a mechanistic understanding of the biological effects of climate change. Nonlinear phenological responses to climate are one manifestation of species-specificity in rates of shifts in phenology. Nonlinear responses are likely to become more common under continued climate change because linear advancements in the timing of life-history events cannot continue indefinitely [9]. The timing of flowering is a critical life-history event because it determines exposure of plant reproductive organs to abiotic and biotic conditions that affect plant fitness [10–12].

Temperature, the timing of snowmelt and photoperiod all have been shown to act as proximate cues of plant phenology in high-altitude and high-latitude environments, but their relative importance is often unclear [2,13–16]. For example, these abiotic cues may act independently, or they may interact to determine the timing of flowering in a given year [17]. While the timing of spring snowmelt at least partly depends on spring air temperatures, snowmelt and temperature may often act independently of one another to affect flowering phenology [15]. Indeed, the timing of snowmelt also depends on the amount of snowfall and dust deposition over the previous winter, especially in the western USA [18]. Furthermore, seasonal snow cover also provides a vital input of water and nutrients that sustain plant activity through spring [19–21]. Further complicating this issue, as the climate changes, spring snowmelt is advancing through time and temperatures are warming [22], but photoperiod remains constant. A minimum photoperiod requirement in the spring is beneficial if it prevents flowering after unusually early spring snowmelt or anomalous warm spells, which could serve as ‘miscues’, exposing flowers to unfavourable abiotic and biotic conditions [23,24]. Along these lines, photoperiod can cue flowering in alpine plants when snowmelt is early, thereby setting a limit to how early plants can flower [17,25]. At the same time, plants may be able to adjust their photoperiod thresholds to match local site conditions, and temperature can override photoperiod [17,26,27]. Therefore, photoperiod may not always act to limit to how early plants can flower.

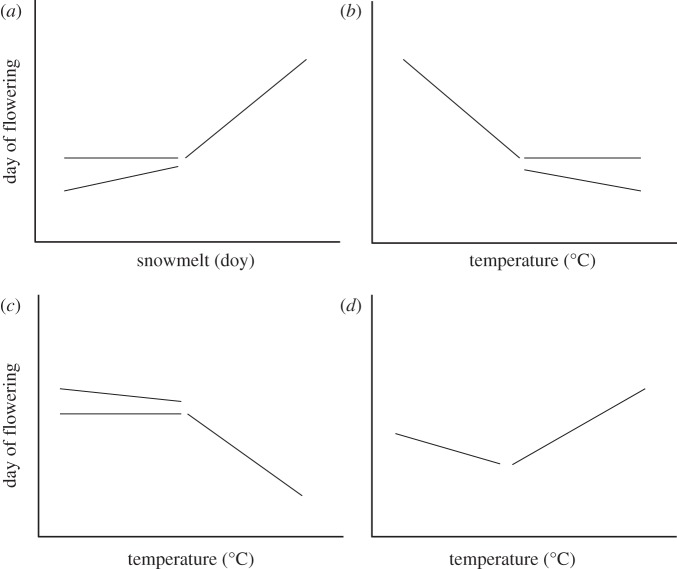
This dynamic interplay among snowmelt, temperature and photoperiod creates the potential for various types of nonlinear phenological responses to interannual variation in climate. For example, flowering may advance through time as temperature increases and as snowmelt becomes earlier, up to a threshold snowmelt date or temperature, beyond which flowering ceases to advance or advances at a slower rate (figure 1a,b) [23]. Such a threshold in the degree to which a plant species advances its flowering time may reflect a minimum photoperiod requirement for flowering that is not met when snowmelt is early and/or when temperatures are warm. This type of nonlinear flowering response may also be caused by a limit to adaptive changes in flowering time, by which the rate of selection for earlier flowering falls behind the rate of change in the abiotic environment [28]. Conversely, flowering may advance in response to increasing temperatures after temperatures reach a minimum threshold of heat accumulation (i.e. degree days; figure 1c), as suggested by degree day requirements for leaf budburst and flowering [29–31]. Finally, temperatures may be so warm that plants fail to meet a vernalization requirement over the winter or early spring (i.e. number of days below a minimum temperature required to initiate flowering), in which case phenology should delay at warm temperatures and advance at cooler temperatures (figure 1d) [32,33].

Figure 1.

Conceptual diagram of types of nonlinearity expected in flowering responses of individual species to (a) interannual variation in snowmelt and (b–d) temperature. Species may either show no response or a smaller response beyond a breakpoint (a and b); a smaller response may be due to variability among individuals in the degree to which they respond to the abiotic environment (i.e. some individuals do not respond but some do, creating a shallower slope beyond the breakpoint). Photoperiodicity or a limit to plasticity may cause the patterns shown in (a and b). Failure to accumulate heat required for flowering may cause the flowering pattern in (c), whereas failure to reach a chilling requirement (vernalization) may cause the pattern in (d).

Nonlinear flowering responses probably represent a threshold in the degree to which plants can adjust their flowering times in accordance with changing abiotic conditions. At least two studies have shown that flowering phenology in a few species can exhibit a threshold or nonlinear response to the timing of spring snowmelt (sensu figure 1a; [15,23]), and plant phenology is often modelled using nonlinear temperature functions [27,34,35]. However, the prevalence of these types of long-term responses within plant communities is largely unknown. We therefore used two long-term phenological time series with annual records of onset, peak and end of flowering, to explore the limits of linear phenological responses to climate in Arctic and subalpine communities of flowering plants. We consider nonlinear trends as evidence that the timing of flowering is not keeping pace with changing abiotic conditions and explore evidence for photoperiod and rate of selection on flowering time as drivers of nonlinear trends.

2. Material and methods

(a). Study sites and data collection

We used two long-term records of flowering phenology from snow-dominated habitats: (i) the Rocky Mountain Biological Laboratory (RMBL) in Gothic, CO, USA (38°57.5′ N, 106°59.3′ W, 2900 m.a.s.l.), and (ii) Zackenberg, Northeast Greenland (74°28′ N, 20°34′ W, 35–50 m.a.s.l.). These sites are sampled frequently enough to examine multiple phenological responses: onset, peak and end of flowering. The timing of snowmelt is measured in permanent locations, and air temperature data are available from nearby weather stations at both sites. A summary of site information is available in table 1.

Table 1.

Site information for two long-term flowering phenology datasets used in this study: Gothic, CO, USA and Zackenberg, Greenland. Mean temperature during the growing season is the average of monthly mean temperatures from the month in which temperatures warm above freezing through when onset of flowering typically ends: Apr–Aug in Gothic and May–Aug in Zackenberg. Phenological stage includes flower buds, open flowers or senescent flowers.

site characteristic	Gothic	Zackenberg
plant community	subalpine meadow	Arctic tundra
elevation	2900 m.a.s.l.	50 m.a.s.l.
mean day of spring snowmelt	20 May	16 June
mean growing season temperature	8.8°C	5.2°C
length of census	38 years	16 years
frequency of census	every other day	weekly
no. plant species	56	6
no. plots	30	25
phenology measurement	no. flowers	phenological stage

(i). Gothic

The landscape surrounding Gothic consists of mesic and wet meadows, dry rocky meadows and mixed conifer forests. This site is characterized by a short growing season, with snowmelt typically occurring in May (38-year mean from a permanent 2 × 2 m plot = 20 May; range = 22 April–19 June) and snowfall beginning in late September to early October. Data on the timing of snowmelt, that is, the first date of bare ground, were obtained from B. Barr's snowpack dataset collected in Gothic (2928 m.a.s.l.) since 1975. Permanent winter snowpack commences at this site in early November (38-year mean = 4 November). In 1973, a series of 30 2 × 2 m plots was established in and around the RMBL to monitor flowering phenology [23]. Most of the plant species in the Gothic phenology dataset are long-lived herbaceous perennials, with a few short-lived perennial and biennial herbaceous species. The farthest distance between two plots is approximately 1 km, and the plots are within 1 km of the snowmelt station [36]. The plots are located in three habitats: mesic or wet meadows (19 plots), relatively dry, rocky meadows (seven plots) and aspen forest understory (two plots). For each plant species present in these long-term plots, either the number of flowers per stalk or the number of flowering inflorescences (for species with numerous small flowers) are counted every other day throughout the growing season (excluding the years 1978 and 1990, for more than 120 species). Mean monthly temperature data (mean of daily max and min temperatures) were obtained from a NOAA weather station located at an altitude of 2704 m in Crested Butte, CO, ca 9.5 km south of the phenology plots (http://www.ncdc.noaa.gov).

(ii). Zackenberg

The brief growing season in this area spans June–August and similarly to Gothic is limited by spring snowmelt and autumn frost. Snowmelt occurs in June (16-year mean = 16 June; range = 16 May to 3 July), and mean daily temperatures fall below 0°C in August (16-year mean = 7 September; range = 27 August to 23 September), both measured at the climate station within 2 km of all plant plots. Four major plant communities compose the study area: fen, grassland, willow snowbed and heath [37]. A series of 25 permanent plots was established in 1996 to measure flowering phenology within an area of ca 2 km². The phenological stage (flower bud, open flower or senescent flower) of six common Arctic plant species ranging from woody to herbaceous perennials (Cassiope tetragona, Dryas octopetala, Papaver radicatum, Salix arctica, Saxifraga oppositifolia and Silene acaulis) is recorded weekly in three to six plots each. Plots vary in size between 1 and 300 m² to allow the recording of the stage of 200 or more inflorescences in each plot during each census. The flowering phenology and environmental data were collected as part of the Zackenberg basic monitoring programme [38].

(b). Data analysis

(i). Datasets

We limited the analysis of the Gothic dataset for each species to years in which five or more flowers per plot were recorded in at least one census, and then to species present in at least 19 years (half of the dataset), leaving a total of 58 species. We used flowering data from 1974 to 2011, excluding the first year of sampling (1973) because of potential errors in plant species identification. The census commenced after flowering by some species had begun in 5 years (1976, 1982, 1985, 1992 and 1994), and species whose flowering onset was missed were excluded from analysis in these years. We first summed floral abundance across plots for each species and then calculated the day of year when 10 (flowering onset), 50 (peak flowering) and 90 per cent (end of flowering) of flowers were counted for each species. For example, the day on which 50 per cent of flowers were counted for a given species was estimated using linear interpolation between the latest census in which less than 50 per cent of flowers were counted and the earliest census in which more than 50 per cent of flowers were counted [39]. Similarly, for the Zackenberg dataset, we used linear interpolation between weekly censuses to calculate onset of flowering as the day on which 50 per cent of buds had opened, end of flowering as the day on which 50 per cent of the flowers had senesced and peak flowering as the mid-point between onset and end of flowering [39]. The day of first flowering, day of maximum floral abundance and last day of flowering are correlated with onset, peak and end of flowering, respectively, within the Gothic dataset (data not shown). We use onset, peak and end as flowering response variables, or phenophases, here because they are likely to be more comparable across years and sites with different floral abundance and sampling intensity.

We compiled two temperature predictors, using monthly mean temperatures from the weather stations, because temperature in the months before flowering is often a good predictor of flowering phenology [1,6,40]. The first was an aggregated temperature response, or the mean monthly air temperature from the month in which temperatures warm above freezing at each site (April at Gothic and May at Zackenberg) through the month of flowering. The second was monthly mean temperature in the month of flowering. We defined the month of flowering as follows: if a species flowered before the 15th of the month, we used temperatures through the month prior to flowering, to avoid using temperature values that largely occurred after flowering to predict a flowering response. If a species flowered on or after the 15th of the month, we used mean temperatures through that month. The timing of snowmelt was the day of year of 100 per cent bare ground at each snowmelt station.

(ii). Statistical analysis

We used piecewise linear regression to determine whether a linear or nonlinear model was a better fit to each flowering response for each species. Snowmelt date and temperature were continuous predictors, and separate models were run for each species, predictor and flowering response. We used piecewise regression with continuous fitting. Continuous fitting requires the intersection point of the two regression lines to fall within the range of the data. In the nonlinear models, we required a minimum of five data points on either side of the threshold or breakpoint value in the predictor [41]. Models were constructed for each possible breakpoint (leaving at least five data points on either side of the breakpoint), and the threshold with the lowest deviance value was used in each nonlinear model. We then used AIC values to determine whether a linear or nonlinear model was a better fit to the flowering data. A linear and a nonlinear model were compared for each species’ flowering response, separately for snowmelt and temperature. Models with ΔAIC ≥ 2 were considered to be different, whereas models with ΔAIC < 2 were considered to have equal fits to the data [42]. In some cases, a continuous piecewise regression could not be fit to the data because the intersection point of the two regression lines did not fall within the range of available data. In those cases, we considered a linear fit to be superior (i.e. conceptually equivalent to ΔAIC ≥ 2).

For flowering onset, we compared the two temperature predictors (aggregated temperature versus temperature only in the month of flowering) for both linear and nonlinear models. Monthly mean temperature in the month prior to flowering was a better predictor than in the several months prior to flowering in only two cases (see the electronic supplementary material, appendix S1). Therefore, for peak and end of flowering, we only compared the two temperature responses for the linear model, and if temperature in the month before flowering was a better predictor in the linear model (which only occurred on four occasions), we also used it in the nonlinear model.

To determine whether nonlinearity depended on the timing of flowering within a growing season, we used t-tests to compare mean flowering dates between species with linear and nonlinear flowering responses, based on AIC values. Only species with model support for either a linear or nonlinear model were included in the analysis. Comparisons were conducted separately for each flowering response (onset, peak and end of flowering). We examined only whether nonlinear responses were predominant among early or late flowering species at Gothic because of insufficient sample sizes for other comparisons (i.e. too few nonlinear temperature responses at Zackenberg).

If photoperiod is responsible for nonlinearity, then we expect characteristic differences in the variation in flowering times before and after the breakpoint, depending on the predictor. For example, this hypothesis is supported if flowering dates are more variable after a threshold snowmelt date than before the threshold date (figure 1a). We used F-tests to compare the variation in flowering times before and after the breakpoint, or threshold value, of snowmelt and temperature. These comparisons were only performed for species in which nonlinear models were supported over linear models (ΔAIC ≥ 2). All analyses were performed in R v. 2.15.1, using the package ‘segmented’ to fit nonlinear models. Flowering and climate data used in analyses are available online in electronic supplementary material, appendix S2.

3. Results

(a). Gothic

At Gothic, snowmelt is advancing at a marginally significant rate of 3.5 ± 2.0 days per decade (±1 s.e. here and throughout; R² = 0.07, F_1,36 = 2.84, p = 0.10). Similarly, spring monthly mean temperatures are increasing at a marginally significant rate (April–May temp: 0.34±0.21°C per decade, R² = 0.07, F_1,36 = 2.66, p = 0.11; April–June temp: 0.29±0.18°C per decade, R² = 0.07, F_1,35 = 2.71, p = 0.11). The aggregated temperature predictors that include mean monthly temperature in the summer months are both increasing (April–July temp: 0.36±0.14°C per decade, R² = 0.15, F_1,35 = 6.35, p = 0.016; April–August temp: 0.36±0.11°C per decade, R² = 0.22, F_1,35 = 9.94, p = 0.0033). Snowmelt and all temperature predictors are negatively correlated at Gothic (see the electronic supplementary material, appendix S3).

The timing of snowmelt and temperature were both good predictors of flowering for all responses, and species generally advanced their flowering as snowmelt advanced and as temperatures increased (figures 2 and 3, respectively, and table 2; electronic supplementary material, appendix S1). The aggregated temperature predictors, or mean monthly air temperature from April through the month of flowering (hereafter, temperature), were almost always a better fit to flowering responses than mean air temperature in the month of flowering (results for flowering onset shown in electronic supplementary material, appendix S1). In only four instances out of 174 was temperature in the month of flowering a better fit. These models are included under ‘temperature’ in summarized data.

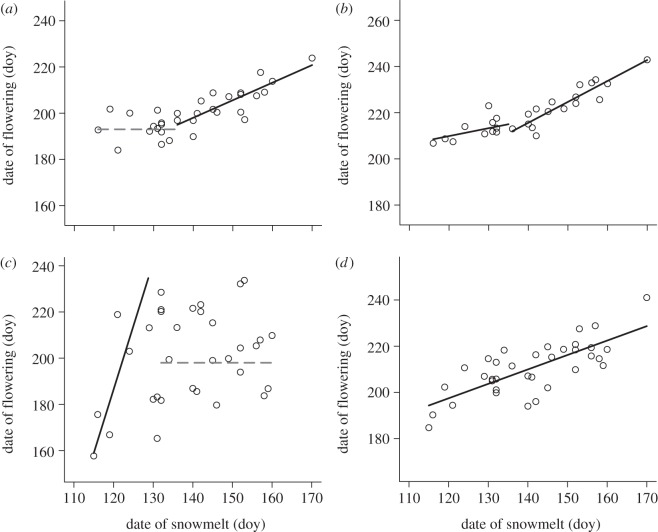
Figure 2.

Examples of types of nonlinear flowering responses to snowmelt using data from one species and one flowering response for each panel (a–d). The percentage of species showing each type of nonlinear flowering response is shown for Gothic in table 2. All nonlinear flowering responses to snowmelt at Zackenberg (Papaver radicatum only) followed (a). Note that axes cover the same range but are not the same values. Solid black lines represent slopes that differ from zero, and slopes that do not differ from zero are shown as horizontal dashed grey lines. (a) Amerosedum lanceolatum peak: R² = 0.70, (b) Campanula rotundifolia peak: R² = 0.85, (c) Boechera stricta end: R² = 0.26 and (d) Linum lewisii end: R² = 0.56.

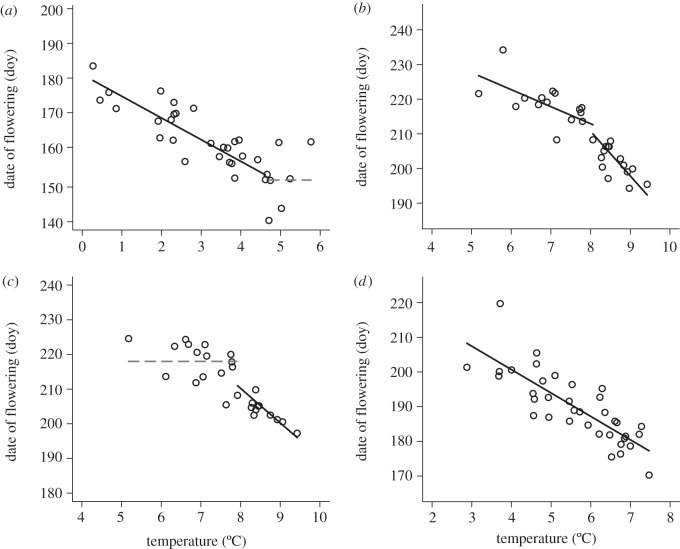
Figure 3.

Examples of types of nonlinear flowering responses to temperature using data from one species and one flowering response for each panel (a–d). The percentage of species showing each type of nonlinear flowering response is shown for Gothic in table 2. Nonlinear flowering responses to temperature were not supported at Zackenberg. Note that axes cover the same range but are not the same values. Solid black lines represent slopes that differ from zero, and slopes that do not differ from zero are shown as horizontal dashed grey lines. (a) Boechera stricta onset: R² = 0.73, (b) Oreochrysum parryi onset: R² = 0.83, (c) Pyrrocoma crocea peak: R² = 0.78 and (d) Potentilla gracilis var. pulcherrima onset: R² = 0.66.

Table 2.

Model selection summary (linear versus nonlinear) of flowering phenology responses to timing of snowmelt and mean air temperature, for 58 species at Gothic, CO, USA (data from 1974 to 2011) and six plant species at Zackenberg, Greenland (data from 1996 to 2011). Summary data are shown for models with ΔAIC ≥ 2 as either linear or nonlinear, and no difference indicates that ΔAIC < 2 between a linear and a nonlinear model. The percentage of species showing each type of response is shown, with the number of species in parentheses. See the electronic supplementary material, appendix S1 for complete list of ΔAIC values and R² values for each species.

		Gothic				Zackenberg
flowering response	model	snowmelt		temperature		snowmelt		temperature
		species	mean R2	species	mean R2	species	mean R2	species	mean R2
onset	linear	34% (20)	0.63	57% (33)	0.57	80% (5)	0.56	67% (4)	0.29
	nonlinear	28% (16)	0.81	7% (4)	0.79	20% (1)	0.85	— (0)	—
	no difference	38% (22)	0.75	36% (21)	0.67	— (0)	—	33% (2)	0.18
peak	linear	38% (22)	0.63	60% (35)	0.59	80% (5)	0.53	80% (5)	0.31
	nonlinear	21% (12)	0.81	5% (3)	0.76	20% (1)	0.83	— (0)	—
	no difference	41% (24)	0.70	34% (20)	0.63	— (0)	—	20% (1)	0.38
end	linear	41% (24)	0.51	43% (25)	0.50	80% (5)	0.44	67% (4)	0.37
	nonlinear	14% (8)	0.65	2% (1)	0.84	20% (1)	0.80	— (0)	—
	no difference	45% (26)	0.67	55% (32)	0.56	— (0)	—	33% (2)	0.41

There was support for either a linear or nonlinear model in response to timing of snowmelt in 55–62% of the 58 species at Gothic, depending on the flowering response (ΔAIC ≥ 2), and snowmelt explained a substantial amount of variation in flowering even when there was no difference between a linear and nonlinear model (mean R² = 0.71; ΔAIC < 2; table 2). Nonlinear flowering responses to snowmelt were present at Gothic for all flowering responses: in 14–28% of species, a nonlinear model was supported, and a linear model was supported in 34–41% of species (table 2). In one type of nonlinear response, flowering advanced at an average rate of 0.93 ± 0.045 days for every day that snowmelt advanced, only up to the mean threshold of 17 May (doy 137; figure 2a). In a similar nonlinear response, flowering advanced at an average rate of 1.24 ± 0.08 days for every day that snowmelt advanced, only up to the mean threshold of 17 May, beyond which flowering advanced by 0.44 ± 0.0 days per day advancement in snowmelt (figure 2b). In supported linear models, flowering advanced by an average of 0.58 ± 0.025 days for every day that snowmelt advanced (figure 2d).

There was support for either a linear or nonlinear model in response to temperature in 45–60% of species, depending on the flowering response. Similarly to snowmelt, temperature explained a substantial amount of variation in flowering even when there was no difference between a linear and nonlinear model (mean R² = 0.62; ΔAIC < 2; table 2). A total of 43–57% of species showed a linear flowering response to temperature, and 2–7% of species showed a nonlinear response to temperature, depending on the flowering response (table 2 and figure 3a–c). On average, species advanced their flowering by 6.6 ± 0.15 days per 1°C increase in mean monthly temperature (figure 3d).

Nonlinearity was rather inconsistent across flowering responses within species (table 3). Of the species showing a nonlinear response to snowmelt, only 12.5 per cent (2/16) consistently showed nonlinearity across all three flowering responses, and 40 per cent (10/25) showed linear responses to snowmelt for all three flowering responses. Only one species consistently responded to temperature in a nonlinear fashion, Pedicularis bracteosa, which advanced at a faster rate at warmer compared with cooler temperatures. Of the species showing a linear response to temperature, 54 per cent (19/35) consistently showed nonlinearity across all three flowering responses. Similarly, individual species often responded in different ways to snowmelt and temperature; for example, a species may show a nonlinear response to snowmelt and a linear response to temperature (table 4).

Table 3.

The percentage of species showing each type of nonlinear flowering response at Gothic. Letters indicate the type of nonlinear response and correspond to panels in figures 2 (snowmelt) and 3 (temperature). Only supported nonlinear models (ΔAIC ≥ 2 in comparison to linear models) are included. The number of species, out of the total number of species showing any type of nonlinear response, is shown in parentheses.

	snowmelt			temperature
flowering response	A	B	C	A	B	C
onset	50% (8/16)	50% (8/16)	—	25% (1/4)	50% (2/4)	25% (1/4)
peak	67% (8/12)	33% (4/12)	—	33% (1/3)	—	67% (2/3)
end	88% (7/8)	—	12% (1/8)	—	—	100% (1/1)

Table 4.

Combinations of flowering responses to climate predictors (snowmelt and temperature) observed in species for which either a linear or nonlinear model was supported for both climate predictors at Gothic (ΔAIC ≥ 2 for each predictor). Shown are the percentages of species with each combination of response, with number out of total species with support for both models in parentheses. For example, of the 20 species with a linear response to snowmelt for flowering onset, 13 also had a linear response to temperature. Results are only summarized for Gothic because almost all flowering responses at Zackenberg were linear, with only one species responding nonlinearly to snowmelt.

flowering response	both linear	both nonlinear	nonlinear snow + linear temp	nonlinear temp + linear snow
onset	65% (13/20)	—	75% (12/16)	—
peak	55% (12/22)	—	75% (9/12)	67% (2/3)
end	38% (9/24)	—	50% (4/8)	100% (1/1)

There was no difference in mean timing of onset, peak or end of flowering between species showing a linear versus a nonlinear response to snowmelt (onset: t = −0.40, p = 0.68; peak: t = −0.20, p = 0.84; end: t = 0.80, p = 0.39). In only one species (out of 24) was variation in flowering time different before versus after the snowmelt breakpoint, for all flowering response variables (table 5; all results shown in electronic supplementary material, appendix S4). The onset of flowering in Pseudocymopterus montanus was less variable before the breakpoint than after it, as one would expect if photoperiod cues flowering (table 5).

Table 5.

Variation in mean flowering time before and after the breakpoint in nonlinear models. F-tests were used to compare the standard deviation in mean flowering onset, peak and end, separately, before and after the breakpoint snowmelt date. Comparisons were only performed for nonlinear models that were supported over linear models (i.e. ΔAIC ≥ 2). Results are only shown for species with significant differences in variation before and after the breakpoint (Pseudocymopterus montanus and Papaver radicatum); all results are shown in electronic supplementary material, appendix S4.

site	predictor	response	species	standard deviation before breakpoint	standard deviation after breakpoint	p-value
Gothic	snowmelt	onset	P. montanus	4.31	9.59	0.052
Zackenberg	snowmelt	onset	P. radicatum	2.36	7.52	0.020
Zackenberg	snowmelt	peak	P. radicatum	2.65	7.69	0.030
Zackenberg	snowmelt	end	P. radicatum	3.19	8.05	0.055

(b). Zackenberg

At Zackenberg, snowmelt is advancing at a marginally significant rate of 10.2±5.7 days per decade (R² = 0.19, F_1,14 = 3.21, p = 0.095). Mean monthly temperature in May has increased at a rate of 2.2±0.66°C per decade (R² = 0.43, F_1,14 = 10.57, p = 0.0058). The aggregated temperature predictor from May to June shows no significant change, though there is a weak warming trend (0.72±0.52°C per decade, R² = 0.12, F_1,14 = 1.89, p = 0.19). The aggregated temperature predictor that includes mean monthly temperature from May to July is also increasing, at a rate of 1.4±0.63°C per decade (R² = 0.25, F_1,14 = 4.76, p = 0.047). Snowmelt and temperature are weakly negatively correlated at Zackenberg (see the electronic supplementary material, appendix S3).

The timing of snowmelt was a good predictor of flowering phenology at Zackenberg, and temperature explained less variation in the timing of flowering (table 2). Flowering advanced with earlier snowmelt and warmer temperatures in all species (see the electronic supplementary material, appendix S1). Only one species showed a nonlinear response to snowmelt at Zackenberg, P. radicatum, whereas all other species responded linearly to snowmelt; this was true for all response variables (see table 2 and electronic supplementary material, appendix S1). Species advanced their flowering at a mean linear rate of 0.38 ± 0.015 days for every day that snowmelt advanced. Papaver radicatum advanced its flowering on average by 1.11 ± 0.023 days per 1 day advancement in snowmelt, until the threshold of 15 June (doy 166; sensu figure 2a). The mean timing of P. radicatum flowering was less variable before the snowmelt threshold than after it (table 5). Linear models were also the best fit of flowering in response to temperature. A linear model was supported over a nonlinear model in 67–80% of species (ΔAIC ≥ 2), depending on the flowering response, and in no cases was a nonlinear model supported over a linear model (table 2; electronic supplementary material, appendix S1). On average, species advanced their flowering by 3.88 ± 0.030 days per 1°C increase in mean monthly temperature.

4. Discussion

Snowmelt and temperature both explain a substantial amount of interannual variation in flowering phenology for almost all species, consistent with other studies of flowering phenology at high altitudes and high latitudes [2,16,43]. Linear advancements of flowering in association with earlier snowmelt and warmer temperatures were the most common type of response at both of our study sites, suggesting that the phenology of the majority of species in our two datasets is tracking changes in abiotic conditions. Yet, nonlinear flowering responses to snowmelt provide evidence that approximately 20 per cent of species are approaching their limits of phenological change in association with changes in the timing of snowmelt. Nonlinear flowering responses to temperature were much less common and were only present at Gothic. Because warm temperatures can override spring photoperiod cues [17,26], plants might be more likely to show a linear response to temperature than to snowmelt. At both sites, mean temperature over the months from spring thaw through the month of flowering was consistently a better predictor than mean temperature in the month of flowering. This finding could reflect the correlation between temperature and snowmelt, making this aggregated temperature response a better predictor, or it could also reflect an extended effect of temperature on plant development through accumulation of degree days [44]. We found no evidence in support of the hypothesis that chilling requirements are not being fulfiled (figure 1d). The current amount of chilling at our study sites may therefore be sufficient to release plants from winter dormancy, although delayed fulfilment of vernalization is predicted to increase under continued climate change [30,45,46].

By far the most common nonlinear flowering response was advancement of flowering phenology only up to a threshold snowmelt date, beyond which flowering did not advance (figure 2a; [23]), or advanced at a slower rate (figure 2b). One explanation for these nonlinear flowering responses is that species are only able to advance their flowering times once a minimum photoperiod has been met [17,25]. This hypothesis is supported for the only species at Zackenberg showing a nonlinear flowering response, P. radicatum. The onset, peak and end of flowering in P. radicatum were all less variable over the range of snowmelt dates over which the species did not change its flowering times compared with the range of snowmelt dates over which it advanced its flowering (table 5). By contrast, we find almost no evidence at Gothic that is consistent with photoperiod as an explanation for nonlinear responses to snowmelt or to temperature (figure 3a). This is in contrast to empirical support for photoperiod as an important flowering cue in alpine plants, especially in species that flower shortly after snowmelt [25].

An alternative hypothesis to explain these nonlinear flowering patterns at Gothic is that the rate of adaptive change in flowering time is falling behind the rate of change in the abiotic environment (described in Anderson et al. [28]). Equally variable flowering times when snowmelt is early and temperatures are warm, compared with when snowmelt is later and temperatures cooler, suggest that the majority of plant species showing nonlinear responses at Gothic have the plasticity in flowering time necessary for tracking changing abiotic conditions. Yet their flowering times are keeping pace with changes in the abiotic environment only over a limited range of abiotic conditions. At Gothic, we observe substantial variation across temporal subsets of the long-term dataset in both the direction and the magnitude of shifts in flowering phenology and in snowmelt through time [47]. Given this large amount of variation in the timing of snowmelt at Gothic, snowmelt is advancing at a marginally significant rate, and the majority of species track changes in snowmelt in a linear fashion. However, our results suggest that there may be a trade-off between tracking changes in the timing of snowmelt over a wider range of snowmelt dates at a slower rate of advancement (i.e. linear responses), compared with tracking snowmelt approximately 1 : 1 over a more limited range of snowmelt dates (i.e. nonlinear response in figure 2a,b). Using the short-lived perennial Boechera stricta from the Gothic dataset, Anderson et al. [28] provide evidence that over 20 per cent of its phenological change is adaptive, and onset of flowering in this species shows a threshold temperature response (figure 3a). This is a species for which we expect adaptation to occur relatively quickly given that it has shorter generations than the majority of species in the Gothic dataset. Therefore, these species showing threshold flowering responses are good candidates for experimental field studies that partition variation in flowering phenology into plasticity and adaptive change, to further investigate whether species are approaching their limits of adaptive phenological change. This approach could be especially powerful if combined with photoperiod manipulations.

The other nonlinear trends we observed were much less common and only occurred at Gothic. Because we had no a priori hypotheses about some of these results (figure 2c) and because they were supported in fewer cases, they should be treated with caution. It is of course possible that spurious relationships could arise in long-term observational data, especially when several statistical tests are performed. The presence of warming thresholds required for flowering [48] may account for stronger advancements in flowering at warmer temperatures relative to cooler temperatures (figure 3b,c). Because heat accumulation is often a good predictor of flowering [29,31], a faster rate of advancement in flowering at warmer temperatures may occur if warming thresholds are not met, or accrue at a slower rate, when temperatures are cooler. The parallel trend of faster advancement of flowering at early snowmelt dates is only evident in one species, B. stricta, and only for its end of flowering (figure 2c). While a much smaller amount of variation is explained by this nonlinear relationship relative to our other results (R² = 0.26; electronic supplementary material, appendix S1), this result is consistent with our observations that B. stricta is one of few species that will flower for a second time when there are heavy July rains following the mid-season dry period at Gothic. Such a flowering pattern has also been reported in the short-lived perennial Androsace septentrionalis at Gothic [49]. When snowmelt is early, there is a longer time window between spring snowmelt and July monsoon rains. Thus, B. stricta may advance the end of its flowering period and fail to flower for a second time in years of early snowmelt, but this hypothesis requires further investigation.

Several species seem to integrate snowmelt and temperature cues in different ways. At Gothic, individual species simultaneously exhibit different flowering responses to temperature and snowmelt, such as a nonlinear response to snowmelt combined with a linear response to temperature, or vice versa (table 4). Along the same lines, we find no instances of species exhibiting nonlinear responses to both cues, and a linear response to snowmelt occurs alongside a linear response to temperature about half of the time at Gothic (mean across flowering responses is 53%; table 4). At Zackenberg, the correlation between temperature and snowmelt was much weaker. This weaker correlation is probably because of relatively cool summer temperatures and because snowpack at the end of winter ranges from a negligible amount to over 1 m of snow, indicating that snowmelt is not merely a function of temperature [50]. Therefore, a particular flowering response to temperature or snowmelt at either site is unlikely to reflect merely the negative correlation between these two cues. These independent responses to snowmelt and temperature may underlie the species-specificity in rates of phenological change through time that is widely reported in the literature [3,6,7], which could lead to changes in community co-flowering patterns within a season. Co-flowering patterns are important because they can affect the intensity of plant–plant interactions and interactions with higher trophic levels, such as pollinators [51]. Indeed, we see evidence of community reshuffling of co-flowering patterns at Gothic [52,53] and changes in community-level flowering duration at Zackenberg [54].

Flowering phenophases also responded to the same abiotic predictor independently of one another. For example, it was common for flowering onset to show a linear response to snowmelt in combination with nonlinear responses in peak and end of flowering. This result is consistent with changes through time in the shapes of phenological flowering curves at Gothic; for example, flowering onset often advances at a faster rate than peak or end of flowering (A. M. Iler, P. J. CaraDonna and D. W. Inouye 1974–2012, unpublished data). Flower longevity, or the lifetime of individual flowers, may account for some of this variation in responses among flowering phenophases within species. The timing of peak and end of flowering are susceptible to effects of floral longevity, whereas flowering onset is not. Floral longevity is often temperature-dependent, generally with shorter floral longevity as temperatures warm [55–58]. Pollination may also influence flower longevity, with some species delaying senescence if they are not pollinated [57,59,60]. Additionally, the timing of snowmelt may affect flowering stages differentially, if changes in soil moisture or mobilization of nutrients occur during the flowering period of individual species. In sum, a variety of mechanisms may affect the timing of each flowering response, highlighting the importance of measuring more than one phenological event in studies of phenology and not focusing solely on the date of first flowering [61].

This study highlights the value of investigating nonlinear phenological responses to abiotic environmental cues and the value of phenological datasets long enough to discern them. Constraining phenological responses to linear climate models may mask nonlinear responses to climate, resulting in shallower linear responses, underestimations of rates of phenological change or even failure to detect a phenological response where one exists. The presence of independent nonlinear responses to both snowmelt and temperature in our study suggests that nonlinearity may account for some of the species-specificity in phenological responses to climate reported in the literature. We find very little evidence for photoperiodicity under extreme climatic conditions (early melt and warm temperatures), but photoperiod could still play an important role in flowering times of species currently showing linear responses to climate. Nonetheless, our results show that the rate of change in the timing of snowmelt may exceed the rate of change in flowering phenology in up to 20 per cent of the species in our study, despite high interannual variation in the timing of snowmelt.

Data accessibility

Research facilities and access to Colorado study sites were provided by the RMBL and John Tuttle.

Funding statement

Research at RMBL was supported by National Science Foundation grant nos. DEB 75-15422, DEB 78-07784, BSR 81-08387, DEB 94-08382, IBN 98-14509, DEB 02-38331 and DEB 09-22080. Funding also came from research grants from the University of Maryland's General Research Board, and assistance from Earthwatch and its Research Corps, awarded to D.W.I. and an International Network grant from the Danish Research Council to T.T.H.